Article contents
SECOND MOMENTS IN THE GENERALIZED GAUSS CIRCLE PROBLEM
Published online by Cambridge University Press: 19 December 2018
Abstract
The generalized Gauss circle problem concerns the lattice point discrepancy of large spheres. We study the Dirichlet series associated to 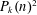 $P_{k}(n)^{2}$, where
$P_{k}(n)^{2}$, where 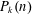 $P_{k}(n)$ is the discrepancy between the volume of the
$P_{k}(n)$ is the discrepancy between the volume of the 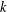 $k$-dimensional sphere of radius
$k$-dimensional sphere of radius 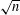 $\sqrt{n}$ and the number of integer lattice points contained in that sphere. We prove asymptotics with improved power-saving error terms for smoothed sums, including
$\sqrt{n}$ and the number of integer lattice points contained in that sphere. We prove asymptotics with improved power-saving error terms for smoothed sums, including 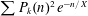 $\sum P_{k}(n)^{2}e^{-n/X}$ and the Laplace transform
$\sum P_{k}(n)^{2}e^{-n/X}$ and the Laplace transform 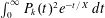 $\int _{0}^{\infty }P_{k}(t)^{2}e^{-t/X}\,dt$, in dimensions
$\int _{0}^{\infty }P_{k}(t)^{2}e^{-t/X}\,dt$, in dimensions 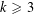 $k\geqslant 3$. We also obtain main terms and power-saving error terms for the sharp sums
$k\geqslant 3$. We also obtain main terms and power-saving error terms for the sharp sums 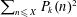 $\sum _{n\leqslant X}P_{k}(n)^{2}$, along with similar results for the sharp integral
$\sum _{n\leqslant X}P_{k}(n)^{2}$, along with similar results for the sharp integral 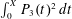 $\int _{0}^{X}P_{3}(t)^{2}\,dt$. This includes producing the first power-saving error term in mean square for the dimension-3 Gauss circle problem.
$\int _{0}^{X}P_{3}(t)^{2}\,dt$. This includes producing the first power-saving error term in mean square for the dimension-3 Gauss circle problem.
MSC classification
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2018
References
- 11
- Cited by


