Hostname: page-component-77c89778f8-fv566 Total loading time: 0 Render date: 2024-07-18T23:20:06.976Z Has data issue: false hasContentIssue false
  • English
  • Français

PARALLEL WEIGHT 2 POINTS ON HILBERT MODULAR EIGENVARIETIES AND THE PARITY CONJECTURE

Part of: Arithmetic algebraic geometry Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  04 September 2019

CHRISTIAN JOHANSSON Open the ORCID record for CHRISTIAN JOHANSSON [Opens in a new window]  and
JAMES NEWTON Open the ORCID record for JAMES NEWTON [Opens in a new window]
CHRISTIAN JOHANSSON
Affiliation:
Department of Mathematical Sciences, Chalmers University of Technology and The University of Gothenburg, SE-412 96 Gothenburg, Sweden; chrjohv@chalmers.se
JAMES NEWTON
Affiliation:
Department of Mathematics, King’s College London, Strand, London WC2R 2LS, UK; j.newton@kcl.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 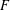$F$ be a totally real field and let 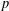$p$ be an odd prime which is totally split in 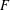$F$. We define and study one-dimensional ‘partial’ eigenvarieties interpolating Hilbert modular forms over 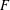$F$ with weight varying only at a single place 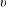$v$ above 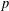$p$. For these eigenvarieties, we show that methods developed by Liu, Wan and Xiao apply and deduce that, over a boundary annulus in weight space of sufficiently small radius, the partial eigenvarieties decompose as a disjoint union of components which are finite over weight space. We apply this result to prove the parity version of the Bloch–Kato conjecture for finite slope Hilbert modular forms with trivial central character (with a technical assumption if 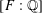$[F:\mathbb{Q}]$ is odd), by reducing to the case of parallel weight 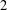$2$. As another consequence of our results on partial eigenvarieties, we show, still under the assumption that 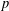$p$ is totally split in 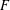$F$, that the ‘full’ (dimension 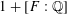$1+[F:\mathbb{Q}]$) cuspidal Hilbert modular eigenvariety has the property that many (all, if 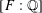$[F:\mathbb{Q}]$ is even) irreducible components contain a classical point with noncritical slopes and parallel weight $2$ (with some character at 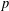$p$ whose conductor can be explicitly bounded), or any other algebraic weight.

MSC classification

Primary: 11F33: Congruences for modular and $p$-adic modular forms
Secondary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e27
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Barrera, D., Dimitrov, M. and Jorza, A., ‘ $p$ -adic $L$ -functions of Hilbert cusp forms and the trivial zero conjecture’. ArXiv e-prints, September 2017.Google Scholar
Bellaïche, J. and Chenevier, G., ‘Families of Galois representations and Selmer groups’, Astérisque 324 (2009), xii+314.Google Scholar
Berger, L., ‘Équations différentielles p-adiques et (𝜙, N)-modules filtrés’, Astérisque 319 (2008), 13–38. Représentations $p$ -adiques de groupes $p$ -adiques. I. Représentations galoisiennes et $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules.Google Scholar
Berger, L. and Colmez, P., ‘Familles de représentations de de Rham et monodromie p-adique’, Astérisque 319 (2008), 303–337. Représentations $p$ -adiques de groupes $p$ -adiques. I. Représentations galoisiennes et $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules.Google Scholar
Buzzard, K., ‘Eigenvarieties’, in L-functions and Galois Representations, London Mathematical Society Lecture Note Series, 320 (Cambridge University Press, Cambridge, 2007), 59–120.Google Scholar
Chenevier, G., ‘Une application des variétés de Hecke des groupes unitaires’, inShimura Varieties, London Mathematical Society Lecture Note Series (Cambridge University Press, Cambridge, in press).Google Scholar
Chenevier, G., ‘Familles p-adiques de formes automorphes pour GLn ’, J. Reine Angew. Math. 570 (2004), 143–217.Google Scholar
Chenevier, G., ‘On the infinite fern of Galois representations of unitary type’, Ann. Sci. Éc. Norm. Supér. (4) 44(6) (2011), 963–1019.Google Scholar
Chenevier, G., ‘The p-adic analytic space of pseudocharacters of a profinite group and pseudorepresentations over arbitrary rings’, inAutomorphic Forms and Galois Representations, Vol. 1, London Mathematical Society Lecture Note Series, 414 (Cambridge University Press, Cambridge, 2014), 221–285.Google Scholar
Chenevier, G. and Harris, M., ‘Construction of automorphic Galois representations, II’, Camb. J. Math. 1(1) (2013), 53–73.Google Scholar
Chojecki, P., Hansen, D. and Johansson, C., ‘Overconvergent modular forms and perfectoid Shimura curves’, Doc. Math. 22 (2017), 191–262.Google Scholar
Coleman, R. and Mazur, B., ‘The eigencurve’, inGalois Representations in Arithmetic Algebraic Geometry (Durham, 1996), London Mathematical Society Lecture Note Series, 254 (Cambridge University Press, Cambridge, 1998), 1–113.Google Scholar
Colmez, P., ‘Représentations triangulines de dimension 2’, Astérisque 319 (2008), 213–258. Représentations $p$ -adiques de groupes $p$ -adiques. I. Représentations galoisiennes et $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules.Google Scholar
Ding, Y., ‘Some results on the locally analytic socle for GLn(ℚp)’, Int. Math. Res. Not. IMRN (2018), rnx287.Google Scholar
Fieseler, K.-H., ‘Zariski’s main theorem für affinoide Kurven’, Math. Ann. 251(2) (1980), 97–110.Google Scholar
Geraghty, D., ‘Modularity lifting theorems for ordinary Galois representations’, Math. Ann. 373(3–4) (2019), 1341–1427.Google Scholar
Hansen, D., ‘Universal eigenvarieties, trianguline Galois representations, and p-adic Langlands functoriality’, J. Reine Angew. Math. 730 (2017), 1–64.Google Scholar
Johansson, C. and Newton, J., ‘Irreducible components of extended eigenvarieties and interpolating Langlands functoriality’, Math. Res. Lett. 26(1) (2019), 159–201.Google Scholar
Johansson, C. and Newton, J., ‘Extended eigenvarieties for overconvergent cohomology’, Algebra Number Theory 13(1) (2019), 93–158.Google Scholar
de Jong, J. and van der Put, M., ‘Étale cohomology of rigid analytic spaces’, Doc. Math. 1(01) (1996), 1–56.Google Scholar
Kedlaya, K. S., Pottharst, J. and Xiao, L., ‘Cohomology of arithmetic families of (𝜑, 𝛤)-modules’, J. Amer. Math. Soc. 27(4) (2014), 1043–1115.Google Scholar
Liu, T., ‘Lattices in filtered (𝜙, N)-modules’, J. Inst. Math. Jussieu 11(3) (2012), 659–693.Google Scholar
Liu, R., Wan, D. and Xiao, L., ‘The eigencurve over the boundary of weight space’, Duke Math. J. 166(9) (2017), 1739–1787.Google Scholar
Loeffler, D., ‘Overconvergent algebraic automorphic forms’, Proc. Lond. Math. Soc. (3) 102(2) (2011), 193–228.Google Scholar
Milne, J. S., Étale Cohomology, Princeton Mathematical Series, 33 (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Nekovář, J., ‘Selmer complexes’, Astérisque 310 (2006), viii+559.Google Scholar
Nekovář, J., ‘On the parity of ranks of Selmer groups. III’, Doc. Math. 12 (2007), 243–274.Google Scholar
Nekovář, J., ‘Some consequences of a formula of Mazur and Rubin for arithmetic local constants’, Algebra Number Theory 7(5) (2013), 1101–1120.Google Scholar
Nekovář, J., ‘Compatibility of arithmetic and algebraic local constants, II: the tame abelian potentially Barsotti–Tate case’, Proc. Lond. Math. Soc. (3) 116(2) (2018), 378–427.Google Scholar
Pottharst, J. and Xiao, L., ‘On the parity conjecture in finite-slope families’, Preprint,http://arxiv.org/abs/1410.5050.Google Scholar
van der Put, M., ‘Cohomology on affinoid spaces’, Compositio Math. 45(2) (1982), 165–198.Google Scholar
Saito, T., ‘Hilbert modular forms and p-adic Hodge theory’, Compositio Math. 145(5) (2009), 1081–1113.Google Scholar
Serre, J.-P., Abelian l-adic Representations and Elliptic Curves, Research Notes in Mathematics, 7 (A K Peters, Ltd, Wellesley, MA, 1998); With the collaboration of Willem Kuyk and John Labute, Revised reprint of the 1968 original.Google Scholar
Skinner, C., ‘A note on the p-adic Galois representations attached to Hilbert modular forms’, Doc. Math. 14 (2009), 241–258.Google Scholar
Templier, N., ‘Large values of modular forms’, Camb. J. Math. 2(1) (2014), 91–116.Google Scholar