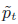Research Article
α-time fractional Brownian motion: PDE connections and local times∗
-
- Published online by Cambridge University Press:
- 09 March 2012, pp. 1-24
-
- Article
- Export citation
Asymptotic properties of autoregressive regime-switching models
-
- Published online by Cambridge University Press:
- 22 March 2012, pp. 25-47
-
- Article
- Export citation
A new proof of Kellerer’s theorem
-
- Published online by Cambridge University Press:
- 26 March 2012, pp. 48-60
-
- Article
- Export citation
Adaptive non-asymptotic confidence balls in density estimation
-
- Published online by Cambridge University Press:
- 02 July 2012, pp. 61-85
-
- Article
- Export citation
Exponential deficiency of convolutions of densities∗
-
- Published online by Cambridge University Press:
- 02 July 2012, pp. 86-96
-
- Article
- Export citation
Estimation of second order parameters using probability weighted moments
-
- Published online by Cambridge University Press:
- 03 July 2012, pp. 97-113
-
- Article
- Export citation
Asymptotic equipartition properties for simple hierarchical and networked structures
-
- Published online by Cambridge University Press:
- 03 July 2012, pp. 114-138
-
- Article
- Export citation
Shrinkage strategies in some multiple multi-factor dynamical systems
-
- Published online by Cambridge University Press:
- 03 July 2012, pp. 139-150
-
- Article
- Export citation
On the asymptotic variance in the central limit theorem for particle filters
-
- Published online by Cambridge University Press:
- 03 July 2012, pp. 151-164
-
- Article
- Export citation
Stationary Gaussian random fields on hyperbolic spaces and on Euclidean spheres∗∗∗
-
- Published online by Cambridge University Press:
- 03 July 2012, pp. 165-221
-
- Article
- Export citation
Manifold indexed fractional fields∗
-
- Published online by Cambridge University Press:
- 11 July 2012, pp. 222-276
-
- Article
- Export citation
Self-stabilizing processes: uniqueness problem for stationary measures and convergence rate in the small-noise limit
-
- Published online by Cambridge University Press:
- 11 July 2012, pp. 277-305
-
- Article
- Export citation
A generalized dual maximizer for the Monge–Kantorovich transport problem∗
-
- Published online by Cambridge University Press:
- 16 July 2012, pp. 306-323
-
- Article
- Export citation
Sojourn time in ℤ+ for the Bernoulli random walk on ℤ
-
- Published online by Cambridge University Press:
- 01 August 2012, pp. 324-351
-
- Article
- Export citation
Lacunary Fractional Brownian Motion
-
- Published online by Cambridge University Press:
- 01 August 2012, pp. 352-374
-
- Article
- Export citation
A Bayesian framework for the ratio of two Poisson rates in the context of vaccine efficacy trials∗
-
- Published online by Cambridge University Press:
- 03 September 2012, pp. 375-398
-
- Article
- Export citation
Density of paths of iterated Lévy transforms of Brownian motion
-
- Published online by Cambridge University Press:
- 31 August 2012, pp. 399-424
-
- Article
- Export citation
Tail approximations for samples from a finite population with applications to permutation tests
-
- Published online by Cambridge University Press:
- 31 August 2012, pp. 425-435
-
- Article
- Export citation
How the initialization affects the stability of the қ-means algorithm∗
-
- Published online by Cambridge University Press:
- 04 September 2012, pp. 436-452
-
- Article
- Export citation
Stochastic Taylor expansions and heat kernel asymptotics∗
-
- Published online by Cambridge University Press:
- 31 October 2012, pp. 453-478
-
- Article
- Export citation