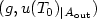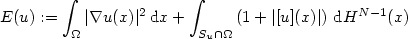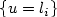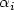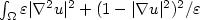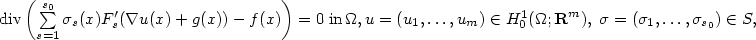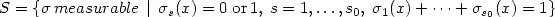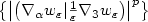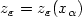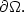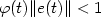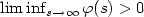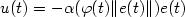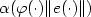Research Article
Unique Localization of Unknown Boundaries in a Conducting Medium from Boundary Measurements
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 1-22
-
- Article
- Export citation
Correcteurs proportionnels-intégraux généralisés
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 23-41
-
- Article
- Export citation
A Model-Based Fault Detection and Diagnosis Scheme for Distributed Parameter Systems: A Learning Systems Approach
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 43-67
-
- Article
- Export citation
An existence result for a nonconvex variational problem via regularity
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 69-95
-
- Article
- Export citation
Feedback in state constrained optimal control
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 97-133
-
- Article
- Export citation
Sensitivity Analysis of a Nonlinear Obstacle Plate Problem
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 135-155
-
- Article
- Export citation
Optimal Control of a Rotating Body Beam
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 157-178
-
- Article
- Export citation
Une approche géométrique du contrôle optimal de l'arc atmosphérique de la navette spatiale
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 179-222
-
- Article
- Export citation
On a Volume Constrained Variational Problem in SBV²(Ω): Part I
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 223-237
-
- Article
- Export citation
Mathematical analysis of the stabilization of lamellar phases by a shear stress
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 239-267
-
- Article
- Export citation
Global non-negative controllability of the semilinear parabolic equation governed by bilinear control
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 269-283
-
- Article
- Export citation
An example in the gradient theory of phase transitions
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 285-289
-
- Article
- Export citation
Regular syntheses and solutions to discontinuous ODEs
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 291-307
-
- Article
- Export citation
Relaxation of Quasilinear Elliptic Systems via A-quasiconvex Envelopes
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 309-334
-
- Article
- Export citation
Stabilization of the wave equation by on-off and positive-negative feedbacks
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 335-377
-
- Article
- Export citation
Univalent σ-harmonic mappings: applications to composites
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 379-406
-
- Article
- Export citation
Sign changing solutions for elliptic equations with critical growth in cylinder type domains
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 407-419
-
- Article
- Export citation
Exponential Stability and Transfer Functions of Processes Governed by Symmetric Hyperbolic Systems
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 421-442
-
- Article
- Export citation
Equi-integrability results for 3D-2D dimension reduction problems
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 443-470
-
- Article
- Export citation
Tracking with prescribed transient behaviour
-
- Published online by Cambridge University Press:
- 15 September 2002, pp. 471-493
-
- Article
- Export citation