Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ilchmann, Achim
and
Trenn, Stephan
2004.
Input constrained funnel control with applications to chemical reactor models.
Systems & Control Letters,
Vol. 53,
Issue. 5,
p.
361.
Ilchmann, A.
Ryan, E.P.
and
Trenn, S.
2004.
Adaptive tracking within prescribed funnels.
Vol. 2,
Issue. ,
p.
1032.
Ilchmann, Achim
Ryan, Eugene P.
and
Trenn, Stephan
2005.
Tracking control: Performance funnels and prescribed transient behaviour.
Systems & Control Letters,
Vol. 54,
Issue. 7,
p.
655.
Schuster, H.
Hackl, C.M.
Westermaier, C.
and
Schroder, D.
2005.
Funnel-control for electrical drives with uncertain parameters.
p.
1.
Ilchmann, Achim
and
Ryan, Eugene P.
2006.
Asymptotic tracking with prescribed transient behaviour for linear systems.
International Journal of Control,
Vol. 79,
Issue. 8,
p.
910.
Hackl, C. M.
and
Schroder, D.
2006.
Funnel-Control for Nonlinear Multi-Mass Flexible Systems.
p.
4707.
Ilchmann, Achim
Ryan, Eugene P.
and
Townsend, Philip
2006.
Tracking control with prescribed transient behaviour for systems of known relative degree.
Systems & Control Letters,
Vol. 55,
Issue. 5,
p.
396.
Hackl, C.M.
Schuster, H.
Westermaier, C.
and
Schroder, D.
2006.
Funnel-control with integrating prefilter for nonlinear, time-varying two-mass flexible servo systems.
p.
456.
Schuster, H.
Westermaier, C.
and
Schroder, D.
2006.
Non-Identifier-Based Adaptive Tracking Control for a Two-Mass System.
p.
190.
Ilchmann, A
Logemann, H
and
Ryan, E P
2006.
Tracking with Prescribed Transient Behaviour for a Class of Nonlinear Functional Differential Equations with Input Hysteresis.
p.
3089.
Mandaloju, Nagendra P.
and
Trenn, Stephan
2006.
Analogue Implementation of the Funnel Controller.
PAMM,
Vol. 6,
Issue. 1,
p.
823.
Schuster, Hans
Westermaier, Christian
and
Schroder, Dierk
2006.
Non-Identifier-Based Adaptive Speed Control for a Two-Mass Flexible Servo System: Consideration of Stability and Steady State Accuracy.
p.
1.
Hackl, Christoph M.
and
Schroder, Dierk
2006.
Extension of High-Gain controllable systems for improved accuracy.
p.
2231.
Schuster, Hans
Westermaier, Christian
and
Schroder, Dierk
2006.
Non-identifier-based adaptive control for a mechatronic system achieving stability and steady state accuracy.
p.
1819.
Ilchmann, Achim
Ryan, Eugene P.
and
Townsend, Philip
2007.
Tracking with Prescribed Transient Behavior for Nonlinear Systems of Known Relative Degree.
SIAM Journal on Control and Optimization,
Vol. 46,
Issue. 1,
p.
210.
Schroder, D.
Schuster, H.
and
Westermaier, C.
2007.
Mechatronic - Advanced Computational Intelligence.
p.
994.
Hackl, C.M.
Ji, Y
and
Schroder, D.
2007.
Enhanced funnel-control with improved performance.
p.
1.
Hackl, C.M.
Ji, Y.
and
Schroder, D.
2007.
Nonidentifier.based adaptive control with saturated control input compensation.
p.
1.
Ilchmann, Achim
and
Ryan, Eugene P.
2008.
High‐gain control without identification: a survey.
GAMM-Mitteilungen,
Vol. 31,
Issue. 1,
p.
115.
Hackl, C. M.
Endisch, C.
and
Schroder, D.
2008.
Funnel-Control in robotics: An introduction.
p.
913.
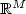 -valued reference signal
r of class W1,∞ (absolutely continuous and bounded
with essentially bounded derivative) and every system of class S, the tracking error e between plant output and reference
signal evolves within a prespecified performance envelope or
funnel in the sense that ${\varphi}(t)\| e(t)\| < 1$
-valued reference signal
r of class W1,∞ (absolutely continuous and bounded
with essentially bounded derivative) and every system of class S, the tracking error e between plant output and reference
signal evolves within a prespecified performance envelope or
funnel in the sense that ${\varphi}(t)\| e(t)\| < 1$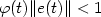 for all t ≥ 0, where φ a prescribed real-valued function of class
W1,∞ with the property that φ(s) > 0 for all s >
0 and $\liminf_{s\rightarrow\infty}{\varphi}(s)>0$
for all t ≥ 0, where φ a prescribed real-valued function of class
W1,∞ with the property that φ(s) > 0 for all s >
0 and $\liminf_{s\rightarrow\infty}{\varphi}(s)>0$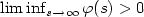 . A simple (neither
adaptive nor dynamic) error feedback control of the form $u(t)=-
\alpha ({\varphi}(t)\|e(t)\|)e(t)$
. A simple (neither
adaptive nor dynamic) error feedback control of the form $u(t)=-
\alpha ({\varphi}(t)\|e(t)\|)e(t)$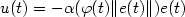 is introduced which achieves the
objective whilst maintaining boundedness of the control and of the
scalar gain
$\alpha ({\varphi}(\cdot )\|e(\cdot )\|)$
is introduced which achieves the
objective whilst maintaining boundedness of the control and of the
scalar gain
$\alpha ({\varphi}(\cdot )\|e(\cdot )\|)$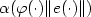 .
.




