Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Figueiredo, Giovany M.
Ikoma, Norihisa
and
Santos Júnior, João R.
2014.
Existence and Concentration Result for the Kirchhoff Type Equations with General Nonlinearities.
Archive for Rational Mechanics and Analysis,
Vol. 213,
Issue. 3,
p.
931.
Liu, Zhisu
and
Guo, Shangjiang
2015.
Existence and concentration of positive ground states for a Kirchhoff equation involving critical Sobolev exponent.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 66,
Issue. 3,
p.
747.
Fan, Haining
2015.
Multiple positive solutions for a class of Kirchhoff type problems involving critical Sobolev exponents.
Journal of Mathematical Analysis and Applications,
Vol. 431,
Issue. 1,
p.
150.
Li, Lin
and
Zhong, Xin
2016.
Infinitely many small solutions for the Kirchhoff equation with local sublinear nonlinearities.
Journal of Mathematical Analysis and Applications,
Vol. 435,
Issue. 1,
p.
955.
Wang, Jun
and
Xiao, Lu
2016.
Existence and concentration of solutions for a Kirchhoff type problem with potentials.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 12,
p.
7137.
Fan, Haining
2016.
Multiple positive solutions for Kirchhoff-type problems in $${\mathbb{R}^3}$$ R 3 involving critical Sobolev exponents.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 67,
Issue. 5,
He, Xiaoming
and
Zou, Wenming
2016.
Existence and concentration result for the fractional Schrödinger equations with critical nonlinearities.
Calculus of Variations and Partial Differential Equations,
Vol. 55,
Issue. 4,
Batkam, Cyril Joel
and
Júnior, João R. Santos
2016.
Schrödinger-Kirchhoff-Poisson type systems.
Communications on Pure and Applied Analysis,
Vol. 15,
Issue. 2,
p.
429.
Zhang, Jian
and
Zou, Wenming
2017.
Multiplicity and concentration behavior of solutions to the critical Kirchhoff-type problem.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 68,
Issue. 3,
Figueiredo, Giovany M.
and
Santos, Jefferson A.
2017.
Existence of least energy nodal solution with two nodal domains for a generalized Kirchhoff problem in an Orlicz–Sobolev space.
Mathematische Nachrichten,
Vol. 290,
Issue. 4,
p.
583.
Shang, Xudong
and
Zhang, Jihui
2018.
Existence and concentration of bound states for a Kirchhoff type problem with potentials vanishing or unbounded at infinity.
Mathematical Methods in the Applied Sciences,
Vol. 41,
Issue. 8,
p.
3018.
JIA, Huifang
and
LI, Gongbao
2018.
Multiplicity and concentration behaviour of positive solutions for Schrödinger-Kirchhoff type equations involving the p-Laplacian inRN.
Acta Mathematica Scientia,
Vol. 38,
Issue. 2,
p.
391.
He, Xiaoming
and
Zou, Wenming
2018.
Multiplicity of concentrating positive solutions for Schrödinger–Poisson equations with critical growth.
Nonlinear Analysis,
Vol. 170,
Issue. ,
p.
142.
Fan, Haining
2018.
Existence of ground state solutions for Kirchhoff‐type problems involving critical Sobolev exponents.
Mathematical Methods in the Applied Sciences,
Vol. 41,
Issue. 1,
p.
371.
Ambrosio, Vincenzo
and
Isernia, Teresa
2018.
Concentration phenomena for a fractional Schrödinger‐Kirchhoff type equation.
Mathematical Methods in the Applied Sciences,
Vol. 41,
Issue. 2,
p.
615.
Alimohammady, Mohsen
Alves, Claudianor O.
and
Amiri, Hassan Kaffash
2019.
Existence and multiplicity of positive solutions for a class of Kirchhoff Laplacian type problems.
Journal of Mathematical Physics,
Vol. 60,
Issue. 10,
Ambrosio, Vincenzo
2019.
Multiplicity and Concentration of Solutions for a Fractional Kirchhoff Equation with Magnetic Field and Critical Growth.
Annales Henri Poincaré,
Vol. 20,
Issue. 8,
p.
2717.
Ambrosio, Vincenzo
and
Servadei, Raffaella
2019.
Supercritical Fractional Kirchhoff Type Problems.
Fractional Calculus and Applied Analysis,
Vol. 22,
Issue. 5,
p.
1351.
Che, Guofeng
and
Chen, Haibo
2020.
Existence and multiplicity of positive solutions for Kirchhoff-Schrödinger-Poisson system with critical growth.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 114,
Issue. 2,
Ambrosio, Vincenzo
2020.
Multiplicity and concentration results for a class of critical fractional Schrödinger–Poisson systems via penalization method.
Communications in Contemporary Mathematics,
Vol. 22,
Issue. 01,
p.
1850078.
 (Pε)ℒεu=f(u)inIR3,u>0inIR3,u∈H1(IR3),
(Pε)ℒεu=f(u)inIR3,u>0inIR3,u∈H1(IR3),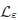 ℒε is a nonlocal
operator defined by
ℒε is a nonlocal
operator defined by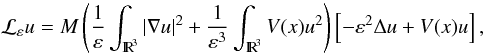 ℒεu=M1ε∫IR3|∇u|2+1ε3∫IR3V(x)u2[−ε2Δu+V(x)u],
ℒεu=M1ε∫IR3|∇u|2+1ε3∫IR3V(x)u2[−ε2Δu+V(x)u],

