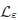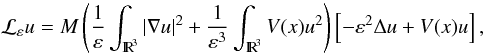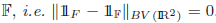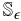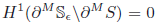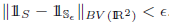Research Article
On torsional rigidity and principal frequencies: an invitation to the Kohler−Jobin rearrangement technique
-
- Published online by Cambridge University Press:
- 06 February 2014, pp. 315-338
-
- Article
- Export citation
Exact boundary synchronization for a coupled system of 1-D wave equations
-
- Published online by Cambridge University Press:
- 06 February 2014, pp. 339-361
-
- Article
- Export citation
Global minimizer of the ground state for two phase conductors in low contrast regime∗∗∗
-
- Published online by Cambridge University Press:
- 03 March 2014, pp. 362-388
-
- Article
- Export citation
Multiplicity and concentration behavior of positive solutions for a Schrödinger–Kirchhoff type problem via penalization method∗∗∗
-
- Published online by Cambridge University Press:
- 03 March 2014, pp. 389-415
-
- Article
- Export citation
A certified reduced basis method for parametrized elliptic optimal control problems∗
-
- Published online by Cambridge University Press:
- 07 March 2014, pp. 416-441
-
- Article
- Export citation
Minimising convex combinations of low eigenvalues∗
-
- Published online by Cambridge University Press:
- 07 March 2014, pp. 442-459
-
- Article
- Export citation
Regularity results for an optimal design problem with a volume constraint
-
- Published online by Cambridge University Press:
- 07 March 2014, pp. 460-487
-
- Article
- Export citation
Adaptive stabilization of coupled PDE–ODE systems with multiple uncertainties∗
-
- Published online by Cambridge University Press:
- 14 March 2014, pp. 488-516
-
- Article
- Export citation
A remark on the compactness for the Cahn–Hilliard functional
-
- Published online by Cambridge University Press:
- 27 March 2014, pp. 517-523
-
- Article
- Export citation
Dual-weighted goal-oriented adaptive finite elements for optimal control of elliptic variational inequalities∗
-
- Published online by Cambridge University Press:
- 27 March 2014, pp. 524-546
-
- Article
- Export citation
Controllability of a simplified model of fluid-structure interaction∗
-
- Published online by Cambridge University Press:
- 28 March 2014, pp. 547-575
-
- Article
- Export citation
Multi-phase structural optimization via a level set method∗∗∗
-
- Published online by Cambridge University Press:
- 27 March 2014, pp. 576-611
-
- Article
- Export citation
On indecomposable sets with applications
-
- Published online by Cambridge University Press:
- 28 March 2014, pp. 612-631
-
- Article
- Export citation