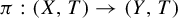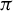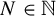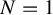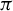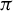1 Introduction
The structure theory of minimal flows originated in Furstenberg’s seminal work [Reference Furstenberg13] for distal minimal flows, and the structure theorem for the general minimal flows was built by Ellis, Glasner, and Shapiro [Reference Ellis, Glasner and Shapiro11], McMahon [Reference McMahon21], Veech [Reference Veech28], and Glasner [Reference Glasner17]. Roughly speaking, the class of minimal flows is the smallest class of flows containing the trivial flow and closed under homomorphisms, inverse limits, and has three ‘building blocks’ which are equicontinuous extensions, proximal extensions, and topologically weakly mixing extensions. In this paper, we mainly study proximal extensions and almost proximal extensions. Refer to [Reference Glasner17] for a systematical study of proximal flows.
In this paper, a flow
![]() $(X,T)$
is a compact metric space X with an infinite countable discrete group T acting continuously on X. Let
$(X,T)$
is a compact metric space X with an infinite countable discrete group T acting continuously on X. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. The proximal relation
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. The proximal relation
![]() $P(X,T)$
is defined by
$P(X,T)$
is defined by
Any pair in
![]() $P(X,T)$
is called a proximal pair and
$P(X,T)$
is called a proximal pair and
![]() $\pi $
is proximal if any pair
$\pi $
is proximal if any pair
![]() $(x,x')$
in the same fiber is proximal, that is,
$(x,x')$
in the same fiber is proximal, that is,
![]() $(x,x')\in P(X,T)$
whenever
$(x,x')\in P(X,T)$
whenever
![]() $\pi (x)=\pi (x')$
. A subset A of X is called an almost periodic set if every finite subset
$\pi (x)=\pi (x')$
. A subset A of X is called an almost periodic set if every finite subset
![]() $\{x_1,x_2,\ldots , x_n\}$
of A,
$\{x_1,x_2,\ldots , x_n\}$
of A,
![]() $(x_1,x_2,\ldots , x_n)$
is a minimal point of the product flow
$(x_1,x_2,\ldots , x_n)$
is a minimal point of the product flow
![]() $(X^n,T)$
. Note that any pair
$(X^n,T)$
. Note that any pair
![]() $(x,x')$
with
$(x,x')$
with
![]() $x\neq x'$
will not be proximal if
$x\neq x'$
will not be proximal if
![]() $(x,x')$
is minimal in
$(x,x')$
is minimal in
![]() $(X^2,T)$
. By this fact, it is easy to show that
$(X^2,T)$
. By this fact, it is easy to show that
![]() $\pi $
is proximal if and only if each almost periodic subset in the fiber of
$\pi $
is proximal if and only if each almost periodic subset in the fiber of
![]() $\pi $
is a singleton. Inspired by this, we call
$\pi $
is a singleton. Inspired by this, we call
![]() $\pi $
an almost proximal extension if there is some
$\pi $
an almost proximal extension if there is some
![]() $N\in \mathbb N$
such that the cardinality of any almost periodic subset in each fiber is not greater than N. When
$N\in \mathbb N$
such that the cardinality of any almost periodic subset in each fiber is not greater than N. When
![]() $N=1$
,
$N=1$
,
![]() $\pi $
is proximal.
$\pi $
is proximal.
An extension
![]() $\pi : (X,T)\rightarrow (Y,T)$
of minimal flows is almost finite to one if some fiber is finite, that is, there is some y where
$\pi : (X,T)\rightarrow (Y,T)$
of minimal flows is almost finite to one if some fiber is finite, that is, there is some y where
![]() $\pi ^{-1}(y)$
is finite. It is not difficult to see that any almost finite-to-one extension is almost proximal (Proposition 3.8). After we study the structure of almost proximal extensions, we show that an extension
$\pi ^{-1}(y)$
is finite. It is not difficult to see that any almost finite-to-one extension is almost proximal (Proposition 3.8). After we study the structure of almost proximal extensions, we show that an extension
![]() $\pi : X\rightarrow Y$
of minimal flows is almost finite-to-one if and only if it is almost proximal and point distal.
$\pi : X\rightarrow Y$
of minimal flows is almost finite-to-one if and only if it is almost proximal and point distal.
It is an open question [Reference Akin, Glasner, Huang, Shao and Ye2, Problem 5.23] that: if a minimal flow
![]() $(X,T)$
is not point distal (that is, for any point
$(X,T)$
is not point distal (that is, for any point
![]() $x\in X$
, there is
$x\in X$
, there is
![]() $x'\neq x$
such that
$x'\neq x$
such that
![]() $(x,x')$
is proximal), is it chaotic in the sense of Li–Yorke? It was showed in [Reference Akin, Glasner, Huang, Shao and Ye2, Theorem 5.17] that if a minimal flow
$(x,x')$
is proximal), is it chaotic in the sense of Li–Yorke? It was showed in [Reference Akin, Glasner, Huang, Shao and Ye2, Theorem 5.17] that if a minimal flow
![]() $(X,T)$
is a proximal but not an almost one-to-one extension of some flow
$(X,T)$
is a proximal but not an almost one-to-one extension of some flow
![]() $(Y,T)$
, then
$(Y,T)$
, then
![]() $(X,T)$
is not point distal and it is Li–Yorke chaotic. In this paper, we generalize this result, and show that any almost proximal extension has the following dichotomy theorem: any almost proximal extension of minimal flows is either almost finite-to-one, or almost all fibers contain an uncountable strongly scrambled subset. In particular, if a minimal flow
$(X,T)$
is not point distal and it is Li–Yorke chaotic. In this paper, we generalize this result, and show that any almost proximal extension has the following dichotomy theorem: any almost proximal extension of minimal flows is either almost finite-to-one, or almost all fibers contain an uncountable strongly scrambled subset. In particular, if a minimal flow
![]() $(X,T)$
is an almost proximal but not almost finite-to-one extension of some flow
$(X,T)$
is an almost proximal but not almost finite-to-one extension of some flow
![]() $(Y,T)$
, then
$(Y,T)$
, then
![]() $(X,T)$
is not point distal and it is Li–Yorke chaotic.
$(X,T)$
is not point distal and it is Li–Yorke chaotic.
Since there are no non-trivial proximal minimal flows under abelian group actions [Reference Glasner17, Theorem 3.4], it is not easy to give a minimal
![]() $\mathbb Z$
-flow which is proximal but not almost one-to-one extension of its maximal equicontinuous factor. In fact, this was a question by Furstenberg several years ago. Using the category method, Glasner and Weiss showed the existence of proximal but not almost one-to-one extensions [Reference Glasner and Weiss19, Theorem 3]. In this paper, using methods in [Reference C̆iklová-Mlíchová7], we will give such explicit examples, and also examples of almost proximal but not almost finite-to-one extensions. In addition, all examples constructed are uniformly rigid.
$\mathbb Z$
-flow which is proximal but not almost one-to-one extension of its maximal equicontinuous factor. In fact, this was a question by Furstenberg several years ago. Using the category method, Glasner and Weiss showed the existence of proximal but not almost one-to-one extensions [Reference Glasner and Weiss19, Theorem 3]. In this paper, using methods in [Reference C̆iklová-Mlíchová7], we will give such explicit examples, and also examples of almost proximal but not almost finite-to-one extensions. In addition, all examples constructed are uniformly rigid.
1.1 Organization of the paper
We organize the paper as follows. In §2, we introduce some basic notions and results needed in the paper. In §3, we introduce the notion of almost proximal and give its structure. In §4, we study chaotic properties of proximal but not almost one-to-one extensions. In §5, we will give a dichotomy theorem: any almost proximal extension of minimal flows is either almost finite-to-one, or almost all fibers contain a strongly scrambled subset. In §6, we will give explicit examples of almost proximal but not almost finite-to-one extensions. In the final section, we will give some questions.
2 Basic facts about abstract topological dynamics
In this section, we recall some basic definitions and results in abstract topological flows. For more details, see [Reference Auslander4, Reference de Vries8, Reference Ellis10, Reference Glasner17, Reference Veech28]. In the article, integers, non-negative integers, and natural numbers are denoted by
![]() $\mathbb Z$
,
$\mathbb Z$
,
![]() $\mathbb Z_+$
, and
$\mathbb Z_+$
, and
![]() $\mathbb N$
, respectively.
$\mathbb N$
, respectively.
2.1 Topological transformation groups
A flow or a topological dynamical system is a triple
![]() $\mathcal {X}=(X, T, \Pi )$
, where X is a compact Hausdorff space, T is a Hausdorff topological group, and
$\mathcal {X}=(X, T, \Pi )$
, where X is a compact Hausdorff space, T is a Hausdorff topological group, and
![]() $\Pi : T\times X\rightarrow X$
is a continuous map such that
$\Pi : T\times X\rightarrow X$
is a continuous map such that
![]() $\Pi (e,x)=x$
and
$\Pi (e,x)=x$
and
![]() $\Pi (s,\Pi (t,x))=\Pi (st,x)$
, where e is the unit of T,
$\Pi (s,\Pi (t,x))=\Pi (st,x)$
, where e is the unit of T,
![]() $s,t\in T$
, and
$s,t\in T$
, and
![]() $x\in X$
. We shall fix T and suppress the action symbol.
$x\in X$
. We shall fix T and suppress the action symbol.
In this paper, we always assume that T is infinite countable and discrete, unless we state it explicitly in some places. Moreover, we always assume that X is a compact metric space with metric
![]() $d(\cdot , \cdot )$
.
$d(\cdot , \cdot )$
.
When
![]() $T=\mathbb Z$
,
$T=\mathbb Z$
,
![]() $(X,T)$
is determined by a homeomorphism f, that is, f is the transformation corresponding to
$(X,T)$
is determined by a homeomorphism f, that is, f is the transformation corresponding to
![]() $1$
of
$1$
of
![]() $\mathbb Z$
. In this case, we usually denote
$\mathbb Z$
. In this case, we usually denote
![]() $(X,\mathbb Z)$
by
$(X,\mathbb Z)$
by
![]() $(X,f)$
, and also call it a discrete flow.
$(X,f)$
, and also call it a discrete flow.
Let
![]() $(X,T)$
be a flow and
$(X,T)$
be a flow and
![]() $x\in X$
. Let
$x\in X$
. Let
![]() $\mathcal{O} (x,T)=\{tx: t\in T\}$
be the orbit of x, which is also denoted by
$\mathcal{O} (x,T)=\{tx: t\in T\}$
be the orbit of x, which is also denoted by
![]() $T x$
. We usually denote the closure of
$T x$
. We usually denote the closure of
![]() $\mathcal{O} (x,T)$
by
$\mathcal{O} (x,T)$
by
![]() $\overline {\mathcal{O} }(x,T)$
or
$\overline {\mathcal{O} }(x,T)$
or
![]() $\overline {Tx}$
. A subset
$\overline {Tx}$
. A subset
![]() $A\subseteq X$
is called invariant if
$A\subseteq X$
is called invariant if
![]() $t a\subseteq A$
for all
$t a\subseteq A$
for all
![]() $a\in A$
and
$a\in A$
and
![]() $t\in T$
. When
$t\in T$
. When
![]() $Y\subseteq X$
is a closed and invariant subset of the flow
$Y\subseteq X$
is a closed and invariant subset of the flow
![]() $(X, T)$
, we say that the flow
$(X, T)$
, we say that the flow
![]() $(Y, T)$
is a subflow of
$(Y, T)$
is a subflow of
![]() $(X, T)$
. If
$(X, T)$
. If
![]() $(X, T)$
and
$(X, T)$
and
![]() $(Y,T)$
are two flows, their product flow is the flow
$(Y,T)$
are two flows, their product flow is the flow
![]() $(X \times Y, T)$
, where
$(X \times Y, T)$
, where
![]() $t(x, y) = (tx, ty)$
for any
$t(x, y) = (tx, ty)$
for any
![]() $t\in T$
and
$t\in T$
and
![]() $x,y\in X$
. For
$x,y\in X$
. For
![]() $n \geq 2$
, we write
$n \geq 2$
, we write
![]() $(X^n,T)$
for the n-fold product flow
$(X^n,T)$
for the n-fold product flow
![]() $(X\times \cdots \times X,T)$
.
$(X\times \cdots \times X,T)$
.
A flow
![]() $(X,T)$
is called minimal if X contains no proper non-empty closed invariant subsets. A point
$(X,T)$
is called minimal if X contains no proper non-empty closed invariant subsets. A point
![]() $x\in X$
is called a minimal point or an almost periodic point if
$x\in X$
is called a minimal point or an almost periodic point if
![]() $(\overline {\mathcal{O} }(x,T), T)$
is a minimal flow.
$(\overline {\mathcal{O} }(x,T), T)$
is a minimal flow.
A flow
![]() $(X,T)$
is called transitive if every invariant open subset of X is dense; and it is point transitive if there is a point with a dense orbit (such a point is called a transitive point). It is easy to verify that a flow is minimal if and only if every orbit is dense.
$(X,T)$
is called transitive if every invariant open subset of X is dense; and it is point transitive if there is a point with a dense orbit (such a point is called a transitive point). It is easy to verify that a flow is minimal if and only if every orbit is dense.
The flow
![]() $(X,T)$
is weakly mixing if the product flow
$(X,T)$
is weakly mixing if the product flow
![]() $(X \times X,T)$
is transitive.
$(X \times X,T)$
is transitive.
A factor map
![]() $\pi : X\rightarrow Y$
between the flow
$\pi : X\rightarrow Y$
between the flow
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y, T)$
is a continuous onto map which intertwines the actions; we say that
$(Y, T)$
is a continuous onto map which intertwines the actions; we say that
![]() $(Y, T)$
is a factor of
$(Y, T)$
is a factor of
![]() $(X,T)$
and that
$(X,T)$
and that
![]() $(X,T)$
is an extension of
$(X,T)$
is an extension of
![]() $(Y,S)$
. The flows are said to be isomorphic if
$(Y,S)$
. The flows are said to be isomorphic if
![]() $\pi $
is bijective.
$\pi $
is bijective.
Let
![]() $(X,T)$
be a flow. Fix
$(X,T)$
be a flow. Fix
![]() $(x,y)\in X^2$
. It is a proximal pair if
$(x,y)\in X^2$
. It is a proximal pair if
![]() $\inf _{t\in T} d(tx, ty)=0$
; it is a distal pair if it is not proximal. Denote by
$\inf _{t\in T} d(tx, ty)=0$
; it is a distal pair if it is not proximal. Denote by
![]() $P(X,T)$
or
$P(X,T)$
or
![]() $P(X)$
the set of proximal pairs of
$P(X)$
the set of proximal pairs of
![]() $(X,T)$
. Here,
$(X,T)$
. Here,
![]() $P(X,T)$
is also called the proximal relation of
$P(X,T)$
is also called the proximal relation of
![]() $(X,T)$
. A flow
$(X,T)$
. A flow
![]() $(X,T)$
is distal if
$(X,T)$
is distal if
![]() $P(X,T)= \Delta _X$
, where
$P(X,T)= \Delta _X$
, where
![]() $\Delta _X=\{(x,x)\in X^2: x\in X\}$
is the diagonal of
$\Delta _X=\{(x,x)\in X^2: x\in X\}$
is the diagonal of
![]() $X\times X$
. A flow
$X\times X$
. A flow
![]() $(X,T)$
is equicontinuous if for any
$(X,T)$
is equicontinuous if for any
![]() $\epsilon>0$
, there is a
$\epsilon>0$
, there is a
![]() $\delta>0$
such that whenever
$\delta>0$
such that whenever
![]() $x,y\in X$
with
$x,y\in X$
with
![]() $d(x,y)<{\delta }$
, then
$d(x,y)<{\delta }$
, then
![]() $d(tx,ty)<\epsilon $
for all
$d(tx,ty)<\epsilon $
for all
![]() $t\in T$
. Any equicontinuous flow is distal.
$t\in T$
. Any equicontinuous flow is distal.
Let
![]() $(X,T)$
be a flow. There is a smallest invariant equivalence relation
$(X,T)$
be a flow. There is a smallest invariant equivalence relation
![]() $S_{\mathrm {eq}}$
such that the quotient flow
$S_{\mathrm {eq}}$
such that the quotient flow
![]() $(X/S_{\mathrm {eq}},T)$
is equicontinuous [Reference Ellis and Gottschalk12, Theorem 1]. The equivalence relation
$(X/S_{\mathrm {eq}},T)$
is equicontinuous [Reference Ellis and Gottschalk12, Theorem 1]. The equivalence relation
![]() $S_{\mathrm {eq}}$
is called the equicontinuous structure relation and the factor
$S_{\mathrm {eq}}$
is called the equicontinuous structure relation and the factor
![]() $(X_{\mathrm {eq}}=X/S_{\mathrm {eq}}, T)$
is called the maximal equicontinuous factor of
$(X_{\mathrm {eq}}=X/S_{\mathrm {eq}}, T)$
is called the maximal equicontinuous factor of
![]() $(X,T)$
.
$(X,T)$
.
2.2 Enveloping semigroups
Given a flow
![]() $(X,T)$
, its enveloping semigroup or Ellis semigroup
$(X,T)$
, its enveloping semigroup or Ellis semigroup
![]() $E(X,T)$
is defined as the closure of the set
$E(X,T)$
is defined as the closure of the set
![]() $\{t: t\in T\}$
in
$\{t: t\in T\}$
in
![]() $X^X$
(with its compact, usually non-metrizable, pointwise convergence topology). For an enveloping semigroup,
$X^X$
(with its compact, usually non-metrizable, pointwise convergence topology). For an enveloping semigroup,
![]() $E(X,T)\rightarrow E(X,T): q\mapsto qp$
and
$E(X,T)\rightarrow E(X,T): q\mapsto qp$
and
![]() $p\mapsto tp$
is continuous for all
$p\mapsto tp$
is continuous for all
![]() $p\in E(X,T)$
and
$p\in E(X,T)$
and
![]() $t\in T$
. Note that
$t\in T$
. Note that
![]() $(X^X,T)$
is a flow and
$(X^X,T)$
is a flow and
![]() $(E(X,T),T)$
is its subflow.
$(E(X,T),T)$
is its subflow.
Definition 2.1. A set E is an
![]() $\mathcal E$
-semigroup if it satisfies the following three conditions:
$\mathcal E$
-semigroup if it satisfies the following three conditions:
-
(1) E is a semigroup;
-
(2) E has a compact Hausdorff topology;
-
(3) the right translation map
 $R_p: E \longrightarrow E, q\longmapsto qp$
is continuous for every
$R_p: E \longrightarrow E, q\longmapsto qp$
is continuous for every
 $p \in E$
.
$p \in E$
.
It is easy to see that for a flow
![]() $(X,T)$
, the enveloping semigroup
$(X,T)$
, the enveloping semigroup
![]() $E(X,T)$
is an
$E(X,T)$
is an
![]() $\mathcal E$
-semigroup.
$\mathcal E$
-semigroup.
For a semigroup, the element u with
![]() $u^2=u$
is called idempotent. Ellis–Numakura theorem says that for any
$u^2=u$
is called idempotent. Ellis–Numakura theorem says that for any
![]() $\mathcal E$
-semigroup E, the set
$\mathcal E$
-semigroup E, the set
![]() $J(E)$
of idempotents of E is not empty (see [Reference Ellis10, Corollary 2.10] or [Reference Glasner17, Ch. I, Lemma 2.2]).
$J(E)$
of idempotents of E is not empty (see [Reference Ellis10, Corollary 2.10] or [Reference Glasner17, Ch. I, Lemma 2.2]).
Let E be an
![]() $\mathcal E$
-semigroup. A non-empty subset
$\mathcal E$
-semigroup. A non-empty subset
![]() $I \subseteq E$
is a left ideal if
$I \subseteq E$
is a left ideal if
![]() $EI \subseteq I$
. A minimal left ideal is a left ideal that does not contain any proper left ideal of E. Every left ideal is a semigroup and every left ideal contains some minimal left ideal.
$EI \subseteq I$
. A minimal left ideal is a left ideal that does not contain any proper left ideal of E. Every left ideal is a semigroup and every left ideal contains some minimal left ideal.
2.3 Universal point transitive flow and universal minimal flow
For a fixed T, there exists a universal point transitive flow
![]() $(S_T,T)$
such that T can densely and equivariantly be embedded in
$(S_T,T)$
such that T can densely and equivariantly be embedded in
![]() $S_T$
(see [Reference Auslander4, Ch. 8], [Reference Glasner17, Ch. I]). The multiplication on T can be extended to a multiplication on
$S_T$
(see [Reference Auslander4, Ch. 8], [Reference Glasner17, Ch. I]). The multiplication on T can be extended to a multiplication on
![]() $S_T$
, and
$S_T$
, and
![]() $S_T$
is an
$S_T$
is an
![]() $\mathcal E$
-semigroup. The universal minimal flow
$\mathcal E$
-semigroup. The universal minimal flow
![]() $\boldsymbol{\mathfrak {M}}=(\mathbf {M},T)$
is isomorphic to any minimal left ideal in
$\boldsymbol{\mathfrak {M}}=(\mathbf {M},T)$
is isomorphic to any minimal left ideal in
![]() $S_T$
and
$S_T$
and
![]() $\mathbf {M}$
is also an
$\mathbf {M}$
is also an
![]() $\mathcal E$
-semigroup. Hence
$\mathcal E$
-semigroup. Hence
![]() $J=J(\mathbf {M})$
of idempotents in
$J=J(\mathbf {M})$
of idempotents in
![]() $\mathbf {M}$
is non-empty.
$\mathbf {M}$
is non-empty.
Proposition 2.2. [Reference Glasner17, Ch. I, Proposition 2.3]
-
(1) For
 $v\in J$
and
$v\in J$
and
 $p\in \mathbf {M}$
,
$p\in \mathbf {M}$
,
 $pv=p$
.
$pv=p$
. -
(2) For each
 $v\in J$
,
$v\in J$
,
 $v\mathbf {M}= \{vp:p\in \mathbf {M}\}=\{p\in \mathbf {M}: vp=p\}$
is a subgroup of
$v\mathbf {M}= \{vp:p\in \mathbf {M}\}=\{p\in \mathbf {M}: vp=p\}$
is a subgroup of
 $\mathbf {M}$
with identity element v. For every
$\mathbf {M}$
with identity element v. For every
 $w\in J$
, the map
$w\in J$
, the map
 $p\mapsto wp$
is a group isomorphism of
$p\mapsto wp$
is a group isomorphism of
 $vI$
onto
$vI$
onto
 $wI$
.
$wI$
. -
(3)
 $ \{v\mathbf {M}:v\in J\}$
is a partition of
$ \{v\mathbf {M}:v\in J\}$
is a partition of
 $\mathbf {M}$
. Thus, if
$\mathbf {M}$
. Thus, if
 $p\in \mathbf {M}$
, then there exists a unique
$p\in \mathbf {M}$
, then there exists a unique
 $v\in J$
such that
$v\in J$
such that
 $p\in v\mathbf {M}$
.
$p\in v\mathbf {M}$
.
Since
![]() $v\mathbf {M}$
is a group (
$v\mathbf {M}$
is a group (
![]() $v\in J$
), for
$v\in J$
), for
![]() $p\in v\mathbf {M}$
, we denote
$p\in v\mathbf {M}$
, we denote
![]() $p^{-1}$
as the inverse of p in
$p^{-1}$
as the inverse of p in
![]() $v\mathbf {M}$
, that is,
$v\mathbf {M}$
, that is,
![]() $p^{-1}\in v\mathbf {M}$
such that
$p^{-1}\in v\mathbf {M}$
such that
![]() $p^{-1}p=pp^{-1}=v$
. If we choose an arbitrary idempotent
$p^{-1}p=pp^{-1}=v$
. If we choose an arbitrary idempotent
![]() $u\in J$
and denote
$u\in J$
and denote
![]() $G=u\mathbf {M}$
, then every element p of
$G=u\mathbf {M}$
, then every element p of
![]() $\mathbf {M}$
has unique representation
$\mathbf {M}$
has unique representation
![]() $p=v{\alpha }$
for
$p=v{\alpha }$
for
![]() $v\in J$
and
$v\in J$
and
![]() ${\alpha }\in G$
. Moreover,
${\alpha }\in G$
. Moreover,
![]() $p^{-1}=v{\alpha }^{-1}$
(see [Reference Glasner17, Ch. I, Proposition 2.3, Corollary 2.4]).
$p^{-1}=v{\alpha }^{-1}$
(see [Reference Glasner17, Ch. I, Proposition 2.3, Corollary 2.4]).
The sets
![]() $S_T$
and
$S_T$
and
![]() $\mathbf {M}$
act on X as semigroups and
$\mathbf {M}$
act on X as semigroups and
![]() $S_T x=\overline {T x}$
, while for a minimal flow
$S_T x=\overline {T x}$
, while for a minimal flow
![]() $(X,T)$
, we have
$(X,T)$
, we have
![]() $\mathbf {M} x=\overline {T x}=X$
for every
$\mathbf {M} x=\overline {T x}=X$
for every
![]() $x\in X$
(see [Reference Glasner17, Ch. I, Proposition 3.1] for details). For
$x\in X$
(see [Reference Glasner17, Ch. I, Proposition 3.1] for details). For
![]() $x\in X$
, set
$x\in X$
, set
![]() $J_x=\{u\in J: ux=x\}$
.
$J_x=\{u\in J: ux=x\}$
.
Proposition 2.3. [Reference Glasner17, Ch. I, Proposition 3.1]
Let
![]() $(X, T)$
be a flow and
$(X, T)$
be a flow and
![]() $x\in X$
. A necessary and sufficient condition for x to be minimal is that
$x\in X$
. A necessary and sufficient condition for x to be minimal is that
![]() $ux=x$
for some
$ux=x$
for some
![]() $u\in J$
.
$u\in J$
.
Thus, for a closed invariant subset A of X,
![]() $JA=\{ua: u\in J, a\in A\}$
is the set of all minimal points contained in A.
$JA=\{ua: u\in J, a\in A\}$
is the set of all minimal points contained in A.
Proposition 2.4. [Reference Glasner17, Ch. I, Proposition 3.2]
Let
![]() $(X,T)$
be a flow,
$(X,T)$
be a flow,
![]() $x,y\in X$
.
$x,y\in X$
.
-
(1) For each
 $u\in J(S_T)$
,
$u\in J(S_T)$
,
 $(x,ux)\in P(X,T)$
.
$(x,ux)\in P(X,T)$
. -
(2) A pair
 $(x,y)\in P(X,T)$
if and only if
$(x,y)\in P(X,T)$
if and only if
 $px=py$
for some
$px=py$
for some
 $p\in S_T$
, if and only if there is some minimal left ideal I of
$p\in S_T$
, if and only if there is some minimal left ideal I of
 $S_T$
such that
$S_T$
such that
 $px=py$
for every
$px=py$
for every
 $p\in I$
.
$p\in I$
. -
(3) If
 $(X,T)$
is a minimal flow, then
$(X,T)$
is a minimal flow, then
 $(x,y)\in P(X)$
if and only if there is a minimal idempotent
$(x,y)\in P(X)$
if and only if there is a minimal idempotent
 $u\in J(S_T)$
such that
$u\in J(S_T)$
such that
 $y=ux$
.
$y=ux$
.
2.4 Hyperspace flow and circle operation
Let X be a compact metric space. Let
![]() $2^X$
be the collection of non-empty closed subsets of X endowed with the Hausdorff topology. Let
$2^X$
be the collection of non-empty closed subsets of X endowed with the Hausdorff topology. Let
![]() $(X,T)$
be a flow. We can induce a flow on
$(X,T)$
be a flow. We can induce a flow on
![]() $2^X$
. The action of T on
$2^X$
. The action of T on
![]() $2^X$
is given by
$2^X$
is given by
![]() $tA=\{ta:a\in A\}$
for each
$tA=\{ta:a\in A\}$
for each
![]() $t\in T$
and
$t\in T$
and
![]() $A \in 2^X$
. Then
$A \in 2^X$
. Then
![]() $(2^X,T)$
is a flow and it is called the hyperspace flow.
$(2^X,T)$
is a flow and it is called the hyperspace flow.
As
![]() $(2^X, T)$
is a flow,
$(2^X, T)$
is a flow,
![]() $S_T$
acts on
$S_T$
acts on
![]() $2^X$
too. To avoid ambiguity, we denote the action of
$2^X$
too. To avoid ambiguity, we denote the action of
![]() $S_T$
on
$S_T$
on
![]() $2^X$
by the circle operation as follows. Let
$2^X$
by the circle operation as follows. Let
![]() $p\in S_T$
and
$p\in S_T$
and
![]() $D\in 2^X$
. Define
$D\in 2^X$
. Define
![]() $p{\circ } D=\lim _{2^X} t_i D$
for any net
$p{\circ } D=\lim _{2^X} t_i D$
for any net
![]() $\{t_i\}_i$
in T with
$\{t_i\}_i$
in T with
![]() $t_i\to p$
. Moreover,
$t_i\to p$
. Moreover,
for any net
![]() $t_i\to p$
in
$t_i\to p$
in
![]() $S_T$
. We always have
$S_T$
. We always have
![]() $pD\subseteq p{\circ } D$
.
$pD\subseteq p{\circ } D$
.
Note that if
![]() $A\in 2^X$
is finite and
$A\in 2^X$
is finite and
![]() $p\in S_T$
, then
$p\in S_T$
, then
![]() $pA=p{\circ } A$
.
$pA=p{\circ } A$
.
2.5 Almost one-to-one extensions and O-diagram
Let
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,T)$
be flows and let
$(Y,T)$
be flows and let
![]() $\pi : X \to Y$
be a factor map. One says that:
$\pi : X \to Y$
be a factor map. One says that:
-
(1)
 $\pi $
is an open extension if it is open as a map;
$\pi $
is an open extension if it is open as a map; -
(2)
 $\pi $
is an almost one-to-one extension if there exists a dense
$\pi $
is an almost one-to-one extension if there exists a dense
 $G_{\delta }$
set
$G_{\delta }$
set
 $X_0\subseteq X$
such that
$X_0\subseteq X$
such that
 $\pi ^{-1}(\{\pi (x)\})=\{x\}$
for any
$\pi ^{-1}(\{\pi (x)\})=\{x\}$
for any
 $x\in X_0$
.
$x\in X_0$
.
The following is a well-known fact about open mappings (see [Reference de Vries8, Appendix A.8], for example).
Theorem 2.5. Let
![]() $\pi :(X,T)\rightarrow (Y,T)$
be a factor map of flow. Then the map
$\pi :(X,T)\rightarrow (Y,T)$
be a factor map of flow. Then the map
![]() $ \pi ^{-1}:Y\rightarrow 2^X, y\mapsto \pi ^{-1}(y)$
is continuous if and only if
$ \pi ^{-1}:Y\rightarrow 2^X, y\mapsto \pi ^{-1}(y)$
is continuous if and only if
![]() $\pi $
is open.
$\pi $
is open.
Every extension of minimal flows can be lifted to an open extension by almost one-to-one modifications ([Reference Veech27, Theorem 3.1], [Reference Auslander and Glasner5, Lemma III.6] or [Reference de Vries8, Ch. VI]). To be precise, we have the following theorem.
Theorem 2.6. For every extension
![]() $\pi :X\rightarrow Y$
of minimal flows, there exists a commutative diagram of extensions (called the O-diagram)
$\pi :X\rightarrow Y$
of minimal flows, there exists a commutative diagram of extensions (called the O-diagram)

with the following properties:
-
(a)
 $\sigma $
and
$\sigma $
and
 $\tau $
are almost one-to-one;
$\tau $
are almost one-to-one; -
(b)
 $\pi ^*$
is an open extension;
$\pi ^*$
is an open extension; -
(c)
 $X^*$
is the unique minimal set in
$X^*$
is the unique minimal set in
 $R_{\pi \tau }=\{(x,y)\in X\times Y^*: \pi (x)=\tau (y)\}$
and
$R_{\pi \tau }=\{(x,y)\in X\times Y^*: \pi (x)=\tau (y)\}$
and
 $\sigma $
and
$\sigma $
and
 $\pi ^*$
are the restrictions to
$\pi ^*$
are the restrictions to
 $X^*$
of the projections of
$X^*$
of the projections of
 $X\times Y^*$
onto X and
$X\times Y^*$
onto X and
 $Y^*$
, respectively.
$Y^*$
, respectively.
We sketch the construction of these factors. Let
![]() $x \in X$
,
$x \in X$
,
![]() $u \in J_{x}$
and
$u \in J_{x}$
and
![]() $y=\pi (x)$
. Let
$y=\pi (x)$
. Let
![]() $y^*=u{\circ } {\pi }^{-1}(y).$
One has that
$y^*=u{\circ } {\pi }^{-1}(y).$
One has that
![]() $y^*$
is a minimal point of
$y^*$
is a minimal point of
![]() $(2^X, T)$
and define
$(2^X, T)$
and define
![]() $Y^*=\{p{\circ } y^*: p \in \mathbf {M}\}$
as the orbit closure of
$Y^*=\{p{\circ } y^*: p \in \mathbf {M}\}$
as the orbit closure of
![]() $y^*$
in
$y^*$
in
![]() $2^X$
for the action of T. Finally,
$2^X$
for the action of T. Finally,
![]() $X^*=\{(px, p{\circ } y^*)\in X\times Y^*: p\in \mathbf {M} \}$
,
$X^*=\{(px, p{\circ } y^*)\in X\times Y^*: p\in \mathbf {M} \}$
,
![]() $\tau (p{\circ } y^*)= p y$
and
$\tau (p{\circ } y^*)= p y$
and
![]() $\sigma ((px,p{\circ } y^*)) =px$
. It can be proved that
$\sigma ((px,p{\circ } y^*)) =px$
. It can be proved that
![]() $X^*=\{(\tilde x,\tilde y)\in X \times Y^* : \tilde x \in \tilde y\}$
.
$X^*=\{(\tilde x,\tilde y)\in X \times Y^* : \tilde x \in \tilde y\}$
.
There is another equivalent way to get an O-diagram. Let
![]() $\pi ^{-1}: Y\rightarrow 2^X, y\mapsto \pi ^{-1}(y)$
. Then
$\pi ^{-1}: Y\rightarrow 2^X, y\mapsto \pi ^{-1}(y)$
. Then
![]() $\pi ^{-1}$
is a u.s.c. map, and the set
$\pi ^{-1}$
is a u.s.c. map, and the set
![]() $Y_c$
of continuous points of
$Y_c$
of continuous points of
![]() $\pi ^{-1}$
is a dense
$\pi ^{-1}$
is a dense
![]() $G_{\delta }$
subset of Y. Let
$G_{\delta }$
subset of Y. Let
where the closure is taken in
![]() $2^X$
. It is obvious that
$2^X$
. It is obvious that
![]() $Y^*\subseteq \widetilde {Y}\subseteq 2^X$
. Note that for each
$Y^*\subseteq \widetilde {Y}\subseteq 2^X$
. Note that for each
![]() $A\in \widetilde {Y}$
, there is some
$A\in \widetilde {Y}$
, there is some
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $A\subseteq \pi ^{-1}(y)$
, and hence
$A\subseteq \pi ^{-1}(y)$
, and hence
![]() $A\mapsto y$
define a map
$A\mapsto y$
define a map
![]() $\tau : \widetilde {Y}\rightarrow Y$
. It is easy to verify that
$\tau : \widetilde {Y}\rightarrow Y$
. It is easy to verify that
![]() $\tau : (\widetilde {Y},T)\rightarrow (Y,T)$
is a factor map. One can show that if
$\tau : (\widetilde {Y},T)\rightarrow (Y,T)$
is a factor map. One can show that if
![]() $(Y,T)$
is minimal, then
$(Y,T)$
is minimal, then
![]() $(Y^*,T)$
is a minimal flow and it is the unique minimal subflow in
$(Y^*,T)$
is a minimal flow and it is the unique minimal subflow in
![]() $(\widetilde {Y},T)$
, and
$(\widetilde {Y},T)$
, and
![]() $\tau : Y^*\rightarrow Y$
is an almost one-to-one extension such that
$\tau : Y^*\rightarrow Y$
is an almost one-to-one extension such that
![]() $\tau ^{-1}(y)=\{\pi ^{-1}(y)\}$
for all
$\tau ^{-1}(y)=\{\pi ^{-1}(y)\}$
for all
![]() $y\in Y_c$
(see [Reference Veech28, §2.3]). When
$y\in Y_c$
(see [Reference Veech28, §2.3]). When
![]() $Y^*$
and
$Y^*$
and
![]() $\tau $
are defined,
$\tau $
are defined,
![]() $X^*, \sigma $
, and
$X^*, \sigma $
, and
![]() $\pi ^*$
are defined as above.
$\pi ^*$
are defined as above.
2.6 Proximal extensions and RIC-diagram
Let
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y, T)$
be flows and let
$(Y, T)$
be flows and let
![]() $\pi : X \to Y$
be a factor map. One says that:
$\pi : X \to Y$
be a factor map. One says that:
-
(1)
 $\pi $
is a distal extension if
$\pi $
is a distal extension if
 $\pi (x_1)=\pi (x_2)$
and
$\pi (x_1)=\pi (x_2)$
and
 $x_1\neq x_2$
implies
$x_1\neq x_2$
implies
 $(x_1,x_2) \not \in P(X,T)$
;
$(x_1,x_2) \not \in P(X,T)$
; -
(2)
 $\pi $
is an equicontinuous or isometric extension if for any
$\pi $
is an equicontinuous or isometric extension if for any
 $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
 ${\delta }>0$
such that
${\delta }>0$
such that
 $\pi (x_1)=\pi (x_2)$
and
$\pi (x_1)=\pi (x_2)$
and
 $d(x_1,x_2)<{\delta }$
imply
$d(x_1,x_2)<{\delta }$
imply
 $d(tx_1,tx_2)<\epsilon $
for any
$d(tx_1,tx_2)<\epsilon $
for any
 $t\in T$
;
$t\in T$
; -
(3)
 $\pi $
is a weakly mixing extension if
$\pi $
is a weakly mixing extension if
 $(R_\pi , T)$
as a subflow of the product flow
$(R_\pi , T)$
as a subflow of the product flow
 $(X\times X, T)$
is transitive, where
$(X\times X, T)$
is transitive, where
 $R_\pi =\{(x_1,x_2)\in X^2: \pi (x_1)=\pi (x_2)\}$
.
$R_\pi =\{(x_1,x_2)\in X^2: \pi (x_1)=\pi (x_2)\}$
.
Let
![]() $\pi : (X,T )\rightarrow (Y,T)$
be a factor map of minimal flows, and
$\pi : (X,T )\rightarrow (Y,T)$
be a factor map of minimal flows, and
![]() $x_0\in X$
,
$x_0\in X$
,
![]() $y_0=\pi (x_0)$
, and
$y_0=\pi (x_0)$
, and
![]() $u\in J_{x_0}$
. We say that
$u\in J_{x_0}$
. We say that
![]() $\pi $
is an RIC (relatively incontractible) extension if for every
$\pi $
is an RIC (relatively incontractible) extension if for every
![]() $y = py_0\in Y$
,
$y = py_0\in Y$
,
![]() $p\in \mathbf {M}$
,
$p\in \mathbf {M}$
,
One can show that
![]() $\pi : X \to Y$
is RIC if and only if it is open and for every
$\pi : X \to Y$
is RIC if and only if it is open and for every
![]() $n \ge 1$
, the minimal points are dense in the relation
$n \ge 1$
, the minimal points are dense in the relation
Note that every distal extension is RIC.
Every factor map between minimal flows can be lifted to an RIC extension by proximal extensions (see [Reference Ellis, Glasner and Shapiro11, Theorem 5.13] or [Reference de Vries8, Ch. VI]).
Theorem 2.7. Given a factor map
![]() $\pi :X\rightarrow Y$
of minimal flows, there exists a commutative diagram of factor maps (called an RIC-diagram)
$\pi :X\rightarrow Y$
of minimal flows, there exists a commutative diagram of factor maps (called an RIC-diagram)

such that:
-
(a)
 $\tau '$
and
$\tau '$
and
 $\sigma '$
are proximal extensions;
$\sigma '$
are proximal extensions; -
(b)
 $\pi '$
is an RIC extension;
$\pi '$
is an RIC extension; -
(c)
 $X '$
is the unique minimal set in
$X '$
is the unique minimal set in
 $R_{\pi \tau ' }=\{(x,y)\in X\times Y ': \pi (x)=\tau '(y)\}$
, and
$R_{\pi \tau ' }=\{(x,y)\in X\times Y ': \pi (x)=\tau '(y)\}$
, and
 $\sigma '$
and
$\sigma '$
and
 $\pi '$
are the restrictions to
$\pi '$
are the restrictions to
 $X '$
of the projections of
$X '$
of the projections of
 $X\times Y '$
onto X and
$X\times Y '$
onto X and
 $Y '$
, respectively.
$Y '$
, respectively.
We sketch the construction of these factors. Let
![]() $x\in X$
,
$x\in X$
,
![]() $u\in J_{x}$
, and
$u\in J_{x}$
, and
![]() $y=\pi (x)$
. Let
$y=\pi (x)$
. Let
![]() $y'=u {\circ } u \pi ^{-1}(y)$
, then
$y'=u {\circ } u \pi ^{-1}(y)$
, then
![]() $y'$
is a minimal point in
$y'$
is a minimal point in
![]() $2^X$
. Define
$2^X$
. Define
![]() $Y'=\{p{\circ } y': p\in \mathbf {M}\}$
to be the orbit closure of
$Y'=\{p{\circ } y': p\in \mathbf {M}\}$
to be the orbit closure of
![]() $y'$
and
$y'$
and
![]() $X'=\{(px, p{\circ } y')\in X\times Y': p\in \mathbf {M}\}$
, and factor maps are given by
$X'=\{(px, p{\circ } y')\in X\times Y': p\in \mathbf {M}\}$
, and factor maps are given by
![]() $\tau ' (p{\circ } y')= p y$
and
$\tau ' (p{\circ } y')= p y$
and
![]() $\sigma '((px,p{\circ } y')) =px$
. It can be proved that
$\sigma '((px,p{\circ } y')) =px$
. It can be proved that
![]() $X'=\{(\tilde x,\tilde y)\in X \times Y' : \tilde x \in \tilde y\}$
.
$X'=\{(\tilde x,\tilde y)\in X \times Y' : \tilde x \in \tilde y\}$
.
3 Almost proximal extensions
In this section, we introduce almost proximal extensions. We will give the structure of almost proximal extensions, and study its relationship with almost finite to one extensions.
3.1 Almost proximal extensions
An almost periodic set for
![]() $(X,T)$
is a subset A of X such that if
$(X,T)$
is a subset A of X such that if
![]() $z\in X^{|A|}$
with
$z\in X^{|A|}$
with
![]() $\mathrm {range} (z)=A$
, then z is a minimal point of the flow
$\mathrm {range} (z)=A$
, then z is a minimal point of the flow
![]() $(X^{|A|},T)$
. (Here,
$(X^{|A|},T)$
. (Here,
![]() $|A|$
denotes the cardinality of A.) For example, a finite set
$|A|$
denotes the cardinality of A.) For example, a finite set
![]() $A=\{x_1,x_2,\ldots , x_n\}$
is an almost periodic set if and only if
$A=\{x_1,x_2,\ldots , x_n\}$
is an almost periodic set if and only if
![]() $(x_1,x_2,\ldots , x_n)$
is a minimal point of
$(x_1,x_2,\ldots , x_n)$
is a minimal point of
![]() $(X^n,T)$
. Using the basis for the Tychonoff topology, we see that a set A is an almost periodic set if and only if every finite subset of A is an almost periodic set. The notion of almost periodic sets was introduced by Auslander, refer to [Reference Auslander4, Ch. 5] for more information.
$(X^n,T)$
. Using the basis for the Tychonoff topology, we see that a set A is an almost periodic set if and only if every finite subset of A is an almost periodic set. The notion of almost periodic sets was introduced by Auslander, refer to [Reference Auslander4, Ch. 5] for more information.
Definition 3.1. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then
![]() $\pi $
is called an almost proximal extension if there is some
$\pi $
is called an almost proximal extension if there is some
![]() $N\in \mathbb N$
such that for each
$N\in \mathbb N$
such that for each
![]() $y\in Y$
, the cardinality of any almost periodic subset in the fiber
$y\in Y$
, the cardinality of any almost periodic subset in the fiber
![]() $\pi ^{-1}(y)$
is not greater than N.
$\pi ^{-1}(y)$
is not greater than N.
Let A be an almost periodic set of
![]() $(X,T)$
. Then for each
$(X,T)$
. Then for each
![]() $z\in X^{|A|}$
with
$z\in X^{|A|}$
with
![]() $\mathrm {range} (z)=A$
, z is a minimal point of
$\mathrm {range} (z)=A$
, z is a minimal point of
![]() $(X^{|A|},T)$
. By Proposition 2.3, there is some
$(X^{|A|},T)$
. By Proposition 2.3, there is some
![]() $u\in J$
such that
$u\in J$
such that
![]() $uz=z$
. It follows that
$uz=z$
. It follows that
![]() $uA=\{ua: a\in A\}=A$
. Thus, for a subset Z of X, a subset
$uA=\{ua: a\in A\}=A$
. Thus, for a subset Z of X, a subset
![]() $A\subseteq Z$
is an almost periodic subset of Z if and only if
$A\subseteq Z$
is an almost periodic subset of Z if and only if
![]() $A\subseteq uZ$
for some
$A\subseteq uZ$
for some
![]() $u\in J$
.
$u\in J$
.
Lemma 3.2. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Let
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Let
![]() $y, y' \in Y$
,
$y, y' \in Y$
,
![]() $u \in J_y$
, and
$u \in J_y$
, and
![]() $v \in J_{y'}$
. Then,
$v \in J_{y'}$
. Then,
![]() $|u\pi ^{-1}(y)|=|v\pi ^{-1}(y')|$
.
$|u\pi ^{-1}(y)|=|v\pi ^{-1}(y')|$
.
Proof. We only show the case when
![]() $u\pi ^{-1}(y), v\pi ^{-1}(y')$
are finite. The same proof works for the general case. Let
$u\pi ^{-1}(y), v\pi ^{-1}(y')$
are finite. The same proof works for the general case. Let
![]() $u\pi ^{-1}(y)=\{x_1,x_2,\ldots , x_n\}$
and
$u\pi ^{-1}(y)=\{x_1,x_2,\ldots , x_n\}$
and
![]() $v\pi ^{-1}(y')=\{x_1',x_2',\ldots , x_m'\}$
for some
$v\pi ^{-1}(y')=\{x_1',x_2',\ldots , x_m'\}$
for some
![]() $n,m\in \mathbb N$
. Then,
$n,m\in \mathbb N$
. Then,
![]() $(x_1,x_2,\ldots , x_n)\in X^n$
is a minimal point of
$(x_1,x_2,\ldots , x_n)\in X^n$
is a minimal point of
![]() $(X^n, T)$
as
$(X^n, T)$
as
![]() $u(x_1,x_2,\ldots , x_n)=(x_1,x_2,\ldots , x_n)$
. Since
$u(x_1,x_2,\ldots , x_n)=(x_1,x_2,\ldots , x_n)$
. Since
![]() $(X,T)$
is minimal, there is
$(X,T)$
is minimal, there is
![]() $p\in \mathbf {M}$
such that
$p\in \mathbf {M}$
such that
![]() $x_1'=px_1$
. Note that
$x_1'=px_1$
. Note that
![]() $x_1'=vx_1'=vpx_1$
and
$x_1'=vx_1'=vpx_1$
and
![]() $x_1,x_2,\ldots , x_n\in \pi ^{-1}(y)$
. It follows that
$x_1,x_2,\ldots , x_n\in \pi ^{-1}(y)$
. It follows that
Since
![]() $x_1,x_2,\ldots ,x_n$
are distinct and
$x_1,x_2,\ldots ,x_n$
are distinct and
![]() $(x_1,x_2,\ldots , x_n)$
is minimal,
$(x_1,x_2,\ldots , x_n)$
is minimal,
![]() $vpx_1, vpx_2, \ldots , vpx_n$
are also distinct. As
$vpx_1, vpx_2, \ldots , vpx_n$
are also distinct. As
we have
![]() $n\le m$
. Similarly, we have
$n\le m$
. Similarly, we have
![]() $m\le n$
. Thus,
$m\le n$
. Thus,
![]() $|u\pi ^{-1}(y)|=|v\pi ^{-1}(y')|$
.
$|u\pi ^{-1}(y)|=|v\pi ^{-1}(y')|$
.
By Lemma 3.2 and the fact that A is an almost periodic subset of subset Z of
![]() $(X,T)$
if and only if
$(X,T)$
if and only if
![]() $A\subseteq uZ$
for some
$A\subseteq uZ$
for some
![]() $u\in J$
, we have the following proposition readily.
$u\in J$
, we have the following proposition readily.
Proposition 3.3. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then the following are equivalent.
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then the following are equivalent.
-
(1)
 $\pi $
is almost proximal.
$\pi $
is almost proximal. -
(2) For some
 $y\in Y$
, there is some
$y\in Y$
, there is some
 $N\in \mathbb N$
such that the cardinality of any almost periodic subset in the fiber
$N\in \mathbb N$
such that the cardinality of any almost periodic subset in the fiber
 $\pi ^{-1}(y)$
is not greater than N.
$\pi ^{-1}(y)$
is not greater than N. -
(3) There is some
 $N\in \mathbb N$
such that for some
$N\in \mathbb N$
such that for some
 $y\in Y$
and
$y\in Y$
and
 $u\in J_y$
,
$u\in J_y$
,
 $|u\pi ^{-1}(y)|=N<\infty $
.
$|u\pi ^{-1}(y)|=N<\infty $
. -
(4) There is some
 $N\in \mathbb N$
such that for each
$N\in \mathbb N$
such that for each
 $y\in Y$
and
$y\in Y$
and
 $u\in J_y$
,
$u\in J_y$
,
 $|u\pi ^{-1}(y)|=N<\infty $
.
$|u\pi ^{-1}(y)|=N<\infty $
.
When
![]() $N=1$
,
$N=1$
,
![]() $\pi $
is proximal.
$\pi $
is proximal.
For
![]() $x\in X$
,
$x\in X$
,
![]() $P[x]=\{x'\in X: (x,x')\in P(X, T)\}$
is called the proximal cell of x. It is clear that
$P[x]=\{x'\in X: (x,x')\in P(X, T)\}$
is called the proximal cell of x. It is clear that
![]() $\pi $
is proximal if and only if for any
$\pi $
is proximal if and only if for any
![]() $y\in Y$
and any
$y\in Y$
and any
![]() $x\in \pi ^{-1}(y)$
,
$x\in \pi ^{-1}(y)$
,
![]() $\pi ^{-1}(y)\subseteq P[x]$
.
$\pi ^{-1}(y)\subseteq P[x]$
.
Corollary 3.4. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If
![]() $\pi $
is almost proximal, then for each
$\pi $
is almost proximal, then for each
![]() $y\in Y$
, there is some finite subset F of
$y\in Y$
, there is some finite subset F of
![]() $\pi ^{-1}(y)$
such that each point of
$\pi ^{-1}(y)$
such that each point of
![]() $\pi ^{-1}(y)$
is proximal to some point of F, that is,
$\pi ^{-1}(y)$
is proximal to some point of F, that is,
![]() $\pi ^{-1}(y)\subseteq \bigcup _{x\in F}P[x]$
.
$\pi ^{-1}(y)\subseteq \bigcup _{x\in F}P[x]$
.
Proof. Let
![]() $y\in Y$
and
$y\in Y$
and
![]() $u\in J_y$
. Then
$u\in J_y$
. Then
![]() $F=u\pi ^{-1}(y)$
is finite by Proposition 3.3. For any
$F=u\pi ^{-1}(y)$
is finite by Proposition 3.3. For any
![]() $x\in \pi ^{-1}(y)$
, by Proposition 2.4,
$x\in \pi ^{-1}(y)$
, by Proposition 2.4,
![]() $(x,ux)\in P(X)$
and
$(x,ux)\in P(X)$
and
![]() $ux\in F$
. The proof is complete.
$ux\in F$
. The proof is complete.
Let
![]() $\pi :(X,T)\rightarrow (Y,T)$
be an extension of flows
$\pi :(X,T)\rightarrow (Y,T)$
be an extension of flows
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,T)$
and
$(Y,T)$
and
![]() $n\in \mathbb N$
. Let
$n\in \mathbb N$
. Let
and
 $$ \begin{align*}2^X_{\pi, n}=\{A\in 2^X_\pi: |A|\le n\}, \quad \text{and}\quad 2^X_{\pi,*}=\{A\in 2^X_\pi: |A|< \infty\}=\bigcup_{n=1}^\infty 2^X_{\pi, n}.\end{align*} $$
$$ \begin{align*}2^X_{\pi, n}=\{A\in 2^X_\pi: |A|\le n\}, \quad \text{and}\quad 2^X_{\pi,*}=\{A\in 2^X_\pi: |A|< \infty\}=\bigcup_{n=1}^\infty 2^X_{\pi, n}.\end{align*} $$
It is clear that
![]() $(2^X_\pi , T)$
,
$(2^X_\pi , T)$
,
![]() $(2^X_{\pi ,n}, T)$
, and
$(2^X_{\pi ,n}, T)$
, and
![]() $(2^X_{\pi ,*}, T)$
are subflows of
$(2^X_{\pi ,*}, T)$
are subflows of
![]() $(2^X,T)$
. Let
$(2^X,T)$
. Let
Then
![]() $\widetilde {\pi }$
is an extension. Note that
$\widetilde {\pi }$
is an extension. Note that
![]() $2^X_{\pi ,1}=\{\{x\}\in 2^X: x\in X\}$
is isomorphic to X and
$2^X_{\pi ,1}=\{\{x\}\in 2^X: x\in X\}$
is isomorphic to X and
![]() $\widetilde {\pi }|_{2^X_{\pi ,1}}$
is the same to
$\widetilde {\pi }|_{2^X_{\pi ,1}}$
is the same to
![]() $\pi $
. Thus,
$\pi $
. Thus,
![]() $\pi : (X,T) \rightarrow (Y,T)$
is proximal if and only if
$\pi : (X,T) \rightarrow (Y,T)$
is proximal if and only if
![]() $\widetilde {\pi }|_{2^X_{\pi ,1}}\!: (2^X_{\pi ,1}, T)\rightarrow (Y,T)$
is proximal.
$\widetilde {\pi }|_{2^X_{\pi ,1}}\!: (2^X_{\pi ,1}, T)\rightarrow (Y,T)$
is proximal.
Proposition 3.5. Let
![]() $\pi :(X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then
$\pi :(X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then
![]() $\pi $
is almost proximal if and only if there is some
$\pi $
is almost proximal if and only if there is some
![]() $n\in \mathbb N$
such that there are no minimal points in
$n\in \mathbb N$
such that there are no minimal points in
![]() $2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
.
$2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
.
Proof. If
![]() $\pi $
is almost proximal, then there is some
$\pi $
is almost proximal, then there is some
![]() $n\in \mathbb N$
such that
$n\in \mathbb N$
such that
![]() $|u\pi ^{-1}(y)|=n$
for all
$|u\pi ^{-1}(y)|=n$
for all
![]() $y\in Y, u\in J_y$
. Let
$y\in Y, u\in J_y$
. Let
![]() $A\in 2^X_{\pi , *} \setminus 2^X_{\pi , n}$
and
$A\in 2^X_{\pi , *} \setminus 2^X_{\pi , n}$
and
![]() $y=\pi (A)$
. Then
$y=\pi (A)$
. Then
![]() $|A|\ge n+1$
. For each
$|A|\ge n+1$
. For each
![]() $u\in J_y$
,
$u\in J_y$
,
![]() $|uA|\le n$
since
$|uA|\le n$
since
![]() $\pi $
is almost proximal. Thus,
$\pi $
is almost proximal. Thus,
![]() $u\circ A=uA\neq A$
, in particular, by Proposition 2.3, A is not minimal.
$u\circ A=uA\neq A$
, in particular, by Proposition 2.3, A is not minimal.
Conversely, assume that there is some
![]() $n\in \mathbb N$
such that there are no minimal points in
$n\in \mathbb N$
such that there are no minimal points in
![]() $2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
. If
$2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
. If
![]() $\pi $
is not almost proximal, then there is some
$\pi $
is not almost proximal, then there is some
![]() $y\in Y$
and
$y\in Y$
and
![]() $u\in J_y$
such that
$u\in J_y$
such that
![]() $|u\pi ^{-1}(y)|=\infty $
. We choose
$|u\pi ^{-1}(y)|=\infty $
. We choose
![]() $A\subseteq u\pi ^{-1}(y)$
with
$A\subseteq u\pi ^{-1}(y)$
with
![]() $|A|= n+1$
. Then
$|A|= n+1$
. Then
which means A is a minimal point of
![]() $2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
, which is a contradiction. The proof is complete.
$2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
, which is a contradiction. The proof is complete.
Remark 3.6. It is well known that each flow has a minimal subflow. Since
![]() $2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
may not be compact, it is an invariant subset of
$2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
may not be compact, it is an invariant subset of
![]() $2^X$
but maybe not a subflow of
$2^X$
but maybe not a subflow of
![]() $2^X$
. So it is possible that
$2^X$
. So it is possible that
![]() $2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
contains no minimal points.
$2^X_{\pi ,*}\setminus 2^X_{\pi , n}$
contains no minimal points.
3.2 Almost finite-to-one extensions
Definition 3.7. Let
![]() $\pi :(X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then
$\pi :(X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then
![]() $\pi $
is called an almost finite-to-one extension if some fiber is finite.
$\pi $
is called an almost finite-to-one extension if some fiber is finite.
Proposition 3.8. [Reference Shoenfeld24, Proposition 3.5], [Reference Huang, Lian, Shao and Ye20, Proposition 2.15]
Let
![]() $\pi :(X,T)\rightarrow (Y,T)$
be an extension of minimal flows. The following statements are equivalent:
$\pi :(X,T)\rightarrow (Y,T)$
be an extension of minimal flows. The following statements are equivalent:
-
(1)
 $\pi $
is almost finite to one, that is, some fiber is finite;
$\pi $
is almost finite to one, that is, some fiber is finite; -
(2) there exists
 $N\in \mathbb N$
such that
$N\in \mathbb N$
such that
 $Y_0=\{y\in Y: |\pi ^{-1}(y)|=N\}$
is a residual subset of Y;
$Y_0=\{y\in Y: |\pi ^{-1}(y)|=N\}$
is a residual subset of Y; -
(3) there exist
 $N\in \mathbb N$
and
$N\in \mathbb N$
and
 $y_0\in Y$
such that
$y_0\in Y$
such that
 $|\pi ^{-1}(y_0)|=N$
and
$|\pi ^{-1}(y_0)|=N$
and
 $\pi ^{-1}(y_0)$
is an almost periodic set;
$\pi ^{-1}(y_0)$
is an almost periodic set; -
(4) the cardinality of each minimal point of
 $(2^X,T)$
in
$(2^X,T)$
in
 $2^X_{\pi }$
is not greater than some fixed integer N.
$2^X_{\pi }$
is not greater than some fixed integer N.
Remark 3.9
-
(1) By Proposition 3.8, almost finite-to-one extensions of minimal flows are almost proximal. In §6, we will give examples which are almost proximal but not almost finite-to-one extensions.
-
(2) By definition, it is obvious that a finite-to-one extension (that is, every fiber is finite) is almost finite-to-one. However, in general, an almost finite-to-one extension may not be finite-to-one. For example, for Rees’ example [Reference Rees22],
 $\pi : (X,T)\rightarrow (X_{\mathrm {eq}},T)$
is an almost one-to-one extension (
$\pi : (X,T)\rightarrow (X_{\mathrm {eq}},T)$
is an almost one-to-one extension (
 $X_{\mathrm {eq}}$
is the maximal equicontinuous factor of X), and for any
$X_{\mathrm {eq}}$
is the maximal equicontinuous factor of X), and for any
 $y\in X_{\mathrm {eq}}$
, either
$y\in X_{\mathrm {eq}}$
, either
 $|\pi ^{-1}(y)|=1$
or
$|\pi ^{-1}(y)|=1$
or
 $|\pi ^{-1}(y)|=\infty $
.
$|\pi ^{-1}(y)|=\infty $
. -
(3) For more discussion about finite-to-one and almost finite-to-one extensions, refer to [Reference Huang, Lian, Shao and Ye20].
By Proposition 3.8, it is easy to check the following corollary.
Corollary 3.10. Let
![]() $\pi :(X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If
$\pi :(X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If
![]() $\pi $
is proximal but not almost one-to-one, then every fiber is infinite, that is,
$\pi $
is proximal but not almost one-to-one, then every fiber is infinite, that is,
![]() $\pi $
is not almost finite-to-one.
$\pi $
is not almost finite-to-one.
3.3 Structure of almost proximal extensions
The following result is well known and it is easy to be verified (one may find a proof in [Reference Huang, Lian, Shao and Ye20, Lemma 2.20]).
Lemma 3.11. Let
![]() $\pi : X \rightarrow Y$
be a finite-to-one extension (that is,
$\pi : X \rightarrow Y$
be a finite-to-one extension (that is,
![]() $\pi ^{-1}(y)$
is finite for all
$\pi ^{-1}(y)$
is finite for all
![]() $y\in Y$
) of the minimal flows
$y\in Y$
) of the minimal flows
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,T)$
. Then the following conditions are equivalent:
$(Y,T)$
. Then the following conditions are equivalent:
-
(1)
 $\pi $
is open;
$\pi $
is open; -
(2)
 $\pi $
is distal;
$\pi $
is distal; -
(3)
 $\pi $
is equicontinuous;
$\pi $
is equicontinuous;
In this case, there exists
![]() $N\in \mathbb N$
such that
$N\in \mathbb N$
such that
![]() $\pi $
is an N-to-one map.
$\pi $
is an N-to-one map.
Theorem 3.12. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an almost proximal extension of minimal flows. Then it has the following structure:
$\pi : (X,T)\rightarrow (Y,T)$
be an almost proximal extension of minimal flows. Then it has the following structure:

where
![]() $\sigma '$
and
$\sigma '$
and
![]() $\tau '$
are proximal,
$\tau '$
are proximal,
![]() $\pi '$
is a finite-to-one equicontinuous extension.
$\pi '$
is a finite-to-one equicontinuous extension.
Moreover,
![]() $\pi $
is almost finite-to-one if and only if
$\pi $
is almost finite-to-one if and only if
![]() $\tau ', \sigma '$
are almost one-to-one.
$\tau ', \sigma '$
are almost one-to-one.
Proof. In light of the construction of the RIC-diagram (Theorem 2.7),
![]() $\sigma '$
and
$\sigma '$
and
![]() $\tau '$
are proximal extensions and
$\tau '$
are proximal extensions and
![]() $\pi '$
is an RIC extension. We show that if
$\pi '$
is an RIC extension. We show that if
![]() $\pi $
is almost proximal, then
$\pi $
is almost proximal, then
![]() $\pi '$
is a finite-to-one equicontinuous extension. Recall the construction of RIC-diagram. Let
$\pi '$
is a finite-to-one equicontinuous extension. Recall the construction of RIC-diagram. Let
![]() $x\in X$
,
$x\in X$
,
![]() $u\in J_{x}$
, and
$u\in J_{x}$
, and
![]() $y=\pi (x)$
. Let
$y=\pi (x)$
. Let
![]() $y'=u {\circ } u \pi ^{-1}(y)\in 2^X$
. Then
$y'=u {\circ } u \pi ^{-1}(y)\in 2^X$
. Then
![]() $Y'=\{p{\circ } y': p\in \mathbf {M}\}$
is the orbit closure of
$Y'=\{p{\circ } y': p\in \mathbf {M}\}$
is the orbit closure of
![]() $y'$
and
$y'$
and
![]() $\tau ' (p{\circ } y')= p y$
. And
$\tau ' (p{\circ } y')= p y$
. And
![]() $X'=\{(px, p{\circ } y')\in X\times Y': p\in \mathbf {M}\}=\{(\tilde x,\tilde y)\in X \times Y' : \tilde x \in \tilde y\}$
is the unique minimal set in
$X'=\{(px, p{\circ } y')\in X\times Y': p\in \mathbf {M}\}=\{(\tilde x,\tilde y)\in X \times Y' : \tilde x \in \tilde y\}$
is the unique minimal set in
![]() $R_{\pi \tau ' }=\{(x,y)\in X\times Y ': \pi (x)=\tau '(y)\}$
, and
$R_{\pi \tau ' }=\{(x,y)\in X\times Y ': \pi (x)=\tau '(y)\}$
, and
![]() $\sigma '$
and
$\sigma '$
and
![]() $\pi '$
are the restrictions to
$\pi '$
are the restrictions to
![]() $X '$
of the projections of
$X '$
of the projections of
![]() $X\times Y '$
onto X and
$X\times Y '$
onto X and
![]() $Y '$
, respectively. Since
$Y '$
, respectively. Since
![]() $\pi $
is almost proximal, we have that
$\pi $
is almost proximal, we have that
![]() $|u\pi ^{-1}(y)|<\infty .$
Thus,
$|u\pi ^{-1}(y)|<\infty .$
Thus,
![]() $y'=u\circ u\pi ^{-1}(y)$
is finite, and for every
$y'=u\circ u\pi ^{-1}(y)$
is finite, and for every
![]() $p\in \mathbf {M}, |p{\circ } y' |<\infty .$
Hence, for every
$p\in \mathbf {M}, |p{\circ } y' |<\infty .$
Hence, for every
![]() $p\in \mathbf {M}$
,
$p\in \mathbf {M}$
,
![]() $|(\pi ')^{-1}(p{\circ } y')|=|\{(\tilde {x}, p\circ y'): \tilde {x}\in p\circ y' \}|=|p{\circ } y' |$
is finite. It follows that
$|(\pi ')^{-1}(p{\circ } y')|=|\{(\tilde {x}, p\circ y'): \tilde {x}\in p\circ y' \}|=|p{\circ } y' |$
is finite. It follows that
![]() $\pi '$
is finite-to-one and open. By Lemma 3.11,
$\pi '$
is finite-to-one and open. By Lemma 3.11,
![]() $\pi '$
is equicontinuous.
$\pi '$
is equicontinuous.
Clearly, if
![]() $\tau ', \sigma '$
are almost one-to-one, then
$\tau ', \sigma '$
are almost one-to-one, then
![]() $\pi $
is almost finite-to-one. Conversely, when
$\pi $
is almost finite-to-one. Conversely, when
![]() $\pi $
is almost finite-to-one, by Proposition 3.8, there exists
$\pi $
is almost finite-to-one, by Proposition 3.8, there exists
![]() $y_0$
such that
$y_0$
such that
![]() $|\pi ^{-1}(y_0)|< \infty $
and
$|\pi ^{-1}(y_0)|< \infty $
and
![]() $\pi ^{-1}(y_0)$
is a minimal point of
$\pi ^{-1}(y_0)$
is a minimal point of
![]() $(2^X,T),$
that is,
$(2^X,T),$
that is,
![]() $u\circ \pi ^{-1}(y_0)=\pi ^{-1}(y_0).$
Hence, the construction of the RIC-diagram coincides with the O-diagram. Therefore,
$u\circ \pi ^{-1}(y_0)=\pi ^{-1}(y_0).$
Hence, the construction of the RIC-diagram coincides with the O-diagram. Therefore,
![]() $\tau ', \sigma '$
are almost one-to-one.
$\tau ', \sigma '$
are almost one-to-one.
If, in addition, the extension is regular (see definition below), an almost proximal extension has a succinct structure. Let
![]() $\mathrm {Aut} (X,T)$
be the group of automorphisms of the flow
$\mathrm {Aut} (X,T)$
be the group of automorphisms of the flow
![]() $(X,T)$
, that is, the group of all self-homeomorphisms
$(X,T)$
, that is, the group of all self-homeomorphisms
![]() $\psi $
of X such that
$\psi $
of X such that
![]() $\psi \circ t=t\circ \psi \text { for all } t\in T$
. For an extension
$\psi \circ t=t\circ \psi \text { for all } t\in T$
. For an extension
![]() $\pi : (X,T)\rightarrow (Y,T)$
, let
$\pi : (X,T)\rightarrow (Y,T)$
, let
that is, elements of
![]() $\mathrm {Aut}(X,T)$
mapping every fiber of
$\mathrm {Aut}(X,T)$
mapping every fiber of
![]() $\pi $
into itself.
$\pi $
into itself.
Definition 3.13. Let
![]() $\pi : (X, T)\rightarrow (Y,T)$
be an extension of minimal flows. One says
$\pi : (X, T)\rightarrow (Y,T)$
be an extension of minimal flows. One says
![]() $\pi $
is regular if for any point
$\pi $
is regular if for any point
![]() $(x_1,x_2)\in R_\pi $
, there exists
$(x_1,x_2)\in R_\pi $
, there exists
![]() $\chi \in \mathrm {Aut}_\pi (X,T)$
such that
$\chi \in \mathrm {Aut}_\pi (X,T)$
such that
![]() $(\chi (x_1),x_2)\in P(X,T)$
. It is equivalent to: for any minimal point
$(\chi (x_1),x_2)\in P(X,T)$
. It is equivalent to: for any minimal point
![]() $(x_1,x_2)$
in
$(x_1,x_2)$
in
![]() $R_\pi $
, there exists
$R_\pi $
, there exists
![]() $\chi \in \mathrm {Aut}_\pi (X,T)$
such that
$\chi \in \mathrm {Aut}_\pi (X,T)$
such that
![]() $\chi (x_1)=x_2$
.
$\chi (x_1)=x_2$
.
The notion of regularity was introduced by Auslander [Reference Auslander3]. Examples of regular extensions are proximal extensions, group extensions. For more information about regularity, refer to [Reference Auslander3, Reference Auslander4, Reference Glasner15].
Theorem 3.14. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If
![]() $\pi $
is regular and almost proximal, then there exists a flow
$\pi $
is regular and almost proximal, then there exists a flow
![]() $(Y^\#,T)$
with the following commutative diagram:
$(Y^\#,T)$
with the following commutative diagram:

where
![]() $\tau ^\#$
is proximal and
$\tau ^\#$
is proximal and
![]() $\pi ^\#$
is a finite-to-one equicontinuous extension. And
$\pi ^\#$
is a finite-to-one equicontinuous extension. And
![]() $\pi $
is almost finite-to-one if and only if
$\pi $
is almost finite-to-one if and only if
![]() $\tau ^\#$
is almost one-to-one.
$\tau ^\#$
is almost one-to-one.
Proof. Let
![]() $y_0\in Y$
and
$y_0\in Y$
and
![]() $u\in J_{y_0}$
, that is,
$u\in J_{y_0}$
, that is,
![]() $uy_0=y_0$
. Since
$uy_0=y_0$
. Since
![]() $\pi $
is almost proximal, by Proposition 3.3, there exits an
$\pi $
is almost proximal, by Proposition 3.3, there exits an
![]() $n\in \mathbb N$
such that
$n\in \mathbb N$
such that
![]() $|v\pi ^{-1}(y)|=n$
for all
$|v\pi ^{-1}(y)|=n$
for all
![]() $y\in Y, v\in J_y$
. Thus,
$y\in Y, v\in J_y$
. Thus,
![]() $|v\pi ^{-1}(py_0)|=n$
for all
$|v\pi ^{-1}(py_0)|=n$
for all
![]() $p\in \mathbf {M}$
and all
$p\in \mathbf {M}$
and all
![]() $v\in J(\mathbf {M})$
with
$v\in J(\mathbf {M})$
with
![]() $vp=p$
.
$vp=p$
.
Let
![]() $\mathbf {y}_0=u\pi ^{-1}(y_0)=\{x_1,x_2,\ldots , x_n\}$
. As
$\mathbf {y}_0=u\pi ^{-1}(y_0)=\{x_1,x_2,\ldots , x_n\}$
. As
![]() $\{x_1,x_2,\ldots , x_n\}$
is an almost periodic set,
$\{x_1,x_2,\ldots , x_n\}$
is an almost periodic set,
![]() $(x_1,\ldots , x_n)$
is a minimal point of
$(x_1,\ldots , x_n)$
is a minimal point of
![]() $(X^n,T)$
, and it follows that for all
$(X^n,T)$
, and it follows that for all
![]() $p\in \mathbf {M}$
,
$p\in \mathbf {M}$
,
![]() $|p\mathbf { y}_0|=|\{px_1,px_2,\ldots , px_n\}|=n$
. Let
$|p\mathbf { y}_0|=|\{px_1,px_2,\ldots , px_n\}|=n$
. Let
It is clear that
![]() $X=\bigcup _{\mathbf {y}\in Y^\#} \mathbf {y}$
. We show that
$X=\bigcup _{\mathbf {y}\in Y^\#} \mathbf {y}$
. We show that
![]() $Y^\#$
is a partition of X, that is, for all
$Y^\#$
is a partition of X, that is, for all
![]() $p,q\in \mathbf {M}$
, either
$p,q\in \mathbf {M}$
, either
![]() $p\mathbf {y}_0=q\mathbf {y}_0$
or
$p\mathbf {y}_0=q\mathbf {y}_0$
or
![]() $p\mathbf {y}_0 \cap q\mathbf {y}_0=\emptyset $
.
$p\mathbf {y}_0 \cap q\mathbf {y}_0=\emptyset $
.
Assume that there are
![]() $p,q\in \mathbf {M}$
such that
$p,q\in \mathbf {M}$
such that
![]() $p\mathbf {y}_0=\{px_1,\ldots , px_n\}\not =\{qx_1, \ldots , qx_n\}=q\mathbf {y}_0$
and
$p\mathbf {y}_0=\{px_1,\ldots , px_n\}\not =\{qx_1, \ldots , qx_n\}=q\mathbf {y}_0$
and
![]() $p\mathbf {y}_0 \cap q\mathbf {y}_0\neq \emptyset $
. Without loss of generality, we assume that
$p\mathbf {y}_0 \cap q\mathbf {y}_0\neq \emptyset $
. Without loss of generality, we assume that
![]() $qx_1=px_j\in p\mathbf {y}_0$
for some
$qx_1=px_j\in p\mathbf {y}_0$
for some
![]() $j\in \{1,2,\ldots , n\}$
and
$j\in \{1,2,\ldots , n\}$
and
![]() $qx_2\not \in p\mathbf {y}_0$
.
$qx_2\not \in p\mathbf {y}_0$
.
Since
![]() $(x_1,\ldots , x_n)$
is a minimal point of
$(x_1,\ldots , x_n)$
is a minimal point of
![]() $(X^n,T)$
,
$(X^n,T)$
,
![]() $(qx_1, \ldots , qx_n)=q(x_1,\ldots , x_n)$
is also a minimal point of
$(qx_1, \ldots , qx_n)=q(x_1,\ldots , x_n)$
is also a minimal point of
![]() $(X^n,T)$
. In particular,
$(X^n,T)$
. In particular,
![]() $(qx_1,qx_2)\in R_\pi $
is a minimal point. As
$(qx_1,qx_2)\in R_\pi $
is a minimal point. As
![]() $\pi $
is regular, there is some
$\pi $
is regular, there is some
![]() $\chi \in \mathrm {Aut}_\pi (X,T)$
such that
$\chi \in \mathrm {Aut}_\pi (X,T)$
such that
![]() $qx_2=\chi (qx_1)$
. Let
$qx_2=\chi (qx_1)$
. Let
![]() $v\in J(\mathbf {M})$
such that
$v\in J(\mathbf {M})$
such that
![]() $vp=p$
(Proposition 2.2). Then,
$vp=p$
(Proposition 2.2). Then,
Thus,
![]() $qx_2\in v\pi ^{-1}(py_0)$
and
$qx_2\in v\pi ^{-1}(py_0)$
and
![]() $v\{px_1,px_2,\ldots , px_n, qx_2\}=\{px_1,px_2,\ldots , px_n, qx_2\}$
. It follows that
$v\{px_1,px_2,\ldots , px_n, qx_2\}=\{px_1,px_2,\ldots , px_n, qx_2\}$
. It follows that
![]() $\{px_1,px_2,\ldots , px_n, qx_2\}$
is an almost periodic subset of
$\{px_1,px_2,\ldots , px_n, qx_2\}$
is an almost periodic subset of
![]() $\pi ^{-1}(py_0)$
, whose cardinality is
$\pi ^{-1}(py_0)$
, whose cardinality is
![]() $n+1$
. In particular,
$n+1$
. In particular,
![]() $|v\pi ^{-1}(py_0)|\ge n+1$
, which contradicts with the fact
$|v\pi ^{-1}(py_0)|\ge n+1$
, which contradicts with the fact
![]() $|v\pi ^{-1}(py_0)|= n$
. Thus,
$|v\pi ^{-1}(py_0)|= n$
. Thus,
![]() $Y^\#$
is a partition of X.
$Y^\#$
is a partition of X.
Since
![]() $Y^\#$
is a partition of X, it induces a map
$Y^\#$
is a partition of X, it induces a map
It is easy to check that
![]() $\pi $
is open, and by Lemma 3.11, it is an n-to-
$\pi $
is open, and by Lemma 3.11, it is an n-to-
![]() $1$
equicontinuous extension.
$1$
equicontinuous extension.
Let
We show that it is proximal. Let
![]() $\tau ^\#(p\mathbf {y}_0)=\tau ^\#(q\mathbf {y}_0)$
for some
$\tau ^\#(p\mathbf {y}_0)=\tau ^\#(q\mathbf {y}_0)$
for some
![]() $p,q\in \mathbf {M}$
. Then,
$p,q\in \mathbf {M}$
. Then,
![]() $py_0=qy_0$
. There are minimal idempotents
$py_0=qy_0$
. There are minimal idempotents
![]() $u_1,u_2\in J(\mathbf {M})$
such that
$u_1,u_2\in J(\mathbf {M})$
such that
Since
![]() $|\mathbf {y}_0|<\infty ,$
we have
$|\mathbf {y}_0|<\infty ,$
we have
Similarly, one has
![]() $q\mathbf {y}_0=u_2\pi ^{-1}(qy_0)$
. Then,
$q\mathbf {y}_0=u_2\pi ^{-1}(qy_0)$
. Then,
So
![]() $p\mathbf {y}_0$
and
$p\mathbf {y}_0$
and
![]() $q\mathbf {y}_0$
are proximal. That is,
$q\mathbf {y}_0$
are proximal. That is,
![]() $\tau ^\#$
is a proximal extension.
$\tau ^\#$
is a proximal extension.
3.4 Relations between almost proximal extensions and almost one-to-one extensions
It is clear that any almost finite-to-one extension is an almost proximal extension. In this subsection, we show that if, in addition, the extension is point distal, then the converse holds.
Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. A point
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. A point
![]() $x\in X$
is called a
$x\in X$
is called a
![]() $\pi $
-distal point whenever
$\pi $
-distal point whenever
![]() $P_\pi [x]\triangleq \{x'\in \pi ^{-1}(\pi (x)): (x,x')\in P(X,T)\}=\{x\}$
, that is,
$P_\pi [x]\triangleq \{x'\in \pi ^{-1}(\pi (x)): (x,x')\in P(X,T)\}=\{x\}$
, that is,
![]() $(x,x')$
is a distal pair for every
$(x,x')$
is a distal pair for every
![]() $x'\in \pi ^{-1}(\pi (x))\setminus \{x\}$
. The extension
$x'\in \pi ^{-1}(\pi (x))\setminus \{x\}$
. The extension
![]() $\pi $
is said to be point distal when there exists a
$\pi $
is said to be point distal when there exists a
![]() $\pi $
-distal point in X. Note that
$\pi $
-distal point in X. Note that
![]() $\pi $
is distal if and only if every point is
$\pi $
is distal if and only if every point is
![]() $\pi $
-distal. It is easy to see that a point x is
$\pi $
-distal. It is easy to see that a point x is
![]() $\pi $
-distal if and only if
$\pi $
-distal if and only if
![]() $ux=x$
for all
$ux=x$
for all
![]() $u\in J_{\pi (x)}$
[Reference de Vries8, Ch. VI(4.3)].
$u\in J_{\pi (x)}$
[Reference de Vries8, Ch. VI(4.3)].
Theorem 3.15. [Reference Veech28, Theorem 2.3.5]
Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then RIC-diagram and O-diagram coincide if and only if there is some
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then RIC-diagram and O-diagram coincide if and only if there is some
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $\bigcap _{u\in J_y} u\circ u\pi ^{-1}(y)\neq \emptyset $
.
$\bigcap _{u\in J_y} u\circ u\pi ^{-1}(y)\neq \emptyset $
.
Theorem 3.16. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then the following are equivalent:
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then the following are equivalent:
-
(1)
 $\pi $
is almost proximal and point distal;
$\pi $
is almost proximal and point distal; -
(2)
 $\pi $
is almost finite-to-one.
$\pi $
is almost finite-to-one.
Proof. If
![]() $\pi $
is almost finite-to-one, it is almost proximal. By Proposition 3.8, there exist
$\pi $
is almost finite-to-one, it is almost proximal. By Proposition 3.8, there exist
![]() $N\in \mathbb N$
and
$N\in \mathbb N$
and
![]() $y_0\in Y$
such that
$y_0\in Y$
such that
![]() $|\pi ^{-1}(y_0)|=N$
and
$|\pi ^{-1}(y_0)|=N$
and
![]() $\pi ^{-1}(y_0)$
is a minimal point of
$\pi ^{-1}(y_0)$
is a minimal point of
![]() $(2^X, T)$
. Each point in
$(2^X, T)$
. Each point in
![]() $\pi ^{-1}(y_0)$
is
$\pi ^{-1}(y_0)$
is
![]() $\pi $
-distal.
$\pi $
-distal.
Conversely, assume that
![]() $\pi $
is almost proximal and point distal. Let
$\pi $
is almost proximal and point distal. Let
![]() $x_0\in X$
be a
$x_0\in X$
be a
![]() $\pi $
-distal point and
$\pi $
-distal point and
![]() $y_0=\pi (x_0)$
. Since
$y_0=\pi (x_0)$
. Since
![]() $x_0$
is
$x_0$
is
![]() $\pi $
-distal,
$\pi $
-distal,
![]() $ux_0=x_0$
for all
$ux_0=x_0$
for all
![]() $u\in J_{y_0}$
. Thus,
$u\in J_{y_0}$
. Thus,
![]() ${x_0\in \bigcap _{u\in J_{y_0}}u\circ u \pi ^{-1}(y_0)}$
. By Theorem 3.15, the RIC-diagram and O-diagram of
${x_0\in \bigcap _{u\in J_{y_0}}u\circ u \pi ^{-1}(y_0)}$
. By Theorem 3.15, the RIC-diagram and O-diagram of
![]() $\pi $
coincide. That is, in the RIC-diagram,
$\pi $
coincide. That is, in the RIC-diagram,

Here,
![]() $\sigma '$
and
$\sigma '$
and
![]() $\tau '$
are almost one-to-one, and
$\tau '$
are almost one-to-one, and
![]() $\pi '$
is a finite-to-one extension. Thus,
$\pi '$
is a finite-to-one extension. Thus,
![]() $\pi $
is almost finite-to-one.
$\pi $
is almost finite-to-one.
Corollary 3.17. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then
![]() $\pi $
is proximal and point distal if and only if
$\pi $
is proximal and point distal if and only if
![]() $\pi $
is almost one-to-one.
$\pi $
is almost one-to-one.
4 Proximal extensions and weakly mixing extensions
In this section, we will study the chaotic properties of proximal but not almost one-to-one extensions.
4.1 Weakly mixing extensions
Let
![]() $(X,T)$
be a flow. A point
$(X,T)$
be a flow. A point
![]() $x\in X$
is recurrent if for each neighborhood U of x, the set of return times of x to U,
$x\in X$
is recurrent if for each neighborhood U of x, the set of return times of x to U,
![]() $N(x,U)=\{t\in T: tx\in U\}$
is infinite. A point x is recurrent if and only if there exists
$N(x,U)=\{t\in T: tx\in U\}$
is infinite. A point x is recurrent if and only if there exists
![]() $p\in S_T\setminus T$
such that
$p\in S_T\setminus T$
such that
![]() $px=x$
, if and only if there exists an idempotent
$px=x$
, if and only if there exists an idempotent
![]() $u\in S_T\setminus T$
such that
$u\in S_T\setminus T$
such that
![]() $ux=x$
[Reference Ellis, Ellis and Nerurkar9, Lemma 5.18].
$ux=x$
[Reference Ellis, Ellis and Nerurkar9, Lemma 5.18].
Definition 4.1. Let
![]() $(X,T)$
be a flow.
$(X,T)$
be a flow.
-
(1) A pair
 $(x,y)\in X^2$
is called a strong Li–Yorke pair if it is proximal and it is also a recurrent point of
$(x,y)\in X^2$
is called a strong Li–Yorke pair if it is proximal and it is also a recurrent point of
 $(X^2, T)$
.
$(X^2, T)$
. -
(2) A subset S of X is called strongly scrambled if every pair of distinct points in S is a strong Li–Yorke pair.
-
(3) The flow
 $(X,T)$
is said to be strongly Li–Yorke chaotic if it contains an uncountable strongly scrambled set.
$(X,T)$
is said to be strongly Li–Yorke chaotic if it contains an uncountable strongly scrambled set.
The following result says that each non-trivial weakly mixing extension contains plenty of strongly scrambled subsets.
Theorem 4.2. [Reference Akin, Glasner, Huang, Shao and Ye2, Theorem 5.10]
Let
![]() $(X,T), (Y,T)$
be a flow and
$(X,T), (Y,T)$
be a flow and
![]() $\pi : (X,T)\rightarrow (Y, T)$
an open non-trivial weakly mixing extension. Then there is a residual subset
$\pi : (X,T)\rightarrow (Y, T)$
an open non-trivial weakly mixing extension. Then there is a residual subset
![]() $Y_0\subseteq Y$
such that for every point
$Y_0\subseteq Y$
such that for every point
![]() $y\in Y_0$
, the set
$y\in Y_0$
, the set
![]() $\pi ^{-1}(y)$
contains a dense uncountable strongly scrambled subset K such that
$\pi ^{-1}(y)$
contains a dense uncountable strongly scrambled subset K such that
where
![]() $ \mathrm {Trans}(R_\pi )$
denotes the set of all transitive points in
$ \mathrm {Trans}(R_\pi )$
denotes the set of all transitive points in
![]() $R_\pi $
, and in particular,
$R_\pi $
, and in particular,
![]() $\pi ^{-1}(y)$
is perfect, and it has the cardinality of the continuum.
$\pi ^{-1}(y)$
is perfect, and it has the cardinality of the continuum.
Definition 4.3. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of flows.
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of flows.
-
(1)
 $\pi $
is called n-weakly mixing (
$\pi $
is called n-weakly mixing (
 $n\ge 2$
) if
$n\ge 2$
) if
 $(R^n_\pi , T)$
is transitive.
$(R^n_\pi , T)$
is transitive. -
(2) If
 $\pi $
is n-weakly mixing for every
$\pi $
is n-weakly mixing for every
 $n\ge 2$
, then
$n\ge 2$
, then
 $\pi $
is called totally weakly mixing.
$\pi $
is called totally weakly mixing.
Note that a
![]() $2$
-weakly mixing extension is just weakly mixing. Totally weakly mixing extensions will present stronger chaotic properties than weakly mixing extensions, see [Reference Akin, Glasner, Huang, Shao and Ye2, Reference Shao and Ye23] for more details. For RIC extensions, weak mixing is equivalent to total weak mixing.
$2$
-weakly mixing extension is just weakly mixing. Totally weakly mixing extensions will present stronger chaotic properties than weakly mixing extensions, see [Reference Akin, Glasner, Huang, Shao and Ye2, Reference Shao and Ye23] for more details. For RIC extensions, weak mixing is equivalent to total weak mixing.
Theorem 4.4. [Reference Auslander, McMahon, van der Woude and Wu6, Theorem 2.12], [Reference Glasner16, Theorem 2.7]
Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an RIC extension of minimal flows. Then the following conditions are equivalent:
$\pi : (X,T)\rightarrow (Y,T)$
be an RIC extension of minimal flows. Then the following conditions are equivalent:
-
(1)
 $\pi $
is weakly mixing;
$\pi $
is weakly mixing; -
(2)
 $\pi $
is n-weakly mixing for some
$\pi $
is n-weakly mixing for some
 $n\ge 2$
;
$n\ge 2$
; -
(3)
 $\pi $
is totally weakly mixing.
$\pi $
is totally weakly mixing.
In general, the fact that
![]() $\pi : (X,T)\rightarrow (Y,T)$
is weakly mixing does not imply that
$\pi : (X,T)\rightarrow (Y,T)$
is weakly mixing does not imply that
![]() $\pi $
is totally weakly mixing. In [Reference Glasner16, Theorem 4.1], for
$\pi $
is totally weakly mixing. In [Reference Glasner16, Theorem 4.1], for
![]() $(Y,T)$
being trivial, the author gave a weakly mixing flow
$(Y,T)$
being trivial, the author gave a weakly mixing flow
![]() $(X,T)$
such that
$(X,T)$
such that
![]() $(X^3,T)$
is not transitive. By Theorem 4.4, such T is not abelian. In §6, we will show that there exists
$(X^3,T)$
is not transitive. By Theorem 4.4, such T is not abelian. In §6, we will show that there exists
![]() $\pi : (X,\mathbb Z)\rightarrow (Y,\mathbb Z)$
which is weakly mixing but not 3-weakly mixing. In fact, we have the following example.
$\pi : (X,\mathbb Z)\rightarrow (Y,\mathbb Z)$
which is weakly mixing but not 3-weakly mixing. In fact, we have the following example.
Example 4.5. There exists a discrete flow
![]() $(X,\mathbb Z)$
such that
$(X,\mathbb Z)$
such that
![]() $\pi : (X,\mathbb Z)\rightarrow (X_{\mathrm {eq}}, \mathbb Z)$
is a proximal extension, and it is weakly mixing but not
$\pi : (X,\mathbb Z)\rightarrow (X_{\mathrm {eq}}, \mathbb Z)$
is a proximal extension, and it is weakly mixing but not
![]() $3$
-weakly mixing. (See Theorem 6.12.)
$3$
-weakly mixing. (See Theorem 6.12.)
4.2 Proximal but not almost one-to-one extensions
Let
![]() $P^{(n)}(X)$
be the subset of
$P^{(n)}(X)$
be the subset of
![]() $X^n$
of all points whose orbit closure intersects the diagonal of
$X^n$
of all points whose orbit closure intersects the diagonal of
![]() $X^n$
. Thus,
$X^n$
. Thus,
![]() $P(X)=P^{(2)}(X)$
. Glasner showed that for a minimal flow
$P(X)=P^{(2)}(X)$
. Glasner showed that for a minimal flow
![]() $(X,T)$
, if
$(X,T)$
, if
![]() $P^{(n)}(X)$
is dense in
$P^{(n)}(X)$
is dense in
![]() $X^n$
for every
$X^n$
for every
![]() $n\ge 2$
, then X is weakly disjoint from all minimal flows, that is,
$n\ge 2$
, then X is weakly disjoint from all minimal flows, that is,
![]() $(X\times Y,T)$
is transitive for all minimal flow
$(X\times Y,T)$
is transitive for all minimal flow
![]() $(Y,T)$
[Reference Glasner17, Ch. II, Proposition 2.1]. In particular, any minimal proximal flow is weakly mixing. This was extended by van der Woude [Reference van der Woude26, Ch. VII, Corollary 2.14] as the following theorem (see also [Reference Glasner16, Corollary 6.4]).
$(Y,T)$
[Reference Glasner17, Ch. II, Proposition 2.1]. In particular, any minimal proximal flow is weakly mixing. This was extended by van der Woude [Reference van der Woude26, Ch. VII, Corollary 2.14] as the following theorem (see also [Reference Glasner16, Corollary 6.4]).
Theorem 4.6. A non-trivial open proximal extension of minimal flows is a weakly mixing extension.
Thus, by Theorem 4.2, we have the following theorem.
Theorem 4.7. [Reference Akin, Glasner, Huang, Shao and Ye2, Theorem 5.17]
Let
![]() $\pi :X\rightarrow Y$
be a proximal but not almost one-to-one extension of minimal flows. Then there is a residual subset
$\pi :X\rightarrow Y$
be a proximal but not almost one-to-one extension of minimal flows. Then there is a residual subset
![]() $Y_0\subseteq Y$
such that for each
$Y_0\subseteq Y$
such that for each
![]() $y\in Y_0$
,
$y\in Y_0$
,
![]() $\pi ^{-1}(y)$
contains an uncountable strongly scrambled subset K.
$\pi ^{-1}(y)$
contains an uncountable strongly scrambled subset K.
In fact, we have the following result which is slightly stronger than Theorem 4.7.
Theorem 4.8. Let
![]() $\pi :X\rightarrow Y$
be a proximal but not almost one-to-one extension of minimal flows. Then there is a residual subset
$\pi :X\rightarrow Y$
be a proximal but not almost one-to-one extension of minimal flows. Then there is a residual subset
![]() $Y_0\subseteq Y$
such that for each
$Y_0\subseteq Y$
such that for each
![]() $y\in Y_0$
,
$y\in Y_0$
,
![]() $\pi ^{-1}(y)$
contains an uncountable strongly scrambled subset K satisfying that for any
$\pi ^{-1}(y)$
contains an uncountable strongly scrambled subset K satisfying that for any
![]() $x_1 \neq x_2\in K$
,
$x_1 \neq x_2\in K$
,
Proof. Let
![]() $\pi :X\rightarrow Y$
be a proximal but not almost one-to-one extension of minimal flows. We consider its O-diagram:
$\pi :X\rightarrow Y$
be a proximal but not almost one-to-one extension of minimal flows. We consider its O-diagram:

Recall the construction of an O-diagram (see Theorem 2.6):
where
![]() $Y_c$
is the set of continuous points of
$Y_c$
is the set of continuous points of
![]() $\pi ^{-1}: Y\rightarrow 2^X$
and it is a residual subset of Y,
$\pi ^{-1}: Y\rightarrow 2^X$
and it is a residual subset of Y,
![]() $X^*$
is the unique minimal set in
$X^*$
is the unique minimal set in
![]() $R_{\pi \tau }=\{(x,y)\in X\times Y^*: \pi (x)=\tau (y)\}$
, and
$R_{\pi \tau }=\{(x,y)\in X\times Y^*: \pi (x)=\tau (y)\}$
, and
![]() $\sigma $
and
$\sigma $
and
![]() $\pi ^*$
are the restrictions to
$\pi ^*$
are the restrictions to
![]() $X^*$
of the projections of
$X^*$
of the projections of
![]() $X\times Y^*$
onto X and
$X\times Y^*$
onto X and
![]() $Y^*$
, respectively. Also
$Y^*$
, respectively. Also
![]() $\tau : Y^*\rightarrow Y$
is an almost one-to-one extension such that
$\tau : Y^*\rightarrow Y$
is an almost one-to-one extension such that
![]() $\tau ^{-1}(y)=\{\pi ^{-1}(y)\}$
for all
$\tau ^{-1}(y)=\{\pi ^{-1}(y)\}$
for all
![]() $y\in Y_c$
.
$y\in Y_c$
.
Since
![]() $\pi $
is proximal but not almost one-to-one,
$\pi $
is proximal but not almost one-to-one,
![]() $\pi ^*$
is open proximal but not almost one-to-one. By Theorem 4.6,
$\pi ^*$
is open proximal but not almost one-to-one. By Theorem 4.6,
![]() $\pi ^*$
is weakly mixing, and hence by Theorem 4.2, there is a residual subset
$\pi ^*$
is weakly mixing, and hence by Theorem 4.2, there is a residual subset
![]() $Y_0^*$
of
$Y_0^*$
of
![]() $Y^*$
such that for each
$Y^*$
such that for each
![]() $\mathbf {y}\in Y_0^*$
,
$\mathbf {y}\in Y_0^*$
,
![]() $(\pi ^*)^{-1}(\mathbf {y})$
contains a dense uncountable strongly scrambled subset
$(\pi ^*)^{-1}(\mathbf {y})$
contains a dense uncountable strongly scrambled subset
![]() $K^*$
such that
$K^*$
such that
Since
![]() $\tau $
is almost one-to-one,
$\tau $
is almost one-to-one,
![]() $\tau (Y_0^*)$
is a residual subset of Y. Let
$\tau (Y_0^*)$
is a residual subset of Y. Let
Then
![]() $Y_0$
is a residual subset of Y. We need to verify that for each
$Y_0$
is a residual subset of Y. We need to verify that for each
![]() $y\in Y_0$
,
$y\in Y_0$
,
![]() $\pi ^{-1}(y)$
contains an uncountable strongly scrambled subset K satisfying that for any
$\pi ^{-1}(y)$
contains an uncountable strongly scrambled subset K satisfying that for any
![]() $x_1 \neq x_2\in K$
,
$x_1 \neq x_2\in K$
,
Let
![]() $y\in Y_0$
. Since
$y\in Y_0$
. Since
![]() $y\in Y_c\cap \tau (Y_0^*) \subseteq Y_c$
, by the property of
$y\in Y_c\cap \tau (Y_0^*) \subseteq Y_c$
, by the property of
![]() $\tau $
, we have that
$\tau $
, we have that
![]() $\tau ^{-1}(y)=\{\pi ^{-1}(y)\}$
. Thus,
$\tau ^{-1}(y)=\{\pi ^{-1}(y)\}$
. Thus,
![]() $\mathbf {y}=\pi ^{-1}(y)\in Y_0^*$
. So by the definition of
$\mathbf {y}=\pi ^{-1}(y)\in Y_0^*$
. So by the definition of
![]() $Y_0^*$
,
$Y_0^*$
,
![]() $(\pi ^*)^{-1}(\mathbf {y})$
contains a dense uncountable strongly scrambled subset
$(\pi ^*)^{-1}(\mathbf {y})$
contains a dense uncountable strongly scrambled subset
![]() $K^*$
such that
$K^*$
such that
![]() $K^*\times K^*\setminus \Delta _{X^*}\subseteq \mathrm {Trans}(R_{\pi ^*}).$
Let
$K^*\times K^*\setminus \Delta _{X^*}\subseteq \mathrm {Trans}(R_{\pi ^*}).$
Let
where
![]() $\Lambda $
is an uncountable index set. Now let
$\Lambda $
is an uncountable index set. Now let
![]() $K=\sigma (K^*)=\{x_{\alpha }\}_{{\alpha }\in \Lambda }$
. First note that
$K=\sigma (K^*)=\{x_{\alpha }\}_{{\alpha }\in \Lambda }$
. First note that
and hence
![]() $K\subseteq \pi ^{-1}(y)$
.
$K\subseteq \pi ^{-1}(y)$
.
Let
![]() $x_1,x_2\in K$
with
$x_1,x_2\in K$
with
![]() $x_1\neq x_2$
. We show that
$x_1\neq x_2$
. We show that
![]() $\pi ^{-1}(y)\times \pi ^{-1}(y)\subseteq \overline {\mathcal{O} }((x_1,x_2),T)$
. Let
$\pi ^{-1}(y)\times \pi ^{-1}(y)\subseteq \overline {\mathcal{O} }((x_1,x_2),T)$
. Let
![]() $y_1,y_2\in \pi ^{-1}(y)=\mathbf {y}$
. Then
$y_1,y_2\in \pi ^{-1}(y)=\mathbf {y}$
. Then
Since
![]() $((x_1,\mathbf {y}), (x_2, \mathbf {y}))\in K^*\times K^*\setminus \Delta _{X^*} \subseteq \mathrm {Trans}(R_{\pi ^*})$
,
$((x_1,\mathbf {y}), (x_2, \mathbf {y}))\in K^*\times K^*\setminus \Delta _{X^*} \subseteq \mathrm {Trans}(R_{\pi ^*})$
,
It follows that
![]() $(y_1,y_2)\in \overline {\mathcal{O} }((x_1,x_2),T)$
. Thus,
$(y_1,y_2)\in \overline {\mathcal{O} }((x_1,x_2),T)$
. Thus,
![]() $ \pi ^{-1}(y)\times \pi ^{-1}(y)\subseteq \overline {\mathcal{O} }((x_1,x_2),T).$
The proof is complete.
$ \pi ^{-1}(y)\times \pi ^{-1}(y)\subseteq \overline {\mathcal{O} }((x_1,x_2),T).$
The proof is complete.
5 A dichotomy theorem on almost proximal extensions
In this section, we show that any almost proximal extension has the following dichotomy theorem: any almost proximal extension of minimal flows is either almost finite-to-one, or almost all fibers contain an uncountable strongly scrambled subset.
Lemma 5.1. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be a distal extension of minimal flows. For any strongly scrambled set K of Y, there is a strongly scrambled set
$\pi : (X,T)\rightarrow (Y,T)$
be a distal extension of minimal flows. For any strongly scrambled set K of Y, there is a strongly scrambled set
![]() $K'$
of X such that
$K'$
of X such that
![]() $\pi |_{K'}: K'\rightarrow K$
is one-to-one.
$\pi |_{K'}: K'\rightarrow K$
is one-to-one.
Proof. Let
![]() $K=\{y_{\alpha }\}_{{\alpha }\in \Lambda }$
, where
$K=\{y_{\alpha }\}_{{\alpha }\in \Lambda }$
, where
![]() $\Lambda $
is an index set. Fix a point
$\Lambda $
is an index set. Fix a point
![]() $y_0\in K$
. By the assumption,
$y_0\in K$
. By the assumption,
![]() $K\subseteq P[y_0].$
Then by Proposition 2.4 for each
$K\subseteq P[y_0].$
Then by Proposition 2.4 for each
![]() ${\alpha }\in \Lambda $
, there is a minimal idempotent
${\alpha }\in \Lambda $
, there is a minimal idempotent
![]() $v_{\alpha }\in J(\mathbf {M})$
such that
$v_{\alpha }\in J(\mathbf {M})$
such that
![]() $y_{\alpha }=v_{\alpha } y_0$
. Thus,
$y_{\alpha }=v_{\alpha } y_0$
. Thus,
Since K is a strongly scrambled set, any pair
![]() $(y_{\alpha },y_\beta )$
is a recurrent point of
$(y_{\alpha },y_\beta )$
is a recurrent point of
![]() $(Y\times Y, T)$
and there is some idempotent
$(Y\times Y, T)$
and there is some idempotent
![]() $u_{{\alpha } \beta }\in J(S_T\setminus T)$
such that
$u_{{\alpha } \beta }\in J(S_T\setminus T)$
such that
Now choose a point
![]() $x_0\in \pi ^{-1}(y_0)$
, and let
$x_0\in \pi ^{-1}(y_0)$
, and let
For any
![]() ${\alpha },\beta \in \Lambda $
, since
${\alpha },\beta \in \Lambda $
, since
![]() $v_{\alpha }, v_\beta $
are minimal idempotents, we have
$v_{\alpha }, v_\beta $
are minimal idempotents, we have
and hence
![]() $(v_{\alpha } x_0, v_\beta x_0) \in P(X,T)$
. By
$(v_{\alpha } x_0, v_\beta x_0) \in P(X,T)$
. By
![]() $u_{{\alpha } \beta } y_{\alpha } = y_{\alpha }$
, we have
$u_{{\alpha } \beta } y_{\alpha } = y_{\alpha }$
, we have
![]() $\pi ( u_{{\alpha } \beta } v_{\alpha } x_0)=u_{{\alpha } \beta } y_{\alpha } = y_{\alpha }= \pi ( v_{\alpha } x_0)$
. Since
$\pi ( u_{{\alpha } \beta } v_{\alpha } x_0)=u_{{\alpha } \beta } y_{\alpha } = y_{\alpha }= \pi ( v_{\alpha } x_0)$
. Since
![]() $\pi $
is distal, it follows that
$\pi $
is distal, it follows that
![]() $u_{{\alpha } \beta } v_{\alpha } x_0 =v_{\alpha } x_0$
. Similarly, we have
$u_{{\alpha } \beta } v_{\alpha } x_0 =v_{\alpha } x_0$
. Similarly, we have
![]() $u_{{\alpha } \beta }v_\beta x_0=v_\beta x_0$
. So
$u_{{\alpha } \beta }v_\beta x_0=v_\beta x_0$
. So
That is,
![]() $(v_{\alpha } x_0, v_\beta x_0)$
is a recurrent point of
$(v_{\alpha } x_0, v_\beta x_0)$
is a recurrent point of
![]() $(X\times X,T)$
. Thus,
$(X\times X,T)$
. Thus,
![]() $K'$
is a strongly scrambled subset of X. As
$K'$
is a strongly scrambled subset of X. As
![]() $\pi $
is distal and each pair in
$\pi $
is distal and each pair in
![]() $K'$
is proximal,
$K'$
is proximal,
![]() $\pi |_{K'}: K'\rightarrow K$
is one-to-one. The proof is complete.
$\pi |_{K'}: K'\rightarrow K$
is one-to-one. The proof is complete.
Theorem 5.2. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an almost proximal extension of minimal flows. Then one of the following holds:
$\pi : (X,T)\rightarrow (Y,T)$
be an almost proximal extension of minimal flows. Then one of the following holds:
-
(1)
 $\pi $
is almost finite-to-one;
$\pi $
is almost finite-to-one; -
(2) there is a residual subset
 $Y_0\subseteq Y$
such that for every
$Y_0\subseteq Y$
such that for every
 $y\in Y_0$
, the fiber
$y\in Y_0$
, the fiber
 $\pi ^{-1}(y)$
contains an uncountable strongly scrambled set.
$\pi ^{-1}(y)$
contains an uncountable strongly scrambled set.
Proof. We show that if
![]() $\pi $
is not almost finite-to-one, then there is a residual subset
$\pi $
is not almost finite-to-one, then there is a residual subset
![]() $Y_0\subseteq Y$
such that for every
$Y_0\subseteq Y$
such that for every
![]() $y\in Y_0$
, the fiber
$y\in Y_0$
, the fiber
![]() $\pi ^{-1}(y)$
contains an uncountable strongly scrambled set.
$\pi ^{-1}(y)$
contains an uncountable strongly scrambled set.
Let
![]() $y_0\in Y$
and
$y_0\in Y$
and
![]() $u\in J(\mathbf {M})$
such that
$u\in J(\mathbf {M})$
such that
![]() $uy_0=y_0$
and let
$uy_0=y_0$
and let
![]() $u\pi ^{-1}(y_0)=\{x_1,x_2,\ldots , x_n\}$
for some
$u\pi ^{-1}(y_0)=\{x_1,x_2,\ldots , x_n\}$
for some
![]() $n\in \mathbb N$
. Let
$n\in \mathbb N$
. Let
![]() $z_0=(x_1,x_2,\ldots , x_n)\in X^n$
. Then
$z_0=(x_1,x_2,\ldots , x_n)\in X^n$
. Then
![]() $z_0$
is a minimal point of
$z_0$
is a minimal point of
![]() $(X^n,T)$
. Let
$(X^n,T)$
. Let
Then
![]() $(X^\#,T)$
is a minimal flow. Let
$(X^\#,T)$
is a minimal flow. Let

We divide the proof into several steps.
Step 1.
![]() $\widetilde {\pi }$
is regular. Let
$\widetilde {\pi }$
is regular. Let
![]() $p_1, p_2\in \mathbf {M}$
such that
$p_1, p_2\in \mathbf {M}$
such that
![]() $\widetilde {\pi }(p_1z_0)=\widetilde {\pi }(p_2z_0)$
and
$\widetilde {\pi }(p_1z_0)=\widetilde {\pi }(p_2z_0)$
and
![]() $(p_1z_0, p_2z_0)$
is minimal. Let
$(p_1z_0, p_2z_0)$
is minimal. Let
![]() $v\in J(\mathbf {M})$
such that
$v\in J(\mathbf {M})$
such that
![]() $v(p_1z_0,p_2z_0)=(p_1z_0,p_2z_0)$
. Since
$v(p_1z_0,p_2z_0)=(p_1z_0,p_2z_0)$
. Since
![]() $\widetilde {\pi }(p_1 z_0)=\widetilde {\pi }(p_2z_0)$
, we have that
$\widetilde {\pi }(p_1 z_0)=\widetilde {\pi }(p_2z_0)$
, we have that
![]() $p_1y_0 = p_2y_0$
. Hence,
$p_1y_0 = p_2y_0$
. Hence,
![]() $up_1^{-1}p_2y_0=y_0$
, where
$up_1^{-1}p_2y_0=y_0$
, where
![]() $p^{-1}_1$
is defined after Proposition 2.2. Now let
$p^{-1}_1$
is defined after Proposition 2.2. Now let
First, we verify that
![]() $\chi $
is well defined. Let
$\chi $
is well defined. Let
![]() $p,q\in \mathbf {M}$
such that
$p,q\in \mathbf {M}$
such that
![]() $pz_0=qz_0$
. Since
$pz_0=qz_0$
. Since
![]() $z_0=(x_1,x_2,\ldots , x_n)$
, it follows that
$z_0=(x_1,x_2,\ldots , x_n)$
, it follows that
![]() $px_j=qx_j, 1\le j\le n$
. By
$px_j=qx_j, 1\le j\le n$
. By
![]() $up_1^{-1}p_2\pi ^{-1}(y_0)=u\pi ^{-1}(y_0)$
,
$up_1^{-1}p_2\pi ^{-1}(y_0)=u\pi ^{-1}(y_0)$
,
Thus,
that is,
![]() $\chi (pz_0)=p(up_1^{-1}p_2)z_0=q(up_1^{-1}p_2)z_0=\chi (qz_0)$
. That is,
$\chi (pz_0)=p(up_1^{-1}p_2)z_0=q(up_1^{-1}p_2)z_0=\chi (qz_0)$
. That is,
![]() $\chi $
is well defined. As
$\chi $
is well defined. As
![]() $\widetilde {\pi }(\chi (pz_0))=p(up_1^{-1}p_2)y_0=py_0=\widetilde {\pi }(pz_0)$
,
$\widetilde {\pi }(\chi (pz_0))=p(up_1^{-1}p_2)y_0=py_0=\widetilde {\pi }(pz_0)$
,
![]() $\chi \in \mathrm { Aut}_{\widetilde {\pi }}(X^\#,T)$
.
$\chi \in \mathrm { Aut}_{\widetilde {\pi }}(X^\#,T)$
.
Finally, note that
Thus,
![]() $\widetilde {\pi }$
is regular.
$\widetilde {\pi }$
is regular.
Step 2.
![]() $\widetilde {\pi }$
is almost proximal and not almost finite-to-one. Since
$\widetilde {\pi }$
is almost proximal and not almost finite-to-one. Since
![]() $\pi $
is not almost finite-to-one, it is easy to see that
$\pi $
is not almost finite-to-one, it is easy to see that
![]() $\widetilde {\pi }$
is also not almost finite-to-one. Next we show it is almost proximal. We show that
$\widetilde {\pi }$
is also not almost finite-to-one. Next we show it is almost proximal. We show that
![]() $|u\widetilde {\pi }^{-1}(y_0)|<\infty $
. Let
$|u\widetilde {\pi }^{-1}(y_0)|<\infty $
. Let
![]() $pz_0\in u\widetilde {\pi }^{-1}(y_0)$
. Then,
$pz_0\in u\widetilde {\pi }^{-1}(y_0)$
. Then,
![]() $up(x_1,x_2,\ldots , x_n)=upz_0=pz_0=(px_1,px_2,\ldots , px_n)$
. It follows that
$up(x_1,x_2,\ldots , x_n)=upz_0=pz_0=(px_1,px_2,\ldots , px_n)$
. It follows that
Thus,
![]() $(px_1,px_2,\ldots , px_n)$
is a permutation of
$(px_1,px_2,\ldots , px_n)$
is a permutation of
![]() $(x_1,x_2,\ldots ,x_n)$
. Hence,
$(x_1,x_2,\ldots ,x_n)$
. Hence,
![]() $|u\widetilde {\pi }^{-1}(y_0)|\le |S_n|<\infty $
, where
$|u\widetilde {\pi }^{-1}(y_0)|\le |S_n|<\infty $
, where
![]() $S_n$
is the symmetric group on
$S_n$
is the symmetric group on
![]() $\{x_1,x_2,\ldots , x_n\}$
. That is,
$\{x_1,x_2,\ldots , x_n\}$
. That is,
![]() $\widetilde {\pi }$
is almost proximal.
$\widetilde {\pi }$
is almost proximal.
Step 3. There is a residual subset
![]() $Y_0\subseteq Y$
such that for every
$Y_0\subseteq Y$
such that for every
![]() $y\in Y_0$
, the fiber
$y\in Y_0$
, the fiber
![]() $\pi ^{-1}(y)$
contains an uncountable strongly scrambled set. Since
$\pi ^{-1}(y)$
contains an uncountable strongly scrambled set. Since
![]() $\widetilde {\pi }$
is regular and almost proximal, by Theorem 3.14, there is a finite-to-one equicontinuous extension
$\widetilde {\pi }$
is regular and almost proximal, by Theorem 3.14, there is a finite-to-one equicontinuous extension
![]() $\phi : X^\#\rightarrow Y^\#$
and a proximal extension
$\phi : X^\#\rightarrow Y^\#$
and a proximal extension
![]() $\pi ^\#: Y^\#\rightarrow Y$
such that
$\pi ^\#: Y^\#\rightarrow Y$
such that
![]() $\widetilde {\pi }=\pi ^\#\circ \phi $
.
$\widetilde {\pi }=\pi ^\#\circ \phi $
.

Since
![]() $\widetilde {\pi }$
is not almost finite-to-one,
$\widetilde {\pi }$
is not almost finite-to-one,
![]() $\pi ^\#$
is proximal but not almost one-to-one. By Theorem 4.8, there is a residual subset
$\pi ^\#$
is proximal but not almost one-to-one. By Theorem 4.8, there is a residual subset
![]() $Y_0\subseteq Y$
such that for every
$Y_0\subseteq Y$
such that for every
![]() $y\in Y_0$
, the fiber
$y\in Y_0$
, the fiber
![]() $(\pi ^\#)^{-1}(y)$
contains a countable strongly scrambled set
$(\pi ^\#)^{-1}(y)$
contains a countable strongly scrambled set
![]() $K^{\prime }_y$
. Since
$K^{\prime }_y$
. Since
![]() $\phi $
is distal, by Lemma 5.1, there is a countable strongly scrambled set
$\phi $
is distal, by Lemma 5.1, there is a countable strongly scrambled set
![]() $K^\#_y$
such that
$K^\#_y$
such that
![]() $\phi (K^\#_y)=K^{\prime }_y$
. Note that
$\phi (K^\#_y)=K^{\prime }_y$
. Note that
![]() $K^\#_y\subseteq X^\#\subseteq X^n$
. Let
$K^\#_y\subseteq X^\#\subseteq X^n$
. Let
![]() $K_j=\pi _j(K^\#_y), 1\le j\le n$
, where
$K_j=\pi _j(K^\#_y), 1\le j\le n$
, where
![]() $\pi _j$
is the projection from
$\pi _j$
is the projection from
![]() $X^n$
to jth coordinate. Since
$X^n$
to jth coordinate. Since
there is some
![]() $j_0\in \{1,2,\ldots , n\}$
such that
$j_0\in \{1,2,\ldots , n\}$
such that
![]() $|K_{j_0}|$
is uncountable. Since
$|K_{j_0}|$
is uncountable. Since
![]() $K^\#_y$
is a strongly scrambled set of
$K^\#_y$
is a strongly scrambled set of
![]() $X^\#$
,
$X^\#$
,
![]() $K_{j_0}$
is a strongly scrambled set of X. As the diagram is commutative, it is easy to check that
$K_{j_0}$
is a strongly scrambled set of X. As the diagram is commutative, it is easy to check that
![]() $K_{j_0}\subseteq \pi ^{-1}(y)$
. The proof is complete.
$K_{j_0}\subseteq \pi ^{-1}(y)$
. The proof is complete.
6 Examples
Since there are no non-trivial proximal minimal flows under abelian group actions [Reference Glasner17, Ch. II, Theorem 3.4], it is not easy to construct a proximal but not almost one-to-one extension of minimal flows. In fact, this was a question by Furstenberg several years ago. Using category method, Glasner and Weiss constructed the first of this kind of extensions of minimal flows and gave a positive answer to this question. In this section, using methods in [Reference C̆iklová-Mlíchová7], we give explicit examples of proximal but not almost one-to-one extensions. And examples constructed are uniformly rigid.
In this section, first we briefly introduce Glasner and Weiss’ results, which will be used later. For Glasner and Weiss’ methods, refer to [Reference Glasner and Weiss19] for more details. Then we show how to give explicit examples of almost proximal but not almost finite-to-one extensions.
6.1 Glasner and Weiss’ results
Let
![]() $(Y,f)$
be a minimal discrete flow and Z be a compact metric space with metric
$(Y,f)$
be a minimal discrete flow and Z be a compact metric space with metric
![]() $d_Z$
. Let
$d_Z$
. Let
![]() $H(Z,Z)$
be the space of all homeomorphisms of Z equipped with the metric
$H(Z,Z)$
be the space of all homeomorphisms of Z equipped with the metric
With this metric,
![]() $H(Z,Z)$
is a complete metric space and a topological group. Let
$H(Z,Z)$
is a complete metric space and a topological group. Let
![]() $X=Y\times Z$
. Let
$X=Y\times Z$
. Let
![]() $H_s(X,X)$
be the subspace of
$H_s(X,X)$
be the subspace of
![]() $H(X,X)$
which consists of homeomorphisms which fix all subspace of X of the form
$H(X,X)$
which consists of homeomorphisms which fix all subspace of X of the form
![]() $\{y\}\times Z, y\in Y$
. Such a homeomorphism G is determined by a continuous map
$\{y\}\times Z, y\in Y$
. Such a homeomorphism G is determined by a continuous map
![]() ${\alpha }: Y\rightarrow H(Z,Z)$
, by
${\alpha }: Y\rightarrow H(Z,Z)$
, by
![]() $G(y,z)=(y, {\alpha }(y)(z))$
. Put
$G(y,z)=(y, {\alpha }(y)(z))$
. Put
(Here, f is identified with
![]() $f\times \mathrm {id}_Z,$
where
$f\times \mathrm {id}_Z,$
where
![]() $\mathrm {id}_Z$
is the identity map on
$\mathrm {id}_Z$
is the identity map on
![]() $Z.$
)
$Z.$
)
If
![]() $\mathcal {G}$
is a subgroup of
$\mathcal {G}$
is a subgroup of
![]() $H(Z,Z)$
, let
$H(Z,Z)$
, let
![]() $\mathcal {G}_s\subseteq H_s(X,X)$
be the subgroup of those elements of
$\mathcal {G}_s\subseteq H_s(X,X)$
be the subgroup of those elements of
![]() $H_s(X,X)$
which come from cocycles (see definition below) of
$H_s(X,X)$
which come from cocycles (see definition below) of
![]() $\mathcal {G}$
. That is,
$\mathcal {G}$
. That is,
Let
Theorem 6.1. [Reference Glasner and Weiss19, Theorem 1]
Let
![]() $\mathcal {G}$
be a pathwise connected subgroup of
$\mathcal {G}$
be a pathwise connected subgroup of
![]() $H(Z,Z)$
such that
$H(Z,Z)$
such that
![]() $(Z,\mathcal {G})$
is a minimal flow. If
$(Z,\mathcal {G})$
is a minimal flow. If
![]() $(Y,f)$
is minimal, then for a residual subset
$(Y,f)$
is minimal, then for a residual subset
![]() $\mathcal {R}\subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
$\mathcal {R}\subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
![]() $(X,F)$
is a minimal flow for every
$(X,F)$
is a minimal flow for every
![]() $F\in \mathcal {R}$
.
$F\in \mathcal {R}$
.
Theorem 6.2. [Reference Glasner and Weiss19, Theorem 3]
Let
![]() $\mathcal {G}$
be a pathwise connected subgroup of
$\mathcal {G}$
be a pathwise connected subgroup of
![]() $H(Z,Z)$
with the following property: for every pair of points
$H(Z,Z)$
with the following property: for every pair of points
![]() $z_1,z_2\in Z$
, there exist neighborhoods U and V of
$z_1,z_2\in Z$
, there exist neighborhoods U and V of
![]() $z_1$
and
$z_1$
and
![]() $z_2$
, respectively, such that for every
$z_2$
, respectively, such that for every
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $h\in \mathcal {G}$
with
$h\in \mathcal {G}$
with
![]() $\mathrm {diam}\ (h(U\cup V))<\epsilon $
. Then for a residual subset
$\mathrm {diam}\ (h(U\cup V))<\epsilon $
. Then for a residual subset
![]() $\mathcal {R}\subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
$\mathcal {R}\subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
![]() $(X,F)$
is a proximal extension of
$(X,F)$
is a proximal extension of
![]() $(Y,f)$
for every
$(Y,f)$
for every
![]() $F \in \mathcal {R}$
.
$F \in \mathcal {R}$
.
According to [Reference Glasner and Weiss19, §1], if we choose
![]() $Z=\mathbf {P}^n, n\ge 1$
to be the projective n-space, and let
$Z=\mathbf {P}^n, n\ge 1$
to be the projective n-space, and let
![]() $\mathcal {G}$
be a pathwise connected component of
$\mathcal {G}$
be a pathwise connected component of
![]() $\mathrm {id}_Z$
in
$\mathrm {id}_Z$
in
![]() $H(Z,Z)$
, then
$H(Z,Z)$
, then
![]() $\mathcal {G}$
satisfies the conditions of Theorems 6.1 and 6.2. Thus, for an arbitrary minimal infinite flow
$\mathcal {G}$
satisfies the conditions of Theorems 6.1 and 6.2. Thus, for an arbitrary minimal infinite flow
![]() $(Y,f)$
, there are many minimal homeomorphisms of
$(Y,f)$
, there are many minimal homeomorphisms of
![]() $Y\times Z$
which are proximal but not almost one-to-one extensions of
$Y\times Z$
which are proximal but not almost one-to-one extensions of
![]() $(Y,f)$
.
$(Y,f)$
.
6.2 Skew-product
Let
![]() $(Y,f)$
be a discrete flow and
$(Y,f)$
be a discrete flow and
![]() $(Z,d_Z)$
a compact metric space. Denote the set of all the homeomorphisms of Z to Z with
$(Z,d_Z)$
a compact metric space. Denote the set of all the homeomorphisms of Z to Z with
![]() $H(Z,Z)$
. For
$H(Z,Z)$
. For
![]() $\varphi _1, \varphi _2\in H(Z,Z)$
, set
$\varphi _1, \varphi _2\in H(Z,Z)$
, set
Assume
![]() $X=Y\times Z$
and let
$X=Y\times Z$
and let
![]() $\rho _X $
denote the max-metric on the product space
$\rho _X $
denote the max-metric on the product space
![]() $Y\times Z$
,
$Y\times Z$
,
where
![]() $d_Y$
is the metric of Y.
$d_Y$
is the metric of Y.
A continuous map
![]() $\sigma : Y\rightarrow H(Z,Z)$
is called a cocycle. By a given cocycle
$\sigma : Y\rightarrow H(Z,Z)$
is called a cocycle. By a given cocycle
![]() $\sigma $
, one can define
$\sigma $
, one can define
The new flow
![]() $(X,f_\sigma )$
is called a skew-product flow.
$(X,f_\sigma )$
is called a skew-product flow.
For
![]() $(y,z)\in X$
, set
$(y,z)\in X$
, set
![]() $f^n_\sigma (y,z)= (f^n (y), \sigma _n(y)(z))$
, where
$f^n_\sigma (y,z)= (f^n (y), \sigma _n(y)(z))$
, where
 $$ \begin{align*}\sigma_n(y)= \begin{cases} \sigma(f^{n-1}y)\cdots \sigma(fy)\sigma(y), & n\ge 1; \\ \mathrm{id}_Z, & n=0 ;\\ \sigma(f^ny)^{-1}\cdots \sigma(f^{-2}y)^{-1}\sigma(f^{-1}y)^{-1}, & n<0. \end{cases} \end{align*} $$
$$ \begin{align*}\sigma_n(y)= \begin{cases} \sigma(f^{n-1}y)\cdots \sigma(fy)\sigma(y), & n\ge 1; \\ \mathrm{id}_Z, & n=0 ;\\ \sigma(f^ny)^{-1}\cdots \sigma(f^{-2}y)^{-1}\sigma(f^{-1}y)^{-1}, & n<0. \end{cases} \end{align*} $$
6.3 A cocycle
Let
![]() $Y=Z(2)=\{0,1\}^{\mathbb N}$
with the metric
$Y=Z(2)=\{0,1\}^{\mathbb N}$
with the metric
The map
is defined as follows: for every
![]() ${\alpha } \in Z(2)$
,
${\alpha } \in Z(2)$
,
![]() $\tau ({\alpha })={\alpha } + 10000\ldots $
, where the addition is modulo
$\tau ({\alpha })={\alpha } + 10000\ldots $
, where the addition is modulo
![]() $2$
from the left to right. Obviously,
$2$
from the left to right. Obviously,
![]() $\tau $
is continuous. Moreover, it can be shown that
$\tau $
is continuous. Moreover, it can be shown that
![]() $\tau $
is invertible and
$\tau $
is invertible and
![]() $(Z(2),\tau )$
is an equicontinuous minimal flow. The flow
$(Z(2),\tau )$
is an equicontinuous minimal flow. The flow
![]() $(Z(2),\tau )$
is called an adding machine or odometer. Similarly, one can define
$(Z(2),\tau )$
is called an adding machine or odometer. Similarly, one can define
![]() ${(Z(k)=\{0,1,\ldots , k-1\}^{\mathbb N}, \tau )}$
.
${(Z(k)=\{0,1,\ldots , k-1\}^{\mathbb N}, \tau )}$
.
In the following, an increasing sequence
![]() $\{n_i\}_{i=1}^\infty \subseteq \mathbb N$
is fixed. For any
$\{n_i\}_{i=1}^\infty \subseteq \mathbb N$
is fixed. For any
![]() ${\alpha }\in Z(2)$
,
${\alpha }\in Z(2)$
,
![]() ${\alpha }$
can be written as
${\alpha }$
can be written as
Let
![]() $e: \bigcup _{j=1}^\infty \{0,1\}^j \rightarrow \mathbb Z_+$
be the evaluation function: for
$e: \bigcup _{j=1}^\infty \{0,1\}^j \rightarrow \mathbb Z_+$
be the evaluation function: for
![]() $x=x_1x_2\ldots x_j \in \{0,1\}^j$
,
$x=x_1x_2\ldots x_j \in \{0,1\}^j$
,
For
![]() $n\in \mathbb Z_+$
, if
$n\in \mathbb Z_+$
, if
![]() $x=x_1x_2\ldots x_j \in \{0,1\}^j$
such that
$x=x_1x_2\ldots x_j \in \{0,1\}^j$
such that
![]() $e(x)=n$
, then let
$e(x)=n$
, then let
where
![]() $0^\infty =000\ldots .$
For example,
$0^\infty =000\ldots .$
For example,
![]() $\underline {0}=0^\infty $
,
$\underline {0}=0^\infty $
,
![]() $\underline {2}=010^\infty $
,
$\underline {2}=010^\infty $
,
![]() $\underline {7}=1110^\infty $
.
$\underline {7}=1110^\infty $
.
Let
![]() $Z={\mathbb S}^1=\{\exp (i 2\pi x): 0\le x\le 1\}$
and
$Z={\mathbb S}^1=\{\exp (i 2\pi x): 0\le x\le 1\}$
and
We use
![]() $\Phi $
to construct a cocycle
$\Phi $
to construct a cocycle
![]() $\sigma : Z(2)\rightarrow H({\mathbb S}^1,{\mathbb S}^1)$
:
$\sigma : Z(2)\rightarrow H({\mathbb S}^1,{\mathbb S}^1)$
:
 $$ \begin{align} \sigma({\alpha})= \begin{cases} \varphi^{e({\alpha}^k)}_{k}, & {\alpha}\neq 1^\infty\text{ and }{\alpha}^k\text{ is the first block in}\ (6.1)\ \text{containing at least one zero}\\ &\quad\text{digit;} \\ \mathrm{id}_{{\mathbb S}^1}, & {\alpha} =1^\infty. \end{cases} \end{align} $$
$$ \begin{align} \sigma({\alpha})= \begin{cases} \varphi^{e({\alpha}^k)}_{k}, & {\alpha}\neq 1^\infty\text{ and }{\alpha}^k\text{ is the first block in}\ (6.1)\ \text{containing at least one zero}\\ &\quad\text{digit;} \\ \mathrm{id}_{{\mathbb S}^1}, & {\alpha} =1^\infty. \end{cases} \end{align} $$
Lemma 6.3. If
![]() $\Phi $
satisfies the following condition:
$\Phi $
satisfies the following condition:
then
![]() $\sigma : Z(2)\rightarrow H({\mathbb S}^1,{\mathbb S}^1)$
is continuous and hence it is a cocycle.
$\sigma : Z(2)\rightarrow H({\mathbb S}^1,{\mathbb S}^1)$
is continuous and hence it is a cocycle.
Proof. Let
![]() $\beta _n, {\alpha } \in Z(2)$
such that
$\beta _n, {\alpha } \in Z(2)$
such that
![]() $\beta _n \to {\alpha }, n\to \infty $
. We show that
$\beta _n \to {\alpha }, n\to \infty $
. We show that
![]() $\lim _{n\to \infty } D_{{\mathbb S}^1}(\sigma (\beta _n), \sigma ({\alpha }))=0$
.
$\lim _{n\to \infty } D_{{\mathbb S}^1}(\sigma (\beta _n), \sigma ({\alpha }))=0$
.
If
![]() ${\alpha } \ne 1^\infty $
, then one has
${\alpha } \ne 1^\infty $
, then one has
![]() $\sigma (\beta _n)=\sigma ({\alpha })$
when n is large enough and
$\sigma (\beta _n)=\sigma ({\alpha })$
when n is large enough and
![]() $D_{{\mathbb S}^1}(\sigma (\beta _n), \sigma ({\alpha }))=0$
. Now assume that
$D_{{\mathbb S}^1}(\sigma (\beta _n), \sigma ({\alpha }))=0$
. Now assume that
![]() ${\alpha } =1^\infty $
. For
${\alpha } =1^\infty $
. For
![]() $\beta _n$
, we have that
$\beta _n$
, we have that
![]() $ \beta _n=\beta _n^1 \beta _n^2 \beta _n^3 \ldots $
, where
$ \beta _n=\beta _n^1 \beta _n^2 \beta _n^3 \ldots $
, where
![]() $\beta _n^k$
is a block of
$\beta _n^k$
is a block of
![]() $n_k$
digits of
$n_k$
digits of
![]() $\beta _n$
. Thus,
$\beta _n$
. Thus,
![]() $\sigma (\beta _n)=\varphi _k^{e(\beta _n^k)}$
, where
$\sigma (\beta _n)=\varphi _k^{e(\beta _n^k)}$
, where
![]() $\beta _n^k$
is the first block containing at least one zero digit. Since
$\beta _n^k$
is the first block containing at least one zero digit. Since
![]() $\beta _n\to {\alpha }, n\to \infty $
, and
$\beta _n\to {\alpha }, n\to \infty $
, and
![]() $\lim _{k\to \infty } \max _{0\le j\le 2^{n_k}-2} D_{{\mathbb S}^1}(\varphi ^{j}_k, \mathrm {id}_{{\mathbb S}^1} ) = 0$
, we have that
$\lim _{k\to \infty } \max _{0\le j\le 2^{n_k}-2} D_{{\mathbb S}^1}(\varphi ^{j}_k, \mathrm {id}_{{\mathbb S}^1} ) = 0$
, we have that
That is,
![]() $\sigma $
is continuous.
$\sigma $
is continuous.
Thus, when (C1) is satisfied,
![]() $\sigma $
is a cocycle. Hence, we have a skew product flow
$\sigma $
is a cocycle. Hence, we have a skew product flow
![]() $(X=Z(2)\times {\mathbb S}^1, F_\Phi )$
:
$(X=Z(2)\times {\mathbb S}^1, F_\Phi )$
:
 $$ \begin{align} F_\Phi\triangleq \tau_\sigma: X\rightarrow X, \, F_\Phi({\alpha}, y)=(\tau({\alpha}), \sigma({\alpha}) y)= \begin{cases} (\tau({\alpha}), \varphi^{e({\alpha}^k)}_{k}(y)), & {\alpha}\neq 1^\infty; \\ (\underline{0}, y), & {\alpha} =1^\infty, \end{cases} \end{align} $$
$$ \begin{align} F_\Phi\triangleq \tau_\sigma: X\rightarrow X, \, F_\Phi({\alpha}, y)=(\tau({\alpha}), \sigma({\alpha}) y)= \begin{cases} (\tau({\alpha}), \varphi^{e({\alpha}^k)}_{k}(y)), & {\alpha}\neq 1^\infty; \\ (\underline{0}, y), & {\alpha} =1^\infty, \end{cases} \end{align} $$
where
![]() ${\alpha }^k$
is the first block in (6.1) containing at least one zero digit when
${\alpha }^k$
is the first block in (6.1) containing at least one zero digit when
![]() ${\alpha }\neq 1^\infty $
.
${\alpha }\neq 1^\infty $
.
6.4 The form of
 $F_\Phi ^n$
$F_\Phi ^n$
Let
![]() ${\alpha }={\alpha }^1{\alpha }^2\ldots \in Z(2)$
as in (6.1) and
${\alpha }={\alpha }^1{\alpha }^2\ldots \in Z(2)$
as in (6.1) and
![]() $z_0\in {\mathbb S}^1$
. Let
$z_0\in {\mathbb S}^1$
. Let
We need to know the formula of
![]() $z_n$
for some special n.
$z_n$
for some special n.
For simplicity, we always assume the following conditions hold:
and
First we have a formula for
![]() ${\alpha }= \underline 0$
. By an easy induction, we have the following lemma.
${\alpha }= \underline 0$
. By an easy induction, we have the following lemma.
Lemma 6.4. Let
![]() $(\underline 0 ,y_0) \in Z(2)\times {\mathbb S}^1$
and
$(\underline 0 ,y_0) \in Z(2)\times {\mathbb S}^1$
and
![]() $(\underline n , y_n)=F_\Phi ^n (\underline 0 , y_0)$
. Let
$(\underline n , y_n)=F_\Phi ^n (\underline 0 , y_0)$
. Let
![]() $m_k=2^{n_1+n_2+\cdots +n_k}$
for all
$m_k=2^{n_1+n_2+\cdots +n_k}$
for all
![]() $k\in \mathbb N$
. Then
$k\in \mathbb N$
. Then
and
Now we see the general case. Let
![]() ${\alpha }={\alpha }^1{\alpha }^2\ldots \in Z(2)$
as in (6.1) and
${\alpha }={\alpha }^1{\alpha }^2\ldots \in Z(2)$
as in (6.1) and
![]() $z_0\in {\mathbb S}^1$
. We denote
$z_0\in {\mathbb S}^1$
. We denote
![]() $F^n_\Phi ({\alpha } ,z_0)=(\tau ^n{\alpha },z_n).$
Let
$F^n_\Phi ({\alpha } ,z_0)=(\tau ^n{\alpha },z_n).$
Let
and
By the assumption (C3), one has that
![]() $(\psi _k ^+)^{-1}=\psi ^-_k.$
$(\psi _k ^+)^{-1}=\psi ^-_k.$
By an easy induction, we have the following lemma.
Lemma 6.5. Let
![]() ${\alpha }={\alpha }^1{\alpha }^2\ldots \in Z(2)$
as in (6.1) and
${\alpha }={\alpha }^1{\alpha }^2\ldots \in Z(2)$
as in (6.1) and
![]() $z_0\in {\mathbb S}^1$
. Let
$z_0\in {\mathbb S}^1$
. Let
![]() $F^n_\Phi ({\alpha } ,z_0)=(\tau ^n{\alpha },z_n).$
Let
$F^n_\Phi ({\alpha } ,z_0)=(\tau ^n{\alpha },z_n).$
Let
![]() $m_k=2^{n_1+n_2+\cdots +n_k}$
for all
$m_k=2^{n_1+n_2+\cdots +n_k}$
for all
![]() $k\in \mathbb N$
. Then
$k\in \mathbb N$
. Then
where
![]() $z_{m_k-e({\alpha }^1{\alpha }^2\ldots {\alpha }^k)}=\varphi ^{e({\alpha }^{k+1})}_{k+1}\circ \psi ^-_k\circ \psi ^-_{k-1}\circ \cdots \circ \psi ^-_1 (z_0). $
And
$z_{m_k-e({\alpha }^1{\alpha }^2\ldots {\alpha }^k)}=\varphi ^{e({\alpha }^{k+1})}_{k+1}\circ \psi ^-_k\circ \psi ^-_{k-1}\circ \cdots \circ \psi ^-_1 (z_0). $
And
where
![]() $z_{m_k}=\psi ^+_1\circ \psi ^+_2\circ \cdots \circ \psi ^+_k \circ \varphi ^{e({\alpha }^{k+1})}_{k+1}\circ \psi ^-_k\circ \cdots \circ \psi ^-_1 (z_0).$
$z_{m_k}=\psi ^+_1\circ \psi ^+_2\circ \cdots \circ \psi ^+_k \circ \varphi ^{e({\alpha }^{k+1})}_{k+1}\circ \psi ^-_k\circ \cdots \circ \psi ^-_1 (z_0).$
Remark 6.6. (i) To simplify the calculation, if we require that
 $$ \begin{align*} \varphi^1_k =\varphi ^2_k &=\cdots =\varphi^{2^{n_k -1}-1}_k\triangleq\varphi_k,\\\varphi^{2^{n_k -1}}_k=\varphi^{2^{n_k -1}+1}_k&=\cdots =\varphi^{2^{n_k}-2}\triangleq \varphi^-_k=(\varphi_k)^{-1}, \end{align*} $$
$$ \begin{align*} \varphi^1_k =\varphi ^2_k &=\cdots =\varphi^{2^{n_k -1}-1}_k\triangleq\varphi_k,\\\varphi^{2^{n_k -1}}_k=\varphi^{2^{n_k -1}+1}_k&=\cdots =\varphi^{2^{n_k}-2}\triangleq \varphi^-_k=(\varphi_k)^{-1}, \end{align*} $$
then
![]() $\psi ^+_k=(\varphi _k)^{c_k}, \psi ^-_k=(\varphi ^-_k)^{c_k},$
where
$\psi ^+_k=(\varphi _k)^{c_k}, \psi ^-_k=(\varphi ^-_k)^{c_k},$
where
![]() $c_k=2^{n_k -1}-1-|e({\alpha }^k)-2^{n_k-1}|.$
Thus, (6.10) will be
$c_k=2^{n_k -1}-1-|e({\alpha }^k)-2^{n_k-1}|.$
Thus, (6.10) will be
(ii) By (6.6), (6.9), for
![]() $j<k, 1\leq s<2^{n_{j+1}}$
, we have
$j<k, 1\leq s<2^{n_{j+1}}$
, we have
where
![]() $z_{m_k -e({\alpha }^1{\alpha }^2\ldots {\alpha }^k)+s\cdot m_j}=\varphi ^{s-1}_{j+1}\circ \varphi ^{s-2}_{j+1}\circ \cdots \circ \varphi ^{1}_{j+1} \circ \varphi ^{0}_{j+1}(z_{m_k -e({\alpha }^1{\alpha }^2\ldots {\alpha }^k)}).$
$z_{m_k -e({\alpha }^1{\alpha }^2\ldots {\alpha }^k)+s\cdot m_j}=\varphi ^{s-1}_{j+1}\circ \varphi ^{s-2}_{j+1}\circ \cdots \circ \varphi ^{1}_{j+1} \circ \varphi ^{0}_{j+1}(z_{m_k -e({\alpha }^1{\alpha }^2\ldots {\alpha }^k)}).$
6.5 Uniform rigidity
A discrete flow
![]() $(X,F)$
is rigid if there exists an increasing sequence
$(X,F)$
is rigid if there exists an increasing sequence
![]() $\{n_i\}_{i\in \mathbb N}$
in
$\{n_i\}_{i\in \mathbb N}$
in
![]() $\mathbb N$
such that
$\mathbb N$
such that
![]() $F^{n_i}x$
converges to x as i goes to infinity for every
$F^{n_i}x$
converges to x as i goes to infinity for every
![]() $x\in X$
(that is,
$x\in X$
(that is,
![]() $F^{n_i}$
converges pointwisely to the identity map). A flow
$F^{n_i}$
converges pointwisely to the identity map). A flow
![]() $(X, F)$
is uniformly rigid if there exists an increasing sequence
$(X, F)$
is uniformly rigid if there exists an increasing sequence
![]() $\{n_i\}_{i\in \mathbb N}$
in
$\{n_i\}_{i\in \mathbb N}$
in
![]() $\mathbb N$
such that
$\mathbb N$
such that
![]() $\sup \nolimits _{x\in X} d(x,F^{n_i}x) \to 0$
as i goes to infinity (that is,
$\sup \nolimits _{x\in X} d(x,F^{n_i}x) \to 0$
as i goes to infinity (that is,
![]() $F^{n_i}$
converges uniformly to the identity map). Refer to [Reference Glasner and Maon18] for more information about topological rigidity.
$F^{n_i}$
converges uniformly to the identity map). Refer to [Reference Glasner and Maon18] for more information about topological rigidity.
Lemma 6.7. Let
![]() $\mathcal F$
be a finite subset of
$\mathcal F$
be a finite subset of
![]() $H(X,X)$
, where
$H(X,X)$
, where
![]() $(X,\rho _X)$
is a compact metric space. Then for any
$(X,\rho _X)$
is a compact metric space. Then for any
![]() $\epsilon>0$
, there is a
$\epsilon>0$
, there is a
![]() ${\delta }>0$
such that for any continuous map
${\delta }>0$
such that for any continuous map
![]() $h: X\rightarrow X$
with
$h: X\rightarrow X$
with
![]() $D_X(h,\mathrm {id}_X)<{\delta }$
, we have
$D_X(h,\mathrm {id}_X)<{\delta }$
, we have
Proof. For any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\delta>0$
such that whenever
$\delta>0$
such that whenever
![]() $\rho _X(x_1,x_2)<\delta ,$
$\rho _X(x_1,x_2)<\delta ,$
Then for continuous map
![]() $h: X\rightarrow X$
with
$h: X\rightarrow X$
with
![]() $D(h,\mathrm {id}_X)<\delta $
, we have that
$D(h,\mathrm {id}_X)<\delta $
, we have that
It follows that
That is,
The proof is complete.
Proposition 6.8. Suppose that
![]() $\Phi $
satisfies (C1), (C2), and (C3). Then the skew product flow
$\Phi $
satisfies (C1), (C2), and (C3). Then the skew product flow
![]() $(Z(2)\times {\mathbb S}^1,F_\Phi )$
is uniformly rigid.
$(Z(2)\times {\mathbb S}^1,F_\Phi )$
is uniformly rigid.
Proof. By (6.10), for any
![]() $({\alpha }, z_0)\in X=Z(2)\times {\mathbb S}^1 ,$
we get
$({\alpha }, z_0)\in X=Z(2)\times {\mathbb S}^1 ,$
we get
 $$ \begin{align*}&F^{m_k}_\Phi ({\alpha},z_0)\\&\quad=({\alpha}^1{\alpha}^2\ldots {\alpha}^k\tau({\alpha}^{k+1}{\alpha}^{k+2}\ldots), \psi({\alpha}^1{\alpha}^2\ldots {\alpha}^k)\varphi ^{e({\alpha}^{k+1})} _{k+1}\psi^{-1}({\alpha}^1{\alpha}^2\ldots {\alpha}^k)(z_0)),\end{align*} $$
$$ \begin{align*}&F^{m_k}_\Phi ({\alpha},z_0)\\&\quad=({\alpha}^1{\alpha}^2\ldots {\alpha}^k\tau({\alpha}^{k+1}{\alpha}^{k+2}\ldots), \psi({\alpha}^1{\alpha}^2\ldots {\alpha}^k)\varphi ^{e({\alpha}^{k+1})} _{k+1}\psi^{-1}({\alpha}^1{\alpha}^2\ldots {\alpha}^k)(z_0)),\end{align*} $$
where
![]() $\psi ({\alpha }^1{\alpha }^2\ldots {\alpha }^k)=\psi ^+_1\circ \psi ^+_2\circ \cdots \circ \psi ^+_k .$
By the assumption (C1) that
$\psi ({\alpha }^1{\alpha }^2\ldots {\alpha }^k)=\psi ^+_1\circ \psi ^+_2\circ \cdots \circ \psi ^+_k .$
By the assumption (C1) that
and Lemma 6.7, we have that
that is,
![]() $(Z(2)\times {\mathbb S}^1,F_\Phi )$
is uniformly rigid.
$(Z(2)\times {\mathbb S}^1,F_\Phi )$
is uniformly rigid.
6.6 Minimality
Now we specify the homeomorphisms
![]() $\{\varphi _{2k-1}^j: 1\le j\le 2^{n_{2k-1}}-2\}_{k=1}^\infty $
to make the flow
$\{\varphi _{2k-1}^j: 1\le j\le 2^{n_{2k-1}}-2\}_{k=1}^\infty $
to make the flow
![]() $(Z(2)\times {\mathbb S}^1,F_\Phi )$
minimal. Let
$(Z(2)\times {\mathbb S}^1,F_\Phi )$
minimal. Let
 $$ \begin{align} \varphi_{2k-1}^j(z)= \begin{cases} \exp{(i\theta_k)}\cdot z, & 1\le j \le 2^{n_{2k-1}-1}-1; \\ \exp{(-i\theta_k)}\cdot z, & 2^{n_{2k-1}-1}-1<j\le 2^{n_{2k-1}}-2 , \end{cases} \end{align} $$
$$ \begin{align} \varphi_{2k-1}^j(z)= \begin{cases} \exp{(i\theta_k)}\cdot z, & 1\le j \le 2^{n_{2k-1}-1}-1; \\ \exp{(-i\theta_k)}\cdot z, & 2^{n_{2k-1}-1}-1<j\le 2^{n_{2k-1}}-2 , \end{cases} \end{align} $$
where
![]() $\theta _k = {2\pi }/({2^{n_{2k-1}-1}-1})$
. That is,
$\theta _k = {2\pi }/({2^{n_{2k-1}-1}-1})$
. That is,
![]() $\varphi ^{j}_{2k-1}$
is a rotation of
$\varphi ^{j}_{2k-1}$
is a rotation of
![]() ${\mathbb S}^1$
with angle
${\mathbb S}^1$
with angle
![]() $\theta _k$
in the anti-clockwise direction if
$\theta _k$
in the anti-clockwise direction if
![]() $1\le j \le 2^{n_{2k-1}-1}-1$
and in the opposite direction otherwise. We remark that this construction satisfies the assumption (C3), that is,
$1\le j \le 2^{n_{2k-1}-1}-1$
and in the opposite direction otherwise. We remark that this construction satisfies the assumption (C3), that is,
![]() $\psi _{2k-1} =\mathrm {id}.$
$\psi _{2k-1} =\mathrm {id}.$
Proposition 6.9. Suppose that
![]() $\Phi $
satisfies (C1), (C2), (C3), and (C4). Then the skew product flow
$\Phi $
satisfies (C1), (C2), (C3), and (C4). Then the skew product flow
![]() $(Z(2)\times {\mathbb S}^1,F_\Phi )$
is uniformly rigid and minimal.
$(Z(2)\times {\mathbb S}^1,F_\Phi )$
is uniformly rigid and minimal.
Proof. Let
![]() ${\alpha }\in Z(2)$
and
${\alpha }\in Z(2)$
and
![]() ${\mathbb S}^1_{{\alpha }}={{\alpha }}\times {\mathbb S}^1.$
First we show that for any
${\mathbb S}^1_{{\alpha }}={{\alpha }}\times {\mathbb S}^1.$
First we show that for any
![]() $y_0\in {\mathbb S}^1$
,
$y_0\in {\mathbb S}^1$
,
By (6.6), for
![]() $1\le s<2^{n_{2k-1}}$
, one has that
$1\le s<2^{n_{2k-1}}$
, one has that
where
![]() $y_{s\cdot m_{2k-2}}=\varphi ^{s-1}_{2k-1}\circ \varphi ^{s-2}_{2k-1}\circ \cdots \circ \varphi ^1_{2k-1}\circ \varphi ^0_{2k-1}(y_0).$
As a result,
$y_{s\cdot m_{2k-2}}=\varphi ^{s-1}_{2k-1}\circ \varphi ^{s-2}_{2k-1}\circ \cdots \circ \varphi ^1_{2k-1}\circ \varphi ^0_{2k-1}(y_0).$
As a result,
![]() $\{y_{s\cdot m_{2k-2}}: 1\le s \le 2^{n_{2k-1}-1}-1\}$
is
$\{y_{s\cdot m_{2k-2}}: 1\le s \le 2^{n_{2k-1}-1}-1\}$
is
![]() $\theta _k = {2\pi }/({2^{n_{2k-1}-1}-1})-$
dense in
$\theta _k = {2\pi }/({2^{n_{2k-1}-1}-1})-$
dense in
![]() ${\mathbb S}^1$
. (Recall the definition of
${\mathbb S}^1$
. (Recall the definition of
![]() $\epsilon $
-dense subsets: if S is a subset of a metric space, then B in S is
$\epsilon $
-dense subsets: if S is a subset of a metric space, then B in S is
![]() $\epsilon $
-dense in S for given
$\epsilon $
-dense in S for given
![]() $\epsilon>0$
if for any
$\epsilon>0$
if for any
![]() $s\in S$
, there is
$s\in S$
, there is
![]() $b\in B$
such that the distance between s and b is
$b\in B$
such that the distance between s and b is
![]() $<\epsilon $
.) Moreover, for any
$<\epsilon $
.) Moreover, for any
![]() $y\in {\mathbb S}^1,$
there exists
$y\in {\mathbb S}^1,$
there exists
![]() $1\le s_k\le 2^{n_{2k-1}-1}-1$
such that
$1\le s_k\le 2^{n_{2k-1}-1}-1$
such that
Thus,
Thus,
![]() ${\mathbb S}^1_{\underline 0} \subseteq \overline {\mathcal{O} }((\underline 0,y_0),F_\Phi ).$
Since
${\mathbb S}^1_{\underline 0} \subseteq \overline {\mathcal{O} }((\underline 0,y_0),F_\Phi ).$
Since
![]() $F^n_\Phi ({\mathbb S}^1_{\underline 0})={\mathbb S}^1_{\underline n},$
we have
$F^n_\Phi ({\mathbb S}^1_{\underline 0})={\mathbb S}^1_{\underline n},$
we have
 $$ \begin{align*}Z(2)\times {\mathbb S}^1=\overline{\bigcup_{n\in \mathbb Z _{+}} {\mathbb S}^1_{\underline n}} \subseteq \overline{\mathcal{O}}((\underline 0,y_0),F_\Phi).\end{align*} $$
$$ \begin{align*}Z(2)\times {\mathbb S}^1=\overline{\bigcup_{n\in \mathbb Z _{+}} {\mathbb S}^1_{\underline n}} \subseteq \overline{\mathcal{O}}((\underline 0,y_0),F_\Phi).\end{align*} $$
Thus,
Now we show that for any
![]() $({\alpha } ,z_0 )\in Z(2)\times {\mathbb S}^1,$
one has
$({\alpha } ,z_0 )\in Z(2)\times {\mathbb S}^1,$
one has
As
![]() $(Z(2),\tau )$
is minimal, there exists some
$(Z(2),\tau )$
is minimal, there exists some
![]() $\{p_k\}$
such that
$\{p_k\}$
such that
Without loss of generality, we may assume that
for some
![]() $y_0 \in {\mathbb S}^1.$
Thus,
$y_0 \in {\mathbb S}^1.$
Thus,
![]() $Z(2)\times {\mathbb S}^1=\overline {\mathcal{O} }( (\underline 0, y_0),F_\Phi ) \subseteq \overline {\mathcal{O} } (({\alpha } , z_0),F_\Phi ).$
Thus,
$Z(2)\times {\mathbb S}^1=\overline {\mathcal{O} }( (\underline 0, y_0),F_\Phi ) \subseteq \overline {\mathcal{O} } (({\alpha } , z_0),F_\Phi ).$
Thus,
Hence,
![]() $(Z(2)\times {\mathbb S}^1,F_\Phi )$
is minimal. Moreover, by Proposition 6.8, it is uniformly rigid. The proof is complete.
$(Z(2)\times {\mathbb S}^1,F_\Phi )$
is minimal. Moreover, by Proposition 6.8, it is uniformly rigid. The proof is complete.
6.7 Proximality
In this subsection, we specify the homeomorphisms
![]() $\{\varphi _{2k}^j: 1\le j\le 2^{n_{2k}}-2\}_{k=1}^\infty $
to make the extension
$\{\varphi _{2k}^j: 1\le j\le 2^{n_{2k}}-2\}_{k=1}^\infty $
to make the extension
![]() $\pi : (Z(2)\times {\mathbb S}^1, F_\Phi )\to (Z(2),\tau ), \ ({\alpha } , z_0)\mapsto {\alpha }$
to be proximal. Recall that
$\pi : (Z(2)\times {\mathbb S}^1, F_\Phi )\to (Z(2),\tau ), \ ({\alpha } , z_0)\mapsto {\alpha }$
to be proximal. Recall that
![]() ${\mathbb S}^1=\{\exp (i 2\pi x): 0\le x<1\}$
. Let
${\mathbb S}^1=\{\exp (i 2\pi x): 0\le x<1\}$
. Let
![]() $\varphi _{2k}^j: {\mathbb S}^1\rightarrow {\mathbb S}^1$
be defined as follows:
$\varphi _{2k}^j: {\mathbb S}^1\rightarrow {\mathbb S}^1$
be defined as follows:
 $$ \begin{align} \varphi_{2k}^j( \exp(i{2\pi x }))= \begin{cases} \exp(i{2\pi x^{t_k} }), & 1< j \le 2^{n_{2k}-1}-1; \\ \exp( {i2\pi x^{1/{t_k}}}), & 2^{n_{2k}-1}-1<j\le 2^{n_{2k}}-2 , \end{cases} \end{align} $$
$$ \begin{align} \varphi_{2k}^j( \exp(i{2\pi x }))= \begin{cases} \exp(i{2\pi x^{t_k} }), & 1< j \le 2^{n_{2k}-1}-1; \\ \exp( {i2\pi x^{1/{t_k}}}), & 2^{n_{2k}-1}-1<j\le 2^{n_{2k}}-2 , \end{cases} \end{align} $$
where
![]() $\{t_k\}_{k\in \mathbb N}$
is a decreasing sequence such that
$\{t_k\}_{k\in \mathbb N}$
is a decreasing sequence such that
![]() $t_k>1$
,
$t_k>1$
,
![]() $\lim _{k\to \infty } t_k=1$
and
$\lim _{k\to \infty } t_k=1$
and
![]() $\lim _{k\to \infty } t_k^{2^{n_{2k}}}=+\infty $
. For example,
$\lim _{k\to \infty } t_k^{2^{n_{2k}}}=+\infty $
. For example,
![]() $\{t_k=3^{2^{-{n_{2k}}/{2}}}\}_{ k\in \mathbb N}$
satisfies the condition. Notice that the construction of
$\{t_k=3^{2^{-{n_{2k}}/{2}}}\}_{ k\in \mathbb N}$
satisfies the condition. Notice that the construction of
![]() $\varphi _{2k} ^j$
also satisfies the convention (C3), that is,
$\varphi _{2k} ^j$
also satisfies the convention (C3), that is,
![]() $\psi _{2k}=\mathrm {id}.$
$\psi _{2k}=\mathrm {id}.$
To verify that
![]() $\pi $
is proximal, we begin with the following lemma.
$\pi $
is proximal, we begin with the following lemma.
Lemma 6.10. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If there exists
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If there exists
![]() $y_0 \in Y$
such that for any
$y_0 \in Y$
such that for any
![]() $x_1 , x_2 \in \pi ^{-1} (y_0) , (x_1,x_2)\in P(X,T),$
then
$x_1 , x_2 \in \pi ^{-1} (y_0) , (x_1,x_2)\in P(X,T),$
then
![]() $\pi $
is proximal.
$\pi $
is proximal.
Proof. Let
![]() $(x_1,x_2)\in R_\pi $
and
$(x_1,x_2)\in R_\pi $
and
![]() $\pi (x_1)=\pi (x_2)=y_1 .$
Since
$\pi (x_1)=\pi (x_2)=y_1 .$
Since
![]() $(Y,T)$
is minimal, we can find
$(Y,T)$
is minimal, we can find
![]() $p\in E(X,T) $
such that
$p\in E(X,T) $
such that
So
![]() $px_1,px_2\in \pi ^{-1}(y_0).$
According to the assumption, there exists
$px_1,px_2\in \pi ^{-1}(y_0).$
According to the assumption, there exists
![]() $q\in E(X,T)$
such that
$q\in E(X,T)$
such that
It follows that
Thus,
![]() $\pi $
is proximal.
$\pi $
is proximal.
Proposition 6.11. Suppose that
![]() $\Phi $
satisfies (C2), (C4), and (C5). Then the extension
$\Phi $
satisfies (C2), (C4), and (C5). Then the extension
![]() $\pi : (Z(2)\times {\mathbb S}^1, F_\Phi )\to (Z(2),\tau ), \ ({\alpha } , z)\mapsto {\alpha }$
is a proximal extension of uniformly rigid minimal flows.
$\pi : (Z(2)\times {\mathbb S}^1, F_\Phi )\to (Z(2),\tau ), \ ({\alpha } , z)\mapsto {\alpha }$
is a proximal extension of uniformly rigid minimal flows.
Proof. First notice that (C4) and (C5) imply (C1) and (C3). It follows that
![]() $(Z(2)\times {\mathbb S}^1, F_\Phi )$
is uniformly rigid and minimal by Proposition 6.9.
$(Z(2)\times {\mathbb S}^1, F_\Phi )$
is uniformly rigid and minimal by Proposition 6.9.
By Lemma 6.10, it suffices to show that for arbitrary
![]() $z_0^{(1)}$
,
$z_0^{(1)}$
,
![]() $z_0^{(2)} \in {\mathbb S}^1$
, one has
$z_0^{(2)} \in {\mathbb S}^1$
, one has
Let
![]() $z_0^{(1)}=\exp {(i{2\pi x_1 })}$
,
$z_0^{(1)}=\exp {(i{2\pi x_1 })}$
,
![]() $z_0^{(2)} =\exp {(i{2\pi x_2 })}$
, where
$z_0^{(2)} =\exp {(i{2\pi x_2 })}$
, where
![]() $0\le x_1,x_2<1$
. Let
$0\le x_1,x_2<1$
. Let
![]() $d_{{\mathbb S}^1}$
be the metric of
$d_{{\mathbb S}^1}$
be the metric of
![]() ${\mathbb S}^1$
. Let
${\mathbb S}^1$
. Let
![]() $F^{m}_\Phi ((\underline 0 ,z_0^{(j)}))=(\underline 0 ,z_m^{(j)})$
for
$F^{m}_\Phi ((\underline 0 ,z_0^{(j)}))=(\underline 0 ,z_m^{(j)})$
for
![]() $j=1,2$
and
$j=1,2$
and
![]() $m\in \mathbb N$
. Let
$m\in \mathbb N$
. Let
![]() $m_k=2^{n_1+n_2+\cdots +n_k}$
for all
$m_k=2^{n_1+n_2+\cdots +n_k}$
for all
![]() $k\in \mathbb N$
. Then by Lemma 6.4,
$k\in \mathbb N$
. Then by Lemma 6.4,
 $$ \begin{align*} \lim _{k\to \infty}\kern-1pt d_{{\mathbb S}^1}\kern-0.7pt(z^{(1)}_{2^{n_{2k}-1}\cdot m_{2k-1}}\kern-1pt,z^{(2)}_{2^{n_{2k}-1}\cdot m_{2k-1}}\kern-1.3pt)\kern1.2pt{=}\kern1.2pt\lim _{k\to \infty} \kern-2pt d_{{\mathbb S}^1} (\exp(i{2\pi x_1^{t_k^{(2^{n_{2k}-1}-1)}} }\kern-1pt), \exp(i{2\pi x_2^{t_k^{(2^{n_{2k}-1}-1)}} }\kern-1pt)\kern-0.3pt). \end{align*} $$
$$ \begin{align*} \lim _{k\to \infty}\kern-1pt d_{{\mathbb S}^1}\kern-0.7pt(z^{(1)}_{2^{n_{2k}-1}\cdot m_{2k-1}}\kern-1pt,z^{(2)}_{2^{n_{2k}-1}\cdot m_{2k-1}}\kern-1.3pt)\kern1.2pt{=}\kern1.2pt\lim _{k\to \infty} \kern-2pt d_{{\mathbb S}^1} (\exp(i{2\pi x_1^{t_k^{(2^{n_{2k}-1}-1)}} }\kern-1pt), \exp(i{2\pi x_2^{t_k^{(2^{n_{2k}-1}-1)}} }\kern-1pt)\kern-0.3pt). \end{align*} $$
Since
![]() $\lim _{k\to \infty } t_k^{2^{n_{2k}}}\kern1.2pt{=}+\infty $
and
$\lim _{k\to \infty } t_k^{2^{n_{2k}}}\kern1.2pt{=}+\infty $
and
![]() $0\kern1.2pt{\le}\kern1.2pt x_j\kern1.2pt{<}\kern1.2pt1, j\kern1.2pt{=}\kern1.2pt1,2$
, we have that
$0\kern1.2pt{\le}\kern1.2pt x_j\kern1.2pt{<}\kern1.2pt1, j\kern1.2pt{=}\kern1.2pt1,2$
, we have that
![]() ${\lim _{k\to \infty } x_j^{t_k^{(2^{n_{2k}-1}-1)}}\kern1pt{=}\kern1.5pt0}$
for
${\lim _{k\to \infty } x_j^{t_k^{(2^{n_{2k}-1}-1)}}\kern1pt{=}\kern1.5pt0}$
for
![]() $j=1,2$
. Thus,
$j=1,2$
. Thus,
 $$ \begin{align*} \begin{split} & \lim _{k\to \infty}d_{{\mathbb S}^1}(z^{(1)}_{2^{n_{2k}-1}\cdot m_{2k-1}},z^{(2)}_{2^{n_{2k}-1}\cdot m_{2k-1}})\\ &\quad =\lim _{k\to \infty} d_{{\mathbb S}^1}\kern-2pt (\exp(i{2\pi x_1^{t_k^{(2^{n_{2k}-1}-1)}} }), \exp(i{2\pi x_2^{t_k^{(2^{n_{2k}-1}-1)}} }))\\ &\quad=d_{{\mathbb S}^1}(1,1)=0. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} & \lim _{k\to \infty}d_{{\mathbb S}^1}(z^{(1)}_{2^{n_{2k}-1}\cdot m_{2k-1}},z^{(2)}_{2^{n_{2k}-1}\cdot m_{2k-1}})\\ &\quad =\lim _{k\to \infty} d_{{\mathbb S}^1}\kern-2pt (\exp(i{2\pi x_1^{t_k^{(2^{n_{2k}-1}-1)}} }), \exp(i{2\pi x_2^{t_k^{(2^{n_{2k}-1}-1)}} }))\\ &\quad=d_{{\mathbb S}^1}(1,1)=0. \end{split} \end{align*} $$
In particular,
It follows that
![]() $((\underline 0 ,z_0^{(1)}),(\underline 0 ,z_0^{(2)}))\in P(Z(2)\times {\mathbb S}^1,F_\Phi )$
.
$((\underline 0 ,z_0^{(1)}),(\underline 0 ,z_0^{(2)}))\in P(Z(2)\times {\mathbb S}^1,F_\Phi )$
.
6.8 Proximal extensions and n-weakly mixing extensions
In §4.1, we mentioned that the fact that
![]() $\pi : (X,T)\rightarrow (Y,T)$
is weakly mixing does not imply that
$\pi : (X,T)\rightarrow (Y,T)$
is weakly mixing does not imply that
![]() $\pi $
is totally weakly mixing. In this subsection, we give such examples. The main result of this subsection is the following theorem.
$\pi $
is totally weakly mixing. In this subsection, we give such examples. The main result of this subsection is the following theorem.
Theorem 6.12
-
(1) There are proximal extensions of discrete minimal flows which are weakly mixing but not
 $3$
-weakly mixing.
$3$
-weakly mixing. -
(2) There are proximal extensions of discrete minimal flows which are totally weakly mixing.
Proof of (1) of Theorem 6.12
Suppose that
![]() $\Phi $
satisfies (C2), (C4), and (C5). We show that the extension
$\Phi $
satisfies (C2), (C4), and (C5). We show that the extension
is weakly mixing but not
![]() $3$
-weakly mixing. Since
$3$
-weakly mixing. Since
![]() $\pi $
is open proximal by Proposition 6.11, it is weakly mixing by Theorem 4.6. Now we show that
$\pi $
is open proximal by Proposition 6.11, it is weakly mixing by Theorem 4.6. Now we show that
![]() $\pi $
is not
$\pi $
is not
![]() $3$
-weakly mixing, that is,
$3$
-weakly mixing, that is,
![]() $(R_\pi ^3,F_\Phi ^{(3)})$
is not transitive.
$(R_\pi ^3,F_\Phi ^{(3)})$
is not transitive.
We may regard
![]() $R_\pi ^3$
as
$R_\pi ^3$
as
![]() $Z(2)\times {\mathbb S}^1 \times {\mathbb S}^1\times {\mathbb S}^1.$
Suppose
$Z(2)\times {\mathbb S}^1 \times {\mathbb S}^1\times {\mathbb S}^1.$
Suppose
![]() $(R_\pi ^3,F_\Phi ^{(3)})$
is transitive, and let
$(R_\pi ^3,F_\Phi ^{(3)})$
is transitive, and let
![]() $({\alpha },x_1,x_2,x_3)\in Z(2)\times {\mathbb S}^1 \times {\mathbb S}^1\times {\mathbb S}^1$
be a transitive point. Let
$({\alpha },x_1,x_2,x_3)\in Z(2)\times {\mathbb S}^1 \times {\mathbb S}^1\times {\mathbb S}^1$
be a transitive point. Let
![]() $y_1, y_2,y_3$
be distinct points of
$y_1, y_2,y_3$
be distinct points of
![]() ${\mathbb S}^1$
and
${\mathbb S}^1$
and
![]() $\beta \in Z(2)$
. Then
$\beta \in Z(2)$
. Then
![]() $(\beta , y_1,y_2,y_3)$
is in the orbit closure of the transitive point
$(\beta , y_1,y_2,y_3)$
is in the orbit closure of the transitive point
![]() $({\alpha },x_1,x_2,x_3)$
. By the construction of
$({\alpha },x_1,x_2,x_3)$
. By the construction of
![]() $\Phi $
((C4) and (C5)),
$\Phi $
((C4) and (C5)),
![]() $F_\Phi $
preserves orientation, that is, for all
$F_\Phi $
preserves orientation, that is, for all
![]() ${\alpha }\in Z(2)$
,
${\alpha }\in Z(2)$
,
![]() $F_\Phi $
maps
$F_\Phi $
maps
![]() $\{{\alpha }\}\times {\mathbb S}^1$
to
$\{{\alpha }\}\times {\mathbb S}^1$
to
![]() $\{\tau {\alpha }\}\times {\mathbb S}^1$
such that it sends the unit circle with the anti-clockwise orientation into the unit circle with the anti-clockwise orientation. It follows that
$\{\tau {\alpha }\}\times {\mathbb S}^1$
such that it sends the unit circle with the anti-clockwise orientation into the unit circle with the anti-clockwise orientation. It follows that
![]() $(\beta , y_1,y_3,y_2)$
can not be in the orbit closure of the transitive point
$(\beta , y_1,y_3,y_2)$
can not be in the orbit closure of the transitive point
![]() $({\alpha },x_1,x_2,x_3)$
. Thus,
$({\alpha },x_1,x_2,x_3)$
. Thus,
![]() $(R_\pi ^3,F_\Phi ^{(3)}) $
is not transitive.
$(R_\pi ^3,F_\Phi ^{(3)}) $
is not transitive.
For the proof of (2) of Theorem 6.12, we need some preparations. We use the notation in §6.1.
Theorem 6.13. [Reference Glasner and Weiss19, Theorem 4]
Let
![]() $\mathcal {G}$
be a pathwise connected subgroup of
$\mathcal {G}$
be a pathwise connected subgroup of
![]() $H(Z,Z)$
such that
$H(Z,Z)$
such that
![]() $(Z,\mathcal {G})$
is a weakly mixing flow. Then for a residual subset
$(Z,\mathcal {G})$
is a weakly mixing flow. Then for a residual subset
![]() $\mathcal {R}\subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
$\mathcal {R}\subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
![]() $(X,F)$
is a weakly mixing extension of
$(X,F)$
is a weakly mixing extension of
![]() $(Y,f)$
for every
$(Y,f)$
for every
![]() $F\in \mathcal {R}$
.
$F\in \mathcal {R}$
.
By the same proof of [Reference Glasner and Weiss19, Theorem 4], we can show the following: if
![]() $\mathcal {G}$
is a pathwise connected subgroup of
$\mathcal {G}$
is a pathwise connected subgroup of
![]() $H(Z,Z)$
such that
$H(Z,Z)$
such that
![]() $(Z^n,\mathcal {G})$
is a transitive flow, then for a residual subset
$(Z^n,\mathcal {G})$
is a transitive flow, then for a residual subset
![]() $\mathcal {R}_n \subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
$\mathcal {R}_n \subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
![]() $(X,F)$
is an n-weakly mixing extension of
$(X,F)$
is an n-weakly mixing extension of
![]() $(Y,f)$
for every
$(Y,f)$
for every
![]() $F\in \mathcal {R}_n$
. Let
$F\in \mathcal {R}_n$
. Let
![]() ${\mathcal R}=\bigcap _{n=2}^\infty {\mathcal R}_n$
. Then we have the following result which slightly generalizes Theorem 6.13.
${\mathcal R}=\bigcap _{n=2}^\infty {\mathcal R}_n$
. Then we have the following result which slightly generalizes Theorem 6.13.
Theorem 6.14. Let
![]() $\mathcal {G}$
be a pathwise connected subgroup of
$\mathcal {G}$
be a pathwise connected subgroup of
![]() $H(Z,Z)$
such that
$H(Z,Z)$
such that
![]() $(Z,\mathcal {G})$
is a flow such that
$(Z,\mathcal {G})$
is a flow such that
![]() $(Z^n, \mathcal {G})$
is transitive for all
$(Z^n, \mathcal {G})$
is transitive for all
![]() $n\ge 2$
. Then for a residual subset
$n\ge 2$
. Then for a residual subset
![]() $\mathcal {R}\subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
$\mathcal {R}\subseteq \overline {\mathcal {S}_{\mathcal {G}}(f)}$
,
![]() $(X,F)$
is a totally weakly mixing extension of
$(X,F)$
is a totally weakly mixing extension of
![]() $(Y,f)$
for every
$(Y,f)$
for every
![]() $F\in \mathcal {R}$
.
$F\in \mathcal {R}$
.
According to [Reference Glasner and Weiss19], if we choose
![]() $Z=\mathbf {P}^n, n\ge 2$
to be the projective n-space, and let
$Z=\mathbf {P}^n, n\ge 2$
to be the projective n-space, and let
![]() $\mathcal {G}$
be a pathwise connected component of
$\mathcal {G}$
be a pathwise connected component of
![]() $\mathrm {id}_Z$
in
$\mathrm {id}_Z$
in
![]() $H(Z,Z)$
, then
$H(Z,Z)$
, then
![]() $\mathcal {G}$
satisfies the conditions of Theorems 6.1, 6.2, and 6.14. Thus, for an arbitrary minimal infinite flow
$\mathcal {G}$
satisfies the conditions of Theorems 6.1, 6.2, and 6.14. Thus, for an arbitrary minimal infinite flow
![]() $(Y,f)$
, there are many minimal homeomorphisms of
$(Y,f)$
, there are many minimal homeomorphisms of
![]() $Y\times Z$
which are proximal and totally weakly mixing extensions of
$Y\times Z$
which are proximal and totally weakly mixing extensions of
![]() $(Y,f)$
. And we have proved (2) of Theorem 6.12.
$(Y,f)$
. And we have proved (2) of Theorem 6.12.
Remark 6.15. Note that the examples in Theorem 6.12(1) are uniformly rigid by Proposition 6.11. By the proof of Proposition 6.5 of [Reference Glasner and Maon18], one may also require that the examples in Theorem 6.12(2) are uniformly rigid.
6.9 Almost proximal
In this subsection, we modify the construction of homeomorphisms
![]() $\{\varphi _{2k}^j: 1\le j\le 2^{n_{2k}}-2\}_{k=1}^\infty $
to make the extension
$\{\varphi _{2k}^j: 1\le j\le 2^{n_{2k}}-2\}_{k=1}^\infty $
to make the extension
almost proximal.
Let
![]() $n\in \mathbb N $
be a fixed number. Let
$n\in \mathbb N $
be a fixed number. Let
![]() $\omega =\exp {(i({2\pi }/{n}))}$
. We always write intervals on
$\omega =\exp {(i({2\pi }/{n}))}$
. We always write intervals on
![]() ${\mathbb S}^1$
anti-clockwise, so
${\mathbb S}^1$
anti-clockwise, so
![]() $[z_1,z_2]$
denotes the anti-clockwise closed interval beginning at
$[z_1,z_2]$
denotes the anti-clockwise closed interval beginning at
![]() $z_1$
and ending at
$z_1$
and ending at
![]() $z_2$
:
$z_2$
:
 $$ \begin{align*}S_q=[\omega^{q-1}, \omega^q]=\bigg[\exp{\bigg(i\frac{2\pi}{n} (q-1) \bigg)}, \exp{\bigg(i\frac{2\pi}{n} q \bigg)}\bigg], \quad q\in\{1,2,\ldots, n\}.\end{align*} $$
$$ \begin{align*}S_q=[\omega^{q-1}, \omega^q]=\bigg[\exp{\bigg(i\frac{2\pi}{n} (q-1) \bigg)}, \exp{\bigg(i\frac{2\pi}{n} q \bigg)}\bigg], \quad q\in\{1,2,\ldots, n\}.\end{align*} $$
Then
Thus,
![]() ${\mathbb S}^1$
is divided into n closed intervals equally. For each
${\mathbb S}^1$
is divided into n closed intervals equally. For each
![]() $q\in \{1,2,\ldots ,n\}$
, we may regard
$q\in \{1,2,\ldots ,n\}$
, we may regard
![]() $S_q$
as
$S_q$
as
![]() $[0,1]$
(via the map
$[0,1]$
(via the map
![]() $S_q=[\exp {(i({2\pi }/{n}) (q-1) )}, \exp {(i({2\pi }/{n}) q )}]\rightarrow [0,1], \exp {(i2\pi x)}\mapsto nx-(q-1)$
, where
$S_q=[\exp {(i({2\pi }/{n}) (q-1) )}, \exp {(i({2\pi }/{n}) q )}]\rightarrow [0,1], \exp {(i2\pi x)}\mapsto nx-(q-1)$
, where
![]() $(({q-1})/{n})\le x\le {q}/{n}$
) and let the map
$(({q-1})/{n})\le x\le {q}/{n}$
) and let the map
![]() $\varphi _{2k}^j|_{S_q}: S_q\rightarrow S_q$
be isomorphic to
$\varphi _{2k}^j|_{S_q}: S_q\rightarrow S_q$
be isomorphic to
![]() $g_k(x)=x^{t_k}: [0,1]\rightarrow [0,1]$
when
$g_k(x)=x^{t_k}: [0,1]\rightarrow [0,1]$
when
![]() $1\le j \le 2^{n_{2k}-1}-1$
; and
$1\le j \le 2^{n_{2k}-1}-1$
; and
![]() $g_k^{-1}(x)=x^{1/t_k}: [0,1]\rightarrow [0,1] $
when
$g_k^{-1}(x)=x^{1/t_k}: [0,1]\rightarrow [0,1] $
when
![]() $2^{n_{2k}-1}-1<j\le 2^{n_{2k}}-2$
, where
$2^{n_{2k}-1}-1<j\le 2^{n_{2k}}-2$
, where
![]() $\{t_k\}_{k\in \mathbb N}$
is a decreasing sequence tending to
$\{t_k\}_{k\in \mathbb N}$
is a decreasing sequence tending to
![]() $1$
and
$1$
and
![]() $\lim _{k\to \infty } t_k^{2^{n_{2k}}}=+\infty $
.
$\lim _{k\to \infty } t_k^{2^{n_{2k}}}=+\infty $
.
To be precise, for each
![]() $q\in \{1,2,\ldots ,n\}$
, when
$q\in \{1,2,\ldots ,n\}$
, when
![]() $z=\exp {(i2\pi x)}\in S_q$
,
$z=\exp {(i2\pi x)}\in S_q$
,
![]() $({q-1})/{n}\le x\le {q}/{n}$
,
$({q-1})/{n}\le x\le {q}/{n}$
,
![]() $\varphi _{2k}^j: S_q\rightarrow S_q$
is defined as follows:
$\varphi _{2k}^j: S_q\rightarrow S_q$
is defined as follows:
 $$ \begin{align} \varphi_{2k}^j(z)&= \varphi_{2k}^j(\exp{(i2\pi x)})\nonumber\\&= \begin{cases} \exp\bigg({i2\pi \dfrac{(nx-(q-1))^{t_k}+(q-1)}{n}}\bigg), & 1\le j \le 2^{n_{2k}-1}-1; \\ \exp\bigg( {i2\pi \dfrac{(nx-(q-1))^{1/t_k}+(q-1)}{n}}\bigg), & 2^{n_{2k}-1}-1< j\le 2^{n_{2k}}-2 , \end{cases} \end{align} $$
$$ \begin{align} \varphi_{2k}^j(z)&= \varphi_{2k}^j(\exp{(i2\pi x)})\nonumber\\&= \begin{cases} \exp\bigg({i2\pi \dfrac{(nx-(q-1))^{t_k}+(q-1)}{n}}\bigg), & 1\le j \le 2^{n_{2k}-1}-1; \\ \exp\bigg( {i2\pi \dfrac{(nx-(q-1))^{1/t_k}+(q-1)}{n}}\bigg), & 2^{n_{2k}-1}-1< j\le 2^{n_{2k}}-2 , \end{cases} \end{align} $$
where
![]() $\{t_k\}$
is a decreasing sequence tending to
$\{t_k\}$
is a decreasing sequence tending to
![]() $1$
and
$1$
and
![]() $\lim _{k\to \infty } t_k^{2^{n_{2k}}}=+\infty $
. Thus, for each
$\lim _{k\to \infty } t_k^{2^{n_{2k}}}=+\infty $
. Thus, for each
![]() $q\in \{1,2,\ldots , n\}$
,
$q\in \{1,2,\ldots , n\}$
,
![]() $\varphi _{2k}^j|_{S_q}: S_q\rightarrow S_q$
has exactly two fixed points. Notice that the construction of
$\varphi _{2k}^j|_{S_q}: S_q\rightarrow S_q$
has exactly two fixed points. Notice that the construction of
![]() $\varphi _{2k} ^j$
also satisfies the convention (C3), that is,
$\varphi _{2k} ^j$
also satisfies the convention (C3), that is,
![]() $\psi _{2k}=\mathrm {id} .$
$\psi _{2k}=\mathrm {id} .$
Note that when
![]() $n=1, S_1$
is exactly
$n=1, S_1$
is exactly
![]() ${\mathbb S}^1$
and (C6) coincides with (C5).
${\mathbb S}^1$
and (C6) coincides with (C5).
Proposition 6.16. Suppose that
![]() $\Phi $
satisfies (C2), (C4), and (C6). Then the extension
$\Phi $
satisfies (C2), (C4), and (C6). Then the extension
is an almost proximal extension of uniformly rigid minimal flows, and the cardinality of maximal almost periodic set in each fiber is n.
Proof. First notice that (C4) and (C6) imply (C1) and (C3). It follows that
![]() $(Z(2)\times {\mathbb S}^1, F_\Phi )$
is uniformly rigid and minimal by Proposition 6.9.
$(Z(2)\times {\mathbb S}^1, F_\Phi )$
is uniformly rigid and minimal by Proposition 6.9.
Let
![]() ${\alpha }\in Z(2)$
and
${\alpha }\in Z(2)$
and
![]() $z_0\in {\mathbb S}^1$
. Let
$z_0\in {\mathbb S}^1$
. Let
 $$ \begin{align*}x_j=\bigg({\alpha}, z_0 \exp{\bigg(i\frac{2\pi}{n}(j-1)\bigg)}\bigg)=({\alpha}, z_0\omega^{j-1})\in \pi^{-1}{\alpha}),\quad 1\le j\le n.\end{align*} $$
$$ \begin{align*}x_j=\bigg({\alpha}, z_0 \exp{\bigg(i\frac{2\pi}{n}(j-1)\bigg)}\bigg)=({\alpha}, z_0\omega^{j-1})\in \pi^{-1}{\alpha}),\quad 1\le j\le n.\end{align*} $$
First we show that
![]() $\{x_1, x_2,\ldots , x_n\}$
is an almost periodic set. To attain that aim, we show
$\{x_1, x_2,\ldots , x_n\}$
is an almost periodic set. To attain that aim, we show
![]() $(x_1,x_2,\ldots , x_n)$
is a minimal point of
$(x_1,x_2,\ldots , x_n)$
is a minimal point of
![]() $(X^n, F_\Phi ^{(n)})$
, where
$(X^n, F_\Phi ^{(n)})$
, where
![]() $F^{(n)}_\Phi =F_\Phi \times \cdots \times F_\Phi $
(n times).
$F^{(n)}_\Phi =F_\Phi \times \cdots \times F_\Phi $
(n times).
By the conditions (C4) and (C6), we have
Let
![]() $(y_1,y_2,\ldots , y_n)$
be a minimal point of
$(y_1,y_2,\ldots , y_n)$
be a minimal point of
![]() $\overline {\mathcal{O} }((x_1,x_2,\ldots , x_n), F_\Phi ^{(n)})$
with
$\overline {\mathcal{O} }((x_1,x_2,\ldots , x_n), F_\Phi ^{(n)})$
with
![]() $y_1=x_1$
. (First we choose any minimal point
$y_1=x_1$
. (First we choose any minimal point
![]() $(y_1', y_2',\ldots , y_n')$
in
$(y_1', y_2',\ldots , y_n')$
in
![]() $\overline {\mathcal{O} }((x_1,x_2,\ldots , x_n), F_\Phi ^{(n)})$
. Since
$\overline {\mathcal{O} }((x_1,x_2,\ldots , x_n), F_\Phi ^{(n)})$
. Since
![]() $(X,F_\Phi )$
is minimal, there is some
$(X,F_\Phi )$
is minimal, there is some
![]() $p\in \mathbf {M}$
such that
$p\in \mathbf {M}$
such that
![]() $py_1'=x_1$
. Let
$py_1'=x_1$
. Let
![]() $(y_1,y_2,\ldots , y_n)=p(y_1', y_2',\ldots , y_n')$
. Then
$(y_1,y_2,\ldots , y_n)=p(y_1', y_2',\ldots , y_n')$
. Then
![]() $(y_1,y_2,\ldots , y_n)$
is a minimal point of
$(y_1,y_2,\ldots , y_n)$
is a minimal point of
![]() $\overline {\mathcal{O} }((x_1,x_2,\ldots , x_n), F_\Phi ^{(n)})$
with
$\overline {\mathcal{O} }((x_1,x_2,\ldots , x_n), F_\Phi ^{(n)})$
with
![]() $y_1=x_1$
.) By (6.13),
$y_1=x_1$
.) By (6.13),
Since
![]() $F_\Phi $
preserves orientation, we have
$F_\Phi $
preserves orientation, we have
and hence
![]() $x_2=y_2$
. By the same reason, we have
$x_2=y_2$
. By the same reason, we have
![]() $x_j=y_j$
for
$x_j=y_j$
for
![]() $3\le j\le n$
. Thus,
$3\le j\le n$
. Thus,
![]() $(x_1,x_2,\ldots , x_n)=(y_1,y_2,\ldots , y_n)$
is minimal.
$(x_1,x_2,\ldots , x_n)=(y_1,y_2,\ldots , y_n)$
is minimal.
Next we show that for each
![]() ${\alpha }\in Z(2), z_1,z_2\in {\mathbb S}^1$
, if
${\alpha }\in Z(2), z_1,z_2\in {\mathbb S}^1$
, if
![]() $\rho _X(({\alpha },z_1),({\alpha },z_2))<{2\pi }/{n}$
, then
$\rho _X(({\alpha },z_1),({\alpha },z_2))<{2\pi }/{n}$
, then
![]() $({\alpha },z_1),({\alpha },z_2)$
are proximal. Without loss of generality, we may assume that
$({\alpha },z_1),({\alpha },z_2)$
are proximal. Without loss of generality, we may assume that
![]() ${\alpha }=\underline {0}$
and
${\alpha }=\underline {0}$
and
![]() $z_1,z_2\in [1,\omega ).$
By (C6), for
$z_1,z_2\in [1,\omega ).$
By (C6), for
![]() $z=\exp {(i2\pi x)}\in S_1=[1,\omega ]$
, (
$z=\exp {(i2\pi x)}\in S_1=[1,\omega ]$
, (
![]() $0\le x\le {1}/{n}$
)
$0\le x\le {1}/{n}$
)
 $$ \begin{align*} \varphi_{2k}^j(z)= \varphi_{2k}^j(\exp{(i2\pi x)})= \begin{cases} \exp\bigg({i2\pi \dfrac{(nx)^{t_k}}{n}}\bigg), & 1\leq j \le 2^{n_{2k}-1}-1; \\ \exp\bigg( {i2\pi \dfrac{(nx)^{1/{t_k}}}{n}}\bigg), & 2^{n_{2k}-1}-1<j\le 2^{n_{2k}}-2. \end{cases} \end{align*} $$
$$ \begin{align*} \varphi_{2k}^j(z)= \varphi_{2k}^j(\exp{(i2\pi x)})= \begin{cases} \exp\bigg({i2\pi \dfrac{(nx)^{t_k}}{n}}\bigg), & 1\leq j \le 2^{n_{2k}-1}-1; \\ \exp\bigg( {i2\pi \dfrac{(nx)^{1/{t_k}}}{n}}\bigg), & 2^{n_{2k}-1}-1<j\le 2^{n_{2k}}-2. \end{cases} \end{align*} $$
Let
![]() $m_k$
and
$m_k$
and
![]() $y_m$
be defined as in Lemma 6.4. According to (6.6), for
$y_m$
be defined as in Lemma 6.4. According to (6.6), for
![]() $1\le s<2^{n_{2k}}$
,
$1\le s<2^{n_{2k}}$
,
where
![]() $y_{s\cdot m_{2k-1}}=\varphi ^{s-1}_{2k}\circ \varphi ^{s-2}_{2k}\circ \cdots \circ \varphi ^1_{2k}\circ \varphi ^0_{2k}(y_0).$
Let
$y_{s\cdot m_{2k-1}}=\varphi ^{s-1}_{2k}\circ \varphi ^{s-2}_{2k}\circ \cdots \circ \varphi ^1_{2k}\circ \varphi ^0_{2k}(y_0).$
Let
![]() $z_1=\exp {(i2\pi a_1)}, z_2=\exp {(i2\pi a_2)}$
and
$z_1=\exp {(i2\pi a_1)}, z_2=\exp {(i2\pi a_2)}$
and
![]() $s=2^{n_{2k}-1}$
, where
$s=2^{n_{2k}-1}$
, where
![]() $0\le a_1,a_2<{1}/{n}$
. Then for
$0\le a_1,a_2<{1}/{n}$
. Then for
![]() $j=1,2$
, by conditions on
$j=1,2$
, by conditions on
![]() $\{t_k\}_{k\in \mathbb N}$
and
$\{t_k\}_{k\in \mathbb N}$
and
![]() $na_j<1$
, we have that
$na_j<1$
, we have that
![]() $\lim _{k\to \infty }(na_j)^{t_k^{2^{n_{2k}-1}}}=0$
, and
$\lim _{k\to \infty }(na_j)^{t_k^{2^{n_{2k}-1}}}=0$
, and
 $$ \begin{align*}F^{sm_{2k-1}}_\Phi (\underline{0},z_j)=\bigg(0^{n_1+n_2+\cdots n_{2k-1}}\underline s0^\infty, \exp\bigg({i2\pi \frac{(na_j)^{t_k^{2^{n_{2k}-1}}}}{n}}\bigg)\bigg)\to (\underline{0}, 1),\quad k\to\infty. \end{align*} $$
$$ \begin{align*}F^{sm_{2k-1}}_\Phi (\underline{0},z_j)=\bigg(0^{n_1+n_2+\cdots n_{2k-1}}\underline s0^\infty, \exp\bigg({i2\pi \frac{(na_j)^{t_k^{2^{n_{2k}-1}}}}{n}}\bigg)\bigg)\to (\underline{0}, 1),\quad k\to\infty. \end{align*} $$
Thus,
To sum up, we have showed that for
![]() ${\alpha }\in Z(2)$
,
${\alpha }\in Z(2)$
,
![]() $A\subseteq \pi ^{-1}({\alpha })$
is an almost periodic set with maximal cardinality if and only if
$A\subseteq \pi ^{-1}({\alpha })$
is an almost periodic set with maximal cardinality if and only if
![]() $A=\{({\alpha }, z_0 \exp {(i({2\pi }/{n})(j-1))})=({\alpha }, z_0\omega ^{j-1}): 1\le j\le n\}$
for some
$A=\{({\alpha }, z_0 \exp {(i({2\pi }/{n})(j-1))})=({\alpha }, z_0\omega ^{j-1}): 1\le j\le n\}$
for some
![]() $z_0\in {\mathbb S} ^1$
. The proof is complete.
$z_0\in {\mathbb S} ^1$
. The proof is complete.
6.10 Some remarks
The method to construct the flow
![]() $(Z(2)\times {\mathbb S}^1, F_\Phi )$
is modified from the examples in [Reference C̆iklová-Mlíchová7]. This kind of construction originally was from the study of a triangular map of the unit square
$(Z(2)\times {\mathbb S}^1, F_\Phi )$
is modified from the examples in [Reference C̆iklová-Mlíchová7]. This kind of construction originally was from the study of a triangular map of the unit square
![]() $[0,1]^2$
, which is a continuous map
$[0,1]^2$
, which is a continuous map
![]() $F: [0,1]^2\rightarrow [0,1]^2$
of the form
$F: [0,1]^2\rightarrow [0,1]^2$
of the form
![]() $F(x,y)=(f(x),g_x(y))$
. For a short survey of triangular maps, see [Reference Smítal25].
$F(x,y)=(f(x),g_x(y))$
. For a short survey of triangular maps, see [Reference Smítal25].
We may replace
![]() ${\mathbb S}^1$
by
${\mathbb S}^1$
by
![]() $\mathbb T^n$
,
$\mathbb T^n$
,
![]() $\mathbf {P}^n$
, etc., to get similar minimal flows. Since
$\mathbf {P}^n$
, etc., to get similar minimal flows. Since
![]() ${\mathbb S}^1$
is enough for our purpose, we do not use them in this paper. However, for different purposes, using manifolds with higher dimension may be useful.
${\mathbb S}^1$
is enough for our purpose, we do not use them in this paper. However, for different purposes, using manifolds with higher dimension may be useful.
7 Further discussion
In this section, we give some questions.
7.1 Proximality and chaos
First we restate Problem 5.23. in [Reference Akin, Glasner, Huang, Shao and Ye2].
Question 1. If a minimal flow is not point distal (that is, for any point
![]() $x\in X$
, there is
$x\in X$
, there is
![]() $x'\neq x$
such that
$x'\neq x$
such that
![]() $(x,x')$
is proximal), is it chaotic in the sense of Li–Yorke?
$(x,x')$
is proximal), is it chaotic in the sense of Li–Yorke?
In this paper, we show that if a minimal flow
![]() $(X,T)$
is an almost proximal but not almost finite-to-one extension of some flow
$(X,T)$
is an almost proximal but not almost finite-to-one extension of some flow
![]() $(Y,T)$
, then
$(Y,T)$
, then
![]() $(X,T)$
is not point distal and it is Li–Yorke chaotic. See [Reference Akin, Glasner, Huang, Shao and Ye2, §5] for another special case about Question 1.
$(X,T)$
is not point distal and it is Li–Yorke chaotic. See [Reference Akin, Glasner, Huang, Shao and Ye2, §5] for another special case about Question 1.
7.2 Proximality and weak mixing
As mentioned before, any minimal proximal flow is weakly mixing. In fact, for minimal proximal flows, one can say more.
Theorem 7.1. Let
![]() $(X,T)$
be a proximal minimal flow. Then for every
$(X,T)$
be a proximal minimal flow. Then for every
![]() $x\in X$
, the set
$x\in X$
, the set
is residual in X.
Proof. First we show that for any non-empty open subsets
![]() $V , U',V'$
of X, there is some
$V , U',V'$
of X, there is some
![]() $t\in T$
such that
$t\in T$
such that
Since
![]() $(X,T)$
is minimal, there is a finite subset
$(X,T)$
is minimal, there is a finite subset
![]() $\{t_1,t_2,\ldots , t_n\}$
of T such that
$\{t_1,t_2,\ldots , t_n\}$
of T such that
![]() $X=\bigcup _{i=1}^n t_i V$
. As
$X=\bigcup _{i=1}^n t_i V$
. As
![]() $(X,T)$
is proximal,
$(X,T)$
is proximal,
![]() $(t_1x, t_2x, \ldots , t_n x)\in P^{(n)}.$
And there is some
$(t_1x, t_2x, \ldots , t_n x)\in P^{(n)}.$
And there is some
![]() $t_0\in T$
such that
$t_0\in T$
such that
Note that
![]() $t_0^{-1}V'\cap \bigcup _{i=1}^n t_iV= t_0^{-1}V'\cap X\neq \emptyset $
, there is some
$t_0^{-1}V'\cap \bigcup _{i=1}^n t_iV= t_0^{-1}V'\cap X\neq \emptyset $
, there is some
![]() $j\in \{1,2, \ldots , n\}$
such that
$j\in \{1,2, \ldots , n\}$
such that
![]() $t_0^{-1}V'\cap t_j V\neq \emptyset $
. Thus,
$t_0^{-1}V'\cap t_j V\neq \emptyset $
. Thus,
So we have (7.1).
Let
![]() $\{U_i\}_{i=1}^\infty $
be a base for
$\{U_i\}_{i=1}^\infty $
be a base for
![]() $X\times X$
. By (7.1), the set
$X\times X$
. By (7.1), the set
is a dense open subset of X. It follows that
 $$ \begin{align*}\{y\in X: \overline{\mathcal{O}}((x,y),T)=X\times X\}=\bigcap_{i=1}^\infty A_i\end{align*} $$
$$ \begin{align*}\{y\in X: \overline{\mathcal{O}}((x,y),T)=X\times X\}=\bigcap_{i=1}^\infty A_i\end{align*} $$
is residual in X.
Our question is does the relative version of the theorem above hold?
Question 2. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be a non-trivial open proximal extension of minimal flows. For each
$\pi : (X,T)\rightarrow (Y,T)$
be a non-trivial open proximal extension of minimal flows. For each
![]() $y\in Y$
and each
$y\in Y$
and each
![]() $x\in \pi ^{-1}(y)$
, is the subset
$x\in \pi ^{-1}(y)$
, is the subset
residual in
![]() $\pi ^{-1}(y)$
?
$\pi ^{-1}(y)$
?
7.3 Openness and perfectness
It is a well-known fact that for a homomorphism of ergodic measure-preserving systems, either almost all fibers have constant, finite cardinality or almost all fibers have the cardinality of the continuum. In Theorems 4.2 and 4.7, almost all fibers are perfect. In fact, in the topological case, we have the following general result.
Theorem 7.2. [Reference Akin, Auslander and Glasner1, Theorem 6.31]
Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then one of the following holds:
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. Then one of the following holds:
-
(1)
 $\pi $
is almost finite to one;
$\pi $
is almost finite to one; -
(2) every fiber
 $\pi ^{-1}(y)$
is infinite and
$\pi ^{-1}(y)$
is infinite and
 $\{y\in Y: \pi ^{-1}(y) $
is perfect
$\{y\in Y: \pi ^{-1}(y) $
is perfect
 $\}$
is a residual subset of Y.
$\}$
is a residual subset of Y.
However, the proof of theorem above does not imply that in (2), every fiber is perfect even for open extensions. Thus we have the following question.
Question 3. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If
$\pi : (X,T)\rightarrow (Y,T)$
be an extension of minimal flows. If
![]() $\pi $
is open and is not finite-to-one, is every fiber
$\pi $
is open and is not finite-to-one, is every fiber
![]() $\pi ^{-1}(y)$
perfect?
$\pi ^{-1}(y)$
perfect?
7.3.1 Some special cases
For some special cases, we have positive answer for Question 3. First, we have that for some special weakly mixing extensions, each fiber is perfect.
Theorem 7.3. [Reference Shao and Ye23]
Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be a non-trivial weakly mixing RIC extension of minimal flows. Then each fiber is perfect.
$\pi : (X,T)\rightarrow (Y,T)$
be a non-trivial weakly mixing RIC extension of minimal flows. Then each fiber is perfect.
In the rest of the section, we show that if a distal extension is not finite-to-one, each fiber is perfect. To prove this result, we need the Furstenberg–Ellis structure theorem.
Furstenberg’s structure theorem for distal flows [Reference Furstenberg13] says that any distal minimal flow can be constructed by equicontinuous extensions. We state the result in its relative version of Ellis [Reference Ellis10]. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be a distal extension of minimal flows. Then there is an ordinal
$\pi : (X,T)\rightarrow (Y,T)$
be a distal extension of minimal flows. Then there is an ordinal
![]() $\eta $
(which is countable when X is metrizable) and a family of flows
$\eta $
(which is countable when X is metrizable) and a family of flows
![]() $\{(Z_n,T)\}_{n\le \eta }$
such that:
$\{(Z_n,T)\}_{n\le \eta }$
such that:
-
(i)
 $Z_0=Y$
;
$Z_0=Y$
; -
(ii) for every
 $n <\eta $
there exists a homomorphism
$n <\eta $
there exists a homomorphism
 $\rho _{n+1} :Z_{n+1}\to Z_{n}$
which is equicontinuous;
$\rho _{n+1} :Z_{n+1}\to Z_{n}$
which is equicontinuous; -
(iii) for a limit ordinal
 $\nu \le \eta $
the flow
$\nu \le \eta $
the flow
 $Z_\nu $
is the inverse limit of the flows
$Z_\nu $
is the inverse limit of the flows
 $\{Z_\iota \}_{\iota <\nu }$
;
$\{Z_\iota \}_{\iota <\nu }$
; -
(iv)
 $Z_\eta =X$
.
$Z_\eta =X$
.
When
![]() $Y=\{pt\}$
is the trivial flow, we have the structure theorem for a distal minimal flow.
$Y=\{pt\}$
is the trivial flow, we have the structure theorem for a distal minimal flow.
Theorem 7.4. Let
![]() $\pi : (X,T)\rightarrow (Y,T)$
be a distal extension of minimal flows. If
$\pi : (X,T)\rightarrow (Y,T)$
be a distal extension of minimal flows. If
![]() $\pi $
is not finite-to-one, then each fiber is perfect.
$\pi $
is not finite-to-one, then each fiber is perfect.
Proof. We need an equivalent characterization of an equicontinuous extension. Let M be a homogeneous compact metric space. By this, we mean a compact metric space such that for any two points
![]() $x,y\in M$
, there is an isometry of M taking x into y. The isometries of M form a compact group H, M may be identified with a coset space
$x,y\in M$
, there is an isometry of M taking x into y. The isometries of M form a compact group H, M may be identified with a coset space
![]() $H/H_0$
, where
$H/H_0$
, where
![]() $H_0$
is the subgroup of H leaving a given point of M fixed.
$H_0$
is the subgroup of H leaving a given point of M fixed.
Let
![]() $\pi : X\rightarrow Y$
be an extension of flows. Then
$\pi : X\rightarrow Y$
be an extension of flows. Then
![]() $\pi $
is equicontinuous if and only if there exists a continuous map
$\pi $
is equicontinuous if and only if there exists a continuous map
![]() $\rho : R_\pi \rightarrow \mathbb R$
such that for each
$\rho : R_\pi \rightarrow \mathbb R$
such that for each
![]() $y\in Y$
,
$y\in Y$
,
![]() $\rho $
defines a metric on the fiber
$\rho $
defines a metric on the fiber
![]() $X_y=\pi ^{-1}(y)$
under which
$X_y=\pi ^{-1}(y)$
under which
![]() $X_y$
is isometric to M, and
$X_y$
is isometric to M, and
![]() $\rho (tx_1,tx_2)=\rho (x_1,x_2)$
for all
$\rho (tx_1,tx_2)=\rho (x_1,x_2)$
for all
![]() $t\in T$
and
$t\in T$
and
![]() $(x_1,x_2)\in R_\pi $
[Reference Furstenberg13]. Thus, if
$(x_1,x_2)\in R_\pi $
[Reference Furstenberg13]. Thus, if
![]() $\pi $
is equicontinuous, then each fiber is isometric to
$\pi $
is equicontinuous, then each fiber is isometric to
![]() $M=H/H_0$
. Hence, if
$M=H/H_0$
. Hence, if
![]() $\pi $
is not finite-to-one, then each fiber is perfect.
$\pi $
is not finite-to-one, then each fiber is perfect.
To deal with distal extensions, we use the Furstenberg–Ellis structure theorem as stated above. Let
![]() $\{(Z_n,T)\}_{n\le \eta }$
be the factors. Since
$\{(Z_n,T)\}_{n\le \eta }$
be the factors. Since
![]() $\pi $
is not finite-to-one, either
$\pi $
is not finite-to-one, either
![]() $\eta $
is not finite ordinal and each
$\eta $
is not finite ordinal and each
![]() $\rho _n$
is finite-to-one, or there is some
$\rho _n$
is finite-to-one, or there is some
![]() $n\le \eta $
such that
$n\le \eta $
such that
![]() $\rho _n$
is not finite-to-one. In the first case, each fiber is an inverse limit of finite sets and it is a Cantor set; in the second case,
$\rho _n$
is not finite-to-one. In the first case, each fiber is an inverse limit of finite sets and it is a Cantor set; in the second case,
![]() $\rho _n$
is an infinite-to-one equicontinuous extension and each fiber of
$\rho _n$
is an infinite-to-one equicontinuous extension and each fiber of
![]() $\rho _n$
is perfect and by this, we claim that each fiber of
$\rho _n$
is perfect and by this, we claim that each fiber of
![]() $\pi $
is also perfect. To prove the second case, we need the following claim: if
$\pi $
is also perfect. To prove the second case, we need the following claim: if
![]() $\pi _1:(X_1,T)\to (X_2,T), \pi _2:(X_2,T)\to (X_3,T)$
are open extensions such that each fiber of
$\pi _1:(X_1,T)\to (X_2,T), \pi _2:(X_2,T)\to (X_3,T)$
are open extensions such that each fiber of
![]() $\pi _1$
or
$\pi _1$
or
![]() $\pi _2$
is perfect, then each fiber of
$\pi _2$
is perfect, then each fiber of
![]() $\pi _2 \circ \pi _1$
is perfect. First, by definition, it is easy to see that when each fiber of
$\pi _2 \circ \pi _1$
is perfect. First, by definition, it is easy to see that when each fiber of
![]() $\pi _1$
is perfect, we have each fiber of
$\pi _1$
is perfect, we have each fiber of
![]() $\pi _2 \circ \pi _1$
is perfect. Next, we show the other case. Suppose that each fiber of
$\pi _2 \circ \pi _1$
is perfect. Next, we show the other case. Suppose that each fiber of
![]() $\pi _2$
is perfect. We show that for each
$\pi _2$
is perfect. We show that for each
![]() $z\in X_3$
,
$z\in X_3$
,
![]() $(\pi _2 \circ \pi _1)^{-1} (z)$
is perfect. Let
$(\pi _2 \circ \pi _1)^{-1} (z)$
is perfect. Let
![]() $x\in (\pi _2 \circ \pi _1)^{-1} (z)$
and
$x\in (\pi _2 \circ \pi _1)^{-1} (z)$
and
![]() $y=\pi _1(x).$
Clearly,
$y=\pi _1(x).$
Clearly,
![]() $y\in \pi _2^{-1}(z),$
and by perfectness of
$y\in \pi _2^{-1}(z),$
and by perfectness of
![]() $\pi _2^{-1}(z)$
, one can find
$\pi _2^{-1}(z)$
, one can find
![]() $y_n \in \pi _2^{-1}(z)$
such that
$y_n \in \pi _2^{-1}(z)$
such that
![]() $y_n \to y$
as
$y_n \to y$
as
![]() $n\to \infty .$
Since
$n\to \infty .$
Since
![]() $\pi _1$
is open, there exists
$\pi _1$
is open, there exists
![]() $x_n\in X$
such that
$x_n\in X$
such that
![]() $\pi _1(x_n)=y_n$
and
$\pi _1(x_n)=y_n$
and
![]() $x_n \to x$
as
$x_n \to x$
as
![]() $n\to \infty $
. To sum up, there are
$n\to \infty $
. To sum up, there are
![]() $x_n \in (\pi _2 \circ \pi _1)^{-1} (z)$
such that
$x_n \in (\pi _2 \circ \pi _1)^{-1} (z)$
such that
![]() $x_n \to x$
,
$x_n \to x$
,
![]() $n\to \infty .$
Thus, each point of
$n\to \infty .$
Thus, each point of
![]() $(\pi _2 \circ \pi _1)^{-1} (z)$
is not isolated and
$(\pi _2 \circ \pi _1)^{-1} (z)$
is not isolated and
![]() $(\pi _2 \circ \pi _1)^{-1} (z)$
is perfect. Thus, we have the claim. By this claim and the Furstenberg–Ellis structure theorem (7.2), one can show that each fiber of
$(\pi _2 \circ \pi _1)^{-1} (z)$
is perfect. Thus, we have the claim. By this claim and the Furstenberg–Ellis structure theorem (7.2), one can show that each fiber of
![]() $\pi $
is perfect.
$\pi $
is perfect.
7.4 Open proximality and entropy
Our last question is about entropy. Let
![]() $\pi : (X,\mathbb Z)\rightarrow (Y,\mathbb Z)$
be an extension of discrete flows. If
$\pi : (X,\mathbb Z)\rightarrow (Y,\mathbb Z)$
be an extension of discrete flows. If
![]() $h_{\mathrm {top}}(X)> h_{\mathrm {top}} (Y)$
, then lots of fibers will have very complex properties (see [Reference Zhang29] for example). We are not sure that open proximal extensions can reach those kinds of complexity. Thus, we have the following question.
$h_{\mathrm {top}}(X)> h_{\mathrm {top}} (Y)$
, then lots of fibers will have very complex properties (see [Reference Zhang29] for example). We are not sure that open proximal extensions can reach those kinds of complexity. Thus, we have the following question.
Question 4. Let
![]() $\pi : (X,\mathbb Z)\rightarrow (Y,\mathbb Z)$
be an open proximal extension of discrete minimal flows. Is it true that
$\pi : (X,\mathbb Z)\rightarrow (Y,\mathbb Z)$
be an open proximal extension of discrete minimal flows. Is it true that
![]() $h_{\mathrm {top}}(X)=h_{\mathrm {top}} (Y)$
?
$h_{\mathrm {top}}(X)=h_{\mathrm {top}} (Y)$
?
Note that in Question 4, openness is a necessary condition, since there are many minimal flows which are almost one-to-one extensions of their maximal equicontinuous factors, and they have positive entropy by [Reference Furstenberg and Weiss14, Theorem 1].
Acknowledgements
We would like to thank Professors Wen Huang and Xiangdong Ye for their very useful comments. In particular, we thank the referee for the very careful reading and many useful comments, which helped us to improve the writing of the paper and clarify some proofs. This research is supported by NNSF of China (11971455, 11571335).