1. Formal theories in mathematics and the empirical sciences
A recent article in this journal claimed that ‘team reasoning can be viewed as a particular type of payoff transformation’ and that ‘there is a payoff transformation theory, which relies on participatory motivations, that does yield the same action recommendations as team reasoning’ (Duijf Reference Duijf2021: 413, 436). The article is well written, cites an impressive range of relevant literature, and provides a clear explanation of the puzzling phenomenon under investigation, namely, strategic coordination in games with payoff-dominant (or Pareto-dominant) Nash equilibria. The argument appears to be technically correct within the mathematical framework developed to formalize it, but the interpretation of the mathematical results, summarized in the quotations above, seems unjustified. The problems appear to lie in the formalization. First, the model fails to capture the essence of team reasoning as understood by game theorists who introduced the concept and by researchers who have used it subsequently. Second, Duijf’s key possibility result applies only to what he calls ‘material games’ and not to games in which the payoffs represent the players’ utilities, as assumed in orthodox game theory. The counterargument in the pages that follow is self-contained. It applies to any payoff transformation intended to simulate team reasoning, and it generalizes to any payoff transformation intended to simulate any theory that predicts what strategies players will choose in a specified game. However, a reader who wishes to examine the details of Duijf’s payoff transformation in particular should, of course, read his article also.
An important distinction exists between formal models in pure mathematics on the one hand and in the empirical sciences on the other. A major part of mathematics involves defining formal structures from a small number of undefined primitive terms and unproved axioms or postulates, and then proving theorems within these structures to develop mathematical theories. Historically, one of the earliest definitions of the word theory in the Oxford English Dictionary is ‘a collection of theorems forming a connected system’, leading to such phrases as theory of probability, set theory, group theory, and so on. Mathematical theories are ends in themselves, valued by mathematicians independently of any relevance that they may or may not have to real-world phenomena.
Mathematical models in the empirical sciences are different. They are deliberately simplified abstractions of real-world phenomena, and researchers value them for what they reveal about those phenomena. Because real-world phenomena are too complex and sometimes too fleeting to be clearly perceived and properly understood, they are replaced by mathematical models that, like their counterparts in pure mathematics, consist of primitive terms and unproved assumptions from which other properties are then inferred and conclusions deduced by logical reasoning, but they differ from pure mathematical models in an important way. Although the conclusions drawn from scientific models are necessarily true in a formal sense, provided that no mathematical errors are made, they are valued for their usefulness in explaining or illuminating the real-world phenomena that they model.
I draw attention to this distinction to explain how a game-theoretic model of an empirical phenomenon, such as Duijf’s payoff-transformational model of team reasoning, can be mathematically correct while failing to explain the phenomenon that it purports to model. Duijf’s contribution cannot be judged solely on its internal consistency and mathematical soundness. A scientific model can be formally correct but nevertheless wrong as an interpretation of the phenomenon that it seeks to model, as I believe Duijf’s is. I focus initially on Duijf’s theory because it is the most ambitious and thoroughly worked out payoff-transformational model of team reasoning. But I shall prove that any theory – not just the theory of team reasoning – that predicts what strategies players will choose can be mimicked by a simple payoff transformation with a natural psychological interpretation, but that such a payoff transformation cannot be viewed as a valid representation of the theory that it mimics.
2. Game theory, payoff dominance, and team reasoning
Game theory, at least as it has been applied in the behavioural sciences, notably experimental economics (Smith Reference Smith and Weintraub1992) and more recently behavioural economics (Camerer and Loewenstein Reference Camerer, Loewenstein, Camerer, Loewenstein and Rabin2004), is an example of a mathematical theory from which models of specific classes of interactive decisions are built. Although game theory has been described as ‘central to understanding the dynamics of life forms in general, and humans in particular’ and ‘an indispensable tool in modeling human behavior’ (Gintis Reference Gintis2009: xiii, 248), one of its most striking shortcomings is its inability to confirm what is already known about the elementary case of coordination in games with payoff-dominant Nash equilibria. A prominent solution to this problem is team reasoning, which requires a non-standard form of game-theoretic reasoning. Duijf (Reference Duijf2021) claimed to have derived the same solution without any non-standard reasoning, using a particular type of payoff transformation. I shall show why his game-theoretic model of coordination fails to represent team reasoning adequately, why it does not provide an alternative account of team reasoning, and how his result can be proved more simply and with far greater generality.
The standard assumptions of game theory are as follows. (a) The players know everything about the game, including their own and the other players’ payoff functions – for a simple two-player static game, they know everything displayed in the game’s payoff matrix – and this information is common knowledge in the sense that all players know it, know that they all know it, and so on, indefinitely.Footnote 1 (b) The players are instrumentally rational in the sense that they always choose individually payoff-maximizing strategies, given their knowledge and beliefs. In the Hi-Lo game (Figure 1), which Duijf reasonably identified as the acid test of any explanation of strategic coordination, the outcomes (High, High) and (Low, Low) are both Nash equilibria, but (High, High) is payoff-dominant because it yields better payoffs to both players than (Low, Low). Almost all people who reflect on this game share the powerful intuition that High is the rational strategy choice for both players, and almost all experimental subjects choose it in practice (Bardsley et al. Reference Bardsley, Mehta, Starmer and Sugden2010).
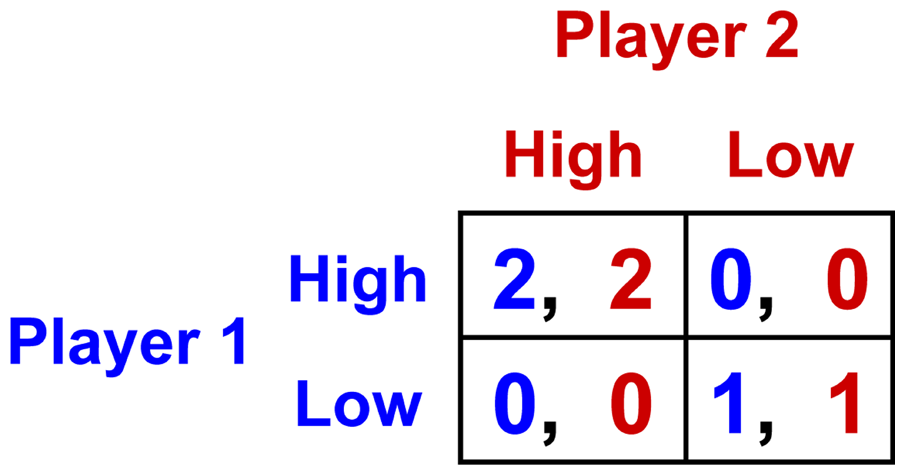
Figure 1. The Hi-Lo game.
It therefore comes as a considerable surprise to find that game theory provides no reason for players to choose their High strategies in this elementary case. According to the standard assumptions (a) and (b) above, a player has a reason (individual payoff maximization) to choose High if and only if there is a reason to expect the other player to choose High. But alas, there can be no such reason, because the game is perfectly symmetric, and the other player has a reason to choose High if and only if there is a reason to expect the first player to choose it. Consequently, any attempt to derive a reason for choosing High from the sparse assumptions of game theory leads to a vicious circle – for a review of various spurious attempts, see Colman et al. (Reference Colman, Pulford and Rose2008) and Colman et al. (Reference Colman, Pulford and Lawrence2014). That is why some researchers have claimed that ‘the action recommendations yielded by team reasoning cannot be explained by payoff transformations – at least, not in a credible way’ (Duijf Reference Duijf2021: 414). Duijf called this the incompatibility claim, and he sought to show that he had found a way of refuting it.
Theories of team reasoning, notably the most prominent theories of Sugden (Reference Sugden1993) and Bacharach (Reference Bacharach, Gold and Sugden2006), solve the problem by altering the rationality assumption of orthodox game theory, labelled (b) above. Instead of assuming that players are instrumentally rational, in the sense of always choosing individually payoff-maximizing strategies, they assume instead that players adopt the following distinctive mode of instrumentally rational reasoning. Switching from an ‘I’ to a ‘we’ point of view, they first examine the game and attempt to identify an outcome or profile of strategies that is best for the players as a group – obviously, in the Hi-Lo game it is (High, High). If the optimal outcome is unique, they then play their component strategies of the corresponding strategy profile – in this game, they both choose High. The players retain the instrumental rationality implied by assumption (b), but the unit of agency changes so that they act together in maximizing a joint utility function. If the optimal outcome is not unique, then team reasoning is indeterminate in the game being examined. This mode of reasoning solves the coordination problem in any game that has a unique payoff-dominant outcome, and it performs better than competing theories of coordination in rigorous experimental tests (Colman et al. Reference Colman, Pulford and Rose2008, Reference Colman, Pulford and Lawrence2014).
Because team reasoning is a theory of instrumental rationality, it makes no sense without a concept of an agent with an objective, but the agent is not an individual. Team reasoning and individualistic reasoning are incompatible in several ways, the most crucial being whether the agent is ‘I’ or ‘we’, respectively. It is therefore impossible to reduce team reasoning to individual reasoning without an agency switch, as Duijf (Reference Duijf2021) purported to do through a particular payoff transformation. An instrumental argument about what one agent ought to do cannot be equivalent to an instrumental argument about what a different agent ought to do. In certain circumstances, it might be good for each of us (reasoning individualistically) to agree to use team reasoning in an interactive decision. Equivalently, in other circumstances it might be good for us collectively (reasoning as ‘we’) to decide that each of us will use individual reasoning, but there cannot be a rational choice about which unit of agency to use. Who would be the agent to make such a decision?
3. Payoff transformations
Duijf (Reference Duijf2021: 415, 431) attempted to disprove the incompatibility claim by demonstrating that ‘a rather unorthodox payoff transformation’ yields reasons to choose High strategies in the Hi-Lo game without any agency switch or special mode of reasoning. To understand this properly, we first need to clarify the status of payoffs in game theory. Strictly speaking, payoffs are utilities, and utilities represent players’ preferences as defined or revealed by their actual choices. This interpretation of utility goes right back to von Neumann and Morgenstern (Reference von Neumann and Morgenstern1947), was endorsed in the classic text on game theory by Luce and Raiffa (Reference Luce and Raiffa1957: 23–31), and was acknowledged by Duijf in footnote 1 of his article. What follows from this is that no payoff transformation can solve the coordination problem in a Hi-Lo game in which the payoffs represent utilities, because the solution would apply to the transformed game and not to the original coordination game. But Duijf began with a Hi-Lo game and payoff-transformed it into what he called a ‘motivational game’ that ‘takes into account some motivationally relevant factors’ (Duijf Reference Duijf2021: 414).
Payoff transformations are intended to deal with material games in which the payoffs are not utilities but objective (typically monetary) gains and losses, and the purpose of transforming such payoffs is to change them into utilities, reflecting the players’ actual preferences. Duijf’s (Reference Duijf2021) payoff transformation is unjustified because its purpose is not to change the payoffs of the Hi-Lo game to utilities. Its explicit purpose is to transform the Hi-Lo game into a game with a different strategic structure in which rational players, using standard individualistic reasoning, choose High strategies. If the payoffs in an untransformed Hi-Lo game represent the players’ preferences, then there is no justification for transforming them. In such a game, team reasoning would cause both players to choose High strategies, whereas Duijf’s payoff transformation, and indeed any transformation that changed the strategic structure of the game would, at best, solve a different game. This seems to invalidate any attempt to derive team reasoning from payoff transformations.
Experimental researchers are constrained to work with material games, because their experimental subjects or participants, who are usually incentivized with monetary rewards, have unknown utilities, and experimenters sometimes transform the payoffs to take account of motivationally relevant factors aside from individual monetary gain. Payoff transformations were (I believe) originally introduced by Edgeworth (1881 [Reference Edgeworth1967]: 101–102), long before the dawn of experimental games. They were first applied to experimental games by Deutsch (Reference Deutsch1949 a, Reference Deutsch1949 b), and developed into modern social value orientations by Messick and McClintock (Reference Messick and McClintock1968) and McClintock (Reference McClintock1972) to solve the problem that the material payoffs in experimental games take no account of players’ other-regarding preferences – cooperation, competition, altruism, and equality-seeking (inequality aversion). Payoff transformations can be justified and are useful when the payoffs in experimental games do not reflect the players’ utilities. Duijf (Reference Duijf2021) examined various standard payoff transformations: social value orientations, Fehr and Schmidt’s (Reference Fehr and Schmidt1999) inequality aversion model, and Rabin’s (Reference Rabin1993) fairness model, all of which are intended to take account of psychological motivations that correspond to intuitions about how people think and feel about interactive decisions. Duijf proved correctly (Theorems 1, 2, 3) that none of them can represent team reasoning, but he claimed that his own payoff transformation can achieve this.
Duijf’s interpretation of his rather unorthodox payoff transformation does not correspond to any obvious psychological motivation or intuition. For example, his ‘participatory motivation function’ implies that, in the Hi-Lo game, if Player i believes that j will choose High, then i’s participatory utility from choosing Low is the utility that the player pair would get if both chose Low. As Duijf expressed i’s thinking: ‘at (low, high) she thinks of herself as having counterfactually participated in (low, low)’ (Duijf Reference Duijf2021: 433). But why would anyone think like that? In orthodox game theory, on which Duijf was supposedly relying to prove that team reasoning’s deviation from orthodox game theory is not required, players are assumed to choose best responses, defined by their utilities, to the strategies they believe their co-players will choose, but that is evidently not the case here. There is no obvious psychological or intuitive justification for Duijf’s payoff transformation, in contrast to team reasoning, which is firmly grounded in a familiar intuition: people often feel that they are acting in the best interests of their sports teams, their families, their universities, or other groups to which they belong rather than in their individual self-interest. I shall show below that there is a much simpler payoff transformation than Duijf’s, with a natural psychological interpretation, that gives the same result as his, although, like Duijf’s, it cannot be viewed as team reasoning.
Those who have claimed that the coordination problem cannot be solved by payoff transformations have usually had standard payoff transformations in mind. For example, Duijf (Reference Duijf2021: 426) quoted the following claim of mine: ‘Team reasoning is inherently non-individualistic and cannot be derived from transformational models of social value orientation’ (Colman Reference Colman2003: 151). The article from which that quotation was taken contains a mathematical proof that these standard transformational models of social value orientation cannot solve the coordination problem. Duijf claimed that his own rather unorthodox payoff transformation does the trick, but team reasoning theorists have never claimed, or at least never intended to claim, that no conceivable payoff transformation could produce the desired result.
What grounds are there for believing that team-reasoning theorists never intended to make such a strong claim? One answer is the fact that there is a trivial sense in which a payoff transformation can obviously mimic team reasoning, and those who made the incompatibility claim in relation to social value orientations and other standard payoff transformations were surely aware of it. For example, let u i be the payoff function – or what Duijf called the ‘personal motivation function’ – of Player i ∈ {1, 2} in the Hi-Lo game of Figure 1, and let s i and s j ∈ {High, Low} be the players’ chosen strategies. Consider the following payoff transformation:
For both players, High is a weakly dominant strategy in this payoff-transformed game, and both players therefore have a reason to choose High according to the individual payoff-maximization assumption of orthodox game theory, just as team-reasoning players do in the untransformed Hi-Lo game. This payoff transformation, unlike Duijf’s, has a natural psychological interpretation. We need to assume no more than that both players are so strongly motivated to achieve the payoff-dominant outcome that they regard all other outcomes as equally bad. But surely no one would claim that this payoff transformation can be viewed as team reasoning, because there is no agency switch, and above all because the transformed game is not a Hi-Lo game. Why, then, should we believe that Duijf’s rather unorthodox payoff transformation, or for that matter any other payoff-transformational interpretation of team reasoning, such as that of Van Lange (Reference Van Lange2008), can be viewed as team reasoning or that it solves the problem of coordination?
Duijf claimed that his payoff transformation, like the simpler one in Equation (1), yields the same strategy choices as team reasoning. This is true in a technical sense, but for this claim to have any theoretical significance, his payoff transformation would have to be entirely distinct from and independent of team reasoning, and that does not appear to be the case. For example, let us examine his ‘participatory motivation function’ (Duijf Reference Duijf2021: 432) more closely:
where
![]() $u_i^{\max }\left( a \right)$
is the ‘motivational utility’ from the strategy profile a that Player i is assumed to maximize, γ
i
is the utility from i’s material payoff, δ
i
is the utility from group actions that i participates in, and
$u_i^{\max }\left( a \right)$
is the ‘motivational utility’ from the strategy profile a that Player i is assumed to maximize, γ
i
is the utility from i’s material payoff, δ
i
is the utility from group actions that i participates in, and
![]() $\max V_i^{conf}\left( {{a_i}} \right)$
is the greatest ‘team utility’ – the ‘participatory utility’ associated with the team in which i participates actively. Note that this last quantity is precisely what players are assumed to maximize in theories of team reasoning. In fact, if we set γ
i
= 0 and δ
i
= 1, suppressing the utility derived from i’s material payoff, we are left with a purely participatory motivation, and i’s utility is that of the team if the other players choose the team-utility best response to a
i
. This amounts to i choosing the strategy that is a component of the team-optimal solution: in effect, i acts as if team reasoning. This analysis seems to expose the participatory motivation function in Equation (2) as an arbitrary and roundabout way of reverse-engineering the team-optimal solution through individualistic reasoning.
$\max V_i^{conf}\left( {{a_i}} \right)$
is the greatest ‘team utility’ – the ‘participatory utility’ associated with the team in which i participates actively. Note that this last quantity is precisely what players are assumed to maximize in theories of team reasoning. In fact, if we set γ
i
= 0 and δ
i
= 1, suppressing the utility derived from i’s material payoff, we are left with a purely participatory motivation, and i’s utility is that of the team if the other players choose the team-utility best response to a
i
. This amounts to i choosing the strategy that is a component of the team-optimal solution: in effect, i acts as if team reasoning. This analysis seems to expose the participatory motivation function in Equation (2) as an arbitrary and roundabout way of reverse-engineering the team-optimal solution through individualistic reasoning.
Duijf’s (Reference Duijf2021: 431) ‘possibility result’ asserts that ‘team reasoning can be viewed as a payoff transformation that incorporates the intuition that people care about the group actions they participate in’. It is possible to prove a theoretical result that is both more general and more intuitive than this. The following proof is a further generalization of the payoff transformation in Equation (1) above.
Consider an arbitrary material game G in strategic form, defined as follows:
where N = {1, …, n} is the set of players, S
i
is Player i’s strategy set, and m
i
is Player i’s material payoff function. Assume that n ≥ 2 and that every S
i
contains two or more pure strategies. I use the notation
![]() $S = {\prod _{i \in N}}{S_i}$
, I write player’s payoff function m
i
:
$S = {\prod _{i \in N}}{S_i}$
, I write player’s payoff function m
i
:
![]() $S \to {\mathbb R}$
, and I write a strategy profile s = (s
1, …, s
n
) ∈ S.
$S \to {\mathbb R}$
, and I write a strategy profile s = (s
1, …, s
n
) ∈ S.
Theorem. Suppose an arbitrary theory T predicts that players will choose the profile of strategies
![]() ${{\bf{s}}^ * } = \left( {s_1^ * , \ldots ,{\rm{ }}s_n^ * } \right)$
in the specified game G. There is a payoff transformation of G that ensures that the players, by maximizing their individual material payoffs using standard game-theoretic reasoning, will play the component strategies of s*.
${{\bf{s}}^ * } = \left( {s_1^ * , \ldots ,{\rm{ }}s_n^ * } \right)$
in the specified game G. There is a payoff transformation of G that ensures that the players, by maximizing their individual material payoffs using standard game-theoretic reasoning, will play the component strategies of s*.
Proof. Define the following payoff-transformation of the material payoffs of G in Equation (3) above:
for all i and all
![]() ${s_i}.$
In Equation 4, every player i receives a utility of 1 if all players choose their component strategies of the strategy profile s*, and 0 otherwise. Figure 2 shows the payoff matrix resulting from the application of this payoff transformation on the Hi-Lo game of Figure 1. In the transformed payoff matrix, the High strategy is weakly dominant for both players and the unique Nash equilibrium is (High, High). Using standard, individualistic, game-theoretic reasoning, both players will therefore choose their component strategies of the unique Nash equilibrium s* in the payoff-transformed game, as required. This applies not merely to the two-player Hi-Lo game in this trivial example but to any game G, as defined in (3) above, and to any particular strategy profile predicted by a theory T, whether or not it specifies that all players will choose the same strategy.
${s_i}.$
In Equation 4, every player i receives a utility of 1 if all players choose their component strategies of the strategy profile s*, and 0 otherwise. Figure 2 shows the payoff matrix resulting from the application of this payoff transformation on the Hi-Lo game of Figure 1. In the transformed payoff matrix, the High strategy is weakly dominant for both players and the unique Nash equilibrium is (High, High). Using standard, individualistic, game-theoretic reasoning, both players will therefore choose their component strategies of the unique Nash equilibrium s* in the payoff-transformed game, as required. This applies not merely to the two-player Hi-Lo game in this trivial example but to any game G, as defined in (3) above, and to any particular strategy profile predicted by a theory T, whether or not it specifies that all players will choose the same strategy.

Figure 2. Payoff transformation using Equation 4 of the Hi-Lo game from Figure 1.
Comment. Duijf’s rather unorthodox payoff transformation is a special case of this more general result, although his payoff transformation is quite different and far more complicated than the simpler and more intuitive payoff transformation of the theorem above. The payoff transformation in Equation 4 achieves the same result for any theory that predicts that players will choose a particular strategy profile in any well-defined 2-player or N-player strategic game. Equation 4 is more general because whatever the theory T is, whether it assumes that individuals act with the intention of contributing to a collective outcome or to conform to some entirely different strategy profile, the payoff transformation in Equation 4 achieves the desired result. Furthermore, there is a coherent psychological interpretation of this more general payoff transformation. Whatever the theory T may be, we assume that players are motivated to act with the intention of participating in whatever strategy profile T predicts: they desire the outcome that the theory predicts and consider all other outcomes as equally undesirable. This resembles Kutz’s (Reference Kutz2000) theory of participatory intentions, cited in footnote 37 of Duijf’s article. However and crucially, although the payoff transformation in Equation 4 predicts the same strategy choices as the arbitrary theory T, it does not provide an alternative interpretation of T in any meaningful sense: it would be unreasonable to claim that T can be ‘viewed as’ the payoff transformation, because every theory can be simulated with precisely the same payoff transformation.
4. Conclusions
Duijf (Reference Duijf2021) proved that team reasoning cannot be derived from or explained by standard payoff transformations (Theorems 1, 2, 3), but that there is a payoff transformation that does yield the same strategy choices as team reasoning, under orthodox game-theoretic individualistic reasoning (Theorems 4 and 5). All of this seems quite correct from a mathematical point of view, although the possibility of a payoff transformation that mimics team reasoning was never in doubt. What seems unjustified is Duijf’s interpretation of these results as evidence that team reasoning can be viewed or interpreted as a payoff transformation. I have shown how a particular profile of strategies predicted by any theory whatsoever can be represented by a simple payoff transformation without that payoff transformation providing a meaningful way of viewing or interpreting the theory.
A fundamental problem with Duijf’s interpretation is that team reasoning involves an agency switch, from the individualistic mode of reasoning of orthodox game theory to a collectivistic mode of team reasoning, and his model ignores this fundamental property. His argument also fails because his result applies to a material coordination game and not to any coordination game in which the payoffs represent von Neumann–Morgenstern utilities, precluding meaningful payoff transformation. A payoff-transformed game is supposed to have payoffs closer to utilities than a material game, but Duijf’s argument begins with a material Hi-Lo game and then proceeds to a payoff-transformed game that is nothing like a Hi-Lo game.
The agency objection is crucial, because team reasoning makes no sense within the framework of individualistic reasoning. Whatever Duijf’s formal analysis has shown, it cannot be that team reasoning can be viewed as a payoff transformation, because the standard, individualistic agency and mode of reasoning remain in operation in his model. The utility objection is also fatal, because by transforming the payoffs of any coordination game appropriately, we can produce a game with dominant strategies and a unique Nash equilibrium in which individualistic reasoning could, in some sense, be said to mimic team reasoning in the original, untransformed coordination game. But if the original game has payoffs representing the players’ preferences, then there can be no justifiable payoff transformation. By transforming payoffs in a game in which the payoffs represent utilities, we can produce another game in which the strategy choices of instrumentally rational players, reasoning individualistically, correspond to those of team reasoning players who are reasoning collectively in the original game, but to describe that as team reasoning seems unjustified and unjustifiable.
Having shown that team reasoning cannot be viewed as a payoff transformation, I conclude by commenting that team reasoning is not the only modification of standard game-theoretic reasoning that can explain strategic coordination in games with payoff-dominant Nash equilibria. Three other notable suggestions are cognitive hierarchy theory (Camerer et al. Reference Camerer, Ho and Chong2004), Berge equilibrium (Colman et al. Reference Colman, Körner, Musy and Tazdaït2011; Salukvadze and Zhukovskiy Reference Salukvadze and Zhukovskiy2020) and strong Stackelberg reasoning (Colman and Bacharach Reference Colman and Bacharach1997; Colman et al. Reference Colman, Pulford and Lawrence2014; Pulford et al. Reference Pulford, Colman and Lawrence2014). Cognitive hierarchy theory abandons the standard common knowledge of rationality assumption in favour of an assumption that players choose best responses to their co-players’ expected strategies given an assumption that their co-players choose their own strategies using a shallower depth of strategic reasoning than they use themselves. Berge equilibrium, which solves many coordination games with payoff-dominant equilibria, though not the Hi-Lo game, and also explains cooperation in the Prisoner’s Dilemma game, abandons Nash equilibrium and the rationality assumption in favour of an alternative equilibrium in which players choose strategies that maximize one another’s payoffs rather than their own. Strong Stackelberg reasoning abandons standard best-responding in favour of a modified form of best-responding constrained by an assumption that any strategy choice will be anticipated by the co-player(s), who will best-respond to it.
Acknowledgements
The writing of this article was supported by the Leicester Judgment and Decision Making Endowment Fund (Grant No. M56TH33). I am grateful to Robert Sugden for helpful comments on an earlier draft of this article.
Andrew M. Colman is Professor of Psychology at the University of Leicester and is a Fellow of the British Psychological Society. He has published over 160 journal articles and book chapters, mainly on aspects of judgement and decision making, game theory and experimental games, and is the author of several books, including Game Theory and its Applications in the Social and Biological Sciences (2nd edn, 1995) and the Oxford Dictionary of Psychology (4th edn, 2015). URL: https://sites.google.com/view/andrew-m-colman/home





