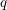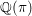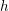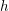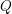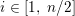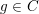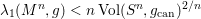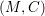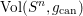Contents
Research Article
Unitary cycles on Shimura curves and the Shimura lift II
- Part of:
- Published online by Cambridge University Press: 15 September 2014, pp. 1963-2002
-
- Article
-
- You have access
- Export citation
-
-
View abstract
We consider two families of arithmetic divisors defined on integral models of Shimura curves. The first was studied by Kudla, Rapoport and Yang, who proved that if one assembles these divisors in a formal generating series, one obtains the
$q$-expansion of a modular form of weight 3/2. The present work concerns the Shimura lift of this modular form: we identify the Shimura lift with a generating series comprising divisors arising in the recent work of Kudla and Rapoport regarding cycles on Shimura varieties of unitary type. In the prequel to this paper, the author considered the geometry of the two families of cycles. These results are combined with the Archimedean calculations found in this work in order to establish the theorem. In particular, we obtain new examples of modular generating series whose coefficients lie in arithmetic Chow groups of Shimura varieties.
-
On fields of rationality for automorphic representations
- Part of:
- Published online by Cambridge University Press: 11 September 2014, pp. 2003-2053
-
- Article
-
- You have access
- Export citation
-
-
View abstract
This paper proves two results on the field of rationality
$\mathbb{Q}({\it\pi})$ for an automorphic representation 
${\it\pi}$, which is the subfield of 
$\mathbb{C}$ fixed under the subgroup of 
$\text{Aut}(\mathbb{C})$ stabilizing the isomorphism class of the finite part of 
${\it\pi}$. For general linear groups and classical groups, our first main result is the finiteness of the set of discrete automorphic representations 
${\it\pi}$ such that 
${\it\pi}$ is unramified away from a fixed finite set of places, 
${\it\pi}_{\infty }$ has a fixed infinitesimal character, and 
$[\mathbb{Q}({\it\pi}):\mathbb{Q}]$ is bounded. The second main result is that for classical groups, 
$[\mathbb{Q}({\it\pi}):\mathbb{Q}]$ grows to infinity in a family of automorphic representations in level aspect whose infinite components are discrete series in a fixed 
$L$-packet under mild conditions.
-
Jordan property for groups of birational selfmaps
- Part of:
- Published online by Cambridge University Press: 17 September 2014, pp. 2054-2072
-
- Article
-
- You have access
- Export citation
-
-
View abstract
Assuming a particular case of the Borisov–Alexeev–Borisov conjecture, we prove that finite subgroups of the automorphism group of a finitely generated field over
$\mathbb{Q}$ have bounded orders. Further, we investigate which algebraic varieties have groups of birational selfmaps satisfying the Jordan property. Unless explicitly stated otherwise, all varieties are assumed to be algebraic, geometrically irreducible and defined over an arbitrary field 
$\Bbbk$ of characteristic zero.
-
Hermitian forms over quaternion algebras
- Part of:
- Published online by Cambridge University Press: 15 September 2014, pp. 2073-2094
-
- Article
-
- You have access
- Export citation
-
-
View abstract
We study a Hermitian form
$h$ over a quaternion division algebra 
$Q$ over a field (
$h$ is supposed to be alternating if the characteristic of the field is two). For generic 
$h$ and 
$Q$, for any integer 
$i\in [1,\;n/2]$, where 
$n:=\dim _{Q}h$, we show that the variety of 
$i$-dimensional (over 
$Q$) totally isotropic right subspaces of 
$h$ is 
$2$-incompressible. The proof is based on a computation of the Chow ring for the classifying space of a certain parabolic subgroup in a split simple adjoint affine algebraic group of type 
$C_{n}$. As an application, we determine the smallest value of the 
$J$-invariant of a non-degenerate quadratic form divisible by a 
$2$-fold Pfister form; we also determine the biggest values of the canonical dimensions of the orthogonal Grassmannians associated to such quadratic forms.
-
The Hardy–Littlewood conjecture and rational points
- Part of:
- Published online by Cambridge University Press: 10 September 2014, pp. 2095-2111
-
- Article
-
- You have access
- Export citation
-
-
View abstract
Schinzel’s Hypothesis (H) was used by Colliot-Thélène and Sansuc, and later by Serre, Swinnerton-Dyer and others, to prove that the Brauer–Manin obstruction controls the Hasse principle and weak approximation on pencils of conics and similar varieties. We show that when the ground field is
$\mathbb{Q}$ and the degenerate geometric fibres of the pencil are all defined over 
$\mathbb{Q}$, one can use this method to obtain unconditional results by replacing Hypothesis (H) with the finite complexity case of the generalised Hardy–Littlewood conjecture recently established by Green, Tao and Ziegler.
-
Spectre et géométrie conforme des variétés compactes à bord
- Part of:
- Published online by Cambridge University Press: 28 October 2014, pp. 2112-2126
-
- Article
-
- You have access
- Export citation
-
-
View abstract
We prove that on any compact manifold
$M^{n}$ with boundary, there exists a conformal class 
$C$ such that for any Riemannian metric 
$g\in C$ of unit volume, the first positive eigenvalue of the Neumann Laplacian satisfies 
${\it\lambda}_{1}(M^{n},g)<n\,\text{Vol}(S^{n},g_{\text{can}})^{2/n}$. We also prove a similar inequality for the first positive Steklov eigenvalue. The proof relies on a handle decomposition of the manifold. We also prove that the conformal volume of 
$(M,C)$ is 
$\text{Vol}(S^{n},g_{\text{can}})$, and that the Friedlander–Nadirashvili invariant and the Möbius volume of 
$M$ are equal to those of the sphere. If 
$M$ is a domain in a space form, 
$C$ is the conformal class of the canonical metric.
-
The real Chevalley involution
- Part of:
- Published online by Cambridge University Press: 27 August 2014, pp. 2127-2142
-
- Article
-
- You have access
- Export citation
-
-
View abstract
The Chevalley involution of a connected, reductive algebraic group over an algebraically closed field takes every semisimple element to a conjugate of its inverse, and this involution is unique up to conjugacy. In the case of the reals we prove the existence of a real Chevalley involution, which is defined over
$\mathbb{R}$, takes every semisimple element of 
$G(\mathbb{R})$ to a 
$G(\mathbb{R})$-conjugate of its inverse, and is unique up to conjugacy by 
$G(\mathbb{R})$. We derive some consequences, including an analysis of groups for which every irreducible representation is self-dual, and a calculation of the Frobenius Schur indicator for such groups.
-
Bounding Lagrangian widths via geodesic paths
- Part of:
- Published online by Cambridge University Press: 17 September 2014, pp. 2143-2183
-
- Article
-
- You have access
- Export citation
-
-
View abstract
The width of a Lagrangian is the largest capacity of a ball that can be symplectically embedded into the ambient manifold such that the ball intersects the Lagrangian exactly along the real part of the ball. Due to Dimitroglou Rizell, finite width is an obstruction to a Lagrangian admitting an exact Lagrangian cap in the sense of Eliashberg–Murphy. In this paper we introduce a new method for bounding the width of a Lagrangian
$Q$ by considering the Lagrangian Floer cohomology of an auxiliary Lagrangian 
$L$ with respect to a Hamiltonian whose chords correspond to geodesic paths in 
$Q$. This is formalized as a wrapped version of the Floer–Hofer–Wysocki capacity and we establish an associated energy–capacity inequality with the help of a closed–open map. For any orientable Lagrangian 
$Q$ admitting a metric of non-positive sectional curvature in a Liouville manifold, we show the width of 
$Q$ is bounded above by four times its displacement energy.
-
Front Cover (OFC, IFC) and matter
COM volume 150 Issue 12 Cover and Front matter
- Published online by Cambridge University Press: 19 December 2014, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
COM volume 150 Issue 12 Cover and Back matter
- Published online by Cambridge University Press: 19 December 2014, pp. b1-b3
-
- Article
-
- You have access
- Export citation