Hostname: page-component-7bb8b95d7b-l4ctd Total loading time: 0 Render date: 2024-09-22T05:36:51.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Unistructurality of cluster algebras

Part of: Arithmetic rings and other special rings

Published online by Cambridge University Press:  17 April 2020

Peigen Cao  and
Fang Li
Peigen Cao
Affiliation:
Department of Mathematics, Zhejiang University (Yuquan Campus), Hangzhou,Zhejiang310027, PR China Université de Paris, UFR de Mathématiques, CNRS, Institut de Mathématiques de Jussieu-Paris Rive Gauche, IMJ-PRG, Batiment Sophie Germain, 75205 Paris Cedex 13, France email peigencao@126.com
Fang Li
Affiliation:
Department of Mathematics, Zhejiang University (Yuquan Campus), Hangzhou, Zhejiang310027, PR China email fangli@zju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that any skew-symmetrizable cluster algebra is unistructural, which is a conjecture by Assem, Schiffler and Shramchenko. As a corollary, we obtain that a cluster automorphism of a cluster algebra 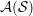${\mathcal{A}}({\mathcal{S}})$ is just an automorphism of the ambient field 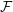${\mathcal{F}}$ which restricts to a permutation of the cluster variables of 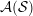${\mathcal{A}}({\mathcal{S}})$.

Keywords

cluster algebrasunistructurality

MSC classification

Primary: 13F60: Cluster algebras
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 5 , May 2020 , pp. 946 - 958
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assem, I., Schiffler, R. and Shramchenko, V., Cluster automorphisms and compatibility of cluster variables, Glasg. Math. J. 56 (2014), 705–720.CrossRefGoogle Scholar
Bazier-Matte, V., Unistructurality of cluster algebras of type Ã, J. Algebra 464 (2016), 297–315.CrossRefGoogle Scholar
Bazier-Matte, V. and Plamondon, P. G., Unistructurality of cluster algebras from unpunctured surfaces, Proc. Amer. Math. Soc. 148 (2020), 2397–2409.CrossRefGoogle Scholar
Cao, P. and Li, F., The enough g-pairs property and denominator vectors of cluster algebras, Preprint (2018), arXiv:1803.05281.Google Scholar
Ceballos, C. and Pilaud, V., Denominator vectors and compatibility degrees in cluster algebras of finite type, Trans. Amer. Math. Soc. 367 (2015), 1421–1439.CrossRefGoogle Scholar
Cerulli Irelli, G., Keller, B., Labardini-Fragoso, D. and Plamondon, P. G., Linear independence of cluster monomials for skew-symmetric cluster algebras, Compos. Math. 149 (2013), 1753–1764.CrossRefGoogle Scholar
Davison, B., Positivity for quantum cluster algebras, Ann. of Math. (2) 187 (2018), 157–219.CrossRefGoogle Scholar
Fomin, S., Shapiro, M. and Thurston, D., Cluster algebras and triangulated surfaces. I. Cluster complexes, Acta Math. 201 (2008), 83–146.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. I. Foundations, J. Amer. Math. Soc. 15 (2002), 497–529 (electronic).CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Y-systems and generalized associahedra, Ann. of Math. (2) 158 (2003), 977–1018.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. II. Finite type classification, Invent. Math. 154 (2003), 63–121.CrossRefGoogle Scholar
Fomin, S. and Zelevinsky, A., Cluster algebras. IV. Coefficients, Compos. Math. 143 (2007), 112–164.CrossRefGoogle Scholar
Gekhtman, M., Shapiro, M. and Vainshtein, A., On the properties of the exchange graph of a cluster algebra, Math. Res. Lett. 15 (2008), 321–330.CrossRefGoogle Scholar
Gross, M., Hacking, P., Keel, S. and Kontsevich, M., Canonical bases for cluster algebras, J. Amer. Math. Soc. 31 (2018), 497–608.CrossRefGoogle Scholar
Lee, K. and Schiffler, R., Positivity for cluster algebras, Ann. of Math. (2) 182 (2015), 73–125.CrossRefGoogle Scholar
Nakanishi, T. and Zelevinsky, A., On tropical dualities in cluster algebras, in Algebraic groups and quantum groups, Contemporary Mathematics, vol. 565 (American Mathematical Society, Providence, RI, 2012), 217–226.CrossRefGoogle Scholar
Zhu, B., BGP-reflection functors and cluster combinatorics, J. Pure Appl. Algebra 209 (2007), 497–506.CrossRefGoogle Scholar