Article contents
Symmetric operations for all primes and Steenrod operations in algebraic cobordism
Published online by Cambridge University Press: 22 December 2015
Abstract
In this article we construct symmetric operations for all primes (previously known only for 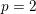 $p=2$). These unstable operations are more subtle than the Landweber–Novikov operations, and encode all
$p=2$). These unstable operations are more subtle than the Landweber–Novikov operations, and encode all 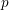 $p$-primary divisibilities of characteristic numbers. Thus, taken together (for all primes) they plug the gap left by the Hurewitz map
$p$-primary divisibilities of characteristic numbers. Thus, taken together (for all primes) they plug the gap left by the Hurewitz map 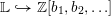 $\mathbb{L}{\hookrightarrow}\mathbb{Z}[b_{1},b_{2},\ldots ]$, providing an important structure on algebraic cobordism. Applications include questions of rationality of Chow group elements, and the structure of the algebraic cobordism. We also construct Steenrod operations of tom Dieck style in algebraic cobordism. These unstable multiplicative operations are more canonical and subtle than Quillen-style operations, and complement the latter.
$\mathbb{L}{\hookrightarrow}\mathbb{Z}[b_{1},b_{2},\ldots ]$, providing an important structure on algebraic cobordism. Applications include questions of rationality of Chow group elements, and the structure of the algebraic cobordism. We also construct Steenrod operations of tom Dieck style in algebraic cobordism. These unstable multiplicative operations are more canonical and subtle than Quillen-style operations, and complement the latter.
- Type
- Research Article
- Information
- Copyright
- © The Author 2015
References
- 3
- Cited by


