Article contents
On the complexity of a putative counterexample to the 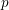 $p$-adic Littlewood conjecture
$p$-adic Littlewood conjecture
Published online by Cambridge University Press: 19 May 2015
Abstract
Let  $\Vert \cdot \Vert$ denote the distance to the nearest integer and, for a prime number
$\Vert \cdot \Vert$ denote the distance to the nearest integer and, for a prime number 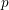 $p$, let
$p$, let  $|\cdot |_{p}$ denote the
$|\cdot |_{p}$ denote the 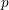 $p$-adic absolute value. Over a decade ago, de Mathan and Teulié [Problèmes diophantiens simultanés, Monatsh. Math. 143 (2004), 229–245] asked whether
$p$-adic absolute value. Over a decade ago, de Mathan and Teulié [Problèmes diophantiens simultanés, Monatsh. Math. 143 (2004), 229–245] asked whether 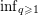 $\inf _{q\geqslant 1}$
$\inf _{q\geqslant 1}$ $q\cdot \Vert q{\it\alpha}\Vert \cdot |q|_{p}=0$ holds for every badly approximable real number
$q\cdot \Vert q{\it\alpha}\Vert \cdot |q|_{p}=0$ holds for every badly approximable real number 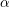 ${\it\alpha}$ and every prime number
${\it\alpha}$ and every prime number 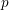 $p$. Among other results, we establish that, if the complexity of the sequence of partial quotients of a real number
$p$. Among other results, we establish that, if the complexity of the sequence of partial quotients of a real number 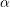 ${\it\alpha}$ grows too rapidly or too slowly, then their conjecture is true for the pair
${\it\alpha}$ grows too rapidly or too slowly, then their conjecture is true for the pair 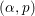 $({\it\alpha},p)$ with
$({\it\alpha},p)$ with 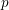 $p$ an arbitrary prime.
$p$ an arbitrary prime.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2015
References
- 5
- Cited by


