Article contents
Motohashi’s fourth moment identity for non-archimedean test functions and applications
Published online by Cambridge University Press: 17 April 2020
Abstract
Motohashi established an explicit identity between the fourth moment of the Riemann zeta function weighted by some test function and a spectral cubic moment of automorphic 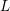 $L$-functions. By an entirely different method, we prove a generalization of this formula to a fourth moment of Dirichlet
$L$-functions. By an entirely different method, we prove a generalization of this formula to a fourth moment of Dirichlet 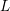 $L$-functions modulo
$L$-functions modulo 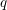 $q$ weighted by a non-archimedean test function. This establishes a new reciprocity formula. As an application, we obtain sharp upper bounds for the fourth moment twisted by the square of a Dirichlet polynomial of length
$q$ weighted by a non-archimedean test function. This establishes a new reciprocity formula. As an application, we obtain sharp upper bounds for the fourth moment twisted by the square of a Dirichlet polynomial of length 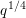 $q^{1/4}$. An auxiliary result of independent interest is a sharp upper bound for a certain sixth moment for automorphic
$q^{1/4}$. An auxiliary result of independent interest is a sharp upper bound for a certain sixth moment for automorphic 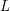 $L$-functions, which we also use to improve the best known subconvexity bounds for automorphic
$L$-functions, which we also use to improve the best known subconvexity bounds for automorphic 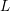 $L$-functions in the level aspect.
$L$-functions in the level aspect.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2020
Footnotes
The first author is supported in part by DFG grant BL 915/2-2. The second author is supported by the European Research Council grant agreement 670239. The third author is supported by the Simons Foundation (award 630985).
References
- 9
- Cited by


