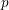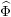1 Introduction
The theory of Rankin–Selberg integrals for  $\operatorname{GL}_{n}\times \operatorname{GL}_{n^{\prime }}$, studied by Jacquet, Piatetski-Shapiro and Shalika in a series of papers starting in the late 1970s (notably [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83]), is a basic tool in the theory of automorphic forms with an abundance of applications. The theory is based on global zeta integrals (which involve Eisenstein series in the case
$\operatorname{GL}_{n}\times \operatorname{GL}_{n^{\prime }}$, studied by Jacquet, Piatetski-Shapiro and Shalika in a series of papers starting in the late 1970s (notably [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83]), is a basic tool in the theory of automorphic forms with an abundance of applications. The theory is based on global zeta integrals (which involve Eisenstein series in the case  $n^{\prime }=n$) that unfold to adelic integrals of Whittaker–Fourier coefficients of cuspidal representations. By local multiplicity one, these integrals factorize into a product of local zeta integrals pertaining to generic representations and their Whittaker models.
$n^{\prime }=n$) that unfold to adelic integrals of Whittaker–Fourier coefficients of cuspidal representations. By local multiplicity one, these integrals factorize into a product of local zeta integrals pertaining to generic representations and their Whittaker models.
The purpose of this paper is to study a modification of the local Rankin–Selberg integrals in the equal-rank case for a class of representations  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ where
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ where  $\unicode[STIX]{x1D70B}$ is an irreducible generic representation of
$\unicode[STIX]{x1D70B}$ is an irreducible generic representation of  $\operatorname{GL}_{n}$ over a
$\operatorname{GL}_{n}$ over a  $p$-adic field and
$p$-adic field and  $m\geqslant 1$ is an integer. If
$m\geqslant 1$ is an integer. If  $\unicode[STIX]{x1D70B}$ is unitarizable (and generic),
$\unicode[STIX]{x1D70B}$ is unitarizable (and generic),  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is the Langlands quotient of the parabolic induction of
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is the Langlands quotient of the parabolic induction of  $\unicode[STIX]{x1D70B}|\det |^{(m-1)/2}\otimes \unicode[STIX]{x1D70B}|\det |^{(m-3)/2}\otimes \cdots \otimes \unicode[STIX]{x1D70B}|\det |^{(1-m)/2}$. In particular, if
$\unicode[STIX]{x1D70B}|\det |^{(m-1)/2}\otimes \unicode[STIX]{x1D70B}|\det |^{(m-3)/2}\otimes \cdots \otimes \unicode[STIX]{x1D70B}|\det |^{(1-m)/2}$. In particular, if  $\unicode[STIX]{x1D70B}$ is discrete series,
$\unicode[STIX]{x1D70B}$ is discrete series,  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is the usual ‘Speh representation’. These representations (of
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is the usual ‘Speh representation’. These representations (of  $\operatorname{GL}_{mn}$) are not generic if
$\operatorname{GL}_{mn}$) are not generic if  $m>1$ (i.e. they do not admit a Whittaker model). Instead, the integrals involve a different model which for simplicity we will call a Shalika model. (We caution, however, that it does not exactly coincide with the standard notion of the Shalika model in the literature.) It is known that any
$m>1$ (i.e. they do not admit a Whittaker model). Instead, the integrals involve a different model which for simplicity we will call a Shalika model. (We caution, however, that it does not exactly coincide with the standard notion of the Shalika model in the literature.) It is known that any  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ admits a unique Shalika model, a fact that reflects the ‘smallness’ of
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ admits a unique Shalika model, a fact that reflects the ‘smallness’ of  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$. Structurally, the new integrals look very much like the classical ones and in fact they can be explicitly related. In particular, the unramified computation reduces to that of the classical Rankin–Selberg integrals [Reference Jacquet and ShalikaJS81] (which in turn uses Cauchy’s identity and Shintani’s formula for the unramified Whittaker function of
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$. Structurally, the new integrals look very much like the classical ones and in fact they can be explicitly related. In particular, the unramified computation reduces to that of the classical Rankin–Selberg integrals [Reference Jacquet and ShalikaJS81] (which in turn uses Cauchy’s identity and Shintani’s formula for the unramified Whittaker function of  $\operatorname{GL}_{n}$ [Reference ShintaniShi76]).
$\operatorname{GL}_{n}$ [Reference ShintaniShi76]).
Just as the Whittaker model gives rise to the so-called Kirillov model [Reference Gel’fand and KajdanGK75] (by restriction to the mirabolic subgroup, namely, the stabilizer of a vector in  $\operatorname{GL}_{n}$ in its standard
$\operatorname{GL}_{n}$ in its standard  $n$-dimensional representation) the Shalika model gives rise to a closely related object which we call the Kirillov–Shalika model. The role of the mirabolic subgroup is now played by the joint stabilizer of
$n$-dimensional representation) the Shalika model gives rise to a closely related object which we call the Kirillov–Shalika model. The role of the mirabolic subgroup is now played by the joint stabilizer of  $m$ linearly independent vectors in
$m$ linearly independent vectors in  $\operatorname{GL}_{mn}$. The argument of Gelfand and Kazhdan shows that the Kirillov–Shalika model contains all functions that are compactly supported modulo the equivariance subgroup.
$\operatorname{GL}_{mn}$. The argument of Gelfand and Kazhdan shows that the Kirillov–Shalika model contains all functions that are compactly supported modulo the equivariance subgroup.
There are, however, some differences between the classical theory and its suggested analogue. First, in the unramified case, we are unaware of a simple closed formula for the spherical function in the Shalika model, except if  $n\leqslant 2$ or if
$n\leqslant 2$ or if  $n=3$ and
$n=3$ and  $m=2$. A related, equally difficult, problem is the asymptotic behavior of a function in the Shalika model. Apart from the above-mentioned cases, both problems go beyond the ‘comfort zone’ of spherical varieties, for which the works of Sakellaridis [Reference SakellaridisSak13] and Sakellaridis and Venkatesh [Reference Sakellaridis and VenkateshSV17] provide a conceptual framework and satisfactory answers to the questions above. Moreover, at this stage it is not clear whether there is an analogue of the Bernstein–Zelevinsky theory of derivatives [Reference Bernšten̆ and ZelevinskyBZ76, Reference Bernshtein and ZelevinskyBZ77] in the case at hand. In particular, we do not know whether the restriction of
$m=2$. A related, equally difficult, problem is the asymptotic behavior of a function in the Shalika model. Apart from the above-mentioned cases, both problems go beyond the ‘comfort zone’ of spherical varieties, for which the works of Sakellaridis [Reference SakellaridisSak13] and Sakellaridis and Venkatesh [Reference Sakellaridis and VenkateshSV17] provide a conceptual framework and satisfactory answers to the questions above. Moreover, at this stage it is not clear whether there is an analogue of the Bernstein–Zelevinsky theory of derivatives [Reference Bernšten̆ and ZelevinskyBZ76, Reference Bernshtein and ZelevinskyBZ77] in the case at hand. In particular, we do not know whether the restriction of  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ to a parabolic subgroup of type
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ to a parabolic subgroup of type  $((n-1)m,m)$ is of finite length.
$((n-1)m,m)$ is of finite length.
Another aspect of the paper is to provide an explicit, manifestly positive, unitary structure for the Speh representation in its Shalika model. (By this we mean that the positive-definiteness is ‘clear and obvious’ from the definition.) Once again, this is modeled on the case of generic unitarizable representations, in which Bernstein gives a unitary structure for their Whittaker models by taking the  $L^{2}$-inner product of Whittaker functions restricted to the mirabolic subgroup [Reference BernsteinBer84]. For
$L^{2}$-inner product of Whittaker functions restricted to the mirabolic subgroup [Reference BernsteinBer84]. For  $m>1$ we use instead the joint stabilizer of
$m>1$ we use instead the joint stabilizer of  $m$ vectors, as before.
$m$ vectors, as before.
Along with the above-mentioned Shalika model, the representations  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ admit various other models, for instance the degenerate Whittaker model considered by Zelevinsky (for any irreducible representation) in [Reference ZelevinskyZel80]. We can think of this as a sequence of models starting from the Zelevinsky model and ending with the Shalika model. They all involve a character on a unipotent subgroup and are covered by the general construction of Mœglin and Waldspurger [Reference Mœglin and WaldspurgerMW87]. The unipotent subgroups in the sequence are decreasing. One can write down explicit isomorphisms (transition maps) between these models. This idea has been used by many authors, most recently and systematically by Gomez, Gourevitch and Sahi [Reference Gomez, Gourevitch and SahiGGS16, Reference Gomez, Gourevitch and SahiGGS17]. It also played a role in the recent work of Cai, Friedberg and Kaplan on new doubling constructions of
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ admit various other models, for instance the degenerate Whittaker model considered by Zelevinsky (for any irreducible representation) in [Reference ZelevinskyZel80]. We can think of this as a sequence of models starting from the Zelevinsky model and ending with the Shalika model. They all involve a character on a unipotent subgroup and are covered by the general construction of Mœglin and Waldspurger [Reference Mœglin and WaldspurgerMW87]. The unipotent subgroups in the sequence are decreasing. One can write down explicit isomorphisms (transition maps) between these models. This idea has been used by many authors, most recently and systematically by Gomez, Gourevitch and Sahi [Reference Gomez, Gourevitch and SahiGGS16, Reference Gomez, Gourevitch and SahiGGS17]. It also played a role in the recent work of Cai, Friedberg and Kaplan on new doubling constructions of  $L$-functions [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Cai, Friedberg and KaplanCFK18]. We write an inner product for each of these models and show that the transition maps are unitary.
$L$-functions [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Cai, Friedberg and KaplanCFK18]. We write an inner product for each of these models and show that the transition maps are unitary.
As far as we know, this is the first time a purely local, manifestly positive hermitian form for a general Speh representation is explicitly given. Of course, the intertwining operator on the standard module whose image is the Speh representation induces its unitary structure – a fact that is true in general for any unitarizable representation on a reductive group (cf. [Reference Knapp and ZuckermanKZ77, §4]). (In the case at hand we will explicitly relate this unitary structure to that on the Shalika model.) However, the semidefiniteness of the intertwining operator is far from obvious – in fact it is equivalent to unitarizability, which is known to be a difficult problem in general, as is evident from the work of Vogan and many others. Another realization of the inner product is obtained by using global theory to embed Speh representations as local constituents of automorphic forms in the discrete spectrum of  $\operatorname{GL}_{mn}$ over the adeles [Reference SpehSpe83]. Finally, in the
$\operatorname{GL}_{mn}$ over the adeles [Reference SpehSpe83]. Finally, in the  $m=2$ case one can also realize a Speh representation in the discrete spectrum of
$m=2$ case one can also realize a Speh representation in the discrete spectrum of  $L^{2}(H\backslash \!\operatorname{GL}_{2n})$ where
$L^{2}(H\backslash \!\operatorname{GL}_{2n})$ where  $H$ is the symplectic group of rank
$H$ is the symplectic group of rank  $n$ [Reference SmithSmi18, Reference Lapid and OffenLO19]. However, there is no such analogue for
$n$ [Reference SmithSmi18, Reference Lapid and OffenLO19]. However, there is no such analogue for  $m>2$.
$m>2$.
In principle, the new local integrals are the local counterpart of certain global integrals, just as in the classical case. However, in addition to Eisenstein series, these global integrals involve automorphic forms in the discrete spectrum, rather than cusp forms, and they unfortunately do not converge (for any value of  $s$). It should be possible (for instance by using the recent work of Zydor [Reference ZydorZyd19]) to carry out a regularization procedure to make sense of these integrals and to justify the unfolding procedure. However, we will not discuss this aspect in the paper. Nor we will discuss the archimedean case, for which we expect many of our results to hold without change.
$s$). It should be possible (for instance by using the recent work of Zydor [Reference ZydorZyd19]) to carry out a regularization procedure to make sense of these integrals and to justify the unfolding procedure. However, we will not discuss this aspect in the paper. Nor we will discuss the archimedean case, for which we expect many of our results to hold without change.
The main new results of this paper are in §§ 4 and 5. The unitary structure for Speh representations (and more generally,  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ for unitarizable generic
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ for unitarizable generic  $\unicode[STIX]{x1D70B}$), on their various models, is given in Theorem 4.3. The new zeta integrals are defined in § 5. The convergence, unramified computation and local functional equations are stated in Theorem 5.1.
$\unicode[STIX]{x1D70B}$), on their various models, is given in Theorem 4.3. The new zeta integrals are defined in § 5. The convergence, unramified computation and local functional equations are stated in Theorem 5.1.
We now give some more details about the contents of the paper. In § 2 we first introduce some notation and recall Zelevinsky’s classification of irreducible representations of the general linear group over a local non-archimedean field  $F$. We then introduce the class of
$F$. We then introduce the class of  $m$-homogeneous representations, which includes the usual Speh representations and which is the main focus of the paper. In terms of Zelevinsky’s classification, they simply correspond to multisegments consisting of segments of length
$m$-homogeneous representations, which includes the usual Speh representations and which is the main focus of the paper. In terms of Zelevinsky’s classification, they simply correspond to multisegments consisting of segments of length  $m$, where
$m$, where  $m\geqslant 1$ is a fixed integer parameter. The case
$m\geqslant 1$ is a fixed integer parameter. The case  $m=1$ exactly corresponds to generic representations (i.e. the classical theory). In § 3 we introduce the models pertaining to
$m=1$ exactly corresponds to generic representations (i.e. the classical theory). In § 3 we introduce the models pertaining to  $m$-homogeneous representations, following Mœglin–Waldspurger. (In order to use their results, we assume from § 3 onward that
$m$-homogeneous representations, following Mœglin–Waldspurger. (In order to use their results, we assume from § 3 onward that  $F$ is of characteristic
$F$ is of characteristic  $0$. As was pointed out to us by Dmitry Gourevitch, this assumption can be lifted. Details will appear elsewhere.) We also introduce the transition maps between the models. They are given by integrals which entail no convergence issues. Finally, we introduce the Kirillov–Shalika model which is the analogue of the classical Kirillov model for generic representations. In § 4 we introduce a family of bilinear forms on a pair of models of
$0$. As was pointed out to us by Dmitry Gourevitch, this assumption can be lifted. Details will appear elsewhere.) We also introduce the transition maps between the models. They are given by integrals which entail no convergence issues. Finally, we introduce the Kirillov–Shalika model which is the analogue of the classical Kirillov model for generic representations. In § 4 we introduce a family of bilinear forms on a pair of models of  $m$-homogeneous representations. In the case where the two representations are in duality, these bilinear forms specialize to an invariant pairing, at least under some restrictions. In the unitarizable case this gives rise to a manifestly positive invariant unitary structure. The invariance is proved by induction on
$m$-homogeneous representations. In the case where the two representations are in duality, these bilinear forms specialize to an invariant pairing, at least under some restrictions. In the unitarizable case this gives rise to a manifestly positive invariant unitary structure. The invariance is proved by induction on  $m$ using Bernstein’s theorem on invariant distributions with respect to the mirabolic subgroup. In § 5 we define the local Rankin–Selberg integrals for
$m$ using Bernstein’s theorem on invariant distributions with respect to the mirabolic subgroup. In § 5 we define the local Rankin–Selberg integrals for  $m$-homogeneous representations using their Shalika models. Applying the transition maps, we can express these integrals in terms of the Zelevinsky model. Hence, we get their rationality in
$m$-homogeneous representations using their Shalika models. Applying the transition maps, we can express these integrals in terms of the Zelevinsky model. Hence, we get their rationality in  $q^{s}$, the unramified computation and functional equations. In § 6 we obtain more information about the poles of the zeta functions and relate them to the above-mentioned bilinear forms and, in particular, to the invariant pairing. In § 7 we go back to the Kirillov–Shalika model and analyze in detail the case of Speh representations of
$q^{s}$, the unramified computation and functional equations. In § 6 we obtain more information about the poles of the zeta functions and relate them to the above-mentioned bilinear forms and, in particular, to the invariant pairing. In § 7 we go back to the Kirillov–Shalika model and analyze in detail the case of Speh representations of  $\operatorname{GL}_{4}$ pertaining to supercuspidal representations of
$\operatorname{GL}_{4}$ pertaining to supercuspidal representations of  $\operatorname{GL}_{2}$. We study the asymptotic behavior of a function in the Kirillov–Shalika model. At this stage, it is hard to tell whether the result is representative of the general case or merely a low-rank fluke. In § 8 we write an informal global expression, modeled after the classical Rankin–Selberg integrals, whose regularization is expected to unfold to the local integrals studied in the paper. The regularization is necessary as the integral does not converge. (It would also eliminate extraneous terms in the unfolding procedure.) However, we do not discuss the regularization procedure and only give a purely heuristic argument. Finally, in Appendix A we relate the pairing of § 4 to that induced by the intertwining operator on the standard module.
$\operatorname{GL}_{2}$. We study the asymptotic behavior of a function in the Kirillov–Shalika model. At this stage, it is hard to tell whether the result is representative of the general case or merely a low-rank fluke. In § 8 we write an informal global expression, modeled after the classical Rankin–Selberg integrals, whose regularization is expected to unfold to the local integrals studied in the paper. The regularization is necessary as the integral does not converge. (It would also eliminate extraneous terms in the unfolding procedure.) However, we do not discuss the regularization procedure and only give a purely heuristic argument. Finally, in Appendix A we relate the pairing of § 4 to that induced by the intertwining operator on the standard module.
2 Preliminaries
2.1 Notation
Throughout the paper, fix a non-archimedean local field  $F$ with ring of integers
$F$ with ring of integers  ${\mathcal{O}}$ and absolute value
${\mathcal{O}}$ and absolute value  $|\cdot |$. In principle it should be possible to deal with the archimedean case as well with proper adjustments, but we do not consider this case here.
$|\cdot |$. In principle it should be possible to deal with the archimedean case as well with proper adjustments, but we do not consider this case here.
From § 3 onward,  $F$ is assumed to be of characteristic
$F$ is assumed to be of characteristic  $0$.
$0$.
If  $H$ is an algebraic group over
$H$ is an algebraic group over  $F$, we often also use
$F$, we often also use  $H$ to denote
$H$ to denote  $H(F)$.
$H(F)$.
We will consider complex, smooth representations of finite length of the groups  $\operatorname{GL}_{n}(F)$,
$\operatorname{GL}_{n}(F)$,  $n\geqslant 0$. We denote the set of irreducible representations of
$n\geqslant 0$. We denote the set of irreducible representations of  $\operatorname{GL}_{n}(F)$ (up to equivalence) by
$\operatorname{GL}_{n}(F)$ (up to equivalence) by  $\operatorname{Irr}\operatorname{GL}_{n}$ and set
$\operatorname{Irr}\operatorname{GL}_{n}$ and set  $\operatorname{Irr}=\bigcup _{n\geqslant 0}\operatorname{Irr}\operatorname{GL}_{n}$. We write
$\operatorname{Irr}=\bigcup _{n\geqslant 0}\operatorname{Irr}\operatorname{GL}_{n}$. We write  $\operatorname{Irr}\operatorname{GL}_{0}=\{\mathbf{1}\}$. (In contrast, the one-dimensional trivial character of
$\operatorname{Irr}\operatorname{GL}_{0}=\{\mathbf{1}\}$. (In contrast, the one-dimensional trivial character of  $\operatorname{GL}_{1}$ will be denoted by
$\operatorname{GL}_{1}$ will be denoted by  $\mathbf{1}_{F^{\ast }}$.) The subset of supercuspidal (respectively, square-integrable, essentially square-integrable, tempered, generic) representations will be denoted by
$\mathbf{1}_{F^{\ast }}$.) The subset of supercuspidal (respectively, square-integrable, essentially square-integrable, tempered, generic) representations will be denoted by  $\operatorname{Irr}_{\operatorname{cusp}}$ (respectively,
$\operatorname{Irr}_{\operatorname{cusp}}$ (respectively,  $\operatorname{Irr}_{\operatorname{sqr}}$,
$\operatorname{Irr}_{\operatorname{sqr}}$,  $\operatorname{Irr}_{\operatorname{esqr}}$,
$\operatorname{Irr}_{\operatorname{esqr}}$,  $\operatorname{Irr}_{\operatorname{tmp}}$,
$\operatorname{Irr}_{\operatorname{tmp}}$,  $\operatorname{Irr}_{\operatorname{gen}}$). Thus,
$\operatorname{Irr}_{\operatorname{gen}}$). Thus,
 $$\begin{eqnarray}\operatorname{Irr}_{\operatorname{cusp}}\subset \operatorname{Irr}_{\operatorname{sqr}}\subset \operatorname{Irr}_{\operatorname{esqr}}\quad \text{and}\quad \operatorname{Irr}_{\operatorname{esqr}},\operatorname{Irr}_{\operatorname{tmp}}\subset \operatorname{Irr}_{\operatorname{gen}}\!.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Irr}_{\operatorname{cusp}}\subset \operatorname{Irr}_{\operatorname{sqr}}\subset \operatorname{Irr}_{\operatorname{esqr}}\quad \text{and}\quad \operatorname{Irr}_{\operatorname{esqr}},\operatorname{Irr}_{\operatorname{tmp}}\subset \operatorname{Irr}_{\operatorname{gen}}\!.\end{eqnarray}$$ By convention  $\mathbf{1}\in \operatorname{Irr}_{\operatorname{tmp}}$ but
$\mathbf{1}\in \operatorname{Irr}_{\operatorname{tmp}}$ but  $\mathbf{1}\notin \operatorname{Irr}_{\operatorname{esqr}}$.
$\mathbf{1}\notin \operatorname{Irr}_{\operatorname{esqr}}$.
Let  $\unicode[STIX]{x1D70B}$ be a representation of
$\unicode[STIX]{x1D70B}$ be a representation of  $\operatorname{GL}_{n}(F)$. We denote by
$\operatorname{GL}_{n}(F)$. We denote by  $\unicode[STIX]{x1D70B}^{\vee }$ the contragredient of
$\unicode[STIX]{x1D70B}^{\vee }$ the contragredient of  $\unicode[STIX]{x1D70B}$ and by
$\unicode[STIX]{x1D70B}$ and by  $\operatorname{soc}(\unicode[STIX]{x1D70B})$ the socle of
$\operatorname{soc}(\unicode[STIX]{x1D70B})$ the socle of  $\unicode[STIX]{x1D70B}$ (the maximal semisimple subrepresentation of
$\unicode[STIX]{x1D70B}$ (the maximal semisimple subrepresentation of  $\unicode[STIX]{x1D70B}$). If
$\unicode[STIX]{x1D70B}$). If  $\unicode[STIX]{x1D70B}$ is non-zero, then we write
$\unicode[STIX]{x1D70B}$ is non-zero, then we write  $\deg \unicode[STIX]{x1D70B}=n$, the degree of
$\deg \unicode[STIX]{x1D70B}=n$, the degree of  $\unicode[STIX]{x1D70B}$. For any character
$\unicode[STIX]{x1D70B}$. For any character  $\unicode[STIX]{x1D714}$ of
$\unicode[STIX]{x1D714}$ of  $F^{\ast }$ (i.e.
$F^{\ast }$ (i.e.  $\unicode[STIX]{x1D714}\in \operatorname{Irr}\operatorname{GL}_{1}$) we denote by
$\unicode[STIX]{x1D714}\in \operatorname{Irr}\operatorname{GL}_{1}$) we denote by  $\unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}$ the representation obtained from
$\unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}$ the representation obtained from  $\unicode[STIX]{x1D70B}$ by twisting by the character
$\unicode[STIX]{x1D70B}$ by twisting by the character  $\unicode[STIX]{x1D714}\circ \det$. For instance,
$\unicode[STIX]{x1D714}\circ \det$. For instance,  $\unicode[STIX]{x1D70B}|\cdot |$ is the twist of
$\unicode[STIX]{x1D70B}|\cdot |$ is the twist of  $\unicode[STIX]{x1D70B}$ by
$\unicode[STIX]{x1D70B}$ by  $|\det |$. We also write
$|\det |$. We also write  $J_{P}(\unicode[STIX]{x1D70B})$ for the (normalized) Jacquet module of
$J_{P}(\unicode[STIX]{x1D70B})$ for the (normalized) Jacquet module of  $\unicode[STIX]{x1D70B}$ with respect to a parabolic subgroup
$\unicode[STIX]{x1D70B}$ with respect to a parabolic subgroup  $P$ of
$P$ of  $\operatorname{GL}_{n}$, defined over
$\operatorname{GL}_{n}$, defined over  $F$. If
$F$. If  $\unicode[STIX]{x1D70F}\in \operatorname{Irr}\operatorname{GL}_{n}$, then we write
$\unicode[STIX]{x1D70F}\in \operatorname{Irr}\operatorname{GL}_{n}$, then we write  $\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D70B}$ if
$\unicode[STIX]{x1D70F}\leqslant \unicode[STIX]{x1D70B}$ if  $\unicode[STIX]{x1D70F}$ occurs as a subquotient of
$\unicode[STIX]{x1D70F}$ occurs as a subquotient of  $\unicode[STIX]{x1D70B}$, that is, if
$\unicode[STIX]{x1D70B}$, that is, if  $\unicode[STIX]{x1D70F}$ occurs in the Jordan–Hölder sequence of
$\unicode[STIX]{x1D70F}$ occurs in the Jordan–Hölder sequence of  $\unicode[STIX]{x1D70B}$. If
$\unicode[STIX]{x1D70B}$. If  $\unicode[STIX]{x1D70F}$ occurs with multiplicity one in the Jordan–Hölder sequence of
$\unicode[STIX]{x1D70F}$ occurs with multiplicity one in the Jordan–Hölder sequence of  $\unicode[STIX]{x1D70B}$, then we write
$\unicode[STIX]{x1D70B}$, then we write  $\unicode[STIX]{x1D70F}\,{\leqslant}_{\operatorname{unq}}\unicode[STIX]{x1D70B}$.
$\unicode[STIX]{x1D70F}\,{\leqslant}_{\operatorname{unq}}\unicode[STIX]{x1D70B}$.
If  $\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{k}$ are representations of
$\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{k}$ are representations of  $\operatorname{GL}_{n_{1}}(F),\ldots ,\operatorname{GL}_{n_{k}}(F)$ respectively, then we denote the representation parabolically induced from
$\operatorname{GL}_{n_{1}}(F),\ldots ,\operatorname{GL}_{n_{k}}(F)$ respectively, then we denote the representation parabolically induced from  $\unicode[STIX]{x1D70B}_{1}\otimes \cdots \otimes \unicode[STIX]{x1D70B}_{k}$ (normalized induction), with respect to the standard parabolic subgroup of block upper triangular matrices, by
$\unicode[STIX]{x1D70B}_{1}\otimes \cdots \otimes \unicode[STIX]{x1D70B}_{k}$ (normalized induction), with respect to the standard parabolic subgroup of block upper triangular matrices, by  $\unicode[STIX]{x1D70B}_{1}\times \cdots \times \unicode[STIX]{x1D70B}_{k}$ and refer to it as the product representation. We also use the notation
$\unicode[STIX]{x1D70B}_{1}\times \cdots \times \unicode[STIX]{x1D70B}_{k}$ and refer to it as the product representation. We also use the notation  $\operatorname{Ind}_{H}^{G}$ and
$\operatorname{Ind}_{H}^{G}$ and  $\operatorname{ind}_{H}^{G}$ to denote induction and induction with compact support (both normalized) from a subgroup
$\operatorname{ind}_{H}^{G}$ to denote induction and induction with compact support (both normalized) from a subgroup  $H$ of
$H$ of  $G$.
$G$.
For any  $\unicode[STIX]{x1D70F}\in \operatorname{Irr}_{\operatorname{esqr}}$, let
$\unicode[STIX]{x1D70F}\in \operatorname{Irr}_{\operatorname{esqr}}$, let  $\mathbf{e}(\unicode[STIX]{x1D70F})$ be the unique real number
$\mathbf{e}(\unicode[STIX]{x1D70F})$ be the unique real number  $s$ such that the twisted representation
$s$ such that the twisted representation  $\unicode[STIX]{x1D70F}|\cdot |^{-s}$ is unitarizable (i.e. has a unitary central character). Note that
$\unicode[STIX]{x1D70F}|\cdot |^{-s}$ is unitarizable (i.e. has a unitary central character). Note that  $\mathbf{e}(\unicode[STIX]{x1D70F}^{\vee })=-\mathbf{e}(\unicode[STIX]{x1D70F})$. Any
$\mathbf{e}(\unicode[STIX]{x1D70F}^{\vee })=-\mathbf{e}(\unicode[STIX]{x1D70F})$. Any  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}$ can be written uniquely (up to permutation) as
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}$ can be written uniquely (up to permutation) as  $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70F}_{1}\times \cdots \times \unicode[STIX]{x1D70F}_{k}$ where
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70F}_{1}\times \cdots \times \unicode[STIX]{x1D70F}_{k}$ where  $\unicode[STIX]{x1D70F}_{i}$ are essentially square-integrable. Let
$\unicode[STIX]{x1D70F}_{i}$ are essentially square-integrable. Let  $\mathbf{e}(\unicode[STIX]{x1D70B})=\min \mathbf{e}(\unicode[STIX]{x1D70F}_{i})$. (For consistency we write
$\mathbf{e}(\unicode[STIX]{x1D70B})=\min \mathbf{e}(\unicode[STIX]{x1D70F}_{i})$. (For consistency we write  $\mathbf{e}(\mathbf{1})=0$.) Then
$\mathbf{e}(\mathbf{1})=0$.) Then  $\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\vee })\leqslant 0$ with equality if and only if
$\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\vee })\leqslant 0$ with equality if and only if  $\unicode[STIX]{x1D70B}$ is essentially tempered. Moreover,
$\unicode[STIX]{x1D70B}$ is essentially tempered. Moreover,  $\unicode[STIX]{x1D70B}$ is tempered if and only if
$\unicode[STIX]{x1D70B}$ is tempered if and only if  $\mathbf{e}(\unicode[STIX]{x1D70B})=\mathbf{e}(\unicode[STIX]{x1D70B}^{\vee })=0$. More generally, we will say that
$\mathbf{e}(\unicode[STIX]{x1D70B})=\mathbf{e}(\unicode[STIX]{x1D70B}^{\vee })=0$. More generally, we will say that  $\unicode[STIX]{x1D70B}$ is ‘approximately tempered’ (AT) if
$\unicode[STIX]{x1D70B}$ is ‘approximately tempered’ (AT) if  $\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\vee })+1>0$. Equivalently,
$\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\vee })+1>0$. Equivalently,  $\mathbf{e}(\unicode[STIX]{x1D70F}_{i})-\mathbf{e}(\unicode[STIX]{x1D70F}_{j})<1$ for all
$\mathbf{e}(\unicode[STIX]{x1D70F}_{i})-\mathbf{e}(\unicode[STIX]{x1D70F}_{j})<1$ for all  $i,j$. It is known that every unitarizable
$i,j$. It is known that every unitarizable  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}$ is (AT). (This follows from the classification of the unitary dual of
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}$ is (AT). (This follows from the classification of the unitary dual of  $\operatorname{GL}_{n}(F)$ by Tadić [Reference TadićTad86].) We denote by
$\operatorname{GL}_{n}(F)$ by Tadić [Reference TadićTad86].) We denote by  $\operatorname{Irr}_{(AT)}$ the set of (AT) representations.
$\operatorname{Irr}_{(AT)}$ the set of (AT) representations.
For any set  $A$ we denote by
$A$ we denote by  ${\mathcal{M}}(A)$ the free commutative monoid generated by
${\mathcal{M}}(A)$ the free commutative monoid generated by  $A$, considered as an ordered monoid. Thus, an element of
$A$, considered as an ordered monoid. Thus, an element of  ${\mathcal{M}}(A)$ (a multiset of
${\mathcal{M}}(A)$ (a multiset of  $A$) is a finite (possibly empty) formal sum of element of
$A$) is a finite (possibly empty) formal sum of element of  $A$.
$A$.
2.2 Zelevinsky classification
We recall the well-known results and terminology of [Reference ZelevinskyZel80].
A segment  $\unicode[STIX]{x1D6E5}$ (of length
$\unicode[STIX]{x1D6E5}$ (of length  $l>0$ and center
$l>0$ and center  $\unicode[STIX]{x1D70C}\in \operatorname{Irr}_{\operatorname{cusp}}$) is a non-empty finite subset of
$\unicode[STIX]{x1D70C}\in \operatorname{Irr}_{\operatorname{cusp}}$) is a non-empty finite subset of  $\operatorname{Irr}_{\operatorname{cusp}}$ of the form
$\operatorname{Irr}_{\operatorname{cusp}}$ of the form
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}}^{(l)}=\{\unicode[STIX]{x1D70C}|\cdot |^{(1-l)/2},\unicode[STIX]{x1D70C}|\cdot |^{(3-l)/2},\ldots ,\unicode[STIX]{x1D70C}|\cdot |^{(l-1)/2}\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}}^{(l)}=\{\unicode[STIX]{x1D70C}|\cdot |^{(1-l)/2},\unicode[STIX]{x1D70C}|\cdot |^{(3-l)/2},\ldots ,\unicode[STIX]{x1D70C}|\cdot |^{(l-1)/2}\}.\end{eqnarray}$$ We define  $\deg \unicode[STIX]{x1D6E5}=l\deg \unicode[STIX]{x1D70C}$ and write
$\deg \unicode[STIX]{x1D6E5}=l\deg \unicode[STIX]{x1D70C}$ and write  $e(\unicode[STIX]{x1D6E5})=\unicode[STIX]{x1D70C}|\cdot |^{(l-1)/2}\in \operatorname{Irr}_{\operatorname{cusp}}$ (the endpoint of
$e(\unicode[STIX]{x1D6E5})=\unicode[STIX]{x1D70C}|\cdot |^{(l-1)/2}\in \operatorname{Irr}_{\operatorname{cusp}}$ (the endpoint of  $\unicode[STIX]{x1D6E5}$),
$\unicode[STIX]{x1D6E5}$),
 $$\begin{eqnarray}\mathfrak{c}(\unicode[STIX]{x1D6E5})=\unicode[STIX]{x1D70C}|\cdot |^{(1-l)/2}+\unicode[STIX]{x1D70C}|\cdot |^{(3-l)/2}+\cdots +\unicode[STIX]{x1D70C}|\cdot |^{(l-1)/2}\in {\mathcal{M}}(\operatorname{Irr}_{\operatorname{ cusp}})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{c}(\unicode[STIX]{x1D6E5})=\unicode[STIX]{x1D70C}|\cdot |^{(1-l)/2}+\unicode[STIX]{x1D70C}|\cdot |^{(3-l)/2}+\cdots +\unicode[STIX]{x1D70C}|\cdot |^{(l-1)/2}\in {\mathcal{M}}(\operatorname{Irr}_{\operatorname{ cusp}})\end{eqnarray}$$ and  $\unicode[STIX]{x1D6E5}^{\vee }=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}^{\vee }}^{(l)}$. For compatibility we also write
$\unicode[STIX]{x1D6E5}^{\vee }=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}^{\vee }}^{(l)}$. For compatibility we also write  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}}^{(0)}=\emptyset$. Denote by
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}}^{(0)}=\emptyset$. Denote by  ${\mathcal{S}}{\mathcal{E}}{\mathcal{G}}$ the set of all segments. We extend
${\mathcal{S}}{\mathcal{E}}{\mathcal{G}}$ the set of all segments. We extend  $\deg$ additively to a function
$\deg$ additively to a function  ${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})\rightarrow \mathbb{Z}_{{\geqslant}0}$. Similarly, we extend
${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})\rightarrow \mathbb{Z}_{{\geqslant}0}$. Similarly, we extend  $e$ and
$e$ and  $\mathfrak{c}$ additively to functions
$\mathfrak{c}$ additively to functions  ${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})\rightarrow {\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})$.
${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})\rightarrow {\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})$.
For any  $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}}^{(l)}\in {\mathcal{S}}{\mathcal{E}}{\mathcal{G}}$, let
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}}^{(l)}\in {\mathcal{S}}{\mathcal{E}}{\mathcal{G}}$, let
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D6E5})=\operatorname{soc}(\unicode[STIX]{x1D70C}|\cdot |^{(1-l)/2}\times \unicode[STIX]{x1D70C}|\cdot |^{(3-l)/2}\times \cdots \times \unicode[STIX]{x1D70C}|\cdot |^{(l-1)/2})\in \operatorname{Irr}\operatorname{GL}_{ deg\unicode[STIX]{x1D6E5}}.\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D6E5})=\operatorname{soc}(\unicode[STIX]{x1D70C}|\cdot |^{(1-l)/2}\times \unicode[STIX]{x1D70C}|\cdot |^{(3-l)/2}\times \cdots \times \unicode[STIX]{x1D70C}|\cdot |^{(l-1)/2})\in \operatorname{Irr}\operatorname{GL}_{ deg\unicode[STIX]{x1D6E5}}.\end{eqnarray}$$ (For compatibility we also set  $Z(\emptyset )=\mathbf{1}$.) Then
$Z(\emptyset )=\mathbf{1}$.) Then  $Z(\unicode[STIX]{x1D6E5})^{\vee }=Z(\unicode[STIX]{x1D6E5}^{\vee })$. Given
$Z(\unicode[STIX]{x1D6E5})^{\vee }=Z(\unicode[STIX]{x1D6E5}^{\vee })$. Given  $\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2}\in {\mathcal{S}}{\mathcal{E}}{\mathcal{G}}$, we write
$\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2}\in {\mathcal{S}}{\mathcal{E}}{\mathcal{G}}$, we write  $\unicode[STIX]{x1D6E5}_{2}\prec \unicode[STIX]{x1D6E5}_{1}$ if
$\unicode[STIX]{x1D6E5}_{2}\prec \unicode[STIX]{x1D6E5}_{1}$ if  $\unicode[STIX]{x1D6E5}_{i}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{i}}^{(l_{i})}$ with
$\unicode[STIX]{x1D6E5}_{i}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{i}}^{(l_{i})}$ with  $\unicode[STIX]{x1D70C}_{2}|\cdot |^{(1-l_{2})/2+\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D70C}_{1}|\cdot |^{(1-l_{1})/2}$ for some
$\unicode[STIX]{x1D70C}_{2}|\cdot |^{(1-l_{2})/2+\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D70C}_{1}|\cdot |^{(1-l_{1})/2}$ for some  $\unicode[STIX]{x1D6FC}\in \mathbb{Z}_{{>}0}$ such that
$\unicode[STIX]{x1D6FC}\in \mathbb{Z}_{{>}0}$ such that  $l_{2}-l_{1}<\unicode[STIX]{x1D6FC}\leqslant l_{2}$. If either
$l_{2}-l_{1}<\unicode[STIX]{x1D6FC}\leqslant l_{2}$. If either  $\unicode[STIX]{x1D6E5}_{2}\prec \unicode[STIX]{x1D6E5}_{1}$ or
$\unicode[STIX]{x1D6E5}_{2}\prec \unicode[STIX]{x1D6E5}_{1}$ or  $\unicode[STIX]{x1D6E5}_{1}\prec \unicode[STIX]{x1D6E5}_{2}$, then we say that
$\unicode[STIX]{x1D6E5}_{1}\prec \unicode[STIX]{x1D6E5}_{2}$, then we say that  $\unicode[STIX]{x1D6E5}_{1}$ and
$\unicode[STIX]{x1D6E5}_{1}$ and  $\unicode[STIX]{x1D6E5}_{2}$ are linked. The induced representation
$\unicode[STIX]{x1D6E5}_{2}$ are linked. The induced representation  $Z(\unicode[STIX]{x1D6E5}_{1})\times Z(\unicode[STIX]{x1D6E5}_{2})$ is reducible if and only if
$Z(\unicode[STIX]{x1D6E5}_{1})\times Z(\unicode[STIX]{x1D6E5}_{2})$ is reducible if and only if  $\unicode[STIX]{x1D6E5}_{1}$ and
$\unicode[STIX]{x1D6E5}_{1}$ and  $\unicode[STIX]{x1D6E5}_{2}$ are linked.
$\unicode[STIX]{x1D6E5}_{2}$ are linked.
The well-known classification result of Zelevinsky [Reference ZelevinskyZel80, Theorem 6.5] extends the map  $\unicode[STIX]{x1D6E5}\mapsto Z(\unicode[STIX]{x1D6E5})$ to a degree-preserving bijection
$\unicode[STIX]{x1D6E5}\mapsto Z(\unicode[STIX]{x1D6E5})$ to a degree-preserving bijection
 $$\begin{eqnarray}\mathfrak{m}\mapsto Z(\mathfrak{m})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}\mapsto Z(\mathfrak{m})\end{eqnarray}$$ between  ${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$ and
${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$ and  $\operatorname{Irr}$. If
$\operatorname{Irr}$. If  $\mathfrak{m}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$ and
$\mathfrak{m}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$ and  $\unicode[STIX]{x1D6E5}_{i}\not \prec \unicode[STIX]{x1D6E5}_{j}$ for any
$\unicode[STIX]{x1D6E5}_{i}\not \prec \unicode[STIX]{x1D6E5}_{j}$ for any  $i<j$ (which can always be arranged), then
$i<j$ (which can always be arranged), then  $Z(\mathfrak{m})=\operatorname{soc}(Z(\unicode[STIX]{x1D6E5}_{1})\times \cdots \times Z(\unicode[STIX]{x1D6E5}_{k}))$. An element of
$Z(\mathfrak{m})=\operatorname{soc}(Z(\unicode[STIX]{x1D6E5}_{1})\times \cdots \times Z(\unicode[STIX]{x1D6E5}_{k}))$. An element of  ${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$ is called a multisegment. We have
${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$ is called a multisegment. We have  $Z(\mathfrak{m})^{\vee }=Z(\mathfrak{m}^{\vee })$, where we extend
$Z(\mathfrak{m})^{\vee }=Z(\mathfrak{m}^{\vee })$, where we extend  $^{\vee }$ from
$^{\vee }$ from  ${\mathcal{S}}{\mathcal{E}}{\mathcal{G}}$ to
${\mathcal{S}}{\mathcal{E}}{\mathcal{G}}$ to  ${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$ additively. For any
${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$ additively. For any  $\mathfrak{m}_{1},\mathfrak{m}_{2}\in {\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$ we have
$\mathfrak{m}_{1},\mathfrak{m}_{2}\in {\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$ we have  $Z(\mathfrak{m}_{1}+\mathfrak{m}_{2})\,{\leqslant}_{\operatorname{unq}}Z(\mathfrak{m}_{1})\times Z(\mathfrak{m}_{2})$ [Reference Lapid and MínguezLM16, Proposition 3.5]. In particular, if
$Z(\mathfrak{m}_{1}+\mathfrak{m}_{2})\,{\leqslant}_{\operatorname{unq}}Z(\mathfrak{m}_{1})\times Z(\mathfrak{m}_{2})$ [Reference Lapid and MínguezLM16, Proposition 3.5]. In particular, if  $Z(\mathfrak{m}_{1})\times Z(\mathfrak{m}_{2})$ is irreducible, then it is equal to
$Z(\mathfrak{m}_{1})\times Z(\mathfrak{m}_{2})$ is irreducible, then it is equal to  $Z(\mathfrak{m}_{1}+\mathfrak{m}_{2})$.
$Z(\mathfrak{m}_{1}+\mathfrak{m}_{2})$.
We note the following fact.

By identifying an irreducible supercuspidal representation with a singleton segment we view  ${\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})$ as a submonoid of
${\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})$ as a submonoid of  ${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$. The map
${\mathcal{M}}({\mathcal{S}}{\mathcal{E}}{\mathcal{G}})$. The map  $Z$ restricts to a bijection
$Z$ restricts to a bijection
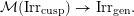 $$\begin{eqnarray}{\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})\rightarrow \operatorname{Irr}_{\operatorname{gen}}\!.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})\rightarrow \operatorname{Irr}_{\operatorname{gen}}\!.\end{eqnarray}$$ An element of  ${\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})$ is called a cuspidal datum. We write
${\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})$ is called a cuspidal datum. We write  $\mathfrak{c}(Z(\mathfrak{m}))=\mathfrak{c}(\mathfrak{m})$. The resulting map
$\mathfrak{c}(Z(\mathfrak{m}))=\mathfrak{c}(\mathfrak{m})$. The resulting map
 $$\begin{eqnarray}\mathfrak{c}:\operatorname{Irr}\rightarrow {\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{c}:\operatorname{Irr}\rightarrow {\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})\end{eqnarray}$$ is the supercuspidal support (which of course can be defined without reference to the Zelevinsky classification). The restriction of  $\mathfrak{c}$ to
$\mathfrak{c}$ to  $\operatorname{Irr}_{\operatorname{gen}}$ is the inverse of (2).
$\operatorname{Irr}_{\operatorname{gen}}$ is the inverse of (2).
For any segment  $\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}}^{(l)}$ let
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}}^{(l)}$ let  $\unicode[STIX]{x1D6E5}^{-}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}|\cdot |^{-1/2}}^{(l-1)}$ denote either the segment obtained by removing the endpoint
$\unicode[STIX]{x1D6E5}^{-}=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}|\cdot |^{-1/2}}^{(l-1)}$ denote either the segment obtained by removing the endpoint  $e(\unicode[STIX]{x1D6E5})$ of
$e(\unicode[STIX]{x1D6E5})$ of  $\unicode[STIX]{x1D6E5}$ if
$\unicode[STIX]{x1D6E5}$ if  $l>1$ or the empty set otherwise.
$l>1$ or the empty set otherwise.
Now let  $\unicode[STIX]{x1D70E}=Z(\mathfrak{m})$, where
$\unicode[STIX]{x1D70E}=Z(\mathfrak{m})$, where  $\mathfrak{m}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$. Let
$\mathfrak{m}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$. Let
 $$\begin{eqnarray}\mathfrak{m}^{-}=\unicode[STIX]{x1D6E5}_{1}^{-}+\cdots +\unicode[STIX]{x1D6E5}_{k}^{-}\quad \text{(disregarding empty sets)}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}^{-}=\unicode[STIX]{x1D6E5}_{1}^{-}+\cdots +\unicode[STIX]{x1D6E5}_{k}^{-}\quad \text{(disregarding empty sets)}.\end{eqnarray}$$ Define recursively  $\mathfrak{m}^{(0)}=\mathfrak{m}$ and
$\mathfrak{m}^{(0)}=\mathfrak{m}$ and  $\mathfrak{m}^{(k)}=(\mathfrak{m}^{(k-1)})^{-}$,
$\mathfrak{m}^{(k)}=(\mathfrak{m}^{(k-1)})^{-}$,  $k>0$, with
$k>0$, with  $\mathfrak{m}^{(l)}=0$,
$\mathfrak{m}^{(l)}=0$,  $l$ minimal. Let
$l$ minimal. Let  $n_{k}=\deg e(\mathfrak{m}^{(k-1)})$,
$n_{k}=\deg e(\mathfrak{m}^{(k-1)})$,  $k=1,\ldots ,l$, so that
$k=1,\ldots ,l$, so that  $n_{1}+\cdots +n_{l}=\deg \unicode[STIX]{x1D70E}$ and let
$n_{1}+\cdots +n_{l}=\deg \unicode[STIX]{x1D70E}$ and let  $\unicode[STIX]{x1D714}_{k}=Z(e(\mathfrak{m}^{(k-1)}))\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n_{k}}$. Let
$\unicode[STIX]{x1D714}_{k}=Z(e(\mathfrak{m}^{(k-1)}))\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n_{k}}$. Let  $P=P_{\unicode[STIX]{x1D70E}}=M_{\unicode[STIX]{x1D70E}}\ltimes U_{\unicode[STIX]{x1D70E}}=M\ltimes U$ be the standard parabolic subgroup of type
$P=P_{\unicode[STIX]{x1D70E}}=M_{\unicode[STIX]{x1D70E}}\ltimes U_{\unicode[STIX]{x1D70E}}=M\ltimes U$ be the standard parabolic subgroup of type  $(n_{l},\ldots ,n_{1})$. By [Reference ZelevinskyZel80, §8.3] the Jordan–Hölder sequence of
$(n_{l},\ldots ,n_{1})$. By [Reference ZelevinskyZel80, §8.3] the Jordan–Hölder sequence of  $J_{P}(\unicode[STIX]{x1D70E})$ admits a unique generic irreducible representation
$J_{P}(\unicode[STIX]{x1D70E})$ admits a unique generic irreducible representation  $\unicode[STIX]{x1D714}$ of
$\unicode[STIX]{x1D714}$ of  $M$ and, moreover,
$M$ and, moreover,  $\unicode[STIX]{x1D714}\,{\leqslant}_{\operatorname{unq}}J_{P}(\unicode[STIX]{x1D70E})$. Equivalently (by the uniqueness of the Whittaker model), this means that
$\unicode[STIX]{x1D714}\,{\leqslant}_{\operatorname{unq}}J_{P}(\unicode[STIX]{x1D70E})$. Equivalently (by the uniqueness of the Whittaker model), this means that
 $$\begin{eqnarray}\operatorname{Hom}_{N_{M}}(J_{P}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D713}_{P})=\operatorname{Hom}_{N}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D713}_{P})=\operatorname{Hom}_{G}(\unicode[STIX]{x1D70E},\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D713}_{P})\text{ is one-dimensional},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{N_{M}}(J_{P}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D713}_{P})=\operatorname{Hom}_{N}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D713}_{P})=\operatorname{Hom}_{G}(\unicode[STIX]{x1D70E},\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D713}_{P})\text{ is one-dimensional},\end{eqnarray}$$ where  $N$ is the maximal nilpotent group of upper unitriangular matrices and
$N$ is the maximal nilpotent group of upper unitriangular matrices and  $\unicode[STIX]{x1D713}_{P}$ is a character of
$\unicode[STIX]{x1D713}_{P}$ is a character of  $N$ which is trivial on
$N$ which is trivial on  $U$ and non-degenerate on
$U$ and non-degenerate on  $N_{M}=N\cap M$. (This property determines
$N_{M}=N\cap M$. (This property determines  $P$ uniquely up to association.) Moreover,
$P$ uniquely up to association.) Moreover,  $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{l}\otimes \cdots \otimes \unicode[STIX]{x1D714}_{1}$ (see, for example, [Reference Mínguez and SécherreMS14, Lemma 9.17]). (For an arbitrary
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{l}\otimes \cdots \otimes \unicode[STIX]{x1D714}_{1}$ (see, for example, [Reference Mínguez and SécherreMS14, Lemma 9.17]). (For an arbitrary  $P$,
$P$,  $\operatorname{Hom}_{N}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D713}_{P})$ is finite-dimensional.) We will call the image of
$\operatorname{Hom}_{N}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D713}_{P})$ is finite-dimensional.) We will call the image of  $\unicode[STIX]{x1D70E}$ in
$\unicode[STIX]{x1D70E}$ in  $\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D713}_{P}$ the Zelevinsky model of
$\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D713}_{P}$ the Zelevinsky model of  $\unicode[STIX]{x1D70E}$. In general,
$\unicode[STIX]{x1D70E}$. In general,  $\unicode[STIX]{x1D70E}\not \leqslant \unicode[STIX]{x1D714}_{l}\times \cdots \times \unicode[STIX]{x1D714}_{1}$. For example, if
$\unicode[STIX]{x1D70E}\not \leqslant \unicode[STIX]{x1D714}_{l}\times \cdots \times \unicode[STIX]{x1D714}_{1}$. For example, if  $\unicode[STIX]{x1D70E}=Z(\{\mathbf{1}_{F^{\ast }},|\cdot |\}+\{\mathbf{1}_{F^{\ast }}\})$, then
$\unicode[STIX]{x1D70E}=Z(\{\mathbf{1}_{F^{\ast }},|\cdot |\}+\{\mathbf{1}_{F^{\ast }}\})$, then  $l=2$,
$l=2$,  $\unicode[STIX]{x1D714}_{2}=\mathbf{1}_{F^{\ast }}$,
$\unicode[STIX]{x1D714}_{2}=\mathbf{1}_{F^{\ast }}$,  $\unicode[STIX]{x1D714}_{1}=Z(\{|\cdot |\}+\{\mathbf{1}_{F^{\ast }}\})$ and
$\unicode[STIX]{x1D714}_{1}=Z(\{|\cdot |\}+\{\mathbf{1}_{F^{\ast }}\})$ and  $\unicode[STIX]{x1D714}_{2}\times \unicode[STIX]{x1D714}_{1}$ is irreducible (and generic).
$\unicode[STIX]{x1D714}_{2}\times \unicode[STIX]{x1D714}_{1}$ is irreducible (and generic).
2.3 Ladder representations
A multisegment  $\mathfrak{m}$ is called a (strict) ladder if it can be written as
$\mathfrak{m}$ is called a (strict) ladder if it can be written as  $\mathfrak{m}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$ where
$\mathfrak{m}=\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k}$ where  $\unicode[STIX]{x1D6E5}_{i+1}\prec \unicode[STIX]{x1D6E5}_{i}$ for all
$\unicode[STIX]{x1D6E5}_{i+1}\prec \unicode[STIX]{x1D6E5}_{i}$ for all  $i=1,\ldots ,k-1$. The corresponding irreducible representation
$i=1,\ldots ,k-1$. The corresponding irreducible representation  $Z(\mathfrak{m})$ is called a ladder representation.
$Z(\mathfrak{m})$ is called a ladder representation.
Lemma 2.1 [Reference Lapid and MínguezLM16].
The following two statements hold.
(i) [Reference Lapid and MínguezLM16, Lemma 6.17] Let
 $\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{k}$ be ladder representations. Then
$\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{k}$ be ladder representations. Then  $\unicode[STIX]{x1D70B}_{1}\times \cdots \times \unicode[STIX]{x1D70B}_{k}$ is irreducible if and only if
$\unicode[STIX]{x1D70B}_{1}\times \cdots \times \unicode[STIX]{x1D70B}_{k}$ is irreducible if and only if  $\unicode[STIX]{x1D70B}_{i}\times \unicode[STIX]{x1D70B}_{j}$ is irreducible for all
$\unicode[STIX]{x1D70B}_{i}\times \unicode[STIX]{x1D70B}_{j}$ is irreducible for all  $i,j$.Footnote 1
$i,j$.Footnote 1(ii) [Reference Lapid and MínguezLM16, Lemma 6.21] Suppose that
 $Z(\mathfrak{m}_{1})$ and
$Z(\mathfrak{m}_{1})$ and  $Z(\mathfrak{m}_{2})$ are two ladder representations and that each segment of
$Z(\mathfrak{m}_{2})$ are two ladder representations and that each segment of  $\mathfrak{m}_{1}$ also occurs in
$\mathfrak{m}_{1}$ also occurs in  $\mathfrak{m}_{2}$. Then
$\mathfrak{m}_{2}$. Then  $Z(\mathfrak{m}_{1})\times Z(\mathfrak{m}_{2})$ is irreducible.
$Z(\mathfrak{m}_{1})\times Z(\mathfrak{m}_{2})$ is irreducible.
The Jacquet module of ladder representations was described in [Reference Kret and LapidKL12]. The following lemma is an immediate consequence.
Lemma 2.2 [Reference Kret and LapidKL12].
Let  $\unicode[STIX]{x1D70B}=Z(\mathfrak{m})$ be a ladder representation and
$\unicode[STIX]{x1D70B}=Z(\mathfrak{m})$ be a ladder representation and  $P$ a maximal parabolic subgroup. The following statements hold.
$P$ a maximal parabolic subgroup. The following statements hold.
(i)
 $J_{P}(\unicode[STIX]{x1D70B})$ is a direct sum of irreducible representations of the form
$J_{P}(\unicode[STIX]{x1D70B})$ is a direct sum of irreducible representations of the form  $\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D714}$ where both
$\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D714}$ where both  $\unicode[STIX]{x1D70F}$ and
$\unicode[STIX]{x1D70F}$ and  $\unicode[STIX]{x1D714}$ are products of ladder representations.
$\unicode[STIX]{x1D714}$ are products of ladder representations.(ii) If
 $\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D714}\leqslant J_{P}(\unicode[STIX]{x1D70B})$ and
$\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D714}\leqslant J_{P}(\unicode[STIX]{x1D70B})$ and  $\unicode[STIX]{x1D714}\notin \operatorname{Irr}_{\operatorname{gen}}$, then there exists
$\unicode[STIX]{x1D714}\notin \operatorname{Irr}_{\operatorname{gen}}$, then there exists  $\unicode[STIX]{x1D70C}\in \operatorname{Irr}_{\operatorname{cusp}}$ such that
$\unicode[STIX]{x1D70C}\in \operatorname{Irr}_{\operatorname{cusp}}$ such that  $\unicode[STIX]{x1D70C}\leqslant \mathfrak{c}(\unicode[STIX]{x1D714})$,
$\unicode[STIX]{x1D70C}\leqslant \mathfrak{c}(\unicode[STIX]{x1D714})$,  $\unicode[STIX]{x1D70C}|\cdot |\leqslant e(\mathfrak{m})$ but
$\unicode[STIX]{x1D70C}|\cdot |\leqslant e(\mathfrak{m})$ but  $\unicode[STIX]{x1D70C}\not \leqslant e(\mathfrak{m})$.
$\unicode[STIX]{x1D70C}\not \leqslant e(\mathfrak{m})$.(iii) If
 $\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D714}\leqslant J_{P}(\unicode[STIX]{x1D70B})$ with
$\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D714}\leqslant J_{P}(\unicode[STIX]{x1D70B})$ with  $\unicode[STIX]{x1D714}\in \operatorname{Irr}_{\operatorname{gen}}$, then
$\unicode[STIX]{x1D714}\in \operatorname{Irr}_{\operatorname{gen}}$, then  $\mathfrak{c}(\unicode[STIX]{x1D714})\leqslant e(\mathfrak{m})$. Moreover, if
$\mathfrak{c}(\unicode[STIX]{x1D714})\leqslant e(\mathfrak{m})$. Moreover, if  $\unicode[STIX]{x1D70C}\in \operatorname{Irr}_{\operatorname{cusp}}$ is such that
$\unicode[STIX]{x1D70C}\in \operatorname{Irr}_{\operatorname{cusp}}$ is such that  $\unicode[STIX]{x1D70C}\leqslant e(\mathfrak{m})$ and
$\unicode[STIX]{x1D70C}\leqslant e(\mathfrak{m})$ and  $\unicode[STIX]{x1D70C}|\cdot |\leqslant \mathfrak{c}(\unicode[STIX]{x1D714})$, then
$\unicode[STIX]{x1D70C}|\cdot |\leqslant \mathfrak{c}(\unicode[STIX]{x1D714})$, then  $\unicode[STIX]{x1D70C}\leqslant \mathfrak{c}(\unicode[STIX]{x1D714})$.
$\unicode[STIX]{x1D70C}\leqslant \mathfrak{c}(\unicode[STIX]{x1D714})$.(iv) If
 $\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D714}\leqslant J_{P}(\unicode[STIX]{x1D70B})$ and
$\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D714}\leqslant J_{P}(\unicode[STIX]{x1D70B})$ and  $\unicode[STIX]{x1D70C}\in \operatorname{Irr}_{\operatorname{cusp}}$ is such that
$\unicode[STIX]{x1D70C}\in \operatorname{Irr}_{\operatorname{cusp}}$ is such that  $\unicode[STIX]{x1D70C}|\cdot |\not \leqslant \mathfrak{c}(\unicode[STIX]{x1D714})$, then
$\unicode[STIX]{x1D70C}|\cdot |\not \leqslant \mathfrak{c}(\unicode[STIX]{x1D714})$, then  $\unicode[STIX]{x1D70C}$ occurs in
$\unicode[STIX]{x1D70C}$ occurs in  $\mathfrak{c}(\unicode[STIX]{x1D714})$ with multiplicity at most one.
$\mathfrak{c}(\unicode[STIX]{x1D714})$ with multiplicity at most one.
Strictly speaking, the results of [Reference Kret and LapidKL12] are stated in terms of the Langlands classification. However, they are also valid in the form above (for the Zelevinsky classification) by either repeating the arguments, or using the Zelevinsky involution.
2.4  $m$-homogeneous representationsFootnote 2
$m$-homogeneous representationsFootnote 2
From now on let  $m,n\geqslant 1$ be integers and
$m,n\geqslant 1$ be integers and  $G=\operatorname{GL}_{mn}$. We say that
$G=\operatorname{GL}_{mn}$. We say that  $\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$ is
$\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$ is  $m$-homogeneous if
$m$-homogeneous if  $\unicode[STIX]{x1D70E}=Z(\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k})$ where each
$\unicode[STIX]{x1D70E}=Z(\unicode[STIX]{x1D6E5}_{1}+\cdots +\unicode[STIX]{x1D6E5}_{k})$ where each  $\unicode[STIX]{x1D6E5}_{i}$ is of length
$\unicode[STIX]{x1D6E5}_{i}$ is of length  $m$. (If
$m$. (If  $m=1$ this simply means that
$m=1$ this simply means that  $\unicode[STIX]{x1D70E}$ is generic.) We denote by
$\unicode[STIX]{x1D70E}$ is generic.) We denote by  $\operatorname{Irr}_{m\operatorname{-hmgns}}G$ the set of irreducible
$\operatorname{Irr}_{m\operatorname{-hmgns}}G$ the set of irreducible  $m$-homogeneous representations of
$m$-homogeneous representations of  $G$. For any
$G$. For any  $\unicode[STIX]{x1D70B}=Z(\{\unicode[STIX]{x1D70C}_{1}\}+\cdots +\{\unicode[STIX]{x1D70C}_{k}\})\in \operatorname{Irr}_{\operatorname{gen}}$, define
$\unicode[STIX]{x1D70B}=Z(\{\unicode[STIX]{x1D70C}_{1}\}+\cdots +\{\unicode[STIX]{x1D70C}_{k}\})\in \operatorname{Irr}_{\operatorname{gen}}$, define
 $$\begin{eqnarray}\operatorname{Sp}(\unicode[STIX]{x1D70B},m)=Z(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{1}}^{(m)}+\cdots +\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{k}}^{(m)})\in \operatorname{Irr}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sp}(\unicode[STIX]{x1D70B},m)=Z(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{1}}^{(m)}+\cdots +\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{k}}^{(m)})\in \operatorname{Irr}.\end{eqnarray}$$The following result is clear.
Lemma 2.3. The map  $\unicode[STIX]{x1D70B}\mapsto \operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ defines a bijection between
$\unicode[STIX]{x1D70B}\mapsto \operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ defines a bijection between  $\operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ and
$\operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ and  $\operatorname{Irr}_{m\operatorname{-hmgns}}G$. We have
$\operatorname{Irr}_{m\operatorname{-hmgns}}G$. We have  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)^{\vee }=\operatorname{Sp}(\unicode[STIX]{x1D70B}^{\vee },m)$ for any
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)^{\vee }=\operatorname{Sp}(\unicode[STIX]{x1D70B}^{\vee },m)$ for any  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}$.
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}$.
Remark 2.4. The notion of  $m$-homogeneous representations is very close to the concept of ‘representations of type
$m$-homogeneous representations is very close to the concept of ‘representations of type  $(n,m)$’ introduced in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] and studied further in [Reference Cai, Friedberg and KaplanCFK18]. The difference is that we only consider irreducible representations and emphasize the roles of the Mœglin–Waldspurger models.
$(n,m)$’ introduced in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19] and studied further in [Reference Cai, Friedberg and KaplanCFK18]. The difference is that we only consider irreducible representations and emphasize the roles of the Mœglin–Waldspurger models.
Remark 2.5. If  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{sqr}}\operatorname{GL}_{n}$, then
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{sqr}}\operatorname{GL}_{n}$, then  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is known as a ‘Speh representation’. (Strictly speaking, these representations were introduced by Speh in the archimedean case.)
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is known as a ‘Speh representation’. (Strictly speaking, these representations were introduced by Speh in the archimedean case.)
Remark 2.6. In general, if  $\unicode[STIX]{x1D70B}$ is unramified (and generic), then
$\unicode[STIX]{x1D70B}$ is unramified (and generic), then  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is not necessarily unramified if
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is not necessarily unramified if  $m>1$. More precisely, if
$m>1$. More precisely, if  $\unicode[STIX]{x1D70B}=Z(\{\unicode[STIX]{x1D70C}_{1}\}+\cdots +\{\unicode[STIX]{x1D70C}_{k}\})$ is unramified (so that
$\unicode[STIX]{x1D70B}=Z(\{\unicode[STIX]{x1D70C}_{1}\}+\cdots +\{\unicode[STIX]{x1D70C}_{k}\})$ is unramified (so that  $\unicode[STIX]{x1D70C}_{i}$ are unramified characters of
$\unicode[STIX]{x1D70C}_{i}$ are unramified characters of  $F^{\ast }$ and
$F^{\ast }$ and  $\unicode[STIX]{x1D70C}_{i}\neq \unicode[STIX]{x1D70C}_{j}|\cdot |$ for all
$\unicode[STIX]{x1D70C}_{i}\neq \unicode[STIX]{x1D70C}_{j}|\cdot |$ for all  $i,j$), then
$i,j$), then  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is unramified if and only if
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is unramified if and only if  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{1}}^{(m)},\ldots ,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{k}}^{(m)}$ are mutually unlinked. For instance, this is the case if
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{1}}^{(m)},\ldots ,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{k}}^{(m)}$ are mutually unlinked. For instance, this is the case if  $\unicode[STIX]{x1D70B}$ is (AT).
$\unicode[STIX]{x1D70B}$ is (AT).
Suppose that  $\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ with
$\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ with  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$. Then, in the notation of (2),
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$. Then, in the notation of (2),  $P_{\unicode[STIX]{x1D70E}}=P_{m,n}=M\ltimes U$ is the standard parabolic subgroup of
$P_{\unicode[STIX]{x1D70E}}=P_{m,n}=M\ltimes U$ is the standard parabolic subgroup of  $G$ of type
$G$ of type  $(\overbrace{n,\ldots ,n}^{m})$, consisting of the block upper triangular matrices with blocks of size
$(\overbrace{n,\ldots ,n}^{m})$, consisting of the block upper triangular matrices with blocks of size  $n\times n$. Thus,
$n\times n$. Thus,  $M\simeq \overbrace{\operatorname{GL}_{n}\times \cdots \times \operatorname{GL}_{n}}^{m}$.
$M\simeq \overbrace{\operatorname{GL}_{n}\times \cdots \times \operatorname{GL}_{n}}^{m}$.
Just as in the case  $m=1$, there are simple building blocks for
$m=1$, there are simple building blocks for  $m$-homogeneous representations.
$m$-homogeneous representations.
Proposition 2.7. Let  $\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)\in \operatorname{Irr}G$ be
$\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)\in \operatorname{Irr}G$ be  $m$-homogeneous. Then there exist
$m$-homogeneous. Then there exist  $\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{t}\in \operatorname{Irr}_{\operatorname{gen}}$ such that the following statements hold.
$\unicode[STIX]{x1D70B}_{1},\ldots ,\unicode[STIX]{x1D70B}_{t}\in \operatorname{Irr}_{\operatorname{gen}}$ such that the following statements hold.
(i)
 $\unicode[STIX]{x1D70E}_{i}:=\operatorname{Sp}(\unicode[STIX]{x1D70B}_{i},m)$ is a ladder representation for all
$\unicode[STIX]{x1D70E}_{i}:=\operatorname{Sp}(\unicode[STIX]{x1D70B}_{i},m)$ is a ladder representation for all  $i$.
$i$.(ii)
 $\operatorname{Sp}(\unicode[STIX]{x1D70B},l)=\operatorname{Sp}(\unicode[STIX]{x1D70B}_{1},l)\times \cdots \times \operatorname{Sp}(\unicode[STIX]{x1D70B}_{t},l)$ for all
$\operatorname{Sp}(\unicode[STIX]{x1D70B},l)=\operatorname{Sp}(\unicode[STIX]{x1D70B}_{1},l)\times \cdots \times \operatorname{Sp}(\unicode[STIX]{x1D70B}_{t},l)$ for all  $l=1,\ldots ,m$. In particular,
$l=1,\ldots ,m$. In particular,  $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{1}\times \cdots \times \unicode[STIX]{x1D70B}_{t}$ and
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{1}\times \cdots \times \unicode[STIX]{x1D70B}_{t}$ and  $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{1}\times \cdots \times \unicode[STIX]{x1D70E}_{t}$.
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{1}\times \cdots \times \unicode[STIX]{x1D70E}_{t}$.
Moreover, let  $Q$ be the maximal standard parabolic subgroup of type
$Q$ be the maximal standard parabolic subgroup of type  $((m-1)n,n)$ and denote by
$((m-1)n,n)$ and denote by  $J_{Q}(\unicode[STIX]{x1D70E})_{;\mathfrak{d}}$ the direct summand of
$J_{Q}(\unicode[STIX]{x1D70E})_{;\mathfrak{d}}$ the direct summand of  $J_{Q}(\unicode[STIX]{x1D70E})$ pertaining to the supercuspidal data
$J_{Q}(\unicode[STIX]{x1D70E})$ pertaining to the supercuspidal data  $\mathfrak{d}\in {\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})$ in the second (
$\mathfrak{d}\in {\mathcal{M}}(\operatorname{Irr}_{\operatorname{cusp}})$ in the second ( $\operatorname{GL}_{n}$) factor. Then
$\operatorname{GL}_{n}$) factor. Then
 $$\begin{eqnarray}J_{Q}(\unicode[STIX]{x1D70E})_{;\mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)|\cdot |^{-1/2}\otimes \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}.\end{eqnarray}$$
$$\begin{eqnarray}J_{Q}(\unicode[STIX]{x1D70E})_{;\mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)|\cdot |^{-1/2}\otimes \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}.\end{eqnarray}$$Remark 2.8. For  $m=1$,
$m=1$,  $\unicode[STIX]{x1D70B}_{i}$ is essentially a discrete series. This is not the case for
$\unicode[STIX]{x1D70B}_{i}$ is essentially a discrete series. This is not the case for  $m>1$ in general.
$m>1$ in general.
Proof. Write  $\unicode[STIX]{x1D70B}=Z(\sum _{i\in I}\{\unicode[STIX]{x1D70C}_{i}\})$ with
$\unicode[STIX]{x1D70B}=Z(\sum _{i\in I}\{\unicode[STIX]{x1D70C}_{i}\})$ with  $\unicode[STIX]{x1D70C}_{i}\in \operatorname{Irr}_{\operatorname{cusp}}$ and let
$\unicode[STIX]{x1D70C}_{i}\in \operatorname{Irr}_{\operatorname{cusp}}$ and let  $l\geqslant 1$. We say that a subset
$l\geqslant 1$. We say that a subset  $J$ of
$J$ of  $I$ is an
$I$ is an  $l$-chain if it can be written, necessarily uniquely, as
$l$-chain if it can be written, necessarily uniquely, as  $J=\{i_{1},\ldots ,i_{r}\}$ where for all
$J=\{i_{1},\ldots ,i_{r}\}$ where for all  $j=1,\ldots ,r-1$ we have
$j=1,\ldots ,r-1$ we have  $\unicode[STIX]{x1D70C}_{i_{j}}=\unicode[STIX]{x1D70C}_{i_{j+1}}|\cdot |^{\unicode[STIX]{x1D6FC}_{j}}$ with
$\unicode[STIX]{x1D70C}_{i_{j}}=\unicode[STIX]{x1D70C}_{i_{j+1}}|\cdot |^{\unicode[STIX]{x1D6FC}_{j}}$ with  $\unicode[STIX]{x1D6FC}_{j}\in \{1,\ldots ,l\}$. (For example, for a
$\unicode[STIX]{x1D6FC}_{j}\in \{1,\ldots ,l\}$. (For example, for a  $1$-chain,
$1$-chain,  $\unicode[STIX]{x1D70C}_{i_{r}},\ldots ,\unicode[STIX]{x1D70C}_{i_{1}}$ is a segment.) Clearly,
$\unicode[STIX]{x1D70C}_{i_{r}},\ldots ,\unicode[STIX]{x1D70C}_{i_{1}}$ is a segment.) Clearly,  $J$ is an
$J$ is an  $l$-chain if and only if
$l$-chain if and only if  $Z(\sum _{j\in J}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{j}}^{(l)})$ is a ladder representation.
$Z(\sum _{j\in J}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{j}}^{(l)})$ is a ladder representation.
We say that two partitions of  $I$ are equivalent if one can be obtained from the other by applying a permutation
$I$ are equivalent if one can be obtained from the other by applying a permutation  $\unicode[STIX]{x1D70F}$ of
$\unicode[STIX]{x1D70F}$ of  $I$ such that
$I$ such that  $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70F}(i)}=\unicode[STIX]{x1D70C}_{i}$ for all
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70F}(i)}=\unicode[STIX]{x1D70C}_{i}$ for all  $i$. It is easy to see that for any
$i$. It is easy to see that for any  $l\geqslant 1$ there exists a partition
$l\geqslant 1$ there exists a partition  ${\mathcal{P}}^{(l)}(I)$ of
${\mathcal{P}}^{(l)}(I)$ of  $I$ consisting of
$I$ consisting of  $l$-chains, such that for any
$l$-chains, such that for any  $J,J^{\prime }\in {\mathcal{P}}^{(l)}(I)$ at least one of the following conditions holds:
$J,J^{\prime }\in {\mathcal{P}}^{(l)}(I)$ at least one of the following conditions holds:
(i)
 $\{\unicode[STIX]{x1D70C}_{j}:j\in J\}\subset \{\unicode[STIX]{x1D70C}_{j}:j\in J^{\prime }\}$;
$\{\unicode[STIX]{x1D70C}_{j}:j\in J\}\subset \{\unicode[STIX]{x1D70C}_{j}:j\in J^{\prime }\}$;(ii)
 $\{\unicode[STIX]{x1D70C}_{j}:j\in J^{\prime }\}\subset \{\unicode[STIX]{x1D70C}_{j}:j\in J\}$;
$\{\unicode[STIX]{x1D70C}_{j}:j\in J^{\prime }\}\subset \{\unicode[STIX]{x1D70C}_{j}:j\in J\}$;(iii) for every
 $j\in J$ and
$j\in J$ and  $j^{\prime }\in J^{\prime }$ the segments
$j^{\prime }\in J^{\prime }$ the segments  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{j}}^{(l)}$ and
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{j}}^{(l)}$ and  $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{j^{\prime }}}^{(l)}$ are unlinked.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D70C}_{j^{\prime }}}^{(l)}$ are unlinked.
Moreover,  ${\mathcal{P}}^{(l)}(I)$ is unique up to equivalence. Indeed,
${\mathcal{P}}^{(l)}(I)$ is unique up to equivalence. Indeed,  ${\mathcal{P}}^{(l)}(I)$ can be defined inductively by taking a maximal
${\mathcal{P}}^{(l)}(I)$ can be defined inductively by taking a maximal  $l$-chain
$l$-chain  $J$ of
$J$ of  $I$ (with respect to inclusion) together with the partition
$I$ (with respect to inclusion) together with the partition  ${\mathcal{P}}^{(l)}(I\setminus J)$. It follows from this description that if
${\mathcal{P}}^{(l)}(I\setminus J)$. It follows from this description that if  $l\leqslant m$, then up to equivalence,
$l\leqslant m$, then up to equivalence,  ${\mathcal{P}}^{(l)}(J)=\{J^{\prime }\in {\mathcal{P}}^{(l)}(I):J^{\prime }\subset J\}$ for any
${\mathcal{P}}^{(l)}(J)=\{J^{\prime }\in {\mathcal{P}}^{(l)}(I):J^{\prime }\subset J\}$ for any  $J\in {\mathcal{P}}^{(m)}(I)$ and, in particular,
$J\in {\mathcal{P}}^{(m)}(I)$ and, in particular,  ${\mathcal{P}}^{(l)}(I)$ is a refinement of
${\mathcal{P}}^{(l)}(I)$ is a refinement of  ${\mathcal{P}}^{(m)}(I)$.
${\mathcal{P}}^{(m)}(I)$.
For any  $J\subset I$, let
$J\subset I$, let  $\unicode[STIX]{x1D70B}_{J}=Z(\sum _{j\in J}\{\unicode[STIX]{x1D70C}_{j}\})\in \operatorname{Irr}_{\operatorname{gen}}$ and
$\unicode[STIX]{x1D70B}_{J}=Z(\sum _{j\in J}\{\unicode[STIX]{x1D70C}_{j}\})\in \operatorname{Irr}_{\operatorname{gen}}$ and  $\unicode[STIX]{x1D70E}_{J}=\operatorname{Sp}(\unicode[STIX]{x1D70B}_{J},m)$. Then
$\unicode[STIX]{x1D70E}_{J}=\operatorname{Sp}(\unicode[STIX]{x1D70B}_{J},m)$. Then  $\unicode[STIX]{x1D70E}_{J}$ is an (
$\unicode[STIX]{x1D70E}_{J}$ is an ( $m$-homogeneous) ladder representation for any
$m$-homogeneous) ladder representation for any  $J\in {\mathcal{P}}^{(m)}(I)$. It follows from the defining property of
$J\in {\mathcal{P}}^{(m)}(I)$. It follows from the defining property of  ${\mathcal{P}}^{(m)}(I)$, (1) and Lemma 2.1 that
${\mathcal{P}}^{(m)}(I)$, (1) and Lemma 2.1 that  is irreducible, hence equals
is irreducible, hence equals  $\unicode[STIX]{x1D70E}$. Likewise, for any
$\unicode[STIX]{x1D70E}$. Likewise, for any  $l\leqslant m$, we have
$l\leqslant m$, we have  Since we may assume that
Since we may assume that  for all
for all  $J\in {\mathcal{P}}^{(m)}(I)$, we infer that
$J\in {\mathcal{P}}^{(m)}(I)$, we infer that
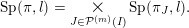
In particular,  $\unicode[STIX]{x1D70B}=\times _{J\in {\mathcal{P}}^{(m)}(I)}\unicode[STIX]{x1D70B}_{J}$.
$\unicode[STIX]{x1D70B}=\times _{J\in {\mathcal{P}}^{(m)}(I)}\unicode[STIX]{x1D70B}_{J}$.
By [Reference Kret and LapidKL12], we have
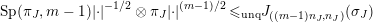 $$\begin{eqnarray}\operatorname{Sp}(\unicode[STIX]{x1D70B}_{J},m-1)|\cdot |^{-1/2}\otimes \unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}\,{\leqslant}_{\operatorname{unq}}J_{((m-1)n_{J},n_{J})}(\unicode[STIX]{x1D70E}_{J})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sp}(\unicode[STIX]{x1D70B}_{J},m-1)|\cdot |^{-1/2}\otimes \unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}\,{\leqslant}_{\operatorname{unq}}J_{((m-1)n_{J},n_{J})}(\unicode[STIX]{x1D70E}_{J})\end{eqnarray}$$ for all  $J\in {\mathcal{P}}^{(m)}(I)$ where
$J\in {\mathcal{P}}^{(m)}(I)$ where  $n_{J}=\deg \unicode[STIX]{x1D70B}_{J}$. Therefore, by the geometric lemma of Bernstein and Zelevinsky [Reference Bernshtein and ZelevinskyBZ77],
$n_{J}=\deg \unicode[STIX]{x1D70B}_{J}$. Therefore, by the geometric lemma of Bernstein and Zelevinsky [Reference Bernshtein and ZelevinskyBZ77],
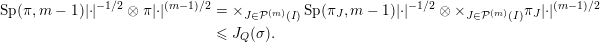 $$\begin{eqnarray}\displaystyle \operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)|\cdot |^{-1/2}\otimes \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2} & = & \displaystyle \times _{J\in {\mathcal{P}}^{(m)}(I)}\operatorname{Sp}(\unicode[STIX]{x1D70B}_{J},m-1)|\cdot |^{-1/2}\otimes \times _{J\in {\mathcal{P}}^{(m)}(I)}\unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle J_{Q}(\unicode[STIX]{x1D70E}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)|\cdot |^{-1/2}\otimes \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2} & = & \displaystyle \times _{J\in {\mathcal{P}}^{(m)}(I)}\operatorname{Sp}(\unicode[STIX]{x1D70B}_{J},m-1)|\cdot |^{-1/2}\otimes \times _{J\in {\mathcal{P}}^{(m)}(I)}\unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle J_{Q}(\unicode[STIX]{x1D70E}).\nonumber\end{eqnarray}$$ On the other hand, suppose that  $\unicode[STIX]{x1D70F}_{J},\unicode[STIX]{x1D714}_{J}\in \operatorname{Irr}$ with
$\unicode[STIX]{x1D70F}_{J},\unicode[STIX]{x1D714}_{J}\in \operatorname{Irr}$ with  $\unicode[STIX]{x1D70F}_{J}\otimes \unicode[STIX]{x1D714}_{J}\leqslant J_{P}(\unicode[STIX]{x1D70E}_{J})$,
$\unicode[STIX]{x1D70F}_{J}\otimes \unicode[STIX]{x1D714}_{J}\leqslant J_{P}(\unicode[STIX]{x1D70E}_{J})$,  $J\in {\mathcal{P}}^{(m)}(I)$ and
$J\in {\mathcal{P}}^{(m)}(I)$ and
 $$\begin{eqnarray}\mathop{\sum }_{J\in {\mathcal{P}}^{(m)}(I)}\mathfrak{c}(\unicode[STIX]{x1D714}_{J})=\mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{J\in {\mathcal{P}}^{(m)}(I)}\mathfrak{c}(\unicode[STIX]{x1D714}_{J})=\mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}.\end{eqnarray}$$ We claim that this is possible only if  $\unicode[STIX]{x1D70F}_{J}=\operatorname{Sp}(\unicode[STIX]{x1D70B}_{J},m-1)|\cdot |^{-1/2}$ and
$\unicode[STIX]{x1D70F}_{J}=\operatorname{Sp}(\unicode[STIX]{x1D70B}_{J},m-1)|\cdot |^{-1/2}$ and  $\unicode[STIX]{x1D714}_{J}=\unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}$ for all
$\unicode[STIX]{x1D714}_{J}=\unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}$ for all  $J$. We prove it by induction on
$J$. We prove it by induction on  $\deg \unicode[STIX]{x1D70B}$ using the geometric lemma. The base of the induction is trivial. For the induction step, it is enough to prove that if
$\deg \unicode[STIX]{x1D70B}$ using the geometric lemma. The base of the induction is trivial. For the induction step, it is enough to prove that if  $J$ is a maximal
$J$ is a maximal  $m$-chain, then
$m$-chain, then  $\unicode[STIX]{x1D714}_{J}=\unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}$. We use Lemma 2.2. By part (ii), if
$\unicode[STIX]{x1D714}_{J}=\unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}$. We use Lemma 2.2. By part (ii), if  $J$ is a maximal
$J$ is a maximal  $m$-chain, then
$m$-chain, then  $\unicode[STIX]{x1D714}_{J}$ is generic. For otherwise, since
$\unicode[STIX]{x1D714}_{J}$ is generic. For otherwise, since  $\mathfrak{c}(\unicode[STIX]{x1D714}_{J})\leqslant \mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}$, there would exist
$\mathfrak{c}(\unicode[STIX]{x1D714}_{J})\leqslant \mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}$, there would exist  $i\in I$ such that
$i\in I$ such that  $\unicode[STIX]{x1D70C}_{i}\notin \{\unicode[STIX]{x1D70C}_{j}:j\in J\}$ but
$\unicode[STIX]{x1D70C}_{i}\notin \{\unicode[STIX]{x1D70C}_{j}:j\in J\}$ but  $\unicode[STIX]{x1D70C}_{i}|\cdot |\in \{\unicode[STIX]{x1D70C}_{j}:j\in J\}$ in contradiction to the maximality of
$\unicode[STIX]{x1D70C}_{i}|\cdot |\in \{\unicode[STIX]{x1D70C}_{j}:j\in J\}$ in contradiction to the maximality of  $J$. On the other hand, by part (iv), if
$J$. On the other hand, by part (iv), if  $\unicode[STIX]{x1D70C}|\cdot |\not \leqslant \mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}$, then
$\unicode[STIX]{x1D70C}|\cdot |\not \leqslant \mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}$, then  $\unicode[STIX]{x1D70C}$ can occur in
$\unicode[STIX]{x1D70C}$ can occur in  $\mathfrak{c}(\unicode[STIX]{x1D714}_{J})$ at most once for any
$\mathfrak{c}(\unicode[STIX]{x1D714}_{J})$ at most once for any  $J\in {\mathcal{P}}^{(m)}(I)$. It follows from (4) that if
$J\in {\mathcal{P}}^{(m)}(I)$. It follows from (4) that if  $\unicode[STIX]{x1D70C}|\cdot |\not \leqslant \mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}$, then
$\unicode[STIX]{x1D70C}|\cdot |\not \leqslant \mathfrak{c}(\unicode[STIX]{x1D70B})|\cdot |^{(m-1)/2}$, then  $\unicode[STIX]{x1D70C}\leqslant \mathfrak{c}(\unicode[STIX]{x1D714}_{J})$ if and only if
$\unicode[STIX]{x1D70C}\leqslant \mathfrak{c}(\unicode[STIX]{x1D714}_{J})$ if and only if  $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{j}|\cdot |^{(m-1)/2}$ for some
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{j}|\cdot |^{(m-1)/2}$ for some  $j\in J$. By part (iii), it now follows that if
$j\in J$. By part (iii), it now follows that if  $J$ is a maximal
$J$ is a maximal  $m$-chain, then
$m$-chain, then  $\mathfrak{c}(\unicode[STIX]{x1D714}_{J})=\sum _{j\in J}\{\unicode[STIX]{x1D70C}_{j}|\cdot |^{(m-1)/2}\}$ and hence
$\mathfrak{c}(\unicode[STIX]{x1D714}_{J})=\sum _{j\in J}\{\unicode[STIX]{x1D70C}_{j}|\cdot |^{(m-1)/2}\}$ and hence  $\unicode[STIX]{x1D714}_{J}=\unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}$ (since
$\unicode[STIX]{x1D714}_{J}=\unicode[STIX]{x1D70B}_{J}|\cdot |^{(m-1)/2}$ (since  $\unicode[STIX]{x1D714}_{J}$ is generic) as required.
$\unicode[STIX]{x1D714}_{J}$ is generic) as required.
This concludes the proof of the proposition. ◻
Remark 2.9. It can be shown that up to permutation,  $\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{t}$ are the unique ladder representations such that
$\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{t}$ are the unique ladder representations such that  $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{1}\times \cdots \times \unicode[STIX]{x1D70E}_{t}$. We will not need to use this fact.
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{1}\times \cdots \times \unicode[STIX]{x1D70E}_{t}$. We will not need to use this fact.
By Frobenius reciprocity and [Reference Lapid and MínguezLM16, Corollary 4.10], we have the following corollary.
Corollary 2.10. For any  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$,
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$,
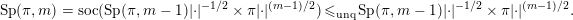 $$\begin{eqnarray}\operatorname{Sp}(\unicode[STIX]{x1D70B},m)=\operatorname{soc}(\operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)|\cdot |^{-1/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2})\,{\leqslant}_{\operatorname{ unq}}\operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)|\cdot |^{-1/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sp}(\unicode[STIX]{x1D70B},m)=\operatorname{soc}(\operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)|\cdot |^{-1/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2})\,{\leqslant}_{\operatorname{ unq}}\operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)|\cdot |^{-1/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}.\end{eqnarray}$$ By induction on  $m$, we get the following result.
$m$, we get the following result.
Corollary 2.11. For any  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$,
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$,  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is a subrepresentation of
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is a subrepresentation of
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}:=\unicode[STIX]{x1D70B}|\cdot |^{(1-m)/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(3-m)/2}\times \cdots \times \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}:=\unicode[STIX]{x1D70B}|\cdot |^{(1-m)/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(3-m)/2}\times \cdots \times \unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}.\end{eqnarray}$$ Equivalently (by passing to the contragredient),  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is a quotient of
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is a quotient of
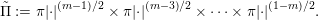 $$\begin{eqnarray}\tilde{\unicode[STIX]{x1D6F1}}:=\unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(m-3)/2}\times \cdots \times \unicode[STIX]{x1D70B}|\cdot |^{(1-m)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D6F1}}:=\unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(m-3)/2}\times \cdots \times \unicode[STIX]{x1D70B}|\cdot |^{(1-m)/2}.\end{eqnarray}$$Remark 2.12. If  $\unicode[STIX]{x1D70B}$ is (AT), then
$\unicode[STIX]{x1D70B}$ is (AT), then  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is the Langlands quotient of
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is the Langlands quotient of  $\tilde{\unicode[STIX]{x1D6F1}}$, In particular, in this case
$\tilde{\unicode[STIX]{x1D6F1}}$, In particular, in this case  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is the image of the standard intertwining operator from
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ is the image of the standard intertwining operator from  $\tilde{\unicode[STIX]{x1D6F1}}$ to
$\tilde{\unicode[STIX]{x1D6F1}}$ to  $\unicode[STIX]{x1D6F1}$ and
$\unicode[STIX]{x1D6F1}$ and  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)=\operatorname{soc}(\unicode[STIX]{x1D6F1})\,{\leqslant}_{\operatorname{unq}}\,\unicode[STIX]{x1D6F1}$. However, in general for
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)=\operatorname{soc}(\unicode[STIX]{x1D6F1})\,{\leqslant}_{\operatorname{unq}}\,\unicode[STIX]{x1D6F1}$. However, in general for  $m>2$ and
$m>2$ and  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ it is not true that
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ it is not true that  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)\,{\leqslant}_{\operatorname{unq}}\,\unicode[STIX]{x1D6F1}$. For instance, if
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)\,{\leqslant}_{\operatorname{unq}}\,\unicode[STIX]{x1D6F1}$. For instance, if  $\unicode[STIX]{x1D70B}=|\cdot |\times |\cdot |^{-1}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{2}$, then
$\unicode[STIX]{x1D70B}=|\cdot |\times |\cdot |^{-1}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{2}$, then  $\operatorname{Sp}(\unicode[STIX]{x1D70B},3)$ occurs with multiplicity two in the Jordan–Hölder sequence of
$\operatorname{Sp}(\unicode[STIX]{x1D70B},3)$ occurs with multiplicity two in the Jordan–Hölder sequence of  $\unicode[STIX]{x1D70B}|\cdot |^{-1}\times \unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}|\cdot |$. Note that in this case we still have
$\unicode[STIX]{x1D70B}|\cdot |^{-1}\times \unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}|\cdot |$. Note that in this case we still have  $\operatorname{Sp}(\unicode[STIX]{x1D70B},m)=\operatorname{soc}(\unicode[STIX]{x1D6F1})$ but we do not know whether this holds in general, that is, whether
$\operatorname{Sp}(\unicode[STIX]{x1D70B},m)=\operatorname{soc}(\unicode[STIX]{x1D6F1})$ but we do not know whether this holds in general, that is, whether  $\operatorname{soc}(\unicode[STIX]{x1D6F1})$ is always irreducible.
$\operatorname{soc}(\unicode[STIX]{x1D6F1})$ is always irreducible.
3 The models
3.1 Definition of models
Throughout this section, fix  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$, let
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$, let  $\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)\in \operatorname{Irr}G$ and let
$\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)\in \operatorname{Irr}G$ and let  $P=P_{\unicode[STIX]{x1D70E}}=P_{m,n}=M\ltimes U$ be the standard parabolic subgroup of
$P=P_{\unicode[STIX]{x1D70E}}=P_{m,n}=M\ltimes U$ be the standard parabolic subgroup of  $G$ of type
$G$ of type  $\overbrace{(n,\ldots ,n)}^{m}$. Let
$\overbrace{(n,\ldots ,n)}^{m}$. Let  $\bar{U}=\,^{t}U$ be the opposite of
$\bar{U}=\,^{t}U$ be the opposite of  $U$. Fix a non-trivial character
$U$. Fix a non-trivial character  $\unicode[STIX]{x1D713}$ of
$\unicode[STIX]{x1D713}$ of  $F$. Let
$F$. Let  $\unicode[STIX]{x1D6F9}$ be the function on
$\unicode[STIX]{x1D6F9}$ be the function on  $G$ given by
$G$ given by
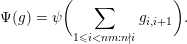 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}(g)=\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{1\leqslant i<nm:n\nmid i}g_{i,i+1}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}(g)=\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{1\leqslant i<nm:n\nmid i}g_{i,i+1}\biggr).\end{eqnarray}$$ We denote the restriction of  $\unicode[STIX]{x1D6F9}$ to a subset
$\unicode[STIX]{x1D6F9}$ to a subset  $A$ of
$A$ of  $G$ by
$G$ by  $\unicode[STIX]{x1D6F9}_{A}$. Let
$\unicode[STIX]{x1D6F9}_{A}$. Let  $N=N_{mn}$ (respectively,
$N=N_{mn}$ (respectively,  $\bar{N}=\,^{t}N$) be the group of upper (respectively, lower) unitriangular matrices in
$\bar{N}=\,^{t}N$) be the group of upper (respectively, lower) unitriangular matrices in  $G$. Then
$G$. Then  $\unicode[STIX]{x1D6F9}_{N}$ is a (degenerate) character on
$\unicode[STIX]{x1D6F9}_{N}$ is a (degenerate) character on  $N$ that is trivial on
$N$ that is trivial on  $U$ and non-degenerate on
$U$ and non-degenerate on  $N_{M}:=N\cap M$. Recall that by (3),
$N_{M}:=N\cap M$. Recall that by (3),  $\operatorname{Hom}_{G}(\unicode[STIX]{x1D70E},\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N})$ is one-dimensional.
$\operatorname{Hom}_{G}(\unicode[STIX]{x1D70E},\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N})$ is one-dimensional.
Denote by  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ the image of
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ the image of  $\unicode[STIX]{x1D70E}$ in
$\unicode[STIX]{x1D70E}$ in  $\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N}$, that is, the Zelevinsky model of
$\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N}$, that is, the Zelevinsky model of  $\unicode[STIX]{x1D70E}$. By Corollaries 2.10 and 2.11, for any
$\unicode[STIX]{x1D70E}$. By Corollaries 2.10 and 2.11, for any  $W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$, we have
$W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$, we have
 $$\begin{eqnarray}(|\det |^{(1-n)/2}\otimes |\det |^{(m-1)(n-1)/2})W_{\operatorname{ Ze}}|_{\operatorname{GL}_{(m-1)n}\times \operatorname{GL}_{n}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N\cap (\operatorname{GL}_{(m-1)n}\times \operatorname{GL}_{n})}}(\operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)\otimes \unicode[STIX]{x1D70B}),\end{eqnarray}$$
$$\begin{eqnarray}(|\det |^{(1-n)/2}\otimes |\det |^{(m-1)(n-1)/2})W_{\operatorname{ Ze}}|_{\operatorname{GL}_{(m-1)n}\times \operatorname{GL}_{n}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N\cap (\operatorname{GL}_{(m-1)n}\times \operatorname{GL}_{n})}}(\operatorname{Sp}(\unicode[STIX]{x1D70B},m-1)\otimes \unicode[STIX]{x1D70B}),\end{eqnarray}$$ $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{P}^{-1/2}\unicode[STIX]{x1D6FF}^{\prime }W_{\operatorname{ Ze}}|_{M}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{P}^{-1/2}\unicode[STIX]{x1D6FF}^{\prime }W_{\operatorname{ Ze}}|_{M}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m}),\end{eqnarray}$$ $\unicode[STIX]{x1D70B}^{\otimes m}=\overbrace{\unicode[STIX]{x1D70B}\otimes \cdots \otimes \unicode[STIX]{x1D70B}}^{m}$,
$\unicode[STIX]{x1D70B}^{\otimes m}=\overbrace{\unicode[STIX]{x1D70B}\otimes \cdots \otimes \unicode[STIX]{x1D70B}}^{m}$,  $\unicode[STIX]{x1D6FF}_{P}$ is the modulus character of
$\unicode[STIX]{x1D6FF}_{P}$ is the modulus character of 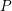 $P$ and
$P$ and 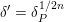 $\unicode[STIX]{x1D6FF}^{\prime }=\unicode[STIX]{x1D6FF}_{P}^{1/2n}$ is the character of
$\unicode[STIX]{x1D6FF}^{\prime }=\unicode[STIX]{x1D6FF}_{P}^{1/2n}$ is the character of 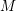 $M$ given by
$M$ given by 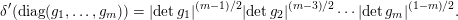 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{\prime }(\operatorname{diag}(g_{1},\ldots ,g_{m}))=|\det g_{1}|^{(m-1)/2}|\det g_{2}|^{(m-3)/2}\cdots |\det g_{m}|^{(1-m)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{\prime }(\operatorname{diag}(g_{1},\ldots ,g_{m}))=|\det g_{1}|^{(m-1)/2}|\det g_{2}|^{(m-3)/2}\cdots |\det g_{m}|^{(1-m)/2}.\end{eqnarray}$$ The model  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ is a particular case of more general models considered in [Reference Mœglin and WaldspurgerMW87] (for any reductive group). Let us recall the setup. Let
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ is a particular case of more general models considered in [Reference Mœglin and WaldspurgerMW87] (for any reductive group). Let us recall the setup. Let  $\mathfrak{g}=\operatorname{Mat}_{nm,nm}$ be the Lie algebra of
$\mathfrak{g}=\operatorname{Mat}_{nm,nm}$ be the Lie algebra of  $G$ over
$G$ over  $F$. For any cocharacter
$F$. For any cocharacter  $\unicode[STIX]{x1D711}$ of the diagonal torus
$\unicode[STIX]{x1D711}$ of the diagonal torus  $T$, let
$T$, let  $\mathfrak{g}=\bigoplus _{j\in \mathbb{Z}}\mathfrak{g}_{j}^{\unicode[STIX]{x1D711}}$ be the corresponding grading
$\mathfrak{g}=\bigoplus _{j\in \mathbb{Z}}\mathfrak{g}_{j}^{\unicode[STIX]{x1D711}}$ be the corresponding grading
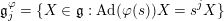 $$\begin{eqnarray}\mathfrak{g}_{j}^{\unicode[STIX]{x1D711}}=\{X\in \mathfrak{g}:\operatorname{Ad}(\unicode[STIX]{x1D711}(s))X=s^{j}X\}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}_{j}^{\unicode[STIX]{x1D711}}=\{X\in \mathfrak{g}:\operatorname{Ad}(\unicode[STIX]{x1D711}(s))X=s^{j}X\}\end{eqnarray}$$ and let  $\mathfrak{g}_{{\geqslant}j}^{\unicode[STIX]{x1D711}}=\bigoplus _{k\geqslant j}\mathfrak{g}_{k}^{\unicode[STIX]{x1D711}}$,
$\mathfrak{g}_{{\geqslant}j}^{\unicode[STIX]{x1D711}}=\bigoplus _{k\geqslant j}\mathfrak{g}_{k}^{\unicode[STIX]{x1D711}}$,  $j\in \mathbb{Z}$, be the corresponding filtration. Let
$j\in \mathbb{Z}$, be the corresponding filtration. Let  $P_{\unicode[STIX]{x1D711}}$ be the semistandard parabolic subgroup such that
$P_{\unicode[STIX]{x1D711}}$ be the semistandard parabolic subgroup such that  $\operatorname{Lie}P_{\unicode[STIX]{x1D711}}=\mathfrak{g}_{{\geqslant}0}^{\unicode[STIX]{x1D711}}$. Then
$\operatorname{Lie}P_{\unicode[STIX]{x1D711}}=\mathfrak{g}_{{\geqslant}0}^{\unicode[STIX]{x1D711}}$. Then  $P_{\unicode[STIX]{x1D711}}=M_{\unicode[STIX]{x1D711}}\ltimes U_{\unicode[STIX]{x1D711}}$ where
$P_{\unicode[STIX]{x1D711}}=M_{\unicode[STIX]{x1D711}}\ltimes U_{\unicode[STIX]{x1D711}}$ where  $M_{\unicode[STIX]{x1D711}}$ is the centralizer of
$M_{\unicode[STIX]{x1D711}}$ is the centralizer of  $\unicode[STIX]{x1D711}$,
$\unicode[STIX]{x1D711}$,  $\operatorname{Lie}M_{\unicode[STIX]{x1D711}}=\mathfrak{g}_{0}^{\unicode[STIX]{x1D711}}$ and
$\operatorname{Lie}M_{\unicode[STIX]{x1D711}}=\mathfrak{g}_{0}^{\unicode[STIX]{x1D711}}$ and  $\operatorname{Lie}U_{\unicode[STIX]{x1D711}}=\mathfrak{g}_{{>}0}^{\unicode[STIX]{x1D711}}$. Concretely, if
$\operatorname{Lie}U_{\unicode[STIX]{x1D711}}=\mathfrak{g}_{{>}0}^{\unicode[STIX]{x1D711}}$. Concretely, if  $\unicode[STIX]{x1D711}(s)=\operatorname{diag}(s^{\unicode[STIX]{x1D706}_{1}^{\unicode[STIX]{x1D711}}},\ldots ,s^{\unicode[STIX]{x1D706}_{mn}^{\unicode[STIX]{x1D711}}})$ where
$\unicode[STIX]{x1D711}(s)=\operatorname{diag}(s^{\unicode[STIX]{x1D706}_{1}^{\unicode[STIX]{x1D711}}},\ldots ,s^{\unicode[STIX]{x1D706}_{mn}^{\unicode[STIX]{x1D711}}})$ where  $(\unicode[STIX]{x1D706}_{1}^{\unicode[STIX]{x1D711}},\ldots ,\unicode[STIX]{x1D706}_{mn}^{\unicode[STIX]{x1D711}})\in \mathbb{Z}^{mn}$, then
$(\unicode[STIX]{x1D706}_{1}^{\unicode[STIX]{x1D711}},\ldots ,\unicode[STIX]{x1D706}_{mn}^{\unicode[STIX]{x1D711}})\in \mathbb{Z}^{mn}$, then
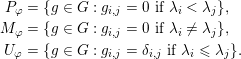 $$\begin{eqnarray}\displaystyle P_{\unicode[STIX]{x1D711}} & = & \displaystyle \{g\in G:g_{i,j}=0\text{ if }\unicode[STIX]{x1D706}_{i}<\unicode[STIX]{x1D706}_{j}\},\nonumber\\ \displaystyle M_{\unicode[STIX]{x1D711}} & = & \displaystyle \{g\in G:g_{i,j}=0\text{ if }\unicode[STIX]{x1D706}_{i}\neq \unicode[STIX]{x1D706}_{j}\},\nonumber\\ \displaystyle U_{\unicode[STIX]{x1D711}} & = & \displaystyle \{g\in G:g_{i,j}=\unicode[STIX]{x1D6FF}_{i,j}\text{ if }\unicode[STIX]{x1D706}_{i}\leqslant \unicode[STIX]{x1D706}_{j}\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{\unicode[STIX]{x1D711}} & = & \displaystyle \{g\in G:g_{i,j}=0\text{ if }\unicode[STIX]{x1D706}_{i}<\unicode[STIX]{x1D706}_{j}\},\nonumber\\ \displaystyle M_{\unicode[STIX]{x1D711}} & = & \displaystyle \{g\in G:g_{i,j}=0\text{ if }\unicode[STIX]{x1D706}_{i}\neq \unicode[STIX]{x1D706}_{j}\},\nonumber\\ \displaystyle U_{\unicode[STIX]{x1D711}} & = & \displaystyle \{g\in G:g_{i,j}=\unicode[STIX]{x1D6FF}_{i,j}\text{ if }\unicode[STIX]{x1D706}_{i}\leqslant \unicode[STIX]{x1D706}_{j}\}.\nonumber\end{eqnarray}$$ Consider the nilpotent  $nm\times nm$ matrix
$nm\times nm$ matrix  $J_{m,n}$ consisting of
$J_{m,n}$ consisting of  $m$ lower triangular Jordan blocks of size
$m$ lower triangular Jordan blocks of size  $n\times n$ each. We say that
$n\times n$ each. We say that  $\unicode[STIX]{x1D711}$ is of type
$\unicode[STIX]{x1D711}$ is of type  $(m,n)$ if
$(m,n)$ if  $\operatorname{Ad}(\unicode[STIX]{x1D711}(s))J_{m,n}=s^{-1}J_{m,n}$, or equivalently, if
$\operatorname{Ad}(\unicode[STIX]{x1D711}(s))J_{m,n}=s^{-1}J_{m,n}$, or equivalently, if  $\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D711}}-\unicode[STIX]{x1D706}_{i+1}^{\unicode[STIX]{x1D711}}=1$ for all
$\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D711}}-\unicode[STIX]{x1D706}_{i+1}^{\unicode[STIX]{x1D711}}=1$ for all  $i$ not dividing
$i$ not dividing  $n$. If
$n$. If  $\unicode[STIX]{x1D711}$ is of type
$\unicode[STIX]{x1D711}$ is of type  $(m,n)$, then
$(m,n)$, then  $\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}}$ is a character of
$\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}}$ is a character of  $U_{\unicode[STIX]{x1D711}}$. By [Reference Mœglin and WaldspurgerMW87] (in particular, § II.2) we obtain the following theorem.Footnote 3
$U_{\unicode[STIX]{x1D711}}$. By [Reference Mœglin and WaldspurgerMW87] (in particular, § II.2) we obtain the following theorem.Footnote 3
Theorem 3.1 [Reference Mœglin and WaldspurgerMW87].
Suppose that  $\unicode[STIX]{x1D711}$ is of type
$\unicode[STIX]{x1D711}$ is of type  $(m,n)$. Then the space
$(m,n)$. Then the space
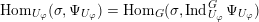 $$\begin{eqnarray}\operatorname{Hom}_{U_{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}})=\operatorname{Hom}_{G}(\unicode[STIX]{x1D70E},\operatorname{Ind}_{U_{\unicode[STIX]{x1D711}}}^{G}\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{U_{\unicode[STIX]{x1D711}}}(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}})=\operatorname{Hom}_{G}(\unicode[STIX]{x1D70E},\operatorname{Ind}_{U_{\unicode[STIX]{x1D711}}}^{G}\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}})\end{eqnarray}$$is one-dimensional.
In the setting of [Reference Mœglin and WaldspurgerMW87] the data pertaining to Theorem 3.1 is the pair  $(\unicode[STIX]{x1D711}^{2},J_{m,n})$. (The more general context of [Reference Mœglin and WaldspurgerMW87] applies to cocharacters which are not necessarily even. However, we will not discuss them here.)
$(\unicode[STIX]{x1D711}^{2},J_{m,n})$. (The more general context of [Reference Mœglin and WaldspurgerMW87] applies to cocharacters which are not necessarily even. However, we will not discuss them here.)
We denote by  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D70E})$ the image of
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}}}(\unicode[STIX]{x1D70E})$ the image of  $\unicode[STIX]{x1D70E}$ in
$\unicode[STIX]{x1D70E}$ in  $\operatorname{Ind}_{U_{\unicode[STIX]{x1D711}}}^{G}\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}}$. It consists of functions that are left equivariant (with respect to some character) under the centralizer of
$\operatorname{Ind}_{U_{\unicode[STIX]{x1D711}}}^{G}\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}}$. It consists of functions that are left equivariant (with respect to some character) under the centralizer of  $\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}}$ in
$\unicode[STIX]{x1D6F9}_{U_{\unicode[STIX]{x1D711}}}$ in  $P_{\unicode[STIX]{x1D711}}$.
$P_{\unicode[STIX]{x1D711}}$.
Clearly, any  $\unicode[STIX]{x1D711}$ of type
$\unicode[STIX]{x1D711}$ of type  $(m,n)$ is determined by the
$(m,n)$ is determined by the  $m$-tuple
$m$-tuple  $(\unicode[STIX]{x1D706}_{n}^{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D706}_{2n}^{\unicode[STIX]{x1D711}},\ldots ,\unicode[STIX]{x1D706}_{mn}^{\unicode[STIX]{x1D711}})$. We consider
$(\unicode[STIX]{x1D706}_{n}^{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D706}_{2n}^{\unicode[STIX]{x1D711}},\ldots ,\unicode[STIX]{x1D706}_{mn}^{\unicode[STIX]{x1D711}})$. We consider  $(m-1)n+1$ cocharacters
$(m-1)n+1$ cocharacters  $\unicode[STIX]{x1D711}_{0},\ldots ,\unicode[STIX]{x1D711}_{(m-1)n}$ of
$\unicode[STIX]{x1D711}_{0},\ldots ,\unicode[STIX]{x1D711}_{(m-1)n}$ of  $T$ of type
$T$ of type  $(m,n)$ such that
$(m,n)$ such that  $\unicode[STIX]{x1D706}_{nk}^{\unicode[STIX]{x1D711}_{i}}-\unicode[STIX]{x1D706}_{n(k+1)}^{\unicode[STIX]{x1D711}_{i}}=\max (0,nk-i)$,
$\unicode[STIX]{x1D706}_{nk}^{\unicode[STIX]{x1D711}_{i}}-\unicode[STIX]{x1D706}_{n(k+1)}^{\unicode[STIX]{x1D711}_{i}}=\max (0,nk-i)$,  $k=1,\ldots ,m-1$. (Up to a cocharacter of the center of
$k=1,\ldots ,m-1$. (Up to a cocharacter of the center of  $G$, the cocharacter
$G$, the cocharacter  $\unicode[STIX]{x1D711}_{(m-1)n}^{2}$ corresponds to the
$\unicode[STIX]{x1D711}_{(m-1)n}^{2}$ corresponds to the  $\operatorname{SL}_{2}$-triple pertaining to
$\operatorname{SL}_{2}$-triple pertaining to  $J_{m,n}$.) For simplicity we write
$J_{m,n}$.) For simplicity we write  $P_{i}=P_{\unicode[STIX]{x1D711}_{i}}$,
$P_{i}=P_{\unicode[STIX]{x1D711}_{i}}$,  $M_{i}=M_{\unicode[STIX]{x1D711}_{i}}$,
$M_{i}=M_{\unicode[STIX]{x1D711}_{i}}$,  $U_{i}=U_{\unicode[STIX]{x1D711}_{i}}$. If
$U_{i}=U_{\unicode[STIX]{x1D711}_{i}}$. If  $i=nd+r$ where
$i=nd+r$ where  $d=\lfloor i/n\rfloor$ and
$d=\lfloor i/n\rfloor$ and  $0\leqslant r<n$, then
$0\leqslant r<n$, then  $U_{i}$ consists of the matrices whose
$U_{i}$ consists of the matrices whose  $n\times n$ blocks
$n\times n$ blocks  $A_{j,k}$ satisfy:
$A_{j,k}$ satisfy:
(i)
 $A_{j,j}$ is upper unitriangular for all
$A_{j,j}$ is upper unitriangular for all  $j=1,\ldots ,m$;
$j=1,\ldots ,m$;(ii)
 $A_{j,k}$ is strictly upper triangular if
$A_{j,k}$ is strictly upper triangular if  $j\neq k$ and
$j\neq k$ and  $j,k\leqslant d+1$;
$j,k\leqslant d+1$;(iii) for any
 $k<d+2$,
$k<d+2$,  $(A_{d+2,k})_{a,b}=0$ if
$(A_{d+2,k})_{a,b}=0$ if  $b-a\leqslant n-r$ and
$b-a\leqslant n-r$ and  $(A_{k,d+2})_{a,b}=0$ if
$(A_{k,d+2})_{a,b}=0$ if  $a-b\geqslant n-r$;
$a-b\geqslant n-r$;(iv)
 $A_{j,k}=0$ if
$A_{j,k}=0$ if  $j>k$ and
$j>k$ and  $j>d+2$.
$j>d+2$.
(There is no constraint on  $A_{j,k}$ if
$A_{j,k}$ if  $j<k$ and
$j<k$ and  $d+2<k$.)
$d+2<k$.)
In particular,  $U_{0}=N$ while
$U_{0}=N$ while  $U_{(m-1)n}$ consists of the matrices whose difference from the identity matrix is strictly upper triangular in each
$U_{(m-1)n}$ consists of the matrices whose difference from the identity matrix is strictly upper triangular in each  $n\times n$ block. Also,
$n\times n$ block. Also,  $U_{i+1}\cap N\subset U_{i}\cap N$ and
$U_{i+1}\cap N\subset U_{i}\cap N$ and  $U_{i}\cap \bar{N}\subset U_{i+1}\cap \bar{N}$ for all
$U_{i}\cap \bar{N}\subset U_{i+1}\cap \bar{N}$ for all  $i$.
$i$.
For brevity we write  $P^{\prime }=P_{(m-1)n}$,
$P^{\prime }=P_{(m-1)n}$,  $M^{\prime }=M_{(m-1)n}\simeq \overbrace{\operatorname{GL}_{m}\times \cdots \times \operatorname{GL}_{m}}^{n}$,
$M^{\prime }=M_{(m-1)n}\simeq \overbrace{\operatorname{GL}_{m}\times \cdots \times \operatorname{GL}_{m}}^{n}$,  $U^{\prime }=U_{(m-1)n}$. In analogy with the case
$U^{\prime }=U_{(m-1)n}$. In analogy with the case  $m=2$ we will refer to
$m=2$ we will refer to  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ as the Shalika model of
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ as the Shalika model of  $\unicode[STIX]{x1D70E}$. We caution, however, that in the literature, this terminology usually refers to the image of
$\unicode[STIX]{x1D70E}$. We caution, however, that in the literature, this terminology usually refers to the image of  $\unicode[STIX]{x1D70F}\in \operatorname{Irr}\operatorname{GL}_{2n}$ (possibly generic) in
$\unicode[STIX]{x1D70F}\in \operatorname{Irr}\operatorname{GL}_{2n}$ (possibly generic) in 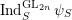 $\operatorname{Ind}_{S}^{\operatorname{GL}_{2n}}\unicode[STIX]{x1D713}_{S}$ under a non-trivial intertwining operator, if it exists (in which case it is unique up to a scalar [Reference Jacquet and RallisJR96]), where
$\operatorname{Ind}_{S}^{\operatorname{GL}_{2n}}\unicode[STIX]{x1D713}_{S}$ under a non-trivial intertwining operator, if it exists (in which case it is unique up to a scalar [Reference Jacquet and RallisJR96]), where  $S$ is the Shalika group
$S$ is the Shalika group
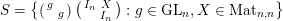 $$\begin{eqnarray}S=\big\{\!\left(\begin{smallmatrix}g & \\ & g\end{smallmatrix}\right)\left(\begin{smallmatrix}I_{n} & X\\ & I_{n}\end{smallmatrix}\right):g\in \operatorname{GL}_{n},X\in \operatorname{Mat}_{n,n}\!\big\}\end{eqnarray}$$
$$\begin{eqnarray}S=\big\{\!\left(\begin{smallmatrix}g & \\ & g\end{smallmatrix}\right)\left(\begin{smallmatrix}I_{n} & X\\ & I_{n}\end{smallmatrix}\right):g\in \operatorname{GL}_{n},X\in \operatorname{Mat}_{n,n}\!\big\}\end{eqnarray}$$ and  $\unicode[STIX]{x1D713}_{S}$ is the character on
$\unicode[STIX]{x1D713}_{S}$ is the character on  $S$ given by
$S$ given by  $\unicode[STIX]{x1D713}(\operatorname{tr}X)$. In the case at hand, any
$\unicode[STIX]{x1D713}(\operatorname{tr}X)$. In the case at hand, any  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ automatically satisfies an equivariance property under the centralizer of
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ automatically satisfies an equivariance property under the centralizer of  $\unicode[STIX]{x1D6F9}_{U^{\prime }}$ in
$\unicode[STIX]{x1D6F9}_{U^{\prime }}$ in  $P^{\prime }$ (which is conjugate to
$P^{\prime }$ (which is conjugate to  $S$ in the case
$S$ in the case  $m=2$), which justifies our terminology. In general, even for
$m=2$), which justifies our terminology. In general, even for  $m=2$,
$m=2$,  $\operatorname{Hom}_{U^{\prime }}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6F9}_{U^{\prime }})$ is infinite-dimensional for
$\operatorname{Hom}_{U^{\prime }}(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D6F9}_{U^{\prime }})$ is infinite-dimensional for  $\unicode[STIX]{x1D70F}\in \operatorname{Irr}G$.
$\unicode[STIX]{x1D70F}\in \operatorname{Irr}G$.
Letting  $G$ act on right on the vector space
$G$ act on right on the vector space  $F^{mn}$ of row vectors with standard basis
$F^{mn}$ of row vectors with standard basis  $e_{1},\ldots ,e_{mn}$,
$e_{1},\ldots ,e_{mn}$,  $P^{\prime }$ is the stabilizer of the flag
$P^{\prime }$ is the stabilizer of the flag
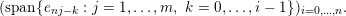 $$\begin{eqnarray}(\operatorname{span}\{e_{nj-k}:j=1,\ldots ,m,~k=0,\ldots ,i-1\})_{i=0,\ldots ,n}.\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{span}\{e_{nj-k}:j=1,\ldots ,m,~k=0,\ldots ,i-1\})_{i=0,\ldots ,n}.\end{eqnarray}$$ We denote by  $\unicode[STIX]{x1D705}:\overbrace{\operatorname{GL}_{m}\times \cdots \times \operatorname{GL}_{m}}^{n}\rightarrow M^{\prime }$ the isomorphism such that the
$\unicode[STIX]{x1D705}:\overbrace{\operatorname{GL}_{m}\times \cdots \times \operatorname{GL}_{m}}^{n}\rightarrow M^{\prime }$ the isomorphism such that the  $i$th copy of
$i$th copy of  $\operatorname{GL}_{m}$ acts on
$\operatorname{GL}_{m}$ acts on  $\operatorname{span}\{e_{nj+i}:j=0,\ldots ,m-1\}$.
$\operatorname{span}\{e_{nj+i}:j=0,\ldots ,m-1\}$.
If  $X$ is a matrix over
$X$ is a matrix over  $F$, then we write
$F$, then we write  $\Vert X\Vert$ for the maximum of the absolute value of its entries.
$\Vert X\Vert$ for the maximum of the absolute value of its entries.
Lemma 3.2. Suppose that  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$. Then there exists
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$. Then there exists  $C>0$ with the following property. Suppose that
$C>0$ with the following property. Suppose that  $g\in G$ with
$g\in G$ with  $W_{\operatorname{Sh}}(g)\neq 0$. Write
$W_{\operatorname{Sh}}(g)\neq 0$. Write  $g=u^{\prime }l^{\prime }k$ where
$g=u^{\prime }l^{\prime }k$ where  $u^{\prime }\in U^{\prime }$,
$u^{\prime }\in U^{\prime }$,  $l^{\prime }=\unicode[STIX]{x1D705}(g_{1},\ldots ,g_{n})\in M^{\prime }$ and
$l^{\prime }=\unicode[STIX]{x1D705}(g_{1},\ldots ,g_{n})\in M^{\prime }$ and  $k\in G({\mathcal{O}})$. Then
$k\in G({\mathcal{O}})$. Then  $\Vert g_{i+1}^{-1}g_{i}\Vert \leqslant C$ for all
$\Vert g_{i+1}^{-1}g_{i}\Vert \leqslant C$ for all  $i<n$.
$i<n$.
Proof. It is enough to consider the case  $g=\unicode[STIX]{x1D705}(g_{1},\ldots ,g_{n})\in M^{\prime }$. Assume that
$g=\unicode[STIX]{x1D705}(g_{1},\ldots ,g_{n})\in M^{\prime }$. Assume that  $W_{\operatorname{Sh}}(g)\neq 0$. Fix
$W_{\operatorname{Sh}}(g)\neq 0$. Fix  $1\leqslant i<n$. For any
$1\leqslant i<n$. For any  $X\in \operatorname{Mat}_{m,m}(F)$, let
$X\in \operatorname{Mat}_{m,m}(F)$, let 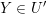 $Y\in U^{\prime }$ be the matrix such that
$Y\in U^{\prime }$ be the matrix such that  $Y_{nj+i,nk+i+1}=X_{j+1,k+1}$ for all
$Y_{nj+i,nk+i+1}=X_{j+1,k+1}$ for all  $0\leqslant j,k<m$ and all other non-diagonal entries of
$0\leqslant j,k<m$ and all other non-diagonal entries of  $Y$ are zero. Then
$Y$ are zero. Then  $W_{\operatorname{Sh}}(gY)=\unicode[STIX]{x1D713}(\operatorname{tr}g_{i}Xg_{i+1}^{-1})W_{\operatorname{Sh}}(g)$. It follows that there exists
$W_{\operatorname{Sh}}(gY)=\unicode[STIX]{x1D713}(\operatorname{tr}g_{i}Xg_{i+1}^{-1})W_{\operatorname{Sh}}(g)$. It follows that there exists  $C_{1}>0$ depending only on
$C_{1}>0$ depending only on  $W_{\operatorname{Sh}}$ such that if
$W_{\operatorname{Sh}}$ such that if  $W_{\operatorname{Sh}}(g)\not =0$, then
$W_{\operatorname{Sh}}(g)\not =0$, then  $\unicode[STIX]{x1D713}(\operatorname{tr}g_{i}Xg_{i+1}^{-1})=\unicode[STIX]{x1D713}(\operatorname{tr}g_{i+1}^{-1}g_{i}X)=1$ for all
$\unicode[STIX]{x1D713}(\operatorname{tr}g_{i}Xg_{i+1}^{-1})=\unicode[STIX]{x1D713}(\operatorname{tr}g_{i+1}^{-1}g_{i}X)=1$ for all  $X\in \operatorname{Mat}_{m,m}(F)$ with
$X\in \operatorname{Mat}_{m,m}(F)$ with  $\Vert X\Vert \leqslant C_{1}$. The lemma follows.◻
$\Vert X\Vert \leqslant C_{1}$. The lemma follows.◻
3.2 Model transition part I
We denote by  $M_{i}^{\unicode[STIX]{x1D6F9}}$ (respectively,
$M_{i}^{\unicode[STIX]{x1D6F9}}$ (respectively,  $P_{i}^{\unicode[STIX]{x1D6F9}}=M_{i}^{\unicode[STIX]{x1D6F9}}\ltimes U_{i}$) the stabilizer of
$P_{i}^{\unicode[STIX]{x1D6F9}}=M_{i}^{\unicode[STIX]{x1D6F9}}\ltimes U_{i}$) the stabilizer of  $\unicode[STIX]{x1D6F9}_{U_{i}}$ in
$\unicode[STIX]{x1D6F9}_{U_{i}}$ in  $M_{i}$ (respectively,
$M_{i}$ (respectively,  $P_{i}$). (Note that
$P_{i}$). (Note that  $M_{i}$ determines
$M_{i}$ determines  $i$ so this notation is unambiguous.) We also write
$i$ so this notation is unambiguous.) We also write  ${M^{\prime }}^{\unicode[STIX]{x1D6F9}}=M_{(m-1)n}^{\unicode[STIX]{x1D6F9}}$ and
${M^{\prime }}^{\unicode[STIX]{x1D6F9}}=M_{(m-1)n}^{\unicode[STIX]{x1D6F9}}$ and  ${P^{\prime }}^{\unicode[STIX]{x1D6F9}}=P_{(m-1)n}^{\unicode[STIX]{x1D6F9}}={M^{\prime }}^{\unicode[STIX]{x1D6F9}}\ltimes U^{\prime }$. Note that
${P^{\prime }}^{\unicode[STIX]{x1D6F9}}=P_{(m-1)n}^{\unicode[STIX]{x1D6F9}}={M^{\prime }}^{\unicode[STIX]{x1D6F9}}\ltimes U^{\prime }$. Note that  ${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ is unimodular. Explicitly,
${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ is unimodular. Explicitly,  ${M^{\prime }}^{\unicode[STIX]{x1D6F9}}$ is the image under
${M^{\prime }}^{\unicode[STIX]{x1D6F9}}$ is the image under  $\unicode[STIX]{x1D705}$ of
$\unicode[STIX]{x1D705}$ of  $\operatorname{GL}_{m}$ diagonally embedded in
$\operatorname{GL}_{m}$ diagonally embedded in  $\overbrace{\operatorname{GL}_{m}\times \cdots \times \operatorname{GL}_{m}}^{n}$. It consists of the matrices in
$\overbrace{\operatorname{GL}_{m}\times \cdots \times \operatorname{GL}_{m}}^{n}$. It consists of the matrices in  $G$ whose
$G$ whose  $n\times n$ blocks are all scalar matrices. Let
$n\times n$ blocks are all scalar matrices. Let  $\unicode[STIX]{x1D704}:\operatorname{GL}_{m}\rightarrow {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$ be the resulting identification.
$\unicode[STIX]{x1D704}:\operatorname{GL}_{m}\rightarrow {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$ be the resulting identification.
In general, write  $i=nd+r$,
$i=nd+r$,  $0\leqslant r<n$. Then the reductive part of
$0\leqslant r<n$. Then the reductive part of  $M_{i}^{\unicode[STIX]{x1D6F9}}$ is the image under
$M_{i}^{\unicode[STIX]{x1D6F9}}$ is the image under  $\unicode[STIX]{x1D704}$ of the subgroup
$\unicode[STIX]{x1D704}$ of the subgroup
 $$\begin{eqnarray}\{\operatorname{diag}(l,t_{d+2},\ldots ,t_{m}):l\in \operatorname{GL}_{d+1},t_{d+2},\ldots ,t_{m}\in F^{\ast }\}.\end{eqnarray}$$
$$\begin{eqnarray}\{\operatorname{diag}(l,t_{d+2},\ldots ,t_{m}):l\in \operatorname{GL}_{d+1},t_{d+2},\ldots ,t_{m}\in F^{\ast }\}.\end{eqnarray}$$ The unipotent radical of  $M_{i}^{\unicode[STIX]{x1D6F9}}$ consists of the matrices whose
$M_{i}^{\unicode[STIX]{x1D6F9}}$ consists of the matrices whose  $n\times n$ blocks
$n\times n$ blocks  $A_{j,k}$ satisfy the following requirements.
$A_{j,k}$ satisfy the following requirements.
(i)
 $A_{j,j}=I_{n}$ for all
$A_{j,j}=I_{n}$ for all  $j$.
$j$.(ii) If
 $j\neq k$, then
$j\neq k$, then  $A_{j,k}=0$ unless
$A_{j,k}=0$ unless  $k=d+2$ and
$k=d+2$ and  $j<k$, in which case
$j<k$, in which case  $(A_{j,k})_{a,b}=0$ unless
$(A_{j,k})_{a,b}=0$ unless  $a-b=n-r$. Moreover, all the entries of
$a-b=n-r$. Moreover, all the entries of  $A_{j,k}$ on the diagonal
$A_{j,k}$ on the diagonal  $a-b=n-r$ coincide.
$a-b=n-r$ coincide.
This group is trivial if  $i$ is divisible by
$i$ is divisible by  $n$, and is of dimension
$n$, and is of dimension  $d+1$ otherwise.
$d+1$ otherwise.
Lemma 3.3. Let  $0\leqslant i<(m-1)n$. Then the following statements hold.
$0\leqslant i<(m-1)n$. Then the following statements hold.
(i) The commutator
 $[U_{i},U_{i+1}]$ is contained in
$[U_{i},U_{i+1}]$ is contained in  $U_{i}\cap U_{i+1}$. Thus,
$U_{i}\cap U_{i+1}$. Thus,  $U_{i}\cdot U_{i+1}$ is a subgroup of
$U_{i}\cdot U_{i+1}$ is a subgroup of  $G$ which contains
$G$ which contains  $U_{i}$ and
$U_{i}$ and  $U_{i+1}$ as normal subgroups and the quotients
$U_{i+1}$ as normal subgroups and the quotients  $U_{i}U_{i+1}/U_{i}\simeq U_{i+1}/U_{i}\cap U_{i+1}$ and
$U_{i}U_{i+1}/U_{i}\simeq U_{i+1}/U_{i}\cap U_{i+1}$ and  $U_{i}U_{i+1}/U_{i+1}\simeq U_{i}/U_{i}\cap U_{i+1}$ are abelian. Moreover, (6)
$U_{i}U_{i+1}/U_{i+1}\simeq U_{i}/U_{i}\cap U_{i+1}$ are abelian. Moreover, (6) $$\begin{eqnarray}U_{i+1}=(M_{i}\cap U_{i+1})\ltimes (U_{i}\cap U_{i+1})\quad \text{and}\quad U_{i}=(M_{i+1}\cap U_{i})\ltimes (U_{i}\cap U_{i+1}).\end{eqnarray}$$
$$\begin{eqnarray}U_{i+1}=(M_{i}\cap U_{i+1})\ltimes (U_{i}\cap U_{i+1})\quad \text{and}\quad U_{i}=(M_{i+1}\cap U_{i})\ltimes (U_{i}\cap U_{i+1}).\end{eqnarray}$$(ii) We have a short exact sequence
where
 $\mathfrak{c}_{i}$ denotes the map
$\mathfrak{c}_{i}$ denotes the map  $u\mapsto \unicode[STIX]{x1D6F9}([\cdot ,u])$ and
$u\mapsto \unicode[STIX]{x1D6F9}([\cdot ,u])$ and  $PD$ denotes the Pontryagin dual. Dually,where
$PD$ denotes the Pontryagin dual. Dually,where
 $\mathfrak{c}_{i}^{\prime }$ is defined by the same formula as
$\mathfrak{c}_{i}^{\prime }$ is defined by the same formula as  $\mathfrak{c}_{i}$.
$\mathfrak{c}_{i}$.
Proof. For any  $j,k$, we have
$j,k$, we have  $\unicode[STIX]{x1D706}_{j}^{\unicode[STIX]{x1D711}_{i}}-\unicode[STIX]{x1D706}_{k}^{\unicode[STIX]{x1D711}_{i}}-(\unicode[STIX]{x1D706}_{j}^{\unicode[STIX]{x1D711}_{i+1}}-\unicode[STIX]{x1D706}_{k}^{\unicode[STIX]{x1D711}_{i+1}})\in \{-1,0,1\}$. It follows that
$\unicode[STIX]{x1D706}_{j}^{\unicode[STIX]{x1D711}_{i}}-\unicode[STIX]{x1D706}_{k}^{\unicode[STIX]{x1D711}_{i}}-(\unicode[STIX]{x1D706}_{j}^{\unicode[STIX]{x1D711}_{i+1}}-\unicode[STIX]{x1D706}_{k}^{\unicode[STIX]{x1D711}_{i+1}})\in \{-1,0,1\}$. It follows that
 $$\begin{eqnarray}\mathfrak{g}_{{\geqslant}j+1}^{\unicode[STIX]{x1D711}_{i+1}}\subset \mathfrak{g}_{{\geqslant}j}^{\unicode[STIX]{x1D711}_{i}}\subset \mathfrak{g}_{{\geqslant}j-1}^{\unicode[STIX]{x1D711}_{i+1}}\quad \text{for all }j.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}_{{\geqslant}j+1}^{\unicode[STIX]{x1D711}_{i+1}}\subset \mathfrak{g}_{{\geqslant}j}^{\unicode[STIX]{x1D711}_{i}}\subset \mathfrak{g}_{{\geqslant}j-1}^{\unicode[STIX]{x1D711}_{i+1}}\quad \text{for all }j.\end{eqnarray}$$ Therefore,  $U_{i}\subset P_{i+1}$ and
$U_{i}\subset P_{i+1}$ and  $U_{i+1}\subset P_{i}$. Hence,
$U_{i+1}\subset P_{i}$. Hence,  $U_{i}$ and
$U_{i}$ and  $U_{i+1}$ normalize each other, so that
$U_{i+1}$ normalize each other, so that  $U_{i}\cdot U_{i+1}$ is a subgroup of
$U_{i}\cdot U_{i+1}$ is a subgroup of  $G$ that contains
$G$ that contains  $U_{i}$ and
$U_{i}$ and  $U_{i+1}$ as normal subgroups. The equalities (6) are now clear since
$U_{i+1}$ as normal subgroups. The equalities (6) are now clear since  $T\subset M_{i},M_{i+1}$. By (7), we have
$T\subset M_{i},M_{i+1}$. By (7), we have  $\operatorname{Lie}M_{i+1}\cap U_{i}=\mathfrak{g}_{{>}0}^{\unicode[STIX]{x1D711}_{i}}\cap \mathfrak{g}_{0}^{\unicode[STIX]{x1D711}_{i+1}}\subset \mathfrak{g}_{1}^{\unicode[STIX]{x1D711}_{i}}$. It follows that
$\operatorname{Lie}M_{i+1}\cap U_{i}=\mathfrak{g}_{{>}0}^{\unicode[STIX]{x1D711}_{i}}\cap \mathfrak{g}_{0}^{\unicode[STIX]{x1D711}_{i+1}}\subset \mathfrak{g}_{1}^{\unicode[STIX]{x1D711}_{i}}$. It follows that  $M_{i+1}\cap U_{i}$ is abelian since
$M_{i+1}\cap U_{i}$ is abelian since  $[\mathfrak{g}_{1}^{\unicode[STIX]{x1D711}_{i}},\mathfrak{g}_{1}^{\unicode[STIX]{x1D711}_{i}}]\subset \mathfrak{g}_{2}^{\unicode[STIX]{x1D711}_{i}}$. Similarly,
$[\mathfrak{g}_{1}^{\unicode[STIX]{x1D711}_{i}},\mathfrak{g}_{1}^{\unicode[STIX]{x1D711}_{i}}]\subset \mathfrak{g}_{2}^{\unicode[STIX]{x1D711}_{i}}$. Similarly,  $M_{i}\cap U_{i+1}$ is abelian. The rest of the lemma follows easily from the fact that
$M_{i}\cap U_{i+1}$ is abelian. The rest of the lemma follows easily from the fact that  $U_{i+1}\cap M_{i}^{\unicode[STIX]{x1D6F9}}=1$.◻
$U_{i+1}\cap M_{i}^{\unicode[STIX]{x1D6F9}}=1$.◻
Remark 3.4. If  $i=nd+r$,
$i=nd+r$,  $0\leqslant r<n$, then
$0\leqslant r<n$, then  $U_{i}\cap M_{i+1}^{\unicode[STIX]{x1D6F9}}$ consists of the upper unitriangular matrices whose
$U_{i}\cap M_{i+1}^{\unicode[STIX]{x1D6F9}}$ consists of the upper unitriangular matrices whose  $n\times n$ blocks
$n\times n$ blocks  $A_{j,k}$ satisfy the following requirements.
$A_{j,k}$ satisfy the following requirements.
(i)
 $A_{j,j}=I_{n}$ for all
$A_{j,j}=I_{n}$ for all  $j$.
$j$.(ii) If
 $j<k$, then
$j<k$, then  $A_{j,k}=0$ unless
$A_{j,k}=0$ unless  $k=d+2$, in which case
$k=d+2$, in which case  $(A_{j,k})_{a,b}=0$ unless
$(A_{j,k})_{a,b}=0$ unless  $a-b=n-r-1$ and all entries of
$a-b=n-r-1$ and all entries of  $A_{j,k}$ along the diagonal
$A_{j,k}$ along the diagonal  $a-b=n-r-1$ are identical.
$a-b=n-r-1$ are identical.
This group is of dimension  $d+1$. (It coincides with the unipotent radical of
$d+1$. (It coincides with the unipotent radical of  $M_{i+1}^{\unicode[STIX]{x1D6F9}}$ unless
$M_{i+1}^{\unicode[STIX]{x1D6F9}}$ unless  $i+1$ is divisible by
$i+1$ is divisible by  $n$.)
$n$.)
In the rest of the section we endow various unipotent subgroups of  $G$ with Haar measures. Thanks to the choice of basis
$G$ with Haar measures. Thanks to the choice of basis  $e_{1},\ldots ,e_{mn}$, the Lie algebra of any of these unipotent groups has a natural basis as a vector space over
$e_{1},\ldots ,e_{mn}$, the Lie algebra of any of these unipotent groups has a natural basis as a vector space over  $F$. Our convention will be to take the measure corresponding to the product measure where the Haar measure on
$F$. Our convention will be to take the measure corresponding to the product measure where the Haar measure on  $F$ is the one which is self-dual with respect to
$F$ is the one which is self-dual with respect to  $\unicode[STIX]{x1D713}$.
$\unicode[STIX]{x1D713}$.
The following is a special case of [Reference Gomez, Gourevitch and SahiGGS16] (see also [Reference Gomez, Gourevitch and SahiGGS17]). For future reference and in order to be self-contained we provide the (elementary) proof. We refer the reader to [Reference Gomez, Gourevitch and SahiGGS16, Reference Gomez, Gourevitch and SahiGGS17] for a more thorough discussion about interplay between models.
Proposition 3.5. For any  $i=0,\ldots ,(m-1)n-1$, the map
$i=0,\ldots ,(m-1)n-1$, the map
 $$\begin{eqnarray}\displaystyle W_{i}\mapsto \int _{U_{i}\cap U_{i+1}\backslash U_{i+1}}W_{i}(u^{\prime }\cdot )\unicode[STIX]{x1D6F9}_{U_{i+1}}(u^{\prime })^{-1}\,du^{\prime } & = & \displaystyle \int _{U_{i}\cap U^{\prime }\backslash U_{i+1}\cap U^{\prime }}W_{i}(u^{\prime }\cdot )\unicode[STIX]{x1D6F9}_{U_{i+1}}(u^{\prime })^{-1}\,du^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{i}\cap \bar{N}\backslash U_{i+1}\cap \bar{N}}W_{i}(u^{\prime }\cdot )\,du^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W_{i}\mapsto \int _{U_{i}\cap U_{i+1}\backslash U_{i+1}}W_{i}(u^{\prime }\cdot )\unicode[STIX]{x1D6F9}_{U_{i+1}}(u^{\prime })^{-1}\,du^{\prime } & = & \displaystyle \int _{U_{i}\cap U^{\prime }\backslash U_{i+1}\cap U^{\prime }}W_{i}(u^{\prime }\cdot )\unicode[STIX]{x1D6F9}_{U_{i+1}}(u^{\prime })^{-1}\,du^{\prime }\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{i}\cap \bar{N}\backslash U_{i+1}\cap \bar{N}}W_{i}(u^{\prime }\cdot )\,du^{\prime }\end{eqnarray}$$ defines an isomorphism  ${\mathcal{T}}_{i}={\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}:{\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\rightarrow {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i+1}}}(\unicode[STIX]{x1D70E})$. Its inverse is given by
${\mathcal{T}}_{i}={\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}:{\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\rightarrow {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i+1}}}(\unicode[STIX]{x1D70E})$. Its inverse is given by
 $$\begin{eqnarray}W_{i+1}\mapsto \int _{U_{i}\cap P_{i+1}^{\unicode[STIX]{x1D6F9}}\backslash U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du.\end{eqnarray}$$
$$\begin{eqnarray}W_{i+1}\mapsto \int _{U_{i}\cap P_{i+1}^{\unicode[STIX]{x1D6F9}}\backslash U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du.\end{eqnarray}$$In both cases the integrands are compactly supported.
Proof. For any  $W_{i}\in \operatorname{Ind}_{U_{i}}^{G}\unicode[STIX]{x1D6F9}_{U_{i}}$,
$W_{i}\in \operatorname{Ind}_{U_{i}}^{G}\unicode[STIX]{x1D6F9}_{U_{i}}$,  $u\in U_{i}$ and
$u\in U_{i}$ and  $u^{\prime }\in U_{i+1}$, we have
$u^{\prime }\in U_{i+1}$, we have  $W_{i}(u^{\prime }u)=\mathfrak{c}_{i}(u)(u^{\prime })\unicode[STIX]{x1D6F9}_{U_{i}}(u)W_{i}(u^{\prime })$. It follows from Lemma 3.3 and the smoothness of
$W_{i}(u^{\prime }u)=\mathfrak{c}_{i}(u)(u^{\prime })\unicode[STIX]{x1D6F9}_{U_{i}}(u)W_{i}(u^{\prime })$. It follows from Lemma 3.3 and the smoothness of  $W_{i}$ that
$W_{i}$ that  $W_{i}|_{U_{i+1}}$ is compactly supported modulo
$W_{i}|_{U_{i+1}}$ is compactly supported modulo  $U_{i}\cap U_{i+1}$ and that, for any
$U_{i}\cap U_{i+1}$ and that, for any  $u\in U_{i}$,
$u\in U_{i}$,

Recall that any  $W_{i+1}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i+1}}}(\unicode[STIX]{x1D70E})$ is left-
$W_{i+1}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i+1}}}(\unicode[STIX]{x1D70E})$ is left- $M_{i+1}^{\unicode[STIX]{x1D6F9}}$-equivariant under a character and, in particular, is left-invariant under any unipotent subgroup of
$M_{i+1}^{\unicode[STIX]{x1D6F9}}$-equivariant under a character and, in particular, is left-invariant under any unipotent subgroup of  $M_{i+1}^{\unicode[STIX]{x1D6F9}}$. Also,
$M_{i+1}^{\unicode[STIX]{x1D6F9}}$. Also,  $U_{i}\cap P_{i+1}^{\unicode[STIX]{x1D6F9}}=(U_{i}\cap M_{i+1}^{\unicode[STIX]{x1D6F9}})\ltimes (U_{i}\cap U_{i+1})$. By similar reasoning as before,
$U_{i}\cap P_{i+1}^{\unicode[STIX]{x1D6F9}}=(U_{i}\cap M_{i+1}^{\unicode[STIX]{x1D6F9}})\ltimes (U_{i}\cap U_{i+1})$. By similar reasoning as before,  $W_{i+1}|_{U_{i}}$ is compactly supported modulo
$W_{i+1}|_{U_{i}}$ is compactly supported modulo  $U_{i}\cap P_{i+1}^{\unicode[STIX]{x1D6F9}}$. By Lemma 3.3 and Fourier inversion, the map (9) defines a
$U_{i}\cap P_{i+1}^{\unicode[STIX]{x1D6F9}}$. By Lemma 3.3 and Fourier inversion, the map (9) defines a  $G$-equivariant left inverse to
$G$-equivariant left inverse to  ${\mathcal{T}}_{i}$. Since the spaces are irreducible, it is also a right inverse.◻
${\mathcal{T}}_{i}$. Since the spaces are irreducible, it is also a right inverse.◻
Remark 3.6. Suppose that  $\unicode[STIX]{x1D70E}$ is unramified,
$\unicode[STIX]{x1D70E}$ is unramified,  $\unicode[STIX]{x1D713}$ has conductor
$\unicode[STIX]{x1D713}$ has conductor  ${\mathcal{O}}$ and
${\mathcal{O}}$ and  $W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$ is the unramified vector such that
$W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$ is the unramified vector such that  $W_{i}(e)=1$. Then
$W_{i}(e)=1$. Then  ${\mathcal{T}}_{i}W_{i}(e)=1$. This follows immediately from the proof of Proposition 3.5.
${\mathcal{T}}_{i}W_{i}(e)=1$. This follows immediately from the proof of Proposition 3.5.
We write
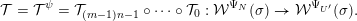 $$\begin{eqnarray}{\mathcal{T}}={\mathcal{T}}^{\unicode[STIX]{x1D713}}={\mathcal{T}}_{(m-1)n-1}\circ \ldots \circ {\mathcal{T}}_{0}:{\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})\rightarrow {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}={\mathcal{T}}^{\unicode[STIX]{x1D713}}={\mathcal{T}}_{(m-1)n-1}\circ \ldots \circ {\mathcal{T}}_{0}:{\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})\rightarrow {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E}).\end{eqnarray}$$This operator was considered in [Reference Cai, Friedberg and KaplanCFK18, §2.4].
3.3 Model transition part II
We now introduce a subgroup of  $G$ that will play an important role in what follows. Let
$G$ that will play an important role in what follows. Let  $D=D_{m,n}$ be the joint stabilizer of the vectors
$D=D_{m,n}$ be the joint stabilizer of the vectors  $e_{jn}$,
$e_{jn}$,  $j=1,\ldots ,m$, in
$j=1,\ldots ,m$, in  $G$ and let
$G$ and let  $N_{D}=N\cap D\supset N_{M}$. Note that
$N_{D}=N\cap D\supset N_{M}$. Note that  $U^{\prime }\subset D$. (In the case
$U^{\prime }\subset D$. (In the case  $m=1$,
$m=1$,  $D$ is the standard mirabolic subgroup.)
$D$ is the standard mirabolic subgroup.)
The following lemma is straightforward.
Lemma 3.7. We have  $M_{i+1}\cap U_{i}=(M_{i+1}\cap U_{i}\cap D)\times (U_{i}\cap M_{i+1}^{\unicode[STIX]{x1D6F9}})$. Hence, the restriction of
$M_{i+1}\cap U_{i}=(M_{i+1}\cap U_{i}\cap D)\times (U_{i}\cap M_{i+1}^{\unicode[STIX]{x1D6F9}})$. Hence, the restriction of  $\mathfrak{c}_{i}$ to
$\mathfrak{c}_{i}$ to  $D\cap U_{i}/D\cap U_{i}\cap U_{i+1}\simeq D\cap M_{i+1}\cap U_{i}$ is an isomorphism. Dually,
$D\cap U_{i}/D\cap U_{i}\cap U_{i+1}\simeq D\cap M_{i+1}\cap U_{i}$ is an isomorphism. Dually,  $\mathfrak{c}_{i}^{\prime }$ defines an isomorphism between
$\mathfrak{c}_{i}^{\prime }$ defines an isomorphism between  $U_{i+1}/U_{i}\cap U_{i+1}\simeq M_{i}\cap U_{i+1}$ and the Pontryagin dual of
$U_{i+1}/U_{i}\cap U_{i+1}\simeq M_{i}\cap U_{i+1}$ and the Pontryagin dual of  $D\cap U_{i}/D\cap U_{i}\cap U_{i+1}\simeq D\cap M_{i+1}\cap U_{i}\simeq U_{i}\cap M_{i+1}/U_{i}\cap M_{i+1}^{\unicode[STIX]{x1D6F9}}$.
$D\cap U_{i}/D\cap U_{i}\cap U_{i+1}\simeq D\cap M_{i+1}\cap U_{i}\simeq U_{i}\cap M_{i+1}/U_{i}\cap M_{i+1}^{\unicode[STIX]{x1D6F9}}$.
Hence, we can rewrite (9) as
 $$\begin{eqnarray}W_{i+1}\mapsto \int _{D\cap U_{i}\cap U_{i+1}\backslash D\cap U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du=\int _{N_{D}\cap U_{i+1}\backslash N_{D}\cap U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du.\end{eqnarray}$$
$$\begin{eqnarray}W_{i+1}\mapsto \int _{D\cap U_{i}\cap U_{i+1}\backslash D\cap U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du=\int _{N_{D}\cap U_{i+1}\backslash N_{D}\cap U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du.\end{eqnarray}$$Lemma 3.8. Any  $W_{\operatorname{Ze}}\in \operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N}$ is compactly supported on
$W_{\operatorname{Ze}}\in \operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N}$ is compactly supported on  $D\cap \bar{N}$. Hence,
$D\cap \bar{N}$. Hence,
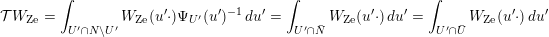 $$\begin{eqnarray}{\mathcal{T}}W_{\operatorname{Ze}}=\int _{U^{\prime }\cap N\backslash U^{\prime }}W_{\operatorname{Ze}}(u^{\prime }\cdot )\unicode[STIX]{x1D6F9}_{U^{\prime }}(u^{\prime })^{-1}\,du^{\prime }=\int _{U^{\prime }\cap \bar{N}}W_{\operatorname{Ze}}(u^{\prime }\cdot )\,du^{\prime }=\int _{U^{\prime }\cap \bar{U}}W_{\operatorname{Ze}}(u^{\prime }\cdot )\,du^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{T}}W_{\operatorname{Ze}}=\int _{U^{\prime }\cap N\backslash U^{\prime }}W_{\operatorname{Ze}}(u^{\prime }\cdot )\unicode[STIX]{x1D6F9}_{U^{\prime }}(u^{\prime })^{-1}\,du^{\prime }=\int _{U^{\prime }\cap \bar{N}}W_{\operatorname{Ze}}(u^{\prime }\cdot )\,du^{\prime }=\int _{U^{\prime }\cap \bar{U}}W_{\operatorname{Ze}}(u^{\prime }\cdot )\,du^{\prime }\end{eqnarray}$$where the integrand is compactly supported.
Proof. Let  $g=ank\in G$ with
$g=ank\in G$ with  $a=\operatorname{diag}(a_{1},\ldots ,a_{nm})$,
$a=\operatorname{diag}(a_{1},\ldots ,a_{nm})$,  $n\in N$ and
$n\in N$ and  $k\in G({\mathcal{O}})$. It is well known and easy to prove that if
$k\in G({\mathcal{O}})$. It is well known and easy to prove that if  $g\in \bar{N}$, then
$g\in \bar{N}$, then  $\Vert g\Vert \leqslant \max _{i=1,\ldots ,mn}|\prod _{j=i}^{nm}a_{j}|$. On the other hand, it is also easy to see that if
$\Vert g\Vert \leqslant \max _{i=1,\ldots ,mn}|\prod _{j=i}^{nm}a_{j}|$. On the other hand, it is also easy to see that if  $g\in D$, then
$g\in D$, then  $|a_{jn}|\leqslant 1$ for
$|a_{jn}|\leqslant 1$ for  $j=1,\ldots ,m$. Thus, if
$j=1,\ldots ,m$. Thus, if  $g\in D$ and
$g\in D$ and  $W_{\operatorname{Ze}}(g)\neq 0$, then by the support condition for Whittaker functions we get
$W_{\operatorname{Ze}}(g)\neq 0$, then by the support condition for Whittaker functions we get  $|a_{i}|\leqslant C_{1}$ for all
$|a_{i}|\leqslant C_{1}$ for all  $i$ where
$i$ where  $C_{1}$ depends only on
$C_{1}$ depends only on  $W_{\operatorname{Ze}}$. By the above, if moreover
$W_{\operatorname{Ze}}$. By the above, if moreover  $g\in \bar{N}$, then
$g\in \bar{N}$, then  $\Vert g\Vert$ is bounded in terms of
$\Vert g\Vert$ is bounded in terms of  $W_{\operatorname{Ze}}$ as required.◻
$W_{\operatorname{Ze}}$ as required.◻
Recall that any  $W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$ is
$W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$ is  $M_{i}^{\unicode[STIX]{x1D6F9}}$-equivariant with respect to some character
$M_{i}^{\unicode[STIX]{x1D6F9}}$-equivariant with respect to some character  $\unicode[STIX]{x1D712}_{i}$ of
$\unicode[STIX]{x1D712}_{i}$ of  $M_{i}^{\unicode[STIX]{x1D6F9}}$ (depending only on
$M_{i}^{\unicode[STIX]{x1D6F9}}$ (depending only on  $\unicode[STIX]{x1D70E}$). As in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Cai, Friedberg and KaplanCFK18] we can easily explicate this character.
$\unicode[STIX]{x1D70E}$). As in [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Reference Cai, Friedberg and KaplanCFK18] we can easily explicate this character.
Lemma 3.9 (Cf. [Reference Cai, Friedberg, Ginzburg and KaplanCFGK19, Proposition 24], [Reference Cai, Friedberg and KaplanCFK18, §2.6]).
For any  $i=nd+r$,
$i=nd+r$,  $0\leqslant r<n$,
$0\leqslant r<n$,  $l\in \operatorname{GL}_{d+1}$ and
$l\in \operatorname{GL}_{d+1}$ and  $t_{d+2},\ldots ,t_{m}\in F^{\ast }$, we have
$t_{d+2},\ldots ,t_{m}\in F^{\ast }$, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D712}_{i}(\unicode[STIX]{x1D704}(\operatorname{diag}(l,t_{d+2},\ldots ,t_{m})))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(t_{d+2}\ldots t_{m}\det l)|\det l|^{-\binom{r}{2}+\binom{n}{2}(m-d-1)}|t_{d+2}|^{\binom{r}{2}(d+1)}\mathop{\prod }_{j=d+2}^{m}|t_{j}|^{n(n-1)((m+1)/2-j)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D712}_{i}(\unicode[STIX]{x1D704}(\operatorname{diag}(l,t_{d+2},\ldots ,t_{m})))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(t_{d+2}\ldots t_{m}\det l)|\det l|^{-\binom{r}{2}+\binom{n}{2}(m-d-1)}|t_{d+2}|^{\binom{r}{2}(d+1)}\mathop{\prod }_{j=d+2}^{m}|t_{j}|^{n(n-1)((m+1)/2-j)}\nonumber\end{eqnarray}$$ where  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$ is the central character of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$ is the central character of  $\unicode[STIX]{x1D70B}$. In particular, for any
$\unicode[STIX]{x1D70B}$. In particular, for any  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
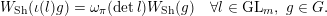 $$\begin{eqnarray}W_{\operatorname{Sh}}(\unicode[STIX]{x1D704}(l)g)=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\det l)W_{\operatorname{Sh}}(g)\quad \forall l\in \operatorname{GL}_{m},~g\in G.\end{eqnarray}$$
$$\begin{eqnarray}W_{\operatorname{Sh}}(\unicode[STIX]{x1D704}(l)g)=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\det l)W_{\operatorname{Sh}}(g)\quad \forall l\in \operatorname{GL}_{m},~g\in G.\end{eqnarray}$$Proof. It is enough to evaluate  $\unicode[STIX]{x1D712}_{i}$ on an element
$\unicode[STIX]{x1D712}_{i}$ on an element  $\unicode[STIX]{x1D704}(t)$ where
$\unicode[STIX]{x1D704}(t)$ where  $t=\operatorname{diag}(t_{1},\ldots ,t_{m})$ is in the diagonal torus of
$t=\operatorname{diag}(t_{1},\ldots ,t_{m})$ is in the diagonal torus of  $\operatorname{GL}_{m}$. Note that
$\operatorname{GL}_{m}$. Note that  $\unicode[STIX]{x1D704}(t)$ lies in the center
$\unicode[STIX]{x1D704}(t)$ lies in the center  $Z_{M}$ of
$Z_{M}$ of 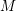 $M$. Writing
$M$. Writing  $W_{i}=\int _{\bar{N}\cap U_{i}}W_{\operatorname{Ze}}(u\cdot )\,du$ with
$W_{i}=\int _{\bar{N}\cap U_{i}}W_{\operatorname{Ze}}(u\cdot )\,du$ with  $W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ (the integrand is compactly supported by Lemma 3.8), the required relation follows from the equality
$W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ (the integrand is compactly supported by Lemma 3.8), the required relation follows from the equality
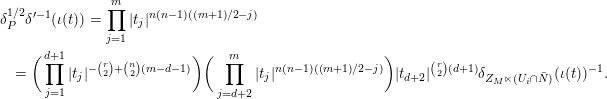 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}_{P}^{1/2}{\unicode[STIX]{x1D6FF}^{\prime }}^{-1}(\unicode[STIX]{x1D704}(t))=\mathop{\prod }_{j=1}^{m}|t_{j}|^{n(n-1)((m+1)/2-j)}\nonumber\\ \displaystyle & & \displaystyle \quad =\bigg(\mathop{\prod }_{j=1}^{d+1}|t_{j}|^{-\binom{r}{2}+\binom{n}{2}(m-d-1)}\bigg)\bigg(\mathop{\prod }_{j=d+2}^{m}|t_{j}|^{n(n-1)((m+1)/2-j)}\bigg)|t_{d+2}|^{\binom{r}{2}(d+1)}\unicode[STIX]{x1D6FF}_{Z_{M}\ltimes (U_{i}\cap \bar{N})}(\unicode[STIX]{x1D704}(t))^{-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}_{P}^{1/2}{\unicode[STIX]{x1D6FF}^{\prime }}^{-1}(\unicode[STIX]{x1D704}(t))=\mathop{\prod }_{j=1}^{m}|t_{j}|^{n(n-1)((m+1)/2-j)}\nonumber\\ \displaystyle & & \displaystyle \quad =\bigg(\mathop{\prod }_{j=1}^{d+1}|t_{j}|^{-\binom{r}{2}+\binom{n}{2}(m-d-1)}\bigg)\bigg(\mathop{\prod }_{j=d+2}^{m}|t_{j}|^{n(n-1)((m+1)/2-j)}\bigg)|t_{d+2}|^{\binom{r}{2}(d+1)}\unicode[STIX]{x1D6FF}_{Z_{M}\ltimes (U_{i}\cap \bar{N})}(\unicode[STIX]{x1D704}(t))^{-1}.\nonumber\end{eqnarray}$$◻
Remark 3.10. Let  (alternating signs on the non-principal diagonal) and
(alternating signs on the non-principal diagonal) and  $\tilde{w}_{m,n}=\unicode[STIX]{x1D704}(\tilde{w}_{m})$. By Lemma 3.9, we have
$\tilde{w}_{m,n}=\unicode[STIX]{x1D704}(\tilde{w}_{m})$. By Lemma 3.9, we have
 $$\begin{eqnarray}W_{\operatorname{Sh}}(\tilde{w}_{m,n}g)=W_{\operatorname{Sh}}(g)\end{eqnarray}$$
$$\begin{eqnarray}W_{\operatorname{Sh}}(\tilde{w}_{m,n}g)=W_{\operatorname{Sh}}(g)\end{eqnarray}$$ for any  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$.
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$.
Lemma 3.11. The inverse of  ${\mathcal{T}}$ is given by
${\mathcal{T}}$ is given by
 $$\begin{eqnarray}W_{\operatorname{Sh}}\mapsto \int _{N\cap U^{\prime }\backslash N_{D}}W_{\operatorname{Sh}}(u\cdot )\unicode[STIX]{x1D6F9}_{N}(u)^{-1}\,du\end{eqnarray}$$
$$\begin{eqnarray}W_{\operatorname{Sh}}\mapsto \int _{N\cap U^{\prime }\backslash N_{D}}W_{\operatorname{Sh}}(u\cdot )\unicode[STIX]{x1D6F9}_{N}(u)^{-1}\,du\end{eqnarray}$$where the integrand is compactly supported.
Proof. From Proposition 3.5 we only need to check that the integrand is compactly supported. Assume that  $W_{\operatorname{Sh}}={\mathcal{T}}W_{\operatorname{Ze}}$. By Remark 3.10, the integral equals
$W_{\operatorname{Sh}}={\mathcal{T}}W_{\operatorname{Ze}}$. By Remark 3.10, the integral equals
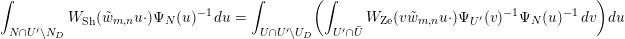 $$\begin{eqnarray}\int _{N\cap U^{\prime }\backslash N_{D}}W_{\operatorname{Sh}}(\tilde{w}_{m,n}u\cdot )\unicode[STIX]{x1D6F9}_{N}(u)^{-1}\,du=\int _{U\cap U^{\prime }\backslash U_{D}}\biggl(\int _{U^{\prime }\cap \bar{U}}W_{\operatorname{Ze}}(v\tilde{w}_{m,n}u\cdot )\unicode[STIX]{x1D6F9}_{U^{\prime }}(v)^{-1}\unicode[STIX]{x1D6F9}_{N}(u)^{-1}\,dv\biggr)du\end{eqnarray}$$
$$\begin{eqnarray}\int _{N\cap U^{\prime }\backslash N_{D}}W_{\operatorname{Sh}}(\tilde{w}_{m,n}u\cdot )\unicode[STIX]{x1D6F9}_{N}(u)^{-1}\,du=\int _{U\cap U^{\prime }\backslash U_{D}}\biggl(\int _{U^{\prime }\cap \bar{U}}W_{\operatorname{Ze}}(v\tilde{w}_{m,n}u\cdot )\unicode[STIX]{x1D6F9}_{U^{\prime }}(v)^{-1}\unicode[STIX]{x1D6F9}_{N}(u)^{-1}\,dv\biggr)du\end{eqnarray}$$ where  $U_{D}=U\cap D$. The latter double integral is
$U_{D}=U\cap D$. The latter double integral is
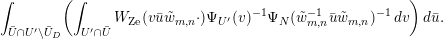 $$\begin{eqnarray}\int _{\bar{U}\cap U^{\prime }\backslash \bar{U}_{D}}\biggl(\int _{U^{\prime }\cap \bar{U}}W_{\operatorname{Ze}}(v\bar{u}\tilde{w}_{m,n}\cdot )\unicode[STIX]{x1D6F9}_{U^{\prime }}(v)^{-1}\unicode[STIX]{x1D6F9}_{N}({\tilde{w}_{m,n}}^{-1}\bar{u}\tilde{w}_{m,n})^{-1}\,dv\biggr)\,d\bar{u}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}\cap U^{\prime }\backslash \bar{U}_{D}}\biggl(\int _{U^{\prime }\cap \bar{U}}W_{\operatorname{Ze}}(v\bar{u}\tilde{w}_{m,n}\cdot )\unicode[STIX]{x1D6F9}_{U^{\prime }}(v)^{-1}\unicode[STIX]{x1D6F9}_{N}({\tilde{w}_{m,n}}^{-1}\bar{u}\tilde{w}_{m,n})^{-1}\,dv\biggr)\,d\bar{u}.\end{eqnarray}$$ By Lemma 3.8 the integrand is compactly supported in  $v$,
$v$,  $\bar{u}$. Thus, the integrand on the right-hand side of (11) is compactly supported.◻
$\bar{u}$. Thus, the integrand on the right-hand side of (11) is compactly supported.◻
3.4 Kirillov–Shalika model
The following lemma is an analogue of [Reference Gel’fand and KajdanGK75, Proposition 2].
Lemma 3.12. Any non-zero  $D$-invariant subspace of
$D$-invariant subspace of  $\operatorname{Ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$ contains
$\operatorname{Ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$ contains  $\operatorname{ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$. In particular,
$\operatorname{ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$. In particular,  $\operatorname{ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$ is irreducible.
$\operatorname{ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$ is irreducible.
The proof of [Reference Gel’fand and KajdanGK75, pp. 110–111] (for the case  $m=1$) applies verbatim. One only needs to observe that the unipotent radical
$m=1$) applies verbatim. One only needs to observe that the unipotent radical  $V$ of
$V$ of  $D$ is abelian, the stabilizer of the character
$D$ is abelian, the stabilizer of the character  $\unicode[STIX]{x1D6F9}_{V}$ under the action of
$\unicode[STIX]{x1D6F9}_{V}$ under the action of  $D$ modulo
$D$ modulo  $V$ is isomorphic to
$V$ is isomorphic to  $D_{m,n-1}$ and the map
$D_{m,n-1}$ and the map  $p\mapsto \unicode[STIX]{x1D6F9}_{V}(p^{-1}\cdot p)$ defines an open map from
$p\mapsto \unicode[STIX]{x1D6F9}_{V}(p^{-1}\cdot p)$ defines an open map from  $D$ to the Pontryagin dual of
$D$ to the Pontryagin dual of  $V$.
$V$.
Let  $Q$ be the stabilizer of
$Q$ be the stabilizer of  $\operatorname{span}\{e_{ni}:i=1,\ldots ,m\}$ in
$\operatorname{span}\{e_{ni}:i=1,\ldots ,m\}$ in  $G$ – a maximal parabolic subgroup of
$G$ – a maximal parabolic subgroup of  $G$ of type
$G$ of type  $((n-1)m,m)$. Thus,
$((n-1)m,m)$. Thus,  $Q=D\rtimes {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$ and
$Q=D\rtimes {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$ and  $\unicode[STIX]{x1D6FF}_{Q}|_{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}}\equiv 1$.
$\unicode[STIX]{x1D6FF}_{Q}|_{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}}\equiv 1$.
Corollary 3.13. For any  $m$-homogeneous
$m$-homogeneous  $\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$, the image of the restriction map
$\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$, the image of the restriction map
 $$\begin{eqnarray}W_{\operatorname{Sh}}\mapsto W_{\operatorname{Sh}}|_{D},\quad {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})\rightarrow \operatorname{Ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}\end{eqnarray}$$
$$\begin{eqnarray}W_{\operatorname{Sh}}\mapsto W_{\operatorname{Sh}}|_{D},\quad {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})\rightarrow \operatorname{Ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}\end{eqnarray}$$ contains  $\operatorname{ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$. Equivalently, by Lemmas 2.3 and 3.9, if
$\operatorname{ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$. Equivalently, by Lemmas 2.3 and 3.9, if  $\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$, then the image
$\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$, then the image  ${\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$ of the restriction map
${\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$ of the restriction map
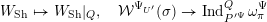 $$\begin{eqnarray}W_{\operatorname{Sh}}\mapsto W_{\operatorname{Sh}}|_{Q},\quad {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})\rightarrow \operatorname{Ind}_{{P^{\prime }}^{\unicode[STIX]{x1D6F9}}}^{Q}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}\end{eqnarray}$$
$$\begin{eqnarray}W_{\operatorname{Sh}}\mapsto W_{\operatorname{Sh}}|_{Q},\quad {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})\rightarrow \operatorname{Ind}_{{P^{\prime }}^{\unicode[STIX]{x1D6F9}}}^{Q}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}\end{eqnarray}$$ contains  $\operatorname{ind}_{{P^{\prime }}^{\unicode[STIX]{x1D6F9}}}^{Q}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}$ where
$\operatorname{ind}_{{P^{\prime }}^{\unicode[STIX]{x1D6F9}}}^{Q}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}$ where  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}$ is the character of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}$ is the character of  ${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ such that
${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ such that  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}|_{U^{\prime }}=\unicode[STIX]{x1D6F9}_{U^{\prime }}$ and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}|_{U^{\prime }}=\unicode[STIX]{x1D6F9}_{U^{\prime }}$ and  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\circ \det$.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\circ \det$.
We will call  ${\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$ the Kirillov–Shalika model of
${\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$ the Kirillov–Shalika model of  $\unicode[STIX]{x1D70E}$.
$\unicode[STIX]{x1D70E}$.
Lemma 3.14. For any  $i=0,\ldots ,(m-1)n-1$, the map
$i=0,\ldots ,(m-1)n-1$, the map
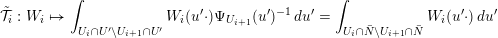 $$\begin{eqnarray}\tilde{{\mathcal{T}}}_{i}:W_{i}\mapsto \int _{U_{i}\cap U^{\prime }\backslash U_{i+1}\cap U^{\prime }}W_{i}(u^{\prime }\cdot )\unicode[STIX]{x1D6F9}_{U_{i+1}}(u^{\prime })^{-1}\,du^{\prime }=\int _{U_{i}\cap \bar{N}\backslash U_{i+1}\cap \bar{N}}W_{i}(u^{\prime }\cdot )\,du^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\mathcal{T}}}_{i}:W_{i}\mapsto \int _{U_{i}\cap U^{\prime }\backslash U_{i+1}\cap U^{\prime }}W_{i}(u^{\prime }\cdot )\unicode[STIX]{x1D6F9}_{U_{i+1}}(u^{\prime })^{-1}\,du^{\prime }=\int _{U_{i}\cap \bar{N}\backslash U_{i+1}\cap \bar{N}}W_{i}(u^{\prime }\cdot )\,du^{\prime }\end{eqnarray}$$ is an isomorphism between  $\operatorname{Ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$ and
$\operatorname{Ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$ and  $\operatorname{Ind}_{D\cap U_{i+1}}^{D}\unicode[STIX]{x1D6F9}_{U_{i+1}}$, whose inverse is given by
$\operatorname{Ind}_{D\cap U_{i+1}}^{D}\unicode[STIX]{x1D6F9}_{U_{i+1}}$, whose inverse is given by
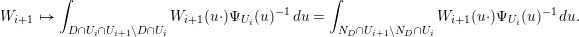 $$\begin{eqnarray}W_{i+1}\mapsto \int _{D\cap U_{i}\cap U_{i+1}\backslash D\cap U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du=\int _{N_{D}\cap U_{i+1}\backslash N_{D}\cap U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du.\end{eqnarray}$$
$$\begin{eqnarray}W_{i+1}\mapsto \int _{D\cap U_{i}\cap U_{i+1}\backslash D\cap U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du=\int _{N_{D}\cap U_{i+1}\backslash N_{D}\cap U_{i}}W_{i+1}(u\cdot )\unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}\,du.\end{eqnarray}$$Moreover,
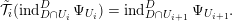 $$\begin{eqnarray}\tilde{{\mathcal{T}}}_{i}(\operatorname{ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}})=\operatorname{ind}_{D\cap U_{i+1}}^{D}\unicode[STIX]{x1D6F9}_{U_{i+1}}.\end{eqnarray}$$
$$\begin{eqnarray}\tilde{{\mathcal{T}}}_{i}(\operatorname{ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}})=\operatorname{ind}_{D\cap U_{i+1}}^{D}\unicode[STIX]{x1D6F9}_{U_{i+1}}.\end{eqnarray}$$ Finally, the  $D$-module
$D$-module  $\operatorname{ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$ is irreducible.
$\operatorname{ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$ is irreducible.
Proof. Let  $W_{i}\in \operatorname{Ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$. As in the proof of Proposition 3.5, by Lemma 3.7 the function
$W_{i}\in \operatorname{Ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$. As in the proof of Proposition 3.5, by Lemma 3.7 the function
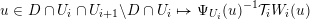 $$\begin{eqnarray}u\in D\cap U_{i}\cap U_{i+1}\backslash D\cap U_{i}\mapsto \unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}{\mathcal{T}}_{i}W_{i}(u)\end{eqnarray}$$
$$\begin{eqnarray}u\in D\cap U_{i}\cap U_{i+1}\backslash D\cap U_{i}\mapsto \unicode[STIX]{x1D6F9}_{U_{i}}(u)^{-1}{\mathcal{T}}_{i}W_{i}(u)\end{eqnarray}$$ is the Fourier transform of the function  $W_{i}\unicode[STIX]{x1D6F9}_{U_{i+1}}^{-1}|_{U_{i}\cap U^{\prime }\backslash U_{i+1}\cap U^{\prime }}$ at
$W_{i}\unicode[STIX]{x1D6F9}_{U_{i+1}}^{-1}|_{U_{i}\cap U^{\prime }\backslash U_{i+1}\cap U^{\prime }}$ at  $\mathfrak{c}_{i}(u)$. The first claim follows by Fourier inversion.
$\mathfrak{c}_{i}(u)$. The first claim follows by Fourier inversion.
Suppose that  $W_{i}\in \operatorname{ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$. From the definition (and since
$W_{i}\in \operatorname{ind}_{D\cap U_{i}}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$. From the definition (and since  $U^{\prime }\subset D$),
$U^{\prime }\subset D$),  $\tilde{{\mathcal{T}}}_{i}W_{i}$ is supported on
$\tilde{{\mathcal{T}}}_{i}W_{i}$ is supported on  $(D\cap U_{i}\cdot U_{i+1})\unicode[STIX]{x1D6FA}$, where
$(D\cap U_{i}\cdot U_{i+1})\unicode[STIX]{x1D6FA}$, where  $\unicode[STIX]{x1D6FA}$ is a compact subset of
$\unicode[STIX]{x1D6FA}$ is a compact subset of  $D$. Fix
$D$. Fix  $g\in \unicode[STIX]{x1D6FA}$. It follows from the above that the function
$g\in \unicode[STIX]{x1D6FA}$. It follows from the above that the function  $\tilde{{\mathcal{T}}}_{i}W_{i}(g)$ is compactly supported modulo
$\tilde{{\mathcal{T}}}_{i}W_{i}(g)$ is compactly supported modulo  $D\cap U_{i}\cap U_{i+1}$. Hence,
$D\cap U_{i}\cap U_{i+1}$. Hence,  $\tilde{{\mathcal{T}}}_{i}W_{i}$ is compactly supported modulo
$\tilde{{\mathcal{T}}}_{i}W_{i}$ is compactly supported modulo  $D\cap U_{i+1}$.
$D\cap U_{i+1}$.
The last part now follows from the fact that  $\operatorname{ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$ is irreducible.◻
$\operatorname{ind}_{U^{\prime }}^{D}\unicode[STIX]{x1D6F9}_{U^{\prime }}$ is irreducible.◻
From Lemma 3.14, Proposition 3.5 and Corollary 3.13 we obtain the following result.
Corollary 3.15. For any  $m$-homogeneous
$m$-homogeneous  $\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$ and for any
$\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$ and for any  $i=0,\ldots ,(m-1)n$, the image of the restriction map
$i=0,\ldots ,(m-1)n$, the image of the restriction map
 $$\begin{eqnarray}W_{i}\mapsto W_{i}|_{D},\quad {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\rightarrow \operatorname{Ind}_{U_{i}\cap D}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}\end{eqnarray}$$
$$\begin{eqnarray}W_{i}\mapsto W_{i}|_{D},\quad {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\rightarrow \operatorname{Ind}_{U_{i}\cap D}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}\end{eqnarray}$$ contains  $\operatorname{ind}_{U_{i}\cap D}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$.
$\operatorname{ind}_{U_{i}\cap D}^{D}\unicode[STIX]{x1D6F9}_{U_{i}}$.
Once again, in analogy with the case  $m=1$ (conjectured in [Reference Gel’fand and KajdanGK75], proved in [Reference Bernšten̆ and ZelevinskyBZ76, Reference Bernshtein and ZelevinskyBZ77]) it is natural to make the following conjecture.
$m=1$ (conjectured in [Reference Gel’fand and KajdanGK75], proved in [Reference Bernšten̆ and ZelevinskyBZ76, Reference Bernshtein and ZelevinskyBZ77]) it is natural to make the following conjecture.
Conjecture 3.16. For any  $m$-homogeneous
$m$-homogeneous  $\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$, the restriction map (12) (or equivalently, (13)) is injective.
$\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$, the restriction map (12) (or equivalently, (13)) is injective.
We will prove a special case in Corollary 4.4 below.
We do not know whether, in general, the restriction of  $\unicode[STIX]{x1D70E}$ to
$\unicode[STIX]{x1D70E}$ to  $Q$ is of finite length. (See Proposition 7.1 for a very special case.) Recall that in the case
$Q$ is of finite length. (See Proposition 7.1 for a very special case.) Recall that in the case  $m=1$ this is known (for any
$m=1$ this is known (for any  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}$, not necessarily generic) using the theory of derivatives of Bernstein and Zelevinsky [Reference Bernšten̆ and ZelevinskyBZ76, Reference Bernshtein and ZelevinskyBZ77]. It would be very interesting to have an analogous theory for
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}$, not necessarily generic) using the theory of derivatives of Bernstein and Zelevinsky [Reference Bernšten̆ and ZelevinskyBZ76, Reference Bernshtein and ZelevinskyBZ77]. It would be very interesting to have an analogous theory for  $m>1$.
$m>1$.
4 Unitary structure
We take the unnormalized Tamagawa measure on  $\operatorname{GL}_{r}$ with respect to
$\operatorname{GL}_{r}$ with respect to  $\unicode[STIX]{x1D713}$, that is, the Haar measure associated to the standard gauge form
$\unicode[STIX]{x1D713}$, that is, the Haar measure associated to the standard gauge form  $(\bigwedge _{i,j=1,\ldots ,r}dg_{i,j})/(\det g^{r})$ on
$(\bigwedge _{i,j=1,\ldots ,r}dg_{i,j})/(\det g^{r})$ on  $\operatorname{GL}_{r}$ and the self-dual Haar measure on
$\operatorname{GL}_{r}$ and the self-dual Haar measure on  $F$ with respect to
$F$ with respect to  $\unicode[STIX]{x1D713}$. Following our convention on Haar measures for unipotent groups (see § 3.2), we obtain a (right) Haar measure on the
$\unicode[STIX]{x1D713}$. Following our convention on Haar measures for unipotent groups (see § 3.2), we obtain a (right) Haar measure on the  $F$-points of any algebraic group whose reductive part is a product of general linear groups. This will cover all algebraic groups considered here.
$F$-points of any algebraic group whose reductive part is a product of general linear groups. This will cover all algebraic groups considered here.
Throughout this section let  $\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ and let
$\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ and let  $\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ and
$\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ and  $\unicode[STIX]{x1D70E}^{\prime }=\operatorname{Sp}(\unicode[STIX]{x1D70B}^{\prime },m)$. We will work with the models considered in the previous section.
$\unicode[STIX]{x1D70E}^{\prime }=\operatorname{Sp}(\unicode[STIX]{x1D70B}^{\prime },m)$. We will work with the models considered in the previous section.
For any  $0\leqslant i\leqslant (m-1)n$ and
$0\leqslant i\leqslant (m-1)n$ and  $s\in \mathbb{C}$, we define a bilinear form on
$s\in \mathbb{C}$, we define a bilinear form on  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\times {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ by
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\times {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ by
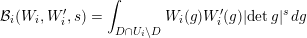 $$\begin{eqnarray}{\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s)=\int _{D\cap U_{i}\backslash D}W_{i}(g)W_{i}^{\prime }(g)|\det g|^{s}\,dg\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s)=\int _{D\cap U_{i}\backslash D}W_{i}(g)W_{i}^{\prime }(g)|\det g|^{s}\,dg\end{eqnarray}$$ (assuming convergence). In particular, for  $W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$,  $W_{\operatorname{Ze}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$,
$W_{\operatorname{Ze}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$,
 $$\begin{eqnarray}{\mathcal{B}}_{0}(W_{\operatorname{Ze}},W_{\operatorname{Ze}}^{\prime },s)=\int _{N_{D}\backslash D}W_{\operatorname{Ze}}(g)W_{\operatorname{Ze}}^{\prime }(g)|\det g|^{s}\,dg,\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{0}(W_{\operatorname{Ze}},W_{\operatorname{Ze}}^{\prime },s)=\int _{N_{D}\backslash D}W_{\operatorname{Ze}}(g)W_{\operatorname{Ze}}^{\prime }(g)|\det g|^{s}\,dg,\end{eqnarray}$$ and for  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,  $W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$,
$W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$,
 $$\begin{eqnarray}{\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s):={\mathcal{B}}_{(m-1)n}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s)=\int _{U^{\prime }\backslash D}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)|\det g|^{s}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s):={\mathcal{B}}_{(m-1)n}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s)=\int _{U^{\prime }\backslash D}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)|\det g|^{s}\,dg.\end{eqnarray}$$ It follows from Lemma 3.2 that  $|\det |$ is bounded above on the support of
$|\det |$ is bounded above on the support of  $W_{\operatorname{Sh}}|_{D}$. Hence,
$W_{\operatorname{Sh}}|_{D}$. Hence,

A similar statement holds for any  ${\mathcal{B}}_{i}$, although we will not use it.
${\mathcal{B}}_{i}$, although we will not use it.
We also write  ${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime })={\mathcal{B}}(W_{i},W_{i}^{\prime },0)$ assuming the latter is well defined (either as a convergent integral, or by analytic continuation), in which case it is
${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime })={\mathcal{B}}(W_{i},W_{i}^{\prime },0)$ assuming the latter is well defined (either as a convergent integral, or by analytic continuation), in which case it is  $D$-invariant.
$D$-invariant.
In general, we do not know whether  ${\mathcal{B}}_{i}(\cdot ,\cdot )$ is always defined. (See § 6 and in particular Example 6.5 for further discussion.)
${\mathcal{B}}_{i}(\cdot ,\cdot )$ is always defined. (See § 6 and in particular Example 6.5 for further discussion.)
Proposition 4.1. The integral defining  ${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s)$ converges for
${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s)$ converges for  $\operatorname{Re}s+\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })+1>0$. Moreover, for all
$\operatorname{Re}s+\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })+1>0$. Moreover, for all  $0\leqslant i<(m-1)n$,
$0\leqslant i<(m-1)n$,  $W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$,
$W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$,  $W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$, we have
$W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$, we have
 $$\begin{eqnarray}{\mathcal{B}}_{i+1}({\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i},{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime },s)={\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{i+1}({\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i},{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime },s)={\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s).\end{eqnarray}$$ Finally, there exist  $W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$ and
$W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$ and  $W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ such that
$W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ such that  ${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s)\equiv 1$ for all
${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s)\equiv 1$ for all  $s\in \mathbb{C}$.
$s\in \mathbb{C}$.
Remark 4.2. In Proposition 6.2 below we prove that  ${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s)$ admits meromorphic continuation in
${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },s)$ admits meromorphic continuation in  $s$ to a rational function in
$s$ to a rational function in  $q^{s}$.
$q^{s}$.
Proof. First note that the last statement follows from Corollary 3.15.
Next, we show the convergence of the integral defining  ${\mathcal{B}}_{0}$. Upon twisting
${\mathcal{B}}_{0}$. Upon twisting  $\unicode[STIX]{x1D70B}$ and
$\unicode[STIX]{x1D70B}$ and  $\unicode[STIX]{x1D70B}^{\prime }$ by
$\unicode[STIX]{x1D70B}^{\prime }$ by  $|\cdot |^{(s+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })-\mathbf{e}(\unicode[STIX]{x1D70B}))/2}$ and
$|\cdot |^{(s+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })-\mathbf{e}(\unicode[STIX]{x1D70B}))/2}$ and  $|\cdot |^{(s+\mathbf{e}(\unicode[STIX]{x1D70B})-\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime }))/2}$ respectively and using the inequality
$|\cdot |^{(s+\mathbf{e}(\unicode[STIX]{x1D70B})-\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime }))/2}$ respectively and using the inequality  $|xy|\leqslant (|x|^{2}+|y^{2}|)/2$, we may assume without loss of generality that
$|xy|\leqslant (|x|^{2}+|y^{2}|)/2$, we may assume without loss of generality that  $\unicode[STIX]{x1D70B}^{\prime }=\overline{\unicode[STIX]{x1D70B}}$,
$\unicode[STIX]{x1D70B}^{\prime }=\overline{\unicode[STIX]{x1D70B}}$,  $W_{\operatorname{Ze}}^{\prime }=\overline{W_{\operatorname{Ze}}}$ and
$W_{\operatorname{Ze}}^{\prime }=\overline{W_{\operatorname{Ze}}}$ and  $s=0$. Thus, we need to show the convergence of
$s=0$. Thus, we need to show the convergence of
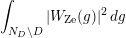 $$\begin{eqnarray}\int _{N_{D}\backslash D}|W_{\operatorname{Ze}}(g)|^{2}\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{D}\backslash D}|W_{\operatorname{Ze}}(g)|^{2}\,dg\end{eqnarray}$$ provided that  $\mathbf{e}(\unicode[STIX]{x1D70B})>-\frac{1}{2}$. In fact, we show a slightly stronger assertion, namely the convergence of
$\mathbf{e}(\unicode[STIX]{x1D70B})>-\frac{1}{2}$. In fact, we show a slightly stronger assertion, namely the convergence of
 $$\begin{eqnarray}\int _{D\backslash G}\int _{N_{D}\backslash D}|W_{\operatorname{Ze}}(lg)|^{2}dl\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{D\backslash G}\int _{N_{D}\backslash D}|W_{\operatorname{Ze}}(lg)|^{2}dl\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}\,dg\end{eqnarray}$$ for any  $0\leqslant \unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$ where
$0\leqslant \unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$ where  $\unicode[STIX]{x1D702}\in \operatorname{Mat}_{m,nm}(F)$ is the matrix whose
$\unicode[STIX]{x1D702}\in \operatorname{Mat}_{m,nm}(F)$ is the matrix whose  $i$th row is
$i$th row is  $e_{ni}$,
$e_{ni}$,  $i=1,\ldots ,m$. Note that the stabilizer of
$i=1,\ldots ,m$. Note that the stabilizer of  $\unicode[STIX]{x1D702}$ under the right
$\unicode[STIX]{x1D702}$ under the right  $G$-action on
$G$-action on  $\operatorname{Mat}_{m,nm}(F)$ is
$\operatorname{Mat}_{m,nm}(F)$ is  $D$. Since the modulus character of
$D$. Since the modulus character of  $D$ is
$D$ is  $|\det |^{m}$, (17) is formally well defined and can be rewritten as
$|\det |^{m}$, (17) is formally well defined and can be rewritten as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{N_{D}\backslash G}|W_{\operatorname{Ze}}(g)|^{2}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{P\backslash G}\int _{N\backslash P}|W_{\operatorname{Ze}}(lg)|^{2}\int _{N_{D}\backslash N}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}ulg)\,du~|\det l|^{m}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}\,dl~|\det g|^{m}\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{P\backslash G}\int _{N_{M}\backslash M}|W_{\operatorname{Ze}}(lg)|^{2}\int _{U_{D}\backslash U}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}ulg)\,du~|\det l|^{m}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}\,dl~|\det g|^{m}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{N_{D}\backslash G}|W_{\operatorname{Ze}}(g)|^{2}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{P\backslash G}\int _{N\backslash P}|W_{\operatorname{Ze}}(lg)|^{2}\int _{N_{D}\backslash N}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}ulg)\,du~|\det l|^{m}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}\,dl~|\det g|^{m}\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{P\backslash G}\int _{N_{M}\backslash M}|W_{\operatorname{Ze}}(lg)|^{2}\int _{U_{D}\backslash U}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}ulg)\,du~|\det l|^{m}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}\,dl~|\det g|^{m}\,dg.\end{eqnarray}$$ We may identify the vector space  $\operatorname{Mat}_{m,nm}(F)$ with
$\operatorname{Mat}_{m,nm}(F)$ with  $\operatorname{Mat}_{m,m}(F^{n})$. Observe that, for any
$\operatorname{Mat}_{m,m}(F^{n})$. Observe that, for any  $l=\operatorname{diag}(g_{1},\ldots ,g_{m})\in M$,
$l=\operatorname{diag}(g_{1},\ldots ,g_{m})\in M$,  $g\in G$, we have
$g\in G$, we have
 $$\begin{eqnarray}|\det l|^{(m-1)/2}\int _{U_{D}\backslash U}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}ulg)\,du=\tilde{\unicode[STIX]{x1D6F7}}_{g}(e_{n}g_{1},\ldots ,e_{n}g_{m})\unicode[STIX]{x1D6FF}^{\prime }(l)\end{eqnarray}$$
$$\begin{eqnarray}|\det l|^{(m-1)/2}\int _{U_{D}\backslash U}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}ulg)\,du=\tilde{\unicode[STIX]{x1D6F7}}_{g}(e_{n}g_{1},\ldots ,e_{n}g_{m})\unicode[STIX]{x1D6FF}^{\prime }(l)\end{eqnarray}$$ where  $\tilde{\unicode[STIX]{x1D6F7}}_{g}\in {\mathcal{S}}((F^{n})^{m})$ is the function
$\tilde{\unicode[STIX]{x1D6F7}}_{g}\in {\mathcal{S}}((F^{n})^{m})$ is the function
 $$\begin{eqnarray}\tilde{\unicode[STIX]{x1D6F7}}_{g}(v_{1},\ldots ,v_{m})=\int \unicode[STIX]{x1D6F7}(Xg)\,dX,\quad v_{1},\ldots ,v_{m}\in F^{n},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D6F7}}_{g}(v_{1},\ldots ,v_{m})=\int \unicode[STIX]{x1D6F7}(Xg)\,dX,\quad v_{1},\ldots ,v_{m}\in F^{n},\end{eqnarray}$$ where the integral is taken over the  $n\binom{m}{2}$-dimensional affine space of upper triangular
$n\binom{m}{2}$-dimensional affine space of upper triangular  $F^{n}$-valued
$F^{n}$-valued  $m\times m$-matrices whose diagonal entries are
$m\times m$-matrices whose diagonal entries are  $v_{1},\ldots ,v_{m}$. Thus, (18) is equal to
$v_{1},\ldots ,v_{m}$. Thus, (18) is equal to
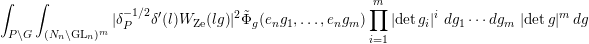 $$\begin{eqnarray}\int _{P\backslash G}\int _{(N_{n}\backslash \!\operatorname{GL}_{n})^{m}}|\unicode[STIX]{x1D6FF}_{P}^{-1/2}\unicode[STIX]{x1D6FF}^{\prime }(l)W_{\operatorname{ Ze}}(lg)|^{2}\tilde{\unicode[STIX]{x1D6F7}}_{g}(e_{n}g_{1},\ldots ,e_{n}g_{m})\mathop{\prod }_{i=1}^{m}|\det g_{i}|^{i}~dg_{1}\cdots dg_{m}~|\det g|^{m}\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{P\backslash G}\int _{(N_{n}\backslash \!\operatorname{GL}_{n})^{m}}|\unicode[STIX]{x1D6FF}_{P}^{-1/2}\unicode[STIX]{x1D6FF}^{\prime }(l)W_{\operatorname{ Ze}}(lg)|^{2}\tilde{\unicode[STIX]{x1D6F7}}_{g}(e_{n}g_{1},\ldots ,e_{n}g_{m})\mathop{\prod }_{i=1}^{m}|\det g_{i}|^{i}~dg_{1}\cdots dg_{m}~|\det g|^{m}\,dg\end{eqnarray}$$ where  $l=\operatorname{diag}(g_{1},\ldots ,g_{m})\in M$. Thus, by (5b) the inner integral is a finite linear combination of products of Rankin–Selberg integrals for
$l=\operatorname{diag}(g_{1},\ldots ,g_{m})\in M$. Thus, by (5b) the inner integral is a finite linear combination of products of Rankin–Selberg integrals for  $\unicode[STIX]{x1D70B}\times \bar{\unicode[STIX]{x1D70B}}$ at
$\unicode[STIX]{x1D70B}\times \bar{\unicode[STIX]{x1D70B}}$ at  $i$,
$i$,  $i=1,\ldots ,m$. The assumption that
$i=1,\ldots ,m$. The assumption that  $\mathbf{e}(\unicode[STIX]{x1D70B})>-\frac{1}{2}$ guarantees that these Rankin–Selberg integrals converge. Since the outer integral is a finite sum, we obtain the convergence of (17).
$\mathbf{e}(\unicode[STIX]{x1D70B})>-\frac{1}{2}$ guarantees that these Rankin–Selberg integrals converge. Since the outer integral is a finite sum, we obtain the convergence of (17).
Now let  $0\leqslant i<(m-1)n$,
$0\leqslant i<(m-1)n$,  $W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$,
$W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$,  $W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$. Recall that
$W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$. Recall that  $W_{i}|_{U_{i+1}}$ (respectively,
$W_{i}|_{U_{i+1}}$ (respectively,  ${\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i}|_{U_{i}\cap D}$) is compactly supported modulo
${\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i}|_{U_{i}\cap D}$) is compactly supported modulo  $U_{i}\cap U_{i+1}$ (respectively,
$U_{i}\cap U_{i+1}$ (respectively,  $U_{i}\cap U_{i+1}\cap D$).
$U_{i}\cap U_{i+1}\cap D$).
Moreover, by the unitarity of the Fourier transform and the argument of Proposition 3.5 (cf. (10)) we have
 $$\begin{eqnarray}\displaystyle \int _{D\cap U_{i+1}\backslash D\cap U_{i}U_{i+1}}{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i}(u){\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime }(u)\,du & = & \displaystyle \int _{N_{D}\cap U_{i+1}\backslash N_{D}\cap U_{i}}{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i}(u){\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime }(u)\,du\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{i}\backslash U_{i}U_{i+1}}W_{i}(u)W_{i}^{\prime }(u)\,du\nonumber\\ \displaystyle & = & \displaystyle \int _{D\cap U_{i}\backslash D\cap U_{i}U_{i+1}}W_{i}(u)W_{i}^{\prime }(u)\,du\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{D\cap U_{i+1}\backslash D\cap U_{i}U_{i+1}}{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i}(u){\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime }(u)\,du & = & \displaystyle \int _{N_{D}\cap U_{i+1}\backslash N_{D}\cap U_{i}}{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i}(u){\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime }(u)\,du\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{i}\backslash U_{i}U_{i+1}}W_{i}(u)W_{i}^{\prime }(u)\,du\nonumber\\ \displaystyle & = & \displaystyle \int _{D\cap U_{i}\backslash D\cap U_{i}U_{i+1}}W_{i}(u)W_{i}^{\prime }(u)\,du\end{eqnarray}$$where the integrals are absolutely convergent. (We can also write the integrals as
 $$\begin{eqnarray}\int _{U_{i}\cap U^{\prime }\backslash U_{i+1}\cap U^{\prime }}W_{i}(u)W_{i}^{\prime }(u)\,du=\int _{U_{i}\cap \bar{N}\backslash U_{i+1}\cap \bar{N}}W_{i}(u)W_{i}^{\prime }(u)\,du.)\end{eqnarray}$$
$$\begin{eqnarray}\int _{U_{i}\cap U^{\prime }\backslash U_{i+1}\cap U^{\prime }}W_{i}(u)W_{i}^{\prime }(u)\,du=\int _{U_{i}\cap \bar{N}\backslash U_{i+1}\cap \bar{N}}W_{i}(u)W_{i}^{\prime }(u)\,du.)\end{eqnarray}$$It follows that if at least one of integrals
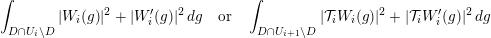 $$\begin{eqnarray}\int _{D\cap U_{i}\backslash D}|W_{i}(g)|^{2}+|W_{i}^{\prime }(g)|^{2}\,dg\quad \text{or}\quad \int _{D\cap U_{i+1}\backslash D}|{\mathcal{T}}_{i}W_{i}(g)|^{2}+|{\mathcal{T}}_{i}W_{i}^{\prime }(g)|^{2}\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{D\cap U_{i}\backslash D}|W_{i}(g)|^{2}+|W_{i}^{\prime }(g)|^{2}\,dg\quad \text{or}\quad \int _{D\cap U_{i+1}\backslash D}|{\mathcal{T}}_{i}W_{i}(g)|^{2}+|{\mathcal{T}}_{i}W_{i}^{\prime }(g)|^{2}\,dg\end{eqnarray}$$converges, then so does the other and
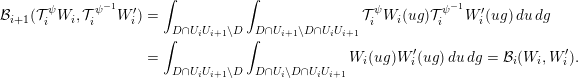 $$\begin{eqnarray}\displaystyle {\mathcal{B}}_{i+1}({\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i},{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime }) & = & \displaystyle \int _{D\cap U_{i}U_{i+1}\backslash D}\int _{D\cap U_{i+1}\backslash D\cap U_{i}U_{i+1}}{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i}(ug){\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime }(ug)\,du\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{D\cap U_{i}U_{i+1}\backslash D}\int _{D\cap U_{i}\backslash D\cap U_{i}U_{i+1}}W_{i}(ug)W_{i}^{\prime }(ug)\,du\,dg={\mathcal{B}}_{i}(W_{i},W_{i}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{B}}_{i+1}({\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i},{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime }) & = & \displaystyle \int _{D\cap U_{i}U_{i+1}\backslash D}\int _{D\cap U_{i+1}\backslash D\cap U_{i}U_{i+1}}{\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}}W_{i}(ug){\mathcal{T}}_{i}^{\unicode[STIX]{x1D713}^{-1}}W_{i}^{\prime }(ug)\,du\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{D\cap U_{i}U_{i+1}\backslash D}\int _{D\cap U_{i}\backslash D\cap U_{i}U_{i+1}}W_{i}(ug)W_{i}^{\prime }(ug)\,du\,dg={\mathcal{B}}_{i}(W_{i},W_{i}^{\prime }).\nonumber\end{eqnarray}$$ We can now conclude the convergence for all  $i$ and the identity (16) since they clearly reduce to the case
$i$ and the identity (16) since they clearly reduce to the case  $i=0$.◻
$i=0$.◻
Theorem 4.3. Suppose that  $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$ (or equivalently,
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$ (or equivalently,  $\unicode[STIX]{x1D70E}^{\prime }=\unicode[STIX]{x1D70E}^{\vee }$) and
$\unicode[STIX]{x1D70E}^{\prime }=\unicode[STIX]{x1D70E}^{\vee }$) and  $\unicode[STIX]{x1D70B}$ is (AT) (see § 2.1). Then
$\unicode[STIX]{x1D70B}$ is (AT) (see § 2.1). Then  ${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime })$ is a well-defined
${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime })$ is a well-defined  $G$-invariant pairing on
$G$-invariant pairing on  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\times {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$. In particular, if
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\times {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$. In particular, if  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ is unitarizable, then
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ is unitarizable, then  ${\mathcal{B}}_{i}$ gives a unitary structure on
${\mathcal{B}}_{i}$ gives a unitary structure on  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$.
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$.
Proof. By Proposition 4.1  ${\mathcal{B}}_{i}(\cdot ,\cdot )$ is well defined and not identically zero. To show invariance it suffices to consider
${\mathcal{B}}_{i}(\cdot ,\cdot )$ is well defined and not identically zero. To show invariance it suffices to consider  $i=0$. We use induction on
$i=0$. We use induction on  $m$. The case
$m$. The case  $m=1$ (in which
$m=1$ (in which  $D$ is the standard mirabolic subgroup) is well known and follows from Bernstein’s theorem [Reference BernsteinBer84]. For the induction step, let
$D$ is the standard mirabolic subgroup) is well known and follows from Bernstein’s theorem [Reference BernsteinBer84]. For the induction step, let  $m>1$ and let
$m>1$ and let  $Q^{\prime }$ be the subgroup of the standard maximal parabolic subgroup of
$Q^{\prime }$ be the subgroup of the standard maximal parabolic subgroup of  $G$ of type
$G$ of type  $((m-1)n,n)$ consisting of the matrices whose lower right
$((m-1)n,n)$ consisting of the matrices whose lower right  $n\times n$ corner is upper unitriangular. Write
$n\times n$ corner is upper unitriangular. Write
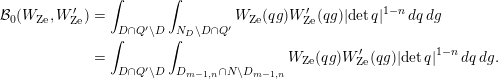 $$\begin{eqnarray}\displaystyle {\mathcal{B}}_{0}(W_{\operatorname{Ze}},W_{\operatorname{Ze}}^{\prime }) & = & \displaystyle \int _{D\cap Q^{\prime }\backslash D}\int _{N_{D}\backslash D\cap Q^{\prime }}W_{\operatorname{Ze}}(qg)W_{\operatorname{Ze}}^{\prime }(qg)|\det q|^{1-n}\,dq\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{D\cap Q^{\prime }\backslash D}\int _{D_{m-1,n}\cap N\backslash D_{m-1,n}}W_{\operatorname{Ze}}(qg)W_{\operatorname{Ze}}^{\prime }(qg)|\det q|^{1-n}\,dq\,dg.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{B}}_{0}(W_{\operatorname{Ze}},W_{\operatorname{Ze}}^{\prime }) & = & \displaystyle \int _{D\cap Q^{\prime }\backslash D}\int _{N_{D}\backslash D\cap Q^{\prime }}W_{\operatorname{Ze}}(qg)W_{\operatorname{Ze}}^{\prime }(qg)|\det q|^{1-n}\,dq\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{D\cap Q^{\prime }\backslash D}\int _{D_{m-1,n}\cap N\backslash D_{m-1,n}}W_{\operatorname{Ze}}(qg)W_{\operatorname{Ze}}^{\prime }(qg)|\det q|^{1-n}\,dq\,dg.\nonumber\end{eqnarray}$$ Here we consider  $\operatorname{GL}_{(m-1)n}$ (and hence,
$\operatorname{GL}_{(m-1)n}$ (and hence,  $D_{m-1,n}$) as a subgroup of
$D_{m-1,n}$) as a subgroup of  $G$. (Note that
$G$. (Note that  $\unicode[STIX]{x1D6FF}_{D}=|\det |^{m}$ while
$\unicode[STIX]{x1D6FF}_{D}=|\det |^{m}$ while  $\unicode[STIX]{x1D6FF}_{D\cap Q^{\prime }}=|\det |^{n+m-1}$.) By (5a) and the induction hypothesis, the inner integral is left-
$\unicode[STIX]{x1D6FF}_{D\cap Q^{\prime }}=|\det |^{n+m-1}$.) By (5a) and the induction hypothesis, the inner integral is left- $(Q^{\prime },|\det |^{n-1})$-equivariant in
$(Q^{\prime },|\det |^{n-1})$-equivariant in  $g$. Hence, we can replace the domain of outer integration by
$g$. Hence, we can replace the domain of outer integration by  $Q^{\prime }\backslash D_{1,mn}$ where
$Q^{\prime }\backslash D_{1,mn}$ where  $D_{1,mn}$ is the standard mirabolic subgroup of
$D_{1,mn}$ is the standard mirabolic subgroup of  $G$ (the stabilizer of
$G$ (the stabilizer of  $e_{mn}$). (Note that
$e_{mn}$). (Note that  $\unicode[STIX]{x1D6FF}_{D_{1,mn}}=|\det |$ and
$\unicode[STIX]{x1D6FF}_{D_{1,mn}}=|\det |$ and  $\unicode[STIX]{x1D6FF}_{Q^{\prime }}=|\det |^{n}$.) It follows that
$\unicode[STIX]{x1D6FF}_{Q^{\prime }}=|\det |^{n}$.) It follows that  ${\mathcal{B}}_{0}(\cdot ,\cdot )$ is
${\mathcal{B}}_{0}(\cdot ,\cdot )$ is  $D_{1,mn}$-invariant. By Bernstein’s theorem, it is
$D_{1,mn}$-invariant. By Bernstein’s theorem, it is  $G$-invariant as required.◻
$G$-invariant as required.◻
We immediately deduce a special case of Conjecture 3.16.
Corollary 4.4. Conjecture 3.16 holds for any  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{(AT)}\operatorname{GL}_{n}$. In particular, it holds for any unitarizable
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{(AT)}\operatorname{GL}_{n}$. In particular, it holds for any unitarizable  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$.
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$.
Remark 4.5. By analytic continuation it is easy to prove Conjecture 3.16 for  $\unicode[STIX]{x1D70B}$ of the form
$\unicode[STIX]{x1D70B}$ of the form  $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70F}_{1}|\cdot |^{\unicode[STIX]{x1D706}_{1}}\times \cdots \times \unicode[STIX]{x1D70F}_{k}|\cdot |^{\unicode[STIX]{x1D706}_{k}}$ where
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70F}_{1}|\cdot |^{\unicode[STIX]{x1D706}_{1}}\times \cdots \times \unicode[STIX]{x1D70F}_{k}|\cdot |^{\unicode[STIX]{x1D706}_{k}}$ where  $\unicode[STIX]{x1D70F}_{i}\in \operatorname{Irr}_{\operatorname{sqr}}$ are fixed and
$\unicode[STIX]{x1D70F}_{i}\in \operatorname{Irr}_{\operatorname{sqr}}$ are fixed and  $(q^{\unicode[STIX]{x1D706}_{1}},\ldots ,q^{\unicode[STIX]{x1D706}_{k}})$ is in general position.
$(q^{\unicode[STIX]{x1D706}_{1}},\ldots ,q^{\unicode[STIX]{x1D706}_{k}})$ is in general position.
In view of Theorem 4.3 and Bernstein’s theorem, it is natural to make following related conjecture.
Conjecture 4.6. For any  $m$-homogeneous
$m$-homogeneous  $\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$, every
$\unicode[STIX]{x1D70E}\in \operatorname{Irr}G$, every  $D$-invariant bilinear form on
$D$-invariant bilinear form on  $\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70E}^{\vee }$ is
$\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70E}^{\vee }$ is  $G$-invariant.
$G$-invariant.
Perhaps even more is true.
Conjecture 4.7. For any  $m$-homogeneous
$m$-homogeneous  $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }\in \operatorname{Irr}G$, there is a unique up to scalar
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }\in \operatorname{Irr}G$, there is a unique up to scalar  $D$-invariant bilinear form on
$D$-invariant bilinear form on  $\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70E}^{\prime }$.
$\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70E}^{\prime }$.
(We do not know whether this is known even in the case  $m=1$.)
$m=1$.)
5 Local zeta integrals
Throughout this section let  $\unicode[STIX]{x1D70B}$,
$\unicode[STIX]{x1D70B}$,  $\unicode[STIX]{x1D70B}^{\prime }\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ and
$\unicode[STIX]{x1D70B}^{\prime }\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$ and  $\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m),\unicode[STIX]{x1D70E}^{\prime }=\operatorname{Sp}(\unicode[STIX]{x1D70B}^{\prime },m)\in \operatorname{Irr}G$. Let
$\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m),\unicode[STIX]{x1D70E}^{\prime }=\operatorname{Sp}(\unicode[STIX]{x1D70B}^{\prime },m)\in \operatorname{Irr}G$. Let  $L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })$ and
$L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })$ and  $\unicode[STIX]{x1D6FE}(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime },\unicode[STIX]{x1D713})$ be the local factors defined by Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83]. (See § 5.2 below.)
$\unicode[STIX]{x1D6FE}(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime },\unicode[STIX]{x1D713})$ be the local factors defined by Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83]. (See § 5.2 below.)
5.1 Statement of the result
We write an analogue of the Rankin–Selberg integral for  $\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70E}^{\prime }$ on the Shalika model as follows. Recall that
$\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70E}^{\prime }$ on the Shalika model as follows. Recall that  $\unicode[STIX]{x1D702}\in \operatorname{Mat}_{m,nm}(F)$ is the matrix whose
$\unicode[STIX]{x1D702}\in \operatorname{Mat}_{m,nm}(F)$ is the matrix whose  $i$th row is
$i$th row is  $e_{ni}$,
$e_{ni}$,  $i=1,\ldots ,m$, so that
$i=1,\ldots ,m$, so that  $D$ is the stabilizer of
$D$ is the stabilizer of  $\unicode[STIX]{x1D702}$ in
$\unicode[STIX]{x1D702}$ in  $G$. For any
$G$. For any  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,  $W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$,
$W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$,  $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$, consider
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$, consider
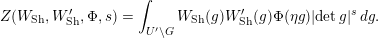 $$\begin{eqnarray}Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)=\int _{U^{\prime }\backslash G}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{s}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)=\int _{U^{\prime }\backslash G}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{s}\,dg.\end{eqnarray}$$This expression was already considered in some form in the proof of Proposition 4.1.
Note that in the case  $n=1$ (where
$n=1$ (where  $U^{\prime }=1$)
$U^{\prime }=1$)  $Z$ reduces to the generalized Tate integral for (a character of)
$Z$ reduces to the generalized Tate integral for (a character of)  $\operatorname{GL}_{m}$ considered by Godement and Jacquet [Reference Godement and JacquetGJ72].
$\operatorname{GL}_{m}$ considered by Godement and Jacquet [Reference Godement and JacquetGJ72].
For any  $k$, let
$k$, let
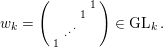
Theorem 5.1. The integral  $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ has the following properties.
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ has the following properties.
(i) The integral defining
 $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ is absolutely convergent for
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ is absolutely convergent for  $$\begin{eqnarray}\operatorname{Re}s+\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })+1>m.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Re}s+\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })+1>m.\end{eqnarray}$$(ii) The function
is a Laurent polynomial in $$\begin{eqnarray}\bigg(\mathop{\prod }_{i=0}^{m-1}L(s-i,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })\bigg)^{-1}Z(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)\end{eqnarray}$$
$$\begin{eqnarray}\bigg(\mathop{\prod }_{i=0}^{m-1}L(s-i,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })\bigg)^{-1}Z(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)\end{eqnarray}$$ $q^{s}$, hence entire.
$q^{s}$, hence entire.(iii) If
 $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }$ are unramified,
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }$ are unramified,  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,  $W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E})$ are the unramified vectors such that
$W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E})$ are the unramified vectors such that  $W_{\operatorname{Sh}}(e)=W_{\operatorname{Sh}}(e)=1$,
$W_{\operatorname{Sh}}(e)=W_{\operatorname{Sh}}(e)=1$,  $\unicode[STIX]{x1D6F7}$ is the characteristic function of
$\unicode[STIX]{x1D6F7}$ is the characteristic function of  $\operatorname{Mat}_{m,nm}({\mathcal{O}})$ and
$\operatorname{Mat}_{m,nm}({\mathcal{O}})$ and  $\unicode[STIX]{x1D713}$ has conductor
$\unicode[STIX]{x1D713}$ has conductor  ${\mathcal{O}}$, thenwhere
${\mathcal{O}}$, thenwhere
 $c$ is a measure-theoretic constant (depending only on
$c$ is a measure-theoretic constant (depending only on  $F$,
$F$,  $m$ and
$m$ and  $n$).
$n$).(iv) We have a local functional equation
(22)where
 $\widehat{W_{\operatorname{Sh}}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ is given by
$\widehat{W_{\operatorname{Sh}}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ is given by  $\widehat{W_{\operatorname{Sh}}}(g)=W_{\operatorname{Sh}}(w_{nm}^{t}g^{-1})$ and
$\widehat{W_{\operatorname{Sh}}}(g)=W_{\operatorname{Sh}}(w_{nm}^{t}g^{-1})$ and  $\widehat{\unicode[STIX]{x1D6F7}}$ is the Fourier transform
$\widehat{\unicode[STIX]{x1D6F7}}$ is the Fourier transform
We will prove the theorem below by relating  $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ to the usual Rankin–Selberg integrals.
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ to the usual Rankin–Selberg integrals.
5.2 A result of Jacquet, Piatetski-Shapiro and Shalika
Recall the  $\operatorname{GL}_{n}\times \operatorname{GL}_{n}$ local Rankin–Selberg integrals studied by Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83]. They are given by
$\operatorname{GL}_{n}\times \operatorname{GL}_{n}$ local Rankin–Selberg integrals studied by Jacquet, Piatetski-Shapiro and Shalika [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83]. They are given by
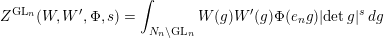 $$\begin{eqnarray}Z^{\operatorname{GL}_{n}}(W,W^{\prime },\unicode[STIX]{x1D6F7},s)=\int _{N_{n}\backslash \!\operatorname{GL}_{n}}W(g)W^{\prime }(g)\unicode[STIX]{x1D6F7}(e_{n}g)|\det g|^{s}\,dg\end{eqnarray}$$
$$\begin{eqnarray}Z^{\operatorname{GL}_{n}}(W,W^{\prime },\unicode[STIX]{x1D6F7},s)=\int _{N_{n}\backslash \!\operatorname{GL}_{n}}W(g)W^{\prime }(g)\unicode[STIX]{x1D6F7}(e_{n}g)|\det g|^{s}\,dg\end{eqnarray}$$ where  $W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}}(\unicode[STIX]{x1D70B})$,
$W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}}(\unicode[STIX]{x1D70B})$,  $W^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}^{-1}}(\unicode[STIX]{x1D70B}^{\prime })$,
$W^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}^{-1}}(\unicode[STIX]{x1D70B}^{\prime })$,  $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(F^{n})$ and
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(F^{n})$ and  $s\in \mathbb{C}$. The integral converges for
$s\in \mathbb{C}$. The integral converges for  $\operatorname{Re}s+\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })>0$ and admits a meromorphic continuation in
$\operatorname{Re}s+\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })>0$ and admits a meromorphic continuation in  $s$ to a rational function in
$s$ to a rational function in  $q^{s}$. The quotient
$q^{s}$. The quotient
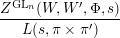 $$\begin{eqnarray}\frac{Z^{\operatorname{GL}_{n}}(W,W^{\prime },\unicode[STIX]{x1D6F7},s)}{L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })}\end{eqnarray}$$
$$\begin{eqnarray}\frac{Z^{\operatorname{GL}_{n}}(W,W^{\prime },\unicode[STIX]{x1D6F7},s)}{L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })}\end{eqnarray}$$ is a Laurent polynomial in  $q^{s}$ which can be made non-zero at any given
$q^{s}$ which can be made non-zero at any given  $s\in \mathbb{C}$ by an appropriate choice of
$s\in \mathbb{C}$ by an appropriate choice of  $W$,
$W$,  $W^{\prime }$,
$W^{\prime }$,  $\unicode[STIX]{x1D6F7}$. Moreover, we have a functional equation
$\unicode[STIX]{x1D6F7}$. Moreover, we have a functional equation
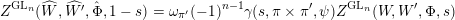 $$\begin{eqnarray}Z^{\operatorname{GL}_{n}}(\widehat{W},\widehat{W^{\prime }},\hat{\unicode[STIX]{x1D6F7}},1-s)=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}(-1)^{n-1}\unicode[STIX]{x1D6FE}(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime },\unicode[STIX]{x1D713})Z^{\operatorname{GL}_{n}}(W,W^{\prime },\unicode[STIX]{x1D6F7},s)\end{eqnarray}$$
$$\begin{eqnarray}Z^{\operatorname{GL}_{n}}(\widehat{W},\widehat{W^{\prime }},\hat{\unicode[STIX]{x1D6F7}},1-s)=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}(-1)^{n-1}\unicode[STIX]{x1D6FE}(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime },\unicode[STIX]{x1D713})Z^{\operatorname{GL}_{n}}(W,W^{\prime },\unicode[STIX]{x1D6F7},s)\end{eqnarray}$$ where  $\widehat{W}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}}(\unicode[STIX]{x1D70B}^{\vee })$,
$\widehat{W}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}}(\unicode[STIX]{x1D70B}^{\vee })$,  $\widehat{W^{\prime }}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}^{-1}}({\unicode[STIX]{x1D70B}^{\prime }}^{\vee })$ are given by
$\widehat{W^{\prime }}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}^{-1}}({\unicode[STIX]{x1D70B}^{\prime }}^{\vee })$ are given by
 $$\begin{eqnarray}\widehat{W}(g)=W(w_{n}\,^{t}g^{-1}),\quad \widehat{W^{\prime }}(g)=W^{\prime }(w_{n}\,^{t}g^{-1})\end{eqnarray}$$
$$\begin{eqnarray}\widehat{W}(g)=W(w_{n}\,^{t}g^{-1}),\quad \widehat{W^{\prime }}(g)=W^{\prime }(w_{n}\,^{t}g^{-1})\end{eqnarray}$$ and  $\hat{\unicode[STIX]{x1D6F7}}$ is the Fourier transform of
$\hat{\unicode[STIX]{x1D6F7}}$ is the Fourier transform of  $\unicode[STIX]{x1D6F7}$ given by
$\unicode[STIX]{x1D6F7}$ given by
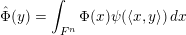 $$\begin{eqnarray}\hat{\unicode[STIX]{x1D6F7}}(y)=\int _{F^{n}}\unicode[STIX]{x1D6F7}(x)\unicode[STIX]{x1D713}(\left\langle x,y\right\rangle )\,dx\end{eqnarray}$$
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D6F7}}(y)=\int _{F^{n}}\unicode[STIX]{x1D6F7}(x)\unicode[STIX]{x1D713}(\left\langle x,y\right\rangle )\,dx\end{eqnarray}$$ where  $\left\langle (x_{1},\ldots ,x_{n}),(y_{1},\ldots ,y_{n})\right\rangle =\sum _{i}x_{i}y_{i}$ denotes the standard pairing on
$\left\langle (x_{1},\ldots ,x_{n}),(y_{1},\ldots ,y_{n})\right\rangle =\sum _{i}x_{i}y_{i}$ denotes the standard pairing on  $F^{n}$.
$F^{n}$.
Slightly more generally, for  $W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m})$,
$W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m})$,  $W^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}}(\unicode[STIX]{x1D70B}^{\prime \otimes m})$,
$W^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}}(\unicode[STIX]{x1D70B}^{\prime \otimes m})$,  $\tilde{\unicode[STIX]{x1D6F7}}\in {\mathcal{S}}((F^{n})^{m})$ and
$\tilde{\unicode[STIX]{x1D6F7}}\in {\mathcal{S}}((F^{n})^{m})$ and  $(s_{1},\ldots ,s_{m})\in \mathbb{C}^{m}$, we write
$(s_{1},\ldots ,s_{m})\in \mathbb{C}^{m}$, we write
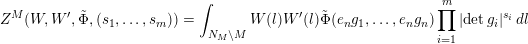 $$\begin{eqnarray}Z^{M}(W,W^{\prime },\tilde{\unicode[STIX]{x1D6F7}},(s_{1},\ldots ,s_{m}))=\int _{N_{M}\backslash M}W(l)W^{\prime }(l)\tilde{\unicode[STIX]{x1D6F7}}(e_{n}g_{1},\ldots ,e_{n}g_{n})\mathop{\prod }_{i=1}^{m}|\det g_{i}|^{s_{i}}\,dl\end{eqnarray}$$
$$\begin{eqnarray}Z^{M}(W,W^{\prime },\tilde{\unicode[STIX]{x1D6F7}},(s_{1},\ldots ,s_{m}))=\int _{N_{M}\backslash M}W(l)W^{\prime }(l)\tilde{\unicode[STIX]{x1D6F7}}(e_{n}g_{1},\ldots ,e_{n}g_{n})\mathop{\prod }_{i=1}^{m}|\det g_{i}|^{s_{i}}\,dl\end{eqnarray}$$ where  $l=\operatorname{diag}(g_{1},\ldots ,g_{m})\in M$. This is a linear combination of products
$l=\operatorname{diag}(g_{1},\ldots ,g_{m})\in M$. This is a linear combination of products
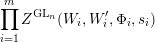 $$\begin{eqnarray}\mathop{\prod }_{i=1}^{m}Z^{\operatorname{GL}_{n}}(W_{i},W_{i}^{\prime },\unicode[STIX]{x1D6F7}_{i},s_{i})\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{i=1}^{m}Z^{\operatorname{GL}_{n}}(W_{i},W_{i}^{\prime },\unicode[STIX]{x1D6F7}_{i},s_{i})\end{eqnarray}$$ where  $W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}}(\unicode[STIX]{x1D70B})$,
$W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}}(\unicode[STIX]{x1D70B})$,  $W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}^{-1}}(\unicode[STIX]{x1D70B}^{\prime })$ and
$W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{n}}^{-1}}(\unicode[STIX]{x1D70B}^{\prime })$ and  $\unicode[STIX]{x1D6F7}_{i}\in {\mathcal{S}}(F^{n})$. Thus,
$\unicode[STIX]{x1D6F7}_{i}\in {\mathcal{S}}(F^{n})$. Thus,

Moreover, we have a functional equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle Z^{M}(\widehat{W}^{M},\widehat{W}^{\prime M},\widehat{\tilde{\unicode[STIX]{x1D6F7}}}^{M},(1-s_{1},\ldots ,1-s_{m}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}(-1)^{m(n-1)}\mathop{\prod }_{i=1}^{m}\unicode[STIX]{x1D6FE}(s_{i},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime },\unicode[STIX]{x1D713})Z^{M}(W,W^{\prime },\tilde{\unicode[STIX]{x1D6F7}},(s_{1},\ldots ,s_{m}))\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle Z^{M}(\widehat{W}^{M},\widehat{W}^{\prime M},\widehat{\tilde{\unicode[STIX]{x1D6F7}}}^{M},(1-s_{1},\ldots ,1-s_{m}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}(-1)^{m(n-1)}\mathop{\prod }_{i=1}^{m}\unicode[STIX]{x1D6FE}(s_{i},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime },\unicode[STIX]{x1D713})Z^{M}(W,W^{\prime },\tilde{\unicode[STIX]{x1D6F7}},(s_{1},\ldots ,s_{m}))\end{eqnarray}$$ where  $\widehat{W}^{M}(l)=W(\operatorname{diag}(\overbrace{w_{n},\ldots ,w_{n}}^{m})\,^{t}l^{-1})$ and
$\widehat{W}^{M}(l)=W(\operatorname{diag}(\overbrace{w_{n},\ldots ,w_{n}}^{m})\,^{t}l^{-1})$ and
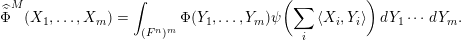 $$\begin{eqnarray}\widehat{\tilde{\unicode[STIX]{x1D6F7}}}^{M}(X_{1},\ldots ,X_{m})=\int _{(F^{n})^{m}}\unicode[STIX]{x1D6F7}(Y_{1},\ldots ,Y_{m})\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{i}\left\langle X_{i},Y_{i}\right\rangle \biggr)\,dY_{1}\cdots \,dY_{m}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{\tilde{\unicode[STIX]{x1D6F7}}}^{M}(X_{1},\ldots ,X_{m})=\int _{(F^{n})^{m}}\unicode[STIX]{x1D6F7}(Y_{1},\ldots ,Y_{m})\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{i}\left\langle X_{i},Y_{i}\right\rangle \biggr)\,dY_{1}\cdots \,dY_{m}.\end{eqnarray}$$5.3 Proof of the theorem
The fulcrum for Theorem 5.1 is the following proposition.
Proposition 5.2. For any  $W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$,  $W_{\operatorname{Ze}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ and
$W_{\operatorname{Ze}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ and  $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$, we have
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$, we have
 $$\begin{eqnarray}Z({\mathcal{T}}^{\unicode[STIX]{x1D713}}W_{\operatorname{Ze}},{\mathcal{T}}^{\unicode[STIX]{x1D713}^{-1}}W_{\operatorname{Ze}}^{\prime },\unicode[STIX]{x1D6F7},s)=\int _{P\backslash G}Z^{M}((W_{\operatorname{ Ze}})_{g},(W_{\operatorname{Ze}}^{\prime })_{g},\tilde{\unicode[STIX]{x1D6F7}}_{g},(s-m+1,\ldots ,s))|\det g|^{s}\,dg\end{eqnarray}$$
$$\begin{eqnarray}Z({\mathcal{T}}^{\unicode[STIX]{x1D713}}W_{\operatorname{Ze}},{\mathcal{T}}^{\unicode[STIX]{x1D713}^{-1}}W_{\operatorname{Ze}}^{\prime },\unicode[STIX]{x1D6F7},s)=\int _{P\backslash G}Z^{M}((W_{\operatorname{ Ze}})_{g},(W_{\operatorname{Ze}}^{\prime })_{g},\tilde{\unicode[STIX]{x1D6F7}}_{g},(s-m+1,\ldots ,s))|\det g|^{s}\,dg\end{eqnarray}$$ where  $(W_{\operatorname{Ze}})_{g}=\unicode[STIX]{x1D6FF}_{P}^{-1/2}\unicode[STIX]{x1D6FF}^{\prime }W_{\operatorname{Ze}}(\cdot g)\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m})$,
$(W_{\operatorname{Ze}})_{g}=\unicode[STIX]{x1D6FF}_{P}^{-1/2}\unicode[STIX]{x1D6FF}^{\prime }W_{\operatorname{Ze}}(\cdot g)\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m})$,  $(W_{\operatorname{Ze}}^{\prime })_{g}=\unicode[STIX]{x1D6FF}_{P}^{-1/2}\unicode[STIX]{x1D6FF}^{\prime }W_{\operatorname{Ze}}^{\prime }(\cdot g)\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}}(\unicode[STIX]{x1D70B}^{\prime \otimes m})$ and
$(W_{\operatorname{Ze}}^{\prime })_{g}=\unicode[STIX]{x1D6FF}_{P}^{-1/2}\unicode[STIX]{x1D6FF}^{\prime }W_{\operatorname{Ze}}^{\prime }(\cdot g)\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}}(\unicode[STIX]{x1D70B}^{\prime \otimes m})$ and  $\tilde{\unicode[STIX]{x1D6F7}}_{g}$ is given by (20). The integral on the right-hand side is absolutely convergent for
$\tilde{\unicode[STIX]{x1D6F7}}_{g}$ is given by (20). The integral on the right-hand side is absolutely convergent for  $\operatorname{Re}s+\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })+1>m$.
$\operatorname{Re}s+\mathbf{e}(\unicode[STIX]{x1D70B})+\mathbf{e}(\unicode[STIX]{x1D70B}^{\prime })+1>m$.
Proof. Write  $Z({\mathcal{T}}^{\unicode[STIX]{x1D713}}W_{\operatorname{Ze}},{\mathcal{T}}^{\unicode[STIX]{x1D713}^{-1}}W_{\operatorname{Ze}}^{\prime },\unicode[STIX]{x1D6F7},s)$ as
$Z({\mathcal{T}}^{\unicode[STIX]{x1D713}}W_{\operatorname{Ze}},{\mathcal{T}}^{\unicode[STIX]{x1D713}^{-1}}W_{\operatorname{Ze}}^{\prime },\unicode[STIX]{x1D6F7},s)$ as
 $$\begin{eqnarray}\int _{D\backslash G}\int _{U^{\prime }\backslash D}{\mathcal{T}}^{\unicode[STIX]{x1D713}}W_{\operatorname{ Ze}}(lg){\mathcal{T}}^{\unicode[STIX]{x1D713}^{-1}}W_{\operatorname{Ze}}^{\prime }(lg)|\det l|^{s-m}\,dl~\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{s}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{D\backslash G}\int _{U^{\prime }\backslash D}{\mathcal{T}}^{\unicode[STIX]{x1D713}}W_{\operatorname{ Ze}}(lg){\mathcal{T}}^{\unicode[STIX]{x1D713}^{-1}}W_{\operatorname{Ze}}^{\prime }(lg)|\det l|^{s-m}\,dl~\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{s}\,dg.\end{eqnarray}$$By Proposition 4.1 we get
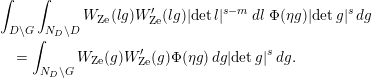 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{D\backslash G}\int _{N_{D}\backslash D}W_{\operatorname{Ze}}(lg)W_{\operatorname{Ze}}^{\prime }(lg)|\det l|^{s-m}\,dl~\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{s}\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{N_{D}\backslash G}W_{\operatorname{Ze}}(g)W_{\operatorname{Ze}}^{\prime }(g)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)\,dg|\det g|^{s}\,dg.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{D\backslash G}\int _{N_{D}\backslash D}W_{\operatorname{Ze}}(lg)W_{\operatorname{Ze}}^{\prime }(lg)|\det l|^{s-m}\,dl~\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{s}\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{N_{D}\backslash G}W_{\operatorname{Ze}}(g)W_{\operatorname{Ze}}^{\prime }(g)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)\,dg|\det g|^{s}\,dg.\nonumber\end{eqnarray}$$We write this as
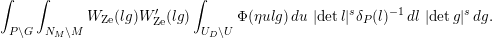 $$\begin{eqnarray}\int _{P\backslash G}\int _{N_{M}\backslash M}W_{\operatorname{Ze}}(lg)W_{\operatorname{Ze}}^{\prime }(lg)\int _{U_{D}\backslash U}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}ulg)\,du~|\det l|^{s}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}\,dl~|\det g|^{s}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{P\backslash G}\int _{N_{M}\backslash M}W_{\operatorname{Ze}}(lg)W_{\operatorname{Ze}}^{\prime }(lg)\int _{U_{D}\backslash U}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}ulg)\,du~|\det l|^{s}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}\,dl~|\det g|^{s}\,dg.\end{eqnarray}$$ The required identity now follows from (19). For convergence, as in the proof of Proposition 4.1, we may assume that  $\unicode[STIX]{x1D6F7}\geqslant 0$,
$\unicode[STIX]{x1D6F7}\geqslant 0$,  $s\in \mathbb{R}$,
$s\in \mathbb{R}$,  $\unicode[STIX]{x1D70B}^{\prime }=\bar{\unicode[STIX]{x1D70B}}$ and
$\unicode[STIX]{x1D70B}^{\prime }=\bar{\unicode[STIX]{x1D70B}}$ and  $W_{2}=\overline{W_{1}}$, so that all the integrands considered above are non-negative. Therefore, the manipulations are justified for
$W_{2}=\overline{W_{1}}$, so that all the integrands considered above are non-negative. Therefore, the manipulations are justified for  $s+2\mathbf{e}(\unicode[STIX]{x1D70B})+1>m$ by (23).◻
$s+2\mathbf{e}(\unicode[STIX]{x1D70B})+1>m$ by (23).◻
Proposition 5.2 immediately implies the first part of Theorem 5.1 (absolute convergence). In view of Remark 3.6, Proposition 5.2 also reduces the second and third parts of Theorem 5.1 (analyticity and unramified computation) to the analogous statements for the usual Rankin–Selberg integrals.
Remark 5.3. If  $\unicode[STIX]{x1D70E}$ and
$\unicode[STIX]{x1D70E}$ and  $\unicode[STIX]{x1D70E}^{\prime }$ are unramified, then
$\unicode[STIX]{x1D70E}^{\prime }$ are unramified, then
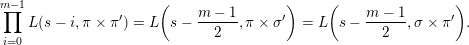 $$\begin{eqnarray}\mathop{\prod }_{i=0}^{m-1}L(s-i,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })=L\biggl(s-\frac{m-1}{2},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70E}^{\prime }\biggr)=L\biggl(s-\frac{m-1}{2},\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70B}^{\prime }\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{i=0}^{m-1}L(s-i,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })=L\biggl(s-\frac{m-1}{2},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70E}^{\prime }\biggr)=L\biggl(s-\frac{m-1}{2},\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70B}^{\prime }\biggr).\end{eqnarray}$$ However, in general for  $\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$, the equality
$\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$, the equality
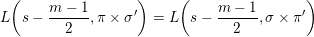 $$\begin{eqnarray}L\biggl(s-\frac{m-1}{2},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70E}^{\prime }\biggr)=L\biggl(s-\frac{m-1}{2},\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70B}^{\prime }\biggr)\end{eqnarray}$$
$$\begin{eqnarray}L\biggl(s-\frac{m-1}{2},\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70E}^{\prime }\biggr)=L\biggl(s-\frac{m-1}{2},\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70B}^{\prime }\biggr)\end{eqnarray}$$does not always hold.
Finally, we prove the functional equation (last part of Theorem 5.1).
For any  $W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$, define
$W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$, define  $\widehat{W_{\operatorname{Ze}}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ by
$\widehat{W_{\operatorname{Ze}}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ by  $\widehat{W_{\operatorname{Ze}}}(g)=W_{\operatorname{Ze}}(w_{nm}\,^{t}g^{-1})$. Then
$\widehat{W_{\operatorname{Ze}}}(g)=W_{\operatorname{Ze}}(w_{nm}\,^{t}g^{-1})$. Then  $\widehat{{\mathcal{T}}W_{\operatorname{Ze}}}={\mathcal{T}}(\widehat{W_{\operatorname{Ze}}})$. Note that
$\widehat{{\mathcal{T}}W_{\operatorname{Ze}}}={\mathcal{T}}(\widehat{W_{\operatorname{Ze}}})$. Note that  $w_{mn}=\operatorname{diag}(\overbrace{w_{n},\ldots ,w_{n}}^{m})w_{m,n}$ where
$w_{mn}=\operatorname{diag}(\overbrace{w_{n},\ldots ,w_{n}}^{m})w_{m,n}$ where  $w_{m,n}=\unicode[STIX]{x1D704}(w_{m})$; write
$w_{m,n}=\unicode[STIX]{x1D704}(w_{m})$; write  $g^{\prime }=w_{m,n}\,^{t}g^{-1}$,
$g^{\prime }=w_{m,n}\,^{t}g^{-1}$,  $g\in G$. Then, for any
$g\in G$. Then, for any  $g\in G$, we have
$g\in G$, we have
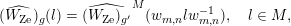 $$\begin{eqnarray}(\widehat{W_{\operatorname{Ze}}})_{g}(l)=\widehat{(W_{\operatorname{Ze}})_{g^{\prime }}}^{M}(w_{m,n}lw_{m,n}^{-1}),\quad l\in M,\end{eqnarray}$$
$$\begin{eqnarray}(\widehat{W_{\operatorname{Ze}}})_{g}(l)=\widehat{(W_{\operatorname{Ze}})_{g^{\prime }}}^{M}(w_{m,n}lw_{m,n}^{-1}),\quad l\in M,\end{eqnarray}$$and by Fourier inversion
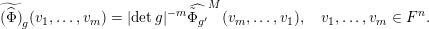 $$\begin{eqnarray}\widetilde{(\widehat{\unicode[STIX]{x1D6F7}})}_{g}(v_{1},\ldots ,v_{m})=|\det g|^{-m}\widehat{\tilde{\unicode[STIX]{x1D6F7}}_{g^{\prime }}}^{M}(v_{m},\ldots ,v_{1}),\quad v_{1},\ldots ,v_{m}\in F^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{(\widehat{\unicode[STIX]{x1D6F7}})}_{g}(v_{1},\ldots ,v_{m})=|\det g|^{-m}\widehat{\tilde{\unicode[STIX]{x1D6F7}}_{g^{\prime }}}^{M}(v_{m},\ldots ,v_{1}),\quad v_{1},\ldots ,v_{m}\in F^{n}.\end{eqnarray}$$ The last part of Theorem 5.1 therefore follows from Proposition 5.2 and the functional equation (24) using the change of variable  $g\mapsto g^{\prime }$ in the integral on the right-hand side of (25).
$g\mapsto g^{\prime }$ in the integral on the right-hand side of (25).
This finishes the proof of Theorem 5.1.
6 More analytic results
In this section we prove some more analytic properties of the zeta integrals defined in the previous section, as well as the bilinear forms of § 4. Some of these properties are well known in the case  $m=1$. However, there are also some new phenomena.
$m=1$. However, there are also some new phenomena.
6.1 Relation between zeta integrals and  ${\mathcal{B}}_{\operatorname{Sh}}$
${\mathcal{B}}_{\operatorname{Sh}}$
Recall that  $Q=D\rtimes {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$,
$Q=D\rtimes {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$,  $\unicode[STIX]{x1D6FF}_{Q}|_{D}=\unicode[STIX]{x1D6FF}_{D}=|\det |^{m}$ and
$\unicode[STIX]{x1D6FF}_{Q}|_{D}=\unicode[STIX]{x1D6FF}_{D}=|\det |^{m}$ and  $\unicode[STIX]{x1D6FF}_{Q}|_{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}}=1$. Hence, we can write
$\unicode[STIX]{x1D6FF}_{Q}|_{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}}=1$. Hence, we can write  $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ as
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ as
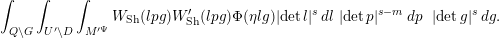 $$\begin{eqnarray}\int _{Q\backslash G}\int _{U^{\prime }\backslash D}\int _{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}}W_{\operatorname{Sh}}(lpg)W_{\operatorname{Sh}}^{\prime }(lpg)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}lg)|\det l|^{s}\,dl~|\det p|^{s-m}\,dp~~|\det g|^{s}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{Q\backslash G}\int _{U^{\prime }\backslash D}\int _{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}}W_{\operatorname{Sh}}(lpg)W_{\operatorname{Sh}}^{\prime }(lpg)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}lg)|\det l|^{s}\,dl~|\det p|^{s-m}\,dp~~|\det g|^{s}\,dg.\end{eqnarray}$$ Using Lemma 3.9 and the identification  $\unicode[STIX]{x1D704}:\operatorname{GL}_{m}\rightarrow {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$, we get
$\unicode[STIX]{x1D704}:\operatorname{GL}_{m}\rightarrow {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$, we get
 $$\begin{eqnarray}Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)=\int _{Q\backslash G}{\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}}(\cdot g),W_{\operatorname{Sh}}^{\prime }(\cdot g),s-m)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }},s}(g)\,dg\end{eqnarray}$$
$$\begin{eqnarray}Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)=\int _{Q\backslash G}{\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}}(\cdot g),W_{\operatorname{Sh}}^{\prime }(\cdot g),s-m)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }},s}(g)\,dg\end{eqnarray}$$ where, for any character  $\unicode[STIX]{x1D714}$ of
$\unicode[STIX]{x1D714}$ of  $F^{\ast }$,
$F^{\ast }$,
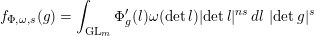 $$\begin{eqnarray}f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)=\int _{\operatorname{GL}_{m}}\unicode[STIX]{x1D6F7}_{g}^{\prime }(l)\unicode[STIX]{x1D714}(\det l)|\det l|^{ns}\,dl~|\det g|^{s}\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)=\int _{\operatorname{GL}_{m}}\unicode[STIX]{x1D6F7}_{g}^{\prime }(l)\unicode[STIX]{x1D714}(\det l)|\det l|^{ns}\,dl~|\det g|^{s}\end{eqnarray}$$ and  $\unicode[STIX]{x1D6F7}_{g}^{\prime }\in {\mathcal{S}}(\operatorname{Mat}_{m,m}(F))$ is given by
$\unicode[STIX]{x1D6F7}_{g}^{\prime }\in {\mathcal{S}}(\operatorname{Mat}_{m,m}(F))$ is given by  $\unicode[STIX]{x1D6F7}_{g}^{\prime }(X)=\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}(X)g)$ where
$\unicode[STIX]{x1D6F7}_{g}^{\prime }(X)=\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}(X)g)$ where  $\unicode[STIX]{x1D707}(X)\in \operatorname{Mat}_{m\times nm}$ is the matrix whose
$\unicode[STIX]{x1D707}(X)\in \operatorname{Mat}_{m\times nm}$ is the matrix whose  $i$th row is
$i$th row is  $\sum _{j=1}^{m}X_{i,j}e_{nj}$. Note that
$\sum _{j=1}^{m}X_{i,j}e_{nj}$. Note that  $\unicode[STIX]{x1D6F7}\mapsto f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}$ is an intertwining map from
$\unicode[STIX]{x1D6F7}\mapsto f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}$ is an intertwining map from  ${\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))\otimes |\det |^{s}$ to
${\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))\otimes |\det |^{s}$ to  $\operatorname{Ind}_{Q}^{G}\unicode[STIX]{x1D708}_{s}$ where
$\operatorname{Ind}_{Q}^{G}\unicode[STIX]{x1D708}_{s}$ where  $\unicode[STIX]{x1D708}_{s}$ is the character on
$\unicode[STIX]{x1D708}_{s}$ is the character on  $Q$ such that
$Q$ such that  $\unicode[STIX]{x1D708}_{s}|_{D}=|\det |^{s-m/2}$ and
$\unicode[STIX]{x1D708}_{s}|_{D}=|\det |^{s-m/2}$ and  $\unicode[STIX]{x1D708}_{s}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D714}^{-1}\circ \det$.
$\unicode[STIX]{x1D708}_{s}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D714}^{-1}\circ \det$.
Lemma 6.1. There exist  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,  $W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ and
$W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ and  $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$ such that
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$ such that  $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)\equiv 1$.
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)\equiv 1$.
Proof. This follows from Corollary 3.13 and (26) by taking  $W_{\operatorname{Sh}}$ such that
$W_{\operatorname{Sh}}$ such that  $W_{\operatorname{Sh}}|_{D}$ is supported in
$W_{\operatorname{Sh}}|_{D}$ is supported in  $U^{\prime }\unicode[STIX]{x1D6FA}$ for a small neighborhood
$U^{\prime }\unicode[STIX]{x1D6FA}$ for a small neighborhood  $\unicode[STIX]{x1D6FA}$ of
$\unicode[STIX]{x1D6FA}$ of  $e$ and
$e$ and  $\unicode[STIX]{x1D6F7}$ supported in a small neighborhood of
$\unicode[STIX]{x1D6F7}$ supported in a small neighborhood of  $\unicode[STIX]{x1D702}$.◻
$\unicode[STIX]{x1D702}$.◻
Let  $\operatorname{ord}_{{\mathcal{B}}}(s)=\operatorname{ord}_{{\mathcal{B}};\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }}(s)$ be the maximal order of pole of
$\operatorname{ord}_{{\mathcal{B}}}(s)=\operatorname{ord}_{{\mathcal{B}};\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }}(s)$ be the maximal order of pole of  ${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },\cdot )$ at
${\mathcal{B}}_{i}(W_{i},W_{i}^{\prime },\cdot )$ at  $s$ for
$s$ for  $i=0,\ldots ,(m-1)n$ as we vary
$i=0,\ldots ,(m-1)n$ as we vary  $W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$,
$W_{i}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})$,  $W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$. (Recall that this does not depend on
$W_{i}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$. (Recall that this does not depend on  $i$ by (16).) By Corollary 3.13, we have
$i$ by (16).) By Corollary 3.13, we have  $\operatorname{ord}_{{\mathcal{B}}}(s)\geqslant 0$ for all
$\operatorname{ord}_{{\mathcal{B}}}(s)\geqslant 0$ for all  $s$.
$s$.
Similarly, let  $\operatorname{ord}_{Z}(s)=\operatorname{ord}_{Z;\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }}(s)\geqslant 0$ be the maximal order of pole of
$\operatorname{ord}_{Z}(s)=\operatorname{ord}_{Z;\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}^{\prime }}(s)\geqslant 0$ be the maximal order of pole of  $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},\cdot )$ at
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},\cdot )$ at  $s$ as we vary
$s$ as we vary  $W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
$W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,  $W^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ and
$W^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ and  $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$. By Lemma 6.1, we have
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$. By Lemma 6.1, we have  $\operatorname{ord}_{Z}(s)\geqslant 0$ for all
$\operatorname{ord}_{Z}(s)\geqslant 0$ for all  $s$. We can sharpen this as follows.
$s$. We can sharpen this as follows.
Proposition 6.2. The bilinear form  ${\mathcal{B}}_{i}(\cdot ,\cdot ,s)$ on
${\mathcal{B}}_{i}(\cdot ,\cdot ,s)$ on  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\times {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ admits meromorphic continuation in
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}}(\unicode[STIX]{x1D70E})\times {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{i}}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$ admits meromorphic continuation in  $s$ to a rational function in
$s$ to a rational function in  $q^{s}$. Moreover, for every
$q^{s}$. Moreover, for every  $s\in \mathbb{C}$, we have
$s\in \mathbb{C}$, we have  $\operatorname{ord}_{{\mathcal{B}}}(s-m)\leqslant \operatorname{ord}_{Z}(s)$ with equality unless
$\operatorname{ord}_{{\mathcal{B}}}(s-m)\leqslant \operatorname{ord}_{Z}(s)$ with equality unless  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}=|\cdot |^{j-ns}$ for some
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}=|\cdot |^{j-ns}$ for some  $j\in \{0,\ldots ,m-1\}$, in which case
$j\in \{0,\ldots ,m-1\}$, in which case  $\operatorname{ord}_{Z}(s)\leqslant \operatorname{ord}_{{\mathcal{B}}}(s-m)+1$. In particular, if
$\operatorname{ord}_{Z}(s)\leqslant \operatorname{ord}_{{\mathcal{B}}}(s-m)+1$. In particular, if  $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$, then
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$, then  ${\mathcal{B}}_{0}(\cdot ,\cdot )$ is defined if and only if
${\mathcal{B}}_{0}(\cdot ,\cdot )$ is defined if and only if  $Z(\cdot ,\cdot ,\cdot ,s)$ is holomorphic at
$Z(\cdot ,\cdot ,\cdot ,s)$ is holomorphic at  $s=m$ for all data.
$s=m$ for all data.
Proof. It is enough to prove the meromorphic continuation for  $i=(m-1)n$, that is, for
$i=(m-1)n$, that is, for  ${\mathcal{B}}_{\operatorname{Sh}}$. This case follows from equality (26). Indeed, taking
${\mathcal{B}}_{\operatorname{Sh}}$. This case follows from equality (26). Indeed, taking  $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}$ and
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}$ and  $\unicode[STIX]{x1D6F7}$ to be the characteristic function of a small neighborhood of
$\unicode[STIX]{x1D6F7}$ to be the characteristic function of a small neighborhood of  $\unicode[STIX]{x1D702}$,
$\unicode[STIX]{x1D702}$,  $f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}$ is supported in
$f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}$ is supported in  $Q\unicode[STIX]{x1D6FA}$ for a small neighborhood
$Q\unicode[STIX]{x1D6FA}$ for a small neighborhood  $\unicode[STIX]{x1D6FA}$ of
$\unicode[STIX]{x1D6FA}$ of  $e$ and hence
$e$ and hence  $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ is a non-zero constant multiple of
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ is a non-zero constant multiple of  ${\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s-m)$. We also get that
${\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s-m)$. We also get that  $\operatorname{ord}_{{\mathcal{B}}}(s-m)\leqslant \operatorname{ord}_{Z}(s)$ for all
$\operatorname{ord}_{{\mathcal{B}}}(s-m)\leqslant \operatorname{ord}_{Z}(s)$ for all  $s$.
$s$.
On the other hand,  $f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)$ is a generalized Tate integral with respect to
$f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)$ is a generalized Tate integral with respect to  $\operatorname{GL}_{m}$, and hence
$\operatorname{GL}_{m}$, and hence
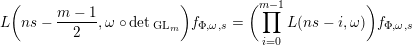 $$\begin{eqnarray}L\biggl(ns-\frac{m-1}{2},\unicode[STIX]{x1D714}\circ \det _{\operatorname{GL}_{m}}\biggr)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}=\biggl(\mathop{\prod }_{i=0}^{m-1}L(ns-i,\unicode[STIX]{x1D714})\biggr)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}\end{eqnarray}$$
$$\begin{eqnarray}L\biggl(ns-\frac{m-1}{2},\unicode[STIX]{x1D714}\circ \det _{\operatorname{GL}_{m}}\biggr)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}=\biggl(\mathop{\prod }_{i=0}^{m-1}L(ns-i,\unicode[STIX]{x1D714})\biggr)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}\end{eqnarray}$$ is entire. We get from (26) that  $\operatorname{ord}_{Z}(s)\leqslant \operatorname{ord}_{{\mathcal{B}}}(s-m)$ unless
$\operatorname{ord}_{Z}(s)\leqslant \operatorname{ord}_{{\mathcal{B}}}(s-m)$ unless  $\unicode[STIX]{x1D714}=|\cdot |^{j-ns}$ for some
$\unicode[STIX]{x1D714}=|\cdot |^{j-ns}$ for some  $j\in \{0,\ldots ,m-1\}$, in which case
$j\in \{0,\ldots ,m-1\}$, in which case  $\operatorname{ord}_{Z}(s)\leqslant \operatorname{ord}_{{\mathcal{B}}}(s-m)+1$. The corollary follows.◻
$\operatorname{ord}_{Z}(s)\leqslant \operatorname{ord}_{{\mathcal{B}}}(s-m)+1$. The corollary follows.◻
Remark 6.3. Note that if  $\unicode[STIX]{x1D70B}$ and
$\unicode[STIX]{x1D70B}$ and  $\unicode[STIX]{x1D70B}^{\prime }$ are tempered, then it follows from Theorem 5.1 part (ii) that
$\unicode[STIX]{x1D70B}^{\prime }$ are tempered, then it follows from Theorem 5.1 part (ii) that  $\operatorname{ord}_{Z}(s)=0$ unless
$\operatorname{ord}_{Z}(s)=0$ unless  $\operatorname{Re}s\in \frac{1}{2}\mathbb{Z}$ and
$\operatorname{Re}s\in \frac{1}{2}\mathbb{Z}$ and  $\operatorname{Re}s\leqslant m$. Thus, in general, many poles of
$\operatorname{Re}s\leqslant m$. Thus, in general, many poles of  $f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }},s}$ do not contribute a pole for
$f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }},s}$ do not contribute a pole for  $Z(\cdot ,\cdot ,\cdot ,s)$.
$Z(\cdot ,\cdot ,\cdot ,s)$.
Remark 6.4. In general, we do not know what precisely is the fractional ideal of  $\mathbb{Z}[q^{\pm s}]$ generated by
$\mathbb{Z}[q^{\pm s}]$ generated by
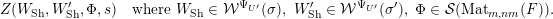 $$\begin{eqnarray}Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)\quad \text{where }W_{\operatorname{ Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E}),~W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E}^{\prime }),~\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F)).\end{eqnarray}$$
$$\begin{eqnarray}Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)\quad \text{where }W_{\operatorname{ Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E}),~W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E}^{\prime }),~\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F)).\end{eqnarray}$$ If both  $\unicode[STIX]{x1D70B}$ and
$\unicode[STIX]{x1D70B}$ and  $\unicode[STIX]{x1D70B}^{\prime }$ are unitarizable, then we expect that this ideal is generated by
$\unicode[STIX]{x1D70B}^{\prime }$ are unitarizable, then we expect that this ideal is generated by  $\prod _{i=0}^{m-1}L(s-i,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })$, that is, part (ii) of Theorem 5.1 is tight in this case.
$\prod _{i=0}^{m-1}L(s-i,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })$, that is, part (ii) of Theorem 5.1 is tight in this case.
Example 6.5. Consider  $n=m=2$ and
$n=m=2$ and  $\unicode[STIX]{x1D70B}=|\cdot |\times |\cdot |^{-1}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{2}$. Then
$\unicode[STIX]{x1D70B}=|\cdot |\times |\cdot |^{-1}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{2}$. Then  $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}^{\vee }$ and
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}^{\vee }$ and  $L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee })=L(s,\mathbf{1}_{F^{\ast }})^{2}L(s+2,\mathbf{1}_{F^{\ast }})L(s-2,\mathbf{1}_{F^{\ast }})$. Therefore,
$L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee })=L(s,\mathbf{1}_{F^{\ast }})^{2}L(s+2,\mathbf{1}_{F^{\ast }})L(s-2,\mathbf{1}_{F^{\ast }})$. Therefore,  $L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })L(s-1,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })$ has a pole at
$L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })L(s-1,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })$ has a pole at  $s=2$. However, we do not know whether
$s=2$. However, we do not know whether  $Z(\cdot ,\cdot ,\cdot ,s)$ is holomorphic at
$Z(\cdot ,\cdot ,\cdot ,s)$ is holomorphic at  $s=2$, or equivalently (by Proposition 6.2) whether
$s=2$, or equivalently (by Proposition 6.2) whether  ${\mathcal{B}}_{0}(\cdot ,\cdot )$ is well defined. Recall that
${\mathcal{B}}_{0}(\cdot ,\cdot )$ is well defined. Recall that  $\operatorname{Sp}(\unicode[STIX]{x1D70B},2)$ is not unramified in this case (cf. Remark 2.6).
$\operatorname{Sp}(\unicode[STIX]{x1D70B},2)$ is not unramified in this case (cf. Remark 2.6).
6.2 More results in the (AT) case
Proposition 6.6. Suppose that  $\unicode[STIX]{x1D70B}$ is (AT) and let
$\unicode[STIX]{x1D70B}$ is (AT) and let  $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$. Then, for any
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$. Then, for any  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,  $W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$, we have
$W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$, we have
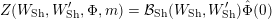 $$\begin{eqnarray}Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},m)={\mathcal{B}}_{\operatorname{ Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime })\hat{\unicode[STIX]{x1D6F7}}(0)\end{eqnarray}$$
$$\begin{eqnarray}Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},m)={\mathcal{B}}_{\operatorname{ Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime })\hat{\unicode[STIX]{x1D6F7}}(0)\end{eqnarray}$$where both sides are well defined.
Proof. By the first part of Theorem 5.1, the integral defining  $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},m)$ is absolutely convergent. Moreover, since the modulus function of
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},m)$ is absolutely convergent. Moreover, since the modulus function of  $D$ is
$D$ is  $|\det |^{m}$, we can write
$|\det |^{m}$, we can write
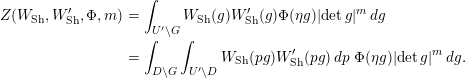 $$\begin{eqnarray}\displaystyle Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},m) & = & \displaystyle \int _{U^{\prime }\backslash G}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{D\backslash G}\int _{U^{\prime }\backslash D}W_{\operatorname{Sh}}(pg)W_{\operatorname{Sh}}^{\prime }(pg)\,dp~\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}\,dg.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},m) & = & \displaystyle \int _{U^{\prime }\backslash G}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{D\backslash G}\int _{U^{\prime }\backslash D}W_{\operatorname{Sh}}(pg)W_{\operatorname{Sh}}^{\prime }(pg)\,dp~\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}\,dg.\nonumber\end{eqnarray}$$ For  $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$, by Theorem 4.3 we get
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$, by Theorem 4.3 we get
 $$\begin{eqnarray}{\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime })\int _{D\backslash G}~\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}dg=\hat{\unicode[STIX]{x1D6F7}}(0){\mathcal{B}}_{\operatorname{ Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime })\int _{D\backslash G}~\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{m}dg=\hat{\unicode[STIX]{x1D6F7}}(0){\mathcal{B}}_{\operatorname{ Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime })\end{eqnarray}$$as required. ◻
From the functional equations (22) we deduce the following corollary.
Corollary 6.7. Suppose that  $\unicode[STIX]{x1D70B}$ is (AT) and let
$\unicode[STIX]{x1D70B}$ is (AT) and let  $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$. Then
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$. Then  $\operatorname{ord}_{Z}(0)$ is equal to the order of the zero of the product of
$\operatorname{ord}_{Z}(0)$ is equal to the order of the zero of the product of  $\unicode[STIX]{x1D6FE}$-factors on the right-hand side of (22) at
$\unicode[STIX]{x1D6FE}$-factors on the right-hand side of (22) at  $s=0$.
$s=0$.
Example 6.8. If  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{sqr}}\operatorname{GL}_{n}$ corresponds to a segment of length
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{sqr}}\operatorname{GL}_{n}$ corresponds to a segment of length  $k$ and
$k$ and  $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$, then
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$, then  $\operatorname{ord}_{Z}(0)=\min (m,k)$. Indeed, in this case
$\operatorname{ord}_{Z}(0)=\min (m,k)$. Indeed, in this case  $(\prod _{j=1}^{k}(1-q^{f(s-j)})/(1-q^{-f(s+j-1)}))\unicode[STIX]{x1D6FE}(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D713})$ is entire for a suitable integer
$(\prod _{j=1}^{k}(1-q^{f(s-j)})/(1-q^{-f(s+j-1)}))\unicode[STIX]{x1D6FE}(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D713})$ is entire for a suitable integer  $f>0$ depending on
$f>0$ depending on  $\unicode[STIX]{x1D70B}$.
$\unicode[STIX]{x1D70B}$.
Under mild assumptions, we can give a lower bound for the real part of the first location of a pole.
Lemma 6.9. Suppose that  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$ is unitary and let
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$ is unitary and let  $\unicode[STIX]{x1D70B}^{\prime }=\overline{\unicode[STIX]{x1D70B}}$. Then, for suitable
$\unicode[STIX]{x1D70B}^{\prime }=\overline{\unicode[STIX]{x1D70B}}$. Then, for suitable  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,  $W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ and
$W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ and  $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$,
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$,  $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ has at least one pole for
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ has at least one pole for  $\operatorname{Re}s\geqslant m-1$.
$\operatorname{Re}s\geqslant m-1$.
Proof. Indeed, taking  $W_{\operatorname{Sh}}^{\prime }=\overline{W_{\operatorname{Sh}}}$ and
$W_{\operatorname{Sh}}^{\prime }=\overline{W_{\operatorname{Sh}}}$ and  $\unicode[STIX]{x1D6F7}\geqslant 0$, the right-hand side of (25) is a power series in
$\unicode[STIX]{x1D6F7}\geqslant 0$, the right-hand side of (25) is a power series in  $q^{-s}$ with non-negative coefficients
$q^{-s}$ with non-negative coefficients  $a_{k}$ which vanish for
$a_{k}$ which vanish for  $k\ll 0$. Assume to the contrary that
$k\ll 0$. Assume to the contrary that  $Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ is holomorphic throughout
$Z(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)$ is holomorphic throughout  $\operatorname{Re}s\geqslant m-1$. Then the power series would converge at
$\operatorname{Re}s\geqslant m-1$. Then the power series would converge at  $s=m-1$. However, the integral on the right-hand side of (25) diverges at
$s=m-1$. However, the integral on the right-hand side of (25) diverges at  $s=m-1$ since it contains
$s=m-1$ since it contains  $\int _{F^{\ast }}\tilde{\unicode[STIX]{x1D6F7}}_{g}(\unicode[STIX]{x1D706}e_{n},e_{n},\ldots ,e_{n})|\unicode[STIX]{x1D706}|^{s-m+1}\,d\unicode[STIX]{x1D706}$ as an inner integral. We obtain a contradiction.◻
$\int _{F^{\ast }}\tilde{\unicode[STIX]{x1D6F7}}_{g}(\unicode[STIX]{x1D706}e_{n},e_{n},\ldots ,e_{n})|\unicode[STIX]{x1D706}|^{s-m+1}\,d\unicode[STIX]{x1D706}$ as an inner integral. We obtain a contradiction.◻
Corollary 6.10. Suppose  $n,m>1$,
$n,m>1$,  $\unicode[STIX]{x1D70B}^{\prime }=\overline{\unicode[STIX]{x1D70B}}$ and
$\unicode[STIX]{x1D70B}^{\prime }=\overline{\unicode[STIX]{x1D70B}}$ and  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$ is unitary. Then any
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$ is unitary. Then any  ${\mathcal{B}}_{i}$ admits a pole in the right half plane
${\mathcal{B}}_{i}$ admits a pole in the right half plane  $\operatorname{Re}s\geqslant -1$. Hence, there exists
$\operatorname{Re}s\geqslant -1$. Hence, there exists  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70B})$ such that the integral defining
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70B})$ such that the integral defining  ${\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},\overline{W_{\operatorname{Sh}}},s)$ diverges for all
${\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},\overline{W_{\operatorname{Sh}}},s)$ diverges for all  $s\leqslant -1$. In particular,
$s\leqslant -1$. In particular,  $\int _{U^{\prime }{M^{\prime }}^{\unicode[STIX]{x1D6F9}}\backslash G}|W_{\operatorname{Sh}}(g)|^{2}\,dg$ diverges.
$\int _{U^{\prime }{M^{\prime }}^{\unicode[STIX]{x1D6F9}}\backslash G}|W_{\operatorname{Sh}}(g)|^{2}\,dg$ diverges.
Proof. Indeed, by Lemma 6.9 we have  $\operatorname{ord}_{Z}(s)>0$ for some
$\operatorname{ord}_{Z}(s)>0$ for some  $s$ with
$s$ with  $\operatorname{Re}s\geqslant m-1$. Hence, by Proposition 6.2,
$\operatorname{Re}s\geqslant m-1$. Hence, by Proposition 6.2,  $\operatorname{ord}_{{\mathcal{B}}}(s-m)>0$ for that
$\operatorname{ord}_{{\mathcal{B}}}(s-m)>0$ for that  $s$ (since
$s$ (since  $n,m>1$). Therefore, the integral defining
$n,m>1$). Therefore, the integral defining  ${\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},\overline{W_{\operatorname{Sh}}},s)$ diverges for all
${\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},\overline{W_{\operatorname{Sh}}},s)$ diverges for all  $s\leqslant -1$ (cf. (15)). In particular,
$s\leqslant -1$ (cf. (15)). In particular,
 $$\begin{eqnarray}\int _{U^{\prime }{M^{\prime }}^{\unicode[STIX]{x1D6F9}}\backslash G}|W_{\operatorname{Sh}}(g)|^{2}\,dg=\int _{Q\backslash G}\int _{U^{\prime }\backslash D}|W_{\operatorname{Sh}}(g)|^{2}|\det g|^{-m}\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{U^{\prime }{M^{\prime }}^{\unicode[STIX]{x1D6F9}}\backslash G}|W_{\operatorname{Sh}}(g)|^{2}\,dg=\int _{Q\backslash G}\int _{U^{\prime }\backslash D}|W_{\operatorname{Sh}}(g)|^{2}|\det g|^{-m}\,dg\end{eqnarray}$$diverges. ◻
Our final result in this section is the following lemma.
Lemma 6.11. Suppose that  $\unicode[STIX]{x1D70B}$ is (AT) and let
$\unicode[STIX]{x1D70B}$ is (AT) and let  $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$. Then
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$. Then  $\operatorname{ord}_{Z}(0)=\operatorname{ord}_{{\mathcal{B}}}(-m)+1$. In particular, if
$\operatorname{ord}_{Z}(0)=\operatorname{ord}_{{\mathcal{B}}}(-m)+1$. In particular, if  $\unicode[STIX]{x1D70B}$ is supercuspidal, then
$\unicode[STIX]{x1D70B}$ is supercuspidal, then  ${\mathcal{B}}$ is holomorphic at
${\mathcal{B}}$ is holomorphic at  $s=-m$ (cf. Example 6.8). Moreover, let
$s=-m$ (cf. Example 6.8). Moreover, let
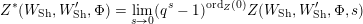 $$\begin{eqnarray}Z^{\ast }(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7})=\lim _{s\rightarrow 0}(q^{s}-1)^{\operatorname{ord}_{Z}(0)}Z(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)\end{eqnarray}$$
$$\begin{eqnarray}Z^{\ast }(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7})=\lim _{s\rightarrow 0}(q^{s}-1)^{\operatorname{ord}_{Z}(0)}Z(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7},s)\end{eqnarray}$$and
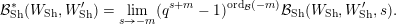 $$\begin{eqnarray}{\mathcal{B}}_{\operatorname{Sh}}^{\ast }(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime })=\lim _{s\rightarrow -m}(q^{s+m}-1)^{\operatorname{ord}_{{\mathcal{B}}}(-m)}{\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{\operatorname{Sh}}^{\ast }(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime })=\lim _{s\rightarrow -m}(q^{s+m}-1)^{\operatorname{ord}_{{\mathcal{B}}}(-m)}{\mathcal{B}}_{\operatorname{Sh}}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s).\end{eqnarray}$$ Then there exists a constant  $c$ (depending only on
$c$ (depending only on  $F$,
$F$,  $m$ and
$m$ and  $n$) such that
$n$) such that
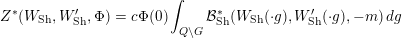 $$\begin{eqnarray}Z^{\ast }(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7})=c\unicode[STIX]{x1D6F7}(0)\int _{Q\backslash G}{\mathcal{B}}_{\operatorname{Sh}}^{\ast }(W_{\operatorname{ Sh}}(\cdot g),W_{\operatorname{Sh}}^{\prime }(\cdot g),-m)\,dg\end{eqnarray}$$
$$\begin{eqnarray}Z^{\ast }(W_{\operatorname{ Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7})=c\unicode[STIX]{x1D6F7}(0)\int _{Q\backslash G}{\mathcal{B}}_{\operatorname{Sh}}^{\ast }(W_{\operatorname{ Sh}}(\cdot g),W_{\operatorname{Sh}}^{\prime }(\cdot g),-m)\,dg\end{eqnarray}$$ for all  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$,  $W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ and
$W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ and  $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$.
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(F))$.
Proof. By the local functional equation and Proposition 6.6,  $Z^{\ast }(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7})=0$ if
$Z^{\ast }(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F7})=0$ if  $\unicode[STIX]{x1D6F7}(0)=0$. Therefore, the argument in the proof of Corollary 6.10 (taking
$\unicode[STIX]{x1D6F7}(0)=0$. Therefore, the argument in the proof of Corollary 6.10 (taking  $\unicode[STIX]{x1D6F7}$ supported near
$\unicode[STIX]{x1D6F7}$ supported near  $\unicode[STIX]{x1D702}$, which localizes
$\unicode[STIX]{x1D702}$, which localizes  $f_{\unicode[STIX]{x1D6F7},\mathbf{1}_{F^{\ast }},s}$ near
$f_{\unicode[STIX]{x1D6F7},\mathbf{1}_{F^{\ast }},s}$ near  $Q$) shows that
$Q$) shows that  $\operatorname{ord}_{Z}(0)=\operatorname{ord}_{{\mathcal{B}}}(-m)+1$. Since
$\operatorname{ord}_{Z}(0)=\operatorname{ord}_{{\mathcal{B}}}(-m)+1$. Since  $\operatorname{Res}_{s=0}f_{\unicode[STIX]{x1D6F7},\mathbf{1}_{F^{\ast }},s}$ is proportional to
$\operatorname{Res}_{s=0}f_{\unicode[STIX]{x1D6F7},\mathbf{1}_{F^{\ast }},s}$ is proportional to  $\unicode[STIX]{x1D6F7}(0)$, we get the required relation from (26).◻
$\unicode[STIX]{x1D6F7}(0)$, we get the required relation from (26).◻
We may view
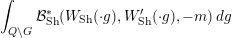 $$\begin{eqnarray}\int _{Q\backslash G}{\mathcal{B}}_{\operatorname{Sh}}^{\ast }(W_{\operatorname{ Sh}}(\cdot g),W_{\operatorname{Sh}}^{\prime }(\cdot g),-m)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{Q\backslash G}{\mathcal{B}}_{\operatorname{Sh}}^{\ast }(W_{\operatorname{ Sh}}(\cdot g),W_{\operatorname{Sh}}^{\prime }(\cdot g),-m)\,dg\end{eqnarray}$$as a regularization of
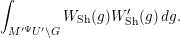 $$\begin{eqnarray}\int _{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}U^{\prime }\backslash G}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}U^{\prime }\backslash G}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)\,dg.\end{eqnarray}$$ (Recall that the latter diverges for  $W_{\operatorname{Sh}}^{\prime }=\overline{W_{\operatorname{Sh}}}$ if
$W_{\operatorname{Sh}}^{\prime }=\overline{W_{\operatorname{Sh}}}$ if  $m>1$.)
$m>1$.)
7 The case  $n=m=2$
$n=m=2$
Given  $\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$, it is natural to ask what is the asymptotic behavior of a function in
$\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$, it is natural to ask what is the asymptotic behavior of a function in  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ or (what is essentially the same thing) in
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ or (what is essentially the same thing) in  ${\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$. In the case
${\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$. In the case  $n=2$ or if
$n=2$ or if  $n=3$ and
$n=3$ and  $m=2$,
$m=2$,  ${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ is a spherical subgroup of
${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ is a spherical subgroup of  $G$ and the problem can in principle be analyzed by the methods of [Reference Sakellaridis and VenkateshSV17]. We will only treat here the case where
$G$ and the problem can in principle be analyzed by the methods of [Reference Sakellaridis and VenkateshSV17]. We will only treat here the case where  $m=n=2$ and
$m=n=2$ and  $\unicode[STIX]{x1D70B}$ is supercuspidal, in a self-contained way, without appealing to the general results of [Reference Sakellaridis and VenkateshSV17]. For
$\unicode[STIX]{x1D70B}$ is supercuspidal, in a self-contained way, without appealing to the general results of [Reference Sakellaridis and VenkateshSV17]. For  $n>2$ and
$n>2$ and  $m>1$ (excluding the case
$m>1$ (excluding the case  $n=3$ and
$n=3$ and  $m=2$),
$m=2$),  ${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ is no longer a spherical subgroup and the problem seems to be more difficult than the analogous problem for
${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ is no longer a spherical subgroup and the problem seems to be more difficult than the analogous problem for  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$. We have little to say about it.
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$. We have little to say about it.
We note that in the case where  $n=2$ and
$n=2$ and  $\unicode[STIX]{x1D70E}$ is unramified, an explicit formula for the unramified
$\unicode[STIX]{x1D70E}$ is unramified, an explicit formula for the unramified  $W_{\operatorname{Sh}}$ was given by Sato [Reference SatoSat05]. This is a special case of a formula of Sakellaridis [Reference SakellaridisSak06]. In general, it would be an interesting problem to obtain such an explicit formula in the unramified case for any
$W_{\operatorname{Sh}}$ was given by Sato [Reference SatoSat05]. This is a special case of a formula of Sakellaridis [Reference SakellaridisSak06]. In general, it would be an interesting problem to obtain such an explicit formula in the unramified case for any  $m,n$. Once again, this goes beyond the scope of [Reference SakellaridisSak13].
$m,n$. Once again, this goes beyond the scope of [Reference SakellaridisSak13].
For the rest of this section we consider the very special case where  $n=m=2$. Fix an infinite-dimensional
$n=m=2$. Fix an infinite-dimensional  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}\operatorname{GL}_{2}$ and
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}\operatorname{GL}_{2}$ and  $\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},2)$. The transition map
$\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},2)$. The transition map  ${\mathcal{T}}:{\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})\rightarrow {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ is
${\mathcal{T}}:{\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})\rightarrow {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ is
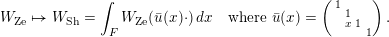 $$\begin{eqnarray}W_{\operatorname{Ze}}\mapsto W_{\operatorname{Sh}}=\int _{F}W_{\operatorname{Ze}}(\bar{u}(x)\cdot )\,dx\quad \text{where }\bar{u}(x)=\left(\begin{smallmatrix}1 & & & \\ & 1 & & \\ & x & 1 & \\ & & & 1\!\end{smallmatrix}\right).\end{eqnarray}$$
$$\begin{eqnarray}W_{\operatorname{Ze}}\mapsto W_{\operatorname{Sh}}=\int _{F}W_{\operatorname{Ze}}(\bar{u}(x)\cdot )\,dx\quad \text{where }\bar{u}(x)=\left(\begin{smallmatrix}1 & & & \\ & 1 & & \\ & x & 1 & \\ & & & 1\!\end{smallmatrix}\right).\end{eqnarray}$$ Recall that  $\unicode[STIX]{x1D70B}^{\vee }\simeq \unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{-1}$. Let
$\unicode[STIX]{x1D70B}^{\vee }\simeq \unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{-1}$. Let  $\unicode[STIX]{x1D70B}_{s}=\unicode[STIX]{x1D70B}|\cdot |^{s}$. Fix a pairing
$\unicode[STIX]{x1D70B}_{s}=\unicode[STIX]{x1D70B}|\cdot |^{s}$. Fix a pairing  $\unicode[STIX]{x1D6E5}:\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}\rightarrow \mathbb{C}$ such that
$\unicode[STIX]{x1D6E5}:\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}\rightarrow \mathbb{C}$ such that  $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70B}_{1/2}(g)v_{1}\otimes \unicode[STIX]{x1D70B}_{-1/2}(g)v_{2})=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\det g)\unicode[STIX]{x1D6E5}(v_{1}\otimes v_{2})$ for all
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D70B}_{1/2}(g)v_{1}\otimes \unicode[STIX]{x1D70B}_{-1/2}(g)v_{2})=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\det g)\unicode[STIX]{x1D6E5}(v_{1}\otimes v_{2})$ for all  $g\in \operatorname{GL}_{2}$. For any
$g\in \operatorname{GL}_{2}$. For any  $v\in \unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}$, let
$v\in \unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}$, let  $\operatorname{MC}_{v}:\operatorname{GL}_{2}\times \operatorname{GL}_{2}\rightarrow \mathbb{C}$ be the twisted matrix coefficient
$\operatorname{MC}_{v}:\operatorname{GL}_{2}\times \operatorname{GL}_{2}\rightarrow \mathbb{C}$ be the twisted matrix coefficient  $\operatorname{MC}_{v}(g_{1},g_{2})=\unicode[STIX]{x1D6E5}((\unicode[STIX]{x1D70B}_{1/2}(g_{1})\otimes \unicode[STIX]{x1D70B}_{-1/2}(g_{2}))(v))$. Thus,
$\operatorname{MC}_{v}(g_{1},g_{2})=\unicode[STIX]{x1D6E5}((\unicode[STIX]{x1D70B}_{1/2}(g_{1})\otimes \unicode[STIX]{x1D70B}_{-1/2}(g_{2}))(v))$. Thus,  $v\mapsto \operatorname{MC}_{v}$ defines an equivariant map from
$v\mapsto \operatorname{MC}_{v}$ defines an equivariant map from  $\unicode[STIX]{x1D70B}_{1/2}\,\otimes \,\unicode[STIX]{x1D70B}_{-1/2}$ to
$\unicode[STIX]{x1D70B}_{1/2}\,\otimes \,\unicode[STIX]{x1D70B}_{-1/2}$ to  $\operatorname{Ind}_{(Z\times Z)\operatorname{GL}_{2}^{\operatorname{diag}}}^{\operatorname{GL}_{2}\times \operatorname{GL}_{2}}\unicode[STIX]{x1D712}$ where
$\operatorname{Ind}_{(Z\times Z)\operatorname{GL}_{2}^{\operatorname{diag}}}^{\operatorname{GL}_{2}\times \operatorname{GL}_{2}}\unicode[STIX]{x1D712}$ where  $Z$ is the center of
$Z$ is the center of  $\operatorname{GL}_{2}$,
$\operatorname{GL}_{2}$,  $\operatorname{GL}_{2}^{\operatorname{diag}}$ is
$\operatorname{GL}_{2}^{\operatorname{diag}}$ is  $\operatorname{GL}_{2}$ diagonally embedded in
$\operatorname{GL}_{2}$ diagonally embedded in  $\operatorname{GL}_{2}\times \operatorname{GL}_{2}$ and
$\operatorname{GL}_{2}\times \operatorname{GL}_{2}$ and  $\unicode[STIX]{x1D712}((\unicode[STIX]{x1D706}_{1}I_{2},\unicode[STIX]{x1D706}_{2}I_{2})(g,g))=|\unicode[STIX]{x1D706}_{1}/\unicode[STIX]{x1D706}_{2}|\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}\det g)$. If
$\unicode[STIX]{x1D712}((\unicode[STIX]{x1D706}_{1}I_{2},\unicode[STIX]{x1D706}_{2}I_{2})(g,g))=|\unicode[STIX]{x1D706}_{1}/\unicode[STIX]{x1D706}_{2}|\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D706}_{2}\det g)$. If  $\unicode[STIX]{x1D70B}$ is supercuspidal, then the image is contained in
$\unicode[STIX]{x1D70B}$ is supercuspidal, then the image is contained in  $\operatorname{ind}_{(Z\times Z)\operatorname{GL}_{2}^{\operatorname{diag}}}^{\operatorname{GL}_{2}\times \operatorname{GL}_{2}}\unicode[STIX]{x1D712}$. If
$\operatorname{ind}_{(Z\times Z)\operatorname{GL}_{2}^{\operatorname{diag}}}^{\operatorname{GL}_{2}\times \operatorname{GL}_{2}}\unicode[STIX]{x1D712}$. If  $\unicode[STIX]{x1D70B}$ is (AT), then upon identifying
$\unicode[STIX]{x1D70B}$ is (AT), then upon identifying  $\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}$ with
$\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}$ with  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2})$ we may realize
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2})$ we may realize  $\unicode[STIX]{x1D6E5}$ as the convergent integral
$\unicode[STIX]{x1D6E5}$ as the convergent integral
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}(W)=\int _{F^{\ast }}W(\operatorname{diag}(1,-t,1,t))\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(t)^{-1}\,d^{\ast }t,\quad W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(W)=\int _{F^{\ast }}W(\operatorname{diag}(1,-t,1,t))\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(t)^{-1}\,d^{\ast }t,\quad W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}).\end{eqnarray}$$ It follows from the Schur orthogonality relations that if  $\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }\in \operatorname{Irr}_{\operatorname{cusp}}\operatorname{GL}_{2}$ with
$\unicode[STIX]{x1D70B},\unicode[STIX]{x1D70B}^{\prime }\in \operatorname{Irr}_{\operatorname{cusp}}\operatorname{GL}_{2}$ with  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}=1$, then
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}=1$, then  $\unicode[STIX]{x1D70B}^{\prime }$ is equivalent to
$\unicode[STIX]{x1D70B}^{\prime }$ is equivalent to  $\unicode[STIX]{x1D70B}^{\vee }$ if and only if
$\unicode[STIX]{x1D70B}^{\vee }$ if and only if
 $$\begin{eqnarray}\int _{Z\backslash \!\operatorname{GL}_{2}}\operatorname{MC}_{v}(g,1)\operatorname{MC}_{v^{\prime }}(g,1)\frac{dg}{|\det g|}\neq 0\end{eqnarray}$$
$$\begin{eqnarray}\int _{Z\backslash \!\operatorname{GL}_{2}}\operatorname{MC}_{v}(g,1)\operatorname{MC}_{v^{\prime }}(g,1)\frac{dg}{|\det g|}\neq 0\end{eqnarray}$$ for some  $v\in \unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}$,
$v\in \unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}$,  $v^{\prime }\in \unicode[STIX]{x1D70B}_{1/2}^{\prime }\otimes \unicode[STIX]{x1D70B}_{-1/2}^{\prime }$.
$v^{\prime }\in \unicode[STIX]{x1D70B}_{1/2}^{\prime }\otimes \unicode[STIX]{x1D70B}_{-1/2}^{\prime }$.
Recall that in the case at hand,  $Q=P^{\prime }=P^{w}$ where
$Q=P^{\prime }=P^{w}$ where  $w=\left(\begin{smallmatrix}1 & & & \\ & & 1 & \\ & 1 & & \\ & & & 1\!\end{smallmatrix}\right),$ and that
$w=\left(\begin{smallmatrix}1 & & & \\ & & 1 & \\ & 1 & & \\ & & & 1\!\end{smallmatrix}\right),$ and that  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}$ is the character of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}$ is the character of  ${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ whose restriction to
${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$ whose restriction to 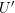 $U^{\prime }$ is
$U^{\prime }$ is  $\unicode[STIX]{x1D6F9}_{U^{\prime }}$ and whose composition with
$\unicode[STIX]{x1D6F9}_{U^{\prime }}$ and whose composition with  $\unicode[STIX]{x1D704}$ is
$\unicode[STIX]{x1D704}$ is  $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\circ \det$. Also,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\circ \det$. Also,  $\Vert \left(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\right)\Vert =\max (|a|,|b|,|c|,|d|)$.
$\Vert \left(\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\right)\Vert =\max (|a|,|b|,|c|,|d|)$.
Proposition 7.1. Suppose that  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{cusp}}\operatorname{GL}_{2}$. Then we have a short exact sequence of
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{cusp}}\operatorname{GL}_{2}$. Then we have a short exact sequence of  $Q$-modules
$Q$-modules
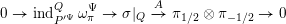 $$\begin{eqnarray}0\rightarrow \operatorname{ind}_{{P^{\prime }}^{\unicode[STIX]{x1D6F9}}}^{Q}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}\rightarrow \unicode[STIX]{x1D70E}|_{Q}\xrightarrow[{}]{A}\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \operatorname{ind}_{{P^{\prime }}^{\unicode[STIX]{x1D6F9}}}^{Q}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{\unicode[STIX]{x1D6F9}}\rightarrow \unicode[STIX]{x1D70E}|_{Q}\xrightarrow[{}]{A}\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}\rightarrow 0\end{eqnarray}$$ where  $Q$ acts on
$Q$ acts on  $\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}$ through
$\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2}$ through  $M^{\prime }$ (identified with
$M^{\prime }$ (identified with  $\operatorname{GL}_{2}\times \operatorname{GL}_{2}$ via
$\operatorname{GL}_{2}\times \operatorname{GL}_{2}$ via  $\unicode[STIX]{x1D705}$). Upon identifying
$\unicode[STIX]{x1D705}$). Upon identifying  $\unicode[STIX]{x1D70E}|_{Q}$ with
$\unicode[STIX]{x1D70E}|_{Q}$ with  ${\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$, the map
${\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$, the map  $A$ is characterized by the property that, for any
$A$ is characterized by the property that, for any  $L\in {\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$, there exists
$L\in {\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$, there exists  $c>0$ such that
$c>0$ such that

where  $\unicode[STIX]{x1D711}=A(L)$. Moreover,
$\unicode[STIX]{x1D711}=A(L)$. Moreover,

Proof. First note that property (29) determines  $\unicode[STIX]{x1D711}$ uniquely (if it exists). It then also follows that if (29) is satisfied, then
$\unicode[STIX]{x1D711}$ uniquely (if it exists). It then also follows that if (29) is satisfied, then  $A$ necessarily intertwines the
$A$ necessarily intertwines the  $Q$-action. Moreover, if (30) is satisfied, then
$Q$-action. Moreover, if (30) is satisfied, then  $\unicode[STIX]{x1D711}=0$ if and only if
$\unicode[STIX]{x1D711}=0$ if and only if  $L$ is compactly supported modulo
$L$ is compactly supported modulo  ${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$. Also note that in relation (29) it is enough to consider
${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$. Also note that in relation (29) it is enough to consider  $g_{2}=1$ since both sides are
$g_{2}=1$ since both sides are  $(\operatorname{GL}_{2}^{\operatorname{diag}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\circ \det )$-equivariant. (For simplicity write
$(\operatorname{GL}_{2}^{\operatorname{diag}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\circ \det )$-equivariant. (For simplicity write  $g=g_{1}$.)
$g=g_{1}$.)
Recall that, by Lemma 3.2, there exists a constant  $C_{1}>1$ such that
$C_{1}>1$ such that  $L(\unicode[STIX]{x1D705}(g,1))=0$ unless
$L(\unicode[STIX]{x1D705}(g,1))=0$ unless  $\Vert g\Vert \leqslant C_{1}$.
$\Vert g\Vert \leqslant C_{1}$.
Suppose that  $L={\mathcal{T}}(W_{\operatorname{Ze}})|_{Q}$. Write
$L={\mathcal{T}}(W_{\operatorname{Ze}})|_{Q}$. Write  $g=u^{\prime }(y)\operatorname{diag}(t_{1},t_{2})k$ where
$g=u^{\prime }(y)\operatorname{diag}(t_{1},t_{2})k$ where  $u^{\prime }(y)=\left(\begin{smallmatrix}1 & y\\ & 1\end{smallmatrix}\right)$ with
$u^{\prime }(y)=\left(\begin{smallmatrix}1 & y\\ & 1\end{smallmatrix}\right)$ with  $k\in \operatorname{GL}_{2}({\mathcal{O}})$. We claim that there exists
$k\in \operatorname{GL}_{2}({\mathcal{O}})$. We claim that there exists  $C_{3}$ such that
$C_{3}$ such that
 $$\begin{eqnarray}W_{\operatorname{Ze}}(\bar{u}(x)\unicode[STIX]{x1D705}(g,1))=|x|^{-1}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(x)W_{\operatorname{Ze}}(\operatorname{diag}(1,-x^{-1},1,x^{-1})\operatorname{diag}(g,I_{2})w)\end{eqnarray}$$
$$\begin{eqnarray}W_{\operatorname{Ze}}(\bar{u}(x)\unicode[STIX]{x1D705}(g,1))=|x|^{-1}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(x)W_{\operatorname{Ze}}(\operatorname{diag}(1,-x^{-1},1,x^{-1})\operatorname{diag}(g,I_{2})w)\end{eqnarray}$$ for all  $x\in F$ such that
$x\in F$ such that  $|x|>C_{3}|t_{2}|$.
$|x|>C_{3}|t_{2}|$.
Indeed, write
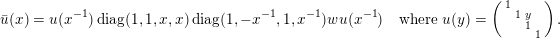 $$\begin{eqnarray}\bar{u}(x)=u(x^{-1})\operatorname{diag}(1,1,x,x)\operatorname{diag}(1,-x^{-1},1,x^{-1})wu(x^{-1})\quad \text{where }u(y)=\left(\begin{smallmatrix}1 & & & \\ & 1 & y & \\ & & 1 & \\ & & & 1\end{smallmatrix}\right).\end{eqnarray}$$
$$\begin{eqnarray}\bar{u}(x)=u(x^{-1})\operatorname{diag}(1,1,x,x)\operatorname{diag}(1,-x^{-1},1,x^{-1})wu(x^{-1})\quad \text{where }u(y)=\left(\begin{smallmatrix}1 & & & \\ & 1 & y & \\ & & 1 & \\ & & & 1\end{smallmatrix}\right).\end{eqnarray}$$Then
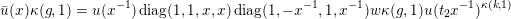 $$\begin{eqnarray}\bar{u}(x)\unicode[STIX]{x1D705}(g,1)=u(x^{-1})\operatorname{diag}(1,1,x,x)\operatorname{diag}(1,-x^{-1},1,x^{-1})w\unicode[STIX]{x1D705}(g,1)u(t_{2}x^{-1})^{\unicode[STIX]{x1D705}(k,1)}\end{eqnarray}$$
$$\begin{eqnarray}\bar{u}(x)\unicode[STIX]{x1D705}(g,1)=u(x^{-1})\operatorname{diag}(1,1,x,x)\operatorname{diag}(1,-x^{-1},1,x^{-1})w\unicode[STIX]{x1D705}(g,1)u(t_{2}x^{-1})^{\unicode[STIX]{x1D705}(k,1)}\end{eqnarray}$$ where the superscript denotes conjugation. Our claim follows since  $w\unicode[STIX]{x1D705}(g,1)w^{-1}=\operatorname{diag}(g,I_{2})$.
$w\unicode[STIX]{x1D705}(g,1)w^{-1}=\operatorname{diag}(g,I_{2})$.
Next, we show that there exists a compact set  $C$ of
$C$ of  $\operatorname{GL}_{2}(F)$ such that if
$\operatorname{GL}_{2}(F)$ such that if  $\Vert g\Vert \leqslant C_{1}$ and
$\Vert g\Vert \leqslant C_{1}$ and  $g\notin C$, then both sides of (31) vanish if
$g\notin C$, then both sides of (31) vanish if  $|x|\leqslant C_{3}|t_{2}|$.
$|x|\leqslant C_{3}|t_{2}|$.
First, note that the condition  $\Vert g\Vert \leqslant C_{1}$ means that
$\Vert g\Vert \leqslant C_{1}$ means that  $|t_{1}|,|t_{2}|,|t_{2}y|\leqslant C_{1}$. Now
$|t_{1}|,|t_{2}|,|t_{2}y|\leqslant C_{1}$. Now
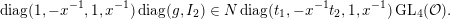 $$\begin{eqnarray}\operatorname{diag}(1,-x^{-1},1,x^{-1})\operatorname{diag}(g,I_{2})\in N\operatorname{diag}(t_{1},-x^{-1}t_{2},1,x^{-1})\operatorname{GL}_{4}({\mathcal{O}}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{diag}(1,-x^{-1},1,x^{-1})\operatorname{diag}(g,I_{2})\in N\operatorname{diag}(t_{1},-x^{-1}t_{2},1,x^{-1})\operatorname{GL}_{4}({\mathcal{O}}).\end{eqnarray}$$ Therefore, if the right-hand side of (31) is non-zero, then by the supercuspidality of  $\unicode[STIX]{x1D70B}$,
$\unicode[STIX]{x1D70B}$,  $x$ and
$x$ and  $t_{1}t_{2}^{-1}$ are confined to a compact subset of
$t_{1}t_{2}^{-1}$ are confined to a compact subset of  $F^{\ast }$. Since
$F^{\ast }$. Since  $|x|\leqslant C_{3}|t_{2}|$, we infer that
$|x|\leqslant C_{3}|t_{2}|$, we infer that  $t_{2}$ belongs to a compact set of
$t_{2}$ belongs to a compact set of  $F^{\ast }$, and hence also
$F^{\ast }$, and hence also  $t_{1}$. Finally,
$t_{1}$. Finally,  $|y|$ is bounded since
$|y|$ is bounded since  $|t_{2}y|\leqslant C_{1}$. Hence,
$|t_{2}y|\leqslant C_{1}$. Hence,  $g$ belongs to a compact set.
$g$ belongs to a compact set.
On the other hand,
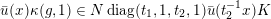 $$\begin{eqnarray}\bar{u}(x)\unicode[STIX]{x1D705}(g,1)\in N\operatorname{diag}(t_{1},1,t_{2},1)\bar{u}(t_{2}^{-1}x)K\end{eqnarray}$$
$$\begin{eqnarray}\bar{u}(x)\unicode[STIX]{x1D705}(g,1)\in N\operatorname{diag}(t_{1},1,t_{2},1)\bar{u}(t_{2}^{-1}x)K\end{eqnarray}$$ and since  $|t_{2}^{-1}x|\leqslant C_{3}$ we infer from the supercuspidality of
$|t_{2}^{-1}x|\leqslant C_{3}$ we infer from the supercuspidality of  $\unicode[STIX]{x1D70B}$ that if the left-hand side of (31) is non-zero, then
$\unicode[STIX]{x1D70B}$ that if the left-hand side of (31) is non-zero, then  $t_{1}$,
$t_{1}$,  $t_{2}$ belong to a compact subset of
$t_{2}$ belong to a compact subset of  $F^{\ast }$. As before,
$F^{\ast }$. As before,  $g$ belongs to a compact set. Our claim follows.
$g$ belongs to a compact set. Our claim follows.
In conclusion, (31) holds for all  $x\in F$ provided that
$x\in F$ provided that  $\Vert g\Vert \leqslant C_{1}$ and
$\Vert g\Vert \leqslant C_{1}$ and  $g\notin C$. Integrating (31) over
$g\notin C$. Integrating (31) over  $x\in F$, we conclude that if
$x\in F$, we conclude that if  $\Vert g\Vert \leqslant C_{1}$ and
$\Vert g\Vert \leqslant C_{1}$ and  $g\notin C$, then
$g\notin C$, then
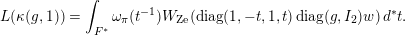 $$\begin{eqnarray}L(\unicode[STIX]{x1D705}(g,1))=\int _{F^{\ast }}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(t^{-1})W_{\operatorname{ Ze}}(\operatorname{diag}(1,-t,1,t)\operatorname{diag}(g,I_{2})w)\,d^{\ast }t.\end{eqnarray}$$
$$\begin{eqnarray}L(\unicode[STIX]{x1D705}(g,1))=\int _{F^{\ast }}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(t^{-1})W_{\operatorname{ Ze}}(\operatorname{diag}(1,-t,1,t)\operatorname{diag}(g,I_{2})w)\,d^{\ast }t.\end{eqnarray}$$ By (27), this is equal to  $\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)$ where
$\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)$ where  $\unicode[STIX]{x1D711}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2})$ is the restriction of
$\unicode[STIX]{x1D711}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}_{1/2}\otimes \unicode[STIX]{x1D70B}_{-1/2})$ is the restriction of  $W_{\operatorname{Ze}}(\cdot w)$ to
$W_{\operatorname{Ze}}(\cdot w)$ to  $M$. Thus, (29) and (30) hold. In view of Corollary 3.13, this proves the proposition. (Note that
$M$. Thus, (29) and (30) hold. In view of Corollary 3.13, this proves the proposition. (Note that  $W_{\operatorname{Ze}}\mapsto \unicode[STIX]{x1D711}$ is
$W_{\operatorname{Ze}}\mapsto \unicode[STIX]{x1D711}$ is  $Q$-equivariant since
$Q$-equivariant since  $w$ conjugates
$w$ conjugates  $P$ to
$P$ to  $Q$.)◻
$Q$.)◻
Remark 7.2. It follows from (the proof of) Proposition 7.1 that there exists a non-zero  $W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ that vanishes on
$W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ that vanishes on  $M$ (in which case
$M$ (in which case  ${\mathcal{T}}W_{\operatorname{Ze}}(\cdot w)|_{Q}\in {\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$ is compactly supported modulo
${\mathcal{T}}W_{\operatorname{Ze}}(\cdot w)|_{Q}\in {\mathcal{K}}^{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D70E})$ is compactly supported modulo  ${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$). This can be also shown directly by realizing
${P^{\prime }}^{\unicode[STIX]{x1D6F9}}$). This can be also shown directly by realizing  $\unicode[STIX]{x1D70E}$ as the image of the intertwining operator
$\unicode[STIX]{x1D70E}$ as the image of the intertwining operator
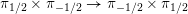 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1/2}\times \unicode[STIX]{x1D70B}_{-1/2}\rightarrow \unicode[STIX]{x1D70B}_{-1/2}\times \unicode[STIX]{x1D70B}_{1/2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{1/2}\times \unicode[STIX]{x1D70B}_{-1/2}\rightarrow \unicode[STIX]{x1D70B}_{-1/2}\times \unicode[STIX]{x1D70B}_{1/2}\end{eqnarray}$$ and taking the image of a suitable vector in  $\unicode[STIX]{x1D70B}_{1/2}\times \unicode[STIX]{x1D70B}_{-1/2}$ that is supported in the big cell.
$\unicode[STIX]{x1D70B}_{1/2}\times \unicode[STIX]{x1D70B}_{-1/2}$ that is supported in the big cell.
Corollary 7.3. Suppose that  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{cusp}}\operatorname{GL}_{2}$ and let
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{\operatorname{cusp}}\operatorname{GL}_{2}$ and let  $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$. Then the poles of the bilinear form
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}^{\vee }$. Then the poles of the bilinear form  ${\mathcal{B}}_{i}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s)$, as we vary
${\mathcal{B}}_{i}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },s)$, as we vary  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ and
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\unicode[STIX]{x1D70E})$ and  $W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$, coincide with those of
$W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\unicode[STIX]{x1D70E}^{\prime })$, coincide with those of  $L(s+1,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee })$.
$L(s+1,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee })$.
Proof. We may assume without loss of generality that  $\unicode[STIX]{x1D70B}$ is unitary. Then
$\unicode[STIX]{x1D70B}$ is unitary. Then
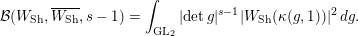 $$\begin{eqnarray}{\mathcal{B}}(W_{\operatorname{Sh}},\overline{W_{\operatorname{Sh}}},s-1)=\int _{\operatorname{GL}_{2}}|\det g|^{s-1}|W_{\operatorname{ Sh}}(\unicode[STIX]{x1D705}(g,1))|^{2}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}(W_{\operatorname{Sh}},\overline{W_{\operatorname{Sh}}},s-1)=\int _{\operatorname{GL}_{2}}|\det g|^{s-1}|W_{\operatorname{ Sh}}(\unicode[STIX]{x1D705}(g,1))|^{2}\,dg.\end{eqnarray}$$By Proposition 7.1, the analytic properties are governed by those of
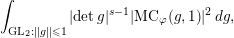 $$\begin{eqnarray}\int _{\operatorname{GL}_{2}:\Vert g\Vert \leqslant 1}|\det g|^{s-1}|\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)|^{2}\,dg,\end{eqnarray}$$
$$\begin{eqnarray}\int _{\operatorname{GL}_{2}:\Vert g\Vert \leqslant 1}|\det g|^{s-1}|\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)|^{2}\,dg,\end{eqnarray}$$which can be written as
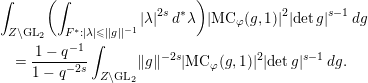 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Z\backslash \!\operatorname{GL}_{2}}\biggl(\int _{F^{\ast }:|\unicode[STIX]{x1D706}|\leqslant \Vert g\Vert ^{-1}}|\unicode[STIX]{x1D706}|^{2s}\,d^{\ast }\unicode[STIX]{x1D706}\biggr)|\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)|^{2}|\det g|^{s-1}\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1-q^{-1}}{1-q^{-2s}}\int _{Z\backslash \!\operatorname{GL}_{2}}\Vert g\Vert ^{-2s}|\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)|^{2}|\det g|^{s-1}\,dg.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{Z\backslash \!\operatorname{GL}_{2}}\biggl(\int _{F^{\ast }:|\unicode[STIX]{x1D706}|\leqslant \Vert g\Vert ^{-1}}|\unicode[STIX]{x1D706}|^{2s}\,d^{\ast }\unicode[STIX]{x1D706}\biggr)|\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)|^{2}|\det g|^{s-1}\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1-q^{-1}}{1-q^{-2s}}\int _{Z\backslash \!\operatorname{GL}_{2}}\Vert g\Vert ^{-2s}|\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)|^{2}|\det g|^{s-1}\,dg.\nonumber\end{eqnarray}$$ Thus, the poles are simple and are confined to  $q^{2s}=1$. If
$q^{2s}=1$. If  $q^{s}=1$, then the residue is clearly non-zero. If
$q^{s}=1$, then the residue is clearly non-zero. If  $q^{s}=-1$, then the residue is a constant multiple of
$q^{s}=-1$, then the residue is a constant multiple of
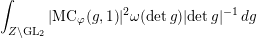 $$\begin{eqnarray}\int _{Z\backslash \!\operatorname{GL}_{2}}|\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)|^{2}\unicode[STIX]{x1D714}(\det g)|\det g|^{-1}\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{Z\backslash \!\operatorname{GL}_{2}}|\operatorname{MC}_{\unicode[STIX]{x1D711}}(g,1)|^{2}\unicode[STIX]{x1D714}(\det g)|\det g|^{-1}\,dg\end{eqnarray}$$ where  $\unicode[STIX]{x1D714}$ is the non-trivial quadratic unramified character of
$\unicode[STIX]{x1D714}$ is the non-trivial quadratic unramified character of  $F^{\ast }$. Thus, by (28), the residue is non-zero if and only if
$F^{\ast }$. Thus, by (28), the residue is non-zero if and only if  $\unicode[STIX]{x1D70B}\simeq \unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}$. This matches exactly with the poles of
$\unicode[STIX]{x1D70B}\simeq \unicode[STIX]{x1D70B}\unicode[STIX]{x1D714}$. This matches exactly with the poles of  $L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee })$ [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83, Proposition 8.1].◻
$L(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee })$ [Reference Jacquet, Piatetskii-Shapiro and ShalikaJPSS83, Proposition 8.1].◻
8 Global heuristics
Let  $F$ be a number field with ring of adeles
$F$ be a number field with ring of adeles  $\mathbb{A}$. We consider
$\mathbb{A}$. We consider  $G=\operatorname{GL}_{nm}$ as a group over
$G=\operatorname{GL}_{nm}$ as a group over  $F$ and write
$F$ and write  $G(\mathbb{A})^{1}=\{g\in G(\mathbb{A}):|\det g|=1\}$. As before, let
$G(\mathbb{A})^{1}=\{g\in G(\mathbb{A}):|\det g|=1\}$. As before, let  $Q$ be the stabilizer of
$Q$ be the stabilizer of  $\operatorname{span}\{e_{ni}:i=1,\ldots ,m\}$ in
$\operatorname{span}\{e_{ni}:i=1,\ldots ,m\}$ in  $G$ – a maximal non-standard parabolic subgroup of
$G$ – a maximal non-standard parabolic subgroup of  $G$ of type
$G$ of type  $((n-1)m,m)$. For any
$((n-1)m,m)$. For any  $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(\mathbb{A}))$ and a Hecke character
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\operatorname{Mat}_{m,nm}(\mathbb{A}))$ and a Hecke character  $\unicode[STIX]{x1D714}$ of
$\unicode[STIX]{x1D714}$ of  $F^{\ast }\backslash \mathbb{A}^{\ast }$, consider the degenerate normalized Eisenstein series that is given by
$F^{\ast }\backslash \mathbb{A}^{\ast }$, consider the degenerate normalized Eisenstein series that is given by
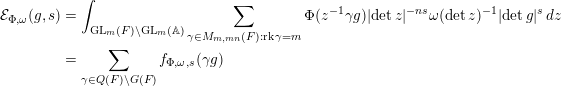 $$\begin{eqnarray}\displaystyle {\mathcal{E}}_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}}(g,s) & = & \displaystyle \int _{\operatorname{GL}_{m}(F)\backslash \!\operatorname{GL}_{m}(\mathbb{A})}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in M_{m,mn}(F):\operatorname{rk}\unicode[STIX]{x1D6FE}=m}\unicode[STIX]{x1D6F7}(z^{-1}\unicode[STIX]{x1D6FE}g)|\det z|^{-ns}\unicode[STIX]{x1D714}(\det z)^{-1}|\det g|^{s}\,dz\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in Q(F)\backslash G(F)}f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(\unicode[STIX]{x1D6FE}g)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}}(g,s) & = & \displaystyle \int _{\operatorname{GL}_{m}(F)\backslash \!\operatorname{GL}_{m}(\mathbb{A})}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in M_{m,mn}(F):\operatorname{rk}\unicode[STIX]{x1D6FE}=m}\unicode[STIX]{x1D6F7}(z^{-1}\unicode[STIX]{x1D6FE}g)|\det z|^{-ns}\unicode[STIX]{x1D714}(\det z)^{-1}|\det g|^{s}\,dz\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in Q(F)\backslash G(F)}f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(\unicode[STIX]{x1D6FE}g)\nonumber\end{eqnarray}$$ for  $\operatorname{Re}s\gg 0$ (more precisely,
$\operatorname{Re}s\gg 0$ (more precisely,  $\operatorname{Re}s>m$ if
$\operatorname{Re}s>m$ if  $\unicode[STIX]{x1D714}$ is unitary) where, as in § 6.1,
$\unicode[STIX]{x1D714}$ is unitary) where, as in § 6.1,
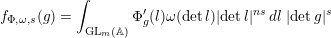 $$\begin{eqnarray}f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)=\int _{\operatorname{GL}_{m}(\mathbb{A})}\unicode[STIX]{x1D6F7}_{g}^{\prime }(l)\unicode[STIX]{x1D714}(\det l)|\det l|^{ns}\,dl~|\det g|^{s}\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)=\int _{\operatorname{GL}_{m}(\mathbb{A})}\unicode[STIX]{x1D6F7}_{g}^{\prime }(l)\unicode[STIX]{x1D714}(\det l)|\det l|^{ns}\,dl~|\det g|^{s}\end{eqnarray}$$ and  $\unicode[STIX]{x1D6F7}_{g}^{\prime }\in {\mathcal{S}}(\operatorname{Mat}_{m,m}(\mathbb{A}))$ is given by
$\unicode[STIX]{x1D6F7}_{g}^{\prime }\in {\mathcal{S}}(\operatorname{Mat}_{m,m}(\mathbb{A}))$ is given by  $\unicode[STIX]{x1D6F7}_{g}^{\prime }(X)=\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}(X)g)$, where
$\unicode[STIX]{x1D6F7}_{g}^{\prime }(X)=\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D707}(X)g)$, where  $\unicode[STIX]{x1D707}(X)\in \operatorname{Mat}_{m,nm}(\mathbb{A})$ is the matrix whose
$\unicode[STIX]{x1D707}(X)\in \operatorname{Mat}_{m,nm}(\mathbb{A})$ is the matrix whose  $i$th row is
$i$th row is  $\sum _{j=1}^{m}X_{i,j}e_{nj}$. By the method of Tate’s thesis (which goes back to Riemann),
$\sum _{j=1}^{m}X_{i,j}e_{nj}$. By the method of Tate’s thesis (which goes back to Riemann),  ${\mathcal{E}}_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}}$ admits a meromorphic continuation with finitely many (simple) poles and a functional equation
${\mathcal{E}}_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}}$ admits a meromorphic continuation with finitely many (simple) poles and a functional equation
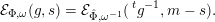 $$\begin{eqnarray}{\mathcal{E}}_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}}(g,s)={\mathcal{E}}_{\hat{\unicode[STIX]{x1D6F7}},\unicode[STIX]{x1D714}^{-1}}(\,^{t}g^{-1},m-s).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}}(g,s)={\mathcal{E}}_{\hat{\unicode[STIX]{x1D6F7}},\unicode[STIX]{x1D714}^{-1}}(\,^{t}g^{-1},m-s).\end{eqnarray}$$ As before, let  $P=M\ltimes U$ be the standard maximal parabolic subgroup of
$P=M\ltimes U$ be the standard maximal parabolic subgroup of  $G$ of type
$G$ of type  $(\overbrace{n,\ldots ,n}^{m})$ and let
$(\overbrace{n,\ldots ,n}^{m})$ and let  $|\cdot |_{M}:M(\mathbb{A})\rightarrow \mathbb{R}_{{>}0}^{m}$ be the homomorphism
$|\cdot |_{M}:M(\mathbb{A})\rightarrow \mathbb{R}_{{>}0}^{m}$ be the homomorphism
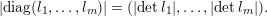 $$\begin{eqnarray}|\operatorname{diag}(l_{1},\ldots ,l_{m})|=(|\det l_{1}|,\ldots ,|\det l_{m}|).\end{eqnarray}$$
$$\begin{eqnarray}|\operatorname{diag}(l_{1},\ldots ,l_{m})|=(|\det l_{1}|,\ldots ,|\det l_{m}|).\end{eqnarray}$$ We extend  $|\cdot |_{M}$ to a left-
$|\cdot |_{M}$ to a left- $U(\mathbb{A})$- and right-
$U(\mathbb{A})$- and right- $K$-invariant function
$K$-invariant function  $|\cdot |_{P}$ on
$|\cdot |_{P}$ on  $G(\mathbb{A})$ where
$G(\mathbb{A})$ where  $K$ is the standard maximal compact subgroup of
$K$ is the standard maximal compact subgroup of  $G(\mathbb{A})$. For any
$G(\mathbb{A})$. For any  $x=(x_{1},\ldots ,x_{m})\in \mathbb{R}_{{>}0}^{m}$ and
$x=(x_{1},\ldots ,x_{m})\in \mathbb{R}_{{>}0}^{m}$ and  $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})\in \mathbb{C}^{m}$, we write
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{m})\in \mathbb{C}^{m}$, we write  $x^{\unicode[STIX]{x1D706}}=\prod _{i}x_{i}^{\unicode[STIX]{x1D706}_{i}}$.
$x^{\unicode[STIX]{x1D706}}=\prod _{i}x_{i}^{\unicode[STIX]{x1D706}_{i}}$.
Let  $\unicode[STIX]{x1D70B}=\otimes \unicode[STIX]{x1D70B}_{v}$ be an irreducible cuspidal representation of
$\unicode[STIX]{x1D70B}=\otimes \unicode[STIX]{x1D70B}_{v}$ be an irreducible cuspidal representation of  $\operatorname{GL}_{n}(\mathbb{A})$. Let
$\operatorname{GL}_{n}(\mathbb{A})$. Let  $\unicode[STIX]{x1D719}:G(\mathbb{A})\rightarrow \mathbb{C}$ be a smooth function such that, for all
$\unicode[STIX]{x1D719}:G(\mathbb{A})\rightarrow \mathbb{C}$ be a smooth function such that, for all  $g\in G(\mathbb{A})$, the function
$g\in G(\mathbb{A})$, the function  $l\in M(\mathbb{A})\mapsto \unicode[STIX]{x1D6FF}_{P}(l)^{-1/2}\unicode[STIX]{x1D719}(lg)$ belongs to the space of
$l\in M(\mathbb{A})\mapsto \unicode[STIX]{x1D6FF}_{P}(l)^{-1/2}\unicode[STIX]{x1D719}(lg)$ belongs to the space of  $\overbrace{\unicode[STIX]{x1D70B}\otimes \cdots \otimes \unicode[STIX]{x1D70B}}^{m}$. The Eisenstein series
$\overbrace{\unicode[STIX]{x1D70B}\otimes \cdots \otimes \unicode[STIX]{x1D70B}}^{m}$. The Eisenstein series
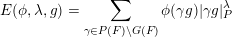 $$\begin{eqnarray}E(\unicode[STIX]{x1D719},\unicode[STIX]{x1D706},g)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(F)\backslash G(F)}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE}g)|\unicode[STIX]{x1D6FE}g|_{P}^{\unicode[STIX]{x1D706}}\end{eqnarray}$$
$$\begin{eqnarray}E(\unicode[STIX]{x1D719},\unicode[STIX]{x1D706},g)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(F)\backslash G(F)}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FE}g)|\unicode[STIX]{x1D6FE}g|_{P}^{\unicode[STIX]{x1D706}}\end{eqnarray}$$ converges if  $\operatorname{Re}(\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1})>n$ for all
$\operatorname{Re}(\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1})>n$ for all  $i=1,\ldots ,m-1$ and admits a meromorphic continuation to
$i=1,\ldots ,m-1$ and admits a meromorphic continuation to  $\mathbb{C}^{m}$. The limit
$\mathbb{C}^{m}$. The limit
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(g)=\lim _{\unicode[STIX]{x1D706}\rightarrow ((m-1)/2,\ldots ,(1-m)/2)}(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}-1)\cdots (\unicode[STIX]{x1D706}_{m-1}-\unicode[STIX]{x1D706}_{m}-1)E(\unicode[STIX]{x1D719},\unicode[STIX]{x1D706},g)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(g)=\lim _{\unicode[STIX]{x1D706}\rightarrow ((m-1)/2,\ldots ,(1-m)/2)}(\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}-1)\cdots (\unicode[STIX]{x1D706}_{m-1}-\unicode[STIX]{x1D706}_{m}-1)E(\unicode[STIX]{x1D719},\unicode[STIX]{x1D706},g)\end{eqnarray}$$ exists and is a square-integrable automorphic form on  $G(F)\backslash G(\mathbb{A})^{1}$ which is non-zero for a suitable
$G(F)\backslash G(\mathbb{A})^{1}$ which is non-zero for a suitable  $\unicode[STIX]{x1D719}$. As we vary
$\unicode[STIX]{x1D719}$. As we vary  $\unicode[STIX]{x1D719}$, we obtain an irreducible automorphic representation of
$\unicode[STIX]{x1D719}$, we obtain an irreducible automorphic representation of  $G(\mathbb{A})$ whose local components are
$G(\mathbb{A})$ whose local components are  $\operatorname{Sp}(\unicode[STIX]{x1D70B}_{v},m)$. (It is well known that as we vary over
$\operatorname{Sp}(\unicode[STIX]{x1D70B}_{v},m)$. (It is well known that as we vary over  $\unicode[STIX]{x1D70B}$ and
$\unicode[STIX]{x1D70B}$ and  $m\geqslant 1$, these representations furnish the entire automorphic discrete spectrum of the general linear group [Reference Mœglin and WaldspurgerMW89].) Similarly, let
$m\geqslant 1$, these representations furnish the entire automorphic discrete spectrum of the general linear group [Reference Mœglin and WaldspurgerMW89].) Similarly, let  $\unicode[STIX]{x1D70B}^{\prime }$ be another irreducible cuspidal representation of
$\unicode[STIX]{x1D70B}^{\prime }$ be another irreducible cuspidal representation of  $\operatorname{GL}_{n}(\mathbb{A})$ and let
$\operatorname{GL}_{n}(\mathbb{A})$ and let  $\unicode[STIX]{x1D719}^{\prime }$ and
$\unicode[STIX]{x1D719}^{\prime }$ and  $\unicode[STIX]{x1D711}^{\prime }$ be analogous functions with respect to
$\unicode[STIX]{x1D711}^{\prime }$ be analogous functions with respect to  $\unicode[STIX]{x1D70B}^{\prime }$.
$\unicode[STIX]{x1D70B}^{\prime }$.
Formally, we would have liked to consider the integral
 $$\begin{eqnarray}\int _{G(F)\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D711}^{\prime }(g){\mathcal{E}}_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}}(g,s)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{G(F)\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D711}^{\prime }(g){\mathcal{E}}_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714}}(g,s)\,dg\end{eqnarray}$$ where  $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}$. For
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{\prime }}$. For  $m=1$, this is of course the classical Rankin–Selberg integral. Unfortunately, for
$m=1$, this is of course the classical Rankin–Selberg integral. Unfortunately, for  $m>1$ this integral does not converge as none of the functions that appear in the integrand is rapidly decreasing. A suitable regularization (in the spirit of [Reference ZagierZag81] or later accounts) is therefore needed in order to make sense of (33). We will not pursue this matter here. Instead, we will be content with a purely heuristic argument, anticipating what a possible regularization of (33) would yield.
$m>1$ this integral does not converge as none of the functions that appear in the integrand is rapidly decreasing. A suitable regularization (in the spirit of [Reference ZagierZag81] or later accounts) is therefore needed in order to make sense of (33). We will not pursue this matter here. Instead, we will be content with a purely heuristic argument, anticipating what a possible regularization of (33) would yield.
As in the case  $m=1$, we unfold (formally) expression (33). For any
$m=1$, we unfold (formally) expression (33). For any  $i=1,\ldots ,m$, let
$i=1,\ldots ,m$, let  $Q_{i}=L_{i}\ltimes V_{i}$ be the stabilizer of the flag
$Q_{i}=L_{i}\ltimes V_{i}$ be the stabilizer of the flag
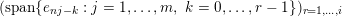 $$\begin{eqnarray}(\operatorname{span}\{e_{nj-k}:j=1,\ldots ,m,~k=0,\ldots ,r-1\})_{r=1,\ldots ,i}\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{span}\{e_{nj-k}:j=1,\ldots ,m,~k=0,\ldots ,r-1\})_{r=1,\ldots ,i}\end{eqnarray}$$ in  $G$. Thus,
$G$. Thus,  $Q_{1}=Q\supset Q_{2}\supset \cdots \supset Q_{n-1}=Q_{n}=P^{\prime }$ and
$Q_{1}=Q\supset Q_{2}\supset \cdots \supset Q_{n-1}=Q_{n}=P^{\prime }$ and  $L_{i}\simeq \operatorname{GL}_{m(n-i)}\times \,L_{i}^{\prime }$ with
$L_{i}\simeq \operatorname{GL}_{m(n-i)}\times \,L_{i}^{\prime }$ with  $L_{i}^{\prime }\simeq \overbrace{\operatorname{GL}_{m}\times \cdots \times \operatorname{GL}_{m}}^{i}$. Let
$L_{i}^{\prime }\simeq \overbrace{\operatorname{GL}_{m}\times \cdots \times \operatorname{GL}_{m}}^{i}$. Let  $p_{i}:Q_{i}\rightarrow L_{i}^{\prime }$ be the resulting projection and let
$p_{i}:Q_{i}\rightarrow L_{i}^{\prime }$ be the resulting projection and let  $Q_{i}^{\prime }$ be the inverse image of
$Q_{i}^{\prime }$ be the inverse image of  $\operatorname{GL}_{m}$ diagonally embedded in
$\operatorname{GL}_{m}$ diagonally embedded in  $L_{i}^{\prime }$. In particular,
$L_{i}^{\prime }$. In particular,  $Q_{1}^{\prime }=Q_{1}=Q$ and
$Q_{1}^{\prime }=Q_{1}=Q$ and  $Q_{n}^{\prime }={M^{\prime }}^{\unicode[STIX]{x1D6F9}}\ltimes U^{\prime }$. Note that, for all
$Q_{n}^{\prime }={M^{\prime }}^{\unicode[STIX]{x1D6F9}}\ltimes U^{\prime }$. Note that, for all  $i=1,\ldots ,n-1$,
$i=1,\ldots ,n-1$,  $Q_{i+1}^{\prime }$ is the stabilizer in
$Q_{i+1}^{\prime }$ is the stabilizer in  $Q_{i}$ of the character
$Q_{i}$ of the character  $\unicode[STIX]{x1D6F9}_{V_{i}}$ and
$\unicode[STIX]{x1D6F9}_{V_{i}}$ and  $V_{i}/V_{i-1}$ is abelian (and can be identified with
$V_{i}/V_{i-1}$ is abelian (and can be identified with  $\operatorname{Mat}_{m,(n-i)m}$), where for consistency we let
$\operatorname{Mat}_{m,(n-i)m}$), where for consistency we let  $V_{0}=0$.
$V_{0}=0$.
In the first step we unfold (33) to write it as
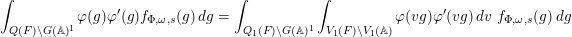 $$\begin{eqnarray}\int _{Q(F)\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D711}^{\prime }(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg=\int _{Q_{1}(F)\backslash G(\mathbb{A})^{1}}\int _{V_{1}(F)\backslash V_{1}(\mathbb{A})}\unicode[STIX]{x1D711}(vg)\unicode[STIX]{x1D711}^{\prime }(vg)\,dv~f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{Q(F)\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D711}^{\prime }(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg=\int _{Q_{1}(F)\backslash G(\mathbb{A})^{1}}\int _{V_{1}(F)\backslash V_{1}(\mathbb{A})}\unicode[STIX]{x1D711}(vg)\unicode[STIX]{x1D711}^{\prime }(vg)\,dv~f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg\end{eqnarray}$$and expand
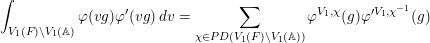 $$\begin{eqnarray}\int _{V_{1}(F)\backslash V_{1}(\mathbb{A})}\unicode[STIX]{x1D711}(vg)\unicode[STIX]{x1D711}^{\prime }(vg)\,dv=\mathop{\sum }_{\unicode[STIX]{x1D712}\in PD(V_{1}(F)\backslash V_{1}(\mathbb{A}))}\unicode[STIX]{x1D711}^{V_{1},\unicode[STIX]{x1D712}}(g){\unicode[STIX]{x1D711}^{\prime }}^{V_{1},\unicode[STIX]{x1D712}^{-1}}(g)\end{eqnarray}$$
$$\begin{eqnarray}\int _{V_{1}(F)\backslash V_{1}(\mathbb{A})}\unicode[STIX]{x1D711}(vg)\unicode[STIX]{x1D711}^{\prime }(vg)\,dv=\mathop{\sum }_{\unicode[STIX]{x1D712}\in PD(V_{1}(F)\backslash V_{1}(\mathbb{A}))}\unicode[STIX]{x1D711}^{V_{1},\unicode[STIX]{x1D712}}(g){\unicode[STIX]{x1D711}^{\prime }}^{V_{1},\unicode[STIX]{x1D712}^{-1}}(g)\end{eqnarray}$$where
 $$\begin{eqnarray}\unicode[STIX]{x1D711}^{V_{1},\unicode[STIX]{x1D712}}(g)=\int _{V_{1}(F)\backslash V_{1}(\mathbb{A})}\unicode[STIX]{x1D711}(vg)\unicode[STIX]{x1D712}(v)^{-1}\,dv.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}^{V_{1},\unicode[STIX]{x1D712}}(g)=\int _{V_{1}(F)\backslash V_{1}(\mathbb{A})}\unicode[STIX]{x1D711}(vg)\unicode[STIX]{x1D712}(v)^{-1}\,dv.\end{eqnarray}$$ The Pontryagin dual of the compact abelian group  $V_{1}(F)\backslash V_{1}(\mathbb{A})$ is isomorphic to
$V_{1}(F)\backslash V_{1}(\mathbb{A})$ is isomorphic to  $\operatorname{Mat}_{m,(n-1)m}(F)$. We consider only the contribution from the non-degenerate
$\operatorname{Mat}_{m,(n-1)m}(F)$. We consider only the contribution from the non-degenerate  $\unicode[STIX]{x1D712}$, that is, those corresponding to matrices of rank
$\unicode[STIX]{x1D712}$, that is, those corresponding to matrices of rank  $m$ (anticipating that the degenerate ones will not contribute, either by the cuspidality of
$m$ (anticipating that the degenerate ones will not contribute, either by the cuspidality of  $\unicode[STIX]{x1D70B}$ or by the regularization procedure itself). The non-degenerate characters form a single orbit under
$\unicode[STIX]{x1D70B}$ or by the regularization procedure itself). The non-degenerate characters form a single orbit under  $Q=Q_{1}$, namely the orbit of
$Q=Q_{1}$, namely the orbit of  $\unicode[STIX]{x1D6F9}_{V_{1}}$, and the stabilizer of
$\unicode[STIX]{x1D6F9}_{V_{1}}$, and the stabilizer of  $\unicode[STIX]{x1D6F9}_{V_{1}}$ is
$\unicode[STIX]{x1D6F9}_{V_{1}}$ is  $Q_{2}^{\prime }$. We thus get
$Q_{2}^{\prime }$. We thus get
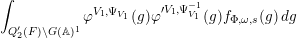 $$\begin{eqnarray}\int _{Q_{2}^{\prime }(F)\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}^{V_{1},\unicode[STIX]{x1D6F9}_{V_{1}}}(g){\unicode[STIX]{x1D711}^{\prime }}^{V_{1},\unicode[STIX]{x1D6F9}_{V_{1}}^{-1}}(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{Q_{2}^{\prime }(F)\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}^{V_{1},\unicode[STIX]{x1D6F9}_{V_{1}}}(g){\unicode[STIX]{x1D711}^{\prime }}^{V_{1},\unicode[STIX]{x1D6F9}_{V_{1}}^{-1}}(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg\end{eqnarray}$$which we write as
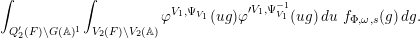 $$\begin{eqnarray}\int _{Q_{2}^{\prime }(F)\backslash G(\mathbb{A})^{1}}\int _{V_{2}(F)\backslash V_{2}(\mathbb{A})}\unicode[STIX]{x1D711}^{V_{1},\unicode[STIX]{x1D6F9}_{V_{1}}}(ug){\unicode[STIX]{x1D711}^{\prime }}^{V_{1},\unicode[STIX]{x1D6F9}_{V_{1}}^{-1}}(ug)\,du~f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{Q_{2}^{\prime }(F)\backslash G(\mathbb{A})^{1}}\int _{V_{2}(F)\backslash V_{2}(\mathbb{A})}\unicode[STIX]{x1D711}^{V_{1},\unicode[STIX]{x1D6F9}_{V_{1}}}(ug){\unicode[STIX]{x1D711}^{\prime }}^{V_{1},\unicode[STIX]{x1D6F9}_{V_{1}}^{-1}}(ug)\,du~f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg.\end{eqnarray}$$ Once again, we expand the inner integral according to characters of the compact abelian group  $V_{2}(\mathbb{A})/V_{1}(\mathbb{A})V_{2}(F)$ and consider only the non-degenerate characters. Continuing in this way, we get, for
$V_{2}(\mathbb{A})/V_{1}(\mathbb{A})V_{2}(F)$ and consider only the non-degenerate characters. Continuing in this way, we get, for  $k=1,\ldots ,n$,
$k=1,\ldots ,n$,
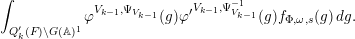 $$\begin{eqnarray}\int _{Q_{k}^{\prime }(F)\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}^{V_{k-1},\unicode[STIX]{x1D6F9}_{V_{k-1}}}(g){\unicode[STIX]{x1D711}^{\prime }}^{V_{k-1},\unicode[STIX]{x1D6F9}_{V_{k-1}}^{-1}}(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{Q_{k}^{\prime }(F)\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}^{V_{k-1},\unicode[STIX]{x1D6F9}_{V_{k-1}}}(g){\unicode[STIX]{x1D711}^{\prime }}^{V_{k-1},\unicode[STIX]{x1D6F9}_{V_{k-1}}^{-1}}(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg.\end{eqnarray}$$ For  $k=n$, we obtain
$k=n$, we obtain
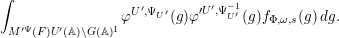 $$\begin{eqnarray}\int _{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}(F)U^{\prime }(\mathbb{A})\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}}(g){\unicode[STIX]{x1D711}^{\prime }}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}(F)U^{\prime }(\mathbb{A})\backslash G(\mathbb{A})^{1}}\unicode[STIX]{x1D711}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}}(g){\unicode[STIX]{x1D711}^{\prime }}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg.\end{eqnarray}$$ Now  $\unicode[STIX]{x1D711}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}}$ is
$\unicode[STIX]{x1D711}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}}$ is  $({M^{\prime }}^{\unicode[STIX]{x1D6F9}}(\mathbb{A}),\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\circ \det )$-equivariant (taking into account the identification
$({M^{\prime }}^{\unicode[STIX]{x1D6F9}}(\mathbb{A}),\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\circ \det )$-equivariant (taking into account the identification  $\unicode[STIX]{x1D704}:\operatorname{GL}_{m}\rightarrow {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$). Therefore, up to a volume factor, we get
$\unicode[STIX]{x1D704}:\operatorname{GL}_{m}\rightarrow {M^{\prime }}^{\unicode[STIX]{x1D6F9}}$). Therefore, up to a volume factor, we get
 $$\begin{eqnarray}\int _{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}(\mathbb{A})U^{\prime }(\mathbb{A})\backslash G(\mathbb{A})}\unicode[STIX]{x1D711}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}}(g){\unicode[STIX]{x1D711}^{\prime }}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\int _{{M^{\prime }}^{\unicode[STIX]{x1D6F9}}(\mathbb{A})U^{\prime }(\mathbb{A})\backslash G(\mathbb{A})}\unicode[STIX]{x1D711}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}}(g){\unicode[STIX]{x1D711}^{\prime }}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(g)f_{\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D714},s}(g)\,dg.\end{eqnarray}$$ This integral (which actually converges for  $\operatorname{Re}s>m$ if
$\operatorname{Re}s>m$ if  $\unicode[STIX]{x1D714}$ is unitary) is Eulerian. Let
$\unicode[STIX]{x1D714}$ is unitary) is Eulerian. Let  $S$ be a finite set of places of
$S$ be a finite set of places of  $F$ containing all the archimedean ones such that, for all
$F$ containing all the archimedean ones such that, for all  $v\notin S$,
$v\notin S$,  $\unicode[STIX]{x1D711}$ and
$\unicode[STIX]{x1D711}$ and  $\unicode[STIX]{x1D711}^{\prime }$ are
$\unicode[STIX]{x1D711}^{\prime }$ are  $G({\mathcal{O}}_{v})$-invariant (and, in particular,
$G({\mathcal{O}}_{v})$-invariant (and, in particular,  $\unicode[STIX]{x1D70B}_{v}$ and
$\unicode[STIX]{x1D70B}_{v}$ and  $\unicode[STIX]{x1D70B}_{v}^{\prime }$ are unramified),
$\unicode[STIX]{x1D70B}_{v}^{\prime }$ are unramified),  $\unicode[STIX]{x1D713}_{v}$ has conductor
$\unicode[STIX]{x1D713}_{v}$ has conductor  ${\mathcal{O}}_{v}$,
${\mathcal{O}}_{v}$,  $\unicode[STIX]{x1D6F7}$ is invariant under translation by
$\unicode[STIX]{x1D6F7}$ is invariant under translation by  $\operatorname{Mat}_{m,mn}({\mathcal{O}}_{v})$ and
$\operatorname{Mat}_{m,mn}({\mathcal{O}}_{v})$ and  $\unicode[STIX]{x1D6F7}(X)=0$ unless
$\unicode[STIX]{x1D6F7}(X)=0$ unless  $X_{v}\in \operatorname{Mat}_{m,mn}({\mathcal{O}}_{v})$. Using (26) and Theorem 5.1 part (iii), up to a measure-theoretic constant, the integral (34) is equal to
$X_{v}\in \operatorname{Mat}_{m,mn}({\mathcal{O}}_{v})$. Using (26) and Theorem 5.1 part (iii), up to a measure-theoretic constant, the integral (34) is equal to
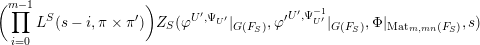 $$\begin{eqnarray}\biggl(\mathop{\prod }_{i=0}^{m-1}L^{S}(s-i,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })\biggr)Z_{S}(\unicode[STIX]{x1D711}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}}|_{G(F_{S})},{\unicode[STIX]{x1D711}^{\prime }}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}|_{G(F_{S})},\unicode[STIX]{x1D6F7}|_{\operatorname{Mat}_{m,mn}(F_{S})},s)\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\mathop{\prod }_{i=0}^{m-1}L^{S}(s-i,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })\biggr)Z_{S}(\unicode[STIX]{x1D711}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}}|_{G(F_{S})},{\unicode[STIX]{x1D711}^{\prime }}^{U^{\prime },\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}|_{G(F_{S})},\unicode[STIX]{x1D6F7}|_{\operatorname{Mat}_{m,mn}(F_{S})},s)\end{eqnarray}$$ where  $L^{S}(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })$ is the partial Rankin–Selberg
$L^{S}(s,\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\prime })$ is the partial Rankin–Selberg  $L$-function and, for any
$L$-function and, for any  $W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\operatorname{Sp}(\unicode[STIX]{x1D70B}_{S},m))$ and
$W_{\operatorname{Sh}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}}(\operatorname{Sp}(\unicode[STIX]{x1D70B}_{S},m))$ and  $W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\operatorname{Sp}(\unicode[STIX]{x1D70B}_{S}^{\prime },m))$,
$W_{\operatorname{Sh}}^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U^{\prime }}^{-1}}(\operatorname{Sp}(\unicode[STIX]{x1D70B}_{S}^{\prime },m))$,
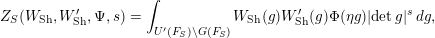 $$\begin{eqnarray}Z_{S}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F9},s)=\int _{U^{\prime }(F_{S})\backslash G(F_{S})}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{s}\,dg,\end{eqnarray}$$
$$\begin{eqnarray}Z_{S}(W_{\operatorname{Sh}},W_{\operatorname{Sh}}^{\prime },\unicode[STIX]{x1D6F9},s)=\int _{U^{\prime }(F_{S})\backslash G(F_{S})}W_{\operatorname{Sh}}(g)W_{\operatorname{Sh}}^{\prime }(g)\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D702}g)|\det g|^{s}\,dg,\end{eqnarray}$$ which is essentially the product over  $v\in S$ of the integrals considered in § 5. (We tacitly assume that much of the analysis of §§ 3–5 carries over to the archimedean case.)
$v\in S$ of the integrals considered in § 5. (We tacitly assume that much of the analysis of §§ 3–5 carries over to the archimedean case.)
Acknowledgements
We thank Raphaël Beuzart-Plessis, Tobias Finis, Wee Teck Gan, Dmitry Gourevitch, Maxim Gurevich, Hervé Jacquet, Yiannis Sakellaridis and Akshay Venkatesh for useful discussions. The paper was conceived while the first-named author was a member at the Institute for Advanced Study in Princeton during the winter semester of 2018. He thanks the IAS warmly for its support and wonderful working conditions.
Finally, we would like to thank the referees for providing many useful suggestions.
Appendix A Relation to intertwining operators
For this appendix assume that  $\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{(AT)}\operatorname{GL}_{n}$. Let
$\unicode[STIX]{x1D70B}\in \operatorname{Irr}_{(AT)}\operatorname{GL}_{n}$. Let
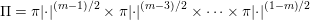 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(m-3)/2}\times \cdots \times \unicode[STIX]{x1D70B}|\cdot |^{(1-m)/2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D70B}|\cdot |^{(m-1)/2}\times \unicode[STIX]{x1D70B}|\cdot |^{(m-3)/2}\times \cdots \times \unicode[STIX]{x1D70B}|\cdot |^{(1-m)/2}\end{eqnarray}$$ be the standard module which admits  $\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ as the Langlands quotient. We realize
$\unicode[STIX]{x1D70E}=\operatorname{Sp}(\unicode[STIX]{x1D70B},m)$ as the Langlands quotient. We realize  $\unicode[STIX]{x1D6F1}$ in the subspace
$\unicode[STIX]{x1D6F1}$ in the subspace  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})$ of
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})$ of  $\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N}$ consisting of functions
$\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N}$ consisting of functions  $W$ such that
$W$ such that  $l\in M\mapsto \unicode[STIX]{x1D6FF}_{P}^{-1/2}(l){\unicode[STIX]{x1D6FF}^{\prime }}^{-1}(l)W(lg)\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m})$ for all
$l\in M\mapsto \unicode[STIX]{x1D6FF}_{P}^{-1/2}(l){\unicode[STIX]{x1D6FF}^{\prime }}^{-1}(l)W(lg)\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m})$ for all  $g\in G$. Define an intertwining operator on
$g\in G$. Define an intertwining operator on  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})$ by
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})$ by
 $$\begin{eqnarray}W\mapsto MW(\cdot )=\int _{U}W({\tilde{w}_{m,n}}^{-1}u\cdot )\,du\end{eqnarray}$$
$$\begin{eqnarray}W\mapsto MW(\cdot )=\int _{U}W({\tilde{w}_{m,n}}^{-1}u\cdot )\,du\end{eqnarray}$$ where  $\tilde{w}_{m,n}$ is as in Remark 3.10. The integral defining
$\tilde{w}_{m,n}$ is as in Remark 3.10. The integral defining  $MW$ is absolutely convergent and its image is
$MW$ is absolutely convergent and its image is  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$. Similarly, define
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$. Similarly, define  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D6F1}^{\vee })\simeq \unicode[STIX]{x1D6F1}^{\vee }$ to be the subspace of
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D6F1}^{\vee })\simeq \unicode[STIX]{x1D6F1}^{\vee }$ to be the subspace of  $\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N}^{-1}$ consisting of functions
$\operatorname{Ind}_{N}^{G}\unicode[STIX]{x1D6F9}_{N}^{-1}$ consisting of functions  $W^{\vee }$ such that
$W^{\vee }$ such that  $l\in M\mapsto \unicode[STIX]{x1D6FF}_{P}^{-1/2}(l)\unicode[STIX]{x1D6FF}^{\prime }(l)W^{\vee }(lg)\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}}((\unicode[STIX]{x1D70B}^{\vee })^{\otimes m})$ for all
$l\in M\mapsto \unicode[STIX]{x1D6FF}_{P}^{-1/2}(l)\unicode[STIX]{x1D6FF}^{\prime }(l)W^{\vee }(lg)\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}}((\unicode[STIX]{x1D70B}^{\vee })^{\otimes m})$ for all  $g\in G$. Then the bilinear form
$g\in G$. Then the bilinear form
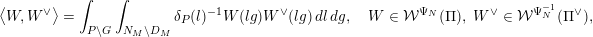 $$\begin{eqnarray}\left\langle W,W^{\vee }\right\rangle =\int _{P\backslash G}\int _{N_{M}\backslash D_{M}}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}W(lg)W^{\vee }(lg)\,dl\,dg,\quad W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1}),~W^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D6F1}^{\vee }),\end{eqnarray}$$
$$\begin{eqnarray}\left\langle W,W^{\vee }\right\rangle =\int _{P\backslash G}\int _{N_{M}\backslash D_{M}}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}W(lg)W^{\vee }(lg)\,dl\,dg,\quad W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1}),~W^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D6F1}^{\vee }),\end{eqnarray}$$ converges absolutely and defines a  $G$-invariant pairing on
$G$-invariant pairing on  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})\times {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D6F1}^{\vee })$ where
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})\times {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D6F1}^{\vee })$ where  $D_{M}=D\cap M$ is the product of
$D_{M}=D\cap M$ is the product of  $m$ copies of the mirabolic subgroup of
$m$ copies of the mirabolic subgroup of  $\operatorname{GL}_{n}$. Since
$\operatorname{GL}_{n}$. Since  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ is the socle of
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ is the socle of  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D6F1}^{\vee })$, for any
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D6F1}^{\vee })$, for any 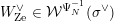 $W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ the linear form
$W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ the linear form  $W\mapsto \left\langle W,W_{\operatorname{Ze}}^{\vee }\right\rangle$ factors through
$W\mapsto \left\langle W,W_{\operatorname{Ze}}^{\vee }\right\rangle$ factors through  $MW$ and it is a scalar multiple (independent of
$MW$ and it is a scalar multiple (independent of  $W$) of
$W$) of  ${\mathcal{B}}_{0}(MW,W_{\operatorname{Ze}}^{\vee })$. In the rest of the appendix we prove the following identity.
${\mathcal{B}}_{0}(MW,W_{\operatorname{Ze}}^{\vee })$. In the rest of the appendix we prove the following identity.
Proposition A.1. For any  $W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})$ and
$W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})$ and  $W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$, we have
$W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$, we have
 $$\begin{eqnarray}\left\langle W,W_{\operatorname{Ze}}^{\vee }\right\rangle ={\mathcal{B}}_{0}(MW,W_{\operatorname{Ze}}^{\vee }).\end{eqnarray}$$
$$\begin{eqnarray}\left\langle W,W_{\operatorname{Ze}}^{\vee }\right\rangle ={\mathcal{B}}_{0}(MW,W_{\operatorname{Ze}}^{\vee }).\end{eqnarray}$$The identity will follow from a series of identities proved below.
For  $i=1,\ldots ,m-1$, let
$i=1,\ldots ,m-1$, let  $U^{i}$ be the unipotent radical of the standard parabolic subgroup
$U^{i}$ be the unipotent radical of the standard parabolic subgroup  $P^{i}$ of
$P^{i}$ of  $G$ of type
$G$ of type  $(in,n,n,\ldots ,n)$. Let
$(in,n,n,\ldots ,n)$. Let  $\bar{U}^{i}=^{t}U^{i}$ be its opposite.
$\bar{U}^{i}=^{t}U^{i}$ be its opposite.
Lemma A.2. Let  $\unicode[STIX]{x1D70F}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$. Then, for any
$\unicode[STIX]{x1D70F}\in \operatorname{Irr}_{\operatorname{gen}}\operatorname{GL}_{n}$. Then, for any  $W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\operatorname{Sp}(\unicode[STIX]{x1D70F},m))$, we have
$W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\operatorname{Sp}(\unicode[STIX]{x1D70F},m))$, we have
 $$\begin{eqnarray}\int _{D\cap \bar{U}^{i}}W_{\operatorname{Ze}}(\bar{u})\,d\bar{u}=W_{\operatorname{Ze}}(\unicode[STIX]{x1D704}({\hat{w}}_{i}))\end{eqnarray}$$
$$\begin{eqnarray}\int _{D\cap \bar{U}^{i}}W_{\operatorname{Ze}}(\bar{u})\,d\bar{u}=W_{\operatorname{Ze}}(\unicode[STIX]{x1D704}({\hat{w}}_{i}))\end{eqnarray}$$where the integrand on the left-hand side is compactly supported. Here
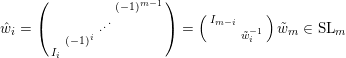
where the signs on the upper right  $(m-i)\times (m-i)$-corner are alternating. Thus,
$(m-i)\times (m-i)$-corner are alternating. Thus,
 $$\begin{eqnarray}\int _{D\cap \bar{U}^{i}}W_{\operatorname{Ze}}(\bar{u}\bar{v})\,d\bar{u}=\int _{D\cap \bar{U}^{i}}W_{\operatorname{Ze}}(\bar{u})\,d\bar{u}\end{eqnarray}$$
$$\begin{eqnarray}\int _{D\cap \bar{U}^{i}}W_{\operatorname{Ze}}(\bar{u}\bar{v})\,d\bar{u}=\int _{D\cap \bar{U}^{i}}W_{\operatorname{Ze}}(\bar{u})\,d\bar{u}\end{eqnarray}$$ for all  $\bar{v}\in \bar{U}^{i}$. In particular, for
$\bar{v}\in \bar{U}^{i}$. In particular, for  $i=1$,
$i=1$,
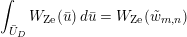 $$\begin{eqnarray}\int _{\bar{U}_{D}}W_{\operatorname{Ze}}(\bar{u})\,d\bar{u}=W_{\operatorname{Ze}}(\tilde{w}_{m,n})\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}_{D}}W_{\operatorname{Ze}}(\bar{u})\,d\bar{u}=W_{\operatorname{Ze}}(\tilde{w}_{m,n})\end{eqnarray}$$ where  $\bar{U}_{D}=\bar{U}\cap D$.
$\bar{U}_{D}=\bar{U}\cap D$.
Proof. Let  $W_{\operatorname{Sh}}^{i}={\mathcal{T}}_{(i-1)n}W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{(i-1)n}}}(\operatorname{Sp}(\unicode[STIX]{x1D70F},m))$. Recall that
$W_{\operatorname{Sh}}^{i}={\mathcal{T}}_{(i-1)n}W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{U_{(i-1)n}}}(\operatorname{Sp}(\unicode[STIX]{x1D70F},m))$. Recall that  $U_{(i-1)n}$ is the subgroup of
$U_{(i-1)n}$ is the subgroup of  $P^{i}$ consisting of matrices whose
$P^{i}$ consisting of matrices whose  $n\times n$ blocks
$n\times n$ blocks  $A_{j,k}$ satisfy:
$A_{j,k}$ satisfy:
–
 $A_{j,j}$ is upper unitriangular for all
$A_{j,j}$ is upper unitriangular for all  $j=1,\ldots ,m$;
$j=1,\ldots ,m$;–
 $A_{j,k}$ is strictly upper triangular if
$A_{j,k}$ is strictly upper triangular if  $j\neq k$ and
$j\neq k$ and  $j,k\leqslant i$;
$j,k\leqslant i$;–
 $A_{j,k}=0$ if
$A_{j,k}=0$ if  $j>k$ and
$j>k$ and  $j>i$.
$j>i$.
(There are no conditions on  $A_{j,k}$ if
$A_{j,k}$ if  $k>j$ and
$k>j$ and  $k>i$.)
$k>i$.)
The inverse transform in Proposition 3.5 gives
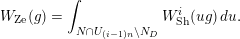 $$\begin{eqnarray}W_{\operatorname{Ze}}(g)=\int _{N\cap U_{(i-1)n}\backslash N_{D}}W_{\operatorname{Sh}}^{i}(ug)\,du.\end{eqnarray}$$
$$\begin{eqnarray}W_{\operatorname{Ze}}(g)=\int _{N\cap U_{(i-1)n}\backslash N_{D}}W_{\operatorname{Sh}}^{i}(ug)\,du.\end{eqnarray}$$ We may replace the domain of integration by  $(N\cap U_{(i-1)n}\cap \operatorname{GL}_{in})\backslash (N_{D}\cap \operatorname{GL}_{in})$ where
$(N\cap U_{(i-1)n}\cap \operatorname{GL}_{in})\backslash (N_{D}\cap \operatorname{GL}_{in})$ where  $\operatorname{GL}_{in}$ is embedded in
$\operatorname{GL}_{in}$ is embedded in  $G$ by
$G$ by  $h\mapsto \big(\begin{smallmatrix}h & \\ & I_{(m-i)n}\end{smallmatrix}\big)$. Let
$h\mapsto \big(\begin{smallmatrix}h & \\ & I_{(m-i)n}\end{smallmatrix}\big)$. Let  $U_{i}^{\prime }=U_{(i-1)n}\cap \operatorname{GL}_{in}=U^{\prime }\cap \operatorname{GL}_{in}$ and
$U_{i}^{\prime }=U_{(i-1)n}\cap \operatorname{GL}_{in}=U^{\prime }\cap \operatorname{GL}_{in}$ and  $D_{i}=D\cap \operatorname{GL}_{in}$. Thus, the above integral can be taken over
$D_{i}=D\cap \operatorname{GL}_{in}$. Thus, the above integral can be taken over  $N\cap U_{i}^{\prime }\backslash N\cap D_{i}$, and by Lemma 3.11 the integrand is compactly supported.
$N\cap U_{i}^{\prime }\backslash N\cap D_{i}$, and by Lemma 3.11 the integrand is compactly supported.
The expression on the left-hand side of (A.3) is
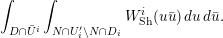 $$\begin{eqnarray}\int _{D\cap \bar{U}^{i}}\int _{N\cap U_{i}^{\prime }\backslash N\cap D_{i}}W_{\operatorname{Sh}}^{i}(u\bar{u})\,du\,d\bar{u}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{D\cap \bar{U}^{i}}\int _{N\cap U_{i}^{\prime }\backslash N\cap D_{i}}W_{\operatorname{Sh}}^{i}(u\bar{u})\,du\,d\bar{u}.\end{eqnarray}$$ The same argument as in Lemma 3.8 shows that the function  $W_{\operatorname{Sh}}^{i}(u\bar{u})$ is compactly supported in
$W_{\operatorname{Sh}}^{i}(u\bar{u})$ is compactly supported in  $\bar{u}$ uniformly in
$\bar{u}$ uniformly in  $u$. Thus, the above double integral is absolutely convergent. Changing the order of integration and making a change of variable in
$u$. Thus, the above double integral is absolutely convergent. Changing the order of integration and making a change of variable in  $\bar{u}$, we get
$\bar{u}$, we get
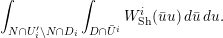 $$\begin{eqnarray}\int _{N\cap U_{i}^{\prime }\backslash N\cap D_{i}}\int _{D\cap \bar{U}^{i}}W_{\operatorname{Sh}}^{i}(\bar{u}u)\,d\bar{u}\,du.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N\cap U_{i}^{\prime }\backslash N\cap D_{i}}\int _{D\cap \bar{U}^{i}}W_{\operatorname{Sh}}^{i}(\bar{u}u)\,d\bar{u}\,du.\end{eqnarray}$$ Notice that the partial integration over  $U^{\prime }\cap \bar{U}^{i}\subset D\cap \bar{U}^{i}$ is the composition of the transforms
$U^{\prime }\cap \bar{U}^{i}\subset D\cap \bar{U}^{i}$ is the composition of the transforms  ${\mathcal{T}}_{j}$ defined in Proposition 3.5 for
${\mathcal{T}}_{j}$ defined in Proposition 3.5 for  $j=(i-1)n,\ldots ,(m-1)n-1$. Thus, the above expression is
$j=(i-1)n,\ldots ,(m-1)n-1$. Thus, the above expression is
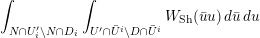 $$\begin{eqnarray}\int _{N\cap U_{i}^{\prime }\backslash N\cap D_{i}}\int _{U^{\prime }\cap \bar{U}^{i}\backslash D\cap \bar{U}^{i}}W_{\operatorname{Sh}}(\bar{u}u)\,d\bar{u}\,du\end{eqnarray}$$
$$\begin{eqnarray}\int _{N\cap U_{i}^{\prime }\backslash N\cap D_{i}}\int _{U^{\prime }\cap \bar{U}^{i}\backslash D\cap \bar{U}^{i}}W_{\operatorname{Sh}}(\bar{u}u)\,d\bar{u}\,du\end{eqnarray}$$ where  $W_{\operatorname{Sh}}={\mathcal{T}}W_{\operatorname{Ze}}$. By Lemma 3.9,
$W_{\operatorname{Sh}}={\mathcal{T}}W_{\operatorname{Ze}}$. By Lemma 3.9,  $W_{\operatorname{Sh}}(\unicode[STIX]{x1D704}({\hat{w}}_{i})g)=W_{\operatorname{Sh}}(g)$. The above expression becomes
$W_{\operatorname{Sh}}(\unicode[STIX]{x1D704}({\hat{w}}_{i})g)=W_{\operatorname{Sh}}(g)$. The above expression becomes
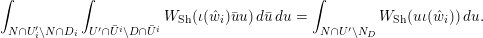 $$\begin{eqnarray}\int _{N\cap U_{i}^{\prime }\backslash N\cap D_{i}}\int _{U^{\prime }\cap \bar{U}^{i}\backslash D\cap \bar{U}^{i}}W_{\operatorname{Sh}}(\unicode[STIX]{x1D704}({\hat{w}}_{i})\bar{u}u)\,d\bar{u}\,du=\int _{N\cap U^{\prime }\backslash N_{D}}W_{\operatorname{Sh}}(u\unicode[STIX]{x1D704}({\hat{w}}_{i}))\,du.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N\cap U_{i}^{\prime }\backslash N\cap D_{i}}\int _{U^{\prime }\cap \bar{U}^{i}\backslash D\cap \bar{U}^{i}}W_{\operatorname{Sh}}(\unicode[STIX]{x1D704}({\hat{w}}_{i})\bar{u}u)\,d\bar{u}\,du=\int _{N\cap U^{\prime }\backslash N_{D}}W_{\operatorname{Sh}}(u\unicode[STIX]{x1D704}({\hat{w}}_{i}))\,du.\end{eqnarray}$$ Now Lemma 3.11 gives (A.3). For the second part, we only need to note that, for all  $\bar{v}\in \bar{U}^{i}$, we have
$\bar{v}\in \bar{U}^{i}$, we have  $W_{\operatorname{Ze}}(\unicode[STIX]{x1D704}({\hat{w}}_{i})\bar{v})=W_{\operatorname{Ze}}(\unicode[STIX]{x1D704}({\hat{w}}_{i}))$.◻
$W_{\operatorname{Ze}}(\unicode[STIX]{x1D704}({\hat{w}}_{i})\bar{v})=W_{\operatorname{Ze}}(\unicode[STIX]{x1D704}({\hat{w}}_{i}))$.◻
Write  $\bar{U}$ as a (semidirect) product of abelian groups
$\bar{U}$ as a (semidirect) product of abelian groups  $\bar{U}_{2}\bar{U}_{3}\cdots \bar{U}_{m}$, where
$\bar{U}_{2}\bar{U}_{3}\cdots \bar{U}_{m}$, where  $\bar{U}_{i}$ consists of the elements
$\bar{U}_{i}$ consists of the elements  $\bar{u}$ in
$\bar{u}$ in  $\bar{U}$ such that
$\bar{U}$ such that  $\bar{u}_{j,k}=\unicode[STIX]{x1D6FF}_{j,k}$ if
$\bar{u}_{j,k}=\unicode[STIX]{x1D6FF}_{j,k}$ if  $j\leqslant n(i-1)$ or
$j\leqslant n(i-1)$ or  $j>ni$. For brevity, for any
$j>ni$. For brevity, for any  $i=1,\ldots ,m$, we denote the iterated integral
$i=1,\ldots ,m$, we denote the iterated integral
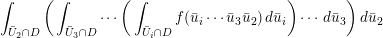 $$\begin{eqnarray}\int _{\bar{U}_{2}\cap D}\bigg(\int _{\bar{U}_{3}\cap D}\cdots \bigg(\int _{\bar{U}_{i}\cap D}f(\bar{u}_{i}\cdots \bar{u}_{3}\bar{u}_{2})\,d\bar{u}_{i}\bigg)\cdots \,d\bar{u}_{3}\bigg)\,d\bar{u}_{2}\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}_{2}\cap D}\bigg(\int _{\bar{U}_{3}\cap D}\cdots \bigg(\int _{\bar{U}_{i}\cap D}f(\bar{u}_{i}\cdots \bar{u}_{3}\bar{u}_{2})\,d\bar{u}_{i}\bigg)\cdots \,d\bar{u}_{3}\bigg)\,d\bar{u}_{2}\end{eqnarray}$$(assuming convergence) by
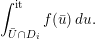 $$\begin{eqnarray}\int _{\bar{U}\cap D_{i}}^{\operatorname{it}}f(\bar{u})\,du.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}\cap D_{i}}^{\operatorname{it}}f(\bar{u})\,du.\end{eqnarray}$$Lemma A.3. Let  $W_{\operatorname{Ze}}$ be as before and let
$W_{\operatorname{Ze}}$ be as before and let  $\unicode[STIX]{x1D719}\in {\mathcal{S}}(\bar{U})$. Then
$\unicode[STIX]{x1D719}\in {\mathcal{S}}(\bar{U})$. Then
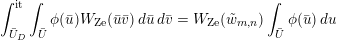 $$\begin{eqnarray}\int _{\bar{U}_{D}}^{\operatorname{it}}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{u}\bar{v})\,d\bar{u}\,d\bar{v}=W_{\operatorname{Ze}}(\tilde{w}_{m,n})\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})\,du\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}_{D}}^{\operatorname{it}}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{u}\bar{v})\,d\bar{u}\,d\bar{v}=W_{\operatorname{Ze}}(\tilde{w}_{m,n})\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})\,du\end{eqnarray}$$where each integrand in the iterated integral on the left-hand side is compactly supported.
Proof. We show by descending induction on  $i=1,\ldots ,m$ that the left-hand side is equal to
$i=1,\ldots ,m$ that the left-hand side is equal to
 $$\begin{eqnarray}\int _{\bar{U}\cap D_{i}}^{\operatorname{it}}\int _{\bar{U}^{i}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}\bar{u}\bar{v}^{\prime })\,d\bar{u}\,d\bar{v}\,d\bar{v}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}\cap D_{i}}^{\operatorname{it}}\int _{\bar{U}^{i}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}\bar{u}\bar{v}^{\prime })\,d\bar{u}\,d\bar{v}\,d\bar{v}^{\prime }.\end{eqnarray}$$ Note that the integrand is compactly supported in  $\bar{u}$ and
$\bar{u}$ and  $\bar{v}$. For
$\bar{v}$. For  $i=m$ this is clear, while for
$i=m$ this is clear, while for  $i=1$ we obtain the statement of the lemma by Lemma A.2.
$i=1$ we obtain the statement of the lemma by Lemma A.2.
For the induction step, we assume  $i>1$ and use Lemma A.2 to rewrite (A.4) as
$i>1$ and use Lemma A.2 to rewrite (A.4) as
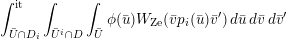 $$\begin{eqnarray}\int _{\bar{U}\cap D_{i}}^{\operatorname{it}}\int _{\bar{U}^{i}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}p_{i}(\bar{u})\bar{v}^{\prime })\,d\bar{u}\,d\bar{v}\,d\bar{v}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}\cap D_{i}}^{\operatorname{it}}\int _{\bar{U}^{i}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}p_{i}(\bar{u})\bar{v}^{\prime })\,d\bar{u}\,d\bar{v}\,d\bar{v}^{\prime }\end{eqnarray}$$ where  $p_{i}:\operatorname{GL}_{in}\ltimes \bar{U}^{i}\rightarrow \operatorname{GL}_{in}$ is the projection. Now write
$p_{i}:\operatorname{GL}_{in}\ltimes \bar{U}^{i}\rightarrow \operatorname{GL}_{in}$ is the projection. Now write  $\bar{v}^{\prime }=\bar{v}_{1}\bar{v}_{2}$ where
$\bar{v}^{\prime }=\bar{v}_{1}\bar{v}_{2}$ where  $\bar{v}_{1}\in \bar{U}_{i}\cap D$ and
$\bar{v}_{1}\in \bar{U}_{i}\cap D$ and  $\bar{v}_{2}\in \bar{U}\cap D_{i-1}$ and note that
$\bar{v}_{2}\in \bar{U}\cap D_{i-1}$ and note that  $p_{i}(\bar{u})\in \operatorname{GL}_{in}\cap \,\bar{U}$ normalizes
$p_{i}(\bar{u})\in \operatorname{GL}_{in}\cap \,\bar{U}$ normalizes  $\bar{U}_{i}\cap D$. Therefore, (A.4) is equal to
$\bar{U}_{i}\cap D$. Therefore, (A.4) is equal to
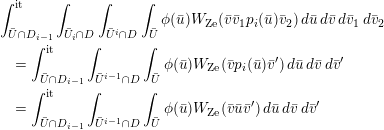 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\bar{U}\cap D_{i-1}}^{\operatorname{it}}\int _{\bar{U}_{i}\cap D}\int _{\bar{U}^{i}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}\bar{v}_{1}p_{i}(\bar{u})\bar{v}_{2})\,d\bar{u}\,d\bar{v}\,d\bar{v}_{1}\,d\bar{v}_{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\bar{U}\cap D_{i-1}}^{\operatorname{it}}\int _{\bar{U}^{i-1}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}p_{i}(\bar{u})\bar{v}^{\prime })\,d\bar{u}\,d\bar{v}\,d\bar{v}^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\bar{U}\cap D_{i-1}}^{\operatorname{it}}\int _{\bar{U}^{i-1}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}\bar{u}\bar{v}^{\prime })\,d\bar{u}\,d\bar{v}\,d\bar{v}^{\prime }\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\bar{U}\cap D_{i-1}}^{\operatorname{it}}\int _{\bar{U}_{i}\cap D}\int _{\bar{U}^{i}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}\bar{v}_{1}p_{i}(\bar{u})\bar{v}_{2})\,d\bar{u}\,d\bar{v}\,d\bar{v}_{1}\,d\bar{v}_{2}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\bar{U}\cap D_{i-1}}^{\operatorname{it}}\int _{\bar{U}^{i-1}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}p_{i}(\bar{u})\bar{v}^{\prime })\,d\bar{u}\,d\bar{v}\,d\bar{v}^{\prime }\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\bar{U}\cap D_{i-1}}^{\operatorname{it}}\int _{\bar{U}^{i-1}\cap D}\int _{\bar{U}}\unicode[STIX]{x1D719}(\bar{u})W_{\operatorname{Ze}}(\bar{v}\bar{u}\bar{v}^{\prime })\,d\bar{u}\,d\bar{v}\,d\bar{v}^{\prime }\nonumber\end{eqnarray}$$as required.◻
Denote by  $\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}(l)$ the character of
$\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}(l)$ the character of  $D_{M}$ given by
$D_{M}$ given by  $d(l\bar{u}l^{-1})=\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}(l)\,d\bar{u}$ where
$d(l\bar{u}l^{-1})=\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}(l)\,d\bar{u}$ where  $d\bar{u}$ is a Haar measure on
$d\bar{u}$ is a Haar measure on  $\bar{U}_{D}$.
$\bar{U}_{D}$.
Let  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})_{\sharp }$ be the linear subspace of
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})_{\sharp }$ be the linear subspace of  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})$ generated by the functions
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})$ generated by the functions  $W$ of the form
$W$ of the form
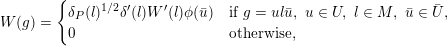 $$\begin{eqnarray}W(g)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FF}_{P}(l)^{1/2}\unicode[STIX]{x1D6FF}^{\prime }(l)W^{\prime }(l)\unicode[STIX]{x1D719}(\bar{u})\quad & \text{if }g=ul\bar{u},~u\in U,~l\in M,~\bar{u}\in \bar{U},\\ 0\quad & \text{otherwise,}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}W(g)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6FF}_{P}(l)^{1/2}\unicode[STIX]{x1D6FF}^{\prime }(l)W^{\prime }(l)\unicode[STIX]{x1D719}(\bar{u})\quad & \text{if }g=ul\bar{u},~u\in U,~l\in M,~\bar{u}\in \bar{U},\\ 0\quad & \text{otherwise,}\end{array}\right.\end{eqnarray}$$ where  $\unicode[STIX]{x1D719}\in {\mathcal{S}}(\bar{U})$,
$\unicode[STIX]{x1D719}\in {\mathcal{S}}(\bar{U})$,  $W^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m})$ and
$W^{\prime }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N_{M}}}(\unicode[STIX]{x1D70B}^{\otimes m})$ and  $W^{\prime }|_{D_{M}}$ is compactly supported modulo
$W^{\prime }|_{D_{M}}$ is compactly supported modulo  $N_{M}$.
$N_{M}$.
Lemma A.4. For any  $W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})_{\sharp }$ and
$W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})_{\sharp }$ and  $W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$, we have
$W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$, we have
 $$\begin{eqnarray}\int _{\bar{U}_{D}}^{\operatorname{it}}\left\langle W,W_{\operatorname{ Ze}}^{\vee }(\cdot \bar{v})\right\rangle \,d\bar{v}=\int _{N_{M}\backslash D_{M}}MW(\tilde{w}_{m,n}l)W_{\operatorname{Ze}}^{\vee }(\tilde{w}_{m,n}l)\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}^{-1}(l)\,dl.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}_{D}}^{\operatorname{it}}\left\langle W,W_{\operatorname{ Ze}}^{\vee }(\cdot \bar{v})\right\rangle \,d\bar{v}=\int _{N_{M}\backslash D_{M}}MW(\tilde{w}_{m,n}l)W_{\operatorname{Ze}}^{\vee }(\tilde{w}_{m,n}l)\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}^{-1}(l)\,dl.\end{eqnarray}$$Proof. The left-hand side is
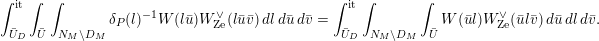 $$\begin{eqnarray}\int _{\bar{U}_{D}}^{\operatorname{it}}\int _{\bar{U}}\int _{N_{M}\backslash D_{M}}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}W(l\bar{u})W_{\operatorname{ Ze}}^{\vee }(l\bar{u}\bar{v})\,dl\,d\bar{u}\,d\bar{v}=\int _{\bar{U}_{D}}^{\operatorname{it}}\int _{N_{M}\backslash D_{M}}\int _{\bar{U}}W(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{u}l\bar{v})\,d\bar{u}\,dl\,d\bar{v}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}_{D}}^{\operatorname{it}}\int _{\bar{U}}\int _{N_{M}\backslash D_{M}}\unicode[STIX]{x1D6FF}_{P}(l)^{-1}W(l\bar{u})W_{\operatorname{ Ze}}^{\vee }(l\bar{u}\bar{v})\,dl\,d\bar{u}\,d\bar{v}=\int _{\bar{U}_{D}}^{\operatorname{it}}\int _{N_{M}\backslash D_{M}}\int _{\bar{U}}W(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{u}l\bar{v})\,d\bar{u}\,dl\,d\bar{v}.\end{eqnarray}$$ As  $M$ normalizes
$M$ normalizes  $\bar{U}_{i}$ for any
$\bar{U}_{i}$ for any  $i$, this equals
$i$, this equals
 $$\begin{eqnarray}\int _{N_{M}\backslash D_{M}}\int _{\bar{U}_{D}}^{\operatorname{it}}\int _{\bar{U}}W(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{u}\bar{v}l)\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}^{-1}(l)\,d\bar{u}\,d\bar{v}\,dl.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N_{M}\backslash D_{M}}\int _{\bar{U}_{D}}^{\operatorname{it}}\int _{\bar{U}}W(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{u}\bar{v}l)\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}^{-1}(l)\,d\bar{u}\,d\bar{v}\,dl.\end{eqnarray}$$ Here we can interchange the order of integration as  $l$ is integrated over a fixed compact set, by the choice of
$l$ is integrated over a fixed compact set, by the choice of  $W$. The claim now follows from Lemma A.3 and (A.1).◻
$W$. The claim now follows from Lemma A.3 and (A.1).◻
Let  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })_{\flat }$ be the subspace of
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })_{\flat }$ be the subspace of  ${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ consisting of the functions
${\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })$ consisting of the functions  $W_{\operatorname{Ze}}^{\vee }$ such that
$W_{\operatorname{Ze}}^{\vee }$ such that  $W_{\operatorname{Ze}}^{\vee }|_{D}$ is contained in
$W_{\operatorname{Ze}}^{\vee }|_{D}$ is contained in  $\operatorname{ind}_{N_{D}}^{D}\unicode[STIX]{x1D6F9}_{N}$ and
$\operatorname{ind}_{N_{D}}^{D}\unicode[STIX]{x1D6F9}_{N}$ and  $W_{\operatorname{Ze}}^{\vee }|_{D}$ is supported in
$W_{\operatorname{Ze}}^{\vee }|_{D}$ is supported in  $P\bar{U}\cap D$.
$P\bar{U}\cap D$.
Lemma A.5. For any  $W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ and
$W_{\operatorname{Ze}}\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D70E})$ and  $W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })_{\flat }$, we have
$W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })_{\flat }$, we have
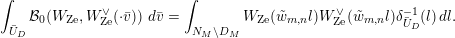 $$\begin{eqnarray}\int _{\bar{U}_{D}}{\mathcal{B}}_{0}(W_{\operatorname{Ze}},W_{\operatorname{Ze}}^{\vee }(\cdot \bar{v}))~d\bar{v}=\int _{N_{M}\backslash D_{M}}W_{\operatorname{Ze}}(\tilde{w}_{m,n}l)W_{\operatorname{Ze}}^{\vee }(\tilde{w}_{m,n}l)\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}^{-1}(l)\,dl.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\bar{U}_{D}}{\mathcal{B}}_{0}(W_{\operatorname{Ze}},W_{\operatorname{Ze}}^{\vee }(\cdot \bar{v}))~d\bar{v}=\int _{N_{M}\backslash D_{M}}W_{\operatorname{Ze}}(\tilde{w}_{m,n}l)W_{\operatorname{Ze}}^{\vee }(\tilde{w}_{m,n}l)\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}^{-1}(l)\,dl.\end{eqnarray}$$Proof. Note that  $P\bar{U}\cap D=U_{D}D_{M}\bar{U}_{D}$. Thus, the left-hand side is
$P\bar{U}\cap D=U_{D}D_{M}\bar{U}_{D}$. Thus, the left-hand side is
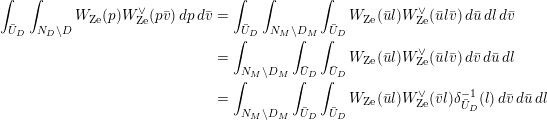 $$\begin{eqnarray}\displaystyle \int _{\bar{U}_{D}}\int _{N_{D}\backslash D}W_{\operatorname{Ze}}(p)W_{\operatorname{Ze}}^{\vee }(p\bar{v})\,dp\,d\bar{v} & = & \displaystyle \int _{\bar{U}_{D}}\int _{N_{M}\backslash D_{M}}\int _{\bar{U}_{D}}W_{\operatorname{Ze}}(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{u}l\bar{v})\,d\bar{u}\,dl\,d\bar{v}\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{M}\backslash D_{M}}\int _{\bar{U}_{D}}\int _{\bar{U}_{D}}W_{\operatorname{Ze}}(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{u}l\bar{v})\,d\bar{v}\,d\bar{u}\,dl\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{M}\backslash D_{M}}\int _{\bar{U}_{D}}\int _{\bar{U}_{D}}W_{\operatorname{Ze}}(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{v}l)\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}^{-1}(l)\,d\bar{v}\,d\bar{u}\,dl\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\bar{U}_{D}}\int _{N_{D}\backslash D}W_{\operatorname{Ze}}(p)W_{\operatorname{Ze}}^{\vee }(p\bar{v})\,dp\,d\bar{v} & = & \displaystyle \int _{\bar{U}_{D}}\int _{N_{M}\backslash D_{M}}\int _{\bar{U}_{D}}W_{\operatorname{Ze}}(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{u}l\bar{v})\,d\bar{u}\,dl\,d\bar{v}\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{M}\backslash D_{M}}\int _{\bar{U}_{D}}\int _{\bar{U}_{D}}W_{\operatorname{Ze}}(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{u}l\bar{v})\,d\bar{v}\,d\bar{u}\,dl\nonumber\\ \displaystyle & = & \displaystyle \int _{N_{M}\backslash D_{M}}\int _{\bar{U}_{D}}\int _{\bar{U}_{D}}W_{\operatorname{Ze}}(\bar{u}l)W_{\operatorname{Ze}}^{\vee }(\bar{v}l)\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}^{-1}(l)\,d\bar{v}\,d\bar{u}\,dl\nonumber\end{eqnarray}$$ where we made a change of variable  $\bar{v}\mapsto l^{-1}\bar{u}^{-1}\bar{v}l$. By the condition on
$\bar{v}\mapsto l^{-1}\bar{u}^{-1}\bar{v}l$. By the condition on  $W_{\operatorname{Ze}}^{\vee }|_{D}$ and Lemma 3.8, the integrand is compactly supported, which justifies the previous steps. Applying Lemma A.2 for both integrals over
$W_{\operatorname{Ze}}^{\vee }|_{D}$ and Lemma 3.8, the integrand is compactly supported, which justifies the previous steps. Applying Lemma A.2 for both integrals over  $\bar{U}_{D}$, we get the required statement.◻
$\bar{U}_{D}$, we get the required statement.◻
Since (A.2) holds up to a scalar, in order to conclude Proposition A.1, it suffices, in view of Lemmas A.4 and A.5, to show the existence of  $W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})_{\sharp }$ and
$W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})_{\sharp }$ and  $W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })_{\flat }$ such that the right-hand side of (A.5) is non-zero. By Corollary 3.15, given
$W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })_{\flat }$ such that the right-hand side of (A.5) is non-zero. By Corollary 3.15, given  $\unicode[STIX]{x1D719}\in {\mathcal{S}}(\bar{U}_{D})$ and
$\unicode[STIX]{x1D719}\in {\mathcal{S}}(\bar{U}_{D})$ and  $W^{\prime }\in \operatorname{ind}_{N_{M}}^{D_{M}}\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}$, there exists (a unique)
$W^{\prime }\in \operatorname{ind}_{N_{M}}^{D_{M}}\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}$, there exists (a unique)  $W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })_{\flat }$ such that
$W_{\operatorname{Ze}}^{\vee }\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}^{-1}}(\unicode[STIX]{x1D70E}^{\vee })_{\flat }$ such that
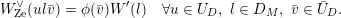 $$\begin{eqnarray}W_{\operatorname{Ze}}^{\vee }(ul\bar{v})=\unicode[STIX]{x1D719}(\bar{v})W^{\prime }(l)\quad \forall u\in U_{D},~l\in D_{M},~\bar{v}\in \bar{U}_{D}.\end{eqnarray}$$
$$\begin{eqnarray}W_{\operatorname{Ze}}^{\vee }(ul\bar{v})=\unicode[STIX]{x1D719}(\bar{v})W^{\prime }(l)\quad \forall u\in U_{D},~l\in D_{M},~\bar{v}\in \bar{U}_{D}.\end{eqnarray}$$Thus,
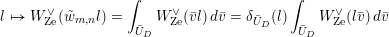 $$\begin{eqnarray}l\mapsto W_{\operatorname{Ze}}^{\vee }(\tilde{w}_{m,n}l)=\int _{\bar{U}_{D}}W_{\operatorname{Ze}}^{\vee }(\bar{v}l)\,d\bar{v}=\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}(l)\int _{\bar{U}_{D}}W_{\operatorname{Ze}}^{\vee }(l\bar{v})\,d\bar{v}\end{eqnarray}$$
$$\begin{eqnarray}l\mapsto W_{\operatorname{Ze}}^{\vee }(\tilde{w}_{m,n}l)=\int _{\bar{U}_{D}}W_{\operatorname{Ze}}^{\vee }(\bar{v}l)\,d\bar{v}=\unicode[STIX]{x1D6FF}_{\bar{U}_{D}}(l)\int _{\bar{U}_{D}}W_{\operatorname{Ze}}^{\vee }(l\bar{v})\,d\bar{v}\end{eqnarray}$$ can be taken to be an arbitrary function in  $\operatorname{ind}_{N_{M}}^{D_{M}}\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}$ Thus, we only need to show that
$\operatorname{ind}_{N_{M}}^{D_{M}}\unicode[STIX]{x1D6F9}_{N_{M}}^{-1}$ Thus, we only need to show that  $MW(\tilde{w}_{m,n})$ is non-zero for some
$MW(\tilde{w}_{m,n})$ is non-zero for some  $W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})_{\sharp }$. However, this is clear since
$W\in {\mathcal{W}}^{\unicode[STIX]{x1D6F9}_{N}}(\unicode[STIX]{x1D6F1})_{\sharp }$. However, this is clear since  $MW(\tilde{w}_{m,n})=\int _{\bar{U}}W(\bar{u})\,d\bar{u}$.
$MW(\tilde{w}_{m,n})=\int _{\bar{U}}W(\bar{u})\,d\bar{u}$.
This finishes the proof of Proposition A.1.
Remark A.6. Let us return to the setup of § 8. It is well known that the Petersson inner product of cusp forms in  $\unicode[STIX]{x1D70B}$ factorizes as the product over
$\unicode[STIX]{x1D70B}$ factorizes as the product over  $v$ of the Bernstein inner product on the Whittaker model of
$v$ of the Bernstein inner product on the Whittaker model of  $\unicode[STIX]{x1D70B}_{v}$. Now let
$\unicode[STIX]{x1D70B}_{v}$. Now let  $\unicode[STIX]{x1D711}$ be as in (32). The
$\unicode[STIX]{x1D711}$ be as in (32). The  $\unicode[STIX]{x1D6F9}_{N}$th Fourier coefficient of
$\unicode[STIX]{x1D6F9}_{N}$th Fourier coefficient of  $\unicode[STIX]{x1D711}$ is the
$\unicode[STIX]{x1D711}$ is the  $\unicode[STIX]{x1D6F9}_{N_{M}}$th Whittaker coefficient of the constant term of
$\unicode[STIX]{x1D6F9}_{N_{M}}$th Whittaker coefficient of the constant term of  $\unicode[STIX]{x1D711}$, which is given by the iterated residue
$\unicode[STIX]{x1D711}$, which is given by the iterated residue  $M_{-1}$ of the global intertwining operator. Proposition A.1 (assumed to work in the archimedean case as well) gives a factorization of the square of the Petersson norm of
$M_{-1}$ of the global intertwining operator. Proposition A.1 (assumed to work in the archimedean case as well) gives a factorization of the square of the Petersson norm of  $\unicode[STIX]{x1D711}$ in terms of the local inner product (14) on the Zelevinsky model of
$\unicode[STIX]{x1D711}$ in terms of the local inner product (14) on the Zelevinsky model of  $\operatorname{Sp}(\unicode[STIX]{x1D70B}_{v},m)$. Indeed, by the Maass–Selberg relations, the Petersson inner product is given by
$\operatorname{Sp}(\unicode[STIX]{x1D70B}_{v},m)$. Indeed, by the Maass–Selberg relations, the Petersson inner product is given by  $M_{-1}$ and Proposition A.1 will reduce the statement to the classical case.
$M_{-1}$ and Proposition A.1 will reduce the statement to the classical case.