Article contents
Homogeneity of cohomology classes associated with Koszul matrix factorizations
Published online by Cambridge University Press: 20 July 2016
Abstract
In this work we prove the so-called dimension property for the cohomological field theory associated with a homogeneous polynomial 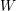 $W$ with an isolated singularity, in the algebraic framework of [A. Polishchuk and A. Vaintrob, Matrix factorizations and cohomological field theories, J. Reine Angew. Math. 714 (2016), 1–122]. This amounts to showing that some cohomology classes on the Deligne–Mumford moduli spaces of stable curves, constructed using Fourier–Mukai-type functors associated with matrix factorizations, live in prescribed dimension. The proof is based on a homogeneity result established in [A. Polishchuk and A. Vaintrob, Algebraic construction of Witten’s top Chern class, in Advances in algebraic geometry motivated by physics (Lowell, MA, 2000) (American Mathematical Society, Providence, RI, 2001), 229–249] for certain characteristic classes of Koszul matrix factorizations of
$W$ with an isolated singularity, in the algebraic framework of [A. Polishchuk and A. Vaintrob, Matrix factorizations and cohomological field theories, J. Reine Angew. Math. 714 (2016), 1–122]. This amounts to showing that some cohomology classes on the Deligne–Mumford moduli spaces of stable curves, constructed using Fourier–Mukai-type functors associated with matrix factorizations, live in prescribed dimension. The proof is based on a homogeneity result established in [A. Polishchuk and A. Vaintrob, Algebraic construction of Witten’s top Chern class, in Advances in algebraic geometry motivated by physics (Lowell, MA, 2000) (American Mathematical Society, Providence, RI, 2001), 229–249] for certain characteristic classes of Koszul matrix factorizations of 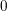 $0$. To reduce to this result, we use the theory of Fourier–Mukai-type functors involving matrix factorizations and the natural rational lattices in the relevant Hochschild homology spaces, as well as a version of Hodge–Riemann bilinear relations for Hochschild homology of matrix factorizations. Our approach also gives a proof of the dimension property for the cohomological field theories associated with some quasihomogeneous polynomials with an isolated singularity.
$0$. To reduce to this result, we use the theory of Fourier–Mukai-type functors involving matrix factorizations and the natural rational lattices in the relevant Hochschild homology spaces, as well as a version of Hodge–Riemann bilinear relations for Hochschild homology of matrix factorizations. Our approach also gives a proof of the dimension property for the cohomological field theories associated with some quasihomogeneous polynomials with an isolated singularity.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2016
References
- 1
- Cited by


