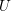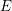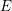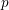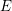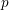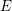1 Introduction
Families of automorphic forms have been a rather fruitful area of research since their introduction by Hida [Reference HidaHid86] in 1986 for ordinary modular forms and their generalizations, notably the Coleman–Mazur eigencurve, but also to other groups than
![]() $\operatorname{GL}_{2}$
. Among examples of applications we can for example cite some cases of the Artin conjecture, for many modular forms the parity conjecture, and generalizations to a bigger class of automorphic representations of instances of Langlands’ philosophy (together with local–global compatibility).
$\operatorname{GL}_{2}$
. Among examples of applications we can for example cite some cases of the Artin conjecture, for many modular forms the parity conjecture, and generalizations to a bigger class of automorphic representations of instances of Langlands’ philosophy (together with local–global compatibility).
The goal of this article is to present a new construction of what is called an ‘eigenvariety’, i.e. a
![]() $p$
-adically rigid-analytic variety which parameterizes Hecke eigensystems. More precisely, the idea is to construct families of eigenvalues for an appropriate Hecke algebra acting on certain rather complicated cohomology groups which are large
$p$
-adically rigid-analytic variety which parameterizes Hecke eigensystems. More precisely, the idea is to construct families of eigenvalues for an appropriate Hecke algebra acting on certain rather complicated cohomology groups which are large
![]() $\mathbb{Q}_{p}$
-Banach spaces, into which we can identify classical Hecke eigenvalues. For example Hida and Emerton consider for these cohomology groups some projective systems of étale cohomology on a tower of Shimura varieties, whereas Ash and Stevens [Reference Ash and StevensAS08] and Urban [Reference UrbanUrb11] instead consider cohomology of a large system of coefficients on a Shimura variety. Another construction which was introduced for
$\mathbb{Q}_{p}$
-Banach spaces, into which we can identify classical Hecke eigenvalues. For example Hida and Emerton consider for these cohomology groups some projective systems of étale cohomology on a tower of Shimura varieties, whereas Ash and Stevens [Reference Ash and StevensAS08] and Urban [Reference UrbanUrb11] instead consider cohomology of a large system of coefficients on a Shimura variety. Another construction which was introduced for
![]() $\operatorname{GL}_{2}$
by Andreatta, Iovita and Stevens [Reference Andreatta, Iovita and StevensAIS14] and Pilloni [Reference PilloniPil13] was to construct large coherent Banach sheaves on some open neighborhood of the rigid modular curve (more precisely on strict neighborhoods of the ordinary locus at
$\operatorname{GL}_{2}$
by Andreatta, Iovita and Stevens [Reference Andreatta, Iovita and StevensAIS14] and Pilloni [Reference PilloniPil13] was to construct large coherent Banach sheaves on some open neighborhood of the rigid modular curve (more precisely on strict neighborhoods of the ordinary locus at
![]() $p$
) indexed by
$p$
) indexed by
![]() $p$
-adic weights and that vary
$p$
-adic weights and that vary
![]() $p$
-adically. Their approach was then improved in [Reference Andreatta, Iovita and PilloniAIP15, Reference Andreatta, Bijakowski, Iovita, Kassaei, Pilloni, Stroh, Tian and XiaoABI+16] to treat the case of Siegel and Hilbert modular forms, still interpolating classical automorphic sheaves by large (coherent) Banach sheaves. This method relies heavily on the construction of the Banach sheaves for which the theory of the canonical subgroup is central. For example in the case of
$p$
-adically. Their approach was then improved in [Reference Andreatta, Iovita and PilloniAIP15, Reference Andreatta, Bijakowski, Iovita, Kassaei, Pilloni, Stroh, Tian and XiaoABI+16] to treat the case of Siegel and Hilbert modular forms, still interpolating classical automorphic sheaves by large (coherent) Banach sheaves. This method relies heavily on the construction of the Banach sheaves for which the theory of the canonical subgroup is central. For example in the case of
![]() $\operatorname{GL}_{2}$
, the idea is to construct a fibration in open ball centered in the images through the Hodge–Tate map of generators of the (dual of the) canonical subgroup inside the line bundle associated to the conormal sheaf
$\operatorname{GL}_{2}$
, the idea is to construct a fibration in open ball centered in the images through the Hodge–Tate map of generators of the (dual of the) canonical subgroup inside the line bundle associated to the conormal sheaf
![]() $\unicode[STIX]{x1D714}$
on the modular curve
$\unicode[STIX]{x1D714}$
on the modular curve
![]() $X_{0}(p)$
. This rigid sub-bundle has then more functions but as the canonical subgroup does not exist on the entire modular curve this fibration in open balls only exists on a strict neighborhood of the ordinary locus. Following the strategy of [Reference Andreatta, Iovita and PilloniAIP15, Reference Andreatta, Bijakowski, Iovita, Kassaei, Pilloni, Stroh, Tian and XiaoABI+16], Brasca [Reference BrascaBra16] extended this eigenvariety construction to groups that are associated to PEL Shimura varieties whose ordinary locus (at
$X_{0}(p)$
. This rigid sub-bundle has then more functions but as the canonical subgroup does not exist on the entire modular curve this fibration in open balls only exists on a strict neighborhood of the ordinary locus. Following the strategy of [Reference Andreatta, Iovita and PilloniAIP15, Reference Andreatta, Bijakowski, Iovita, Kassaei, Pilloni, Stroh, Tian and XiaoABI+16], Brasca [Reference BrascaBra16] extended this eigenvariety construction to groups that are associated to PEL Shimura varieties whose ordinary locus (at
![]() $p$
) is non-empty, still using the canonical subgroup theory as developed in [Reference FarguesFar11].
$p$
) is non-empty, still using the canonical subgroup theory as developed in [Reference FarguesFar11].
As soon as the ordinary locus is empty, the canonical subgroup theory gives no information and without a generalization of it the previous strategy seems vacuous. To my knowledge no eigenvarieties has been constructed using coherent cohomology when the ordinary locus is empty. Fortunately we developed in [Reference HernandezHer19] a generalization of this theory, called the canonical filtration, for (unramified at
![]() $p$
) PEL Shimura varieties. The first example when this happens is the case of
$p$
) PEL Shimura varieties. The first example when this happens is the case of
![]() $U(2,1)_{E/\mathbb{Q}}$
, where
$U(2,1)_{E/\mathbb{Q}}$
, where
![]() $E$
is a quadratic imaginary field, as the associated Picard modular surface has a non-empty ordinary locus if and only if
$E$
is a quadratic imaginary field, as the associated Picard modular surface has a non-empty ordinary locus if and only if
![]() $p$
splits in
$p$
splits in
![]() $E$
. In this article we present a construction of an eigenvariety interpolating
$E$
. In this article we present a construction of an eigenvariety interpolating
![]() $p$
-adically (cuspidal) Picard modular forms when
$p$
-adically (cuspidal) Picard modular forms when
![]() $p$
is inert in
$p$
is inert in
![]() $E$
. The strategy is then to construct new coherent Banach sheaves on strict neighborhoods of the
$E$
. The strategy is then to construct new coherent Banach sheaves on strict neighborhoods of the
![]() $\unicode[STIX]{x1D707}$
-ordinary locus using the (two-step) canonical filtration, and we get the following result,
$\unicode[STIX]{x1D707}$
-ordinary locus using the (two-step) canonical filtration, and we get the following result,
Theorem 1.1. Let
![]() $E$
be a quadratic imaginary field and
$E$
be a quadratic imaginary field and
![]() $p\neq 2$
a prime, inert in
$p\neq 2$
a prime, inert in
![]() $E$
. Fix a neat level
$E$
. Fix a neat level
![]() $K$
outside
$K$
outside
![]() $p$
, and a typeFootnote
1
$p$
, and a typeFootnote
1
![]() $(K_{J},J)$
outside
$(K_{J},J)$
outside
![]() $p$
, i.e. a compact open
$p$
, i.e. a compact open
![]() $K_{J}$
trivial at
$K_{J}$
trivial at
![]() $p$
, together with
$p$
, together with
![]() $J$
a finite dimensional complex representation of
$J$
a finite dimensional complex representation of
![]() $K_{J}$
, and we assume moreover that
$K_{J}$
, and we assume moreover that
![]() $K\subset \operatorname{Ker}J\subset K_{J}$
. Let
$K\subset \operatorname{Ker}J\subset K_{J}$
. Let
![]() $N$
be the places where
$N$
be the places where
![]() $K$
is not hyperspecial (or very special) and
$K$
is not hyperspecial (or very special) and
![]() $I_{p}$
a Iwahori subgroup at
$I_{p}$
a Iwahori subgroup at
![]() $p$
. There exists two equidimensional of dimension-
$p$
. There exists two equidimensional of dimension-
![]() $3$
rigid spaces,
$3$
rigid spaces,
with
![]() $\unicode[STIX]{x1D705}$
locally finite, together with dense inclusions
$\unicode[STIX]{x1D705}$
locally finite, together with dense inclusions
![]() $\mathbb{Z}^{3}\subset {\mathcal{W}}$
and
$\mathbb{Z}^{3}\subset {\mathcal{W}}$
and
![]() ${\mathcal{Z}}\subset {\mathcal{E}}$
such that
${\mathcal{Z}}\subset {\mathcal{E}}$
such that
![]() $\unicode[STIX]{x1D705}({\mathcal{Z}})\subset \mathbb{Z}^{3}$
, and each
$\unicode[STIX]{x1D705}({\mathcal{Z}})\subset \mathbb{Z}^{3}$
, and each
![]() $z\in {\mathcal{Z}}$
coincides with Hecke eigensystem for
$z\in {\mathcal{Z}}$
coincides with Hecke eigensystem for
![]() ${\mathcal{H}}={\mathcal{H}}^{Np}\otimes \mathbb{Z}[U_{p},S_{p}]$
acting on cuspidal Picard modular forms of weight
${\mathcal{H}}={\mathcal{H}}^{Np}\otimes \mathbb{Z}[U_{p},S_{p}]$
acting on cuspidal Picard modular forms of weight
![]() $\unicode[STIX]{x1D705}(z)$
, type
$\unicode[STIX]{x1D705}(z)$
, type
![]() $(K_{J}I_{p},J)$
that are finite slope for the action of
$(K_{J}I_{p},J)$
that are finite slope for the action of
![]() $U_{p}$
. More precisely, we have a map
$U_{p}$
. More precisely, we have a map
![]() ${\mathcal{H}}\longrightarrow {\mathcal{O}}({\mathcal{E}})$
, which induces an injection,
${\mathcal{H}}\longrightarrow {\mathcal{O}}({\mathcal{E}})$
, which induces an injection,
and such that for all
![]() $w\in {\mathcal{W}}(\overline{\mathbb{Q}_{p}})$
,
$w\in {\mathcal{W}}(\overline{\mathbb{Q}_{p}})$
,
![]() $\unicode[STIX]{x1D705}^{-1}(w)$
is identified by the previous map with eigenvalues for
$\unicode[STIX]{x1D705}^{-1}(w)$
is identified by the previous map with eigenvalues for
![]() ${\mathcal{H}}$
on the space of cuspidal, overconvergent and locally analytic Picard modular forms of weight
${\mathcal{H}}$
on the space of cuspidal, overconvergent and locally analytic Picard modular forms of weight
![]() $w$
, type
$w$
, type
![]() $(K_{J},J)$
which are finite slope for the action of
$(K_{J},J)$
which are finite slope for the action of
![]() $U_{p}$
. When
$U_{p}$
. When
![]() $z\in {\mathcal{Z}}$
is of weight
$z\in {\mathcal{Z}}$
is of weight
![]() $w$
(necessarily in
$w$
(necessarily in
![]() $\mathbb{Z}^{3}$
), then the system of Hecke eigenvalues for
$\mathbb{Z}^{3}$
), then the system of Hecke eigenvalues for
![]() ${\mathcal{H}}$
moreover coincide with one of
${\mathcal{H}}$
moreover coincide with one of
![]() ${\mathcal{H}}$
acting on classical previous such forms.
${\mathcal{H}}$
acting on classical previous such forms.
In order to get the previous result we need to have a control on the global sections of the Banach sheaves mentioned before the theorem. A general strategy to prove such a control result is developed in [Reference Andreatta, Iovita and PilloniAIP15] and rely on a vanishing theorem for cuspidal functions on the toroidal and minimal compactifications of the corresponding Shimura varieties. This kind of vanishing results have been proven in great generality in [Reference LanLan13] (though it does not apply here directly), but in the simpler case of
![]() $U(2,1)$
, as the boundary of the toroidal compactification is quite simple, we managed to simplify a part of the argument of [Reference Andreatta, Iovita and PilloniAIP15]. In a forthcoming work, we will use this method together with the technics developed in [Reference HernandezHer19] to construct eigenvarieties for more general PEL Shimura datum.
$U(2,1)$
, as the boundary of the toroidal compactification is quite simple, we managed to simplify a part of the argument of [Reference Andreatta, Iovita and PilloniAIP15]. In a forthcoming work, we will use this method together with the technics developed in [Reference HernandezHer19] to construct eigenvarieties for more general PEL Shimura datum.
The second part of this article focuses on a very nice application of eigenvarieties to construct Galois extensions in certain Selmer groups. The method follows the strategy initiated by Ribet [Reference RibetRib76] in the case of unequal characteristics to prove the converse to Herbrand theorem. It was then understood by Mazur and Wiles how to apply this technic in equal characteristics using Hida families to prove Iwasawa’s main conjecture. In his PhD [Reference BellaïcheBel02], Bellaïche understood that using a certain endoscopic representation together with a generalization of Ribet’s lemma he could produce some extensions of Galois representations, and then how to delete the wrong extensions to only keep the one predicted by the Bloch–Kato conjecture. This method was then improved using
![]() $p$
-adic families and Kisin’s result on triangulations of modular forms to construct the desired extensions in Selmer groups as in [Reference Bellaïche and ChenevierBC04] for imaginary quadratic Hecke character and [Reference Skinner and UrbanSU02] for modular forms using Saito–Kurokawa lifts to
$p$
-adic families and Kisin’s result on triangulations of modular forms to construct the desired extensions in Selmer groups as in [Reference Bellaïche and ChenevierBC04] for imaginary quadratic Hecke character and [Reference Skinner and UrbanSU02] for modular forms using Saito–Kurokawa lifts to
![]() $\operatorname{GSp}_{4}$
. In the previous constructions, it seemed necessary that the sign at the center of the functional equation is
$\operatorname{GSp}_{4}$
. In the previous constructions, it seemed necessary that the sign at the center of the functional equation is
![]() $-1$
, in order to get an endoscopic automorphic representation for a bigger group (
$-1$
, in order to get an endoscopic automorphic representation for a bigger group (
![]() $U(3)$
in [Reference Bellaïche and ChenevierBC04],
$U(3)$
in [Reference Bellaïche and ChenevierBC04],
![]() $\operatorname{GSp}_{4}$
in [Reference Skinner and UrbanSU02]) related the one we started with. In this article, we study the simplest case with a sign
$\operatorname{GSp}_{4}$
in [Reference Skinner and UrbanSU02]) related the one we started with. In this article, we study the simplest case with a sign
![]() $+1$
.
$+1$
.
Let
![]() $\unicode[STIX]{x1D712}$
be an algebraic Hecke character of
$\unicode[STIX]{x1D712}$
be an algebraic Hecke character of
![]() $E$
satisfying the polarization
$E$
satisfying the polarization
and let
![]() $L(\unicode[STIX]{x1D712},s)$
be its
$L(\unicode[STIX]{x1D712},s)$
be its
![]() $L$
-function. In particular
$L$
-function. In particular
![]() $\unicode[STIX]{x1D712}_{\infty }(z)=z^{a}\overline{z}^{1-a}$
for all
$\unicode[STIX]{x1D712}_{\infty }(z)=z^{a}\overline{z}^{1-a}$
for all
![]() $z\in \mathbb{C}^{\times }$
where
$z\in \mathbb{C}^{\times }$
where
![]() $a\in \mathbb{Z}$
. Denote by
$a\in \mathbb{Z}$
. Denote by
![]() $\unicode[STIX]{x1D712}_{p}:G_{E}\longrightarrow F^{\times }$
, where
$\unicode[STIX]{x1D712}_{p}:G_{E}\longrightarrow F^{\times }$
, where
![]() $F/\mathbb{Q}_{p}$
is a finite extension, the associated
$F/\mathbb{Q}_{p}$
is a finite extension, the associated
![]() $p$
-adic Galois character, and
$p$
-adic Galois character, and
![]() $H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
the Selmer group of
$H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
the Selmer group of
![]() $\unicode[STIX]{x1D712}_{p}$
, which is the sub-
$\unicode[STIX]{x1D712}_{p}$
, which is the sub-
![]() $F$
-vector space of
$F$
-vector space of
![]() $H^{1}(E,\unicode[STIX]{x1D712}_{p})$
generated by the extensions,
$H^{1}(E,\unicode[STIX]{x1D712}_{p})$
generated by the extensions,
such that for
![]() $v\!\not |~p$
$v\!\not |~p$
and for
![]() $v|p$
$v|p$
We will say that such an extension has good reduction everywhere. The conjecture of Bloch and Kato predicts the equality
![]() $\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)=\dim _{F}H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
, and in particular the following result, due to Rubin [Reference RubinRub91].
$\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)=\dim _{F}H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
, and in particular the following result, due to Rubin [Reference RubinRub91].
Theorem 1.2 (Rubin).
Suppose
![]() $p\!\not |~|{\mathcal{O}}_{E}^{\times }|$
. If
$p\!\not |~|{\mathcal{O}}_{E}^{\times }|$
. If
![]() $L(\unicode[STIX]{x1D712},0)=0$
, then
$L(\unicode[STIX]{x1D712},0)=0$
, then
![]() $H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})\neq \{0\}$
.
$H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})\neq \{0\}$
.
The previous result follows from Rubin’s work on Iwasawa’s main conjecture for elliptic curves with complex multiplication (CM) and its proof uses Euler systems. In particular this construction proves that the Selmer group is non-trivial but does not really construct a particular extension. For example it is not possible to know if the extension that exists is geometric or automorphic in nature. Another proof of this result [Reference Bellaïche and ChenevierBC04] uses families of modular forms given by the corresponding eigenvarieties, a particular case of transfer as predicted by Langland’s philosophy, together with a generalization of Ribet’s ‘change of lattice’ lemma. More precisely, if
![]() $p$
is split in
$p$
is split in
![]() $E$
,
$E$
,
![]() $p\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
, and the order of vanishing
$p\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
, and the order of vanishing
![]() $\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)$
is odd, then Bellaïche and Chenevier can construct the predicted extension in
$\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)$
is odd, then Bellaïche and Chenevier can construct the predicted extension in
![]() $H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
by deformation of a non-tempered automorphic form
$H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
by deformation of a non-tempered automorphic form
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
for
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
for
![]() $U(3)$
, the compact at infinity unitary group in three variables. It is a natural question to ask why this condition of the order of vanishing being odd is necessary. If the order of vanishing is even, following multiplicity results on automorphic representations for unitary groups on three variables of Rogawski [Reference RogawskiRog92, Reference RogawskiRog90], there exists a non-tempered automorphic representation
$U(3)$
, the compact at infinity unitary group in three variables. It is a natural question to ask why this condition of the order of vanishing being odd is necessary. If the order of vanishing is even, following multiplicity results on automorphic representations for unitary groups on three variables of Rogawski [Reference RogawskiRog92, Reference RogawskiRog90], there exists a non-tempered automorphic representation
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
for
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
for
![]() $U(2,1)$
with Galois representation
$U(2,1)$
with Galois representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712}),p}=1\oplus \unicode[STIX]{x1D712}_{p}\oplus \unicode[STIX]{x1D712}_{p}^{\bot }$
. In this article we check that we can indeed deform this representation such that the associate Galois deformation is generically irreducible, and that we can control the reduction at each place, thus constructing an extension in the Selmer group. More precisely we can reprove the following case of Rubin’s result.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712}),p}=1\oplus \unicode[STIX]{x1D712}_{p}\oplus \unicode[STIX]{x1D712}_{p}^{\bot }$
. In this article we check that we can indeed deform this representation such that the associate Galois deformation is generically irreducible, and that we can control the reduction at each place, thus constructing an extension in the Selmer group. More precisely we can reprove the following case of Rubin’s result.
Theorem 1.3. Let
![]() $p$
a prime, unramified in
$p$
a prime, unramified in
![]() $E$
, such that
$E$
, such that
![]() $p\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
. Suppose moreover that
$p\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
. Suppose moreover that
![]() $p\neq 2$
if
$p\neq 2$
if
![]() $p$
is inert. If
$p$
is inert. If
![]() $L(\unicode[STIX]{x1D712},0)=0$
and
$L(\unicode[STIX]{x1D712},0)=0$
and
![]() $\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)$
is even, then
$\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)$
is even, then
In particular, we can extend the result of [Reference Bellaïche and ChenevierBC04] when the order of vanishing is even, and also to the case of an inert prime
![]() $p$
using the corresponding eigenvariety (in this case the ordinary locus is empty). An advantage of the construction of the eigenvariety presented here is that if a Hecke eigensystem appears in the classical cuspidal global sections of a coherent automorphic sheaf, then there is an associated point on the eigenvariety. This argument might be more complicated with other constructions, as the representation
$p$
using the corresponding eigenvariety (in this case the ordinary locus is empty). An advantage of the construction of the eigenvariety presented here is that if a Hecke eigensystem appears in the classical cuspidal global sections of a coherent automorphic sheaf, then there is an associated point on the eigenvariety. This argument might be more complicated with other constructions, as the representation
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
is not a regular discrete series (it does not even appear in the cohomology in middle degree). Another advantage of using coherent cohomology is that we can also deal with the limit case where
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
is not a regular discrete series (it does not even appear in the cohomology in middle degree). Another advantage of using coherent cohomology is that we can also deal with the limit case where
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
does not appear in the étale cohomologyFootnote
2
(but it was known to Bellaïche [Reference BellaïcheBel12] how to get this limit case). Apart from this fact, the deformation when
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
does not appear in the étale cohomologyFootnote
2
(but it was known to Bellaïche [Reference BellaïcheBel12] how to get this limit case). Apart from this fact, the deformation when
![]() $p$
is split follows the lines of [Reference Bellaïche and ChenevierBC04], whereas when
$p$
is split follows the lines of [Reference Bellaïche and ChenevierBC04], whereas when
![]() $p$
is inert the geometry of the eigenvariety is quite different. In particular, there are fewer refinements (and thus only one point on
$p$
is inert the geometry of the eigenvariety is quite different. In particular, there are fewer refinements (and thus only one point on
![]() ${\mathcal{E}}$
corresponding to
${\mathcal{E}}$
corresponding to
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
instead of three) and we need a bit more care to isolate the right extension. We also need to be slightly more careful with
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
instead of three) and we need a bit more care to isolate the right extension. We also need to be slightly more careful with
![]() $p$
-adic Hodge theory to understand the local–global compatibility at
$p$
-adic Hodge theory to understand the local–global compatibility at
![]() $p$
and a generalization of Kisin’s result on triangulation of refined families as provided by [Reference LiuLiu15]. Let us also remark that a consequence of this construction and Chenevier’s method [Reference ChenevierChe05] to compare the eigenvarieties for
$p$
and a generalization of Kisin’s result on triangulation of refined families as provided by [Reference LiuLiu15]. Let us also remark that a consequence of this construction and Chenevier’s method [Reference ChenevierChe05] to compare the eigenvarieties for
![]() $U(3)$
and
$U(3)$
and
![]() $U(2,1)$
(say when
$U(2,1)$
(say when
![]() $p$
splits) is that the point
$p$
splits) is that the point
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
when the sign at infinity is
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
when the sign at infinity is
![]() $+1$
together with its good refinement also appears in the eigenvariety of
$+1$
together with its good refinement also appears in the eigenvariety of
![]() $U(3)$
, despite not being a classical point for this group.
$U(3)$
, despite not being a classical point for this group.
A lot of the ideas developed in this article extend to more general Shimura varieties, and in particular to Picard modular varieties associated to a general CM field
![]() $E$
. More precisely, the result on the canonical filtration (Theorem 5.8) in this last case remains true as soon as
$E$
. More precisely, the result on the canonical filtration (Theorem 5.8) in this last case remains true as soon as
![]() $p\geqslant 3$
. For more general groups the bound on the prime
$p\geqslant 3$
. For more general groups the bound on the prime
![]() $p$
will grow with the group as predicted in [Reference HernandezHer19]. This is also why we cannot use
$p$
will grow with the group as predicted in [Reference HernandezHer19]. This is also why we cannot use
![]() $p=2$
in this article. With this restriction on the prime, we should also be able to construct the associated eigenvariety, and we hope to come back on this matter in a following article. For the second part, which deals with the Bloch–Kato conjecture, it is less clear what to expect. Already for
$p=2$
in this article. With this restriction on the prime, we should also be able to construct the associated eigenvariety, and we hope to come back on this matter in a following article. For the second part, which deals with the Bloch–Kato conjecture, it is less clear what to expect. Already for
![]() $U(2,1)_{E/F}$
with
$U(2,1)_{E/F}$
with
![]() $E$
a CM extension, we can use the work of Rogawski and prove that the Galois representation passing through a particular refinement is irreducible; unfortunately, just as in [Reference Bellaïche and ChenevierBC09], we cannot get rid of the bad extension in
$E$
a CM extension, we can use the work of Rogawski and prove that the Galois representation passing through a particular refinement is irreducible; unfortunately, just as in [Reference Bellaïche and ChenevierBC09], we cannot get rid of the bad extension in
![]() $H_{f}^{1}(E,\unicode[STIX]{x1D714}_{p})$
anymore (see § 11.5). For higher-dimensional groups, we could probably have similar results as the one in the book [Reference Bellaïche and ChenevierBC09], but, in addition to the previous remark, results in this case would be conditional on Arthur’s conjecture, as in [Reference Bellaïche and ChenevierBC09].
$H_{f}^{1}(E,\unicode[STIX]{x1D714}_{p})$
anymore (see § 11.5). For higher-dimensional groups, we could probably have similar results as the one in the book [Reference Bellaïche and ChenevierBC09], but, in addition to the previous remark, results in this case would be conditional on Arthur’s conjecture, as in [Reference Bellaïche and ChenevierBC09].
2 Shimura datum
2.1 Global datum
Let
![]() $E/\mathbb{Q}$
a quadratic imaginary field and denote by
$E/\mathbb{Q}$
a quadratic imaginary field and denote by
![]() $\overline{\bullet }$
the complex conjugation of
$\overline{\bullet }$
the complex conjugation of
![]() $E$
. Let
$E$
. Let
![]() $(V=E^{3},\unicode[STIX]{x1D713})$
be the hermitian space of dimension
$(V=E^{3},\unicode[STIX]{x1D713})$
be the hermitian space of dimension
![]() $3$
over E, of signature
$3$
over E, of signature
![]() $(2,1)$
at infinity given by the matrix
$(2,1)$
at infinity given by the matrix
 $$\begin{eqnarray}J=\left(\begin{array}{@{}ccc@{}} & & 1\\ & 1 & \\ 1 & & \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}J=\left(\begin{array}{@{}ccc@{}} & & 1\\ & 1 & \\ 1 & & \end{array}\right).\end{eqnarray}$$
Let us then denote by
the reductive group over
![]() $\mathbb{Q}$
of unitary similitudes of
$\mathbb{Q}$
of unitary similitudes of
![]() $(V,\unicode[STIX]{x1D713})$
.
$(V,\unicode[STIX]{x1D713})$
.
Let
![]() $p$
be a prime number, unramified in
$p$
be a prime number, unramified in
![]() $E$
. If
$E$
. If
![]() $p=v\overline{v}$
is split in
$p=v\overline{v}$
is split in
![]() $E$
, then
$E$
, then
where the action of
![]() $E_{v}$
is by
$E_{v}$
is by
![]() $\overline{v}$
on
$\overline{v}$
on
![]() $\overline{V\otimes _{E}E_{v}}$
. Moreover, the complex conjugation exchanges
$\overline{V\otimes _{E}E_{v}}$
. Moreover, the complex conjugation exchanges
![]() $V\otimes _{E}E_{v}$
and
$V\otimes _{E}E_{v}$
and
![]() $\overline{V\otimes _{E}E_{v}}$
. In particular,
$\overline{V\otimes _{E}E_{v}}$
. In particular,
![]() $G\otimes _{\mathbb{Q}}\mathbb{Q}_{p}\simeq \operatorname{GL}(V\otimes _{E}E_{v})\times \mathbb{G}_{m}$
(this isomorphism depends on the choice of
$G\otimes _{\mathbb{Q}}\mathbb{Q}_{p}\simeq \operatorname{GL}(V\otimes _{E}E_{v})\times \mathbb{G}_{m}$
(this isomorphism depends on the choice of
![]() $v$
over
$v$
over
![]() $p$
).
$p$
).
We will be particularly interested in the case where
![]() $p$
is inert in
$p$
is inert in
![]() $E$
; the case when
$E$
; the case when
![]() $p$
split has been studied before (see for example [Reference BrascaBra16]).
$p$
split has been studied before (see for example [Reference BrascaBra16]).
Remark 2.1. We could more generally work in the setting of
![]() $(B,\star )$
a simple
$(B,\star )$
a simple
![]() $E$
-algebra of rank
$E$
-algebra of rank
![]() $9$
with an involution of the second kind, such that
$9$
with an involution of the second kind, such that
![]() $(B\otimes \mathbb{Q}_{p},\star )$
is isomorphic to
$(B\otimes \mathbb{Q}_{p},\star )$
is isomorphic to
![]() $(\operatorname{End}(V\otimes \mathbb{Q}_{p}),\star _{V})$
,Footnote
3
and replace
$(\operatorname{End}(V\otimes \mathbb{Q}_{p}),\star _{V})$
,Footnote
3
and replace
![]() $G$
with the group,
$G$
with the group,
The construction of the eigenvarieties in the case where
![]() $B$
is not split is easier as the associated Shimura varieties are compact, but some non-tempered automorphic form, for example the one constructed by Rogawski and studied in [Reference Bellaïche and ChenevierBC04] and the second part of this article, will never be automorphic for such non-split
$B$
is not split is easier as the associated Shimura varieties are compact, but some non-tempered automorphic form, for example the one constructed by Rogawski and studied in [Reference Bellaïche and ChenevierBC04] and the second part of this article, will never be automorphic for such non-split
![]() $B$
.
$B$
.
The Shimura datum we consider is given by
 $$\begin{eqnarray}h:\begin{array}{@{}ccc@{}}\mathbb{S} & \longrightarrow & G_{\mathbb{R}}\\ z=x+iy & \longmapsto & \left(\begin{array}{@{}ccc@{}}x & & iy\\ & z & \\ iy & & x\end{array}\right).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}h:\begin{array}{@{}ccc@{}}\mathbb{S} & \longrightarrow & G_{\mathbb{R}}\\ z=x+iy & \longmapsto & \left(\begin{array}{@{}ccc@{}}x & & iy\\ & z & \\ iy & & x\end{array}\right).\end{array}\end{eqnarray}$$
2.2 Complex Picard modular forms and automorphic forms
Classically, Picard modular forms are introduced using the unitary group
![]() $U(2,1)$
, but we can treat the case of
$U(2,1)$
, but we can treat the case of
![]() $GU(2,1)$
similarly. Let
$GU(2,1)$
similarly. Let
![]() $G(\mathbb{R})=GU(2,1)(\mathbb{R})$
the group stabilizing (up to scalar) the signature matrix
$G(\mathbb{R})=GU(2,1)(\mathbb{R})$
the group stabilizing (up to scalar) the signature matrix
![]() $J$
and let
$J$
and let
be the symmetric space associated to
![]() $G(\mathbb{R})$
, it is isomorphic to the two-dimensional complex unit ball
$G(\mathbb{R})$
, it is isomorphic to the two-dimensional complex unit ball
On
![]() $Y$
, there is an action of
$Y$
, there is an action of
![]() $G(\mathbb{R})$
through
$G(\mathbb{R})$
through
Remark 2.2. It is known that
![]() $U(2,1)(\mathbb{R})$
stabilizes
$U(2,1)(\mathbb{R})$
stabilizes
![]() $Y$
, and
$Y$
, and
![]() $GU(2,1)(\mathbb{R})$
stabilizes
$GU(2,1)(\mathbb{R})$
stabilizes
![]() $X$
too as if
$X$
too as if
![]() $^{t}\overline{A}JA=cJ$
with
$^{t}\overline{A}JA=cJ$
with
![]() $c\in \mathbb{R}^{\times }$
, we get
$c\in \mathbb{R}^{\times }$
, we get
![]() $\overline{\det A}\det A=|\text{det}A|^{2}=c^{3}$
thus
$\overline{\det A}\det A=|\text{det}A|^{2}=c^{3}$
thus
![]() $c>0$
.
$c>0$
.
This action is transitive and identifies
![]() $Y$
with
$Y$
with
![]() $G(\mathbb{R})/K_{\infty }$
where
$G(\mathbb{R})/K_{\infty }$
where
![]() $K_{\infty }=\operatorname{Stab}((i,0))\subset$
$K_{\infty }=\operatorname{Stab}((i,0))\subset$
![]() $\{(A,e)\in GU(2)(\mathbb{R})\times GU(1)(\mathbb{R})\}$
can be identified with
$\{(A,e)\in GU(2)(\mathbb{R})\times GU(1)(\mathbb{R})\}$
can be identified with
![]() $\{(A,e)\in GU(2)(\mathbb{R})\times \mathbb{C}^{\times }:c(A)=N(e)\}$
. We write
$\{(A,e)\in GU(2)(\mathbb{R})\times \mathbb{C}^{\times }:c(A)=N(e)\}$
. We write
![]() $(i,0)=x_{0}$
.
$(i,0)=x_{0}$
.
The subgroup
![]() $K_{\infty }$
is not compact but can be written
$K_{\infty }$
is not compact but can be written
![]() $Z(\mathbb{R})^{0}(U(2)(\mathbb{R})\times U(1)(\mathbb{R}))$
, with
$Z(\mathbb{R})^{0}(U(2)(\mathbb{R})\times U(1)(\mathbb{R}))$
, with
![]() $Z$
the center of
$Z$
the center of
![]() $GU(2,1)$
. Let
$GU(2,1)$
. Let
![]() $L$
be the
$L$
be the
![]() $\mathbb{C}$
-points of
$\mathbb{C}$
-points of
![]() $K_{\infty }$
. Then
$K_{\infty }$
. Then
![]() $L\simeq (\operatorname{GL}_{2}\times \operatorname{GL}_{1})\times \operatorname{GL}_{1}(\mathbb{C})$
is the Levi of a parabolic
$L\simeq (\operatorname{GL}_{2}\times \operatorname{GL}_{1})\times \operatorname{GL}_{1}(\mathbb{C})$
is the Levi of a parabolic
![]() $P$
in
$P$
in
![]() $\operatorname{GL}_{3}\times \operatorname{GL}_{1}(\mathbb{C})$
. For any
$\operatorname{GL}_{3}\times \operatorname{GL}_{1}(\mathbb{C})$
. For any
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3},r)\in \mathbb{Z}^{4}$
such that
$\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3},r)\in \mathbb{Z}^{4}$
such that
![]() $k_{1}\geqslant k_{2}$
, there is an associated (irreducible) representation
$k_{1}\geqslant k_{2}$
, there is an associated (irreducible) representation
![]() $S_{\unicode[STIX]{x1D705}}(\mathbb{C})$
of
$S_{\unicode[STIX]{x1D705}}(\mathbb{C})$
of
![]() $P$
, of highest weight
$P$
, of highest weight
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}t_{1} & & \\ & t_{2} & \\ & & t_{3}\end{array}\right),c\in (\operatorname{GL}_{2}\times \operatorname{GL}_{1})\times \operatorname{GL}_{1}(\mathbb{C})\longmapsto t_{1}^{k_{1}}t_{2}^{k_{2}}t_{3}^{k_{3}}c^{r}.\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}t_{1} & & \\ & t_{2} & \\ & & t_{3}\end{array}\right),c\in (\operatorname{GL}_{2}\times \operatorname{GL}_{1})\times \operatorname{GL}_{1}(\mathbb{C})\longmapsto t_{1}^{k_{1}}t_{2}^{k_{2}}t_{3}^{k_{3}}c^{r}.\end{eqnarray}$$
The subgroup
![]() $K_{\infty }$
embeds in
$K_{\infty }$
embeds in
![]() $L\subset P$
by
$L\subset P$
by
![]() $(A,e)\mapsto ((\overline{A},e),N(e))$
.
$(A,e)\mapsto ((\overline{A},e),N(e))$
.
Following [Reference HarrisHar90b, Reference HarrisHar84, Reference MilneMil88], such a representation gives
![]() $\unicode[STIX]{x1D6FA}^{\unicode[STIX]{x1D705}}$
a locally free sheaf with
$\unicode[STIX]{x1D6FA}^{\unicode[STIX]{x1D705}}$
a locally free sheaf with
![]() $G(\mathbb{C})$
-action on
$G(\mathbb{C})$
-action on
![]() $G(\mathbb{C})/P$
, whose structure as sheaf does not depend on
$G(\mathbb{C})/P$
, whose structure as sheaf does not depend on
![]() $r$
. Restricting it to
$r$
. Restricting it to
![]() $G(\mathbb{R})/K_{\infty }=Y$
we get a sheaf
$G(\mathbb{R})/K_{\infty }=Y$
we get a sheaf
![]() $\unicode[STIX]{x1D6FA}^{\unicode[STIX]{x1D705}}$
whose sections over
$\unicode[STIX]{x1D6FA}^{\unicode[STIX]{x1D705}}$
whose sections over
![]() $X$
can be seen as holomorphic functions,
$X$
can be seen as holomorphic functions,
such that
![]() $f(gk)=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D705}}(k)^{-1}f(g)$
, for
$f(gk)=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D705}}(k)^{-1}f(g)$
, for
![]() $g\in G(\mathbb{R}),k\in K_{\infty }$
, which we call (meromorphic at infinity) modular forms of weight
$g\in G(\mathbb{R}),k\in K_{\infty }$
, which we call (meromorphic at infinity) modular forms of weight
![]() $\unicode[STIX]{x1D705}$
. In an informal way, the choice of the previous integer
$\unicode[STIX]{x1D705}$
. In an informal way, the choice of the previous integer
![]() $r$
normalizes the action of the Hecke operators and corresponds to normalizing the (norm of the) central character of the modular forms. We will not use this description of the sheaves, and instead introduced a modular description of these automorphic sheaves.
$r$
normalizes the action of the Hecke operators and corresponds to normalizing the (norm of the) central character of the modular forms. We will not use this description of the sheaves, and instead introduced a modular description of these automorphic sheaves.
Fix
![]() $\unicode[STIX]{x1D70F}_{\infty }:E\longrightarrow \mathbb{C}$
an embedding, and
$\unicode[STIX]{x1D70F}_{\infty }:E\longrightarrow \mathbb{C}$
an embedding, and
![]() $\unicode[STIX]{x1D70E}\neq 1\in \operatorname{Gal}(E/\mathbb{Q})$
; thus
$\unicode[STIX]{x1D70E}\neq 1\in \operatorname{Gal}(E/\mathbb{Q})$
; thus
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}_{\infty }=\overline{\unicode[STIX]{x1D70F}_{\infty }}$
is the other embedding of
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}_{\infty }=\overline{\unicode[STIX]{x1D70F}_{\infty }}$
is the other embedding of
![]() $E$
. Over
$E$
. Over
![]() $\mathbb{C}$
, for any sufficiently small compact open
$\mathbb{C}$
, for any sufficiently small compact open
![]() $K$
in
$K$
in
![]() $G(\mathbb{A}_{f})$
, the Picard variety
$G(\mathbb{A}_{f})$
, the Picard variety
![]() $Y_{K}(\mathbb{C})$
of level
$Y_{K}(\mathbb{C})$
of level
![]() $K$
can be identified with a (disjoint union of some) quotient of
$K$
can be identified with a (disjoint union of some) quotient of
![]() $B=GU(2,1)/K_{\infty }$
, but also with the moduli space parametrizing quadruples
$B=GU(2,1)/K_{\infty }$
, but also with the moduli space parametrizing quadruples
![]() $(A,\unicode[STIX]{x1D704},\unicode[STIX]{x1D706},\unicode[STIX]{x1D702})$
where
$(A,\unicode[STIX]{x1D704},\unicode[STIX]{x1D706},\unicode[STIX]{x1D702})$
where
![]() $A$
is an abelian scheme of genus
$A$
is an abelian scheme of genus
![]() $3$
,
$3$
,
![]() $\unicode[STIX]{x1D704}:{\mathcal{O}}_{E}\longrightarrow \operatorname{End}(A)$
is an injection,
$\unicode[STIX]{x1D704}:{\mathcal{O}}_{E}\longrightarrow \operatorname{End}(A)$
is an injection,
![]() $\unicode[STIX]{x1D706}$
is a polarization for which Rosati involution corresponds to the conjugation
$\unicode[STIX]{x1D706}$
is a polarization for which Rosati involution corresponds to the conjugation
![]() $\overline{\cdot }$
on
$\overline{\cdot }$
on
![]() ${\mathcal{O}}$
, and
${\mathcal{O}}$
, and
![]() $\unicode[STIX]{x1D702}$
is a type-
$\unicode[STIX]{x1D702}$
is a type-
![]() $K$
-level structure such that the action of
$K$
-level structure such that the action of
![]() ${\mathcal{O}}_{E}$
on the conormal sheaf
${\mathcal{O}}_{E}$
on the conormal sheaf
![]() $\unicode[STIX]{x1D714}_{A}=e_{A/S}^{\ast }\unicode[STIX]{x1D6FA}_{A/S}^{1}$
Footnote
4
decomposes under the embeddings
$\unicode[STIX]{x1D714}_{A}=e_{A/S}^{\ast }\unicode[STIX]{x1D6FA}_{A/S}^{1}$
Footnote
4
decomposes under the embeddings
![]() $\unicode[STIX]{x1D70F}_{\infty },\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}_{\infty }$
into two direct factors of respective dimensions
$\unicode[STIX]{x1D70F}_{\infty },\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}_{\infty }$
into two direct factors of respective dimensions
![]() $1$
and
$1$
and
![]() $2$
. This is done, for example, explicitly in [Reference de Shalit and GorendSG16, § 1.2.2–1.2.4], and we will be especially interested in the description by ‘moving lattice’ given in [Reference de Shalit and GorendSG16, § 1.2.4]. Thus, to every
$2$
. This is done, for example, explicitly in [Reference de Shalit and GorendSG16, § 1.2.2–1.2.4], and we will be especially interested in the description by ‘moving lattice’ given in [Reference de Shalit and GorendSG16, § 1.2.4]. Thus, to every
![]() $x=(z_{1},z_{2})\in B$
, we can associate a complex abelian variety,
$x=(z_{1},z_{2})\in B$
, we can associate a complex abelian variety,
where
![]() $L_{x}$
is the
$L_{x}$
is the
![]() ${\mathcal{O}}_{E}$
-module given in [Reference de Shalit and GorendSG16, (1.25)], and the action of
${\mathcal{O}}_{E}$
-module given in [Reference de Shalit and GorendSG16, (1.25)], and the action of
![]() ${\mathcal{O}}_{E}$
on
${\mathcal{O}}_{E}$
on
![]() $A_{x}$
is given by
$A_{x}$
is given by
 $$\begin{eqnarray}a\in {\mathcal{O}}_{E}\longmapsto \left(\begin{array}{@{}ccc@{}}\overline{\unicode[STIX]{x1D70F}}_{\infty }(a) & & \\ & \overline{\unicode[STIX]{x1D70F}}_{\infty }(a) & \\ & & \unicode[STIX]{x1D70F}_{\infty }(a)\end{array}\right)\in M_{3}(\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}a\in {\mathcal{O}}_{E}\longmapsto \left(\begin{array}{@{}ccc@{}}\overline{\unicode[STIX]{x1D70F}}_{\infty }(a) & & \\ & \overline{\unicode[STIX]{x1D70F}}_{\infty }(a) & \\ & & \unicode[STIX]{x1D70F}_{\infty }(a)\end{array}\right)\in M_{3}(\mathbb{C}).\end{eqnarray}$$
There is, moreover,
![]() $\unicode[STIX]{x1D702}_{x}$
a canonical (
$\unicode[STIX]{x1D702}_{x}$
a canonical (
![]() $K$
-orbit of) level-
$K$
-orbit of) level-
![]() $N$
-structure (for
$N$
-structure (for
![]() $K(N)\subset K\subset G(\mathbb{A}_{f})$
). Over
$K(N)\subset K\subset G(\mathbb{A}_{f})$
). Over
![]() $Y_{K}(\mathbb{C})$
we thus have a sheaf
$Y_{K}(\mathbb{C})$
we thus have a sheaf
![]() $\unicode[STIX]{x1D714}_{A}$
that can be decomposed
$\unicode[STIX]{x1D714}_{A}$
that can be decomposed
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F},A}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},A}$
according to the action of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F},A}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},A}$
according to the action of
![]() ${\mathcal{O}}_{E}$
, and we can consider the sheaf
${\mathcal{O}}_{E}$
, and we can consider the sheaf
for
![]() $(k_{1},k_{2},k_{3})$
a dominant (i.e.
$(k_{1},k_{2},k_{3})$
a dominant (i.e.
![]() $k_{1}\geqslant k_{2}$
) weight. Using the previous description, if we denote by
$k_{1}\geqslant k_{2}$
) weight. Using the previous description, if we denote by
![]() $\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}$
the coordinates on
$\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2},\unicode[STIX]{x1D701}_{3}$
the coordinates on
![]() $\mathbb{C}^{3}$
,
$\mathbb{C}^{3}$
,
![]() $\unicode[STIX]{x1D714}_{A_{x},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
is generated by
$\unicode[STIX]{x1D714}_{A_{x},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
is generated by
![]() $d\unicode[STIX]{x1D701}_{1},\,d\unicode[STIX]{x1D701}_{2}$
and
$d\unicode[STIX]{x1D701}_{1},\,d\unicode[STIX]{x1D701}_{2}$
and
![]() $\unicode[STIX]{x1D714}_{A_{x},\unicode[STIX]{x1D70F}}$
by
$\unicode[STIX]{x1D714}_{A_{x},\unicode[STIX]{x1D70F}}$
by
![]() $d\unicode[STIX]{x1D701}_{3}$
.
$d\unicode[STIX]{x1D701}_{3}$
.
There is also
![]() $X_{K}(\mathbb{C})$
a toroidal compactification of
$X_{K}(\mathbb{C})$
a toroidal compactification of
![]() $Y_{K}(\mathbb{C})$
, [Reference LarsenLar92] and [Reference BellaïcheBel06b], on which
$Y_{K}(\mathbb{C})$
, [Reference LarsenLar92] and [Reference BellaïcheBel06b], on which
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
extends as
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
extends as
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
(the canonical sheaf of Picard modular forms) and
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
(the canonical sheaf of Picard modular forms) and
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}(-D)$
(the sheaf of cuspidal forms) where
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}(-D)$
(the sheaf of cuspidal forms) where
![]() $D$
here is the closed subscheme
$D$
here is the closed subscheme
![]() $X_{K}\backslash Y_{K}$
together with its reduced structure.
$X_{K}\backslash Y_{K}$
together with its reduced structure.
Definition 2.3. We call the module
![]() $H^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
(respectively
$H^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
(respectively
![]() $H^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}(-D))=:H_{\text{cusp}}^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
) the space of (respectively, cuspidal) Picard modular forms of level
$H^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}(-D))=:H_{\text{cusp}}^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
) the space of (respectively, cuspidal) Picard modular forms of level
![]() $K$
and weight
$K$
and weight
![]() $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.
We sometimes say ‘classical’ if we want to emphasis the difference with overconvergent modular forms defined later. Denote also by
![]() $V^{\unicode[STIX]{x1D705}}$
the representation of
$V^{\unicode[STIX]{x1D705}}$
the representation of
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
given by
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
given by
Definition 2.4. For all
![]() $g\in G(\mathbb{R})=GU(2,1)(\mathbb{R})$
, write
$g\in G(\mathbb{R})=GU(2,1)(\mathbb{R})$
, write
and for
![]() $x=(z_{1},z_{2})\in B$
, following [Reference ShimuraShi78], define
$x=(z_{1},z_{2})\in B$
, following [Reference ShimuraShi78], define
Finally, define
The following proposition is well known (see [Reference HsiehHsi14, Lemma 3.7]) and probably already in [Reference ShimuraShi78], but we rewrite it to fix the notations,
Proposition 2.5. There is a bijection between
![]() $H^{0}(Y_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
and functions
$H^{0}(Y_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
and functions
![]() $F:B\times G(\mathbb{A}_{\mathbb{Q},f})\longrightarrow V^{\unicode[STIX]{x1D705}}$
such that:
$F:B\times G(\mathbb{A}_{\mathbb{Q},f})\longrightarrow V^{\unicode[STIX]{x1D705}}$
such that:
(i) for all
 $\unicode[STIX]{x1D6FE}\in G(\mathbb{Z}),F(\unicode[STIX]{x1D6FE}x,\unicode[STIX]{x1D6FE}k)=J(\unicode[STIX]{x1D6FE},x)\cdot F(x,k)$
;
$\unicode[STIX]{x1D6FE}\in G(\mathbb{Z}),F(\unicode[STIX]{x1D6FE}x,\unicode[STIX]{x1D6FE}k)=J(\unicode[STIX]{x1D6FE},x)\cdot F(x,k)$
;(ii) for all
 $k^{\prime }\in K,F(x,kk^{\prime })=F(x,k)$
$k^{\prime }\in K,F(x,kk^{\prime })=F(x,k)$
given by
![]() $F(x,k)=f(A_{x},\unicode[STIX]{x1D702}_{x}\circ k^{\unicode[STIX]{x1D70E}},(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2},d\unicode[STIX]{x1D701}_{3}))$
.
$F(x,k)=f(A_{x},\unicode[STIX]{x1D702}_{x}\circ k^{\unicode[STIX]{x1D70E}},(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2},d\unicode[STIX]{x1D701}_{3}))$
.
Proof. For all
![]() $\unicode[STIX]{x1D6FE}\in G(\mathbb{Z})$
, there is an isomorphism between
$\unicode[STIX]{x1D6FE}\in G(\mathbb{Z})$
, there is an isomorphism between
![]() $(A_{x},\unicode[STIX]{x1D702}_{x})$
and
$(A_{x},\unicode[STIX]{x1D702}_{x})$
and
![]() $(A_{\unicode[STIX]{x1D6FE}x},\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FE}x}\circ \unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D70E}})$
, for example described in [Reference de Shalit and GorendSG16, § 1.2.2] or in [Reference GordonGor92], which sends
$(A_{\unicode[STIX]{x1D6FE}x},\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D6FE}x}\circ \unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D70E}})$
, for example described in [Reference de Shalit and GorendSG16, § 1.2.2] or in [Reference GordonGor92], which sends
![]() $(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2},d\unicode[STIX]{x1D701}_{3})$
to
$(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2},d\unicode[STIX]{x1D701}_{3})$
to
![]() $\unicode[STIX]{x1D6FE}^{\ast }(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2},d\unicode[STIX]{x1D701}_{3})=(\unicode[STIX]{x1D6FE}^{\ast }(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2}),\unicode[STIX]{x1D6FE}^{\ast }d\unicode[STIX]{x1D701}_{3})$
as
$\unicode[STIX]{x1D6FE}^{\ast }(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2},d\unicode[STIX]{x1D701}_{3})=(\unicode[STIX]{x1D6FE}^{\ast }(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2}),\unicode[STIX]{x1D6FE}^{\ast }d\unicode[STIX]{x1D701}_{3})$
as
![]() $\unicode[STIX]{x1D6FE}$
preserve the action of
$\unicode[STIX]{x1D6FE}$
preserve the action of
![]() ${\mathcal{O}}_{E}$
;
${\mathcal{O}}_{E}$
;
![]() $\unicode[STIX]{x1D6FE}^{\ast }d\unicode[STIX]{x1D701}_{3}$
is calculated in [Reference de Shalit and GorendSG16, Proposition 1.15] and given by
$\unicode[STIX]{x1D6FE}^{\ast }d\unicode[STIX]{x1D701}_{3}$
is calculated in [Reference de Shalit and GorendSG16, Proposition 1.15] and given by
Moreover, by the Kodaira–Spencer isomorphism
![]() $\unicode[STIX]{x1D714}_{A_{x},\unicode[STIX]{x1D70F}}\otimes \unicode[STIX]{x1D714}_{A_{x},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D6FA}^{1}$
(see [Reference de Shalit and GorendSG16, Proposition 1.22] for example), we only need to determine the action of
$\unicode[STIX]{x1D714}_{A_{x},\unicode[STIX]{x1D70F}}\otimes \unicode[STIX]{x1D714}_{A_{x},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D6FA}^{1}$
(see [Reference de Shalit and GorendSG16, Proposition 1.22] for example), we only need to determine the action of
![]() $\unicode[STIX]{x1D6FE}$
on
$\unicode[STIX]{x1D6FE}$
on
![]() $dz_{1},dz_{2}$
. But this is done in [Reference ShimuraShi78, 1.15] (or an explicit calculation), given by
$dz_{1},dz_{2}$
. But this is done in [Reference ShimuraShi78, 1.15] (or an explicit calculation), given by
![]() $c(\unicode[STIX]{x1D6FE})^{t}\unicode[STIX]{x1D705}^{-1}(\unicode[STIX]{x1D6FE},x)j(\unicode[STIX]{x1D6FE},x)$
, and we get
$c(\unicode[STIX]{x1D6FE})^{t}\unicode[STIX]{x1D705}^{-1}(\unicode[STIX]{x1D6FE},x)j(\unicode[STIX]{x1D6FE},x)$
, and we get
Thus, setting
![]() $F(x,k)=f(A_{x},\unicode[STIX]{x1D702}_{x}\circ k^{\unicode[STIX]{x1D70E}},(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2},d\unicode[STIX]{x1D701}_{3}))$
, we get,
$F(x,k)=f(A_{x},\unicode[STIX]{x1D702}_{x}\circ k^{\unicode[STIX]{x1D70E}},(d\unicode[STIX]{x1D701}_{1},d\unicode[STIX]{x1D701}_{2},d\unicode[STIX]{x1D701}_{3}))$
, we get,
Thus, to
![]() $f\in H^{0}(Y_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
we can associate a function,
$f\in H^{0}(Y_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
we can associate a function,
![]() $\unicode[STIX]{x1D6F7}_{f}:G(\mathbb{Q})\backslash G(\mathbb{A})\longrightarrow V^{\unicode[STIX]{x1D705}}$
, by
$\unicode[STIX]{x1D6F7}_{f}:G(\mathbb{Q})\backslash G(\mathbb{A})\longrightarrow V^{\unicode[STIX]{x1D705}}$
, by
where the action
![]() $\cdot$
is the one on
$\cdot$
is the one on
![]() $V^{\unicode[STIX]{x1D705}}$
, and we use the decomposition
$V^{\unicode[STIX]{x1D705}}$
, and we use the decomposition
![]() $g=g_{\mathbb{Q}}g_{\infty }g_{f}\in G(\mathbb{Q})G(\mathbb{R})G(\mathbb{A}_{f})$
. We can check that this expression does not depend on the choice in the decomposition. This association commutes with Hecke operators. The function
$g=g_{\mathbb{Q}}g_{\infty }g_{f}\in G(\mathbb{Q})G(\mathbb{R})G(\mathbb{A}_{f})$
. We can check that this expression does not depend on the choice in the decomposition. This association commutes with Hecke operators. The function
![]() $\unicode[STIX]{x1D6F7}_{f}$
does not necessarily have a unitary central character, but it is nevertheless normalized by
$\unicode[STIX]{x1D6F7}_{f}$
does not necessarily have a unitary central character, but it is nevertheless normalized by
![]() $\unicode[STIX]{x1D705}$
. Indeed, for
$\unicode[STIX]{x1D705}$
. Indeed, for
![]() $z_{\infty }\in \mathbb{C}^{\times }=Z(\mathbb{R})$
,
$z_{\infty }\in \mathbb{C}^{\times }=Z(\mathbb{R})$
,
Let
![]() $L:V^{\unicode[STIX]{x1D705}}\longrightarrow \mathbb{C}$
a non-zero linear form. Define the injective map of right-
$L:V^{\unicode[STIX]{x1D705}}\longrightarrow \mathbb{C}$
a non-zero linear form. Define the injective map of right-
![]() $K_{\infty }$
-modules,
$K_{\infty }$
-modules,
We denote by
![]() $L_{0}^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\mathbb{C})$
the set of cuspidal
$L_{0}^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\mathbb{C})$
the set of cuspidal
![]() $L^{2}$
-automorphic forms for
$L^{2}$
-automorphic forms for
![]() $G$
. We have the following well-known proposition
$G$
. We have the following well-known proposition
Proposition 2.6. The map
![]() $f\mapsto \unicode[STIX]{x1D711}_{f}=L\circ \unicode[STIX]{x1D6F7}_{f}$
is an isometry from
$f\mapsto \unicode[STIX]{x1D711}_{f}=L\circ \unicode[STIX]{x1D6F7}_{f}$
is an isometry from
![]() $H_{\text{cusp}}^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})=H^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}(-D))$
to the subspace of
$H_{\text{cusp}}^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})=H^{0}(X_{K}(\mathbb{C}),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}(-D))$
to the subspace of
![]() $L_{0}^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\mathbb{C})$
of functions
$L_{0}^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\mathbb{C})$
of functions
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
![]() $C^{\infty }$
in the real variable, such that:
$C^{\infty }$
in the real variable, such that:
(i) for all
 $g\in G(\mathbb{A})$
, the function
$g\in G(\mathbb{A})$
, the function
 $\unicode[STIX]{x1D711}_{g}:k\in K_{\infty }\mapsto \unicode[STIX]{x1D711}(gk)$
is in
$\unicode[STIX]{x1D711}_{g}:k\in K_{\infty }\mapsto \unicode[STIX]{x1D711}(gk)$
is in
 ${\mathcal{L}}(V^{\unicode[STIX]{x1D705}})$
, and in particular
${\mathcal{L}}(V^{\unicode[STIX]{x1D705}})$
, and in particular
 $\unicode[STIX]{x1D711}$
is right
$\unicode[STIX]{x1D711}$
is right
 $K_{\infty }$
-finite;
$K_{\infty }$
-finite;(ii) for all
 $k\in K,\unicode[STIX]{x1D711}(gk)=\unicode[STIX]{x1D711}(g)$
;
$k\in K,\unicode[STIX]{x1D711}(gk)=\unicode[STIX]{x1D711}(g)$
;(iii) for all
 $X\in \mathfrak{p}_{\mathbb{C}}^{-}$
,
$X\in \mathfrak{p}_{\mathbb{C}}^{-}$
,
 $X\unicode[STIX]{x1D711}=0$
, i.e.
$X\unicode[STIX]{x1D711}=0$
, i.e.
 $\unicode[STIX]{x1D711}$
is holomorphic;
$\unicode[STIX]{x1D711}$
is holomorphic;(iv)
 $\unicode[STIX]{x1D711}$
is cuspidal, i.e. for all unipotent radical
$\unicode[STIX]{x1D711}$
is cuspidal, i.e. for all unipotent radical
 $N$
of a proper parabolic
$N$
of a proper parabolic
 $P$
of
$P$
of
 $G$
,
$G$
,  $$\begin{eqnarray}\int _{N(\mathbb{Q})\backslash N(\mathbb{A})}\unicode[STIX]{x1D711}(ng)\,dn=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{N(\mathbb{Q})\backslash N(\mathbb{A})}\unicode[STIX]{x1D711}(ng)\,dn=0.\end{eqnarray}$$
This isometry is equivariant under the Hecke action of
![]() ${\mathcal{H}}^{N}$
(
${\mathcal{H}}^{N}$
(
![]() $K(N)\subset K$
).
$K(N)\subset K$
).
Using the previous proposition, to every
![]() $f\in H_{\text{cusp}}^{0}(X_{K},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
, an eigenvector for the Hecke algebra, we will be able to attach a automorphic form
$f\in H_{\text{cusp}}^{0}(X_{K},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
, an eigenvector for the Hecke algebra, we will be able to attach a automorphic form
![]() $\unicode[STIX]{x1D711}_{f}$
, and an automorphic representation
$\unicode[STIX]{x1D711}_{f}$
, and an automorphic representation
![]() $\unicode[STIX]{x1D6F1}_{f}$
(with same central character).
$\unicode[STIX]{x1D6F1}_{f}$
(with same central character).
2.3 Local groups
In this subsection, we describe the local group at an inert prime. Let
![]() $p$
be a prime, inert in
$p$
be a prime, inert in
![]() $E$
. Let
$E$
. Let
![]() $E_{p}\supset \mathbb{Q}_{p}$
its
$E_{p}\supset \mathbb{Q}_{p}$
its
![]() $p$
-adic completion. Recall that
$p$
-adic completion. Recall that
![]() $V\otimes \mathbb{Q}_{p}=E_{p}^{3}$
and that the hermitian form is given by the matrix,
$V\otimes \mathbb{Q}_{p}=E_{p}^{3}$
and that the hermitian form is given by the matrix,
 $$\begin{eqnarray}J=\left(\begin{array}{@{}ccc@{}} & & 1\\ & 1 & \\ 1 & & \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}J=\left(\begin{array}{@{}ccc@{}} & & 1\\ & 1 & \\ 1 & & \end{array}\right).\end{eqnarray}$$
The diagonal maximal torus
![]() $T$
of
$T$
of
![]() $G_{\mathbb{Q}_{p}}$
is isomorphic to
$G_{\mathbb{Q}_{p}}$
is isomorphic to
![]() $E_{p}^{\times }\times E_{p}^{\times }$
,
$E_{p}^{\times }\times E_{p}^{\times }$
,
 $$\begin{eqnarray}T(\mathbb{Q}_{p})=\left\{\!\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & N(e)\overline{a}^{-1}\end{array}\right),\quad a,e\in E_{p}^{\times }\right\}\end{eqnarray}$$
$$\begin{eqnarray}T(\mathbb{Q}_{p})=\left\{\!\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & N(e)\overline{a}^{-1}\end{array}\right),\quad a,e\in E_{p}^{\times }\right\}\end{eqnarray}$$
and contains
![]() $T^{1}$
, isomorphic to
$T^{1}$
, isomorphic to
![]() $E_{p}^{\times }\times E_{p}^{1}$
, where
$E_{p}^{\times }\times E_{p}^{1}$
, where
![]() $E_{p}^{1}=\{x\in E_{p}:x\overline{x}=1\}=({\mathcal{O}}_{E_{p}})^{1}$
, the torus of
$E_{p}^{1}=\{x\in E_{p}:x\overline{x}=1\}=({\mathcal{O}}_{E_{p}})^{1}$
, the torus of
![]() $U(E^{3},J)$
,
$U(E^{3},J)$
,
 $$\begin{eqnarray}T^{1}(\mathbb{Q}_{p})=\left\{\!\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & \overline{a}^{-1}\end{array}\right),\quad a\in E_{p}^{\times },e\in E_{p}^{1}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}T^{1}(\mathbb{Q}_{p})=\left\{\!\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & \overline{a}^{-1}\end{array}\right),\quad a\in E_{p}^{\times },e\in E_{p}^{1}\right\}.\end{eqnarray}$$
We also have the Borel subgroups
![]() $B=B_{\operatorname{GL}_{3}(E)}\cap G_{\mathbb{Q}_{p}}$
of upper-triangular matrices,
$B=B_{\operatorname{GL}_{3}(E)}\cap G_{\mathbb{Q}_{p}}$
of upper-triangular matrices,
 $$\begin{eqnarray}B(\mathbb{Q}_{p})=\left\{\!\left(\begin{array}{@{}ccc@{}}a & x & y\\ & e & \overline{x}\overline{a}^{-1}e\\ & & N(e)\overline{a}^{-1}\end{array}\right),\quad a,e,x,y\in E_{p}^{\times }\text{and }\operatorname{Tr}(\overline{a}^{-1}y)=N(a^{-1}x)\right\},\end{eqnarray}$$
$$\begin{eqnarray}B(\mathbb{Q}_{p})=\left\{\!\left(\begin{array}{@{}ccc@{}}a & x & y\\ & e & \overline{x}\overline{a}^{-1}e\\ & & N(e)\overline{a}^{-1}\end{array}\right),\quad a,e,x,y\in E_{p}^{\times }\text{and }\operatorname{Tr}(\overline{a}^{-1}y)=N(a^{-1}x)\right\},\end{eqnarray}$$
and
![]() $B^{1}$
the corresponding Borel subgroup, for
$B^{1}$
the corresponding Borel subgroup, for
![]() $U(E^{3},J)$
,
$U(E^{3},J)$
,
 $$\begin{eqnarray}B^{1}(\mathbb{Q}_{p})=\left\{\!\left(\begin{array}{@{}ccc@{}}a & x & y\\ & e & \overline{x}\overline{a}^{-1}e\\ & & \overline{a}^{-1}\end{array}\right),\quad a,x,y\in E_{p}^{\times },e\in E_{p}^{1}\text{ and }\operatorname{Tr}(\overline{a}^{-1}y)=N(a^{-1}x)\right\}.\end{eqnarray}$$
$$\begin{eqnarray}B^{1}(\mathbb{Q}_{p})=\left\{\!\left(\begin{array}{@{}ccc@{}}a & x & y\\ & e & \overline{x}\overline{a}^{-1}e\\ & & \overline{a}^{-1}\end{array}\right),\quad a,x,y\in E_{p}^{\times },e\in E_{p}^{1}\text{ and }\operatorname{Tr}(\overline{a}^{-1}y)=N(a^{-1}x)\right\}.\end{eqnarray}$$
3 Weight space
Write
![]() ${\mathcal{O}}={\mathcal{O}}_{E_{p}}$
, and denote by
${\mathcal{O}}={\mathcal{O}}_{E_{p}}$
, and denote by
![]() $T^{1}(\mathbb{Z}_{p})$
the torus
$T^{1}(\mathbb{Z}_{p})$
the torus
![]() ${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
over
${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
over
![]() $\mathbb{Z}_{p}$
. It is the
$\mathbb{Z}_{p}$
. It is the
![]() $\mathbb{Z}_{p}$
-points of a maximal torus of
$\mathbb{Z}_{p}$
-points of a maximal torus of
![]() $U(2,1)$
. Denote by
$U(2,1)$
. Denote by
![]() $T=T^{1}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}$
the split torus over
$T=T^{1}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}$
the split torus over
![]() $\operatorname{Spec}({\mathcal{O}})$
.
$\operatorname{Spec}({\mathcal{O}})$
.
Definition 3.1. The weight space
![]() ${\mathcal{W}}$
is the rigid space over
${\mathcal{W}}$
is the rigid space over
![]() $\mathbb{Q}_{p}$
given by
$\mathbb{Q}_{p}$
given by
![]() $\operatorname{Hom}_{\text{cont}}(T^{1}(\mathbb{Z}_{p}),\mathbb{G}_{m})$
. It coincides with Berthelot’s rigid fiber [Reference BerthelotBer96], of the formal scheme (called the formal weight space) given by
$\operatorname{Hom}_{\text{cont}}(T^{1}(\mathbb{Z}_{p}),\mathbb{G}_{m})$
. It coincides with Berthelot’s rigid fiber [Reference BerthelotBer96], of the formal scheme (called the formal weight space) given by
If
![]() $K$
is an extension of
$K$
is an extension of
![]() $\mathbb{Q}_{p}$
, the
$\mathbb{Q}_{p}$
, the
![]() $K$
-points of
$K$
-points of
![]() ${\mathcal{W}}$
are given by
${\mathcal{W}}$
are given by
The weight space
![]() ${\mathcal{W}}$
is isomorphic to a union of
${\mathcal{W}}$
is isomorphic to a union of
![]() $(p+1)(p^{2}-1)$
open balls of dimension
$(p+1)(p^{2}-1)$
open balls of dimension
![]() $3$
(see Appendix A, compare with [Reference UrbanUrb11, § 3.4.2]),
$3$
(see Appendix A, compare with [Reference UrbanUrb11, § 3.4.2]),
There is also a universal character,
which is locally analytic. We can write
![]() ${\mathcal{W}}=\bigcup _{w>0}{\mathcal{W}}(w)$
as an increasing union of affinoids using the analycity radius (see Appendix A).
${\mathcal{W}}=\bigcup _{w>0}{\mathcal{W}}(w)$
as an increasing union of affinoids using the analycity radius (see Appendix A).
Definition 3.2. To
![]() $k=(k_{1},k_{2},k_{3})\in \mathbb{Z}^{3}$
is associated a character,
$k=(k_{1},k_{2},k_{3})\in \mathbb{Z}^{3}$
is associated a character,
Characters of this form are called algebraic, or classical if moreover
![]() $k_{1}\geqslant k_{2}$
. They are analytic and Zariski dense in
$k_{1}\geqslant k_{2}$
. They are analytic and Zariski dense in
![]() ${\mathcal{W}}$
.
${\mathcal{W}}$
.
4 Induction
Set
![]() $U=U(2,1)/\mathbb{Z}_{p}$
,
$U=U(2,1)/\mathbb{Z}_{p}$
,
![]() $T^{1}$
its maximal torus,
$T^{1}$
its maximal torus,
![]() $K=\mathbb{Q}_{p^{2}}$
and
$K=\mathbb{Q}_{p^{2}}$
and
![]() ${\mathcal{O}}={\mathcal{O}}_{K}$
. We have
${\mathcal{O}}={\mathcal{O}}_{K}$
. We have
![]() $U\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}\simeq \operatorname{GL}_{3}/{\mathcal{O}}$
, and we denote by
$U\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}\simeq \operatorname{GL}_{3}/{\mathcal{O}}$
, and we denote by
![]() $T$
its torus, and
$T$
its torus, and
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}\subset P$
the Levi of the standard parabolic of
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}\subset P$
the Levi of the standard parabolic of
![]() $\operatorname{GL}_{3}/{\mathcal{O}}$
. Let
$\operatorname{GL}_{3}/{\mathcal{O}}$
. Let
![]() $T\subset B$
the upper triangular Borel subgroup of
$T\subset B$
the upper triangular Borel subgroup of
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
and
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
and
![]() $U$
its unipotent radical.
$U$
its unipotent radical.
Definition 4.1. Let
![]() $\unicode[STIX]{x1D705}\in X^{+}(T)$
. Then there exists an (irreducible) algebraic representation of
$\unicode[STIX]{x1D705}\in X^{+}(T)$
. Then there exists an (irreducible) algebraic representation of
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
(of highest weight
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
(of highest weight
![]() $\unicode[STIX]{x1D705}$
) given by
$\unicode[STIX]{x1D705}$
) given by
where
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
acts by translation on the left (i.e.
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
acts by translation on the left (i.e.
![]() $gf(x)=f(g^{-1}x)$
). The representation
$gf(x)=f(g^{-1}x)$
). The representation
![]() $V_{\unicode[STIX]{x1D705}}$
is called the algebraic induction of highest weight
$V_{\unicode[STIX]{x1D705}}$
is called the algebraic induction of highest weight
![]() $\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D705}$
of
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
.
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
.
Let
![]() $I=I_{1}$
be the Iwahori subgroup of
$I=I_{1}$
be the Iwahori subgroup of
![]() $\operatorname{GL}_{2}({\mathcal{O}})\times \operatorname{GL}_{1}({\mathcal{O}})$
, i.e. matrices that are upper-triangular modulo
$\operatorname{GL}_{2}({\mathcal{O}})\times \operatorname{GL}_{1}({\mathcal{O}})$
, i.e. matrices that are upper-triangular modulo
![]() $p$
. Let
$p$
. Let
![]() $I_{n}$
be the subset of matrices in
$I_{n}$
be the subset of matrices in
![]() $B$
modulo
$B$
modulo
![]() $p^{n}$
, i.e. of the form
$p^{n}$
, i.e. of the form
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}a & b & \\ p^{n}c & d & \\ & & e\end{array}\right),\quad a,b,c,d\in {\mathcal{O}}.\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}a & b & \\ p^{n}c & d & \\ & & e\end{array}\right),\quad a,b,c,d\in {\mathcal{O}}.\end{eqnarray}$$
Denote by
![]() $N^{0}$
the opposite unipotent of
$N^{0}$
the opposite unipotent of
![]() $U$
, and
$U$
, and
![]() $N_{n}^{0}$
the subgroup of
$N_{n}^{0}$
the subgroup of
![]() $N^{0}$
of elements reducing to identity modulo
$N^{0}$
of elements reducing to identity modulo
![]() $p^{n}$
. These are seen as subgroups of
$p^{n}$
. These are seen as subgroups of
![]() $\operatorname{GL}_{2}({\mathcal{O}})\times \operatorname{GL}_{1}({\mathcal{O}})$
rather than formal or rigid spaces, but could be identified with
$\operatorname{GL}_{2}({\mathcal{O}})\times \operatorname{GL}_{1}({\mathcal{O}})$
rather than formal or rigid spaces, but could be identified with
![]() ${\mathcal{O}}$
-points of rigid spaces. Precisely,
${\mathcal{O}}$
-points of rigid spaces. Precisely,
 $$\begin{eqnarray}N^{0}=\left\{\!\left(\begin{array}{@{}ccc@{}}1 & 0 & \\ x & 1 & \\ & & 1\end{array}\right),\quad x\in {\mathcal{O}}\right\}\quad \text{and}\quad N_{n}^{0}=\left\{\!\left(\begin{array}{@{}ccc@{}}1 & 0 & \\ p^{n}x & 1 & \\ & & 1\end{array}\right),\quad x\in {\mathcal{O}}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}N^{0}=\left\{\!\left(\begin{array}{@{}ccc@{}}1 & 0 & \\ x & 1 & \\ & & 1\end{array}\right),\quad x\in {\mathcal{O}}\right\}\quad \text{and}\quad N_{n}^{0}=\left\{\!\left(\begin{array}{@{}ccc@{}}1 & 0 & \\ p^{n}x & 1 & \\ & & 1\end{array}\right),\quad x\in {\mathcal{O}}\right\}.\end{eqnarray}$$
We identify
![]() $N_{n}^{0}$
with
$N_{n}^{0}$
with
![]() $p^{n}{\mathcal{O}}\subset (\mathbb{A}_{{\mathcal{O}}}^{1})^{\text{an}}$
. For
$p^{n}{\mathcal{O}}\subset (\mathbb{A}_{{\mathcal{O}}}^{1})^{\text{an}}$
. For
![]() $\unicode[STIX]{x1D700}>0$
, denote by
$\unicode[STIX]{x1D700}>0$
, denote by
![]() $N_{n,\unicode[STIX]{x1D700}}^{0}$
the affinoid,
$N_{n,\unicode[STIX]{x1D700}}^{0}$
the affinoid,
The affinoid
![]() $N_{n,\unicode[STIX]{x1D700}}^{0}$
is a rigid space. Actually we could define a rigid space
$N_{n,\unicode[STIX]{x1D700}}^{0}$
is a rigid space. Actually we could define a rigid space
![]() ${\mathcal{N}}^{0}$
(which would just be
${\mathcal{N}}^{0}$
(which would just be
![]() $\mathbb{A}^{1}$
here) such that
$\mathbb{A}^{1}$
here) such that
![]() ${\mathcal{N}}^{0}({\mathcal{O}})=N^{0}$
,
${\mathcal{N}}^{0}({\mathcal{O}})=N^{0}$
,
![]() $N_{n,\unicode[STIX]{x1D700}}^{0}$
is an affinoid in
$N_{n,\unicode[STIX]{x1D700}}^{0}$
is an affinoid in
![]() ${\mathcal{N}}^{0}$
and a neighborhood of
${\mathcal{N}}^{0}$
and a neighborhood of
![]() $N_{n}^{0}$
. For
$N_{n}^{0}$
. For
![]() $L$
an extension of
$L$
an extension of
![]() $\mathbb{Q}_{p}$
, denote by
$\mathbb{Q}_{p}$
, denote by
![]() ${\mathcal{F}}^{\unicode[STIX]{x1D700}\text{-an}}(N_{n}^{0},L)$
the set of functions
${\mathcal{F}}^{\unicode[STIX]{x1D700}\text{-an}}(N_{n}^{0},L)$
the set of functions
![]() $N_{n}^{0}\longrightarrow L$
which are restriction of analytic functions on
$N_{n}^{0}\longrightarrow L$
which are restriction of analytic functions on
![]() $N_{n,\unicode[STIX]{x1D700}}^{0}$
. Let
$N_{n,\unicode[STIX]{x1D700}}^{0}$
. Let
![]() $\unicode[STIX]{x1D700}>0$
and
$\unicode[STIX]{x1D700}>0$
and
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}_{\unicode[STIX]{x1D700}}(L)$
an
$\unicode[STIX]{x1D705}\in {\mathcal{W}}_{\unicode[STIX]{x1D700}}(L)$
an
![]() $\unicode[STIX]{x1D700}$
-analytic character; we write
$\unicode[STIX]{x1D700}$
-analytic character; we write
We also write, for
![]() $\unicode[STIX]{x1D700}>0$
and
$\unicode[STIX]{x1D700}>0$
and
![]() $k=\lfloor -\text{log}_{p}(\unicode[STIX]{x1D700})\rfloor$
,
$k=\lfloor -\text{log}_{p}(\unicode[STIX]{x1D700})\rfloor$
,
where
![]() $\lfloor .\rfloor$
denotes the previous integer, and
$\lfloor .\rfloor$
denotes the previous integer, and
Concretely,
![]() $V_{0,\unicode[STIX]{x1D705},L}^{\unicode[STIX]{x1D700}\text{-an}}$
is identified with analytic functions on
$V_{0,\unicode[STIX]{x1D705},L}^{\unicode[STIX]{x1D700}\text{-an}}$
is identified with analytic functions on
![]() $B(0,p^{\lfloor -\text{log}_{p}\unicode[STIX]{x1D700}\rfloor })$
(a ball of dimension
$B(0,p^{\lfloor -\text{log}_{p}\unicode[STIX]{x1D700}\rfloor })$
(a ball of dimension
![]() $1$
).
$1$
).
We can identify
![]() $V_{\unicode[STIX]{x1D705},L}^{l\text{-an}}$
with
$V_{\unicode[STIX]{x1D705},L}^{l\text{-an}}$
with
![]() ${\mathcal{F}}^{l\text{-an}}(p{\mathcal{O}},L)$
by restricting
${\mathcal{F}}^{l\text{-an}}(p{\mathcal{O}},L)$
by restricting
![]() $f\in V_{\unicode[STIX]{x1D705},L}^{l\text{-an}}$
to
$f\in V_{\unicode[STIX]{x1D705},L}^{l\text{-an}}$
to
![]() $N^{0}$
. We can also identify
$N^{0}$
. We can also identify
![]() $V_{0,\unicode[STIX]{x1D705},L}^{l\text{-an}}$
to the germ of locally analytic function on
$V_{0,\unicode[STIX]{x1D705},L}^{l\text{-an}}$
to the germ of locally analytic function on
![]() $0$
.
$0$
.
Let
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}=\left(\begin{array}{@{}ccc@{}}p^{-1} & & \\ & 1 & \\ & & 1\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}=\left(\begin{array}{@{}ccc@{}}p^{-1} & & \\ & 1 & \\ & & 1\end{array}\right),\end{eqnarray}$$
which acts on
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
, stabilizes the Borel subgroup
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
, stabilizes the Borel subgroup
![]() $B(K)$
, and defines an action on
$B(K)$
, and defines an action on
![]() $V_{\unicode[STIX]{x1D705},L}$
for
$V_{\unicode[STIX]{x1D705},L}$
for
![]() $\unicode[STIX]{x1D705}\in X^{+}(T)$
, via
$\unicode[STIX]{x1D705}\in X^{+}(T)$
, via
![]() $(\unicode[STIX]{x1D6FF}\cdot f)(g)=f(\unicode[STIX]{x1D6FF}g\unicode[STIX]{x1D6FF}^{-1})$
. The action by conjugation of
$(\unicode[STIX]{x1D6FF}\cdot f)(g)=f(\unicode[STIX]{x1D6FF}g\unicode[STIX]{x1D6FF}^{-1})$
. The action by conjugation of
![]() $\unicode[STIX]{x1D6FF}$
on
$\unicode[STIX]{x1D6FF}$
on
![]() $I$
does not stabilize it, but it stabilizes
$I$
does not stabilize it, but it stabilizes
![]() $N^{0}$
. We can thus set, for
$N^{0}$
. We can thus set, for
![]() $j\in I$
,
$j\in I$
,
![]() $j=nb$
the Iwahori decomposition of
$j=nb$
the Iwahori decomposition of
![]() $j$
, and set
$j$
, and set
We can thus make
![]() $\unicode[STIX]{x1D6FF}$
act on
$\unicode[STIX]{x1D6FF}$
act on
![]() $V_{\unicode[STIX]{x1D705},L}^{\unicode[STIX]{x1D700}\text{-an}},V_{\unicode[STIX]{x1D705},L}^{l\text{-an}},V_{0,\unicode[STIX]{x1D705},L}^{\unicode[STIX]{x1D700}\text{-an}},V_{0,\unicode[STIX]{x1D705},L}^{l\text{-an}}$
. Via the identification
$V_{\unicode[STIX]{x1D705},L}^{\unicode[STIX]{x1D700}\text{-an}},V_{\unicode[STIX]{x1D705},L}^{l\text{-an}},V_{0,\unicode[STIX]{x1D705},L}^{\unicode[STIX]{x1D700}\text{-an}},V_{0,\unicode[STIX]{x1D705},L}^{l\text{-an}}$
. Via the identification
![]() $V_{\unicode[STIX]{x1D705},L}^{\unicode[STIX]{x1D700}\text{-an}}\simeq {\mathcal{F}}^{l\text{-an}}(p{\mathcal{O}},L)$
,
$V_{\unicode[STIX]{x1D705},L}^{\unicode[STIX]{x1D700}\text{-an}}\simeq {\mathcal{F}}^{l\text{-an}}(p{\mathcal{O}},L)$
,
![]() $\unicode[STIX]{x1D6FF}\cdot f(z)=f(pz)$
. Thus
$\unicode[STIX]{x1D6FF}\cdot f(z)=f(pz)$
. Thus
![]() $\unicode[STIX]{x1D6FF}$
improves the analycity radius. Moreover, its supremum norm is negative.
$\unicode[STIX]{x1D6FF}$
improves the analycity radius. Moreover, its supremum norm is negative.
Proposition 4.2. Let
![]() $f\in V_{0,\unicode[STIX]{x1D705},L}^{l\text{-an}}$
. Suppose
$f\in V_{0,\unicode[STIX]{x1D705},L}^{l\text{-an}}$
. Suppose
![]() $f$
is of finite slope under the action of
$f$
is of finite slope under the action of
![]() $\unicode[STIX]{x1D6FF}$
, i.e.
$\unicode[STIX]{x1D6FF}$
, i.e.
![]() $\unicode[STIX]{x1D6FF}\cdot f=\unicode[STIX]{x1D706}f,\unicode[STIX]{x1D706}\in L^{\times }$
. Then
$\unicode[STIX]{x1D6FF}\cdot f=\unicode[STIX]{x1D706}f,\unicode[STIX]{x1D706}\in L^{\times }$
. Then
![]() $f$
comes (by restriction) from a (unique)
$f$
comes (by restriction) from a (unique)
![]() $f\in V_{\unicode[STIX]{x1D705},L}^{\text{an}}$
.
$f\in V_{\unicode[STIX]{x1D705},L}^{\text{an}}$
.
Proof. We have that
![]() $f\in V_{0,\unicode[STIX]{x1D705},L}^{p^{n}-an}$
for a certain
$f\in V_{0,\unicode[STIX]{x1D705},L}^{p^{n}-an}$
for a certain
![]() $n$
; in particular, it defines a function
$n$
; in particular, it defines a function
 $$\begin{eqnarray}f:\left(\begin{array}{@{}ccc@{}}a & u & \\ p^{n}{\mathcal{O}} & b & \\ & & c\end{array}\right)=I_{n}\longrightarrow L\end{eqnarray}$$
$$\begin{eqnarray}f:\left(\begin{array}{@{}ccc@{}}a & u & \\ p^{n}{\mathcal{O}} & b & \\ & & c\end{array}\right)=I_{n}\longrightarrow L\end{eqnarray}$$
that is identified to a function in
![]() ${\mathcal{F}}^{\text{an}}(p^{n}{\mathcal{O}},L)$
. But
${\mathcal{F}}^{\text{an}}(p^{n}{\mathcal{O}},L)$
. But
![]() $f$
is an eigenform for
$f$
is an eigenform for
![]() $\unicode[STIX]{x1D6FF}$
with eigenvalue
$\unicode[STIX]{x1D6FF}$
with eigenvalue
![]() $\unicode[STIX]{x1D706}\neq 0\in L$
, and thus
$\unicode[STIX]{x1D706}\neq 0\in L$
, and thus
![]() $f=\unicode[STIX]{x1D706}^{-1}\unicode[STIX]{x1D6FF}(f)$
. But if
$f=\unicode[STIX]{x1D706}^{-1}\unicode[STIX]{x1D6FF}(f)$
. But if
![]() $f=f(z)$
, with the identification to
$f=f(z)$
, with the identification to
![]() ${\mathcal{F}}^{\text{an}}(p^{n}{\mathcal{O}},L)$
,
${\mathcal{F}}^{\text{an}}(p^{n}{\mathcal{O}},L)$
,
![]() $\unicode[STIX]{x1D6FF}f$
is identified with
$\unicode[STIX]{x1D6FF}f$
is identified with
![]() $f(pz)$
, thus
$f(pz)$
, thus
![]() $f\in {\mathcal{F}}^{\text{an}}(p^{n-1}{\mathcal{O}},L)$
, i.e.,
$f\in {\mathcal{F}}^{\text{an}}(p^{n-1}{\mathcal{O}},L)$
, i.e.,
![]() $\unicode[STIX]{x1D6FF}^{-1}$
strictly increases the analyticity radius, and, by iterating,
$\unicode[STIX]{x1D6FF}^{-1}$
strictly increases the analyticity radius, and, by iterating,
![]() $f\in {\mathcal{F}}^{\text{an}}(p{\mathcal{O}},L)$
, and thus
$f\in {\mathcal{F}}^{\text{an}}(p{\mathcal{O}},L)$
, and thus
![]() $f\in V_{\unicode[STIX]{x1D705},L}^{\text{an}}$
.◻
$f\in V_{\unicode[STIX]{x1D705},L}^{\text{an}}$
.◻
Proposition 4.3. For
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},r)\in X^{+}(T)$
, there is an inclusion,
$\unicode[STIX]{x1D705}=(k_{1},k_{2},r)\in X^{+}(T)$
, there is an inclusion,
which under the identification of
![]() $V_{\unicode[STIX]{x1D705},L}^{\text{an}}$
with
$V_{\unicode[STIX]{x1D705},L}^{\text{an}}$
with
![]() ${\mathcal{F}}^{\text{an}}(p{\mathcal{O}},L)$
identifies
${\mathcal{F}}^{\text{an}}(p{\mathcal{O}},L)$
identifies
![]() $V_{\unicode[STIX]{x1D705}}$
with polynomial functions of degree less or equal than
$V_{\unicode[STIX]{x1D705}}$
with polynomial functions of degree less or equal than
![]() $k_{1}-k_{2}$
.
$k_{1}-k_{2}$
.
Proposition 4.4. Let
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},r)\in X^{+}(T)$
. The following sequence is exact,
$\unicode[STIX]{x1D705}=(k_{1},k_{2},r)\in X^{+}(T)$
. The following sequence is exact,
where
![]() $d_{\unicode[STIX]{x1D705}}$
is given by
$d_{\unicode[STIX]{x1D705}}$
is given by
and
 $$\begin{eqnarray}Xf(g)=\left(\frac{d}{dt}f\left(g\left(\begin{array}{@{}ccc@{}}1 & & \\ -t & 1 & \\ & & 1\end{array}\right)\right)\right)_{t=0}.\end{eqnarray}$$
$$\begin{eqnarray}Xf(g)=\left(\frac{d}{dt}f\left(g\left(\begin{array}{@{}ccc@{}}1 & & \\ -t & 1 & \\ & & 1\end{array}\right)\right)\right)_{t=0}.\end{eqnarray}$$
Proof. Let us first check that
![]() $d_{\unicode[STIX]{x1D705}}$
is well defined. Indeed, using
$d_{\unicode[STIX]{x1D705}}$
is well defined. Indeed, using
![]() $(k_{1}-k_{2}+1)$
-times the formula
$(k_{1}-k_{2}+1)$
-times the formula
 $$\begin{eqnarray}\displaystyle & & \displaystyle (Xf)\left(g\left(\begin{array}{@{}ccc@{}}t_{1} & & \\ & t_{2} & \\ & & 1\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{d}{dt}f\left(g\left(\begin{array}{@{}ccc@{}}t_{1} & & \\ & t_{2} & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}1 & & \\ -t & 1 & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}t_{1}^{-1} & & \\ & t_{2}^{-1} & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}t_{1} & & \\ & t_{2} & \\ & & 1\end{array}\right)\right)\right)_{t=0}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{d}{dt}f\left(g\left(\begin{array}{@{}ccc@{}}1 & & \\ -t_{2}t_{1}^{-1}t & 1 & \\ & & 1\end{array}\right)\right)t_{1}^{k_{1}}t_{2}^{k_{2}}\right)_{t=0}=t_{2}t_{1}^{-1}(Xf)(g)t_{1}^{k_{1}}t_{2}^{k_{2}}=t_{1}^{k_{1}-1}t_{2}^{k_{2}+1}(Xf)(g)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (Xf)\left(g\left(\begin{array}{@{}ccc@{}}t_{1} & & \\ & t_{2} & \\ & & 1\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{d}{dt}f\left(g\left(\begin{array}{@{}ccc@{}}t_{1} & & \\ & t_{2} & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}1 & & \\ -t & 1 & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}t_{1}^{-1} & & \\ & t_{2}^{-1} & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}t_{1} & & \\ & t_{2} & \\ & & 1\end{array}\right)\right)\right)_{t=0}\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{d}{dt}f\left(g\left(\begin{array}{@{}ccc@{}}1 & & \\ -t_{2}t_{1}^{-1}t & 1 & \\ & & 1\end{array}\right)\right)t_{1}^{k_{1}}t_{2}^{k_{2}}\right)_{t=0}=t_{2}t_{1}^{-1}(Xf)(g)t_{1}^{k_{1}}t_{2}^{k_{2}}=t_{1}^{k_{1}-1}t_{2}^{k_{2}+1}(Xf)(g)\nonumber\end{eqnarray}$$
(and the corresponding formula for the action of
![]() $(\begin{smallmatrix}1 & u & \\ & 1 & \\ & & 1\end{smallmatrix})$
), we deduce that
$(\begin{smallmatrix}1 & u & \\ & 1 & \\ & & 1\end{smallmatrix})$
), we deduce that
![]() $d_{\unicode[STIX]{x1D705}}f$
has the right weight.
$d_{\unicode[STIX]{x1D705}}f$
has the right weight.
We can check (evaluating on
![]() $(\begin{smallmatrix}1 & & \\ u & 1 & \\ & & 1\end{smallmatrix})$
) that on
$(\begin{smallmatrix}1 & & \\ u & 1 & \\ & & 1\end{smallmatrix})$
) that on
![]() ${\mathcal{F}}^{\text{an}}(p{\mathcal{O}},L)$
${\mathcal{F}}^{\text{an}}(p{\mathcal{O}},L)$
![]() $d_{\unicode[STIX]{x1D705}}$
correspond to
$d_{\unicode[STIX]{x1D705}}$
correspond to
![]() $(d/dz)^{k_{1}-k_{2}+1}$
, where
$(d/dz)^{k_{1}-k_{2}+1}$
, where
![]() $z$
is the variable on
$z$
is the variable on
![]() $p{\mathcal{O}}$
. Thus, using the previous identification with
$p{\mathcal{O}}$
. Thus, using the previous identification with
![]() $V_{\unicode[STIX]{x1D705}}$
and polynomials of degree less or equal than
$V_{\unicode[STIX]{x1D705}}$
and polynomials of degree less or equal than
![]() $k_{1}-k_{2}$
, we deduce can check that
$k_{1}-k_{2}$
, we deduce can check that
![]() $V_{\unicode[STIX]{x1D705}}$
is exactly the kernel of
$V_{\unicode[STIX]{x1D705}}$
is exactly the kernel of
![]() $d_{\unicode[STIX]{x1D705}}$
.◻
$d_{\unicode[STIX]{x1D705}}$
.◻
Remark 4.5. A more general version of the previous proposition has been developed by Urban, [Reference UrbanUrb11, Proposition 3.2.12], and Jones [Reference JonesJon11].
5 Hasse Invariants and the canonical subgroups
Let
![]() $p$
be a prime. Fix
$p$
be a prime. Fix
![]() $E\subset \overline{E}\subset \mathbb{C}$
an algebraic closure of
$E\subset \overline{E}\subset \mathbb{C}$
an algebraic closure of
![]() $E$
and fix an isomorphism
$E$
and fix an isomorphism
![]() $\mathbb{C}\simeq \overline{\mathbb{Q}_{p}}$
. Call
$\mathbb{C}\simeq \overline{\mathbb{Q}_{p}}$
. Call
![]() $\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
the two places of
$\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
the two places of
![]() $\overline{\mathbb{Q}_{p}}$
that correspond respectively to
$\overline{\mathbb{Q}_{p}}$
that correspond respectively to
![]() $\unicode[STIX]{x1D70F}_{\infty },\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}_{\infty }$
through the previous isomorphism (sometimes if
$\unicode[STIX]{x1D70F}_{\infty },\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}_{\infty }$
through the previous isomorphism (sometimes if
![]() $p$
splits in
$p$
splits in
![]() $E$
we will instead write
$E$
we will instead write
![]() $v=\unicode[STIX]{x1D70F}$
and
$v=\unicode[STIX]{x1D70F}$
and
![]() $\overline{v}=\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
following the notation of [Reference Bellaïche and ChenevierBC04]). Suppose now
$\overline{v}=\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
following the notation of [Reference Bellaïche and ChenevierBC04]). Suppose now
![]() $p$
is inert in
$p$
is inert in
![]() $E$
. Let us take
$E$
. Let us take
![]() $K=K^{p}K_{p}\subset G(\mathbb{A}_{f})$
a sufficiently small compact open, such that
$K=K^{p}K_{p}\subset G(\mathbb{A}_{f})$
a sufficiently small compact open, such that
![]() $K_{p}$
is hyperspecial, and write
$K_{p}$
is hyperspecial, and write
![]() $Y=Y_{K}/\operatorname{Spec}({\mathcal{O}})$
the integral model of Kottwitz [Reference KottwitzKot92] of the Picard Variety associated to the Shimura datum of the first section and the level
$Y=Y_{K}/\operatorname{Spec}({\mathcal{O}})$
the integral model of Kottwitz [Reference KottwitzKot92] of the Picard Variety associated to the Shimura datum of the first section and the level
![]() $K$
(recall
$K$
(recall
![]() ${\mathcal{O}}={\mathcal{O}}_{E,p}$
). Denote by
${\mathcal{O}}={\mathcal{O}}_{E,p}$
). Denote by
![]() ${\mathcal{I}}=\operatorname{Hom}({\mathcal{O}},\mathbb{C}_{p})=\{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}\}$
the set of embeddings of
${\mathcal{I}}=\operatorname{Hom}({\mathcal{O}},\mathbb{C}_{p})=\{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}\}$
the set of embeddings of
![]() ${\mathcal{O}}$
into an algebraic closure of
${\mathcal{O}}$
into an algebraic closure of
![]() $\mathbb{Q}_{p}$
(
$\mathbb{Q}_{p}$
(
![]() $\mathbb{C}_{p}=\widehat{\overline{\mathbb{Q}_{p}}}$
), where
$\mathbb{C}_{p}=\widehat{\overline{\mathbb{Q}_{p}}}$
), where
![]() $\unicode[STIX]{x1D70E}$
is the Frobenius morphism of
$\unicode[STIX]{x1D70E}$
is the Frobenius morphism of
![]() ${\mathcal{O}}$
, which acts transitively on
${\mathcal{O}}$
, which acts transitively on
![]() ${\mathcal{I}}$
, and
${\mathcal{I}}$
, and
![]() $\operatorname{Gal}(E/\mathbb{Q})=\{\operatorname{id},\unicode[STIX]{x1D70E}\}$
.
$\operatorname{Gal}(E/\mathbb{Q})=\{\operatorname{id},\unicode[STIX]{x1D70E}\}$
.
Recall the (toroidal compactification of the) Picard modular surface
![]() $X=X_{K}$
is the (compactified) moduli space of principally polarized abelian varieties
$X=X_{K}$
is the (compactified) moduli space of principally polarized abelian varieties
![]() ${\mathcal{A}}\longrightarrow S$
of genus
${\mathcal{A}}\longrightarrow S$
of genus
![]() $3$
, endowed with an action of
$3$
, endowed with an action of
![]() ${\mathcal{O}}_{E}$
, and a certain level structure
${\mathcal{O}}_{E}$
, and a certain level structure
![]() $K^{p}$
, and such that, up to extending scalars of
$K^{p}$
, and such that, up to extending scalars of
![]() $S$
, we can decompose the conormal sheaf of
$S$
, we can decompose the conormal sheaf of
![]() ${\mathcal{A}}$
under the action of
${\mathcal{A}}$
under the action of
![]() ${\mathcal{O}}={\mathcal{O}}_{E,p}$
,
${\mathcal{O}}={\mathcal{O}}_{E,p}$
,
and we assume
![]() $\dim _{{\mathcal{O}}_{S}}\unicode[STIX]{x1D714}_{{\mathcal{A}},\unicode[STIX]{x1D70F}}=1$
(and thus
$\dim _{{\mathcal{O}}_{S}}\unicode[STIX]{x1D714}_{{\mathcal{A}},\unicode[STIX]{x1D70F}}=1$
(and thus
![]() $\dim _{{\mathcal{O}}_{S}}\unicode[STIX]{x1D714}_{{\mathcal{A}},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=2$
). These two sheaves extend from
$\dim _{{\mathcal{O}}_{S}}\unicode[STIX]{x1D714}_{{\mathcal{A}},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=2$
). These two sheaves extend from
![]() $Y$
to
$Y$
to
![]() $X$
. One reason is that there is a semi-abelian scheme on
$X$
. One reason is that there is a semi-abelian scheme on
![]() $X$
together with an action of
$X$
together with an action of
![]() ${\mathcal{O}}_{E}$
, thus its conormal sheaf extend
${\mathcal{O}}_{E}$
, thus its conormal sheaf extend
![]() $\unicode[STIX]{x1D714}_{A}$
to the boundary, and the
$\unicode[STIX]{x1D714}_{A}$
to the boundary, and the
![]() ${\mathcal{O}}_{E}$
action allows the splitting to make sense on the boundary too (see for example [Reference LanLan13, Theorem 6.4.1.1]).
${\mathcal{O}}_{E}$
action allows the splitting to make sense on the boundary too (see for example [Reference LanLan13, Theorem 6.4.1.1]).
Remark 5.1. If
![]() $p$
splits in
$p$
splits in
![]() $E$
, there is also a integral model of the Picard Surface, which is above
$E$
, there is also a integral model of the Picard Surface, which is above
![]() $\operatorname{Spec}(\mathbb{Z}_{p})$
, and it has a similar description (of course in this case
$\operatorname{Spec}(\mathbb{Z}_{p})$
, and it has a similar description (of course in this case
![]() ${\mathcal{O}}_{E,p}\simeq \mathbb{Z}_{p}\times \mathbb{Z}_{p}$
).
${\mathcal{O}}_{E,p}\simeq \mathbb{Z}_{p}\times \mathbb{Z}_{p}$
).
Remark 5.2. The case of toroidal compactifications of the Picard modular surface is particularly simple. Contrary to the case of other (PEL) Shimura varieties, there is a unique and thus canonical choice of a rational polyhedral cone decomposition
![]() $\unicode[STIX]{x1D6F4}$
, and thus a unique toroidal compactification. This cone decomposition is the one of
$\unicode[STIX]{x1D6F4}$
, and thus a unique toroidal compactification. This cone decomposition is the one of
![]() $\mathbb{R}_{+}$
, it is smooth and projective. As a result, the toroidal compactification is smooth and projective.
$\mathbb{R}_{+}$
, it is smooth and projective. As a result, the toroidal compactification is smooth and projective.
5.1 Classical modular sheaves and geometric modular forms
On
![]() $X$
, there is a sheaf
$X$
, there is a sheaf
![]() $\unicode[STIX]{x1D714}$
, the conormal sheaf of
$\unicode[STIX]{x1D714}$
, the conormal sheaf of
![]() ${\mathcal{A}}$
, the universal (semi-)abelian scheme, along its unit section, and
${\mathcal{A}}$
, the universal (semi-)abelian scheme, along its unit section, and
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
.
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
.
For any
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})\in \mathbb{Z}^{3}$
such that
$\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})\in \mathbb{Z}^{3}$
such that
![]() $k_{1}\geqslant k_{2}$
, there is associated a ‘classical’ modular sheaf,
$k_{1}\geqslant k_{2}$
, there is associated a ‘classical’ modular sheaf,
Write
![]() $\unicode[STIX]{x1D705}^{\prime }=(-k_{2},-k_{1},-k_{3})$
; this is still a dominant weight, and
$\unicode[STIX]{x1D705}^{\prime }=(-k_{2},-k_{1},-k_{3})$
; this is still a dominant weight, and
![]() $\unicode[STIX]{x1D705}\mapsto \unicode[STIX]{x1D705}^{\prime }$
is an involution. There is another way to see the classical modular sheaves.
$\unicode[STIX]{x1D705}\mapsto \unicode[STIX]{x1D705}^{\prime }$
is an involution. There is another way to see the classical modular sheaves.
Write
![]() ${\mathcal{T}}=\operatorname{Hom}_{X,{\mathcal{O}}}({\mathcal{O}}_{X}^{2}\otimes {\mathcal{O}}_{X},\unicode[STIX]{x1D714})$
where
${\mathcal{T}}=\operatorname{Hom}_{X,{\mathcal{O}}}({\mathcal{O}}_{X}^{2}\otimes {\mathcal{O}}_{X},\unicode[STIX]{x1D714})$
where
![]() ${\mathcal{O}}$
acts by
${\mathcal{O}}$
acts by
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
on the first two-dimensional factor and
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
on the first two-dimensional factor and
![]() $\unicode[STIX]{x1D70F}$
on the other one. Write
$\unicode[STIX]{x1D70F}$
on the other one. Write
![]() ${\mathcal{T}}^{\times }=\operatorname{Isom}_{X,{\mathcal{O}}}({\mathcal{O}}_{X}^{2}\otimes {\mathcal{O}}_{X},\unicode[STIX]{x1D714})$
, the
${\mathcal{T}}^{\times }=\operatorname{Isom}_{X,{\mathcal{O}}}({\mathcal{O}}_{X}^{2}\otimes {\mathcal{O}}_{X},\unicode[STIX]{x1D714})$
, the
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
-torsor of trivializations of
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
-torsor of trivializations of
![]() $\unicode[STIX]{x1D714}$
as a
$\unicode[STIX]{x1D714}$
as a
![]() ${\mathcal{O}}$
-module. There is an action on
${\mathcal{O}}$
-module. There is an action on
![]() ${\mathcal{T}}$
of
${\mathcal{T}}$
of
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
by
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
by
![]() $g\cdot w=w\circ g^{-1}$
.
$g\cdot w=w\circ g^{-1}$
.
Denote by
![]() $\unicode[STIX]{x1D70B}:{\mathcal{T}}^{\times }\longrightarrow X$
the projection. For any dominant
$\unicode[STIX]{x1D70B}:{\mathcal{T}}^{\times }\longrightarrow X$
the projection. For any dominant
![]() $\unicode[STIX]{x1D705}$
as before, define
$\unicode[STIX]{x1D705}$
as before, define
the subsheaf of
![]() $\unicode[STIX]{x1D705}^{\prime }$
-equivariant functions for the action of the upper triangular Borel subgroup
$\unicode[STIX]{x1D705}^{\prime }$
-equivariant functions for the action of the upper triangular Borel subgroup
![]() $B\subset \operatorname{GL}_{2}\times \operatorname{GL}_{1}$
. As the notation suggests, there is an isomorphism, if
$B\subset \operatorname{GL}_{2}\times \operatorname{GL}_{1}$
. As the notation suggests, there is an isomorphism, if
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})$
,
$\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})$
,
Definition 5.3. Recall that
![]() $X$
is the (compactified) Picard variety of level
$X$
is the (compactified) Picard variety of level
![]() $K=K_{p}K^{p}$
. The global sections
$K=K_{p}K^{p}$
. The global sections
![]() $H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
is the module of Picard modular forms of level
$H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
is the module of Picard modular forms of level
![]() $K$
and weight
$K$
and weight
![]() $\unicode[STIX]{x1D705}$
. If
$\unicode[STIX]{x1D705}$
. If
![]() $D$
denotes the (reduced) boundary of
$D$
denotes the (reduced) boundary of
![]() $X$
, the submodule
$X$
, the submodule
![]() $H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}(-D))$
is the submodule of Picard cusp-forms.
$H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}(-D))$
is the submodule of Picard cusp-forms.
In the sequel we will be interested in the case
![]() $K_{p}=I$
, the Iwahori subgroup when we speak about modular forms on the rigid space associated to
$K_{p}=I$
, the Iwahori subgroup when we speak about modular forms on the rigid space associated to
![]() $X$
. But for moduli-theoretic reason we will not directly consider an integral model of
$X$
. But for moduli-theoretic reason we will not directly consider an integral model of
![]() $X_{I}^{\text{rig}}$
, but only an integral model of a particular open subset (the one given by the canonical filtration). Indeed, in this particular setting (
$X_{I}^{\text{rig}}$
, but only an integral model of a particular open subset (the one given by the canonical filtration). Indeed, in this particular setting (
![]() $U(2,1)$
with
$U(2,1)$
with
![]() $p$
inert), the canonical filtration identifies a strict neighborhood of the
$p$
inert), the canonical filtration identifies a strict neighborhood of the
![]() $\unicode[STIX]{x1D707}$
-ordinary locus in
$\unicode[STIX]{x1D707}$
-ordinary locus in
![]() $X$
with an open in the level
$X$
with an open in the level
![]() $I$
-Picard variety.
$I$
-Picard variety.
Remark 5.4. There is a more general construction of automorphic sheaves
![]() $\unicode[STIX]{x1D714}^{k_{1},k_{2},k_{3},r}$
given in [Reference HarrisHar84], they are independent of
$\unicode[STIX]{x1D714}^{k_{1},k_{2},k_{3},r}$
given in [Reference HarrisHar84], they are independent of
![]() $r$
as sheaves on the Picard variety, and only the
$r$
as sheaves on the Picard variety, and only the
![]() $G$
-equivariant action (and thus the action of the Hecke operators) depends on
$G$
-equivariant action (and thus the action of the Hecke operators) depends on
![]() $r$
. We will only use the previous definition of the sheaves. We could get more automorphic forms by twisting by the norm character (which would be equivalent to twist the action of the Hecke operators).
$r$
. We will only use the previous definition of the sheaves. We could get more automorphic forms by twisting by the norm character (which would be equivalent to twist the action of the Hecke operators).
5.2 Local constructions
Let
![]() $G$
be the
$G$
be the
![]() $p$
-divisible group of the universal abelian scheme over
$p$
-divisible group of the universal abelian scheme over
![]() $Y\subset X$
. Later we will explain how to extend our construction to all
$Y\subset X$
. Later we will explain how to extend our construction to all
![]() $X$
. The group
$X$
. The group
![]() $G$
is endowed with an action of
$G$
is endowed with an action of
![]() ${\mathcal{O}}$
, and we have that its signature is given by
${\mathcal{O}}$
, and we have that its signature is given by
which means that if we write
![]() $\unicode[STIX]{x1D714}_{G}=\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
, the two pieces have respective dimensions
$\unicode[STIX]{x1D714}_{G}=\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
, the two pieces have respective dimensions
![]() $p_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=2$
and
$p_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=2$
and
![]() $p_{\unicode[STIX]{x1D70F}}=1$
. Moreover,
$p_{\unicode[STIX]{x1D70F}}=1$
. Moreover,
![]() $G$
carries a polarization
$G$
carries a polarization
![]() $\unicode[STIX]{x1D706}$
, such that
$\unicode[STIX]{x1D706}$
, such that
![]() $\unicode[STIX]{x1D706}:G\overset{{\sim}}{\longrightarrow }G^{D,(\unicode[STIX]{x1D70E})}$
is
$\unicode[STIX]{x1D706}:G\overset{{\sim}}{\longrightarrow }G^{D,(\unicode[STIX]{x1D70E})}$
is
![]() ${\mathcal{O}}$
-equivariant.
${\mathcal{O}}$
-equivariant.
The main result of [Reference HernandezHer18], see also [Reference Goldring and NicoleGN17], is the following,
Definition 5.5. There exists sections,
such that
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
is given by (the determinant of)
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
is given by (the determinant of)
![]() $V^{2}$
,
$V^{2}$
,
and
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70F}}$
is given by a division by
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70F}}$
is given by a division by
![]() $p$
on the Dieudonne crystal of
$p$
on the Dieudonne crystal of
![]() $G$
of
$G$
of
![]() $V^{2}$
, restricted to a lift of the Hodge Filtration
$V^{2}$
, restricted to a lift of the Hodge Filtration
![]() $\unicode[STIX]{x1D714}_{G^{D},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
.
$\unicode[STIX]{x1D714}_{G^{D},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
.
On
![]() $Y\otimes {\mathcal{O}}/p$
, the sheaves
$Y\otimes {\mathcal{O}}/p$
, the sheaves
![]() $\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}$
(respectively
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}$
(respectively
![]() $\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
) are isomorphic. In fact, the previous sections extends to all
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
) are isomorphic. In fact, the previous sections extends to all
![]() $X$
, for example by Koecher’s principle, see [Reference LanLan17, Theorem 8.7].
$X$
, for example by Koecher’s principle, see [Reference LanLan17, Theorem 8.7].
Remark 5.6. (i) These sections are Cartier divisors on
![]() $X$
, i.e. they are invertible on an open and dense subset (cf. [Reference HernandezHer18, Proposition 3.22] and [Reference WedhornWed99]).
$X$
, i.e. they are invertible on an open and dense subset (cf. [Reference HernandezHer18, Proposition 3.22] and [Reference WedhornWed99]).
(ii) Because of the
![]() ${\mathcal{O}}$
-equivariant isomorphism
${\mathcal{O}}$
-equivariant isomorphism
![]() $\unicode[STIX]{x1D706}:G\simeq G^{D,(\unicode[STIX]{x1D70E})}$
, and the compatibility of
$\unicode[STIX]{x1D706}:G\simeq G^{D,(\unicode[STIX]{x1D70E})}$
, and the compatibility of
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
with duality (see [Reference HernandezHer18, § 1.10]), we deduce that
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
with duality (see [Reference HernandezHer18, § 1.10]), we deduce that
Thus, we could use only
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}$
or
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}$
or
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
and define it in this case without using any crystalline construction. We usually write
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
and define it in this case without using any crystalline construction. We usually write
![]() $\widetilde{\text{}^{\unicode[STIX]{x1D707}}\operatorname{ha}}=\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}\otimes \widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}$
, but because of the this remark, we will only use
$\widetilde{\text{}^{\unicode[STIX]{x1D707}}\operatorname{ha}}=\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}\otimes \widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}$
, but because of the this remark, we will only use
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
in this article (which is then reduced, see the appendix).
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
in this article (which is then reduced, see the appendix).
(iii) We use the notation
![]() $\widetilde{\bullet }$
to denote the previous global sections, but if we have
$\widetilde{\bullet }$
to denote the previous global sections, but if we have
![]() $G/\operatorname{Spec}({\mathcal{O}}_{\mathbb{C}_{p}}/p)$
a
$G/\operatorname{Spec}({\mathcal{O}}_{\mathbb{C}_{p}}/p)$
a
![]() $p$
-divisible
$p$
-divisible
![]() ${\mathcal{O}}$
-module of signature
${\mathcal{O}}$
-module of signature
![]() $(2,1)$
, we will also use the notation
$(2,1)$
, we will also use the notation
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)=v(\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)})$
, where the valuation
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)=v(\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)})$
, where the valuation
![]() $v$
on
$v$
on
![]() ${\mathcal{O}}_{\mathbb{C}_{p}}$
is normalized such that
${\mathcal{O}}_{\mathbb{C}_{p}}$
is normalized such that
![]() $v(p)=1$
and truncated by
$v(p)=1$
and truncated by
![]() $1$
.
$1$
.
Definition 5.7. We denote by
![]() $\overline{X}^{\text{ord}}$
the
$\overline{X}^{\text{ord}}$
the
![]() $\unicode[STIX]{x1D707}$
-ordinary locus of
$\unicode[STIX]{x1D707}$
-ordinary locus of
![]() $\overline{X}=X\otimes _{{\mathcal{O}}}{\mathcal{O}}/p$
, which is
$\overline{X}=X\otimes _{{\mathcal{O}}}{\mathcal{O}}/p$
, which is
![]() $\{x\in \overline{X}:\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}\text{ is invertible}\}$
. It is open and dense (see [Reference WedhornWed99]).
$\{x\in \overline{X}:\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}\text{ is invertible}\}$
. It is open and dense (see [Reference WedhornWed99]).
Let us recall the main theorem of [Reference HernandezHer19] in the simple case of Picard varieties. Recall that
![]() $p$
still denotes a prime, inert in
$p$
still denotes a prime, inert in
![]() $E$
, and suppose
$E$
, and suppose
![]() $p>2$
.
$p>2$
.
Theorem 5.8. Let
![]() $n\in \mathbb{N}^{\times }$
. Let
$n\in \mathbb{N}^{\times }$
. Let
![]() $H/\operatorname{Spec}({\mathcal{O}}_{L})$
, where
$H/\operatorname{Spec}({\mathcal{O}}_{L})$
, where
![]() $L$
is a valued extension of
$L$
is a valued extension of
![]() $\mathbb{Q}_{p}$
, a truncated
$\mathbb{Q}_{p}$
, a truncated
![]() $p$
-divisible
$p$
-divisible
![]() ${\mathcal{O}}$
-module of level
${\mathcal{O}}$
-module of level
![]() $n+1$
and signature
$n+1$
and signature
![]() $(p_{\unicode[STIX]{x1D70F}}=1,p_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=2)$
. Suppose
$(p_{\unicode[STIX]{x1D70F}}=1,p_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=2)$
. Suppose
Then there exists a unique filtration (so-called ‘canonical’ of height
![]() $n$
) of
$n$
) of
![]() $H[p^{n}]$
,
$H[p^{n}]$
,
by finite flat sub-
![]() ${\mathcal{O}}$
-modules of
${\mathcal{O}}$
-modules of
![]() $H[p^{n}]$
, of
$H[p^{n}]$
, of
![]() ${\mathcal{O}}$
-heights
${\mathcal{O}}$
-heights
![]() $n$
and
$n$
and
![]() $2n$
respectively. Moreover,
$2n$
respectively. Moreover,
and
In particular, the groups
![]() $H_{\unicode[STIX]{x1D70F}}^{n}$
and
$H_{\unicode[STIX]{x1D70F}}^{n}$
and
![]() $H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
are of high degree. In addition, points of
$H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
are of high degree. In addition, points of
![]() $H_{\unicode[STIX]{x1D70F}}^{n}$
coincide with the kernel of the Hodge–Tate map
$H_{\unicode[STIX]{x1D70F}}^{n}$
coincide with the kernel of the Hodge–Tate map
![]() $\unicode[STIX]{x1D6FC}_{H[p^{n}],\unicode[STIX]{x1D70F},n-((p^{2n}-1)/(p^{2}-1))\operatorname{ha}_{\unicode[STIX]{x1D70F}}(H)}$
and
$\unicode[STIX]{x1D6FC}_{H[p^{n}],\unicode[STIX]{x1D70F},n-((p^{2n}-1)/(p^{2}-1))\operatorname{ha}_{\unicode[STIX]{x1D70F}}(H)}$
and
![]() $H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
with the one of
$H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
with the one of
![]() $\unicode[STIX]{x1D6FC}_{H[p^{n}],\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},n-((p^{2n}-1)/(p^{2}-1))\operatorname{ha}_{\unicode[STIX]{x1D70F}}(H)}$
. They also coincide with steps of the Harder–Narasimhan filtration and are compatible with
$\unicode[STIX]{x1D6FC}_{H[p^{n}],\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},n-((p^{2n}-1)/(p^{2}-1))\operatorname{ha}_{\unicode[STIX]{x1D70F}}(H)}$
. They also coincide with steps of the Harder–Narasimhan filtration and are compatible with
![]() $p^{s}$
-torsion (
$p^{s}$
-torsion (
![]() $s\leqslant n$
) and quotients.
$s\leqslant n$
) and quotients.
Proof. This is exactly [Reference HernandezHer19] if
![]() $p\geqslant 5$
. Here the bound on
$p\geqslant 5$
. Here the bound on
![]() $p$
is slightly better than the one of [Reference HernandezHer19]. The reason is that we construct
$p$
is slightly better than the one of [Reference HernandezHer19]. The reason is that we construct
![]() $H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
using [Reference HernandezHer19, Théorème 8.3 and Remarque 8.4] (with our bound for
$H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
using [Reference HernandezHer19, Théorème 8.3 and Remarque 8.4] (with our bound for
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
). We can then construct
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
). We can then construct
![]() $D_{\unicode[STIX]{x1D70F}}^{n}\subset G[p^{n}]^{D}$
of
$D_{\unicode[STIX]{x1D70F}}^{n}\subset G[p^{n}]^{D}$
of
![]() ${\mathcal{O}}$
-height
${\mathcal{O}}$
-height
![]() $2n$
by the same reason. Then setting
$2n$
by the same reason. Then setting
we can have the asserted bound on
![]() $\deg _{\unicode[STIX]{x1D70F}}H_{\unicode[STIX]{x1D70F}}^{n}$
. For the assertion on the Kernel of the Hodge–Tate map, we get an inclusion with the bound on the degree. We can then use [Reference HernandezHer19, Proposition 7.6]. Then by [Reference HernandezHer19, Remarque 8.4], these groups are steps of the Harder–Narasimhan filtration (the classical one), and thus we get the assertion of the inclusion
$\deg _{\unicode[STIX]{x1D70F}}H_{\unicode[STIX]{x1D70F}}^{n}$
. For the assertion on the Kernel of the Hodge–Tate map, we get an inclusion with the bound on the degree. We can then use [Reference HernandezHer19, Proposition 7.6]. Then by [Reference HernandezHer19, Remarque 8.4], these groups are steps of the Harder–Narasimhan filtration (the classical one), and thus we get the assertion of the inclusion
![]() $H_{\unicode[STIX]{x1D70F}}^{n}\subset H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
. By unicity of the Harder–Narasimhan filtration, we get that
$H_{\unicode[STIX]{x1D70F}}^{n}\subset H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
. By unicity of the Harder–Narasimhan filtration, we get that
![]() $(H_{\unicode[STIX]{x1D70F}}^{n})^{\bot }=H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
.◻
$(H_{\unicode[STIX]{x1D70F}}^{n})^{\bot }=H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
.◻
Definition 5.9. Let
![]() $H/\operatorname{Spec}({\mathcal{O}}_{L})$
as before, with
$H/\operatorname{Spec}({\mathcal{O}}_{L})$
as before, with
![]() $n=2m$
. Then we can consider inside
$n=2m$
. Then we can consider inside
![]() $H[2m]$
the finite flat subgroup,
$H[2m]$
the finite flat subgroup,
It coincides, after reduction to
![]() $\operatorname{Spec}({\mathcal{O}}_{L}/\unicode[STIX]{x1D70B}_{L})$
(the residue field of
$\operatorname{Spec}({\mathcal{O}}_{L}/\unicode[STIX]{x1D70B}_{L})$
(the residue field of
![]() $L$
) with the kernel of
$L$
) with the kernel of
![]() $F^{2m}$
of
$F^{2m}$
of
![]() $H[p^{2m}]$
(see [Reference HernandezHer19, § 2.9.1]).
$H[p^{2m}]$
(see [Reference HernandezHer19, § 2.9.1]).
Recall that we denoted by
![]() $X/\operatorname{Spec}({\mathcal{O}})$
the (schematic) Picard surface. Denote by
$X/\operatorname{Spec}({\mathcal{O}})$
the (schematic) Picard surface. Denote by
![]() $X^{\text{rig}}$
the associated rigid space over
$X^{\text{rig}}$
the associated rigid space over
![]() $E_{p}$
, there is a specialization map,
$E_{p}$
, there is a specialization map,
and we denote by
![]() $X^{\text{ord}}\subset X^{\text{rig}}$
the open subspace defined by
$X^{\text{ord}}\subset X^{\text{rig}}$
the open subspace defined by
![]() $\operatorname{sp}^{-1}(\overline{X}^{\text{ord}})$
.
$\operatorname{sp}^{-1}(\overline{X}^{\text{ord}})$
.
Let us denote, for
![]() $v\in (0,1]$
,
$v\in (0,1]$
,
the strict neighborhoods of
![]() $X^{\text{ord}}$
. The previous theorem and technics introduced in [Reference FarguesFar10] (see [Reference HernandezHer19, § 2.9]) implies, if
$X^{\text{ord}}$
. The previous theorem and technics introduced in [Reference FarguesFar10] (see [Reference HernandezHer19, § 2.9]) implies, if
![]() $v\leqslant 1/4p^{n-1}$
, that we have a filtration in families over the rigid space
$v\leqslant 1/4p^{n-1}$
, that we have a filtration in families over the rigid space
![]() $X(v)$
,
$X(v)$
,
Let us explain how to get this result. On
![]() $Y^{\text{rig}}(v)$
this is simply [Reference HernandezHer19, Théorème 9.1] which is essentially [Reference FarguesFar10, Théorème 4] (again, see proof of Theorem 5.8 about the bound). The problem is that the
$Y^{\text{rig}}(v)$
this is simply [Reference HernandezHer19, Théorème 9.1] which is essentially [Reference FarguesFar10, Théorème 4] (again, see proof of Theorem 5.8 about the bound). The problem is that the
![]() $p$
-divisible group
$p$
-divisible group
![]() $G$
does not extend to the boundary. But by results of Stroh [Reference StrohStr10, § 3.1], there exists
$G$
does not extend to the boundary. But by results of Stroh [Reference StrohStr10, § 3.1], there exists
which is an étale covering of
![]() $X^{\text{rig}}$
(actually
$X^{\text{rig}}$
(actually
![]() $\overline{U}$
is algebraic and exists also integrally) together with
$\overline{U}$
is algebraic and exists also integrally) together with
![]() $\overline{R}\overset{p_{1}}{\underset{p_{2}}{\rightrightarrows }}\overline{U}$
étale maps, such that
$\overline{R}\overset{p_{1}}{\underset{p_{2}}{\rightrightarrows }}\overline{U}$
étale maps, such that
Over
![]() $\overline{U}$
there is a Mumford
$\overline{U}$
there is a Mumford
![]() $1$
-motive
$1$
-motive
![]() $M=[L\longrightarrow \widetilde{G}]$
such that
$M=[L\longrightarrow \widetilde{G}]$
such that
![]() $M[p^{n}]=A[p^{n}]$
(
$M[p^{n}]=A[p^{n}]$
(
![]() $A$
is the semi-abelian scheme), and thus there is a canonical
$A$
is the semi-abelian scheme), and thus there is a canonical
![]() $\widetilde{G}$
semi-abelian scheme with an action of
$\widetilde{G}$
semi-abelian scheme with an action of
![]() ${\mathcal{O}}_{E}$
of (locally) constant toric rank and thus
${\mathcal{O}}_{E}$
of (locally) constant toric rank and thus
![]() $\widetilde{G}[p^{n}]$
is finite flat. Thus applying to
$\widetilde{G}[p^{n}]$
is finite flat. Thus applying to
![]() $\widetilde{G}[p^{n}]$
the results of [Reference HernandezHer19], there exists on
$\widetilde{G}[p^{n}]$
the results of [Reference HernandezHer19], there exists on
![]() $\overline{U}(v)=\overline{U}\times _{X}X(v)$
the two groups
$\overline{U}(v)=\overline{U}\times _{X}X(v)$
the two groups
![]() $H_{\unicode[STIX]{x1D70F}}^{n}\subset H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
. Moreover, over
$H_{\unicode[STIX]{x1D70F}}^{n}\subset H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
. Moreover, over
![]() $R(v)\overset{p_{1}}{\underset{p_{2}}{\rightrightarrows }}U(v)$
, we have
$R(v)\overset{p_{1}}{\underset{p_{2}}{\rightrightarrows }}U(v)$
, we have
![]() $pr_{1}^{\ast }H_{\star }^{n}=pr_{2}^{\ast }H_{\star }^{n}$
as
$pr_{1}^{\ast }H_{\star }^{n}=pr_{2}^{\ast }H_{\star }^{n}$
as
![]() $H_{\star }^{n}$
descend to
$H_{\star }^{n}$
descend to
![]() $Y(v)$
. Over
$Y(v)$
. Over
![]() $\overline{R}$
we have an isomorphism
$\overline{R}$
we have an isomorphism
![]() $pr_{1}^{\ast }G=pr_{2}^{\ast }G$
[Reference StrohStr10, 3.1.5], and thus we have over
$pr_{1}^{\ast }G=pr_{2}^{\ast }G$
[Reference StrohStr10, 3.1.5], and thus we have over
![]() $R(v)$
an isomorphism
$R(v)$
an isomorphism
As
![]() $\overline{R}$
is normal (because smooth) and
$\overline{R}$
is normal (because smooth) and
![]() $R$
is dense in
$R$
is dense in
![]() $\overline{R}$
, by [Reference StrohStr10, Théorème 1.1.2] (due to Faltings and Chai) there is an isomorphism over
$\overline{R}$
, by [Reference StrohStr10, Théorème 1.1.2] (due to Faltings and Chai) there is an isomorphism over
![]() $\overline{R}$
$\overline{R}$
Thus, by faithfully flat descent,
![]() $H_{\unicode[STIX]{x1D70F}}^{n}\subset H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
exist on
$H_{\unicode[STIX]{x1D70F}}^{n}\subset H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n}$
exist on
![]() $X(v)$
. In particular,
$X(v)$
. In particular,
![]() $K_{m}=H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}+H_{\unicode[STIX]{x1D70F}}^{2m}$
also exists on
$K_{m}=H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}+H_{\unicode[STIX]{x1D70F}}^{2m}$
also exists on
![]() $X(v)$
.
$X(v)$
.
A priori, this filtration does not extend to a formal model of
![]() $X(v)$
, but as
$X(v)$
, but as
![]() $X/\operatorname{Spec}({\mathcal{O}})$
is a normal scheme, we will be able to use the following proposition.
$X/\operatorname{Spec}({\mathcal{O}})$
is a normal scheme, we will be able to use the following proposition.
Definition 5.10. For
![]() $K/\mathbb{Q}_{p}$
an extension, define the category
$K/\mathbb{Q}_{p}$
an extension, define the category
![]() $\mathfrak{Adm}$
of admissible
$\mathfrak{Adm}$
of admissible
![]() ${\mathcal{O}}_{K}$
-algebra, i.e. flat quotient of power series ring
${\mathcal{O}}_{K}$
-algebra, i.e. flat quotient of power series ring
![]() ${\mathcal{O}}_{K}\langle \langle X_{1},\ldots ,X_{r}\rangle \rangle$
for some
${\mathcal{O}}_{K}\langle \langle X_{1},\ldots ,X_{r}\rangle \rangle$
for some
![]() $r\in \mathbb{N}$
. Define
$r\in \mathbb{N}$
. Define
![]() $\mathfrak{NAdm}$
the sub-category of normal admissible
$\mathfrak{NAdm}$
the sub-category of normal admissible
![]() ${\mathcal{O}}_{K}$
-algebra.
${\mathcal{O}}_{K}$
-algebra.
Proposition 5.11. Let
![]() $m$
be an integer,
$m$
be an integer,
![]() $S=\operatorname{Spf}R$
a normal formal scheme over
$S=\operatorname{Spf}R$
a normal formal scheme over
![]() ${\mathcal{O}}$
, and
${\mathcal{O}}$
, and
![]() $G\longrightarrow S$
a truncated
$G\longrightarrow S$
a truncated
![]() $p$
-divisible
$p$
-divisible
![]() ${\mathcal{O}}$
-module of level
${\mathcal{O}}$
-module of level
![]() $2m+1$
and signature
$2m+1$
and signature
![]() $(p_{\unicode[STIX]{x1D70F}}=1,p_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=2)$
. Suppose that for all
$(p_{\unicode[STIX]{x1D70F}}=1,p_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=2)$
. Suppose that for all
![]() $x\in S^{\text{rig}}$
,
$x\in S^{\text{rig}}$
,
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(x)<1/4p^{2m-1}$
. Then the subgroup
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(x)<1/4p^{2m-1}$
. Then the subgroup
![]() $K_{m}:=H_{\unicode[STIX]{x1D70F}}^{2m}+H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}\subset G[p^{2m}]$
of
$K_{m}:=H_{\unicode[STIX]{x1D70F}}^{2m}+H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}\subset G[p^{2m}]$
of
![]() $S^{\text{rig}}$
extends to
$S^{\text{rig}}$
extends to
![]() $S$
.
$S$
.
Proof. As we know that
![]() $K_{m}$
coincides with the kernel of some Frobenius morphism on points, this is exactly as [Reference Andreatta, Iovita and PilloniAIP15, Proposition 4.1.3].◻
$K_{m}$
coincides with the kernel of some Frobenius morphism on points, this is exactly as [Reference Andreatta, Iovita and PilloniAIP15, Proposition 4.1.3].◻
6 Construction of torsors
6.1 Hodge–Tate map and image sheaves
Let
![]() $p$
a prime, inert in
$p$
a prime, inert in
![]() $E$
, and
$E$
, and
![]() ${\mathcal{O}}={\mathcal{O}}_{E,p}$
, a degree-
${\mathcal{O}}={\mathcal{O}}_{E,p}$
, a degree-
![]() $2$
unramified extension of
$2$
unramified extension of
![]() $\mathbb{Z}_{p}$
. Let
$\mathbb{Z}_{p}$
. Let
![]() $K$
be a valued extension of
$K$
be a valued extension of
![]() $E_{p}$
. Let
$E_{p}$
. Let
![]() $m\in \mathbb{N}^{\times }$
and
$m\in \mathbb{N}^{\times }$
and
![]() $v<1/4p^{2m-1}$
. Let
$v<1/4p^{2m-1}$
. Let
![]() $S=\operatorname{Spec}(R)$
where
$S=\operatorname{Spec}(R)$
where
![]() $R$
is an object of
$R$
is an object of
![]() $\mathfrak{NAdm}/{\mathcal{O}}_{K}$
, and
$\mathfrak{NAdm}/{\mathcal{O}}_{K}$
, and
![]() $G\longrightarrow S$
a truncated
$G\longrightarrow S$
a truncated
![]() $p$
-divisible
$p$
-divisible
![]() ${\mathcal{O}}$
-module of level
${\mathcal{O}}$
-module of level
![]() $2m$
and signature,
$2m$
and signature,
where
![]() $\unicode[STIX]{x1D70F}:{\mathcal{O}}\longrightarrow {\mathcal{O}}_{S}$
is the fixed embedding. Suppose moreover that for all
$\unicode[STIX]{x1D70F}:{\mathcal{O}}\longrightarrow {\mathcal{O}}_{S}$
is the fixed embedding. Suppose moreover that for all
![]() $x\in S^{\text{rig}}$
,
$x\in S^{\text{rig}}$
,
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(x)\leqslant v$
. According to the previous section, there exists on
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(x)\leqslant v$
. According to the previous section, there exists on
![]() $S^{\text{rig}}$
a filtration of
$S^{\text{rig}}$
a filtration of
![]() $G[p^{2m}]$
by finite flat
$G[p^{2m}]$
by finite flat
![]() ${\mathcal{O}}$
-modules,
${\mathcal{O}}$
-modules,
of
![]() ${\mathcal{O}}$
-heights
${\mathcal{O}}$
-heights
![]() $2m$
and
$2m$
and
![]() $4m$
respectively. Moreover, we have on
$4m$
respectively. Moreover, we have on
![]() $S$
a subgroup
$S$
a subgroup
![]() $K_{m}\subset G[p^{2m}]$
, finite flat of
$K_{m}\subset G[p^{2m}]$
, finite flat of
![]() ${\mathcal{O}}$
-height
${\mathcal{O}}$
-height
![]() $3m$
, étale-locally isomorphic (on
$3m$
, étale-locally isomorphic (on
![]() $S^{\text{rig}}$
) to
$S^{\text{rig}}$
) to
![]() ${\mathcal{O}}/p^{2m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{m}{\mathcal{O}}$
, and on
${\mathcal{O}}/p^{2m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{m}{\mathcal{O}}$
, and on
![]() $S^{\text{rig}}$
,
$S^{\text{rig}}$
,
![]() $K_{m}=H_{\unicode[STIX]{x1D70F}}^{2m}+H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2m}[p^{m}]$
.
$K_{m}=H_{\unicode[STIX]{x1D70F}}^{2m}+H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2m}[p^{m}]$
.
Proposition 6.1. Let
![]() $w_{\unicode[STIX]{x1D70F}},w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\in v({\mathcal{O}}_{K})$
such that
$w_{\unicode[STIX]{x1D70F}},w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\in v({\mathcal{O}}_{K})$
such that
![]() $w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}<m-((p^{2m}-1)/(p^{2}-1))v$
and
$w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}<m-((p^{2m}-1)/(p^{2}-1))v$
and
![]() $w_{\unicode[STIX]{x1D70F}}<2m-((p^{4m}-1)/(p^{2}-1))v$
. Then, the morphism of sheaves on
$w_{\unicode[STIX]{x1D70F}}<2m-((p^{4m}-1)/(p^{2}-1))v$
. Then, the morphism of sheaves on
![]() $S$
$S$
![]() $\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D714}_{G}\longrightarrow \unicode[STIX]{x1D714}_{K_{m}}$
, induce by the inclusion
$\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D714}_{G}\longrightarrow \unicode[STIX]{x1D714}_{K_{m}}$
, induce by the inclusion
![]() $K_{m}\subset G$
, induces isomorphisms,
$K_{m}\subset G$
, induces isomorphisms,
Proof. If
![]() $G/\operatorname{Spec}({\mathcal{O}}_{C})$
(
$G/\operatorname{Spec}({\mathcal{O}}_{C})$
(
![]() $C$
a complete algebraically closed extension of
$C$
a complete algebraically closed extension of
![]() $\mathbb{Q}_{p}$
), the degrees of the canonical filtration of
$\mathbb{Q}_{p}$
), the degrees of the canonical filtration of
![]() $G$
assure that
$G$
assure that
and there is thus an isomorphism,
and also for
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
and
![]() $G[p^{2m}]$
. But there are inclusions
$G[p^{2m}]$
. But there are inclusions
![]() $H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}=H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2m}[p^{m}]\subset K_{m}\subset G$
and
$H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}=H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2m}[p^{m}]\subset K_{m}\subset G$
and
![]() $H_{\unicode[STIX]{x1D70F}}^{2m}\subset K_{m}\subset G$
such that the composite,
$H_{\unicode[STIX]{x1D70F}}^{2m}\subset K_{m}\subset G$
such that the composite,
is an isomorphism, which implies that the first one is. The same reasoning applies for
![]() $\unicode[STIX]{x1D70F}$
. We can thus conclude the following for general
$\unicode[STIX]{x1D70F}$
. We can thus conclude the following for general
![]() $S$
as in [Reference Andreatta, Iovita and PilloniAIP15, Proposition 4.2.1]. Up to reducing
$S$
as in [Reference Andreatta, Iovita and PilloniAIP15, Proposition 4.2.1]. Up to reducing
![]() $R$
we can suppose
$R$
we can suppose
![]() $\unicode[STIX]{x1D714}_{G}$
is a free
$\unicode[STIX]{x1D714}_{G}$
is a free
![]() $R/p^{2m+1}$
-module, and look at the surjection
$R/p^{2m+1}$
-module, and look at the surjection
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}:R^{2}{\twoheadrightarrow}\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}{\twoheadrightarrow}\unicode[STIX]{x1D714}_{K_{m},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}$
; it is enough to prove that for any
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}:R^{2}{\twoheadrightarrow}\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}{\twoheadrightarrow}\unicode[STIX]{x1D714}_{K_{m},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}$
; it is enough to prove that for any
![]() $(x_{1},x_{2})$
in
$(x_{1},x_{2})$
in
![]() $\ker \unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
we have
$\ker \unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
we have
![]() $x_{i}\in p^{w_{\unicode[STIX]{x1D70F}}}R$
, but, as
$x_{i}\in p^{w_{\unicode[STIX]{x1D70F}}}R$
, but, as
![]() $R$
is normal, it suffices to do it for
$R$
is normal, it suffices to do it for
![]() $R_{\mathfrak{p}}$
, and even for
$R_{\mathfrak{p}}$
, and even for
![]() $\widehat{R_{\mathfrak{p}}}$
, for all codimension-
$\widehat{R_{\mathfrak{p}}}$
, for all codimension-
![]() $1$
prime ideals
$1$
prime ideals
![]() $\mathfrak{p}$
that contain
$\mathfrak{p}$
that contain
![]() $(p)$
. But now
$(p)$
. But now
![]() $\widehat{R_{\mathfrak{p}}}$
is a complete, discrete valuation ring of mixed characteristic, and this reduces to the preceding assertion.◻
$\widehat{R_{\mathfrak{p}}}$
is a complete, discrete valuation ring of mixed characteristic, and this reduces to the preceding assertion.◻
Proposition 6.2. Suppose there is an isomorphism
![]() $K_{m}^{D}(R)\simeq {\mathcal{O}}/p^{m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}}$
. Then the cokernel of the
$K_{m}^{D}(R)\simeq {\mathcal{O}}/p^{m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}}$
. Then the cokernel of the
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-Hodge–Tate map,
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-Hodge–Tate map,
is killed by
![]() $p^{(p+v)/(p^{2}-1)}$
, and the cokernel of the
$p^{(p+v)/(p^{2}-1)}$
, and the cokernel of the
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate map,
$\unicode[STIX]{x1D70F}$
-Hodge–Tate map,
is killed by
![]() $p^{v/(p^{2}-1)}$
.
$p^{v/(p^{2}-1)}$
.
Proof. This is true for
![]() $G/\operatorname{Spec}({\mathcal{O}}_{C})$
by [Reference HernandezHer19, Théorème 6.10(2)] with the previous proposition (because
$G/\operatorname{Spec}({\mathcal{O}}_{C})$
by [Reference HernandezHer19, Théorème 6.10(2)] with the previous proposition (because
![]() $(p+v)/(p^{2}-1)<1-v$
, already for
$(p+v)/(p^{2}-1)<1-v$
, already for
![]() $m=1$
). For a general normal
$m=1$
). For a general normal
![]() $R$
, we can reduce to previous case (see also [Reference Andreatta, Iovita and PilloniAIP15, Proposition 4.2.2]): up to reducing
$R$
, we can reduce to previous case (see also [Reference Andreatta, Iovita and PilloniAIP15, Proposition 4.2.2]): up to reducing
![]() $\operatorname{Spec}(R)$
, we have a diagram,
$\operatorname{Spec}(R)$
, we have a diagram,

and
![]() $\operatorname{Fitt}^{1}(\unicode[STIX]{x1D6FE})$
(which is just a determinant here) annihilates the cokernel of
$\operatorname{Fitt}^{1}(\unicode[STIX]{x1D6FE})$
(which is just a determinant here) annihilates the cokernel of
![]() $\unicode[STIX]{x1D6FE}$
, and it suffices to prove that
$\unicode[STIX]{x1D6FE}$
, and it suffices to prove that
![]() $p^{(p+v)/(p^{2}-1)}\in \operatorname{Fitt}^{1}(\unicode[STIX]{x1D6FE})$
. But as
$p^{(p+v)/(p^{2}-1)}\in \operatorname{Fitt}^{1}(\unicode[STIX]{x1D6FE})$
. But as
![]() $R$
is normal, it suffices to prove that
$R$
is normal, it suffices to prove that
![]() $p^{(p+v)/(p^{2}-1)}\in \operatorname{Fitt}^{1}(\unicode[STIX]{x1D6FE})R_{\mathfrak{p}}$
for every codimension-
$p^{(p+v)/(p^{2}-1)}\in \operatorname{Fitt}^{1}(\unicode[STIX]{x1D6FE})R_{\mathfrak{p}}$
for every codimension-
![]() $1$
prime ideal
$1$
prime ideal
![]() $\mathfrak{p}$
that contains
$\mathfrak{p}$
that contains
![]() $(p)$
. But by the previous case, we can conclude. The same works for
$(p)$
. But by the previous case, we can conclude. The same works for
![]() $\unicode[STIX]{x1D70F}$
.◻
$\unicode[STIX]{x1D70F}$
.◻
Proposition 6.3. Suppose we have an isomorphism
![]() $K_{m}^{D}(R)\simeq {\mathcal{O}}/p^{m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}}$
. Then there exist on
$K_{m}^{D}(R)\simeq {\mathcal{O}}/p^{m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}}$
. Then there exist on
![]() $S=\operatorname{Spec}R$
locally free subsheaves
$S=\operatorname{Spec}R$
locally free subsheaves
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},{\mathcal{F}}_{\unicode[STIX]{x1D70F}}$
of
${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},{\mathcal{F}}_{\unicode[STIX]{x1D70F}}$
of
![]() $\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
respectively, of ranks
$\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
respectively, of ranks
![]() $2$
and
$2$
and
![]() $1$
, which contain
$1$
, which contain
![]() $p^{(p+v)/(p^{2}-1)}\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
$p^{(p+v)/(p^{2}-1)}\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
![]() $p^{v/(p^{2}-1)}\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
, and which are equipped, for all
$p^{v/(p^{2}-1)}\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
, and which are equipped, for all
![]() $w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}<m-((p^{2m}-1)/(p^{2}-1))v$
and
$w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}<m-((p^{2m}-1)/(p^{2}-1))v$
and
![]() $w_{\unicode[STIX]{x1D70F}}<2m-((p^{4m}-1)/(p^{2}-1))v$
, with maps,
$w_{\unicode[STIX]{x1D70F}}<2m-((p^{4m}-1)/(p^{2}-1))v$
, with maps,
which are surjective after tensoring
![]() $K_{m}^{D}(R)$
with
$K_{m}^{D}(R)$
with
![]() $R$
over
$R$
over
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
More precisely, via the projection,
we have induced isomorphisms,
and
Proof. This is the same construction as [Reference Andreatta, Iovita and PilloniAIP15, proposition 4.3.1]. To check the assertion about the isomorphism with
![]() $H_{\unicode[STIX]{x1D70F}}^{2m}$
, it suffices to show that the map
$H_{\unicode[STIX]{x1D70F}}^{2m}$
, it suffices to show that the map
![]() $\operatorname{HT}_{\unicode[STIX]{x1D70F},w_{\unicode[STIX]{x1D70F}}}$
factors, but it is true over
$\operatorname{HT}_{\unicode[STIX]{x1D70F},w_{\unicode[STIX]{x1D70F}}}$
factors, but it is true over
![]() $R_{\mathfrak{p}}$
(as the canonical filtration is given by kernels of Hodge–Tate maps) for every codimension-
$R_{\mathfrak{p}}$
(as the canonical filtration is given by kernels of Hodge–Tate maps) for every codimension-
![]() $1$
ideal
$1$
ideal
![]() $\mathfrak{p}$
, and it is moreover surjective, so it globally factors and is globally surjective, but the two free
$\mathfrak{p}$
, and it is moreover surjective, so it globally factors and is globally surjective, but the two free
![]() $R_{w_{\unicode[STIX]{x1D70F}}}$
-modules are free of the same rank
$R_{w_{\unicode[STIX]{x1D70F}}}$
-modules are free of the same rank
![]() $1$
, so it is an isomorphism.◻
$1$
, so it is an isomorphism.◻
Moreover the construction of the sheaves
![]() ${\mathcal{F}}$
is functorial in the following sense.
${\mathcal{F}}$
is functorial in the following sense.
Proposition 6.4. Suppose given
![]() $G,G^{\prime }$
two truncated
$G,G^{\prime }$
two truncated
![]() $p$
-divisible
$p$
-divisible
![]() ${\mathcal{O}}$
-module such that for all
${\mathcal{O}}$
-module such that for all
![]() $x\in S^{\text{rig}}$
$x\in S^{\text{rig}}$
and an
![]() ${\mathcal{O}}_{E}$
-isogeny,
${\mathcal{O}}_{E}$
-isogeny,
Assume moreover that we are given trivializations of the points of
![]() $K_{m}^{D}(G)$
and
$K_{m}^{D}(G)$
and
![]() $K_{m}^{D}(G^{\prime })$
. Then
$K_{m}^{D}(G^{\prime })$
. Then
![]() $\unicode[STIX]{x1D719}^{\ast }$
induces maps
$\unicode[STIX]{x1D719}^{\ast }$
induces maps
that are compatible with inclusion in
![]() $\unicode[STIX]{x1D714}$
, reduction modulo
$\unicode[STIX]{x1D714}$
, reduction modulo
![]() $p^{w}$
and the Hodge–Tate maps of
$p^{w}$
and the Hodge–Tate maps of
![]() $K_{m}^{D}$
.
$K_{m}^{D}$
.
Proof. Once we know that
![]() $\unicode[STIX]{x1D719}$
will send
$\unicode[STIX]{x1D719}$
will send
![]() $K_{m}^{D}(G)$
inside
$K_{m}^{D}(G)$
inside
![]() $K_{m}^{D}(G^{\prime })$
this is straightforward as
$K_{m}^{D}(G^{\prime })$
this is straightforward as
![]() ${\mathcal{F}}_{?}$
corresponds to sections of
${\mathcal{F}}_{?}$
corresponds to sections of
![]() $\unicode[STIX]{x1D714}_{G,?}$
that are modulo
$\unicode[STIX]{x1D714}_{G,?}$
that are modulo
![]() $p^{w_{?}}$
generated by the image of
$p^{w_{?}}$
generated by the image of
![]() $\operatorname{HT}_{?}$
. But
$\operatorname{HT}_{?}$
. But
![]() $K_{m}$
is generated by the subgroup
$K_{m}$
is generated by the subgroup
![]() $H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}$
and
$H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}$
and
![]() $H_{\unicode[STIX]{x1D70F}}^{2m}$
each being a breakpoint of the Harder–Narasimhan filtration
$H_{\unicode[STIX]{x1D70F}}^{2m}$
each being a breakpoint of the Harder–Narasimhan filtration
![]() $\operatorname{HN}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(G[p^{m}])$
and
$\operatorname{HN}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(G[p^{m}])$
and
![]() $\operatorname{HN}_{\unicode[STIX]{x1D70F}}(G[p^{2m}])$
respectively, and thus by functoriality of these filtrations,
$\operatorname{HN}_{\unicode[STIX]{x1D70F}}(G[p^{2m}])$
respectively, and thus by functoriality of these filtrations,
![]() $\unicode[STIX]{x1D719}$
sends each subgroup for
$\unicode[STIX]{x1D719}$
sends each subgroup for
![]() $G$
inside the one for
$G$
inside the one for
![]() $G^{\prime }$
and thus sends
$G^{\prime }$
and thus sends
![]() $K_{m}(G)$
inside
$K_{m}(G)$
inside
![]() $K_{m}(G^{\prime })$
.◻
$K_{m}(G^{\prime })$
.◻
Remark 6.5. Strictly speaking, we cannot apply this section for
![]() $S^{\text{rig}}\subset X(v)$
an affinoid. The reason is that even if
$S^{\text{rig}}\subset X(v)$
an affinoid. The reason is that even if
![]() $H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n},H_{\unicode[STIX]{x1D70F}}^{n}$
descend to
$H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{n},H_{\unicode[STIX]{x1D70F}}^{n}$
descend to
![]() $X(v)$
, it is not the case of
$X(v)$
, it is not the case of
![]() $\widetilde{G}[p^{n}]$
. But we can apply the results of this section with
$\widetilde{G}[p^{n}]$
. But we can apply the results of this section with
![]() $\widetilde{G}[p^{n}]$
for
$\widetilde{G}[p^{n}]$
for
![]() $S^{\text{rig}}$
an affinoid of
$S^{\text{rig}}$
an affinoid of
![]() $\overline{U}$
. As
$\overline{U}$
. As
![]() $\unicode[STIX]{x1D714}_{\widetilde{G}}\simeq \unicode[STIX]{x1D714}\times _{X(v)}\overline{U}(v)$
, it is enough to check Propositions 6.1 and 6.2 over
$\unicode[STIX]{x1D714}_{\widetilde{G}}\simeq \unicode[STIX]{x1D714}\times _{X(v)}\overline{U}(v)$
, it is enough to check Propositions 6.1 and 6.2 over
![]() $\overline{U}/\operatorname{Spec}({\mathcal{O}})$
. Thus Propositions 6.3 and 6.4 remain true over
$\overline{U}/\operatorname{Spec}({\mathcal{O}})$
. Thus Propositions 6.3 and 6.4 remain true over
![]() $S^{\text{rig}}$
and affinoid of
$S^{\text{rig}}$
and affinoid of
![]() $X(v)$
(for Proposition 6.4 we will restrict anyway to the open Picard variety, but it would remain true looking at an isogeny of semi-abelian schemes).
$X(v)$
(for Proposition 6.4 we will restrict anyway to the open Picard variety, but it would remain true looking at an isogeny of semi-abelian schemes).
6.2 The torsors
To simplify the notations, fix
![]() $w=w_{\unicode[STIX]{x1D70F}}=w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}<m-((p^{2m}-1)/(p^{2}-1))v$
to use the previous propositions. Let
$w=w_{\unicode[STIX]{x1D70F}}=w_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}<m-((p^{2m}-1)/(p^{2}-1))v$
to use the previous propositions. Let
![]() $R\in {\mathcal{O}}_{K}-\mathfrak{NAdm}$
and
$R\in {\mathcal{O}}_{K}-\mathfrak{NAdm}$
and
![]() $S=\operatorname{Spf}(R)$
. In rigid fiber, we have a subgroup of
$S=\operatorname{Spf}(R)$
. In rigid fiber, we have a subgroup of
![]() $K_{m}[p^{m}]/S^{\text{rig}}$
,
$K_{m}[p^{m}]/S^{\text{rig}}$
,
![]() $H_{\unicode[STIX]{x1D70F}}^{m}\subset K_{m}[p^{m}]$
which induces a filtration,
$H_{\unicode[STIX]{x1D70F}}^{m}\subset K_{m}[p^{m}]$
which induces a filtration,
of cokernel isomorphic to
![]() $(H_{\unicode[STIX]{x1D70F}}^{m})^{D}(R_{K})$
.
$(H_{\unicode[STIX]{x1D70F}}^{m})^{D}(R_{K})$
.
Suppose we are given a trivialization,
which induces trivializations (first coordinate and quotient),
Let
![]() ${\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\longrightarrow S$
be the Grassmanian of locally direct factor sheaves of rank
${\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\longrightarrow S$
be the Grassmanian of locally direct factor sheaves of rank
![]() $1$
,
$1$
,
![]() $\operatorname{Fil}^{1}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\subset {\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. Let
$\operatorname{Fil}^{1}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\subset {\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. Let
![]() ${\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{+}\longrightarrow {\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
be the
${\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{+}\longrightarrow {\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
be the
![]() $\mathbb{G}_{m}^{2}$
-torsor of trivializations of
$\mathbb{G}_{m}^{2}$
-torsor of trivializations of
![]() $\operatorname{Fil}^{1}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
$\operatorname{Fil}^{1}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}/\text{Fil}^{1}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. Also let
${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}/\text{Fil}^{1}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. Also let
![]() ${\mathcal{G}}r_{\unicode[STIX]{x1D70F}}^{+}\longrightarrow S$
be the
${\mathcal{G}}r_{\unicode[STIX]{x1D70F}}^{+}\longrightarrow S$
be the
![]() $\mathbb{G}_{m}$
-torsor of trivializations of
$\mathbb{G}_{m}$
-torsor of trivializations of
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70F}}$
.
${\mathcal{F}}_{\unicode[STIX]{x1D70F}}$
.
Definition 6.6. We say that a
![]() $A$
-point of
$A$
-point of
![]() ${\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
(respectively
${\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
(respectively
![]() ${\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{+}$
or
${\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{+}$
or
![]() ${\mathcal{G}}r_{\unicode[STIX]{x1D70F}}^{+}$
)
${\mathcal{G}}r_{\unicode[STIX]{x1D70F}}^{+}$
)
is
![]() $w$
-compatible with
$w$
-compatible with
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
if, respectively:
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}},\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
if, respectively:
(i)
 $\operatorname{Fil}^{1}({\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes A)\otimes _{R}R_{w}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}((H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}/H_{\unicode[STIX]{x1D70F}}^{m})^{D}(R_{K})\otimes _{{\mathcal{O}}}R_{w})\otimes _{R}A$
;
$\operatorname{Fil}^{1}({\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes A)\otimes _{R}R_{w}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}((H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{m}/H_{\unicode[STIX]{x1D70F}}^{m})^{D}(R_{K})\otimes _{{\mathcal{O}}}R_{w})\otimes _{R}A$
;(ii)
 $P_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes _{R}R_{w}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}\circ (\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes _{{\mathcal{O}}}R_{w})\otimes _{R}A$
;
$P_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes _{R}R_{w}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}\circ (\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes _{{\mathcal{O}}}R_{w})\otimes _{R}A$
;(iii)
 $P_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes _{R}R_{w}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}\circ (\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}\otimes _{{\mathcal{O}}}R_{w})\otimes _{R}A$
;
$P_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes _{R}R_{w}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}\circ (\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}\otimes _{{\mathcal{O}}}R_{w})\otimes _{R}A$
;(iv)
 $P^{\unicode[STIX]{x1D70F}}\otimes _{R}R_{w}=\operatorname{HT}_{\unicode[STIX]{x1D70F},w}\circ (\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}\otimes _{{\mathcal{O}}}R_{w})\otimes _{R}A$
.
$P^{\unicode[STIX]{x1D70F}}\otimes _{R}R_{w}=\operatorname{HT}_{\unicode[STIX]{x1D70F},w}\circ (\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}\otimes _{{\mathcal{O}}}R_{w})\otimes _{R}A$
.
We can define the functors,
The previous functors are representable by formal schemes, affine over
![]() $S=\operatorname{Spf}(R)$
, and locally isomorphic to
$S=\operatorname{Spf}(R)$
, and locally isomorphic to
where
![]() $\mathfrak{B}(0,1)=\operatorname{Spf}({\mathcal{O}}_{K}\langle T\rangle )$
is the one-dimensional formal unit ball, and
$\mathfrak{B}(0,1)=\operatorname{Spf}({\mathcal{O}}_{K}\langle T\rangle )$
is the one-dimensional formal unit ball, and
We also define
![]() $\mathfrak{I}\mathfrak{W}_{w}^{+}=\mathfrak{I}\mathfrak{W}_{\unicode[STIX]{x1D70F},w}^{+}\times _{S}\mathfrak{I}\mathfrak{W}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}^{+}$
. The previous constructions are independent of
$\mathfrak{I}\mathfrak{W}_{w}^{+}=\mathfrak{I}\mathfrak{W}_{\unicode[STIX]{x1D70F},w}^{+}\times _{S}\mathfrak{I}\mathfrak{W}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}^{+}$
. The previous constructions are independent of
![]() $n=2m$
(because
$n=2m$
(because
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70F}},{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
are).
${\mathcal{F}}_{\unicode[STIX]{x1D70F}},{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
are).
Let
![]() $T^{1}=\operatorname{Res}_{{\mathcal{O}}/\mathbb{Z}_{p}}\mathbb{G}_{m}\times U(1)$
the torus of
$T^{1}=\operatorname{Res}_{{\mathcal{O}}/\mathbb{Z}_{p}}\mathbb{G}_{m}\times U(1)$
the torus of
![]() $U(2,1)$
over
$U(2,1)$
over
![]() $\mathbb{Z}_{p}$
whose
$\mathbb{Z}_{p}$
whose
![]() $\mathbb{Z}_{p}$
-points are
$\mathbb{Z}_{p}$
-points are
![]() ${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
. Its scalar extension
${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
. Its scalar extension
![]() $T=T^{1}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}$
is isomorphic to
$T=T^{1}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}$
is isomorphic to
![]() $\mathbb{G}_{m}^{3}$
, and
$\mathbb{G}_{m}^{3}$
, and
![]() ${\mathcal{G}}r^{+}={\mathcal{G}}r_{\unicode[STIX]{x1D70F}}^{+}\times {\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{+}\longrightarrow {\mathcal{G}}r={\mathcal{G}}r_{\unicode[STIX]{x1D70F}}$
is a
${\mathcal{G}}r^{+}={\mathcal{G}}r_{\unicode[STIX]{x1D70F}}^{+}\times {\mathcal{G}}r_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{+}\longrightarrow {\mathcal{G}}r={\mathcal{G}}r_{\unicode[STIX]{x1D70F}}$
is a
![]() $T$
-torsor. Denote by
$T$
-torsor. Denote by
![]() $\mathfrak{T}\longrightarrow \operatorname{Spf}({\mathcal{O}})$
the formal completion of
$\mathfrak{T}\longrightarrow \operatorname{Spf}({\mathcal{O}})$
the formal completion of
![]() $T$
along its special fiber, and
$T$
along its special fiber, and
![]() $\mathfrak{T}_{w}$
the torus defined by
$\mathfrak{T}_{w}$
the torus defined by
Then
![]() $\mathfrak{I}\mathfrak{W}_{w}^{+}\longrightarrow \mathfrak{I}\mathfrak{W}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}$
is a
$\mathfrak{I}\mathfrak{W}_{w}^{+}\longrightarrow \mathfrak{I}\mathfrak{W}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}$
is a
![]() $\mathfrak{T}_{w}$
-torsor.
$\mathfrak{T}_{w}$
-torsor.
Denote by
![]() ${\mathcal{I}}{\mathcal{W}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w},{\mathcal{I}}{\mathcal{W}}_{\unicode[STIX]{x1D70F},w}^{+},{\mathcal{I}}{\mathcal{W}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}^{+},{\mathcal{I}}{\mathcal{W}}_{w}^{+},{\mathcal{T}}$
the generic fibers of the previous formal schemes.
${\mathcal{I}}{\mathcal{W}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w},{\mathcal{I}}{\mathcal{W}}_{\unicode[STIX]{x1D70F},w}^{+},{\mathcal{I}}{\mathcal{W}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}^{+},{\mathcal{I}}{\mathcal{W}}_{w}^{+},{\mathcal{T}}$
the generic fibers of the previous formal schemes.
7 The Picard surface and overconvergent automorphic sheaves
7.1 Constructing automorphic sheaves
Let us consider the datum
![]() $(E,V,\unicode[STIX]{x1D713},{\mathcal{O}}_{E},\unicode[STIX]{x1D6EC}={\mathcal{O}}_{E}^{3},h)$
, the PEL datum introduced in § 2. Let
$(E,V,\unicode[STIX]{x1D713},{\mathcal{O}}_{E},\unicode[STIX]{x1D6EC}={\mathcal{O}}_{E}^{3},h)$
, the PEL datum introduced in § 2. Let
![]() $p$
be a prime, inert in
$p$
be a prime, inert in
![]() $E$
and
$E$
and
![]() $G$
the reductive group associated over
$G$
the reductive group associated over
![]() $\mathbb{Z}_{p}$
. We fix
$\mathbb{Z}_{p}$
. We fix
![]() $K^{p}$
a compact open subgroup of
$K^{p}$
a compact open subgroup of
![]() $G(\mathbb{A}_{f}^{p})$
sufficiently small and
$G(\mathbb{A}_{f}^{p})$
sufficiently small and
![]() $\mathfrak{C}=G(\mathbb{Z}_{p})$
an hyperspecial subgroup at
$\mathfrak{C}=G(\mathbb{Z}_{p})$
an hyperspecial subgroup at
![]() $p$
. Let
$p$
. Let
![]() $X=X_{K^{p}\mathfrak{C}}/\text{Spec}({\mathcal{O}})$
the (integral) Picard variety associated to the previous datum (cf. [Reference KottwitzKot92, Reference LanLan13, Reference Langlands and RamakrishnanLR92]).
$X=X_{K^{p}\mathfrak{C}}/\text{Spec}({\mathcal{O}})$
the (integral) Picard variety associated to the previous datum (cf. [Reference KottwitzKot92, Reference LanLan13, Reference Langlands and RamakrishnanLR92]).
Let
![]() $K/{\mathcal{O}}[1/p]$
be a finite extension (that we will choose sufficiently large) and still write
$K/{\mathcal{O}}[1/p]$
be a finite extension (that we will choose sufficiently large) and still write
![]() $X=X_{{\mathcal{O}}_{K}}=X\times _{\operatorname{Spec}{\mathcal{O}}}\operatorname{Spec}({\mathcal{O}}_{K})$
.
$X=X_{{\mathcal{O}}_{K}}=X\times _{\operatorname{Spec}{\mathcal{O}}}\operatorname{Spec}({\mathcal{O}}_{K})$
.
Denote by
![]() $A$
the universal semi-abelian scheme,
$A$
the universal semi-abelian scheme,
![]() $X^{\text{rig}}$
the rigid fiber of
$X^{\text{rig}}$
the rigid fiber of
![]() $X$
,
$X$
,
![]() $X^{\text{ord}}$
the ordinary locus and for
$X^{\text{ord}}$
the ordinary locus and for
![]() $v\in v(K)$
,
$v\in v(K)$
,
![]() $X(v)$
the rigid-analytic open
$X(v)$
the rigid-analytic open
![]() $\{x\in X^{\text{rig}}:\operatorname{ha}_{\unicode[STIX]{x1D70F}}(x)<v\}$
. Denote also
$\{x\in X^{\text{rig}}:\operatorname{ha}_{\unicode[STIX]{x1D70F}}(x)<v\}$
. Denote also
![]() $\mathfrak{X}\longrightarrow \operatorname{Spf}({\mathcal{O}}_{K})$
the formal completion of
$\mathfrak{X}\longrightarrow \operatorname{Spf}({\mathcal{O}}_{K})$
the formal completion of
![]() $X$
along its special fiber,
$X$
along its special fiber,
![]() $\widetilde{\mathfrak{X}(v)}$
the admissible blow up of
$\widetilde{\mathfrak{X}(v)}$
the admissible blow up of
![]() $\mathfrak{X}$
along the ideal
$\mathfrak{X}$
along the ideal
![]() $(\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}},p^{v})$
and
$(\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}},p^{v})$
and
![]() $\mathfrak{X}(v)$
its open subscheme where
$\mathfrak{X}(v)$
its open subscheme where
![]() $(\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}},p^{v})$
is generated by
$(\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}},p^{v})$
is generated by
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
.
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
.
Lemma 7.1. The formal scheme
![]() $\mathfrak{X}(v)$
is normal.
$\mathfrak{X}(v)$
is normal.
Proof. As
![]() $X(v)$
is smooth, thus normal, and
$X(v)$
is smooth, thus normal, and
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
is reduced, this follows from the next lemma.
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70F}}}$
is reduced, this follows from the next lemma.
Lemma 7.2. Let
![]() $A\in {\mathcal{O}}_{K}-\mathfrak{Adm}$
such that
$A\in {\mathcal{O}}_{K}-\mathfrak{Adm}$
such that
![]() $A_{K}$
is normal and
$A_{K}$
is normal and
![]() $A/\unicode[STIX]{x1D70B}_{K}$
is reduced. Then
$A/\unicode[STIX]{x1D70B}_{K}$
is reduced. Then
![]() $A$
is normal.
$A$
is normal.
Proof. For
![]() $R$
a (noetherian) ring denote by
$R$
a (noetherian) ring denote by
![]() $R^{\text{norm}}$
its integral closure in its total ring of fractions. Write, for all
$R^{\text{norm}}$
its integral closure in its total ring of fractions. Write, for all
![]() $x\in A_{K}$
,
$x\in A_{K}$
,
Then we can check that
![]() $|f+g|_{A}\leqslant \sup (|f|_{A},|g|_{A})$
and that
$|f+g|_{A}\leqslant \sup (|f|_{A},|g|_{A})$
and that
![]() $|f^{n}|_{A}=|f|_{A}^{n}$
. Indeed,
$|f^{n}|_{A}=|f|_{A}^{n}$
. Indeed,
![]() $\unicode[STIX]{x1D70B}_{K}^{-v_{A}(f)}f\in A\backslash \unicode[STIX]{x1D70B}_{K}A$
. Thus, as
$\unicode[STIX]{x1D70B}_{K}^{-v_{A}(f)}f\in A\backslash \unicode[STIX]{x1D70B}_{K}A$
. Thus, as
![]() $A/\unicode[STIX]{x1D70B}_{K}A$
is reduced,
$A/\unicode[STIX]{x1D70B}_{K}A$
is reduced,
![]() $(\unicode[STIX]{x1D70B}_{K}^{-v_{A}(f)}f)^{n}\in A\backslash \unicode[STIX]{x1D70B}_{K}A$
and thus
$(\unicode[STIX]{x1D70B}_{K}^{-v_{A}(f)}f)^{n}\in A\backslash \unicode[STIX]{x1D70B}_{K}A$
and thus
![]() $v_{A}(f^{n})=nv_{A}(f)$
. For this norm, we have that
$v_{A}(f^{n})=nv_{A}(f)$
. For this norm, we have that
Now let us verify that
![]() $A$
is normal. Let
$A$
is normal. Let
![]() $x\in A^{\text{norm}}$
, in particular,
$x\in A^{\text{norm}}$
, in particular,
![]() $x\in A_{K}^{\text{norm}}$
. However, as
$x\in A_{K}^{\text{norm}}$
. However, as
![]() $A_{K}$
is normal,
$A_{K}$
is normal,
![]() $x\in A_{K}$
. Now write, for
$x\in A_{K}$
. Now write, for
![]() $a_{i}\in A,0\leqslant i\leqslant n$
and
$a_{i}\in A,0\leqslant i\leqslant n$
and
![]() $a_{n}=1$
,
$a_{n}=1$
,
Then
![]() $\sup _{1\leqslant i\leqslant n}|x^{i}a_{n-i}|_{A}=|a_{0}|_{A}\leqslant 1$
, thus
$\sup _{1\leqslant i\leqslant n}|x^{i}a_{n-i}|_{A}=|a_{0}|_{A}\leqslant 1$
, thus
![]() $|x^{n}|_{A}=|x|_{A}^{n}\leqslant 1$
, and
$|x^{n}|_{A}=|x|_{A}^{n}\leqslant 1$
, and
![]() $|x|_{A}\leqslant 1$
. Thus
$|x|_{A}\leqslant 1$
. Thus
![]() $x\in A$
.◻
$x\in A$
.◻
By the previous sections, we have on
![]() $X(v)$
a filtration of
$X(v)$
a filtration of
![]() $G$
by finite flat
$G$
by finite flat
![]() ${\mathcal{O}}$
-modules,
${\mathcal{O}}$
-modules,
locally isomorphic to
![]() ${\mathcal{O}}/p^{2m}{\mathcal{O}}$
and
${\mathcal{O}}/p^{2m}{\mathcal{O}}$
and
![]() $({\mathcal{O}}/p^{2m}{\mathcal{O}})^{2}$
. Moreover, the subgroup
$({\mathcal{O}}/p^{2m}{\mathcal{O}})^{2}$
. Moreover, the subgroup
![]() $K_{m}=H_{\unicode[STIX]{x1D70F}}^{2m}+H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2m}[p^{m}]$
extends to
$K_{m}=H_{\unicode[STIX]{x1D70F}}^{2m}+H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2m}[p^{m}]$
extends to
![]() $\mathfrak{X}(v)$
by Proposition 5.11, and over
$\mathfrak{X}(v)$
by Proposition 5.11, and over
![]() $X(v)$
is locally isomorphic to
$X(v)$
is locally isomorphic to
Definition 7.3. We write
where the condition pol means that we are looking at isomorphisms
![]() $\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2})$
which induce an isomorphism ‘in first coordinate’,
$\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2})$
which induce an isomorphism ‘in first coordinate’,
such that
![]() $(\unicode[STIX]{x1D713}_{1,1})^{D}=((\unicode[STIX]{x1D713}_{1,1})^{(\unicode[STIX]{x1D70E})})^{-1}$
, and such that the quotient morphism,
$(\unicode[STIX]{x1D713}_{1,1})^{D}=((\unicode[STIX]{x1D713}_{1,1})^{(\unicode[STIX]{x1D70E})})^{-1}$
, and such that the quotient morphism,
is zero.
Remark 7.4. The map
![]() $\unicode[STIX]{x1D713}_{1,1}$
is automatically an isomorphism. Moreover,
$\unicode[STIX]{x1D713}_{1,1}$
is automatically an isomorphism. Moreover,
where the last morphism is induced by
![]() $\unicode[STIX]{x1D706}$
, the polarization of
$\unicode[STIX]{x1D706}$
, the polarization of
![]() $A$
.
$A$
.
Denote by
![]() $B_{n}$
the subgroup of
$B_{n}$
the subgroup of
![]() $\operatorname{GL}({\mathcal{O}}/p^{m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}})$
of matrices,
$\operatorname{GL}({\mathcal{O}}/p^{m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}})$
of matrices,
such that
![]() $a^{-1}=a^{(\unicode[STIX]{x1D70E})}$
i.e.
$a^{-1}=a^{(\unicode[STIX]{x1D70E})}$
i.e.
![]() $a\in ({\mathcal{O}}/p^{m}{\mathcal{O}})^{1}$
. We can map
$a\in ({\mathcal{O}}/p^{m}{\mathcal{O}})^{1}$
. We can map
![]() ${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
(diagonally) to
${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
(diagonally) to
![]() $B_{n}$
.
$B_{n}$
.
Write also
which surjects to
![]() $B_{n}$
and that we can embed into
$B_{n}$
and that we can embed into
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
(even in its upper triangular Borel subgroup) via
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
(even in its upper triangular Borel subgroup) via
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}a & b\\ 0 & d\end{array}\right)\longmapsto \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(a) & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(b) & \\ & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(d) & \\ & & \unicode[STIX]{x1D70F}(d)\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}a & b\\ 0 & d\end{array}\right)\longmapsto \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(a) & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(b) & \\ & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(d) & \\ & & \unicode[STIX]{x1D70F}(d)\end{array}\right).\end{eqnarray}$$
We denote by
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
the inverses of the induced isomorphisms,
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
the inverses of the induced isomorphisms,
and the quotient,
We also denote by
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
the normalization of
$\mathfrak{X}_{1}(p^{2m})(v)$
the normalization of
![]() $\mathfrak{X}(v)$
in
$\mathfrak{X}(v)$
in
![]() $X_{1}(p^{2m})(v)$
. Over
$X_{1}(p^{2m})(v)$
. Over
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
, we have, by the previous section, locally free subsheaves of
$\mathfrak{X}_{1}(p^{2m})(v)$
, we have, by the previous section, locally free subsheaves of
![]() ${\mathcal{O}}_{\mathfrak{X}_{1}(p^{2m})(v)}$
-modules
${\mathcal{O}}_{\mathfrak{X}_{1}(p^{2m})(v)}$
-modules
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70F}},{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
of
${\mathcal{F}}_{\unicode[STIX]{x1D70F}},{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
of
![]() $\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
together with morphisms,
$\unicode[STIX]{x1D714}_{G,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
together with morphisms,
and denote by
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}^{\text{can}}$
the image of the second morphism. It is a locally direct factor of
${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}^{\text{can}}$
the image of the second morphism. It is a locally direct factor of
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes {\mathcal{O}}_{K}/p^{w}$
, and, passing through the quotient, we get a map,
${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\otimes {\mathcal{O}}_{K}/p^{w}$
, and, passing through the quotient, we get a map,
Using the construction of torsors of the previous section, we get a chain of maps,
Moreover,
![]() $\unicode[STIX]{x1D70B}_{1}$
is a torsor over the formal torus
$\unicode[STIX]{x1D70B}_{1}$
is a torsor over the formal torus
![]() $\mathfrak{T}_{w}$
,
$\mathfrak{T}_{w}$
,
![]() $\unicode[STIX]{x1D70B}_{2}$
is affine, and we have an action of
$\unicode[STIX]{x1D70B}_{2}$
is affine, and we have an action of
![]() ${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
and
${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
and
![]() $B_{n}$
on
$B_{n}$
on
![]() $\mathfrak{X}_{1}(p^{2m})$
over
$\mathfrak{X}_{1}(p^{2m})$
over
![]() $\mathfrak{X}(v)$
. Denote by
$\mathfrak{X}(v)$
. Denote by
![]() $B$
the Borel subgroup of
$B$
the Borel subgroup of
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
,
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
,
![]() $\mathfrak{B}$
its formal completion along its special fiber, and
$\mathfrak{B}$
its formal completion along its special fiber, and
![]() $\mathfrak{B}_{w}$
,
$\mathfrak{B}_{w}$
,
We can embed
![]() $\mathfrak{T}$
in
$\mathfrak{T}$
in
![]() $\mathfrak{B}$
(which induce an embedding
$\mathfrak{B}$
(which induce an embedding
![]() $\mathfrak{T}_{w}\subset \mathfrak{B}_{w}$
) and
$\mathfrak{T}_{w}\subset \mathfrak{B}_{w}$
) and
![]() ${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
in
${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
in
![]() $\mathfrak{T}$
, via
$\mathfrak{T}$
, via
 $$\begin{eqnarray}(a,b)\in {\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}\longmapsto \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(b) & & \\ & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(a) & \\ & & \unicode[STIX]{x1D70F}(a)\end{array}\right)\in \mathfrak{T},\end{eqnarray}$$
$$\begin{eqnarray}(a,b)\in {\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}\longmapsto \left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(b) & & \\ & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(a) & \\ & & \unicode[STIX]{x1D70F}(a)\end{array}\right)\in \mathfrak{T},\end{eqnarray}$$
such that the action of
![]() ${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
on
${\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}$
on
![]() $X_{1}(p^{2m})(v)$
and via
$X_{1}(p^{2m})(v)$
and via
![]() $\mathfrak{T}$
on
$\mathfrak{T}$
on
![]() ${\mathcal{G}}r^{+}$
preserves
${\mathcal{G}}r^{+}$
preserves
![]() $\mathfrak{I}\mathfrak{W}_{w}^{+}$
(over
$\mathfrak{I}\mathfrak{W}_{w}^{+}$
(over
![]() $\mathfrak{X}(v)$
). More generally, the action of
$\mathfrak{X}(v)$
). More generally, the action of
![]() $B_{\infty }(\mathbb{Z}_{p})$
on
$B_{\infty }(\mathbb{Z}_{p})$
on
![]() $X_{1}(p^{2m})(v)$
(and thus
$X_{1}(p^{2m})(v)$
(and thus
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
) and via
$\mathfrak{X}_{1}(p^{2m})(v)$
) and via
![]() $\mathfrak{B}$
on
$\mathfrak{B}$
on
![]() ${\mathcal{G}}r^{+}$
preserves
${\mathcal{G}}r^{+}$
preserves
![]() $\mathfrak{I}\mathfrak{W}_{w}^{+}$
.
$\mathfrak{I}\mathfrak{W}_{w}^{+}$
.
Let
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}_{w}(L)$
. The character
$\unicode[STIX]{x1D705}\in {\mathcal{W}}_{w}(L)$
. The character
![]() $\unicode[STIX]{x1D705}:{\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}\longrightarrow {\mathcal{O}}_{L}^{\times }$
extends to a character,
$\unicode[STIX]{x1D705}:{\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}\longrightarrow {\mathcal{O}}_{L}^{\times }$
extends to a character,
which can be extended as a character of
where
![]() $\mathfrak{U}_{w}\subset \mathfrak{B}_{w}$
acts trivially, and even as a character,
$\mathfrak{U}_{w}\subset \mathfrak{B}_{w}$
acts trivially, and even as a character,
where
![]() $U(\mathbb{Z}_{p})\mathfrak{U}_{w}$
acts trivially. Let us write
$U(\mathbb{Z}_{p})\mathfrak{U}_{w}$
acts trivially. Let us write
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{3}\circ \unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1}$
.
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{3}\circ \unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1}$
.
Proposition 7.5. The sheaf
![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{I}\mathfrak{W}_{w}^{+}}[\unicode[STIX]{x1D705}]$
is a formal Banach sheaf, in the sense of [Reference Andreatta, Iovita and PilloniAIP15, Definition A.1.2.1].
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{I}\mathfrak{W}_{w}^{+}}[\unicode[STIX]{x1D705}]$
is a formal Banach sheaf, in the sense of [Reference Andreatta, Iovita and PilloniAIP15, Definition A.1.2.1].
Proof. We can use the same dévissage as presented in [Reference Andreatta, Iovita and PilloniAIP15]: denote by
![]() $\unicode[STIX]{x1D705}^{0}$
the restriction of
$\unicode[STIX]{x1D705}^{0}$
the restriction of
![]() $\unicode[STIX]{x1D705}$
to
$\unicode[STIX]{x1D705}$
to
![]() $\mathfrak{T}_{w}$
. Then
$\mathfrak{T}_{w}$
. Then
![]() $(\unicode[STIX]{x1D70B}_{1})_{\ast }{\mathcal{O}}_{\mathfrak{I}\mathfrak{W}_{w}^{+}}[\unicode[STIX]{x1D705}^{0}]$
is an invertible sheaf on
$(\unicode[STIX]{x1D70B}_{1})_{\ast }{\mathcal{O}}_{\mathfrak{I}\mathfrak{W}_{w}^{+}}[\unicode[STIX]{x1D705}^{0}]$
is an invertible sheaf on
![]() $\mathfrak{I}\mathfrak{W}_{w}$
. Its pushforward via
$\mathfrak{I}\mathfrak{W}_{w}$
. Its pushforward via
![]() $\unicode[STIX]{x1D70B}_{2}$
is then a formal Banach sheaf because
$\unicode[STIX]{x1D70B}_{2}$
is then a formal Banach sheaf because
![]() $\unicode[STIX]{x1D70B}_{2}$
is affine, and pushing through
$\unicode[STIX]{x1D70B}_{2}$
is affine, and pushing through
![]() $\unicode[STIX]{x1D70B}_{3}$
and taking invariants over
$\unicode[STIX]{x1D70B}_{3}$
and taking invariants over
![]() $B_{\infty }(\mathbb{Z}_{p})/p^{n}=B_{n},\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{I}\mathfrak{W}_{w}^{+}}[\unicode[STIX]{x1D705}]$
is a formal Banach sheaf.◻
$B_{\infty }(\mathbb{Z}_{p})/p^{n}=B_{n},\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{I}\mathfrak{W}_{w}^{+}}[\unicode[STIX]{x1D705}]$
is a formal Banach sheaf.◻
Definition 7.6. We call
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }:=\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{I}\mathfrak{W}_{w}^{+}}[\unicode[STIX]{x1D705}]$
the sheaf of
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }:=\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{\mathfrak{I}\mathfrak{W}_{w}^{+}}[\unicode[STIX]{x1D705}]$
the sheaf of
![]() $v$
-overconvergent
$v$
-overconvergent
![]() $w$
-analytic modular forms of weight
$w$
-analytic modular forms of weight
![]() $\unicode[STIX]{x1D705}$
. The space of integral
$\unicode[STIX]{x1D705}$
. The space of integral
![]() $v$
-overconvergent,
$v$
-overconvergent,
![]() $w$
-analytic modular forms of weight
$w$
-analytic modular forms of weight
![]() $\unicode[STIX]{x1D705}$
and level (outside
$\unicode[STIX]{x1D705}$
and level (outside
![]() $p$
)
$p$
)
![]() $K^{p}$
, for the group
$K^{p}$
, for the group
![]() $G$
is
$G$
is
Remark 7.7. Unfortunately it does not seem clear how to define an involution
![]() $\unicode[STIX]{x1D705}\mapsto \unicode[STIX]{x1D705}^{\prime }$
on all
$\unicode[STIX]{x1D705}\mapsto \unicode[STIX]{x1D705}^{\prime }$
on all
![]() ${\mathcal{W}}$
which extends the one on classical weights, and thus we only get that classical modular forms of (classical, integral) weight
${\mathcal{W}}$
which extends the one on classical weights, and thus we only get that classical modular forms of (classical, integral) weight
![]() $\unicode[STIX]{x1D705}$
embed in overconvergent forms of weight
$\unicode[STIX]{x1D705}$
embed in overconvergent forms of weight
![]() $\unicode[STIX]{x1D705}^{\prime }\ldots \,$
.
$\unicode[STIX]{x1D705}^{\prime }\ldots \,$
.
7.2 Changing the analytic radius
Let
![]() $m-((p^{2m}-1)/(p^{2}-1))v>w^{\prime }>w$
and
$m-((p^{2m}-1)/(p^{2}-1))v>w^{\prime }>w$
and
![]() $\unicode[STIX]{x1D705}\in \mathfrak{W}_{w}(L)$
, and thus
$\unicode[STIX]{x1D705}\in \mathfrak{W}_{w}(L)$
, and thus
![]() $\unicode[STIX]{x1D705}\in \mathfrak{W}_{w^{\prime }}(L)$
. There is a natural inclusion,
$\unicode[STIX]{x1D705}\in \mathfrak{W}_{w^{\prime }}(L)$
. There is a natural inclusion,
compatible with the action of
![]() $({\mathcal{O}}^{\times }\times {\mathcal{O}}^{1})\mathfrak{B}_{w}$
. This induces a map
$({\mathcal{O}}^{\times }\times {\mathcal{O}}^{1})\mathfrak{B}_{w}$
. This induces a map
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }\longrightarrow \mathfrak{w}_{w^{\prime }}^{\unicode[STIX]{x1D705}\dagger }$
and thus a map,
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }\longrightarrow \mathfrak{w}_{w^{\prime }}^{\unicode[STIX]{x1D705}\dagger }$
and thus a map,
Definition 7.8. The space of integral overconvergent locally analytic Picard modular forms of weight
![]() $\unicode[STIX]{x1D705}$
, and level (outside
$\unicode[STIX]{x1D705}$
, and level (outside
![]() $p$
)
$p$
)
![]() $K^{p}$
, is
$K^{p}$
, is
7.3 Classical and overconvergent forms in rigid fiber
Denote by
![]() $\mathfrak{X}_{Iw^{+}(p^{2m})}(v)$
the quotient of
$\mathfrak{X}_{Iw^{+}(p^{2m})}(v)$
the quotient of
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
by
$\mathfrak{X}_{1}(p^{2m})(v)$
by
![]() $\tilde{U_{m}}\subset B_{m}$
, which is isomorphic to
$\tilde{U_{m}}\subset B_{m}$
, which is isomorphic to
Let us also denote by
![]() $X_{Iw^{+}(p^{2m})}(v)$
the corresponding rigid space. Over the scheme
$X_{Iw^{+}(p^{2m})}(v)$
the corresponding rigid space. Over the scheme
![]() $X$
, we have the locally free sheaf
$X$
, we have the locally free sheaf
![]() $\unicode[STIX]{x1D714}_{A}=\unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
, which is locally isomorphic to
$\unicode[STIX]{x1D714}_{A}=\unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
, which is locally isomorphic to
![]() ${\mathcal{O}}_{X}\oplus {\mathcal{O}}_{X}^{2}$
, with the corresponding action of
${\mathcal{O}}_{X}\oplus {\mathcal{O}}_{X}^{2}$
, with the corresponding action of
![]() ${\mathcal{O}}$
. Denote by
${\mathcal{O}}$
. Denote by
![]() ${\mathcal{T}}$
the scheme
${\mathcal{T}}$
the scheme
![]() $\operatorname{Hom}_{X,{\mathcal{O}}}({\mathcal{O}}_{X}^{2}\oplus {\mathcal{O}}_{X},\unicode[STIX]{x1D714}_{G})$
of trivialization of
$\operatorname{Hom}_{X,{\mathcal{O}}}({\mathcal{O}}_{X}^{2}\oplus {\mathcal{O}}_{X},\unicode[STIX]{x1D714}_{G})$
of trivialization of
![]() $\unicode[STIX]{x1D714}_{G}$
as a
$\unicode[STIX]{x1D714}_{G}$
as a
![]() ${\mathcal{O}}_{X}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}={\mathcal{O}}_{X}\,\oplus \,{\mathcal{O}}_{X}$
-sheaf, and denote by
${\mathcal{O}}_{X}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}={\mathcal{O}}_{X}\,\oplus \,{\mathcal{O}}_{X}$
-sheaf, and denote by
![]() ${\mathcal{T}}^{\times }$
its subsheaf of isomorphisms; it is a
${\mathcal{T}}^{\times }$
its subsheaf of isomorphisms; it is a
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
-torsor over
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
-torsor over
![]() $X$
, where
$X$
, where
![]() $g\in \operatorname{GL}_{2}\times \operatorname{GL}_{1}$
acts on
$g\in \operatorname{GL}_{2}\times \operatorname{GL}_{1}$
acts on
![]() ${\mathcal{T}}^{\times }$
by
${\mathcal{T}}^{\times }$
by
![]() $g\cdot \unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}\circ g^{-1}$
. For
$g\cdot \unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}\circ g^{-1}$
. For
![]() $\unicode[STIX]{x1D705}\in X^{+}(T)$
a classical weight, denote by
$\unicode[STIX]{x1D705}\in X^{+}(T)$
a classical weight, denote by
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
the sheaf
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
the sheaf
![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{T}}^{\times }}[\unicode[STIX]{x1D705}^{\prime }]$
, where
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{{\mathcal{T}}^{\times }}[\unicode[STIX]{x1D705}^{\prime }]$
, where
![]() $\unicode[STIX]{x1D70B}:{\mathcal{T}}^{\times }\longrightarrow X$
is the projection and
$\unicode[STIX]{x1D70B}:{\mathcal{T}}^{\times }\longrightarrow X$
is the projection and
![]() $\unicode[STIX]{x1D705}\longrightarrow \unicode[STIX]{x1D705}^{\prime }$
the involution on classical weights. In down-to-earth terms,
$\unicode[STIX]{x1D705}\longrightarrow \unicode[STIX]{x1D705}^{\prime }$
the involution on classical weights. In down-to-earth terms,
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},l)$
where
$\unicode[STIX]{x1D705}=(k_{1},k_{2},l)$
where
![]() $k_{1}\geqslant k_{2}$
and
$k_{1}\geqslant k_{2}$
and
We have defined
![]() $X(v)$
, which is the rigid fiber of
$X(v)$
, which is the rigid fiber of
![]() $\mathfrak{X}(v)$
. Denote by
$\mathfrak{X}(v)$
. Denote by
![]() ${\mathcal{T}}_{\text{an}},{\mathcal{T}}_{\text{an}}^{\times },(\operatorname{GL}_{2}\times \operatorname{GL}_{1})_{\text{an}}$
the analytification of the schemes
${\mathcal{T}}_{\text{an}},{\mathcal{T}}_{\text{an}}^{\times },(\operatorname{GL}_{2}\times \operatorname{GL}_{1})_{\text{an}}$
the analytification of the schemes
![]() ${\mathcal{T}},{\mathcal{T}}^{\times },\operatorname{GL}_{g}$
, and
${\mathcal{T}},{\mathcal{T}}^{\times },\operatorname{GL}_{g}$
, and
![]() ${\mathcal{T}}_{\text{rig}},{\mathcal{T}}_{\text{rig}}^{\times },(\operatorname{GL}_{2}\times \operatorname{GL}_{1})_{\text{rig}}$
Raynaud’s rigid fiber of the completion along the special fibers of the same schemes. As
${\mathcal{T}}_{\text{rig}},{\mathcal{T}}_{\text{rig}}^{\times },(\operatorname{GL}_{2}\times \operatorname{GL}_{1})_{\text{rig}}$
Raynaud’s rigid fiber of the completion along the special fibers of the same schemes. As
![]() ${\mathcal{T}}^{\times }/B$
is complete,
${\mathcal{T}}^{\times }/B$
is complete,
![]() ${\mathcal{T}}_{\text{an}}^{\times }/B_{\text{an}}={\mathcal{T}}_{\text{rig}}^{\times }/B_{\text{rig}}$
, over which there is the diagram,
${\mathcal{T}}_{\text{an}}^{\times }/B_{\text{an}}={\mathcal{T}}_{\text{rig}}^{\times }/B_{\text{rig}}$
, over which there is the diagram,

where
![]() $f$
is a torsor over
$f$
is a torsor over
![]() $U_{\text{rig}}/B_{\text{rig}}=T_{\text{rig}}$
(the torus, not to be mistaken with
$U_{\text{rig}}/B_{\text{rig}}=T_{\text{rig}}$
(the torus, not to be mistaken with
![]() ${\mathcal{T}}_{\text{rig}}$
) and
${\mathcal{T}}_{\text{rig}}$
) and
![]() $g$
a torsor over
$g$
a torsor over
![]() $T_{\text{an}}$
(same remark).
$T_{\text{an}}$
(same remark).
Definition 7.9. Let
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}_{w}(K)$
. We denote by
$\unicode[STIX]{x1D705}\in {\mathcal{W}}_{w}(K)$
. We denote by
![]() $\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
the rigid fiber of
$\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
the rigid fiber of
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }$
on
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }$
on
![]() $X(v)$
. It exists by [Reference Andreatta, Iovita and PilloniAIP15, Proposition A.2.2.4]. It is called the sheaf of
$X(v)$
. It exists by [Reference Andreatta, Iovita and PilloniAIP15, Proposition A.2.2.4]. It is called the sheaf of
![]() $w$
-analytic overconvergent modular forms of weight
$w$
-analytic overconvergent modular forms of weight
![]() $\unicode[STIX]{x1D705}$
. The space of
$\unicode[STIX]{x1D705}$
. The space of
![]() $v$
-overconvergent,
$v$
-overconvergent,
![]() $w$
-analytic modular forms of weight
$w$
-analytic modular forms of weight
![]() $\unicode[STIX]{x1D705}$
is the space,
$\unicode[STIX]{x1D705}$
is the space,
The space of locally analytic overconvergent Picard modular forms of weight
![]() $\unicode[STIX]{x1D705}$
(and level
$\unicode[STIX]{x1D705}$
(and level
![]() $K^{p}$
) is the space,
$K^{p}$
) is the space,
The injection of
![]() ${\mathcal{O}}_{\mathfrak{X}(v)}$
-modules
${\mathcal{O}}_{\mathfrak{X}(v)}$
-modules
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70F}}\oplus {\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\subset \unicode[STIX]{x1D714}_{A}=\unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
is an isomorphism in generic fiber, and this induces an open immersion,
${\mathcal{F}}_{\unicode[STIX]{x1D70F}}\oplus {\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\subset \unicode[STIX]{x1D714}_{A}=\unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
is an isomorphism in generic fiber, and this induces an open immersion,
We also have an open immersion,
The action of
![]() $B_{n}$
on
$B_{n}$
on
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
(or
$\mathfrak{X}_{1}(p^{2m})(v)$
(or
![]() $X_{1}(p^{2m})(v)$
) lifts to an action on
$X_{1}(p^{2m})(v)$
) lifts to an action on
![]() $\mathfrak{I}\mathfrak{W}_{w}$
(or
$\mathfrak{I}\mathfrak{W}_{w}$
(or
![]() ${\mathcal{I}}{\mathcal{W}}_{w}$
) because being
${\mathcal{I}}{\mathcal{W}}_{w}$
) because being
![]() $w$
-compatible for
$w$
-compatible for
![]() $\operatorname{Fil}^{1}{\mathcal{F}}_{\unicode[STIX]{x1D70F}}$
it only depends on the trivialization of
$\operatorname{Fil}^{1}{\mathcal{F}}_{\unicode[STIX]{x1D70F}}$
it only depends on the trivialization of
![]() $K_{n}^{D}$
modulo
$K_{n}^{D}$
modulo
![]() $B_{n}$
. Similarly the action of
$B_{n}$
. Similarly the action of
![]() $\tilde{U_{n}}$
lifts to
$\tilde{U_{n}}$
lifts to
![]() $\mathfrak{I}\mathfrak{W}_{w}^{+}$
and
$\mathfrak{I}\mathfrak{W}_{w}^{+}$
and
![]() ${\mathcal{I}}{\mathcal{W}}_{w}^{+}$
. We can thus define
${\mathcal{I}}{\mathcal{W}}_{w}^{+}$
. We can thus define
![]() ${\mathcal{I}}{\mathcal{W}}_{w}^{0}$
and
${\mathcal{I}}{\mathcal{W}}_{w}^{0}$
and
![]() ${\mathcal{I}}{\mathcal{W}}_{w}^{+,0}$
the respective quotients of
${\mathcal{I}}{\mathcal{W}}_{w}^{+,0}$
the respective quotients of
![]() ${\mathcal{I}}{\mathcal{W}}_{w}$
and
${\mathcal{I}}{\mathcal{W}}_{w}$
and
![]() ${\mathcal{I}}{\mathcal{W}}_{w}^{+}$
by
${\mathcal{I}}{\mathcal{W}}_{w}^{+}$
by
![]() $B_{n}$
and
$B_{n}$
and
![]() $\tilde{U_{n}}$
, which induces open immersions,
$\tilde{U_{n}}$
, which induces open immersions,
Proposition 7.10. Suppose
![]() $w>m-1+(p+v)/(p^{2}-1)$
. Then there are embeddings
$w>m-1+(p+v)/(p^{2}-1)$
. Then there are embeddings
Proof. Let
![]() $S$
be a set of representatives in
$S$
be a set of representatives in
![]() $I_{\infty }\simeq \Bigl(\begin{smallmatrix}{\mathcal{O}}^{1} & {\mathcal{O}}\\ p{\mathcal{O}} & {\mathcal{O}}^{\times }\end{smallmatrix}\!\Bigr)$
of
$I_{\infty }\simeq \Bigl(\begin{smallmatrix}{\mathcal{O}}^{1} & {\mathcal{O}}\\ p{\mathcal{O}} & {\mathcal{O}}^{\times }\end{smallmatrix}\!\Bigr)$
of
![]() $I_{n}/\widetilde{U_{n}}$
which we can suppose of the form,
$I_{n}/\widetilde{U_{n}}$
which we can suppose of the form,
Here,
![]() $[.]$
denotes any lift. Then
$[.]$
denotes any lift. Then
![]() $h$
is locally (over
$h$
is locally (over
![]() $X(v)$
) isomorphic to
$X(v)$
) isomorphic to
 $$\begin{eqnarray}h:\coprod _{\unicode[STIX]{x1D6FE}\in S}\left(\begin{array}{@{}ccc@{}}1+p^{w}B(0,1) & & \\ p^{w}B(0,1) & 1+p^{w}B(0,1) & \\ & & 1+p^{w}B(0,1)\end{array}\right)M\widetilde{\unicode[STIX]{x1D6FE}}\longrightarrow (\operatorname{GL}_{2}\times \operatorname{GL}_{1}/U)_{\text{an}},\end{eqnarray}$$
$$\begin{eqnarray}h:\coprod _{\unicode[STIX]{x1D6FE}\in S}\left(\begin{array}{@{}ccc@{}}1+p^{w}B(0,1) & & \\ p^{w}B(0,1) & 1+p^{w}B(0,1) & \\ & & 1+p^{w}B(0,1)\end{array}\right)M\widetilde{\unicode[STIX]{x1D6FE}}\longrightarrow (\operatorname{GL}_{2}\times \operatorname{GL}_{1}/U)_{\text{an}},\end{eqnarray}$$
where
![]() $M$
is the matrix which is locally given by the Hodge–Tate map, and thus corresponds to the inclusion
$M$
is the matrix which is locally given by the Hodge–Tate map, and thus corresponds to the inclusion
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70F}}\oplus {\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\subset \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
, and if
${\mathcal{F}}_{\unicode[STIX]{x1D70F}}\oplus {\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\subset \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70F}}\oplus \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
, and if
![]() $\unicode[STIX]{x1D6FE}\in S$
, then
$\unicode[STIX]{x1D6FE}\in S$
, then
![]() $\widetilde{\unicode[STIX]{x1D6FE}}$
is given by
$\widetilde{\unicode[STIX]{x1D6FE}}$
is given by
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FE}}=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(b) & & \\ p\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(c) & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(a) & \\ & & \unicode[STIX]{x1D70F}(a)\end{array}\right)\quad \text{if}\quad \unicode[STIX]{x1D6FE}=\left(\begin{array}{@{}cc@{}}b & \\ pc & a\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6FE}}=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(b) & & \\ p\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(c) & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(a) & \\ & & \unicode[STIX]{x1D70F}(a)\end{array}\right)\quad \text{if}\quad \unicode[STIX]{x1D6FE}=\left(\begin{array}{@{}cc@{}}b & \\ pc & a\end{array}\right).\end{eqnarray}$$
But there exists
![]() $M^{\prime }$
with integral coefficients such that
$M^{\prime }$
with integral coefficients such that
and it is easily checked that
![]() $M^{\prime }\circ h$
is then injective if
$M^{\prime }\circ h$
is then injective if
![]() $w>m-1+(p+v)/(p^{2}-1)$
. The proof for the other embedding is similar (and easier).◻
$w>m-1+(p+v)/(p^{2}-1)$
. The proof for the other embedding is similar (and easier).◻
Remark 7.11. Of course not every
![]() $w$
satisfies
$w$
satisfies
![]() $m-1+(p+v)/(p^{2}-1)<w<m-((p^{2m}-1)/(p^{2}-1))v$
for some
$m-1+(p+v)/(p^{2}-1)<w<m-((p^{2m}-1)/(p^{2}-1))v$
for some
![]() $m$
. But every
$m$
. But every
![]() $w$
-analytic character
$w$
-analytic character
![]() $\unicode[STIX]{x1D705}$
is
$\unicode[STIX]{x1D705}$
is
![]() $w^{\prime }$
-analytic for all
$w^{\prime }$
-analytic for all
![]() $w^{\prime }>w$
, and in particular we can choose a
$w^{\prime }>w$
, and in particular we can choose a
![]() $w^{\prime }$
which satisfies the previous inequalities, a priori for another
$w^{\prime }$
which satisfies the previous inequalities, a priori for another
![]() $m$
(for each choice of
$m$
(for each choice of
![]() $w^{\prime }$
there is a unique such
$w^{\prime }$
there is a unique such
![]() $m$
).
$m$
).
From now on, we suppose that we have fixed
![]() $m$
, and we suppose that
$m$
, and we suppose that
![]() $m-1+(p+v)/(p^{2}-1)<w<m-((p^{2m}-1)/(p^{2}-1))v$
.
$m-1+(p+v)/(p^{2}-1)<w<m-((p^{2m}-1)/(p^{2}-1))v$
.
We could have defined
![]() $\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
directly, by
$\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
directly, by
![]() $g_{\ast }{\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}_{w}^{0,+}}[\unicode[STIX]{x1D705}]$
where
$g_{\ast }{\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}_{w}^{0,+}}[\unicode[STIX]{x1D705}]$
where
![]() $g$
is the composite,
$g$
is the composite,
as shown by the next proposition. Remark that
![]() $X(v)\subset X_{Iw(p)}(v)$
via the canonical filtration of level 1.
$X(v)\subset X_{Iw(p)}(v)$
via the canonical filtration of level 1.
Proposition 7.12. The sheaf
![]() $\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
(defined as the rigid fiber of
$\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
(defined as the rigid fiber of
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }$
) is isomorphic to
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }$
) is isomorphic to
![]() $g_{\ast }{\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}_{w}^{0,+}}[\unicode[STIX]{x1D705}]$
.
$g_{\ast }{\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}_{w}^{0,+}}[\unicode[STIX]{x1D705}]$
.
Proof. In the rigid setting, we did a quotient by
![]() $\widetilde{U_{n}}$
to get
$\widetilde{U_{n}}$
to get
![]() ${\mathcal{I}}{\mathcal{W}}_{w}^{0,+}$
. But
${\mathcal{I}}{\mathcal{W}}_{w}^{0,+}$
. But
![]() $\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
is constructed as
$\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
is constructed as
![]() $((\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1})_{\ast }{\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}^{+}}[\unicode[STIX]{x1D705}^{0}])(-\unicode[STIX]{x1D705})^{B_{n}}$
, and the action of
$((\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1})_{\ast }{\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}^{+}}[\unicode[STIX]{x1D705}^{0}])(-\unicode[STIX]{x1D705})^{B_{n}}$
, and the action of
![]() $\widetilde{U_{n}}$
on
$\widetilde{U_{n}}$
on
![]() $(\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1})_{\ast }{\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}^{+}}[\unicode[STIX]{x1D705}^{0}]$
is trivial and it thus descends to
$(\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1})_{\ast }{\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}^{+}}[\unicode[STIX]{x1D705}^{0}]$
is trivial and it thus descends to
![]() $X_{Iw^{+}(p^{2m})}(v)$
and is isomorphic to the
$X_{Iw^{+}(p^{2m})}(v)$
and is isomorphic to the
![]() $\unicode[STIX]{x1D705}^{0}$
-variant vectors in the pushforward of
$\unicode[STIX]{x1D705}^{0}$
-variant vectors in the pushforward of
![]() ${\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}_{w}^{0,+}}$
.◻
${\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}_{w}^{0,+}}$
.◻
Proposition 7.13. For
![]() $\unicode[STIX]{x1D705}\in X_{+}(T^{0})$
and
$\unicode[STIX]{x1D705}\in X_{+}(T^{0})$
and
![]() $\unicode[STIX]{x1D714}>0$
, there is a restriction map,
$\unicode[STIX]{x1D714}>0$
, there is a restriction map,
induced by the inclusion
![]() ${\mathcal{I}}{\mathcal{W}}_{w}^{0,+}\subset ({\mathcal{T}}^{\text{an}}/U)$
. Moreover, locally for the étale topology, this inclusion is isomorphic to the following composition,
${\mathcal{I}}{\mathcal{W}}_{w}^{0,+}\subset ({\mathcal{T}}^{\text{an}}/U)$
. Moreover, locally for the étale topology, this inclusion is isomorphic to the following composition,
Proof. Locally for the étale topology,
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
is identified with algebraic functions on
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
is identified with algebraic functions on
![]() $\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
which are invariant by
$\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
which are invariant by
![]() $U$
and varies as
$U$
and varies as
![]() $\unicode[STIX]{x1D705}^{\prime }$
under the action of
$\unicode[STIX]{x1D705}^{\prime }$
under the action of
![]() $T$
, i.e. to
$T$
, i.e. to
![]() $V_{\unicode[STIX]{x1D705}^{\prime }}$
. But a function
$V_{\unicode[STIX]{x1D705}^{\prime }}$
. But a function
![]() $f\in \unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}^{\prime }\dagger }$
is locally identified with a function,
$f\in \unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}^{\prime }\dagger }$
is locally identified with a function,
 $$\begin{eqnarray}f:\left\{\!\!\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D70F}(a)(1+p^{w}B(0,1)) & & \\ p^{w}B(0,1) & \unicode[STIX]{x1D70F}(b)(1+p^{w}B(0,1)) & \\ & & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(b)(1+p^{w}B(0,1))\end{array}\!\right)\!\!,a\in {\mathcal{O}}^{1},b\in {\mathcal{O}}^{\times }\!\right\}\!\longrightarrow L,\end{eqnarray}$$
$$\begin{eqnarray}f:\left\{\!\!\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D70F}(a)(1+p^{w}B(0,1)) & & \\ p^{w}B(0,1) & \unicode[STIX]{x1D70F}(b)(1+p^{w}B(0,1)) & \\ & & \unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}(b)(1+p^{w}B(0,1))\end{array}\!\right)\!\!,a\in {\mathcal{O}}^{1},b\in {\mathcal{O}}^{\times }\!\right\}\!\longrightarrow L,\end{eqnarray}$$
which varies as
![]() $\unicode[STIX]{x1D705}^{\prime }$
under the action on the right of
$\unicode[STIX]{x1D705}^{\prime }$
under the action on the right of
![]() $T(\mathbb{Z}_{p})\mathfrak{T}_{w}$
. As
$T(\mathbb{Z}_{p})\mathfrak{T}_{w}$
. As
![]() $\unicode[STIX]{x1D705}^{\prime }=(k_{1},k_{2},k_{3})\in X_{+}(T)$
we can extend
$\unicode[STIX]{x1D705}^{\prime }=(k_{1},k_{2},k_{3})\in X_{+}(T)$
we can extend
![]() $f$
to a
$f$
to a
![]() $\unicode[STIX]{x1D705}^{\prime }$
-varying function on
$\unicode[STIX]{x1D705}^{\prime }$
-varying function on
 $$\begin{eqnarray}I_{p^{w}}=\left\{\!\left(\begin{array}{@{}ccc@{}}\mathbb{G}_{m} & B(0,1) & \\ p^{w}B(0,1) & \mathbb{G}_{m} & \\ & & \mathbb{G}_{m}\end{array}\right)\right\},\end{eqnarray}$$
$$\begin{eqnarray}I_{p^{w}}=\left\{\!\left(\begin{array}{@{}ccc@{}}\mathbb{G}_{m} & B(0,1) & \\ p^{w}B(0,1) & \mathbb{G}_{m} & \\ & & \mathbb{G}_{m}\end{array}\right)\right\},\end{eqnarray}$$
extending it ‘trivially’; i.e.
 $$\begin{eqnarray}\displaystyle f\left(\left(\begin{array}{@{}ccc@{}}x & u & \\ p^{w}z & y & \\ & & t\end{array}\right)\right) & =f\left(\left(\begin{array}{@{}ccc@{}}1 & 0 & \\ p^{w}zx^{-1} & 1 & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}x & u & \\ 0 & y-p^{w}zu & \\ & & t\end{array}\right)\right) & \displaystyle \nonumber\\ \displaystyle & =x^{k_{1}}(y-p^{w}zu)^{k_{2}}t^{k_{3}}f\left(\left(\begin{array}{@{}ccc@{}}1 & 0 & \\ p^{w}zx^{-1} & 1 & \\ & & 1\end{array}\right)\right). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f\left(\left(\begin{array}{@{}ccc@{}}x & u & \\ p^{w}z & y & \\ & & t\end{array}\right)\right) & =f\left(\left(\begin{array}{@{}ccc@{}}1 & 0 & \\ p^{w}zx^{-1} & 1 & \\ & & 1\end{array}\right)\left(\begin{array}{@{}ccc@{}}x & u & \\ 0 & y-p^{w}zu & \\ & & t\end{array}\right)\right) & \displaystyle \nonumber\\ \displaystyle & =x^{k_{1}}(y-p^{w}zu)^{k_{2}}t^{k_{3}}f\left(\left(\begin{array}{@{}ccc@{}}1 & 0 & \\ p^{w}zx^{-1} & 1 & \\ & & 1\end{array}\right)\right). & \displaystyle \nonumber\end{eqnarray}$$
Under this identification, locally for the étale topology
![]() $\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}^{\prime }\dagger }$
is identified with
$\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}^{\prime }\dagger }$
is identified with
![]() $V_{0,\unicode[STIX]{x1D705}^{\prime }}^{w\text{-an}}$
.◻
$V_{0,\unicode[STIX]{x1D705}^{\prime }}^{w\text{-an}}$
.◻
8 Hecke operators, classicity
As explained in [Reference Andreatta, Iovita and PilloniAIP15] and [Reference BrascaBra16], it is not possible to find a toroidal compactification for more general PEL Shimura varieties (already for
![]() $\operatorname{GSp}_{4}$
) that is preserved with all the Hecke correspondences, but this can be overcome by looking at bounded sections on the open variety. For the Picard modular variety, there is only one choice of a toroidal compactification, and thus this problem does not appear, but we will keep the general strategy (and thus we will not have to check that the correspondences extend to the boundary). Thus, instead we will define Hecke operators on the open Picard Variety
$\operatorname{GSp}_{4}$
) that is preserved with all the Hecke correspondences, but this can be overcome by looking at bounded sections on the open variety. For the Picard modular variety, there is only one choice of a toroidal compactification, and thus this problem does not appear, but we will keep the general strategy (and thus we will not have to check that the correspondences extend to the boundary). Thus, instead we will define Hecke operators on the open Picard Variety
![]() ${\mathcal{Y}}_{Iw(p)}$
of Iwahori level, and, as bounded sections on the open variety extend automatically to the compactification (see [Reference Andreatta, Iovita and PilloniAIP15, Theorem 5.5.1, Proposition 5.5.2], which follows from a theorem of Lutkebohmert), we show that Hecke operators send bounded functions to bounded functions, and thus induce operators on overconvergent locally analytic modular forms.
${\mathcal{Y}}_{Iw(p)}$
of Iwahori level, and, as bounded sections on the open variety extend automatically to the compactification (see [Reference Andreatta, Iovita and PilloniAIP15, Theorem 5.5.1, Proposition 5.5.2], which follows from a theorem of Lutkebohmert), we show that Hecke operators send bounded functions to bounded functions, and thus induce operators on overconvergent locally analytic modular forms.
8.1 Hecke operators outside
 $p$
$p$
These operators have been defined already in [Reference BrascaBra16, § 4]. We explain their definition quickly, and refer to [Reference BrascaBra16] (see also [Reference Andreatta, Iovita and PilloniAIP15, § 6.1]) for the details. Let
![]() $\ell \neq p$
be an integer, and suppose
$\ell \neq p$
be an integer, and suppose
![]() $\ell \!\not |~N$
, the set of places where
$\ell \!\not |~N$
, the set of places where
![]() $K_{v}$
is not maximal. Let
$K_{v}$
is not maximal. Let
![]() $\unicode[STIX]{x1D6FE}\in G(\mathbb{Q}_{\ell })\cap \operatorname{End}{\mathcal{O}}_{E,\ell }({\mathcal{O}}_{E,\ell }^{3})\times \mathbb{Q}_{\ell }^{\times }$
, and consider
$\unicode[STIX]{x1D6FE}\in G(\mathbb{Q}_{\ell })\cap \operatorname{End}{\mathcal{O}}_{E,\ell }({\mathcal{O}}_{E,\ell }^{3})\times \mathbb{Q}_{\ell }^{\times }$
, and consider
the moduli space of isogeny
![]() $f:A_{1}\longrightarrow A_{2}$
such that:
$f:A_{1}\longrightarrow A_{2}$
such that:
(i)
 $f$
is
$f$
is
 ${\mathcal{O}}_{E}$
-linear, and of degree a power of
${\mathcal{O}}_{E}$
-linear, and of degree a power of
 $\ell$
;
$\ell$
;(ii)
 $f$
is compatible with polarizations, i.e.
$f$
is compatible with polarizations, i.e.
 $f^{\ast }\unicode[STIX]{x1D706}_{2}$
is a multiple of
$f^{\ast }\unicode[STIX]{x1D706}_{2}$
is a multiple of
 $\unicode[STIX]{x1D706}_{1}$
;
$\unicode[STIX]{x1D706}_{1}$
;(iii)
 $f$
is compatible with the
$f$
is compatible with the
 $K^{p}$
-level structure (at places that divides
$K^{p}$
-level structure (at places that divides
 $N$
) (we remark that
$N$
) (we remark that
 $f$
is an isomorphism on
$f$
is an isomorphism on
 $T_{q}(A_{i})$
when
$T_{q}(A_{i})$
when
 $q\neq \ell$
is a prime);
$q\neq \ell$
is a prime);(iv)
 $f$
is compatible with the filtration given by the Iwahori structure at
$f$
is compatible with the filtration given by the Iwahori structure at
 $p$
;
$p$
;(v) the type of
 $f$
is given by the double class
$f$
is given by the double class
 $G(\mathbb{Z}_{\ell })\unicode[STIX]{x1D6FE}G(\mathbb{Z}_{\ell })$
.
$G(\mathbb{Z}_{\ell })\unicode[STIX]{x1D6FE}G(\mathbb{Z}_{\ell })$
.
Remark 8.1. The space
![]() $C_{\unicode[STIX]{x1D6FE}}$
does not depend on
$C_{\unicode[STIX]{x1D6FE}}$
does not depend on
![]() $\unicode[STIX]{x1D6FE}$
, only on the double class
$\unicode[STIX]{x1D6FE}$
, only on the double class
![]() $G(\mathbb{Z}_{\ell })\unicode[STIX]{x1D6FE}G(\mathbb{Z}_{\ell })$
.
$G(\mathbb{Z}_{\ell })\unicode[STIX]{x1D6FE}G(\mathbb{Z}_{\ell })$
.
We could similarly define
![]() $C_{\unicode[STIX]{x1D6FE}}$
without Iwahori level at
$C_{\unicode[STIX]{x1D6FE}}$
without Iwahori level at
![]() $p$
(i.e. for
$p$
(i.e. for
![]() ${\mathcal{Y}}_{G(\mathbb{Z}_{p})K^{p}}$
) without the condition that
${\mathcal{Y}}_{G(\mathbb{Z}_{p})K^{p}}$
) without the condition that
![]() $f$
is compatible with the filtration given by the Iwahori structure at
$f$
is compatible with the filtration given by the Iwahori structure at
![]() $p$
. In our case, this Iwahori structure at
$p$
. In our case, this Iwahori structure at
![]() $p$
will always be the canonical one, and thus
$p$
will always be the canonical one, and thus
![]() $f$
is automatically compatible as it sends the canonical filtration of
$f$
is automatically compatible as it sends the canonical filtration of
![]() $A_{1}$
in the one of
$A_{1}$
in the one of
![]() $A_{2}$
.
$A_{2}$
.
Denote by
![]() $p_{i}:C_{\unicode[STIX]{x1D6FE}}\longrightarrow {\mathcal{Y}}$
the two (finite) maps that sends
$p_{i}:C_{\unicode[STIX]{x1D6FE}}\longrightarrow {\mathcal{Y}}$
the two (finite) maps that sends
![]() $f$
to
$f$
to
![]() $A_{i}$
. Denote by
$A_{i}$
. Denote by
![]() $C_{\unicode[STIX]{x1D6FE}}(p^{n})$
the fiber product with
$C_{\unicode[STIX]{x1D6FE}}(p^{n})$
the fiber product with
![]() $p_{1}$
of
$p_{1}$
of
![]() $C_{\unicode[STIX]{x1D6FE}}$
with
$C_{\unicode[STIX]{x1D6FE}}$
with
![]() ${\mathcal{Y}}_{1}(p^{n})(v)\longrightarrow {\mathcal{Y}}(v)\subset _{s}{\mathcal{Y}}_{Iw(p)}(v)$
, where
${\mathcal{Y}}_{1}(p^{n})(v)\longrightarrow {\mathcal{Y}}(v)\subset _{s}{\mathcal{Y}}_{Iw(p)}(v)$
, where
![]() $s$
is the canonical filtration of
$s$
is the canonical filtration of
![]() $A[p]$
. Denote by
$A[p]$
. Denote by
![]() $f$
the universal isogeny over
$f$
the universal isogeny over
![]() $G_{\unicode[STIX]{x1D6FE}}(p^{n})$
. It induces an
$G_{\unicode[STIX]{x1D6FE}}(p^{n})$
. It induces an
![]() ${\mathcal{O}}$
-linear isomorphism,
${\mathcal{O}}$
-linear isomorphism,
In particular, we get a
![]() $B(\mathbb{Z}_{p})\mathfrak{B}_{w}$
-equivariant isomorphism,
$B(\mathbb{Z}_{p})\mathfrak{B}_{w}$
-equivariant isomorphism,
We can thus form the composite morphism,
 $$\begin{eqnarray}\displaystyle H^{0}({\mathcal{Y}}_{1}(p^{n})(v),{\mathcal{O}}_{\widetilde{{\mathcal{I}}{\mathcal{W}}}_{w}^{+}})\overset{p_{2}^{\ast }}{\longrightarrow }H^{0}(C_{\unicode[STIX]{x1D6FE}}(p^{n})(v),p_{2}^{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{I}}{\mathcal{W}}}_{w}^{+}})\overset{(f^{\ast })^{-1}}{\longrightarrow }H^{0}(C_{\unicode[STIX]{x1D6FE}}(p^{n})(v),p_{1}^{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{I}}{\mathcal{W}}}_{w}^{+}}) & & \displaystyle \nonumber\\ \displaystyle \overset{Tr(p_{1})}{\longrightarrow }H^{0}({\mathcal{Y}}_{1}(p^{n})(v),{\mathcal{O}}_{\widetilde{{\mathcal{I}}{\mathcal{W}}}_{w}^{+}}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{0}({\mathcal{Y}}_{1}(p^{n})(v),{\mathcal{O}}_{\widetilde{{\mathcal{I}}{\mathcal{W}}}_{w}^{+}})\overset{p_{2}^{\ast }}{\longrightarrow }H^{0}(C_{\unicode[STIX]{x1D6FE}}(p^{n})(v),p_{2}^{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{I}}{\mathcal{W}}}_{w}^{+}})\overset{(f^{\ast })^{-1}}{\longrightarrow }H^{0}(C_{\unicode[STIX]{x1D6FE}}(p^{n})(v),p_{1}^{\ast }{\mathcal{O}}_{\widetilde{{\mathcal{I}}{\mathcal{W}}}_{w}^{+}}) & & \displaystyle \nonumber\\ \displaystyle \overset{Tr(p_{1})}{\longrightarrow }H^{0}({\mathcal{Y}}_{1}(p^{n})(v),{\mathcal{O}}_{\widetilde{{\mathcal{I}}{\mathcal{W}}}_{w}^{+}}). & & \displaystyle \nonumber\end{eqnarray}$$
As
![]() $f^{\ast }$
is an isomorphism, it sends bounded functions to bounded functions, and we can make the following definition.
$f^{\ast }$
is an isomorphism, it sends bounded functions to bounded functions, and we can make the following definition.
Definition 8.2. Let
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}_{w}(K)$
a weight. We define the Hecke operator,
$\unicode[STIX]{x1D705}\in {\mathcal{W}}_{w}(K)$
a weight. We define the Hecke operator,
as the restriction of the previous operator to the bounded,
![]() $\unicode[STIX]{x1D705}$
-equivariant sections under the action of
$\unicode[STIX]{x1D705}$
-equivariant sections under the action of
![]() $B(\mathbb{Z}_{p})\mathfrak{B}_{w}$
. It induces an operator,
$B(\mathbb{Z}_{p})\mathfrak{B}_{w}$
. It induces an operator,
Definition 8.3. Define
![]() ${\mathcal{H}}$
to be the commutative
${\mathcal{H}}$
to be the commutative
![]() $\mathbb{Z}$
-algebra generated by all operators
$\mathbb{Z}$
-algebra generated by all operators
![]() $T_{\unicode[STIX]{x1D6FE}}$
for all
$T_{\unicode[STIX]{x1D6FE}}$
for all
![]() $\ell \!\not |~Np$
and all double classes
$\ell \!\not |~Np$
and all double classes
![]() $\unicode[STIX]{x1D6FE}$
. These operators commute on overconvergent forms, and thus
$\unicode[STIX]{x1D6FE}$
. These operators commute on overconvergent forms, and thus
![]() ${\mathcal{H}}$
acts on them.
${\mathcal{H}}$
acts on them.
8.2 Hecke operator at
 $p$
$p$
Here we stress that, as in the previous sections, the prime
![]() $p$
is inert in
$p$
is inert in
![]() $E$
. We will define a first Hecke operator at
$E$
. We will define a first Hecke operator at
![]() $p$
,
$p$
,
![]() $U_{p}$
. Define
$U_{p}$
. Define
![]() $C$
the moduli space over
$C$
the moduli space over
![]() $K$
which parametrizes data
$K$
which parametrizes data
![]() $(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
where
$(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
where
![]() $(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702})\in X_{K}(v)$
and
$(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702})\in X_{K}(v)$
and
![]() $L\subset A[p^{2}]$
is a totally isotropic
$L\subset A[p^{2}]$
is a totally isotropic
![]() ${\mathcal{O}}$
-module for
${\mathcal{O}}$
-module for
![]() $\unicode[STIX]{x1D706}$
(i.e.
$\unicode[STIX]{x1D706}$
(i.e.
![]() $L\subset L^{\bot }:=(G[p^{2}]/L)^{D}\subset G[p^{2}]^{D}\overset{\unicode[STIX]{x1D706}}{\simeq }G[p^{2}]$
) of
$L\subset L^{\bot }:=(G[p^{2}]/L)^{D}\subset G[p^{2}]^{D}\overset{\unicode[STIX]{x1D706}}{\simeq }G[p^{2}]$
) of
![]() ${\mathcal{O}}$
-height
${\mathcal{O}}$
-height
![]() $p^{3}$
(and thus
$p^{3}$
(and thus
![]() $L=L^{\bot }$
) such that
$L=L^{\bot }$
) such that
As remarked by Bijakowski in [Reference BijakowskiBij16], the second condition is implied by the first one and the isotropy condition. We then define two projections,
where
![]() $p_{1}$
is the forgetful map which sends
$p_{1}$
is the forgetful map which sends
![]() $(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
to
$(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
to
![]() $(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
and
$(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
and
![]() $p_{2}$
sends
$p_{2}$
sends
![]() $(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
to
$(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
to
![]() $(A/L,\unicode[STIX]{x1D706}^{\prime },i^{\prime },\unicode[STIX]{x1D702}^{\prime })$
. To compare the correspondence with the canonical filtration we will need the following lemma.
$(A/L,\unicode[STIX]{x1D706}^{\prime },i^{\prime },\unicode[STIX]{x1D702}^{\prime })$
. To compare the correspondence with the canonical filtration we will need the following lemma.
Lemma 8.4. Let
![]() $p>2$
and
$p>2$
and
![]() $G$
be a
$G$
be a
![]() $p$
-divisible
$p$
-divisible
![]() ${\mathcal{O}}$
-module of unitary type and signature
${\mathcal{O}}$
-module of unitary type and signature
![]() $(2,1)$
. Let
$(2,1)$
. Let
![]() $H$
be a sub-
$H$
be a sub-
![]() ${\mathcal{O}}$
-module of
${\mathcal{O}}$
-module of
![]() $p$
-torsion and of
$p$
-torsion and of
![]() ${\mathcal{O}}$
-height
${\mathcal{O}}$
-height
![]() $1$
. Then the two following assertions are equivalent:
$1$
. Then the two following assertions are equivalent:
(i)
 $\operatorname{Deg}_{\unicode[STIX]{x1D70F}}(H)>1+p-\frac{1}{2}$
;
$\operatorname{Deg}_{\unicode[STIX]{x1D70F}}(H)>1+p-\frac{1}{2}$
;(ii)
 $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<\frac{1}{2}$
and
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<\frac{1}{2}$
and
 $H$
is the canonical subgroup of
$H$
is the canonical subgroup of
 $G[p]$
associated to
$G[p]$
associated to
 $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
Let
![]() $H$
be a sub-
$H$
be a sub-
![]() ${\mathcal{O}}$
-module of
${\mathcal{O}}$
-module of
![]() $p$
-torsion and of
$p$
-torsion and of
![]() ${\mathcal{O}}$
-height 2. Then the two following assertions are equivalent:
${\mathcal{O}}$
-height 2. Then the two following assertions are equivalent:
(i)
 $\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)>p+2-\frac{1}{2}$
;
$\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)>p+2-\frac{1}{2}$
;(ii)
 $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<\frac{1}{2}$
and
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<\frac{1}{2}$
and
 $H$
is the canonical subgroup of
$H$
is the canonical subgroup of
 $G[p]$
associated to
$G[p]$
associated to
 $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
.
In both cases we can be more precise: if
![]() $v=1+p-\operatorname{Deg}_{\unicode[STIX]{x1D70F}}(H)$
(respectively
$v=1+p-\operatorname{Deg}_{\unicode[STIX]{x1D70F}}(H)$
(respectively
![]() $2+p-\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)$
), then
$2+p-\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)$
), then
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)\leqslant v$
.
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)\leqslant v$
.
Proof. In both cases we only need to prove that the first assumption implies the second, by the existence theorem of the canonical filtration
![]() $(\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)=\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(G))$
. Moreover, we only have to prove that
$(\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)=\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(G))$
. Moreover, we only have to prove that
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<\frac{1}{2}$
, because then
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<\frac{1}{2}$
, because then
![]() $G[p]$
will have a canonical filtration, and in both cases,
$G[p]$
will have a canonical filtration, and in both cases,
![]() $H$
will be a group of this filtration because it will correspond to a break-point of the Harder–Narasimhan filtration (for the classical degree, as we only care about filtration in
$H$
will be a group of this filtration because it will correspond to a break-point of the Harder–Narasimhan filtration (for the classical degree, as we only care about filtration in
![]() $G[p]$
). Let us do the second case, as it is the most difficult one (the first case can be treated similarly, even using only technics introduced in [Reference FarguesFar11]). Let
$G[p]$
). Let us do the second case, as it is the most difficult one (the first case can be treated similarly, even using only technics introduced in [Reference FarguesFar11]). Let
![]() $v=2+p-\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)$
. We can check that
$v=2+p-\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)$
. We can check that
![]() $\deg _{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)>2-v$
, thus
$\deg _{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)>2-v$
, thus
![]() $\deg _{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H^{D})<v$
, and thus, for all
$\deg _{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H^{D})<v$
, and thus, for all
![]() $\unicode[STIX]{x1D700}>1-v$
, if
$\unicode[STIX]{x1D700}>1-v$
, if
![]() $E=G[p]/H$
, then
$E=G[p]/H$
, then
But then the cokernel of
![]() $\unicode[STIX]{x1D6FC}_{E,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},\unicode[STIX]{x1D700}}\otimes 1$
is of degree
$\unicode[STIX]{x1D6FC}_{E,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},\unicode[STIX]{x1D700}}\otimes 1$
is of degree
![]() $(1/(p^{2}-1))\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(E)$
(
$(1/(p^{2}-1))\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(E)$
(
![]() $E$
is a Raynaud subgroup of type
$E$
is a Raynaud subgroup of type
![]() $(p\ldots p)$
), and the following square is commutative,
$(p\ldots p)$
), and the following square is commutative,

and thus, in particular,
![]() $\deg \operatorname{Coker}(\unicode[STIX]{x1D6FC}_{E,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},\unicode[STIX]{x1D700}}\otimes 1)=\deg \operatorname{Coker}(\unicode[STIX]{x1D6FC}_{G[p],\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},\unicode[STIX]{x1D700}}\otimes 1)$
. But according to [Reference HernandezHer19, Proposition 5.25], we can check that the image of
$\deg \operatorname{Coker}(\unicode[STIX]{x1D6FC}_{E,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},\unicode[STIX]{x1D700}}\otimes 1)=\deg \operatorname{Coker}(\unicode[STIX]{x1D6FC}_{G[p],\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},\unicode[STIX]{x1D700}}\otimes 1)$
. But according to [Reference HernandezHer19, Proposition 5.25], we can check that the image of
![]() $\unicode[STIX]{x1D6FC}_{G[p],\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
is always included inside
$\unicode[STIX]{x1D6FC}_{G[p],\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
is always included inside
![]() $up^{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(G)/(p^{2}-1)}\mathbb{F}_{p^{2}}+p^{1/p^{2}}{\mathcal{O}}_{C}/p\subset \unicode[STIX]{x1D714}_{G[p]^{D},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\simeq {\mathcal{O}}_{C}/p$
for some
$up^{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(G)/(p^{2}-1)}\mathbb{F}_{p^{2}}+p^{1/p^{2}}{\mathcal{O}}_{C}/p\subset \unicode[STIX]{x1D714}_{G[p]^{D},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\simeq {\mathcal{O}}_{C}/p$
for some
![]() $u\in {\mathcal{O}}_{C}^{\times }$
. Rewriting the inequality with
$u\in {\mathcal{O}}_{C}^{\times }$
. Rewriting the inequality with
![]() $\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(E)=\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(G[p])-\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)$
we get
$\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(E)=\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(G[p])-\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H)$
we get
but as
![]() $v<\frac{1}{2}<1-1/p^{2}$
we get
$v<\frac{1}{2}<1-1/p^{2}$
we get
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)\leqslant v$
.◻
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)\leqslant v$
.◻
Thus, we can deduce the following,
Lemma 8.5. Let
![]() $(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
as before with corresponding
$(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702},L)$
as before with corresponding
![]() $(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702})\in \mathfrak{X}(v)$
and
$(A,\unicode[STIX]{x1D706},i,\unicode[STIX]{x1D702})\in \mathfrak{X}(v)$
and
![]() $v<1/2(p^{2}+1)$
. Then
$v<1/2(p^{2}+1)$
. Then
![]() $A/L\in \mathfrak{X}(v)$
, and
$A/L\in \mathfrak{X}(v)$
, and
![]() $A[p^{2}]/L$
coincides with the group
$A[p^{2}]/L$
coincides with the group
![]() $K_{1}(A/L)$
.
$K_{1}(A/L)$
.
Proof. By hypothesis on
![]() $L$
, the map,
$L$
, the map,
is an isomorphism on generic fiber, thus
![]() $\operatorname{Deg}_{\unicode[STIX]{x1D70F}}(A[p]/L[p])\geqslant \operatorname{Deg}_{\unicode[STIX]{x1D70F}}(H_{\unicode[STIX]{x1D70F}}^{1})>1+p-v$
. Thus by the previous lemma, we get that,
$\operatorname{Deg}_{\unicode[STIX]{x1D70F}}(A[p]/L[p])\geqslant \operatorname{Deg}_{\unicode[STIX]{x1D70F}}(H_{\unicode[STIX]{x1D70F}}^{1})>1+p-v$
. Thus by the previous lemma, we get that,
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(A/L)\leqslant v$
and moreover
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(A/L)\leqslant v$
and moreover
![]() $A[p]/L[p]$
coincide with the first canonical subgroup associated to
$A[p]/L[p]$
coincide with the first canonical subgroup associated to
![]() $\unicode[STIX]{x1D70F}$
. Moreover, we deduce that
$\unicode[STIX]{x1D70F}$
. Moreover, we deduce that
![]() $\deg A[p]/L[p]\geqslant 2-v$
. Now consider the composite map,
$\deg A[p]/L[p]\geqslant 2-v$
. Now consider the composite map,
Because
![]() $H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1}$
is sent inside
$H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1}$
is sent inside
![]() $A[p]/L[p]$
, we get the factorization,
$A[p]/L[p]$
, we get the factorization,
This is a generic isomorphism by the second hypothesis on
![]() $L$
, and thus
$L$
, and thus
![]() $\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(Q)\geqslant \operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2}/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1})$
. But by construction,
$\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(Q)\geqslant \operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2}/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1})$
. But by construction,
![]() $H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2}/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1}$
is the canonical subgroup (for
$H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2}/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1}$
is the canonical subgroup (for
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
) of
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
) of
![]() $A/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1}$
and thus
$A/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1}$
and thus
![]() $\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2}/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1})\geqslant p+2-\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(A/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1})$
, and
$\operatorname{Deg}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{2}/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1})\geqslant p+2-\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(A/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1})$
, and
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(A/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1})\leqslant p^{2}\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(A)$
(this is [Reference HernandezHer19, Proposition 8.1]), and this implies that
$\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(A/H_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{1})\leqslant p^{2}\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(A)$
(this is [Reference HernandezHer19, Proposition 8.1]), and this implies that
![]() $\deg Q>3-p^{2}v$
. Using the exact sequence,
$\deg Q>3-p^{2}v$
. Using the exact sequence,
we get that
![]() $\deg A[p^{2}]/L>5-p^{2}v-v$
. A similar argument also shows that
$\deg A[p^{2}]/L>5-p^{2}v-v$
. A similar argument also shows that
![]() $\deg K_{1}(A/L)\geqslant 5-(p^{2}+1)\operatorname{ha}_{\unicode[STIX]{x1D70F}}(A/L)$
. But using Bijakowski’s proposition recalled in [Reference HernandezHer19, Proposition A.2], we get that if
$\deg K_{1}(A/L)\geqslant 5-(p^{2}+1)\operatorname{ha}_{\unicode[STIX]{x1D70F}}(A/L)$
. But using Bijakowski’s proposition recalled in [Reference HernandezHer19, Proposition A.2], we get that if
![]() $2(p^{2}+1)v\leqslant 1$
, then
$2(p^{2}+1)v\leqslant 1$
, then
![]() $A[p^{2}]/L=K_{1}(A/L)$
.◻
$A[p^{2}]/L=K_{1}(A/L)$
.◻
Lemma 8.6. Suppose
![]() $v<1/2p^{4}$
. Let
$v<1/2p^{4}$
. Let
![]() $G/\operatorname{Spec}({\mathcal{O}}_{C})$
be a
$G/\operatorname{Spec}({\mathcal{O}}_{C})$
be a
![]() $p$
-divisible group such that
$p$
-divisible group such that
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<v$
, then
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<v$
, then
![]() $K_{1}\subset G[p^{2}]$
coincides over
$K_{1}\subset G[p^{2}]$
coincides over
![]() ${\mathcal{O}}_{C}/p^{1/2p^{2}}$
with
${\mathcal{O}}_{C}/p^{1/2p^{2}}$
with
![]() $\operatorname{Ker}F^{2}\subset G[p^{2}]$
. In particular,
$\operatorname{Ker}F^{2}\subset G[p^{2}]$
. In particular,
Proof. This is Appendix B.◻
Proposition 8.7. Let
![]() $v<1/2p^{4}$
. The Hecke correspondence
$v<1/2p^{4}$
. The Hecke correspondence
![]() $U_{p}$
defined by the two previous maps preserves
$U_{p}$
defined by the two previous maps preserves
![]() $X(v)$
. More precisely, if
$X(v)$
. More precisely, if
![]() $y\in p_{2}(p_{1}^{-1}(\{x\}))$
where
$y\in p_{2}(p_{1}^{-1}(\{x\}))$
where
![]() $x\in X(v)$
, then
$x\in X(v)$
, then
![]() $y\in X(v/p^{2})$
.
$y\in X(v/p^{2})$
.
Proof. The proof follows from the two previous lemmas as
![]() $(A/L)/(A[p^{2}]/L)=A$
.◻
$(A/L)/(A[p^{2}]/L)=A$
.◻
Denote the universal isogeny over
![]() $C$
by
$C$
by
which induces maps
![]() $\unicode[STIX]{x1D714}_{A/L,\unicode[STIX]{x1D70F}}\overset{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70F}}^{\star }}{\longrightarrow }\unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70F}}$
and
$\unicode[STIX]{x1D714}_{A/L,\unicode[STIX]{x1D70F}}\overset{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70F}}^{\star }}{\longrightarrow }\unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70F}}$
and
![]() $\unicode[STIX]{x1D714}_{A/L,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\overset{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{\star }}{\longrightarrow }\unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. We define
$\unicode[STIX]{x1D714}_{A/L,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}\overset{\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{\star }}{\longrightarrow }\unicode[STIX]{x1D714}_{A,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. We define
with
![]() $\widetilde{\unicode[STIX]{x1D70B}^{\star }}=\widetilde{\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70F}}\oplus \widetilde{\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
by
$\widetilde{\unicode[STIX]{x1D70B}^{\star }}=\widetilde{\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70F}}\oplus \widetilde{\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
by
![]() $\widetilde{\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70F}}={\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70F}}$
, and
$\widetilde{\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70F}}={\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70F}}$
, and
![]() $\widetilde{\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
sends a basis
$\widetilde{\unicode[STIX]{x1D70B}^{\star }}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
sends a basis
![]() $(e_{1},e_{2})$
of
$(e_{1},e_{2})$
of
![]() $\unicode[STIX]{x1D714}_{A/L,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
to
$\unicode[STIX]{x1D714}_{A/L,\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
to
![]() $((1/p)\unicode[STIX]{x1D70B}^{\star }e_{1},\unicode[STIX]{x1D70B}^{\star }e_{2})$
. This is an isomorphism.
$((1/p)\unicode[STIX]{x1D70B}^{\star }e_{1},\unicode[STIX]{x1D70B}^{\star }e_{2})$
. This is an isomorphism.
We will need to slightly change the objects as in [Reference Andreatta, Iovita and PilloniAIP15, Proposition 6.2.2.2].
Definition 8.8. Denote by
![]() $w_{0}=m-((p^{2m}-1)/(p^{2}-1))v$
and for
$w_{0}=m-((p^{2m}-1)/(p^{2}-1))v$
and for
![]() $\text{}\underline{w}=(w_{1,1},w_{2,1},w_{2,2},w_{\unicode[STIX]{x1D70E}})$
, define
$\text{}\underline{w}=(w_{1,1},w_{2,1},w_{2,2},w_{\unicode[STIX]{x1D70E}})$
, define
![]() ${\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}}^{0,+}$
as the subspace of
${\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}}^{0,+}$
as the subspace of
![]() ${\mathcal{T}}^{\times }/U_{\text{an}}$
(over
${\mathcal{T}}^{\times }/U_{\text{an}}$
(over
![]() $X_{1}(p^{n})(v)$
) of points for a finite extension
$X_{1}(p^{n})(v)$
) of points for a finite extension
![]() $L$
of
$L$
of
![]() $K$
consisting of
$K$
consisting of
![]() $(A,\unicode[STIX]{x1D713}_{N},\operatorname{Fil}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},P_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},P_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},P^{\unicode[STIX]{x1D70F}})$
such that there exists a polarized trivialization
$(A,\unicode[STIX]{x1D713}_{N},\operatorname{Fil}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},P_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},P_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},P^{\unicode[STIX]{x1D70F}})$
such that there exists a polarized trivialization
![]() $\unicode[STIX]{x1D713}$
of
$\unicode[STIX]{x1D713}$
of
![]() $K_{m}^{D}$
satisfying:
$K_{m}^{D}$
satisfying:
(i)
 $\operatorname{Fil}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
is
$\operatorname{Fil}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
is
 $(w_{0},\unicode[STIX]{x1D713})$
-compatible with
$(w_{0},\unicode[STIX]{x1D713})$
-compatible with
 $H_{\unicode[STIX]{x1D70F}}^{m}$
;
$H_{\unicode[STIX]{x1D70F}}^{m}$
;(ii)
 $P_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=a_{1,1}\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w_{0}}(\unicode[STIX]{x1D713}(e_{1}))+a_{2,1}\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w_{0}}(\unicode[STIX]{x1D713}_{e_{2}})\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w_{0}}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}})$
;
$P_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=a_{1,1}\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w_{0}}(\unicode[STIX]{x1D713}(e_{1}))+a_{2,1}\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w_{0}}(\unicode[STIX]{x1D713}_{e_{2}})\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w_{0}}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}})$
;(iii)
 $P_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=a_{2,2}\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w_{0}}(\unicode[STIX]{x1D713}(e_{2}))\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w_{0}}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}+\operatorname{Fil}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}})$
;
$P_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=a_{2,2}\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w_{0}}(\unicode[STIX]{x1D713}(e_{2}))\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w_{0}}{\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}+\operatorname{Fil}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}})$
;(iv)
 $P_{\unicode[STIX]{x1D70F}}=t\operatorname{HT}_{\unicode[STIX]{x1D70F},w_{0}}(\unicode[STIX]{x1D713}(e_{2}))\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w_{0}}{\mathcal{F}}_{\unicode[STIX]{x1D70F}})$
,
$P_{\unicode[STIX]{x1D70F}}=t\operatorname{HT}_{\unicode[STIX]{x1D70F},w_{0}}(\unicode[STIX]{x1D713}(e_{2}))\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w_{0}}{\mathcal{F}}_{\unicode[STIX]{x1D70F}})$
,
where
![]() $a_{1,1}\in B(1,p^{w_{1,1}}),a_{2,2}\in B(1,p^{w_{2,2}}),t\in B(1,p^{w_{\unicode[STIX]{x1D70E}}}),a_{2,1}\in B(0,p^{w_{2,1}})$
.
$a_{1,1}\in B(1,p^{w_{1,1}}),a_{2,2}\in B(1,p^{w_{2,2}}),t\in B(1,p^{w_{\unicode[STIX]{x1D70E}}}),a_{2,1}\in B(0,p^{w_{2,1}})$
.
Let
![]() $\text{}\underline{w}$
as before, with
$\text{}\underline{w}$
as before, with
![]() $w_{2,1},w_{2,2}<m-1-((p^{2m}-1)/(p-1))v$
. Write
$w_{2,1},w_{2,2}<m-1-((p^{2m}-1)/(p-1))v$
. Write
![]() $\text{}\underline{w}^{\prime }=(w_{1,1},w_{2,1}+1,w_{2,2},w_{\unicode[STIX]{x1D70E}})$
.
$\text{}\underline{w}^{\prime }=(w_{1,1},w_{2,1}+1,w_{2,2},w_{\unicode[STIX]{x1D70E}})$
.
Proposition 8.9. The quotient map,
sends
![]() $p_{1}^{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}}^{0,+}$
to
$p_{1}^{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}}^{0,+}$
to
![]() $p_{2}^{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}^{\prime }}^{0,+}$
(i.e. improves the analycity radius).
$p_{2}^{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}^{\prime }}^{0,+}$
(i.e. improves the analycity radius).
Proof. Let
![]() $x=(A,\unicode[STIX]{x1D713}_{N},L)$
be a point of
$x=(A,\unicode[STIX]{x1D713}_{N},L)$
be a point of
![]() $C$
. Let
$C$
. Let
![]() $(e_{1},e_{2})$
be a basis of
$(e_{1},e_{2})$
be a basis of
![]() $K_{m}^{D}$
(
$K_{m}^{D}$
(
![]() $p^{m}{\mathcal{O}}/p^{2m}{\mathcal{O}}e_{1}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}}e_{2}=K_{n}^{D}$
) and denote by
$p^{m}{\mathcal{O}}/p^{2m}{\mathcal{O}}e_{1}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}}e_{2}=K_{n}^{D}$
) and denote by
![]() $(e_{1}^{\prime },e_{2}^{\prime })$
a similar basis for
$(e_{1}^{\prime },e_{2}^{\prime })$
a similar basis for
![]() $A/L$
such that if
$A/L$
such that if
![]() $x_{1},x_{2}$
and
$x_{1},x_{2}$
and
![]() $x_{1}^{\prime },x_{2}^{\prime }$
denote the dual basis then
$x_{1}^{\prime },x_{2}^{\prime }$
denote the dual basis then
![]() $\unicode[STIX]{x1D70B}^{D}:K_{m}^{^{\prime },D}\longrightarrow K_{m}^{D}$
in these basis is given by
$\unicode[STIX]{x1D70B}^{D}:K_{m}^{^{\prime },D}\longrightarrow K_{m}^{D}$
in these basis is given by
Let
![]() $(\operatorname{Fil}^{\prime },w^{\prime })\in p_{2}^{\ast }{\mathcal{T}}_{\text{an}}^{\times }/U_{\text{an}}$
. As
$(\operatorname{Fil}^{\prime },w^{\prime })\in p_{2}^{\ast }{\mathcal{T}}_{\text{an}}^{\times }/U_{\text{an}}$
. As
![]() $\unicode[STIX]{x1D70B}^{D}$
is a generic isomorphism on the multiplicative part, it is enough to check the proposition on
$\unicode[STIX]{x1D70B}^{D}$
is a generic isomorphism on the multiplicative part, it is enough to check the proposition on
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. Suppose
${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. Suppose
![]() $\widetilde{\unicode[STIX]{x1D70B}}^{\ast }(\operatorname{Fil}^{\prime },w^{\prime })=(\operatorname{Fil},w)\in p_{1}^{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}}^{0,+}$
, which means (on the
$\widetilde{\unicode[STIX]{x1D70B}}^{\ast }(\operatorname{Fil}^{\prime },w^{\prime })=(\operatorname{Fil},w)\in p_{1}^{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}}^{0,+}$
, which means (on the
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-factor),
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-factor),
But then,
and thus, as
![]() $p{\mathcal{F}}\subset \unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}}^{\prime }$
,
$p{\mathcal{F}}\subset \unicode[STIX]{x1D70B}^{\ast }{\mathcal{F}}^{\prime }$
,
As
![]() $w_{2,2}\leqslant w_{0}-1$
we get the result.◻
$w_{2,2}\leqslant w_{0}-1$
we get the result.◻
Suppose
![]() $v<1/2(p^{2}+1)$
, and define
$v<1/2(p^{2}+1)$
, and define
![]() $\unicode[STIX]{x1D714}_{\text{}\underline{w}^{\prime }}^{\unicode[STIX]{x1D705}\dagger }=g_{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}^{\prime }}^{0,+}[\unicode[STIX]{x1D705}]$
. Suppose
$\unicode[STIX]{x1D714}_{\text{}\underline{w}^{\prime }}^{\unicode[STIX]{x1D705}\dagger }=g_{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}^{\prime }}^{0,+}[\unicode[STIX]{x1D705}]$
. Suppose
![]() $w<m-1-(((p^{2m}-1))/((p^{2}-1)))v$
. We can then look at the following composition,
$w<m-1-(((p^{2m}-1))/((p^{2}-1)))v$
. We can then look at the following composition,
where
![]() $w_{2,1}^{\prime }=w+1$
(we remark that if
$w_{2,1}^{\prime }=w+1$
(we remark that if
![]() $\unicode[STIX]{x1D705}$
is (
$\unicode[STIX]{x1D705}$
is (
![]() $w+1$
)-analytic, there is an isomorphism between
$w+1$
)-analytic, there is an isomorphism between
![]() $g_{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}^{\prime }}^{0,+}[\unicode[STIX]{x1D705}]$
and
$g_{\ast }{\mathcal{I}}{\mathcal{W}}_{\text{}\underline{w}^{\prime }}^{0,+}[\unicode[STIX]{x1D705}]$
and
![]() $\unicode[STIX]{x1D714}_{w_{2,1}}^{\unicode[STIX]{x1D705}\dagger }$
).
$\unicode[STIX]{x1D714}_{w_{2,1}}^{\unicode[STIX]{x1D705}\dagger }$
).
Remark 8.10. The normalization of the Trace map is the same as in [Reference BijakowskiBij17], the normalization of
![]() $\unicode[STIX]{x1D70B}^{\star }$
giving a factor
$\unicode[STIX]{x1D70B}^{\star }$
giving a factor
![]() $p^{-k_{2}}$
on algebraic weights.
$p^{-k_{2}}$
on algebraic weights.
Definition 8.11. Suppose
![]() $v<1/2(p^{2}+1)$
. The operator
$v<1/2(p^{2}+1)$
. The operator
![]() $U_{p}$
is defined as the previous composition on bounded functions precomposed by
$U_{p}$
is defined as the previous composition on bounded functions precomposed by
![]() $H^{0}({\mathcal{Y}}(v),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }){\hookrightarrow}H^{0}({\mathcal{Y}}(v/p^{2}),\unicode[STIX]{x1D714}_{\text{}\underline{w}^{\prime }}^{\unicode[STIX]{x1D705}\dagger })$
. In particular it is compact as
$H^{0}({\mathcal{Y}}(v),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }){\hookrightarrow}H^{0}({\mathcal{Y}}(v/p^{2}),\unicode[STIX]{x1D714}_{\text{}\underline{w}^{\prime }}^{\unicode[STIX]{x1D705}\dagger })$
. In particular it is compact as
![]() $H^{0}({\mathcal{Y}}(v),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }){\hookrightarrow}H^{0}({\mathcal{Y}}(v/p^{2}),\unicode[STIX]{x1D714}_{\text{}\underline{w}^{\prime }}^{\unicode[STIX]{x1D705}\dagger })$
is.
$H^{0}({\mathcal{Y}}(v),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }){\hookrightarrow}H^{0}({\mathcal{Y}}(v/p^{2}),\unicode[STIX]{x1D714}_{\text{}\underline{w}^{\prime }}^{\unicode[STIX]{x1D705}\dagger })$
is.
Proposition 8.12. Let
![]() $L$
be a finite extension of
$L$
be a finite extension of
![]() $K$
, and
$K$
, and
![]() $x,y\in X(v)(L)$
such that
$x,y\in X(v)(L)$
such that
![]() $y\in p_{2}(p_{1}^{-1}(x))$
, and let
$y\in p_{2}(p_{1}^{-1}(x))$
, and let
![]() $\unicode[STIX]{x1D705}$
be a
$\unicode[STIX]{x1D705}$
be a
![]() $\unicode[STIX]{x1D714}$
-analytic character. Then
$\unicode[STIX]{x1D714}$
-analytic character. Then
![]() $U_{p}$
is identified with
$U_{p}$
is identified with
![]() $\unicode[STIX]{x1D6FF}$
, i.e. there is a commutative diagram as follows.
$\unicode[STIX]{x1D6FF}$
, i.e. there is a commutative diagram as follows.

We can also define an operator
![]() $S_{p}$
, by considering the two maps,
$S_{p}$
, by considering the two maps,
defined by
![]() $p_{1}=\operatorname{id}$
and
$p_{1}=\operatorname{id}$
and
![]() $p_{2}(A,\operatorname{Fil}(A[p]))=(A/A[p],p^{-1}\operatorname{Fil}(A[p])/A[p])$
. The map
$p_{2}(A,\operatorname{Fil}(A[p]))=(A/A[p],p^{-1}\operatorname{Fil}(A[p])/A[p])$
. The map
![]() $p_{2}$
corresponds to multiplication by
$p_{2}$
corresponds to multiplication by
![]() $p$
on
$p$
on
![]() $\unicode[STIX]{x1D714}$
and the universal map
$\unicode[STIX]{x1D714}$
and the universal map
![]() $\unicode[STIX]{x1D70B}:A\longrightarrow A/A[p]$
over
$\unicode[STIX]{x1D70B}:A\longrightarrow A/A[p]$
over
![]() $X_{Iw(p)}$
induces a map,
$X_{Iw(p)}$
induces a map,
Define
![]() $\widetilde{\unicode[STIX]{x1D70B}^{\ast }}=(1/p)\unicode[STIX]{x1D70B}^{\ast }$
and consider the operator,
$\widetilde{\unicode[STIX]{x1D70B}^{\ast }}=(1/p)\unicode[STIX]{x1D70B}^{\ast }$
and consider the operator,
The map
![]() $\unicode[STIX]{x1D70B}^{\ast }$
preserves the Hasse invariant (as
$\unicode[STIX]{x1D70B}^{\ast }$
preserves the Hasse invariant (as
![]() $A[p^{\infty }]/A[p]\simeq A[p^{\infty }]$
) and sends the canonical filtration, if it exists, to itself (if
$A[p^{\infty }]/A[p]\simeq A[p^{\infty }]$
) and sends the canonical filtration, if it exists, to itself (if
![]() $v<1/4p$
). In concrete terms, on the classical sheaf
$v<1/4p$
). In concrete terms, on the classical sheaf
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}^{\prime }}\subset \unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}\dagger }$
, if we write
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}^{\prime }}\subset \unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}\dagger }$
, if we write
![]() $\unicode[STIX]{x1D705}^{\prime }=(k_{1},k_{2},k_{3})\in \mathbb{Z}^{3}$
(and thus
$\unicode[STIX]{x1D705}^{\prime }=(k_{1},k_{2},k_{3})\in \mathbb{Z}^{3}$
(and thus
![]() $\unicode[STIX]{x1D705}=(-k_{2},-k_{1},-k_{3})$
) the previous composition corresponds to a normalization by
$\unicode[STIX]{x1D705}=(-k_{2},-k_{1},-k_{3})$
) the previous composition corresponds to a normalization by
![]() $p^{-k_{1}-k_{2}-k_{3}}$
of the map that sends
$p^{-k_{1}-k_{2}-k_{3}}$
of the map that sends
![]() $f(A,dz_{i})\mapsto f(A,pdz_{i})$
.
$f(A,dz_{i})\mapsto f(A,pdz_{i})$
.
Definition 8.13. Define also the Hecke operator
![]() $S_{p}$
to be the previous composition. The operator
$S_{p}$
to be the previous composition. The operator
![]() $S_{p}$
is invertible as
$S_{p}$
is invertible as
![]() $p$
is invertible in
$p$
is invertible in
![]() ${\mathcal{T}}^{\times }$
.
${\mathcal{T}}^{\times }$
.
We define the Atkin–Lehner algebra at
![]() $p$
as
$p$
as
![]() ${\mathcal{A}}(p)=\mathbb{Z}[1/p][U_{p},S_{p}^{\pm 1}]$
. It acts on the space of (classical) modular forms too.
${\mathcal{A}}(p)=\mathbb{Z}[1/p][U_{p},S_{p}^{\pm 1}]$
. It acts on the space of (classical) modular forms too.
Classically it is also possible to define geometrically operators
![]() $U_{p}$
and
$U_{p}$
and
![]() $S_{p}$
at
$S_{p}$
at
![]() $p$
on classical modular forms of Iwahori level at
$p$
on classical modular forms of Iwahori level at
![]() $p$
, and they obviously coincide with ours through the inclusion of classical forms to overconvergent ones. It is actually proven in [Reference BijakowskiBij16] that these Hecke operators preserve a strict neighborhood of the canonical-
$p$
, and they obviously coincide with ours through the inclusion of classical forms to overconvergent ones. It is actually proven in [Reference BijakowskiBij16] that these Hecke operators preserve a strict neighborhood of the canonical-
![]() $\unicode[STIX]{x1D707}$
-ordinary locus of
$\unicode[STIX]{x1D707}$
-ordinary locus of
![]() $X_{I}$
, given in terms of the degree.
$X_{I}$
, given in terms of the degree.
Remark 8.14. Because of the normalization, the definition of the Hecke operator slightly differs with the one by convolution on automorphic forms. The reason is that the Hodge–Tate or automorphic weights do not vary continuously in families. This is already the case in other constructions. Let us be more specific. Let
![]() $f\in H^{0}(X_{Iw,K},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
a classical automorphic form of weight
$f\in H^{0}(X_{Iw,K},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
a classical automorphic form of weight
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})$
and Iwahori level at
$\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})$
and Iwahori level at
![]() $p$
. To
$p$
. To
![]() $f$
, as explained in Proposition 2.6 is associated a (non-scalar) automorphic form
$f$
, as explained in Proposition 2.6 is associated a (non-scalar) automorphic form
![]() $\unicode[STIX]{x1D6F7}_{f}$
(and a scalar one
$\unicode[STIX]{x1D6F7}_{f}$
(and a scalar one
![]() $\unicode[STIX]{x1D711}_{f}$
whose Hecke eigenvalues are the same as the one of
$\unicode[STIX]{x1D711}_{f}$
whose Hecke eigenvalues are the same as the one of
![]() $\unicode[STIX]{x1D6F7}_{f}$
). The Hecke action on
$\unicode[STIX]{x1D6F7}_{f}$
). The Hecke action on
![]() $f$
and
$f$
and
![]() $\unicode[STIX]{x1D6F7}_{f}$
is equivariant for the classical (i.e. non-renormalized) action at
$\unicode[STIX]{x1D6F7}_{f}$
is equivariant for the classical (i.e. non-renormalized) action at
![]() $p$
, more precisely at
$p$
, more precisely at
![]() $p$
if we denote
$p$
if we denote
![]() $S_{p}$
and
$S_{p}$
and
![]() $U_{p}$
the previous (normalized operators) the classical ones are
$U_{p}$
the previous (normalized operators) the classical ones are
![]() $S_{p}^{\text{class}}=p^{|k|}S_{p}$
and
$S_{p}^{\text{class}}=p^{|k|}S_{p}$
and
![]() $U_{p}^{\text{class}}=p^{k_{2}}U_{p}$
. The operators
$U_{p}^{\text{class}}=p^{k_{2}}U_{p}$
. The operators
![]() $S_{p}^{\text{class}}$
and
$S_{p}^{\text{class}}$
and
![]() $U_{p}^{\text{class}}$
correspond to the two matrices,
$U_{p}^{\text{class}}$
correspond to the two matrices,
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & p\end{array}\right)\quad \text{and}\quad \left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right)\in GU(2,1)(\mathbb{Q}_{p}).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & p\end{array}\right)\quad \text{and}\quad \left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right)\in GU(2,1)(\mathbb{Q}_{p}).\end{eqnarray}$$
Their similitude factor is in both cases
![]() $p^{2}=N(p)$
. Let
$p^{2}=N(p)$
. Let
![]() $f\in H^{0}(X_{Iw,K},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
be a classical eigenform that is proper for the Hecke operator
$f\in H^{0}(X_{Iw,K},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
be a classical eigenform that is proper for the Hecke operator
![]() $U_{p}$
and
$U_{p}$
and
![]() $S_{p}$
, of respective eigenvalues
$S_{p}$
, of respective eigenvalues
![]() $\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}$
, then
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D706}$
, then
![]() $\unicode[STIX]{x1D711}_{f}$
has eigenvalues for the corresponding (non-normalized) Hecke operators at
$\unicode[STIX]{x1D711}_{f}$
has eigenvalues for the corresponding (non-normalized) Hecke operators at
![]() $p$
,
$p$
,
![]() $p^{k_{2}}\unicode[STIX]{x1D707}$
and
$p^{k_{2}}\unicode[STIX]{x1D707}$
and
![]() $p^{k_{1}+k_{2}+k_{3}}\unicode[STIX]{x1D706}$
.
$p^{k_{1}+k_{2}+k_{3}}\unicode[STIX]{x1D706}$
.
8.3 Remarks on the operators on the split case
When
![]() $p$
splits in
$p$
splits in
![]() $E$
, the eigenvariety for
$E$
, the eigenvariety for
![]() $U(2,1)_{E}$
is a particular case of Brasca’s construction (see [Reference BrascaBra16]). Unfortunately as noted by Brasca, there is a slight issue with the normalization of the Hecke operators at
$U(2,1)_{E}$
is a particular case of Brasca’s construction (see [Reference BrascaBra16]). Unfortunately as noted by Brasca, there is a slight issue with the normalization of the Hecke operators at
![]() $p$
constructed in [Reference BrascaBra16, § 4.2.2], where there should be a normalization in families that depends on the weights, as in [Reference BijakowskiBij16, § 2.3.1] for classical sheaves (without this normalization Hecke operators do not vary in family). More explicitly on the split Picard case, we have four Hecke operators at
$p$
constructed in [Reference BrascaBra16, § 4.2.2], where there should be a normalization in families that depends on the weights, as in [Reference BijakowskiBij16, § 2.3.1] for classical sheaves (without this normalization Hecke operators do not vary in family). More explicitly on the split Picard case, we have four Hecke operators at
![]() $p$
(Bijakowski only consider two of them, which are relevant for classicity), written
$p$
(Bijakowski only consider two of them, which are relevant for classicity), written
![]() $U_{i},i=0,\ldots ,3$
, following [Reference BijakowskiBij16, § 2.3.1] (allowing
$U_{i},i=0,\ldots ,3$
, following [Reference BijakowskiBij16, § 2.3.1] (allowing
![]() $i=0$
and
$i=0$
and
![]() $i=3$
). The normalization are the following on classical weights,
$i=3$
). The normalization are the following on classical weights,
where
![]() $U_{i}^{c}$
denotes the classical Hecke operators, and we choose a splitting of the universal
$U_{i}^{c}$
denotes the classical Hecke operators, and we choose a splitting of the universal
![]() $p$
-divisible group
$p$
-divisible group
![]() $A[p^{\infty }]=A[v^{\infty }]\times A[\overline{v}^{\infty }]$
and
$A[p^{\infty }]=A[v^{\infty }]\times A[\overline{v}^{\infty }]$
and
![]() $A[\overline{v}^{\infty }]=A[v^{\infty }]^{D}$
, where
$A[\overline{v}^{\infty }]=A[v^{\infty }]^{D}$
, where
![]() $v$
coincide with
$v$
coincide with
![]() $\unicode[STIX]{x1D70F}_{\infty }$
through the fixed isomorphism
$\unicode[STIX]{x1D70F}_{\infty }$
through the fixed isomorphism
![]() $\mathbb{C}\simeq \overline{\mathbb{Q}_{p}}$
. Thus
$\mathbb{C}\simeq \overline{\mathbb{Q}_{p}}$
. Thus
![]() $G=A[v^{\infty }]$
has height
$G=A[v^{\infty }]$
has height
![]() $3$
and dimension
$3$
and dimension
![]() $1$
, and modular forms of weight
$1$
, and modular forms of weight
![]() $\unicode[STIX]{x1D705}=(k_{1}\geqslant k_{2},k_{3})\in \mathbb{Z}_{\text{dom}}^{3}$
are sections of
$\unicode[STIX]{x1D705}=(k_{1}\geqslant k_{2},k_{3})\in \mathbb{Z}_{\text{dom}}^{3}$
are sections of
8.4 Classicity results
In this section, we will prove a classicity result. As in [Reference Andreatta, Iovita and PilloniAIP15], this is realized in two steps. First show that a section in
![]() $M_{\unicode[STIX]{x1D705}}^{\dagger }$
is actually a section of
$M_{\unicode[STIX]{x1D705}}^{\dagger }$
is actually a section of
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}^{\prime }}$
over
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}^{\prime }}$
over
![]() $X(v)$
(this is called a result of classicity at the level of sheaves), then we show that this section extends to all
$X(v)$
(this is called a result of classicity at the level of sheaves), then we show that this section extends to all
![]() $X_{Iw}$
, but this is done in [Reference BijakowskiBij16].
$X_{Iw}$
, but this is done in [Reference BijakowskiBij16].
If
![]() $n$
is big enough, there is an action of
$n$
is big enough, there is an action of
![]() $I_{p^{n}}\subset \operatorname{GL}_{2}\times \operatorname{GL}_{1}$
on
$I_{p^{n}}\subset \operatorname{GL}_{2}\times \operatorname{GL}_{1}$
on
![]() ${\mathcal{I}}{\mathcal{W}}_{w}^{0,+}$
which can be derived as an action of
${\mathcal{I}}{\mathcal{W}}_{w}^{0,+}$
which can be derived as an action of
![]() $U(\mathfrak{g})$
on
$U(\mathfrak{g})$
on
![]() ${\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}_{w}^{0,+}}$
denoted by
${\mathcal{O}}_{{\mathcal{I}}{\mathcal{W}}_{w}^{0,+}}$
denoted by
![]() $\star$
. As in § 4, let
$\star$
. As in § 4, let
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},r)$
be a classical weight, and we denote by
$\unicode[STIX]{x1D705}=(k_{1},k_{2},r)$
be a classical weight, and we denote by
![]() $d_{\unicode[STIX]{x1D705}}$
the map,
$d_{\unicode[STIX]{x1D705}}$
the map,
which sends
![]() $\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
to
$\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
to
![]() $\unicode[STIX]{x1D714}_{w}^{(k_{2}-1,k_{1}+1,r)\dagger }$
.
$\unicode[STIX]{x1D714}_{w}^{(k_{2}-1,k_{1}+1,r)\dagger }$
.
Proposition 8.15. Let
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},r)$
be a classical weight. There is an exact sequence of sheaves on
$\unicode[STIX]{x1D705}=(k_{1},k_{2},r)$
be a classical weight. There is an exact sequence of sheaves on
![]() $X(v)$
,
$X(v)$
,
Proof. This is exactly as in [Reference Andreatta, Iovita and PilloniAIP15, Proposition 7.2.1] (we do not need assumption on
![]() $w$
as
$w$
as
![]() $V_{\unicode[STIX]{x1D705},L}^{0,w\text{-an}}$
is isomorphic to analytic functions on one ball only, and Jones’ theorem applies [Reference JonesJon11]).◻
$V_{\unicode[STIX]{x1D705},L}^{0,w\text{-an}}$
is isomorphic to analytic functions on one ball only, and Jones’ theorem applies [Reference JonesJon11]).◻
Proposition 8.16. On
![]() $\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
we have the following commutativity,
$\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
we have the following commutativity,
In particular, if
![]() $H^{0}(X(v),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger })^{{<}k_{1}-k_{2}+1}$
denotes the union of generalized eigenspaces for eigenvalues of slope smaller than
$H^{0}(X(v),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger })^{{<}k_{1}-k_{2}+1}$
denotes the union of generalized eigenspaces for eigenvalues of slope smaller than
![]() $k_{1}-k_{2}+1$
, and
$k_{1}-k_{2}+1$
, and
![]() $f\in H^{0}(X(v),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger })^{{<}k_{1}-k_{2}+1}$
, then
$f\in H^{0}(X(v),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger })^{{<}k_{1}-k_{2}+1}$
, then
![]() $f\in H^{0}(X(v),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}^{\prime }})$
.
$f\in H^{0}(X(v),\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}^{\prime }})$
.
Proof. We can work étale-locally, in which case by the previous results on
![]() $\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
locally the first part reduces to § 4. Now, if
$\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}\dagger }$
locally the first part reduces to § 4. Now, if
![]() $f$
is a generalized eigenvector for
$f$
is a generalized eigenvector for
![]() $U_{p}$
of eigenvalue
$U_{p}$
of eigenvalue
![]() $\unicode[STIX]{x1D706}$
of slope (strictly) smaller than
$\unicode[STIX]{x1D706}$
of slope (strictly) smaller than
![]() $k_{1}-k_{2}+1$
, then
$k_{1}-k_{2}+1$
, then
![]() $d_{\unicode[STIX]{x1D705}}f$
is generalized eigenvector of slope
$d_{\unicode[STIX]{x1D705}}f$
is generalized eigenvector of slope
![]() $\unicode[STIX]{x1D706}p^{-k_{1}+k_{2}-1}$
which is of negative valuation, but this is impossible as
$\unicode[STIX]{x1D706}p^{-k_{1}+k_{2}-1}$
which is of negative valuation, but this is impossible as
![]() $U_{p}$
(and étale-locally
$U_{p}$
(and étale-locally
![]() $\unicode[STIX]{x1D6FF}$
) is of norm strictly less than
$\unicode[STIX]{x1D6FF}$
) is of norm strictly less than
![]() $1$
. Thus
$1$
. Thus
![]() $d_{\unicode[STIX]{x1D705}}f=0$
and
$d_{\unicode[STIX]{x1D705}}f=0$
and
![]() $f$
is a section of
$f$
is a section of
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
.◻
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
.◻
The previous result is sometimes referred to as a classicity at the level of sheaves. Moreover, we have the following classicity result of Bijakowski [Reference BijakowskiBij16].
Theorem 8.17 (Bijakowski).
Let
![]() $f$
be an overconvergent section of the sheaf
$f$
be an overconvergent section of the sheaf
![]() $\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
,
$\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}}$
,
![]() $\unicode[STIX]{x1D705}=(k_{1}\geqslant k_{2},k_{3})$
, which is proper for
$\unicode[STIX]{x1D705}=(k_{1}\geqslant k_{2},k_{3})$
, which is proper for
![]() $U_{p}$
of eigenvalue
$U_{p}$
of eigenvalue
![]() $\unicode[STIX]{x1D6FC}$
. Then if
$\unicode[STIX]{x1D6FC}$
. Then if
then
![]() $f$
is a classical form of weight
$f$
is a classical form of weight
![]() $\unicode[STIX]{x1D705}$
and level
$\unicode[STIX]{x1D705}$
and level
![]() $K^{p}I$
.
$K^{p}I$
.
9 Constructing the eigenvariety
In this section we will construct the eigenvariety associated to the algebra
![]() ${\mathcal{H}}\otimes {\mathcal{A}}(p)$
and the spaces of overconvergent modular forms
${\mathcal{H}}\otimes {\mathcal{A}}(p)$
and the spaces of overconvergent modular forms
![]() $M_{\unicode[STIX]{x1D705}}^{\dagger }$
. In order to do this, we will use Buzzard’s construction of eigenvarieties, and we need to show that the spaces
$M_{\unicode[STIX]{x1D705}}^{\dagger }$
. In order to do this, we will use Buzzard’s construction of eigenvarieties, and we need to show that the spaces
![]() $M_{\unicode[STIX]{x1D705}}^{\dagger }$
(and a bit more) are projective. The method of proof follows closely the lines of [Reference Andreatta, Iovita and PilloniAIP15], but as this case is simpler (because the toroidal compactification is) we chose to write the argument in details.
$M_{\unicode[STIX]{x1D705}}^{\dagger }$
(and a bit more) are projective. The method of proof follows closely the lines of [Reference Andreatta, Iovita and PilloniAIP15], but as this case is simpler (because the toroidal compactification is) we chose to write the argument in details.
9.1 Projection to the minimal compactification
Definition 9.1. Let
![]() $X^{\ast }$
be the minimal compactification of
$X^{\ast }$
be the minimal compactification of
![]() $Y$
as a (projective) scheme over
$Y$
as a (projective) scheme over
![]() $\operatorname{Spec}({\mathcal{O}})$
. There is a map
$\operatorname{Spec}({\mathcal{O}})$
. There is a map
from the toroidal to the minimal compactification. Denote by
![]() $X_{\text{rig}}^{\ast }$
the rigid fiber and
$X_{\text{rig}}^{\ast }$
the rigid fiber and
![]() $X^{\ast }(v)$
the image of
$X^{\ast }(v)$
the image of
![]() $X(v)$
in
$X(v)$
in
![]() $X_{\text{rig}}^{\ast }$
. If
$X_{\text{rig}}^{\ast }$
. If
![]() $v\in \mathbb{Q}$
this is an affinoid as
$v\in \mathbb{Q}$
this is an affinoid as
![]() $X_{\text{ord}}^{\ast }$
is (
$X_{\text{ord}}^{\ast }$
is (
![]() $\det \unicode[STIX]{x1D714}$
is ample on the minimal compactification). Denote also by
$\det \unicode[STIX]{x1D714}$
is ample on the minimal compactification). Denote also by
![]() $D$
the boundary in the toroidal compactification
$D$
the boundary in the toroidal compactification
![]() $X$
, and by abuse of notation in
$X$
, and by abuse of notation in
![]() $X_{1}(p^{2m})$
and
$X_{1}(p^{2m})$
and
![]() $X_{1}(p^{2m})(v)$
.
$X_{1}(p^{2m})(v)$
.
The idea to check that our spaces of cuspidal overconvergent modular forms are projective is to push the sheaves to
![]() $X^{\ast }(v)$
, which is affinoid, and use the dévissage of [Reference Andreatta, Iovita and PilloniAIP15, Proposition A.1.2.2]. But we need to show that the pushforward of the family of sheaves
$X^{\ast }(v)$
, which is affinoid, and use the dévissage of [Reference Andreatta, Iovita and PilloniAIP15, Proposition A.1.2.2]. But we need to show that the pushforward of the family of sheaves
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}}(-D)$
is a small Banach sheaf. In order to do this, we will do as in [Reference Andreatta, Iovita and PilloniAIP15] and prove that the pushforward of the trivial sheaf has no higher cohomology, and we will need to calculate this locally.
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}}(-D)$
is a small Banach sheaf. In order to do this, we will do as in [Reference Andreatta, Iovita and PilloniAIP15] and prove that the pushforward of the trivial sheaf has no higher cohomology, and we will need to calculate this locally.
9.1.1 Description of the toroidal compactification
Let
![]() $V={\mathcal{O}}_{E}^{3}$
with the hermitian form
$V={\mathcal{O}}_{E}^{3}$
with the hermitian form
![]() $\langle \,,\rangle$
chosen in the datum. For all totally isotropic factor
$\langle \,,\rangle$
chosen in the datum. For all totally isotropic factor
![]() $V^{\prime }$
, we denote by
$V^{\prime }$
, we denote by
![]() $C(V/(V^{\prime })^{\bot })$
the cone of symmetric hermitian semi-definite positive forms on
$C(V/(V^{\prime })^{\bot })$
the cone of symmetric hermitian semi-definite positive forms on
![]() $(V/(V^{\prime })^{\bot })\,\otimes _{\mathbb{Z}}\,\mathbb{R}$
with rational radical. Denote by
$(V/(V^{\prime })^{\bot })\,\otimes _{\mathbb{Z}}\,\mathbb{R}$
with rational radical. Denote by
![]() $\mathfrak{C}$
the set of such
$\mathfrak{C}$
the set of such
![]() $V^{\prime }$
, and
$V^{\prime }$
, and
Remark 9.2. The subspaces
![]() $V^{\prime }$
are of dimension
$V^{\prime }$
are of dimension
![]() $1$
(if non-zero), and
$1$
(if non-zero), and
![]() $C(V/(V^{\prime })^{\bot })\simeq \mathbb{R}_{+}$
.
$C(V/(V^{\prime })^{\bot })\simeq \mathbb{R}_{+}$
.
Fix
![]() $\unicode[STIX]{x1D713}_{N}$
-level
$\unicode[STIX]{x1D713}_{N}$
-level
![]() $N$
structure,
$N$
structure,
and
![]() $\unicode[STIX]{x1D713}$
of level
$\unicode[STIX]{x1D713}$
of level
![]() $p^{2m}$
,
$p^{2m}$
,
Let
![]() $\unicode[STIX]{x1D6E4}\subset G(\mathbb{Z})$
be the congruence subgroup fixing the level outside
$\unicode[STIX]{x1D6E4}\subset G(\mathbb{Z})$
be the congruence subgroup fixing the level outside
![]() $p$
, and
$p$
, and
![]() $\unicode[STIX]{x1D6E4}_{1}(p^{2m})$
fixing
$\unicode[STIX]{x1D6E4}_{1}(p^{2m})$
fixing
![]() $\unicode[STIX]{x1D713}_{N}$
and
$\unicode[STIX]{x1D713}_{N}$
and
![]() $\unicode[STIX]{x1D713}$
. Suppose that
$\unicode[STIX]{x1D713}$
. Suppose that
![]() $N$
is big enough so that
$N$
is big enough so that
![]() $\unicode[STIX]{x1D6E4}$
is neat. Fix
$\unicode[STIX]{x1D6E4}$
is neat. Fix
![]() ${\mathcal{S}}$
a polyhedral decomposition of
${\mathcal{S}}$
a polyhedral decomposition of
![]() ${\mathcal{C}}$
which is
${\mathcal{C}}$
which is
![]() $\unicode[STIX]{x1D6E4}$
-admissible: on each
$\unicode[STIX]{x1D6E4}$
-admissible: on each
![]() $C(V/(V^{\prime })^{\bot })=\mathbb{R}_{+}$
there is a unique polyhedral decomposition and thus there is a unique decomposition
$C(V/(V^{\prime })^{\bot })=\mathbb{R}_{+}$
there is a unique polyhedral decomposition and thus there is a unique decomposition
![]() ${\mathcal{S}}$
and it is automatically
${\mathcal{S}}$
and it is automatically
![]() $\unicode[STIX]{x1D6E4}$
(or
$\unicode[STIX]{x1D6E4}$
(or
![]() $\unicode[STIX]{x1D6E4}_{1}(p^{2m})$
)-admissible, smooth, and projective.
$\unicode[STIX]{x1D6E4}_{1}(p^{2m})$
)-admissible, smooth, and projective.
Recall the local charts of the toroidal compactification
![]() $X$
. For each
$X$
. For each
![]() $V^{\prime }\in \mathfrak{C}$
non-zero, we have a diagram,
$V^{\prime }\in \mathfrak{C}$
non-zero, we have a diagram,

where
![]() $Y_{E}$
is the moduli space of elliptic curves with complex multiplication by
$Y_{E}$
is the moduli space of elliptic curves with complex multiplication by
![]() ${\mathcal{O}}_{E}$
of principal level
${\mathcal{O}}_{E}$
of principal level
![]() $N$
structure. Denote by
$N$
structure. Denote by
![]() ${\mathcal{E}}$
the universal elliptic curve. Then
${\mathcal{E}}$
the universal elliptic curve. Then
![]() ${\mathcal{B}}_{V^{\prime }}=Ext^{1}({\mathcal{E}},\mathbb{G}_{m}\otimes O_{E})$
is isogenous to
${\mathcal{B}}_{V^{\prime }}=Ext^{1}({\mathcal{E}},\mathbb{G}_{m}\otimes O_{E})$
is isogenous to
![]() $^{t}{\mathcal{E}}$
, and is a
$^{t}{\mathcal{E}}$
, and is a
![]() $\mathbb{G}_{m}$
-torsor,
$\mathbb{G}_{m}$
-torsor,
![]() ${\mathcal{M}}_{V^{\prime }}\longrightarrow {\mathcal{B}}_{V^{\prime }}$
is a
${\mathcal{M}}_{V^{\prime }}\longrightarrow {\mathcal{B}}_{V^{\prime }}$
is a
![]() $\mathbb{G}_{m}$
-torsor; it is the moduli space of principally polarized 1-motives, with
$\mathbb{G}_{m}$
-torsor; it is the moduli space of principally polarized 1-motives, with
![]() $\unicode[STIX]{x1D713}_{N}$
-level structure, and
$\unicode[STIX]{x1D713}_{N}$
-level structure, and
![]() ${\mathcal{M}}_{V^{\prime }}\longrightarrow {\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}$
is an affine toroidal embedding associated to the cone decomposition of
${\mathcal{M}}_{V^{\prime }}\longrightarrow {\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}$
is an affine toroidal embedding associated to the cone decomposition of
![]() $C(V/(V^{\prime })^{\bot })$
, locally isomorphic over
$C(V/(V^{\prime })^{\bot })$
, locally isomorphic over
![]() ${\mathcal{B}}_{V^{\prime }}$
to
${\mathcal{B}}_{V^{\prime }}$
to
![]() $\mathbb{G}_{m}\subset \mathbb{G}_{a}$
.
$\mathbb{G}_{m}\subset \mathbb{G}_{a}$
.
Over
![]() ${\mathcal{B}}_{V^{\prime }}$
we have a semi-abelian scheme of constant toric rank,
${\mathcal{B}}_{V^{\prime }}$
we have a semi-abelian scheme of constant toric rank,
Denote by
![]() $Z_{V^{\prime }}$
the closed stratum of
$Z_{V^{\prime }}$
the closed stratum of
![]() ${\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}$
.
${\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}$
.
Recall that
![]() $X$
is the toroidal compactification of our moduli space
$X$
is the toroidal compactification of our moduli space
![]() $Y$
(it is unique as the polyhedral decomposition
$Y$
(it is unique as the polyhedral decomposition
![]() ${\mathcal{S}}$
is), as defined in [Reference LarsenLar92] or [Reference LanLan13] in full generality, and
${\mathcal{S}}$
is), as defined in [Reference LarsenLar92] or [Reference LanLan13] in full generality, and
![]() $X^{\ast }$
is the minimal compactification. The toroidal compactification
$X^{\ast }$
is the minimal compactification. The toroidal compactification
![]() $X$
is proper and smooth, and
$X$
is proper and smooth, and
![]() $X^{\ast }$
is proper. Moreover, we have a (proper) map,
$X^{\ast }$
is proper. Moreover, we have a (proper) map,
Moreover,
![]() $\unicode[STIX]{x1D702}$
is the identity on
$\unicode[STIX]{x1D702}$
is the identity on
![]() $Y$
. As sets,
$Y$
. As sets,
![]() $X^{\ast }$
is a union of
$X^{\ast }$
is a union of
![]() $Y$
to which we glue points corresponding to elliptic curves with complex multiplication, one for each component of
$Y$
to which we glue points corresponding to elliptic curves with complex multiplication, one for each component of
![]() $D$
, the boundary of
$D$
, the boundary of
![]() $X$
, and, over each
$X$
, and, over each
![]() $x\in X^{\ast }\backslash Y$
,
$x\in X^{\ast }\backslash Y$
,
![]() $\unicode[STIX]{x1D702}^{-1}(x)$
is a CM elliptic curve.
$\unicode[STIX]{x1D702}^{-1}(x)$
is a CM elliptic curve.
Denote by
![]() $\widehat{{\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}}$
the completion of
$\widehat{{\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}}$
the completion of
![]() ${\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}$
along the closed stratum
${\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}$
along the closed stratum
![]() $Z_{V^{\prime }}$
. On
$Z_{V^{\prime }}$
. On
![]() $X$
there is a stratification indexed by
$X$
there is a stratification indexed by
![]() $\mathfrak{C}/\unicode[STIX]{x1D6E4}$
(the open subset
$\mathfrak{C}/\unicode[STIX]{x1D6E4}$
(the open subset
![]() $Y$
corresponds to
$Y$
corresponds to
![]() $V^{\prime }=\{0\}$
). For all non-zero
$V^{\prime }=\{0\}$
). For all non-zero
![]() $V^{\prime }$
, the completion of
$V^{\prime }$
, the completion of
![]() $X$
along the
$X$
along the
![]() $V^{\prime }$
stratum is isomorphic to
$V^{\prime }$
stratum is isomorphic to
![]() $\widehat{{\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}}$
, as
$\widehat{{\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}}$
, as
![]() $\unicode[STIX]{x1D6E4}_{V^{\prime }}$
, the stabilizer of
$\unicode[STIX]{x1D6E4}_{V^{\prime }}$
, the stabilizer of
![]() $V^{\prime }$
, is trivial:
$V^{\prime }$
, is trivial:
![]() $V^{\prime }\simeq {\mathcal{O}}_{E}$
so
$V^{\prime }\simeq {\mathcal{O}}_{E}$
so
![]() $\unicode[STIX]{x1D6E4}_{V^{\prime }}\subset {\mathcal{O}}_{E}^{\times }$
, which is finite as
$\unicode[STIX]{x1D6E4}_{V^{\prime }}\subset {\mathcal{O}}_{E}^{\times }$
, which is finite as
![]() $E$
is quadratic imaginary, and thus because
$E$
is quadratic imaginary, and thus because
![]() $\unicode[STIX]{x1D6E4}$
is neat,
$\unicode[STIX]{x1D6E4}$
is neat,
![]() $\unicode[STIX]{x1D6E4}_{V^{\prime }}=\{1\}$
.
$\unicode[STIX]{x1D6E4}_{V^{\prime }}=\{1\}$
.
As the Hasse invariant on the special fiber of
![]() $X$
is defined as the one of the abelian part of the semi-abelian scheme, we can identify it with the same one on
$X$
is defined as the one of the abelian part of the semi-abelian scheme, we can identify it with the same one on
![]() ${\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}$
, which comes from the special fiber of
${\mathcal{M}}_{V^{\prime },\unicode[STIX]{x1D70E}}$
, which comes from the special fiber of
![]() $Y_{V^{\prime }}\simeq Y_{E}$
. Denote by
$Y_{V^{\prime }}\simeq Y_{E}$
. Denote by
![]() ${\mathcal{Y}}$
,
${\mathcal{Y}}$
,
![]() ${\mathcal{X}}$
the formal completions of
${\mathcal{X}}$
the formal completions of
![]() $Y,X$
along the special fiber. We have defined
$Y,X$
along the special fiber. We have defined
![]() $\mathfrak{X}(v)\longrightarrow \mathfrak{X}$
as an open subset of a blow up. We will describe its boundary locally. Denote by
$\mathfrak{X}(v)\longrightarrow \mathfrak{X}$
as an open subset of a blow up. We will describe its boundary locally. Denote by
![]() $\mathfrak{Y}(v)$
the inverse image of
$\mathfrak{Y}(v)$
the inverse image of
![]() $\mathfrak{Y}$
. Denote by:
$\mathfrak{Y}$
. Denote by:
–
 $\mathfrak{Y}_{E}$
the formal completion along
$\mathfrak{Y}_{E}$
the formal completion along
 $p$
of
$p$
of
 $Y_{V^{\prime }}$
;
$Y_{V^{\prime }}$
;–
 $\mathfrak{Y}_{E}(v)$
the open subset of
$\mathfrak{Y}_{E}(v)$
the open subset of
 ${\mathcal{Y}}_{E}(v)$
along
${\mathcal{Y}}_{E}(v)$
along
 $I=(p^{v},\operatorname{Ha}_{\unicode[STIX]{x1D70F}})$
where
$I=(p^{v},\operatorname{Ha}_{\unicode[STIX]{x1D70F}})$
where
 $I$
is generated by
$I$
is generated by
 $\operatorname{Ha}_{\unicode[STIX]{x1D70F}}$
, but as every
$\operatorname{Ha}_{\unicode[STIX]{x1D70F}}$
, but as every
 $CM$
elliptic curve is
$CM$
elliptic curve is
 $\unicode[STIX]{x1D707}$
-ordinary,
$\unicode[STIX]{x1D707}$
-ordinary,
 $\mathfrak{Y}_{E}(v)=\mathfrak{Y}_{E}$
;
$\mathfrak{Y}_{E}(v)=\mathfrak{Y}_{E}$
;–
 $\mathfrak{B}_{V^{\prime }}$
the formal completion of
$\mathfrak{B}_{V^{\prime }}$
the formal completion of
 ${\mathcal{B}}_{V^{\prime }}$
;
${\mathcal{B}}_{V^{\prime }}$
;– and define
 $\mathfrak{M}_{V^{\prime }},\mathfrak{M}_{V^{\prime },\unicode[STIX]{x1D70E}},\mathfrak{Z}_{V^{\prime }}$
similarly.
$\mathfrak{M}_{V^{\prime }},\mathfrak{M}_{V^{\prime },\unicode[STIX]{x1D70E}},\mathfrak{Z}_{V^{\prime }}$
similarly.
Proposition 9.3. The formal scheme
![]() $\mathfrak{X}(v)$
has a stratification indexed by
$\mathfrak{X}(v)$
has a stratification indexed by
![]() $\mathfrak{C}/\unicode[STIX]{x1D6E4}$
, and the stratum corresponding to
$\mathfrak{C}/\unicode[STIX]{x1D6E4}$
, and the stratum corresponding to
![]() $V^{\prime }$
is isomorphic to
$V^{\prime }$
is isomorphic to
![]() $\mathfrak{Z}_{V^{\prime }}$
if
$\mathfrak{Z}_{V^{\prime }}$
if
![]() $V^{\prime }$
is non-zero, and
$V^{\prime }$
is non-zero, and
![]() $\mathfrak{Y}(v)$
if
$\mathfrak{Y}(v)$
if
![]() $V^{\prime }=\{0\}$
. For all non-zero
$V^{\prime }=\{0\}$
. For all non-zero
![]() $V^{\prime }\in \mathfrak{C}$
the completion of
$V^{\prime }\in \mathfrak{C}$
the completion of
![]() $\mathfrak{X}(v)$
along the
$\mathfrak{X}(v)$
along the
![]() $V^{\prime }$
stratum is isomorphic to
$V^{\prime }$
stratum is isomorphic to
![]() $\widehat{\mathfrak{M}_{V^{\prime },\unicode[STIX]{x1D70E}}}$
(completion along
$\widehat{\mathfrak{M}_{V^{\prime },\unicode[STIX]{x1D70E}}}$
(completion along
![]() $\mathfrak{Z}_{V^{\prime }}$
).
$\mathfrak{Z}_{V^{\prime }}$
).
Proof. We complete and pull back the stratification of
![]() $X$
. The analogous result on
$X$
. The analogous result on
![]() $\mathfrak{X}$
is true since we can invert the completion along
$\mathfrak{X}$
is true since we can invert the completion along
![]() $p$
and the stratum. If
$p$
and the stratum. If
![]() $V^{\prime }\neq 0$
, it is simply that the boundary of
$V^{\prime }\neq 0$
, it is simply that the boundary of
![]() $\mathfrak{X}$
is inside the
$\mathfrak{X}$
is inside the
![]() $\unicode[STIX]{x1D707}$
-ordinary locus. For
$\unicode[STIX]{x1D707}$
-ordinary locus. For
![]() $V^{\prime }=0$
the stratum is the pull back of
$V^{\prime }=0$
the stratum is the pull back of
![]() $\mathfrak{Y}$
inside
$\mathfrak{Y}$
inside
![]() $\mathfrak{X}(v)$
, i.e.
$\mathfrak{X}(v)$
, i.e.
![]() $\mathfrak{Y}(v)$
.◻
$\mathfrak{Y}(v)$
.◻
We used the space
![]() $\mathfrak{X}_{1}(p^{2m})$
in the previous sections, and we would like to describe its boundary.
$\mathfrak{X}_{1}(p^{2m})$
in the previous sections, and we would like to describe its boundary.
Let
![]() $\mathfrak{C}^{\prime }$
be the subset of
$\mathfrak{C}^{\prime }$
be the subset of
![]() $V^{\prime }\in \mathfrak{C}$
such that
$V^{\prime }\in \mathfrak{C}$
such that
![]() $\operatorname{Im}(\unicode[STIX]{x1D713})\subset (V^{\prime })^{\bot }/p^{2m}(V^{\prime })^{\bot }$
. The (unique) polyhedral decomposition previously considered induces also a (unique) polyhedral decomposition on
$\operatorname{Im}(\unicode[STIX]{x1D713})\subset (V^{\prime })^{\bot }/p^{2m}(V^{\prime })^{\bot }$
. The (unique) polyhedral decomposition previously considered induces also a (unique) polyhedral decomposition on
which is
![]() $\unicode[STIX]{x1D6E4}_{1}(p^{2m})$
admissible.
$\unicode[STIX]{x1D6E4}_{1}(p^{2m})$
admissible.
For
![]() $V^{\prime }\in \mathfrak{C}^{\prime }$
non-zero, decompose
$V^{\prime }\in \mathfrak{C}^{\prime }$
non-zero, decompose
and denote by
![]() $W$
the image in
$W$
the image in
![]() $(V^{\prime })^{\bot }/(V^{\prime }+p^{2m}(V^{\prime })^{\bot })$
of
$(V^{\prime })^{\bot }/(V^{\prime }+p^{2m}(V^{\prime })^{\bot })$
of
![]() $\unicode[STIX]{x1D713}({\mathcal{O}}/p^{2m}\oplus p^{m}{\mathcal{O}}/p^{m})$
. This is isomorphic to
$\unicode[STIX]{x1D713}({\mathcal{O}}/p^{2m}\oplus p^{m}{\mathcal{O}}/p^{m})$
. This is isomorphic to
![]() ${\mathcal{O}}/p^{m}$
. Indeed, as
${\mathcal{O}}/p^{m}$
. Indeed, as
![]() $(V^{\prime })^{\bot }$
contains
$(V^{\prime })^{\bot }$
contains
![]() $e_{1},p^{m}e_{2}$
modulo
$e_{1},p^{m}e_{2}$
modulo
![]() $p^{2m}$
,
$p^{2m}$
,
![]() $(V^{\prime })^{\bot }/p^{2m}={\mathcal{O}}/p^{2m}(e_{1},e_{2})$
. Then
$(V^{\prime })^{\bot }/p^{2m}={\mathcal{O}}/p^{2m}(e_{1},e_{2})$
. Then
![]() $\overline{V^{\prime }}=V^{\prime }/p^{2m}$
is totally isotropic inside, i.e. generated by
$\overline{V^{\prime }}=V^{\prime }/p^{2m}$
is totally isotropic inside, i.e. generated by
![]() $ae_{1}+be_{2}$
where
$ae_{1}+be_{2}$
where
![]() $p^{m}|b$
(totally isotropic) and
$p^{m}|b$
(totally isotropic) and
![]() $a\in {\mathcal{O}}^{\times }$
(direct factor). Thus the image of
$a\in {\mathcal{O}}^{\times }$
(direct factor). Thus the image of
![]() $\unicode[STIX]{x1D713}$
is generated in
$\unicode[STIX]{x1D713}$
is generated in
![]() $(V^{\prime })^{\bot }/(V^{\prime }+p^{2m}(V^{\prime })^{\bot })$
by the image of
$(V^{\prime })^{\bot }/(V^{\prime }+p^{2m}(V^{\prime })^{\bot })$
by the image of
![]() $e_{1}=a^{-1}be_{2}$
which is
$e_{1}=a^{-1}be_{2}$
which is
![]() $p^{m}$
-torsion.
$p^{m}$
-torsion.
We specify the following.
(i) Denote by
 ${\mathcal{Y}}_{V^{\prime }}$
the rigid fiber of
${\mathcal{Y}}_{V^{\prime }}$
the rigid fiber of
 $\mathfrak{Y}_{V^{\prime }}$
.
$\mathfrak{Y}_{V^{\prime }}$
.(ii) Denote by
 $H_{m,V^{\prime }}$
the canonical subgroup of level
$H_{m,V^{\prime }}$
the canonical subgroup of level
 $m$
of the universal elliptic scheme
$m$
of the universal elliptic scheme
 $\mathfrak{E}_{V^{\prime }}$
over
$\mathfrak{E}_{V^{\prime }}$
over
 $\mathfrak{Y}_{V^{\prime }}$
.
$\mathfrak{Y}_{V^{\prime }}$
.(iii) Denote by
 ${\mathcal{Y}}_{1}(p^{m})_{V^{\prime }}$
the torsor
${\mathcal{Y}}_{1}(p^{m})_{V^{\prime }}$
the torsor
 $\operatorname{Isom}_{{\mathcal{Y}}_{V^{\prime }}}((H_{m,V^{\prime }})^{D},W^{\vee })$
, and
$\operatorname{Isom}_{{\mathcal{Y}}_{V^{\prime }}}((H_{m,V^{\prime }})^{D},W^{\vee })$
, and
 $\unicode[STIX]{x1D713}_{V^{\prime }}$
the universal isomorphism.
$\unicode[STIX]{x1D713}_{V^{\prime }}$
the universal isomorphism.(iv) Denote by
 $\mathfrak{Y}_{1}(p^{m})$
the normalization of
$\mathfrak{Y}_{1}(p^{m})$
the normalization of
 $\mathfrak{Y}_{V^{\prime }}$
in
$\mathfrak{Y}_{V^{\prime }}$
in
 ${\mathcal{Y}}_{1}(p^{m})_{V^{\prime }}$
.
${\mathcal{Y}}_{1}(p^{m})_{V^{\prime }}$
.(v) There is an isogeny
 $i:\mathfrak{B}_{V^{\prime }}\longrightarrow \mathfrak{E}_{V^{\prime }}$
, and if we write
$i:\mathfrak{B}_{V^{\prime }}\longrightarrow \mathfrak{E}_{V^{\prime }}$
, and if we write
 $i^{\prime }:\mathfrak{E}_{V^{\prime }}\longrightarrow \mathfrak{E}_{V^{\prime }}/H_{m,V^{\prime }}$
, set
$i^{\prime }:\mathfrak{E}_{V^{\prime }}\longrightarrow \mathfrak{E}_{V^{\prime }}/H_{m,V^{\prime }}$
, set  $$\begin{eqnarray}\mathfrak{B}_{1}(p^{m})_{V^{\prime }}(v)=\mathfrak{B}_{V^{\prime }}\times _{i,\mathfrak{E},i^{\prime }}\mathfrak{E}_{V^{\prime }}/H_{m,V^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{B}_{1}(p^{m})_{V^{\prime }}(v)=\mathfrak{B}_{V^{\prime }}\times _{i,\mathfrak{E},i^{\prime }}\mathfrak{E}_{V^{\prime }}/H_{m,V^{\prime }}.\end{eqnarray}$$
(vi) Denote by
 $\mathfrak{M}_{1}(p^{m})_{V^{\prime }},\mathfrak{M}_{1}(p^{m})_{V^{\prime },\unicode[STIX]{x1D70E}},\mathfrak{Z}_{1}(p^{m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
the fibered products of the corresponding formal schemes with
$\mathfrak{M}_{1}(p^{m})_{V^{\prime }},\mathfrak{M}_{1}(p^{m})_{V^{\prime },\unicode[STIX]{x1D70E}},\mathfrak{Z}_{1}(p^{m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
the fibered products of the corresponding formal schemes with
 $\mathfrak{B}_{1}(p^{m})_{V^{\prime }}$
over
$\mathfrak{B}_{1}(p^{m})_{V^{\prime }}$
over
 $\mathfrak{B}_{V^{\prime }}$
.
$\mathfrak{B}_{V^{\prime }}$
.
Proposition 9.4. The formal scheme
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
has a stratification indexed by
$\mathfrak{X}_{1}(p^{2m})(v)$
has a stratification indexed by
![]() $\mathfrak{C}^{\prime }/\unicode[STIX]{x1D6E4}_{1}(p^{2m})$
, for all non-zero
$\mathfrak{C}^{\prime }/\unicode[STIX]{x1D6E4}_{1}(p^{2m})$
, for all non-zero
![]() $V^{\prime }$
, the completion of
$V^{\prime }$
, the completion of
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
along the
$\mathfrak{X}_{1}(p^{2m})(v)$
along the
![]() $V^{\prime }$
-stratum is isomorphic to the completion
$V^{\prime }$
-stratum is isomorphic to the completion
![]() $\widehat{\mathfrak{M}_{1}}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
along
$\widehat{\mathfrak{M}_{1}}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
along
![]() $\mathfrak{Z}_{1}(p^{2m})_{V^{\prime }}$
.
$\mathfrak{Z}_{1}(p^{2m})_{V^{\prime }}$
.
Proof. This is known in rigid fiber, with the same construction, but the previous local charts are normal, and thus coincide with the normalization in their rigid fiber of the level
![]() $\unicode[STIX]{x1D6E4}$
-charts. Thus
$\unicode[STIX]{x1D6E4}$
-charts. Thus
![]() $\mathfrak{M}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
is the normalization of
$\mathfrak{M}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
is the normalization of
![]() $\mathfrak{M}_{V^{\prime },\unicode[STIX]{x1D70E}}$
in
$\mathfrak{M}_{V^{\prime },\unicode[STIX]{x1D70E}}$
in
![]() ${\mathcal{M}}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
. But the completion of
${\mathcal{M}}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
. But the completion of
![]() $\mathfrak{M}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
along
$\mathfrak{M}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
along
![]() $\mathfrak{Z}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
coincides with the normalization of
$\mathfrak{Z}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}$
coincides with the normalization of
![]() $\widehat{\mathfrak{M}_{V^{\prime },\unicode[STIX]{x1D70E}}}^{V^{\prime }}=\widehat{\mathfrak{X}(v)}^{V^{\prime }}$
inside
$\widehat{\mathfrak{M}_{V^{\prime },\unicode[STIX]{x1D70E}}}^{V^{\prime }}=\widehat{\mathfrak{X}(v)}^{V^{\prime }}$
inside
![]() ${\mathcal{M}}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}=\widehat{X_{1}(p^{n})(v)}^{V^{\prime }}$
.◻
${\mathcal{M}}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}=\widehat{X_{1}(p^{n})(v)}^{V^{\prime }}$
.◻
9.2 Minimal compactification
Let
![]() $X^{\ast }$
be the minimal compactification of
$X^{\ast }$
be the minimal compactification of
![]() $Y$
of level
$Y$
of level
![]() $\unicode[STIX]{x1D6E4}$
. As a topological space, it corresponds to adding a finite set of points to
$\unicode[STIX]{x1D6E4}$
. As a topological space, it corresponds to adding a finite set of points to
![]() $Y$
, corresponding to CM elliptic curves.
$Y$
, corresponding to CM elliptic curves.
![]() $X^{\ast }$
is also stratified by
$X^{\ast }$
is also stratified by
![]() $\mathfrak{C}/\unicode[STIX]{x1D6E4}$
. Let
$\mathfrak{C}/\unicode[STIX]{x1D6E4}$
. Let
![]() $\overline{x}\in X^{\ast }\backslash Y$
a geometric point of the boundary, it corresponds to a point
$\overline{x}\in X^{\ast }\backslash Y$
a geometric point of the boundary, it corresponds to a point
![]() $x\in Y_{E}$
.
$x\in Y_{E}$
.
Using the previous description of
![]() $X$
, we can describe the local rings of
$X$
, we can describe the local rings of
![]() $X^{\ast }$
. Let
$X^{\ast }$
. Let
![]() $V^{\prime }\in \mathfrak{C}$
be non-zero. Over
$V^{\prime }\in \mathfrak{C}$
be non-zero. Over
![]() ${\mathcal{B}}_{V^{\prime }}$
,
${\mathcal{B}}_{V^{\prime }}$
,
![]() ${\mathcal{M}}_{V^{\prime }}$
is an affine
${\mathcal{M}}_{V^{\prime }}$
is an affine
![]() $\mathbb{G}_{m}$
-torsor, and we can thus write
$\mathbb{G}_{m}$
-torsor, and we can thus write
where
![]() ${\mathcal{L}}$
is a quasi-coherent
${\mathcal{L}}$
is a quasi-coherent
![]() ${\mathcal{O}}_{{\mathcal{B}}_{V^{\prime }}}$
-algebra endowed with an action of
${\mathcal{O}}_{{\mathcal{B}}_{V^{\prime }}}$
-algebra endowed with an action of
![]() $\mathbb{G}_{m}$
, that can be decomposed,
$\mathbb{G}_{m}$
, that can be decomposed,
For all
![]() $k$
,
$k$
,
![]() ${\mathcal{L}}(k)$
is locally free of rank
${\mathcal{L}}(k)$
is locally free of rank
![]() $1$
over
$1$
over
![]() ${\mathcal{B}}_{V^{\prime }}$
. Denote by
${\mathcal{B}}_{V^{\prime }}$
. Denote by
![]() $\widehat{B_{V^{\prime };\overline{x}}}$
the completion of
$\widehat{B_{V^{\prime };\overline{x}}}$
the completion of
![]() ${\mathcal{B}}_{V^{\prime }}$
along the fiber over
${\mathcal{B}}_{V^{\prime }}$
along the fiber over
![]() $\overline{x}$
. We have the following proposition.
$\overline{x}$
. We have the following proposition.
Proposition 9.5. The scheme
![]() $X^{\ast }$
is stratified by
$X^{\ast }$
is stratified by
![]() $\mathfrak{C}/\unicode[STIX]{x1D6E4}$
and
$\mathfrak{C}/\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x1D702}:X\longrightarrow X^{\ast }$
is compatible with stratifications. Moreover, for all
$\unicode[STIX]{x1D702}:X\longrightarrow X^{\ast }$
is compatible with stratifications. Moreover, for all
![]() $V^{\prime }$
,
$V^{\prime }$
,
![]() $X_{V^{\prime }}^{\ast }$
is isomorphic to
$X_{V^{\prime }}^{\ast }$
is isomorphic to
![]() $Y_{V^{\prime }}$
and for all
$Y_{V^{\prime }}$
and for all
![]() $\overline{x}\in X_{V^{\prime }}^{\star }$
a geometric point,
$\overline{x}\in X_{V^{\prime }}^{\star }$
a geometric point,
where
![]() $\widehat{{\mathcal{O}}_{X^{\ast },\overline{x}}}$
is the completion of the strict henselisation of
$\widehat{{\mathcal{O}}_{X^{\ast },\overline{x}}}$
is the completion of the strict henselisation of
![]() ${\mathcal{O}}_{X^{\ast }}$
at
${\mathcal{O}}_{X^{\ast }}$
at
![]() $\overline{x}$
.
$\overline{x}$
.
Proof. This is Serre’s theorem on global sections of the structure sheaf on proper schemes (as
![]() $\unicode[STIX]{x1D702}$
is proper and
$\unicode[STIX]{x1D702}$
is proper and
![]() $X^{\ast }$
is normal), the theorem of formal functions and the previous description of
$X^{\ast }$
is normal), the theorem of formal functions and the previous description of
![]() $X$
.◻
$X$
.◻
The Hasse invariant
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
descends to the special fiber of
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
descends to the special fiber of
![]() $X^{\ast }$
, and we can thus define
$X^{\ast }$
, and we can thus define
![]() $\mathfrak{X}^{\ast }$
the formal completion of
$\mathfrak{X}^{\ast }$
the formal completion of
![]() $X^{\ast }$
along its special fiber and
$X^{\ast }$
along its special fiber and
![]() $\mathfrak{X}^{\ast }(v)$
the normalization of the open subspace of the blow up of
$\mathfrak{X}^{\ast }(v)$
the normalization of the open subspace of the blow up of
![]() $X^{\ast }$
along
$X^{\ast }$
along
![]() $(p^{v},\operatorname{ha}_{\unicode[STIX]{x1D70F}})$
where this ideal is generated by
$(p^{v},\operatorname{ha}_{\unicode[STIX]{x1D70F}})$
where this ideal is generated by
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
.
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
.
Proposition 9.6. For all
![]() $V^{\prime }\in \mathfrak{C}$
the
$V^{\prime }\in \mathfrak{C}$
the
![]() $V^{\prime }$
-strata of
$V^{\prime }$
-strata of
![]() $\mathfrak{X}^{\ast }(v)$
is
$\mathfrak{X}^{\ast }(v)$
is
![]() $\mathfrak{Y}_{V^{\prime }}(v)$
(and
$\mathfrak{Y}_{V^{\prime }}(v)$
(and
![]() $Y_{E}$
if
$Y_{E}$
if
![]() $V^{\prime }$
is non-zero).
$V^{\prime }$
is non-zero).
Proof. This is known before the blow up, and thus for
![]() $V^{\prime }$
non-zero as the boundary is contained in the
$V^{\prime }$
non-zero as the boundary is contained in the
![]() $\unicode[STIX]{x1D707}$
-ordinary locus. But for
$\unicode[STIX]{x1D707}$
-ordinary locus. But for
![]() $V^{\prime }=0$
this is tautologous.◻
$V^{\prime }=0$
this is tautologous.◻
9.3 Higher cohomology and projectivity of the space of overconvergent automorphic forms
We will look at the following diagram.

Proposition 9.7. Let
![]() $D$
be the boundary of
$D$
be the boundary of
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
. Then for all
$\mathfrak{X}_{1}(p^{2m})(v)$
. Then for all
![]() $q>1$
$q>1$
Proof. It is enough to work locally at
![]() $\overline{x}$
a geometric point of the boundary of
$\overline{x}$
a geometric point of the boundary of
![]() $\mathfrak{X}^{\ast }(v)$
, and by the theorem of formal functions,
$\mathfrak{X}^{\ast }(v)$
, and by the theorem of formal functions,
We will thus show that the right-hand side is zero. But the completion
![]() $\widehat{\mathfrak{X}_{1}(p^{2m})(v)}^{\unicode[STIX]{x1D702}^{-1}(x)}$
is isomorphic to a finite disjoint union of spaces of the form
$\widehat{\mathfrak{X}_{1}(p^{2m})(v)}^{\unicode[STIX]{x1D702}^{-1}(x)}$
is isomorphic to a finite disjoint union of spaces of the form
![]() $\widehat{\mathfrak{M}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}}^{\overline{y}}$
for
$\widehat{\mathfrak{M}_{1}(p^{2m})_{V^{\prime },\unicode[STIX]{x1D70E}}}^{\overline{y}}$
for
![]() $\overline{y}$
a geometric point in
$\overline{y}$
a geometric point in
![]() $Y_{E}$
. Denote by
$Y_{E}$
. Denote by
![]() $M_{\unicode[STIX]{x1D70E}}$
this completed space. As
$M_{\unicode[STIX]{x1D70E}}$
this completed space. As
and thus the morphism,
is affine, we have the equality,
(the product is over
![]() $k>0$
as we take the cohomology in
$k>0$
as we take the cohomology in
![]() ${\mathcal{O}}(-D)$
). But for
${\mathcal{O}}(-D)$
). But for
![]() $k>0$
,
$k>0$
,
![]() ${\mathcal{L}}(k)$
is very ample on the elliptic curve
${\mathcal{L}}(k)$
is very ample on the elliptic curve
![]() $\mathfrak{B}_{1}(p^{m})_{V^{\prime }}$
, and thus
$\mathfrak{B}_{1}(p^{m})_{V^{\prime }}$
, and thus
![]() $H^{q}(\widehat{\mathfrak{B}_{1}(p^{m})_{V^{\prime }}},{\mathcal{L}}(k))=0$
for all
$H^{q}(\widehat{\mathfrak{B}_{1}(p^{m})_{V^{\prime }}},{\mathcal{L}}(k))=0$
for all
![]() $q>0$
.◻
$q>0$
.◻
Theorem 9.8. For
![]() $m\geqslant l$
two integers, we have the following commutative diagram,
$m\geqslant l$
two integers, we have the following commutative diagram,

and the following base change property is satisfied,
In particular,
![]() $\unicode[STIX]{x1D702}_{\ast }\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0}\dagger }(-D)$
is a small Banach sheaf on
$\unicode[STIX]{x1D702}_{\ast }\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0}\dagger }(-D)$
is a small Banach sheaf on
![]() $\mathfrak{X}^{\ast }(v)$
. The same result is true over
$\mathfrak{X}^{\ast }(v)$
. The same result is true over
![]() $\mathfrak{X}^{\ast }(v)\times \mathfrak{W}(w)^{0}$
for
$\mathfrak{X}^{\ast }(v)\times \mathfrak{W}(w)^{0}$
for
Proof. We can just restrict to
![]() $l=m-1$
, but as inductive limit and direct image commute, and as the kernel
$l=m-1$
, but as inductive limit and direct image commute, and as the kernel
![]() $\mathfrak{w}_{w,m}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }\longrightarrow \mathfrak{w}_{w,m-1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is isomorphic to
$\mathfrak{w}_{w,m}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }\longrightarrow \mathfrak{w}_{w,m-1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is isomorphic to
![]() $\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
which is itself a direct limit of sheaves with graded pieces isomorphic to
$\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
which is itself a direct limit of sheaves with graded pieces isomorphic to
![]() ${\mathcal{O}}_{X_{1}(p^{m})}/\unicode[STIX]{x1D70B}$
(see Corollary C.5) and thus by the previous proposition we have the announced equality. We can thus use [Reference Andreatta, Iovita and PilloniAIP15, Proposition A.1.3.1] which proves that
${\mathcal{O}}_{X_{1}(p^{m})}/\unicode[STIX]{x1D70B}$
(see Corollary C.5) and thus by the previous proposition we have the announced equality. We can thus use [Reference Andreatta, Iovita and PilloniAIP15, Proposition A.1.3.1] which proves that
![]() $(\unicode[STIX]{x1D702}\times 1)_{\ast }\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is a small formal Banach sheaf (recall that
$(\unicode[STIX]{x1D702}\times 1)_{\ast }\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is a small formal Banach sheaf (recall that
![]() $\unicode[STIX]{x1D702}$
is proper).◻
$\unicode[STIX]{x1D702}$
is proper).◻
Proposition 9.9. Let
![]() $w>0$
. Write
$w>0$
. Write
![]() $\mathfrak{W}(w)^{0}=\operatorname{Spf}(A)$
. Then
$\mathfrak{W}(w)^{0}=\operatorname{Spf}(A)$
. Then
is a projective
![]() $A[1/p]$
-Banach module. Moreover the specialization map, for
$A[1/p]$
-Banach module. Moreover the specialization map, for
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}(w)^{0}$
,
$\unicode[STIX]{x1D705}\in {\mathcal{W}}(w)^{0}$
,
is surjective.
Proof. This is proved exactly as in [Reference Andreatta, Iovita and PilloniAIP15, Corollary 8.2.3.2]. Let us sketch the ideas. Fix
![]() $(\mathfrak{U}_{i})_{1\geqslant i\geqslant r}$
a (finite) affine covering of
$(\mathfrak{U}_{i})_{1\geqslant i\geqslant r}$
a (finite) affine covering of
![]() $\mathfrak{X}^{\ast }(v)$
, and for
$\mathfrak{X}^{\ast }(v)$
, and for
![]() $\text{}\underline{i}=(i_{1},\ldots ,i_{s})\in \{1,\ldots ,r\}^{s}$
denote by
$\text{}\underline{i}=(i_{1},\ldots ,i_{s})\in \{1,\ldots ,r\}^{s}$
denote by
![]() $\mathfrak{U}_{\text{}\underline{i}}$
the intersection
$\mathfrak{U}_{\text{}\underline{i}}$
the intersection
![]() $\mathfrak{U}_{i_{1}}\cap \ldots \mathfrak{U}_{i_{s}}$
. Then
$\mathfrak{U}_{i_{1}}\cap \ldots \mathfrak{U}_{i_{s}}$
. Then
is isomorphic to the
![]() $p$
-adic completion of a free
$p$
-adic completion of a free
![]() $A$
-module (i.e. is orthonormalizable). This is essentially Corollary C.5 and topological Nakayama’s lemma. But then, as
$A$
-module (i.e. is orthonormalizable). This is essentially Corollary C.5 and topological Nakayama’s lemma. But then, as
![]() $X^{\ast }(v)$
is affinoid, the Cech complex after inverting
$X^{\ast }(v)$
is affinoid, the Cech complex after inverting
![]() $p$
is exact and thus [Reference Andreatta, Iovita and PilloniAIP15, Theorem A.1.2.2] provides a resolution of
$p$
is exact and thus [Reference Andreatta, Iovita and PilloniAIP15, Theorem A.1.2.2] provides a resolution of
![]() $M_{v,w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\text{cusp}}$
by the
$M_{v,w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\text{cusp}}$
by the
![]() $M_{\text{}\underline{i},\infty }[1/p]$
, and thus
$M_{\text{}\underline{i},\infty }[1/p]$
, and thus
![]() $M_{v,w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\text{cusp}}$
is projective. For the surjectivity assertion, fix
$M_{v,w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\text{cusp}}$
is projective. For the surjectivity assertion, fix
![]() $\mathfrak{p}_{\unicode[STIX]{x1D705}}$
the maximal ideal of
$\mathfrak{p}_{\unicode[STIX]{x1D705}}$
the maximal ideal of
![]() $A[1/p]$
corresponding to
$A[1/p]$
corresponding to
![]() $\unicode[STIX]{x1D705}$
and consider the Koszul resolution of
$\unicode[STIX]{x1D705}$
and consider the Koszul resolution of
![]() $A[1/p]/\mathfrak{p}_{\unicode[STIX]{x1D705}}$
. Tensoring this for each
$A[1/p]/\mathfrak{p}_{\unicode[STIX]{x1D705}}$
. Tensoring this for each
![]() $\text{}\underline{i}$
with
$\text{}\underline{i}$
with
![]() $\unicode[STIX]{x1D702}_{\ast }\mathfrak{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }(-D)(\mathfrak{U}_{\text{}\underline{i}})$
gives a resolution of
$\unicode[STIX]{x1D702}_{\ast }\mathfrak{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }(-D)(\mathfrak{U}_{\text{}\underline{i}})$
gives a resolution of
![]() $\unicode[STIX]{x1D702}_{\ast }\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }(-D)(\mathfrak{U}_{\text{}\underline{i}})$
. This gives a double complex where each column (for a fixed index of the Koszul complex) is exact. But each line (for a fixed
$\unicode[STIX]{x1D702}_{\ast }\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }(-D)(\mathfrak{U}_{\text{}\underline{i}})$
. This gives a double complex where each column (for a fixed index of the Koszul complex) is exact. But each line (for a fixed
![]() $\text{}\underline{i}$
non-trivial) is also exact by the previous acyclicity, and thus we have the following bottom right square,
$\text{}\underline{i}$
non-trivial) is also exact by the previous acyclicity, and thus we have the following bottom right square,

which proves that
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D705}}$
is surjective.◻
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D705}}$
is surjective.◻
Proposition 9.10. Write
![]() $\operatorname{Spm}(B)={\mathcal{W}}(w)$
. Then the
$\operatorname{Spm}(B)={\mathcal{W}}(w)$
. Then the
![]() $B$
-module
$B$
-module
is projective. Moreover, for every
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}(w)$
, the specialization map,
$\unicode[STIX]{x1D705}\in {\mathcal{W}}(w)$
, the specialization map,
is surjective.
Proof. We can identify the
![]() $B$
-module,
$B$
-module,
with
![]() $(M_{v,w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\text{cusp}}\otimes _{A[1/p]}B(-\unicode[STIX]{x1D705}^{\text{un}}))^{B_{n}}$
. But now
$(M_{v,w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\text{cusp}}\otimes _{A[1/p]}B(-\unicode[STIX]{x1D705}^{\text{un}}))^{B_{n}}$
. But now
![]() $B_{n}$
is a finite group, and
$B_{n}$
is a finite group, and
![]() $B$
is of characteristic zero, thus
$B$
is of characteristic zero, thus
![]() $M^{\prime }$
is a direct factor in a projective
$M^{\prime }$
is a direct factor in a projective
![]() $B$
-module, and is thus surjective. Moreover, as
$B$
-module, and is thus surjective. Moreover, as
![]() $B_{n}$
is finite, the (higher) group cohomology vanishes, and the specialization map remains surjective.◻
$B_{n}$
is finite, the (higher) group cohomology vanishes, and the specialization map remains surjective.◻
9.4 Types
Let
![]() $K_{f}^{p}$
be a compact open subgroup of
$K_{f}^{p}$
be a compact open subgroup of
![]() $G(\mathbb{A}_{f}^{p})$
. Let
$G(\mathbb{A}_{f}^{p})$
. Let
![]() $K_{f}=K_{f}^{p}I$
where
$K_{f}=K_{f}^{p}I$
where
![]() $I\subset G(\mathbb{Q}_{p})$
is the Iwahori subgroup. Fix
$I\subset G(\mathbb{Q}_{p})$
is the Iwahori subgroup. Fix
![]() $(J,V_{J})$
a complex continuous irreducible representation of
$(J,V_{J})$
a complex continuous irreducible representation of
![]() $K_{f}$
, trivial at
$K_{f}$
, trivial at
![]() $p$
and outside a level
$p$
and outside a level
![]() $N$
, it is of finite dimension and finite image, and thus defined over a number field. Denote by
$N$
, it is of finite dimension and finite image, and thus defined over a number field. Denote by
![]() $K^{0}\subset K_{f}$
its Kernel.
$K^{0}\subset K_{f}$
its Kernel.
Definition 9.11. The space of Picard modular forms of weight
![]() $\unicode[STIX]{x1D705}$
,
$\unicode[STIX]{x1D705}$
,
![]() $v$
-overconvergent,
$v$
-overconvergent,
![]() $w$
-analytic, of type
$w$
-analytic, of type
![]() $(K_{f},J)$
is
$(K_{f},J)$
is
The space of overconvergent locally analytic Picard modular forms of weight
![]() $\unicode[STIX]{x1D705}$
and type
$\unicode[STIX]{x1D705}$
and type
![]() $(K_{f},J)$
is then
$(K_{f},J)$
is then
Remark 9.12. In the beginning of this section we made the assumption that the level
![]() $\unicode[STIX]{x1D6E4}$
, outside
$\unicode[STIX]{x1D6E4}$
, outside
![]() $p$
, is big enough (‘neat’). But using the previous definition we can get rid of this assumption by taking
$p$
, is big enough (‘neat’). But using the previous definition we can get rid of this assumption by taking
![]() $K_{f}^{p}$
big enough to have the neatness assumption, and take
$K_{f}^{p}$
big enough to have the neatness assumption, and take
![]() $J$
the trivial representation to descend our families for any level outside
$J$
the trivial representation to descend our families for any level outside
![]() $p$
, as the following proposition shows.
$p$
, as the following proposition shows.
Proposition 9.13. The space
is a projective
![]() ${\mathcal{O}}_{{\mathcal{W}}(w)}$
-module, and the specialization map is surjective.
${\mathcal{O}}_{{\mathcal{W}}(w)}$
-module, and the specialization map is surjective.
Proof. Suppose
![]() $K(N)=K\subset K^{0}=\operatorname{Ker}(J)$
is neat (outside
$K(N)=K\subset K^{0}=\operatorname{Ker}(J)$
is neat (outside
![]() $p$
, up to enlarging it). Then we have shown that, in level
$p$
, up to enlarging it). Then we have shown that, in level
![]() $K$
,
$K$
,
is projective, and that the corresponding specialization map is surjective. We can thus twist the
![]() $K_{f}/K$
action by
$K_{f}/K$
action by
![]() $V_{J}^{\ast }$
and take the invariants over
$V_{J}^{\ast }$
and take the invariants over
![]() $J$
; as
$J$
; as
![]() $K_{f}/K$
is finite, the space is a direct factor inside
$K_{f}/K$
is finite, the space is a direct factor inside
![]() $H^{0}({\mathcal{X}}(v)\times {\mathcal{W}}(w),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}^{\text{un}}\dagger }(-D))\otimes V_{J}^{\ast }$
and higher cohomology vanishes.◻
$H^{0}({\mathcal{X}}(v)\times {\mathcal{W}}(w),\unicode[STIX]{x1D714}_{w}^{\unicode[STIX]{x1D705}^{\text{un}}\dagger }(-D))\otimes V_{J}^{\ast }$
and higher cohomology vanishes.◻
Remark 9.14. The same argument applies when
![]() $p$
splits in
$p$
splits in
![]() $E$
, for the spaces of overconvergent modular forms defined in [Reference BrascaBra16, Reference Andreatta, Iovita and PilloniAIP15]. In particular we can construct families of Picard modular forms with fixed type when
$E$
, for the spaces of overconvergent modular forms defined in [Reference BrascaBra16, Reference Andreatta, Iovita and PilloniAIP15]. In particular we can construct families of Picard modular forms with fixed type when
![]() $p$
is unramified.
$p$
is unramified.
9.5 Eigenvarieties
Theorem 9.15. Let
![]() $p$
be a prime number, unramified in
$p$
be a prime number, unramified in
![]() $E$
. Let
$E$
. Let
![]() ${\mathcal{W}}$
be the
${\mathcal{W}}$
be the
![]() $p$
-adic weight space of
$p$
-adic weight space of
![]() $U(2,1)$
. When
$U(2,1)$
. When
![]() $p$
is inert, it is defined in § 3, and when
$p$
is inert, it is defined in § 3, and when
![]() $p$
splits it is a disjoint union of three-dimensional balls over
$p$
splits it is a disjoint union of three-dimensional balls over
![]() $\mathbb{Q}_{p}$
. Fix
$\mathbb{Q}_{p}$
. Fix
![]() $(K_{J},J)$
a type outside
$(K_{J},J)$
a type outside
![]() $p$
,
$p$
,
![]() $K\subset \operatorname{Ker}J$
a neat level outside
$K\subset \operatorname{Ker}J$
a neat level outside
![]() $p$
, and let
$p$
, and let
![]() $S$
be the set of places where
$S$
be the set of places where
![]() $K$
is not compact maximal or
$K$
is not compact maximal or
![]() $p$
. There exists an equidimensional, of dimension
$p$
. There exists an equidimensional, of dimension
![]() $3$
, eigenvariety
$3$
, eigenvariety
![]() ${\mathcal{E}}$
and a locally finite map,
${\mathcal{E}}$
and a locally finite map,
such that for any
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}$
,
$\unicode[STIX]{x1D705}\in {\mathcal{W}}$
,
![]() $w^{-1}(\unicode[STIX]{x1D705})$
is in bijection with eigensystems for
$w^{-1}(\unicode[STIX]{x1D705})$
is in bijection with eigensystems for
![]() $\mathbb{T}^{S}\otimes _{\mathbb{Z}}{\mathcal{A}}(p)$
acting on the space of overconvergent, locally analytic, modular forms of weight
$\mathbb{T}^{S}\otimes _{\mathbb{Z}}{\mathcal{A}}(p)$
acting on the space of overconvergent, locally analytic, modular forms of weight
![]() $\unicode[STIX]{x1D705}$
and type-level
$\unicode[STIX]{x1D705}$
and type-level
![]() $(K_{J},J)$
(and Iwahori level at
$(K_{J},J)$
(and Iwahori level at
![]() $p$
), finite slope for
$p$
), finite slope for
![]() $U_{p}$
.
$U_{p}$
.
Proof. If
![]() $p$
is split this is a particular case of the main result of [Reference BrascaBra16] (taking into account the previous remark and the normalization of the Hecke operators). If
$p$
is split this is a particular case of the main result of [Reference BrascaBra16] (taking into account the previous remark and the normalization of the Hecke operators). If
![]() $p$
is inert, this is a consequence of Buzzard and Coleman’s machinery [Reference BuzzardBuz07] using for all compatible
$p$
is inert, this is a consequence of Buzzard and Coleman’s machinery [Reference BuzzardBuz07] using for all compatible
![]() $v,w$
$v,w$
![]() $({\mathcal{W}}(w),M_{\text{cusp},v,w}^{(K,J),\unicode[STIX]{x1D705}^{\text{un}}\dagger },U_{p},{\mathcal{H}}^{Np}\otimes {\mathcal{A}}(p))$
and gluing along
$({\mathcal{W}}(w),M_{\text{cusp},v,w}^{(K,J),\unicode[STIX]{x1D705}^{\text{un}}\dagger },U_{p},{\mathcal{H}}^{Np}\otimes {\mathcal{A}}(p))$
and gluing along
![]() $v,w$
.◻
$v,w$
.◻
9.6 Convention on weights
As in [Reference Bellaïche and ChenevierBC04], we set as convention the Hodge–Tate weight of the cyclotomic character to be
![]() $-$
1. Fix an isomorphism
$-$
1. Fix an isomorphism
![]() $\mathbb{C}\simeq \overline{\mathbb{Q}_{p}}$
compatible with the inclusions
$\mathbb{C}\simeq \overline{\mathbb{Q}_{p}}$
compatible with the inclusions
![]() $\overline{E}\subset \mathbb{C}$
that extend
$\overline{E}\subset \mathbb{C}$
that extend
![]() $\unicode[STIX]{x1D70F}_{\infty }$
and denote by
$\unicode[STIX]{x1D70F}_{\infty }$
and denote by
![]() $\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
the
$\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70F}}$
the
![]() $p$
-adic places at
$p$
-adic places at
![]() $p$
inert corresponding to
$p$
inert corresponding to
![]() $\unicode[STIX]{x1D70F}_{\infty },c\unicode[STIX]{x1D70F}_{\infty }$
. If
$\unicode[STIX]{x1D70F}_{\infty },c\unicode[STIX]{x1D70F}_{\infty }$
. If
![]() $p$
is split, we will instead call
$p$
is split, we will instead call
![]() $v,\overline{v}$
the places corresponding to
$v,\overline{v}$
the places corresponding to
![]() $\unicode[STIX]{x1D70F}_{\infty },c\unicode[STIX]{x1D70F}_{\infty }$
, but in this section we focus on
$\unicode[STIX]{x1D70F}_{\infty },c\unicode[STIX]{x1D70F}_{\infty }$
, but in this section we focus on
![]() $p$
inert, even if a similar result hold with
$p$
inert, even if a similar result hold with
![]() $v,\overline{v}$
.
$v,\overline{v}$
.
Let us recall the different parameters that are associated to an algebraic automorphic representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $GU(2,1)$
that we will need, following partly [Reference SkinnerSki12]. There is
$GU(2,1)$
that we will need, following partly [Reference SkinnerSki12]. There is
![]() $\unicode[STIX]{x1D706}=((\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D706}_{3}),\unicode[STIX]{x1D706}_{0})$
, the Harish-Chandra parameter, there is
$\unicode[STIX]{x1D706}=((\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},\unicode[STIX]{x1D706}_{3}),\unicode[STIX]{x1D706}_{0})$
, the Harish-Chandra parameter, there is
![]() $c=((c_{1},c_{2},c_{3}),c_{0})$
, the highest weight of the algebraic representation which has the same infinitesimal character as
$c=((c_{1},c_{2},c_{3}),c_{0})$
, the highest weight of the algebraic representation which has the same infinitesimal character as
![]() $\unicode[STIX]{x1D70B}_{\infty }$
in the discrete series case and
$\unicode[STIX]{x1D70B}_{\infty }$
in the discrete series case and
![]() $(c_{0},c_{0}^{\prime })$
is the parameter at infinity of
$(c_{0},c_{0}^{\prime })$
is the parameter at infinity of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{c}$
the conjugate of the central character of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{c}$
the conjugate of the central character of
![]() $\unicode[STIX]{x1D70B}$
. There is
$\unicode[STIX]{x1D70B}$
. There is
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})$
the classical weight such that
$\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})$
the classical weight such that
![]() $\unicode[STIX]{x1D70B}_{f}$
appears in
$\unicode[STIX]{x1D70B}_{f}$
appears in
![]() $H^{0}(X_{K},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
(if it exists) and there are the Hodge–Tate weights
$H^{0}(X_{K},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
(if it exists) and there are the Hodge–Tate weights
![]() $((h_{1}^{\unicode[STIX]{x1D70F}},h_{2}^{\unicode[STIX]{x1D70F}},h_{3}^{\unicode[STIX]{x1D70F}}),(h_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},h_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},h_{3}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}))$
of the Galois representation of
$((h_{1}^{\unicode[STIX]{x1D70F}},h_{2}^{\unicode[STIX]{x1D70F}},h_{3}^{\unicode[STIX]{x1D70F}}),(h_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},h_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},h_{3}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}))$
of the Galois representation of
![]() $G_{E}$
associated to
$G_{E}$
associated to
![]() $\unicode[STIX]{x1D70B}$
by Blasius and Rogawski [Reference Blasius and RogawskiBR92] or Skinner [Reference SkinnerSki12]. Let us explain how they are related in the case of discrete series.
$\unicode[STIX]{x1D70B}$
by Blasius and Rogawski [Reference Blasius and RogawskiBR92] or Skinner [Reference SkinnerSki12]. Let us explain how they are related in the case of discrete series.
First denote by
![]() $\unicode[STIX]{x1D70C}_{n}$
the half-sum of the positive non-compact roots and
$\unicode[STIX]{x1D70C}_{n}$
the half-sum of the positive non-compact roots and
![]() $\unicode[STIX]{x1D70C}_{c}$
the half-sum of the positive compact roots (see [Reference GoldringGol14, § 5.3]). We have then, for
$\unicode[STIX]{x1D70C}_{c}$
the half-sum of the positive compact roots (see [Reference GoldringGol14, § 5.3]). We have then, for
![]() $i\geqslant 1,\unicode[STIX]{x1D706}_{i}=(c+\unicode[STIX]{x1D70C}_{n}+\unicode[STIX]{x1D70C}_{c})_{i}$
, and
$i\geqslant 1,\unicode[STIX]{x1D706}_{i}=(c+\unicode[STIX]{x1D70C}_{n}+\unicode[STIX]{x1D70C}_{c})_{i}$
, and
![]() $(c_{0},c_{0}^{\prime })$
is the infinite weight of the dual of the central character. The calculation of Harris and Goldring gives
$(c_{0},c_{0}^{\prime })$
is the infinite weight of the dual of the central character. The calculation of Harris and Goldring gives
![]() $(-k_{3},k_{1},k_{2})=\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C}_{n}-\unicode[STIX]{x1D70C}_{c}$
(forgetting the
$(-k_{3},k_{1},k_{2})=\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C}_{n}-\unicode[STIX]{x1D70C}_{c}$
(forgetting the
![]() $\unicode[STIX]{x1D706}_{0}$
factor here, it is because we only considered three parameters in the weight space). The Hodge–Tate weights of the Galois representation associated to
$\unicode[STIX]{x1D706}_{0}$
factor here, it is because we only considered three parameters in the weight space). The Hodge–Tate weights of the Galois representation associated to
![]() $\unicode[STIX]{x1D70B}$
depends of course on the normalization of the correspondence, but take the one of Skinner [Reference SkinnerSki12, § 4.2, 4.3 and after Theorem 10], we get
$\unicode[STIX]{x1D70B}$
depends of course on the normalization of the correspondence, but take the one of Skinner [Reference SkinnerSki12, § 4.2, 4.3 and after Theorem 10], we get
Remark 9.16. Let
![]() $f\in H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
be a classical form. To
$f\in H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
be a classical form. To
![]() $f$
is associated
$f$
is associated
![]() $\unicode[STIX]{x1D711}_{f}$
an automorphic form, with equivariant Hecke action, cf. Proposition 2.6, and thus an autormorphic representation
$\unicode[STIX]{x1D711}_{f}$
an automorphic form, with equivariant Hecke action, cf. Proposition 2.6, and thus an autormorphic representation
![]() $\unicode[STIX]{x1D70B}_{f}$
.
$\unicode[STIX]{x1D70B}_{f}$
.
Before going further, let us remark that a (algebraic) representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $GU(2,1)$
is equivalent to a pair
$GU(2,1)$
is equivalent to a pair
![]() $(\unicode[STIX]{x1D70B}^{0},\unicode[STIX]{x1D713})$
of
$(\unicode[STIX]{x1D70B}^{0},\unicode[STIX]{x1D713})$
of
![]() $\unicode[STIX]{x1D70B}^{0}$
a (algebraic) automorphic representation of
$\unicode[STIX]{x1D70B}^{0}$
a (algebraic) automorphic representation of
![]() $U(2,1)$
(the restriction of
$U(2,1)$
(the restriction of
![]() $\unicode[STIX]{x1D70B}$
) and a (algebraic) Hecke character of
$\unicode[STIX]{x1D70B}$
) and a (algebraic) Hecke character of
![]() $GU(1)=\text{Res}_{E/\mathbb{Q}}\mathbb{G}_{m}$
(the central character of
$GU(1)=\text{Res}_{E/\mathbb{Q}}\mathbb{G}_{m}$
(the central character of
![]() $\unicode[STIX]{x1D70B}$
) which extend the central character of
$\unicode[STIX]{x1D70B}$
) which extend the central character of
![]() $\unicode[STIX]{x1D70B}^{0}$
(see § 10.4). To an algebraic (nice)
$\unicode[STIX]{x1D70B}^{0}$
(see § 10.4). To an algebraic (nice)
![]() $\unicode[STIX]{x1D70B}$
is associated a (non-necessarily polarized) Galois representation
$\unicode[STIX]{x1D70B}$
is associated a (non-necessarily polarized) Galois representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
, but also a pair
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
, but also a pair
![]() $\unicode[STIX]{x1D70B}^{0},\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70B}}$
, and to
$\unicode[STIX]{x1D70B}^{0},\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D70B}}$
, and to
![]() $\unicode[STIX]{x1D70B}^{0}$
is associated a polarized Galois representation, which is what we will need. Thus from Skinner’s normalization, removing the central character of
$\unicode[STIX]{x1D70B}^{0}$
is associated a polarized Galois representation, which is what we will need. Thus from Skinner’s normalization, removing the central character of
![]() $\unicode[STIX]{x1D70B}$
, we get the following proposition (we could also directly use [Reference Chenevier and HarrisCH13]).
$\unicode[STIX]{x1D70B}$
, we get the following proposition (we could also directly use [Reference Chenevier and HarrisCH13]).
Proposition 9.17. Let
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})\in \mathbb{Z}^{3}$
and
$\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})\in \mathbb{Z}^{3}$
and
![]() $f=H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
which is an eigenvector for the Hecke operators outside p. Write
$f=H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
which is an eigenvector for the Hecke operators outside p. Write
![]() $|k|=k_{1}+k_{2}+k_{3}$
. Let
$|k|=k_{1}+k_{2}+k_{3}$
. Let
![]() $\unicode[STIX]{x1D70B}$
be the automorphic representation corresponding to
$\unicode[STIX]{x1D70B}$
be the automorphic representation corresponding to
![]() $f$
(i.e. a irreducible factor in the representation generated by
$f$
(i.e. a irreducible factor in the representation generated by
![]() $\unicode[STIX]{x1D6F7}_{f}$
of § 2.2).
$\unicode[STIX]{x1D6F7}_{f}$
of § 2.2).
Suppose
![]() $\unicode[STIX]{x1D70B}_{\infty }$
is a (regular) discrete series of Harish-Chandra parameter
$\unicode[STIX]{x1D70B}_{\infty }$
is a (regular) discrete series of Harish-Chandra parameter
![]() $\unicode[STIX]{x1D706}$
, then
$\unicode[STIX]{x1D706}$
, then
(see [Reference GoldringGol14, § 5]) with
![]() $k_{1}\geqslant k_{2}>2-k_{3}$
. Denote by
$k_{1}\geqslant k_{2}>2-k_{3}$
. Denote by
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
the
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
the
![]() $p$
-adic Galois representation associated to
$p$
-adic Galois representation associated to
![]() $\unicode[STIX]{x1D70B}$
by Skinner [Reference SkinnerSki12]. Then
$\unicode[STIX]{x1D70B}$
by Skinner [Reference SkinnerSki12]. Then
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
satisfies the following essentially self-polarization,
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
satisfies the following essentially self-polarization,
where
![]() $\unicode[STIX]{x1D700}$
is the cyclotomic character,
$\unicode[STIX]{x1D700}$
is the cyclotomic character,
![]() $\unicode[STIX]{x1D713}$
is a finite Hecke character, and if
$\unicode[STIX]{x1D713}$
is a finite Hecke character, and if
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
denotes the central character of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
denotes the central character of
![]() $\unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D70B}$
,
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{c}$
is of the form
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}^{c}$
is of the form
![]() $N^{-|k|}\unicode[STIX]{x1D713}$
.
$N^{-|k|}\unicode[STIX]{x1D713}$
.
Then, the
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
are
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
are
and the
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-Hodge–Tate weights are
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-Hodge–Tate weights are
To
![]() $\unicode[STIX]{x1D70B}^{0}=\unicode[STIX]{x1D70B}_{|U(2,1)}$
is associated a polarized continuous Galois representation
$\unicode[STIX]{x1D70B}^{0}=\unicode[STIX]{x1D70B}_{|U(2,1)}$
is associated a polarized continuous Galois representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
verifying
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
verifying
of
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights
![]() $(1-k_{3},k_{2}-1,k_{1})$
and (thus)
$(1-k_{3},k_{2}-1,k_{1})$
and (thus)
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-Hodge–Tate weights
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-Hodge–Tate weights
![]() $(-k_{1},1-k_{2},k_{3}-1)$
.
$(-k_{1},1-k_{2},k_{3}-1)$
.
Proof. The calculation of
![]() $\unicode[STIX]{x1D706}$
in terms of
$\unicode[STIX]{x1D706}$
in terms of
![]() $\unicode[STIX]{x1D705}$
is exactly [Reference GoldringGol14, Theorem 5.5.1]. Remark also that we can calculate in terms of
$\unicode[STIX]{x1D705}$
is exactly [Reference GoldringGol14, Theorem 5.5.1]. Remark also that we can calculate in terms of
![]() $\unicode[STIX]{x1D705}$
which are the discrete series by Harish-Chandra theorem [Reference KnappKna16, Theorem 6.6], and we find
$\unicode[STIX]{x1D705}$
which are the discrete series by Harish-Chandra theorem [Reference KnappKna16, Theorem 6.6], and we find
![]() $k_{1}\geqslant k_{2}>2-k_{3}$
. Thus, the calculation of the Hodge–Tate weights of the Galois representations associated to
$k_{1}\geqslant k_{2}>2-k_{3}$
. Thus, the calculation of the Hodge–Tate weights of the Galois representations associated to
![]() $\unicode[STIX]{x1D70B}$
are [Reference SkinnerSki12, Theorem 10], with the previous calculation of
$\unicode[STIX]{x1D70B}$
are [Reference SkinnerSki12, Theorem 10], with the previous calculation of
![]() $c$
in terms of
$c$
in terms of
![]() $\unicode[STIX]{x1D706}$
. The representation
$\unicode[STIX]{x1D706}$
. The representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
is given by
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
is given by
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}\unicode[STIX]{x1D70C}_{\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}}}^{-1}(1)$
.◻
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}\unicode[STIX]{x1D70C}_{\overline{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}}}^{-1}(1)$
.◻
Remark 9.18. In terms of the
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
, discrete series correspond to
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
, discrete series correspond to
![]() $h_{1}<h_{2}<h_{3}$
. All of this is coherent with the Bernstein–Gelfand–Gelfand (BGG) decomposition, see for example [Reference LanLan12, (2.3)], for
$h_{1}<h_{2}<h_{3}$
. All of this is coherent with the Bernstein–Gelfand–Gelfand (BGG) decomposition, see for example [Reference LanLan12, (2.3)], for
![]() $\text{}\underline{c}=\unicode[STIX]{x1D707}=(a,b,c)$
a highest weight representation of
$\text{}\underline{c}=\unicode[STIX]{x1D707}=(a,b,c)$
a highest weight representation of
![]() $G$
,
$G$
,
Denote by
![]() ${\mathcal{Z}}\subset {\mathcal{E}}$
the set of characters corresponding to regular (i.e.
${\mathcal{Z}}\subset {\mathcal{E}}$
the set of characters corresponding to regular (i.e.
![]() $w_{2}(z)\leqslant w_{1}(z)<-2-w_{3}(z)\in \mathbb{Z}^{3}$
) classical modular forms (recall that if
$w_{2}(z)\leqslant w_{1}(z)<-2-w_{3}(z)\in \mathbb{Z}^{3}$
) classical modular forms (recall that if
![]() $f$
is classical of weight
$f$
is classical of weight
![]() $(k_{1},k_{2},k_{3})$
,
$(k_{1},k_{2},k_{3})$
,
![]() $w(f)=(-k_{2},-k_{1},-k_{3})$
). For each
$w(f)=(-k_{2},-k_{1},-k_{3})$
). For each
![]() $z\in {\mathcal{Z}}$
, there exists
$z\in {\mathcal{Z}}$
, there exists
![]() $f$
a classical form, which determines
$f$
a classical form, which determines
![]() $\unicode[STIX]{x1D6F1}$
an automorphic representation of
$\unicode[STIX]{x1D6F1}$
an automorphic representation of
![]() $GU(2,1)$
(generated by
$GU(2,1)$
(generated by
![]() $\unicode[STIX]{x1D6F7}_{f}$
defined in § 2.2). Such a
$\unicode[STIX]{x1D6F7}_{f}$
defined in § 2.2). Such a
![]() $\unicode[STIX]{x1D6F1}$
corresponds to a packet, to which by the work of Blasius and Rogawski [Reference Blasius and RogawskiBR92, Theorem 1.9.1] (see also for generalization to higher-dimension unitary groups and local global compatibilities the work of many authors, in particular [Reference BellaïcheBel06a, Reference Chenevier and HarrisCH13, Reference SkinnerSki12, Reference Barnet-Lamb, Geraghty, Harris and TaylorBGHT11]) is associated a number field
$\unicode[STIX]{x1D6F1}$
corresponds to a packet, to which by the work of Blasius and Rogawski [Reference Blasius and RogawskiBR92, Theorem 1.9.1] (see also for generalization to higher-dimension unitary groups and local global compatibilities the work of many authors, in particular [Reference BellaïcheBel06a, Reference Chenevier and HarrisCH13, Reference SkinnerSki12, Reference Barnet-Lamb, Geraghty, Harris and TaylorBGHT11]) is associated a number field
![]() $E_{z}$
, and compatible system of Galois representations,
$E_{z}$
, and compatible system of Galois representations,
satisfying local global compatibilities (see for example [Reference SkinnerSki12], where the association is normalized by the previous proposition (the Hodge–Tate weight of the cyclotomic character being
![]() $-1$
) and the previous proposition for a normalization suitable to our needs). In particular, denote
$-1$
) and the previous proposition for a normalization suitable to our needs). In particular, denote
![]() $S$
the set of prime of
$S$
the set of prime of
![]() $E$
where
$E$
where
![]() $\operatorname{Ker}(J)I$
is not hyperspecial, and if
$\operatorname{Ker}(J)I$
is not hyperspecial, and if
![]() $\ell$
a prime under
$\ell$
a prime under
![]() $\unicode[STIX]{x1D706}$
, denote by
$\unicode[STIX]{x1D706}$
, denote by
![]() $S_{\ell }$
the set of places of
$S_{\ell }$
the set of places of
![]() $E$
dividing
$E$
dividing
![]() $\unicode[STIX]{x1D706}$
. Then
$\unicode[STIX]{x1D706}$
. Then
![]() $\unicode[STIX]{x1D70C}_{z,\unicode[STIX]{x1D706}}$
, is unramified outside
$\unicode[STIX]{x1D70C}_{z,\unicode[STIX]{x1D706}}$
, is unramified outside
![]() $SS_{\ell }$
.
$SS_{\ell }$
.
We have the classical proposition, which is one reason why eigenvarieties are so useful (see for example [Reference Bellaïche and ChenevierBC09] proposition 7.5.4),
Proposition 9.19. Let
![]() $p$
be unramified in
$p$
be unramified in
![]() $E$
. To each
$E$
. To each
![]() $z\in {\mathcal{Z}}$
, denote by
$z\in {\mathcal{Z}}$
, denote by
![]() $\unicode[STIX]{x1D70C}_{z}$
the (
$\unicode[STIX]{x1D70C}_{z}$
the (
![]() $p$
-adic) polarized representation associated to
$p$
-adic) polarized representation associated to
![]() $z$
by Proposition 9.17. There exists a unique continuous pseudocharacter
$z$
by Proposition 9.17. There exists a unique continuous pseudocharacter
such that for all
![]() $z\in {\mathcal{Z}}$
,
$z\in {\mathcal{Z}}$
,
![]() $T_{z}=\operatorname{tr}(\unicode[STIX]{x1D70C}_{z})$
. Moreover the pseudocharacter
$T_{z}=\operatorname{tr}(\unicode[STIX]{x1D70C}_{z})$
. Moreover the pseudocharacter
![]() $T$
satisfies
$T$
satisfies
![]() $T^{\bot }=T$
, where
$T^{\bot }=T$
, where
![]() $T^{\bot }(g)=T((\unicode[STIX]{x1D70F}g\unicode[STIX]{x1D70F})^{-1})$
for all
$T^{\bot }(g)=T((\unicode[STIX]{x1D70F}g\unicode[STIX]{x1D70F})^{-1})$
for all
![]() $g\in G_{E}$
.
$g\in G_{E}$
.
Proof.
![]() ${\mathcal{Z}}$
is dense in
${\mathcal{Z}}$
is dense in
![]() ${\mathcal{E}}$
by density of very regular weights in
${\mathcal{E}}$
by density of very regular weights in
![]() ${\mathcal{W}}$
and the two classicity results (8.16 and 8.17). We only need [Reference ChenevierChe04, Proposition 7.1] to finish, the hypothesis
${\mathcal{W}}$
and the two classicity results (8.16 and 8.17). We only need [Reference ChenevierChe04, Proposition 7.1] to finish, the hypothesis
![]() $(H)$
there being verified by the Frobenius classes in
$(H)$
there being verified by the Frobenius classes in
![]() $S$
. The polarization assumption follows from the case of
$S$
. The polarization assumption follows from the case of
![]() $z\in {\mathcal{Z}}$
by density.◻
$z\in {\mathcal{Z}}$
by density.◻
10 Application to a conjecture of Bloch and Kato
Let
![]() $E$
be a quadratic imaginary field, and fix an algebraic Hecke character,
$E$
be a quadratic imaginary field, and fix an algebraic Hecke character,
such that, for all
![]() $z\in \mathbb{C}^{\times },\unicode[STIX]{x1D712}_{\infty }(z)=z^{a}\overline{z}^{b}$
, for some
$z\in \mathbb{C}^{\times },\unicode[STIX]{x1D712}_{\infty }(z)=z^{a}\overline{z}^{b}$
, for some
![]() $a,b\in \mathbb{Z}$
. Call
$a,b\in \mathbb{Z}$
. Call
![]() $w=-a-b$
the motivic weight of
$w=-a-b$
the motivic weight of
![]() $\unicode[STIX]{x1D712}$
. Denote by
$\unicode[STIX]{x1D712}$
. Denote by
![]() $\unicode[STIX]{x1D712}_{p}:G_{E}\longrightarrow K$
, where
$\unicode[STIX]{x1D712}_{p}:G_{E}\longrightarrow K$
, where
![]() $K$
is a finite extension of
$K$
is a finite extension of
![]() $\mathbb{Q}_{p}$
, the
$\mathbb{Q}_{p}$
, the
![]() $p$
-adic realization of
$p$
-adic realization of
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
We are interested in the Selmer group
![]() $H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
, which parameterizes extensions
$H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
, which parameterizes extensions
![]() $U$
,
$U$
,
which have good reduction everywhere ([Reference Bloch and KatoBK90, Reference Fontaine and Perrin-RiouFP94], [Reference Bellaïche and ChenevierBC09, ch. 5] and the introduction of this article).
Associated to
![]() $\unicode[STIX]{x1D712}$
there is also an
$\unicode[STIX]{x1D712}$
there is also an
![]() $L$
-function
$L$
-function
![]() $L(\unicode[STIX]{x1D712},s)$
, where
$L(\unicode[STIX]{x1D712},s)$
, where
![]() $s$
is a complex variable, which is a meromorphic function on
$s$
is a complex variable, which is a meromorphic function on
![]() $\mathbb{C}$
, which satisfies a functional equation,
$\mathbb{C}$
, which satisfies a functional equation,
where
![]() $\unicode[STIX]{x1D712}^{\ast }$
is the contragredient representation,
$\unicode[STIX]{x1D712}^{\ast }$
is the contragredient representation,
![]() $\unicode[STIX]{x1D6EC}(V,s)$
is the completed
$\unicode[STIX]{x1D6EC}(V,s)$
is the completed
![]() $L$
-function of
$L$
-function of
![]() $V$
, a product of
$V$
, a product of
![]() $L(V,s)$
by a finite number of
$L(V,s)$
by a finite number of
![]() $\unicode[STIX]{x1D6E4}$
-factors.
$\unicode[STIX]{x1D6E4}$
-factors.
The conjecture of Bloch and Kato (more precisely a particular case of) in this case is the following equality,
The conjecture is more generally for a Galois representation
![]() $\unicode[STIX]{x1D70C}$
of the Galois group
$\unicode[STIX]{x1D70C}$
of the Galois group
![]() $G_{F}$
of a number field, but in the previous case we have a special case by the theorem of Rubin on Iwasawa’s main conjecture for CM elliptic curves,
$G_{F}$
of a number field, but in the previous case we have a special case by the theorem of Rubin on Iwasawa’s main conjecture for CM elliptic curves,
Conjecture 10.1. Suppose that
![]() $\unicode[STIX]{x1D712}$
is polarized and of weight
$\unicode[STIX]{x1D712}$
is polarized and of weight
![]() $-1$
, i.e.
$-1$
, i.e.
where
![]() $\unicode[STIX]{x1D712}^{\bot }(z)=\unicode[STIX]{x1D712}^{-1}(czc)$
, and
$\unicode[STIX]{x1D712}^{\bot }(z)=\unicode[STIX]{x1D712}^{-1}(czc)$
, and
![]() $c\in G_{\mathbb{Q}}$
induces the complex conjugation in
$c\in G_{\mathbb{Q}}$
induces the complex conjugation in
![]() $E$
. Then
$E$
. Then
Remark 10.2. Under the previous polarization assumption, we have
![]() $L(\unicode[STIX]{x1D712}^{\ast }(1),s)=L(\unicode[STIX]{x1D712},s)$
. The previous conjecture is mainly known by the work of Rubin [Reference RubinRub91] if
$L(\unicode[STIX]{x1D712}^{\ast }(1),s)=L(\unicode[STIX]{x1D712},s)$
. The previous conjecture is mainly known by the work of Rubin [Reference RubinRub91] if
![]() $p\!\not |~|{\mathcal{O}}_{E}^{\times }|$
.
$p\!\not |~|{\mathcal{O}}_{E}^{\times }|$
.
In the rest of the article, we will prove the following theorem.
Theorem 10.3. Suppose that
![]() $\unicode[STIX]{x1D712}$
is polarized and of weight
$\unicode[STIX]{x1D712}$
is polarized and of weight
![]() $-1$
, i.e.
$-1$
, i.e.
where
![]() $\unicode[STIX]{x1D712}^{\bot }(z)=\unicode[STIX]{x1D712}^{-1}(czc)$
, and
$\unicode[STIX]{x1D712}^{\bot }(z)=\unicode[STIX]{x1D712}^{-1}(czc)$
, and
![]() $c\in G_{\mathbb{Q}}$
induces the complex conjugation in
$c\in G_{\mathbb{Q}}$
induces the complex conjugation in
![]() $E$
. Suppose that
$E$
. Suppose that
![]() $p$
is unramified in
$p$
is unramified in
![]() $E$
and that
$E$
and that
![]() $p\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
. If
$p\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
. If
![]() $p$
is inert suppose, moreover, that
$p$
is inert suppose, moreover, that
![]() $p\neq 2$
. Then
$p\neq 2$
. Then
Remark 10.4. The same result but for
![]() $\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)$
odd (and strictly speaking for
$\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)$
odd (and strictly speaking for
![]() $p$
split) is proved in [Reference Bellaïche and ChenevierBC04], and using the same method with the eigenvariety for the group
$p$
split) is proved in [Reference Bellaïche and ChenevierBC04], and using the same method with the eigenvariety for the group
![]() $U(3)$
.
$U(3)$
.
Definition 10.5. To stick with notations of [Reference Bellaïche and ChenevierBC04], denote by
![]() $k$
the positive odd integer such that
$k$
the positive odd integer such that
![]() $\unicode[STIX]{x1D712}_{\infty }(z)=z^{(k+1)/2}\overline{z}^{(1-k)/2}$
(i.e.
$\unicode[STIX]{x1D712}_{\infty }(z)=z^{(k+1)/2}\overline{z}^{(1-k)/2}$
(i.e.
![]() $k=2a-1=1-2b$
). We suppose
$k=2a-1=1-2b$
). We suppose
![]() $k\geqslant 1$
, i.e.
$k\geqslant 1$
, i.e.
![]() $a\geqslant 1$
(which we can always suppose up to changing
$a\geqslant 1$
(which we can always suppose up to changing
![]() $\unicode[STIX]{x1D712}$
by
$\unicode[STIX]{x1D712}$
by
![]() $\unicode[STIX]{x1D712}^{c}$
, which does not change either the
$\unicode[STIX]{x1D712}^{c}$
, which does not change either the
![]() $L$
-function nor the dimension of the Selmer group).
$L$
-function nor the dimension of the Selmer group).
10.1 Endoscopic transfer, after Rogawski
Let
![]() $\unicode[STIX]{x1D712}_{0}=\unicode[STIX]{x1D712}|.|^{-1/2}$
the unitary character as in [Reference Bellaïche and ChenevierBC04]. We will define following Rogawski [Reference RogawskiRog92] an automorphic representation of
$\unicode[STIX]{x1D712}_{0}=\unicode[STIX]{x1D712}|.|^{-1/2}$
the unitary character as in [Reference Bellaïche and ChenevierBC04]. We will define following Rogawski [Reference RogawskiRog92] an automorphic representation of
![]() $U(2,1)$
, by constructing it at each place.
$U(2,1)$
, by constructing it at each place.
10.1.1 If
 $\ell$
is split in
$\ell$
is split in
 $E$
$E$
Write
![]() $\ell =v\overline{v}$
and the choice of say
$\ell =v\overline{v}$
and the choice of say
![]() $v$
induces an isomorphism
$v$
induces an isomorphism
![]() $U(2,1)(\mathbb{Q}_{\ell })\overset{i_{v}}{\simeq }\operatorname{GL}_{3}(\mathbb{Q}_{\ell })$
. Let
$U(2,1)(\mathbb{Q}_{\ell })\overset{i_{v}}{\simeq }\operatorname{GL}_{3}(\mathbb{Q}_{\ell })$
. Let
![]() $P=MN$
be the standard parabolic of
$P=MN$
be the standard parabolic of
![]() $\operatorname{GL}_{3}(\mathbb{Q}_{p})$
with Levi
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
with Levi
![]() $M=\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
. Define
$M=\operatorname{GL}_{2}\times \operatorname{GL}_{1}$
. Define
trivially extended to
![]() $P$
, and denote by
$P$
, and denote by
![]() $\operatorname{ind}-n_{P}^{G}(\widetilde{\unicode[STIX]{x1D712}_{0,\ell }})$
the normalized induction of
$\operatorname{ind}-n_{P}^{G}(\widetilde{\unicode[STIX]{x1D712}_{0,\ell }})$
the normalized induction of
![]() $\widetilde{\unicode[STIX]{x1D712}_{0,\ell }}$
. Then set
$\widetilde{\unicode[STIX]{x1D712}_{0,\ell }}$
. Then set
If
![]() $\unicode[STIX]{x1D712}_{\ell }$
is unramified, then so is
$\unicode[STIX]{x1D712}_{\ell }$
is unramified, then so is
![]() $\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
. Fix in this case
$\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
. Fix in this case
![]() $K_{\ell }$
a maximal compact subgroup of
$K_{\ell }$
a maximal compact subgroup of
![]() $U(2,1)(\mathbb{Q}_{\ell })$
.
$U(2,1)(\mathbb{Q}_{\ell })$
.
10.1.2 If
 $\ell$
is inert or ramified in
$\ell$
is inert or ramified in
 $E$
$E$
In this case write
![]() $T={\mathcal{O}}_{E_{\ell }}^{\times }\times {\mathcal{O}}_{E_{\ell }}^{1}$
the torus of
$T={\mathcal{O}}_{E_{\ell }}^{\times }\times {\mathcal{O}}_{E_{\ell }}^{1}$
the torus of
![]() $U(2,1)(\mathbb{Q}_{\ell })$
, and consider the following character of
$U(2,1)(\mathbb{Q}_{\ell })$
, and consider the following character of
![]() $T$
,
$T$
,
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D712}}_{\ell }:\left(\begin{array}{@{}ccc@{}}a & & \\ & b & \\ & & \overline{a}^{-1}\end{array}\right)\longmapsto \unicode[STIX]{x1D712}_{\ell }(a),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D712}}_{\ell }:\left(\begin{array}{@{}ccc@{}}a & & \\ & b & \\ & & \overline{a}^{-1}\end{array}\right)\longmapsto \unicode[STIX]{x1D712}_{\ell }(a),\end{eqnarray}$$
trivially extended to the Borel subgroup
![]() $B$
of
$B$
of
![]() $U(2,1)(\mathbb{Q}_{\ell })$
. Then the normalized induction
$U(2,1)(\mathbb{Q}_{\ell })$
. Then the normalized induction
![]() $\operatorname{ind}-n_{B}^{U(2,1)(\mathbb{Q}_{\ell })}(\widetilde{\unicode[STIX]{x1D712}_{\ell }})$
has two Jordan–Holder factors, one which is non-tempered that we denote by
$\operatorname{ind}-n_{B}^{U(2,1)(\mathbb{Q}_{\ell })}(\widetilde{\unicode[STIX]{x1D712}_{\ell }})$
has two Jordan–Holder factors, one which is non-tempered that we denote by
![]() $\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
and the other one, which is square integrable, that we denote by
$\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
and the other one, which is square integrable, that we denote by
![]() $\unicode[STIX]{x1D70B}_{\ell }^{2}(\unicode[STIX]{x1D712})$
, see [Reference RogawskiRog92].
$\unicode[STIX]{x1D70B}_{\ell }^{2}(\unicode[STIX]{x1D712})$
, see [Reference RogawskiRog92].
If
![]() $\ell$
is inert and
$\ell$
is inert and
![]() $\unicode[STIX]{x1D712}_{0,\ell }$
is unramified,
$\unicode[STIX]{x1D712}_{0,\ell }$
is unramified,
![]() $\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
is also unramified (Satake) and we can choose
$\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
is also unramified (Satake) and we can choose
![]() $K_{\ell }$
a maximal compact for which
$K_{\ell }$
a maximal compact for which
![]() $\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
has a non-zero fixed vector.
$\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
has a non-zero fixed vector.
If
![]() $\ell$
is ramified and
$\ell$
is ramified and
![]() $\unicode[STIX]{x1D712}_{0,\ell }$
is unramified, there are two conjugacy classes of maximal compact subgroup, but only one of them, denoted
$\unicode[STIX]{x1D712}_{0,\ell }$
is unramified, there are two conjugacy classes of maximal compact subgroup, but only one of them, denoted
![]() $K_{\ell }$
(called very special), verifies that
$K_{\ell }$
(called very special), verifies that
![]() $\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
has a non-zero fixed vector under
$\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})$
has a non-zero fixed vector under
![]() $K_{\ell }$
whereas
$K_{\ell }$
whereas
![]() $\unicode[STIX]{x1D70B}_{\ell }^{2}(\unicode[STIX]{x1D712})$
has none.
$\unicode[STIX]{x1D70B}_{\ell }^{2}(\unicode[STIX]{x1D712})$
has none.
10.1.3 Construction at infinity
As in the inert case, let
![]() $\unicode[STIX]{x1D70B}_{\infty }^{n}(\unicode[STIX]{x1D712})$
be the non-tempered Jordan–Holder factor of
$\unicode[STIX]{x1D70B}_{\infty }^{n}(\unicode[STIX]{x1D712})$
be the non-tempered Jordan–Holder factor of
![]() $\operatorname{ind}-n_{B}^{U(2,1)(\mathbb{R})}(\widetilde{\unicode[STIX]{x1D712}_{\infty }})$
.
$\operatorname{ind}-n_{B}^{U(2,1)(\mathbb{R})}(\widetilde{\unicode[STIX]{x1D712}_{\infty }})$
.
Then we have the following proposition, following Rogawski.
Proposition 10.6 (Rogawski).
Suppose
![]() $a\geqslant 1$
. Recall that
$a\geqslant 1$
. Recall that
![]() $\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)$
is even. Then the representation,
$\operatorname{ord}_{s=0}L(\unicode[STIX]{x1D712},s)$
is even. Then the representation,
is an automorphic representation of
![]() $U(2,1)$
. If moreover
$U(2,1)$
. If moreover
![]() $L(\unicode[STIX]{x1D712},0)=0$
, it is a cuspidal representation. Its Galois representation (associated by the work of [Reference Langlands and RamakrishnanLR92] or see also [Reference Bellaïche and ChenevierBC04, § 3.2.3 and Proposition 4.1])
$L(\unicode[STIX]{x1D712},0)=0$
, it is a cuspidal representation. Its Galois representation (associated by the work of [Reference Langlands and RamakrishnanLR92] or see also [Reference Bellaïche and ChenevierBC04, § 3.2.3 and Proposition 4.1])
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712}),p}:G_{E}\longrightarrow \operatorname{GL}_{3}(\overline{\mathbb{Q}_{p}})$
is
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712}),p}:G_{E}\longrightarrow \operatorname{GL}_{3}(\overline{\mathbb{Q}_{p}})$
is
Moreover, its
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights are
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights are
![]() $(-(k+1)/2,-(k-1)/2,0)=(-a,1-a,0)$
.
$(-(k+1)/2,-(k-1)/2,0)=(-a,1-a,0)$
.
10.2 Accessible refinement (at
 $p$
) for
$p$
) for
 $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
In order to construct a
![]() $p$
-adic family of modular forms passing through
$p$
-adic family of modular forms passing through
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
, we need to construct inside
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
, we need to construct inside
![]() $\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})^{I}$
a form which is proper for the operator
$\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})^{I}$
a form which is proper for the operator
![]() $U_{p}$
previously defined. Strictly speaking,
$U_{p}$
previously defined. Strictly speaking,
![]() $U_{p}$
is defined for
$U_{p}$
is defined for
![]() $GU(2,1)$
, and when
$GU(2,1)$
, and when
![]() $p$
is inert,
$p$
is inert,
![]() $U_{p}$
is associated to the operator of the double Iwahori class
$U_{p}$
is associated to the operator of the double Iwahori class
![]() $IU_{p}^{c}I$
where
$IU_{p}^{c}I$
where
 $$\begin{eqnarray}U_{p}^{c}=\left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}U_{p}^{c}=\left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right).\end{eqnarray}$$
This class is not in
![]() $U(2,1)(\mathbb{Q}_{p})$
, but
$U(2,1)(\mathbb{Q}_{p})$
, but
![]() $p^{-1}U_{p}^{c}$
is. Fix
$p^{-1}U_{p}^{c}$
is. Fix
![]() $T\subset B\subset U(2,1)(\mathbb{Q}_{p})$
. As
$T\subset B\subset U(2,1)(\mathbb{Q}_{p})$
. As
![]() $p$
is unramified, we have as a representation of
$p$
is unramified, we have as a representation of
![]() $T/T^{0}$
(
$T/T^{0}$
(
![]() $T^{0}$
a maximal compact in
$T^{0}$
a maximal compact in
![]() $T$
), for
$T$
), for
![]() $\unicode[STIX]{x1D70B}$
a representation of
$\unicode[STIX]{x1D70B}$
a representation of
![]() $U(2,1)(\mathbb{Q}_{p})$
an isomorphism, see [Reference Bellaïche and ChenevierBC04],
$U(2,1)(\mathbb{Q}_{p})$
an isomorphism, see [Reference Bellaïche and ChenevierBC04],
Thus to understand how the double coset operator
![]() $U_{p}^{c}$
in the Iwahori–Hecke algebra acts, we only need to determine the Jacquet functor
$U_{p}^{c}$
in the Iwahori–Hecke algebra acts, we only need to determine the Jacquet functor
![]() $(\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712}))_{N}$
as a representation of
$(\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712}))_{N}$
as a representation of
![]() $T$
. If
$T$
. If
![]() $p$
splits, this is computed in [Reference Bellaïche and ChenevierBC04] (and [Reference Bellaïche and ChenevierBC09] in greater generality), so suppose that
$p$
splits, this is computed in [Reference Bellaïche and ChenevierBC04] (and [Reference Bellaïche and ChenevierBC09] in greater generality), so suppose that
![]() $p$
is inert.
$p$
is inert.
Proposition 10.7. Let
![]() $\widetilde{\unicode[STIX]{x1D712}}$
be the (unramified) character of the torus
$\widetilde{\unicode[STIX]{x1D712}}$
be the (unramified) character of the torus
![]() $T$
of
$T$
of
![]() $U(2,1)(\mathbb{Q}_{p})$
defined by
$U(2,1)(\mathbb{Q}_{p})$
defined by
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & \overline{a}^{-1}\end{array}\right)\longmapsto \unicode[STIX]{x1D712}_{p}(a).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & \overline{a}^{-1}\end{array}\right)\longmapsto \unicode[STIX]{x1D712}_{p}(a).\end{eqnarray}$$
Denote by
![]() $w\in W_{U(2,1)(\mathbb{Q}_{p})}\simeq \mathbb{Z}/2\mathbb{Z}$
the non-trivial element and
$w\in W_{U(2,1)(\mathbb{Q}_{p})}\simeq \mathbb{Z}/2\mathbb{Z}$
the non-trivial element and
![]() $\widetilde{\unicode[STIX]{x1D712}}^{w}$
the corresponding character of
$\widetilde{\unicode[STIX]{x1D712}}^{w}$
the corresponding character of
![]() $T$
(
$T$
(
![]() $\widetilde{\unicode[STIX]{x1D712}}^{w}=\unicode[STIX]{x1D712}(w\cdot w)$
). Then the unique admissible refinement of
$\widetilde{\unicode[STIX]{x1D712}}^{w}=\unicode[STIX]{x1D712}(w\cdot w)$
). Then the unique admissible refinement of
![]() $\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})$
is given by
$\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})$
is given by
![]() $\widetilde{\unicode[STIX]{x1D712}}^{w}$
, i.e.
$\widetilde{\unicode[STIX]{x1D712}}^{w}$
, i.e.
![]() $\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})_{N}=\widetilde{\unicode[STIX]{x1D712}}^{w}\unicode[STIX]{x1D6FF}_{B}^{1/2}$
.
$\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})_{N}=\widetilde{\unicode[STIX]{x1D712}}^{w}\unicode[STIX]{x1D6FF}_{B}^{1/2}$
.
Proof. Write for the proof
![]() $G=U(2,1)(\mathbb{Q}_{p})$
. According to Rogawski we have
$G=U(2,1)(\mathbb{Q}_{p})$
. According to Rogawski we have
![]() $\operatorname{ind}-n_{B}^{G}(\widetilde{\unicode[STIX]{x1D712}})^{ss}=\{\unicode[STIX]{x1D70B}_{p}^{n},\unicode[STIX]{x1D70B}_{p}^{2}\}$
and
$\operatorname{ind}-n_{B}^{G}(\widetilde{\unicode[STIX]{x1D712}})^{ss}=\{\unicode[STIX]{x1D70B}_{p}^{n},\unicode[STIX]{x1D70B}_{p}^{2}\}$
and
![]() $(\operatorname{ind}-n_{B}^{G}(\widetilde{\unicode[STIX]{x1D712}}))_{N}^{ss}=\{\widetilde{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D6FF}_{B}^{1/2},\widetilde{\unicode[STIX]{x1D712}}^{w}\unicode[STIX]{x1D6FF}_{B}^{1/2}\}$
by Bernstein and Zelevinski’s geometric lemma. Following [Reference Bellaïche and ChenevierBC09], denote for
$(\operatorname{ind}-n_{B}^{G}(\widetilde{\unicode[STIX]{x1D712}}))_{N}^{ss}=\{\widetilde{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D6FF}_{B}^{1/2},\widetilde{\unicode[STIX]{x1D712}}^{w}\unicode[STIX]{x1D6FF}_{B}^{1/2}\}$
by Bernstein and Zelevinski’s geometric lemma. Following [Reference Bellaïche and ChenevierBC09], denote for
![]() $\unicode[STIX]{x1D70E}\in W_{G}$
$\unicode[STIX]{x1D70E}\in W_{G}$
![]() $S(\widetilde{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D70E}})$
the unique subrepresentation of
$S(\widetilde{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D70E}})$
the unique subrepresentation of
![]() $\operatorname{ind}-n_{B}^{G}(\widetilde{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D70E}})$
(this induction is non-split by [Reference KeysKey84] for example). It is also the Jordan–Hölder factor that contains
$\operatorname{ind}-n_{B}^{G}(\widetilde{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D70E}})$
(this induction is non-split by [Reference KeysKey84] for example). It is also the Jordan–Hölder factor that contains
![]() $\widetilde{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D6FF}_{B}^{1/2}$
inside its semi-simplified Jacquet functor. Thus
$\widetilde{\unicode[STIX]{x1D712}}^{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D6FF}_{B}^{1/2}$
inside its semi-simplified Jacquet functor. Thus
![]() $S(\widetilde{\unicode[STIX]{x1D712}})=\unicode[STIX]{x1D70B}_{p}^{2}$
or
$S(\widetilde{\unicode[STIX]{x1D712}})=\unicode[STIX]{x1D70B}_{p}^{2}$
or
![]() $S(\widetilde{\unicode[STIX]{x1D712}})=\unicode[STIX]{x1D70B}_{p}^{n}$
. Also, as changing
$S(\widetilde{\unicode[STIX]{x1D712}})=\unicode[STIX]{x1D70B}_{p}^{n}$
. Also, as changing
![]() $\widetilde{\unicode[STIX]{x1D712}}$
by
$\widetilde{\unicode[STIX]{x1D712}}$
by
![]() $\widetilde{\unicode[STIX]{x1D712}}^{w}$
exchanges the subrepresentation and the quotient in the induced representation,
$\widetilde{\unicode[STIX]{x1D712}}^{w}$
exchanges the subrepresentation and the quotient in the induced representation,
![]() $S(\widetilde{\unicode[STIX]{x1D712}})\neq S(\widetilde{\unicode[STIX]{x1D712}}^{w})$
. So the proposition is equivalent to
$S(\widetilde{\unicode[STIX]{x1D712}})\neq S(\widetilde{\unicode[STIX]{x1D712}}^{w})$
. So the proposition is equivalent to
![]() $\unicode[STIX]{x1D70B}_{p}^{2}=S(\widetilde{\unicode[STIX]{x1D712}})$
. Let us remark that it is announced in [Reference RogawskiRog92], as
$\unicode[STIX]{x1D70B}_{p}^{2}=S(\widetilde{\unicode[STIX]{x1D712}})$
. Let us remark that it is announced in [Reference RogawskiRog92], as
![]() $\unicode[STIX]{x1D70B}_{p}^{n}$
is said to be the Langlands quotient, but let us give an argument for that fact. We can use Casselman’s criterion for
$\unicode[STIX]{x1D70B}_{p}^{n}$
is said to be the Langlands quotient, but let us give an argument for that fact. We can use Casselman’s criterion for
![]() $\unicode[STIX]{x1D70B}_{p}^{2}$
[Reference CasselmanCas95, Theorem 4.4.6]. For
$\unicode[STIX]{x1D70B}_{p}^{2}$
[Reference CasselmanCas95, Theorem 4.4.6]. For
![]() $A=T^{\text{split}}=\mathbb{G}_{m}\subset B$
,
$A=T^{\text{split}}=\mathbb{G}_{m}\subset B$
,
and thus
as
![]() $\unicode[STIX]{x1D712}_{0}$
is unitary, and thus
$\unicode[STIX]{x1D712}_{0}$
is unitary, and thus
![]() $\widetilde{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D6FF}_{B}^{1/2}$
is an exponent of
$\widetilde{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D6FF}_{B}^{1/2}$
is an exponent of
![]() $r_{B}^{G}(\unicode[STIX]{x1D70B}^{2})$
and
$r_{B}^{G}(\unicode[STIX]{x1D70B}^{2})$
and
![]() $\unicode[STIX]{x1D70B}_{p}^{2}\subset \operatorname{ind}-n_{B}^{G}(\widetilde{\unicode[STIX]{x1D712}})$
i.e.
$\unicode[STIX]{x1D70B}_{p}^{2}\subset \operatorname{ind}-n_{B}^{G}(\widetilde{\unicode[STIX]{x1D712}})$
i.e.
When
![]() $p$
is split, the calculation is done in [Reference Bellaïche and ChenevierBC04] and we get the following up to identifying an unramified character of
$p$
is split, the calculation is done in [Reference Bellaïche and ChenevierBC04] and we get the following up to identifying an unramified character of
![]() $T(\mathbb{Q}_{p})\simeq (\mathbb{Q}_{p}^{\times })^{3}$
,
$T(\mathbb{Q}_{p})\simeq (\mathbb{Q}_{p}^{\times })^{3}$
,
 $$\begin{eqnarray}\unicode[STIX]{x1D713}:\begin{array}{@{}ccc@{}}T(\mathbb{Q}_{p}) & \longrightarrow & \mathbb{C}\\ \left(\begin{array}{@{}ccc@{}}x_{1} & & \\ & x_{2} & \\ & & x_{3}\end{array}\right) & \longmapsto & \unicode[STIX]{x1D713}_{1}(x_{1})\unicode[STIX]{x1D713}_{2}(x_{2})\unicode[STIX]{x1D713}_{3}(x_{3})\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}:\begin{array}{@{}ccc@{}}T(\mathbb{Q}_{p}) & \longrightarrow & \mathbb{C}\\ \left(\begin{array}{@{}ccc@{}}x_{1} & & \\ & x_{2} & \\ & & x_{3}\end{array}\right) & \longmapsto & \unicode[STIX]{x1D713}_{1}(x_{1})\unicode[STIX]{x1D713}_{2}(x_{2})\unicode[STIX]{x1D713}_{3}(x_{3})\end{array}\end{eqnarray}$$
with the triple
![]() $(\unicode[STIX]{x1D713}_{1}(p),\unicode[STIX]{x1D713}_{2}(p),\unicode[STIX]{x1D713}_{3}(p))$
.
$(\unicode[STIX]{x1D713}_{1}(p),\unicode[STIX]{x1D713}_{2}(p),\unicode[STIX]{x1D713}_{3}(p))$
.
Proposition 10.8 (Bellaïche–Chenevier [Reference Bellaïche and ChenevierBC04, Reference Bellaïche and ChenevierBC09]).
If
![]() $p=\overline{v}v$
, the accessible refinements of
$p=\overline{v}v$
, the accessible refinements of
![]() $\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})$
are given (with identification with
$\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})$
are given (with identification with
![]() $\operatorname{GL}_{3}(\mathbb{Q}_{p})$
using
$\operatorname{GL}_{3}(\mathbb{Q}_{p})$
using
![]() $v$
) by:
$v$
) by:
–
 $\unicode[STIX]{x1D70E}=1,(1,\unicode[STIX]{x1D712}_{v}^{\bot }(p),\unicode[STIX]{x1D712}_{v}(p))$
;
$\unicode[STIX]{x1D70E}=1,(1,\unicode[STIX]{x1D712}_{v}^{\bot }(p),\unicode[STIX]{x1D712}_{v}(p))$
;–
 $\unicode[STIX]{x1D70E}=(3,2),(\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p))$
;
$\unicode[STIX]{x1D70E}=(3,2),(\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p))$
;–
 $\unicode[STIX]{x1D70E}=(3,2,1),(\unicode[STIX]{x1D712}_{v}^{\bot }(p),\unicode[STIX]{x1D712}_{v}(p),1)$
.
$\unicode[STIX]{x1D70E}=(3,2,1),(\unicode[STIX]{x1D712}_{v}^{\bot }(p),\unicode[STIX]{x1D712}_{v}(p),1)$
.
Proof. Indeed, the Langlands class associated to
![]() $\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})$
is
$\unicode[STIX]{x1D70B}_{p}^{n}(\unicode[STIX]{x1D712})$
is
![]() $(\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p))$
which corresponds, up to a twist of the central character by
$(\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p))$
which corresponds, up to a twist of the central character by
![]() $(\unicode[STIX]{x1D712}_{v}^{\bot })^{-1}$
, to the class
$(\unicode[STIX]{x1D712}_{v}^{\bot })^{-1}$
, to the class
![]() $(1,(\unicode[STIX]{x1D712}_{v}^{\bot }(p))^{-1},|p|)$
which in turn is associated by Satake (up to twist by
$(1,(\unicode[STIX]{x1D712}_{v}^{\bot }(p))^{-1},|p|)$
which in turn is associated by Satake (up to twist by
![]() $\unicode[STIX]{x1D707}^{-1}|.|^{1/2}$
) to the unramified induction studied in [Reference Bellaïche and ChenevierBC09, Lemma 8.2.1],
$\unicode[STIX]{x1D707}^{-1}|.|^{1/2}$
) to the unramified induction studied in [Reference Bellaïche and ChenevierBC09, Lemma 8.2.1],
![]() $n=1,m=3$
and
$n=1,m=3$
and
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D712}_{0}^{c}=\unicode[STIX]{x1D712}_{0}^{-1}$
(which satisfies the hypothesis of [Reference Bellaïche and ChenevierBC09] 6.9.1). Thus
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D712}_{0}^{c}=\unicode[STIX]{x1D712}_{0}^{-1}$
(which satisfies the hypothesis of [Reference Bellaïche and ChenevierBC09] 6.9.1). Thus
![]() $L(\unicode[STIX]{x1D70B}_{p}|.|^{1/2})=(\unicode[STIX]{x1D712}^{\bot }(p))^{-1}$
. The refinements are then given by [Reference Bellaïche and ChenevierBC09, Lemma 8.2.1].◻
$L(\unicode[STIX]{x1D70B}_{p}|.|^{1/2})=(\unicode[STIX]{x1D712}^{\bot }(p))^{-1}$
. The refinements are then given by [Reference Bellaïche and ChenevierBC09, Lemma 8.2.1].◻
10.3 Coherent cohomology
In order to associate to the automorphic representation
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
a point in the eigenvariety constructed in § 8, we need also to show that
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
a point in the eigenvariety constructed in § 8, we need also to show that
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appears in the global sections (over
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appears in the global sections (over
![]() $X$
) of a coherent automorphic sheaf. The full calculation is made in Appendix D. Here we give an alternative proof in the case
$X$
) of a coherent automorphic sheaf. The full calculation is made in Appendix D. Here we give an alternative proof in the case
![]() $a>1$
, which corresponds to a regular weight, as the case
$a>1$
, which corresponds to a regular weight, as the case
![]() $a=1$
will correspond to a singular weight (and for
$a=1$
will correspond to a singular weight (and for
![]() $a=1$
,
$a=1$
,
![]() $\unicode[STIX]{x1D70B}^{2}$
is a non-holomorphic limit of discrete series). Thus suppose
$\unicode[STIX]{x1D70B}^{2}$
is a non-holomorphic limit of discrete series). Thus suppose
![]() $a>1$
. According to Rogawski [Reference RogawskiRog90, Proposition 15.2.1], the (regular) parameter
$a>1$
. According to Rogawski [Reference RogawskiRog90, Proposition 15.2.1], the (regular) parameter
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}(a,b,c)=\unicode[STIX]{x1D711}(a,a-1,0)$
(see [Reference RogawskiRog90, p. 176],
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}(a,b,c)=\unicode[STIX]{x1D711}(a,a-1,0)$
(see [Reference RogawskiRog90, p. 176],
![]() $\unicode[STIX]{x1D712}$
corresponding to
$\unicode[STIX]{x1D712}$
corresponding to
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{-}$
) we already know that
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D711}}^{-}$
) we already know that
for
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D711}}$
the representation of
${\mathcal{F}}_{\unicode[STIX]{x1D711}}$
the representation of
![]() $U(2,1)(\mathbb{R})$
of highest weight
$U(2,1)(\mathbb{R})$
of highest weight
![]() $(a-1,a-1,1)$
, and
$(a-1,a-1,1)$
, and
In particular the system of Hecke Eigenvalues of
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appears in the first intersection cohomology group of a local system associated to
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appears in the first intersection cohomology group of a local system associated to
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee }$
(thus coming from a representation of the group
${\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee }$
(thus coming from a representation of the group
![]() $G$
),
$G$
),
![]() $IH^{1}(X^{\text{BS}},{\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })$
, where
$IH^{1}(X^{\text{BS}},{\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })$
, where
![]() $X^{\text{BS}}$
is the Borel–Serre compactification, or also by a theorem of Borel in
$X^{\text{BS}}$
is the Borel–Serre compactification, or also by a theorem of Borel in
![]() $H_{\text{dR},c}^{1}(Y,(V_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D6FB}))$
the de Rham cohomology with compact support (where
$H_{\text{dR},c}^{1}(Y,(V_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D6FB}))$
the de Rham cohomology with compact support (where
![]() $V_{\unicode[STIX]{x1D711}}={\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee }\otimes {\mathcal{O}}_{X}$
is the associated vector bundle with connection, see [Reference HarrisHar90a, 1.4]). If our Picard surface were compact, then
$V_{\unicode[STIX]{x1D711}}={\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee }\otimes {\mathcal{O}}_{X}$
is the associated vector bundle with connection, see [Reference HarrisHar90a, 1.4]). If our Picard surface were compact, then
![]() $IH^{1}(X^{\text{BS}},{\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })=H_{\acute{\text{e}}\text{t}}^{1}(X,{\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })$
is just étale cohomology and as
$IH^{1}(X^{\text{BS}},{\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })=H_{\acute{\text{e}}\text{t}}^{1}(X,{\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })$
is just étale cohomology and as
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D719}}^{\vee }$
comes from a representation of our group, using the Hodge-decomposition for
${\mathcal{F}}_{\unicode[STIX]{x1D719}}^{\vee }$
comes from a representation of our group, using the Hodge-decomposition for
![]() $H_{\acute{\text{e}}\text{t}}^{1}(X,{\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })$
or for the de Rham cohomology (see [Reference FaltingsFal83] or [Reference Matsushima and MurakamiMM63]), we know that there exists a coherent automorphic sheaf
$H_{\acute{\text{e}}\text{t}}^{1}(X,{\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })$
or for the de Rham cohomology (see [Reference FaltingsFal83] or [Reference Matsushima and MurakamiMM63]), we know that there exists a coherent automorphic sheaf
![]() $V_{\unicode[STIX]{x1D711}}={\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee }\otimes {\mathcal{O}}_{X}$
such that
$V_{\unicode[STIX]{x1D711}}={\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee }\otimes {\mathcal{O}}_{X}$
such that
More generally, if
![]() $X$
is not compact (which is the case here) we still have a BGG-decomposition for the de Rham cohomology with compact support, see [Reference LanLan12, (2.4)],
$X$
is not compact (which is the case here) we still have a BGG-decomposition for the de Rham cohomology with compact support, see [Reference LanLan12, (2.4)],
We thus need to show that the system of Hecke eigenvalues appears in the last factor. But, denote by
![]() $\overline{I}$
the opposite induced representation
$\overline{I}$
the opposite induced representation
![]() $\operatorname{ind}-n_{B}^{U(2,1)(\mathbb{R})}(\unicode[STIX]{x1D712}_{\infty }^{w})$
, so that
$\operatorname{ind}-n_{B}^{U(2,1)(\mathbb{R})}(\unicode[STIX]{x1D712}_{\infty }^{w})$
, so that
![]() $\unicode[STIX]{x1D70B}_{\infty }^{n}$
is the subrepresentation of
$\unicode[STIX]{x1D70B}_{\infty }^{n}$
is the subrepresentation of
![]() $\overline{I}$
and
$\overline{I}$
and
![]() $\unicode[STIX]{x1D70B}^{2}$
its quotient. Writing the long exact sequence of
$\unicode[STIX]{x1D70B}^{2}$
its quotient. Writing the long exact sequence of
![]() $(\mathfrak{g},K)$
-cohomology associated to
$(\mathfrak{g},K)$
-cohomology associated to
we get that
![]() $H^{1}(\mathfrak{g},K,\unicode[STIX]{x1D70B}_{\infty }^{n}\otimes {\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })=H^{1}(\mathfrak{g},K,\overline{I}\otimes {\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })$
. Using Hodge decomposition for this, we get that
$H^{1}(\mathfrak{g},K,\unicode[STIX]{x1D70B}_{\infty }^{n}\otimes {\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })=H^{1}(\mathfrak{g},K,\overline{I}\otimes {\mathcal{F}}_{\unicode[STIX]{x1D711}}^{\vee })$
. Using Hodge decomposition for this, we get that
and using Frobenius reciprocity we can calculate the last term as
and, as we know
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D711}}$
, we can calculate its restriction to
${\mathcal{F}}_{\unicode[STIX]{x1D711}}$
, we can calculate its restriction to
![]() $T\cap K$
, we get
$T\cap K$
, we get
where
 $$\begin{eqnarray}t^{k}e^{l}:\left(\begin{array}{@{}ccc@{}}t & & \\ & e & \\ & & t\end{array}\right)\in T\cap K=U(1)\times U(1)\longmapsto t^{k}e^{l}.\end{eqnarray}$$
$$\begin{eqnarray}t^{k}e^{l}:\left(\begin{array}{@{}ccc@{}}t & & \\ & e & \\ & & t\end{array}\right)\in T\cap K=U(1)\times U(1)\longmapsto t^{k}e^{l}.\end{eqnarray}$$
We can also explicitly calculate that, by conjugacy,
![]() $T\cap K$
acts on
$T\cap K$
acts on
![]() $\mathfrak{p}^{+}$
by
$\mathfrak{p}^{+}$
by
![]() $1\oplus te^{-1}$
and on
$1\oplus te^{-1}$
and on
![]() $\mathfrak{p}^{-}$
by
$\mathfrak{p}^{-}$
by
![]() $1\oplus t^{-1}e$
.
$1\oplus t^{-1}e$
.
Remark 10.9. This is because of our choice of
![]() $h$
. If we change
$h$
. If we change
![]() $h$
by its conjugate, then the action on
$h$
by its conjugate, then the action on
![]() $\mathfrak{p}^{+},\mathfrak{p}^{-}$
would have been exchanged, and
$\mathfrak{p}^{+},\mathfrak{p}^{-}$
would have been exchanged, and
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
would be anti-holomorphic (but we could have used
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
would be anti-holomorphic (but we could have used
![]() $\unicode[STIX]{x1D712}^{c}$
instead of
$\unicode[STIX]{x1D712}^{c}$
instead of
![]() $\unicode[STIX]{x1D712}$
in this case,
$\unicode[STIX]{x1D712}$
in this case,
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712}^{c})$
would have been holomorphic).
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712}^{c})$
would have been holomorphic).
As
![]() $\unicode[STIX]{x1D712}_{T\cap K}^{w}=t^{2a-1}$
, we get that
$\unicode[STIX]{x1D712}_{T\cap K}^{w}=t^{2a-1}$
, we get that
Remark 10.10. Changing
![]() $\unicode[STIX]{x1D712}$
by
$\unicode[STIX]{x1D712}$
by
![]() $\unicode[STIX]{x1D712}^{c}$
inverts the previous result, as predicted by the Hodge structure, so we could have argued without explicitly calculating these spaces.
$\unicode[STIX]{x1D712}^{c}$
inverts the previous result, as predicted by the Hodge structure, so we could have argued without explicitly calculating these spaces.
Proposition 10.11. If
![]() $a>1$
, the Hecke eigensystem corresponding to
$a>1$
, the Hecke eigensystem corresponding to
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appears in
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appears in
![]() $H^{0}(X,F_{s\cdot (\unicode[STIX]{x1D711}^{\vee })}\otimes {\mathcal{O}}_{X}(-D))=H^{0}(X,\unicode[STIX]{x1D714}^{(0,1-a,a)}(-D))$
. More generally, for
$H^{0}(X,F_{s\cdot (\unicode[STIX]{x1D711}^{\vee })}\otimes {\mathcal{O}}_{X}(-D))=H^{0}(X,\unicode[STIX]{x1D714}^{(0,1-a,a)}(-D))$
. More generally, for
![]() $a\geqslant 1$
, the Hecke eigenvalues of
$a\geqslant 1$
, the Hecke eigenvalues of
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appear in the global section of the coherent sheaf
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appear in the global section of the coherent sheaf
![]() $\unicode[STIX]{x1D714}^{(0,1-a,a)}(-D)$
.
$\unicode[STIX]{x1D714}^{(0,1-a,a)}(-D)$
.
Proof. When
![]() $a>1$
we know that the Hecke eigensystem corresponding to
$a>1$
we know that the Hecke eigensystem corresponding to
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appears in the de Rham cohomology associated to
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appears in the de Rham cohomology associated to
![]() $\unicode[STIX]{x1D711}$
. If
$\unicode[STIX]{x1D711}$
. If
![]() $Y$
were compact, the proposition would just be Matsushima’s formula and the Hodge decomposition [Reference YoshidaYos08, Theorem 4.7] of the first
$Y$
were compact, the proposition would just be Matsushima’s formula and the Hodge decomposition [Reference YoshidaYos08, Theorem 4.7] of the first
![]() $(\mathfrak{g},K)$
-cohomology group we calculated above. More generally, the previous calculation still shows that the class corresponding to
$(\mathfrak{g},K)$
-cohomology group we calculated above. More generally, the previous calculation still shows that the class corresponding to
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
cannot be represented by classes in
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
cannot be represented by classes in
![]() $H^{1}(X,\unicode[STIX]{x1D714}^{(1-a,1-a,1)})$
(whose cohomology is calculated by
$H^{1}(X,\unicode[STIX]{x1D714}^{(1-a,1-a,1)})$
(whose cohomology is calculated by
![]() $(\mathfrak{p}^{-},K)$
-cohomology), and thus, by the BGG resolution, it appears in
$(\mathfrak{p}^{-},K)$
-cohomology), and thus, by the BGG resolution, it appears in
![]() $H^{0}(X,\unicode[STIX]{x1D714}^{(0,1-a,a)}(-D))$
.
$H^{0}(X,\unicode[STIX]{x1D714}^{(0,1-a,a)}(-D))$
.
For the general case, this is Appendix D (which proves that the Hecke eigensystem appears in the 0th coherent cohomology group).◻
10.4 Transfer to
 $GU(2,1)$
$GU(2,1)$
From now on, denote by
![]() $G=GU(2,1)$
the algebraic group over
$G=GU(2,1)$
the algebraic group over
![]() $\mathbb{Q}$
of unitary similitudes (relatively to
$\mathbb{Q}$
of unitary similitudes (relatively to
![]() $(E^{3},J)$
). It is endowed with a morphism
$(E^{3},J)$
). It is endowed with a morphism
![]() $\unicode[STIX]{x1D708}$
, and there is an exact sequence,
$\unicode[STIX]{x1D708}$
, and there is an exact sequence,
where
![]() $G_{1}=U(2,1)$
is the unitary group of
$G_{1}=U(2,1)$
is the unitary group of
![]() $(E^{3},J)$
.
$(E^{3},J)$
.
Let
![]() $T=\operatorname{Res}_{E/\mathbb{Q}}\mathbb{G}_{m}$
be the center of
$T=\operatorname{Res}_{E/\mathbb{Q}}\mathbb{G}_{m}$
be the center of
![]() $G$
,
$G$
,
![]() $Nm:T\longrightarrow \mathbb{G}_{m}$
the norm morphism, and
$Nm:T\longrightarrow \mathbb{G}_{m}$
the norm morphism, and
![]() $T^{1}$
its Kernel; the center of
$T^{1}$
its Kernel; the center of
![]() $G_{1}$
. We have the exact sequence,
$G_{1}$
. We have the exact sequence,
where the first map is given by
![]() $\unicode[STIX]{x1D706}\mapsto (\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{-1})$
.
$\unicode[STIX]{x1D706}\mapsto (\unicode[STIX]{x1D706},\unicode[STIX]{x1D706}^{-1})$
.
Let
![]() $\unicode[STIX]{x1D70B}_{1}$
be an automorphic (respectively a smooth admissible local) representation of
$\unicode[STIX]{x1D70B}_{1}$
be an automorphic (respectively a smooth admissible local) representation of
![]() $G_{1}(\mathbb{A}_{\mathbb{Q}})$
(respectively of
$G_{1}(\mathbb{A}_{\mathbb{Q}})$
(respectively of
![]() $G_{1}(\mathbb{Q}_{p})$
or
$G_{1}(\mathbb{Q}_{p})$
or
![]() $G_{1}(\mathbb{R})$
), of central character
$G_{1}(\mathbb{R})$
), of central character
![]() $\unicode[STIX]{x1D712}_{1}$
of
$\unicode[STIX]{x1D712}_{1}$
of
![]() $T^{1}$
. Let
$T^{1}$
. Let
![]() $\unicode[STIX]{x1D712}$
be a character of
$\unicode[STIX]{x1D712}$
be a character of
![]() $T$
(local or global) that extends
$T$
(local or global) that extends
![]() $\unicode[STIX]{x1D712}_{1}$
; we can thus look at the representation,
$\unicode[STIX]{x1D712}_{1}$
; we can thus look at the representation,
of
![]() $T\times G_{1}$
. We can check that it factors through the action of
$T\times G_{1}$
. We can check that it factors through the action of
![]() $T^{1}$
and gives a representation of a subgroup of
$T^{1}$
and gives a representation of a subgroup of
![]() $G$
.
$G$
.
Proposition 10.12. The automorphic representation
![]() $\unicode[STIX]{x1D70B}^{n}$
of
$\unicode[STIX]{x1D70B}^{n}$
of
![]() $U(2,1)$
given in Proposition 10.6 has central character
$U(2,1)$
given in Proposition 10.6 has central character
![]() $\unicode[STIX]{x1D714}$
equal to the restriction of
$\unicode[STIX]{x1D714}$
equal to the restriction of
![]() $\unicode[STIX]{x1D712}$
to
$\unicode[STIX]{x1D712}$
to
![]() $E^{1}$
. We can extend
$E^{1}$
. We can extend
![]() $\unicode[STIX]{x1D714}$
as an algebraic Hecke character
$\unicode[STIX]{x1D714}$
as an algebraic Hecke character
![]() $\widetilde{\unicode[STIX]{x1D714}}$
of
$\widetilde{\unicode[STIX]{x1D714}}$
of
![]() $T$
by the algebraic character
$T$
by the algebraic character
![]() $\widetilde{\unicode[STIX]{x1D714}}=N^{-1}\unicode[STIX]{x1D712}$
, where
$\widetilde{\unicode[STIX]{x1D714}}=N^{-1}\unicode[STIX]{x1D712}$
, where
![]() $N$
is the norm of
$N$
is the norm of
![]() $E$
. Thus, there exists an automorphic representation
$E$
. Thus, there exists an automorphic representation
![]() $\widetilde{\unicode[STIX]{x1D70B}^{n}}$
of
$\widetilde{\unicode[STIX]{x1D70B}^{n}}$
of
![]() $G$
such that for
$G$
such that for
![]() $\ell$
a prime, unramified for
$\ell$
a prime, unramified for
![]() $\unicode[STIX]{x1D712}_{0}$
,
$\unicode[STIX]{x1D712}_{0}$
,
![]() $(\unicode[STIX]{x1D70B}_{\ell }^{n})^{K_{\ell }}=(\widetilde{\unicode[STIX]{x1D70B}_{\ell }^{n}})^{K_{\ell }}$
(where
$(\unicode[STIX]{x1D70B}_{\ell }^{n})^{K_{\ell }}=(\widetilde{\unicode[STIX]{x1D70B}_{\ell }^{n}})^{K_{\ell }}$
(where
![]() $K_{\ell }\subset G(\mathbb{Q}_{\ell })$
is the hyperspecial, respectively special if
$K_{\ell }\subset G(\mathbb{Q}_{\ell })$
is the hyperspecial, respectively special if
![]() $\ell$
ramifies in
$\ell$
ramifies in
![]() $E$
– subgroup) and the Galois representation associated to
$E$
– subgroup) and the Galois representation associated to
![]() $\widetilde{\unicode[STIX]{x1D70B}}^{n}$
by [Reference Blasius and RogawskiBR92, Theorem 1.9.1] (or [Reference SkinnerSki12]) is (with the normalization of [Reference SkinnerSki12])
$\widetilde{\unicode[STIX]{x1D70B}}^{n}$
by [Reference Blasius and RogawskiBR92, Theorem 1.9.1] (or [Reference SkinnerSki12]) is (with the normalization of [Reference SkinnerSki12])
Moreover
![]() $(\unicode[STIX]{x1D70B}_{p}^{n})^{I}=(\widetilde{\unicode[STIX]{x1D70B}_{p}^{n}})^{I}$
.
$(\unicode[STIX]{x1D70B}_{p}^{n})^{I}=(\widetilde{\unicode[STIX]{x1D70B}_{p}^{n}})^{I}$
.
Proof. To calculate
![]() $\unicode[STIX]{x1D714}$
, we only need to look at
$\unicode[STIX]{x1D714}$
, we only need to look at
![]() $\unicode[STIX]{x1D70B}_{p}^{n}$
for every place
$\unicode[STIX]{x1D70B}_{p}^{n}$
for every place
![]() $p$
, and we can use that
$p$
, and we can use that
![]() $\unicode[STIX]{x1D70B}_{p}^{n}=\operatorname{ind}-n_{P}^{\operatorname{GL}_{3}(\mathbb{Q}_{p})}(\unicode[STIX]{x1D712}_{0})$
for split
$\unicode[STIX]{x1D70B}_{p}^{n}=\operatorname{ind}-n_{P}^{\operatorname{GL}_{3}(\mathbb{Q}_{p})}(\unicode[STIX]{x1D712}_{0})$
for split
![]() $p$
, and
$p$
, and
![]() $\unicode[STIX]{x1D70B}_{p}^{n}\subset \operatorname{ind}-n_{B}^{U(3)(\mathbb{Q}_{p})}(\widetilde{\unicode[STIX]{x1D712}}^{w})$
for
$\unicode[STIX]{x1D70B}_{p}^{n}\subset \operatorname{ind}-n_{B}^{U(3)(\mathbb{Q}_{p})}(\widetilde{\unicode[STIX]{x1D712}}^{w})$
for
![]() $p=\infty$
and inert or ramified
$p=\infty$
and inert or ramified
![]() $p$
.
$p$
.
The character
![]() $\widetilde{\unicode[STIX]{x1D714}}$
extends
$\widetilde{\unicode[STIX]{x1D714}}$
extends
![]() $\unicode[STIX]{x1D714}$
. Once we have extended the central character of
$\unicode[STIX]{x1D714}$
. Once we have extended the central character of
![]() $\unicode[STIX]{x1D70B}^{n}$
, the existence of a
$\unicode[STIX]{x1D70B}^{n}$
, the existence of a
![]() $\widetilde{\unicode[STIX]{x1D70B}}^{n}$
is unique and assured by [Reference Clozel, Harris and TaylorCHT08, Proposition 1.1.4] (as
$\widetilde{\unicode[STIX]{x1D70B}}^{n}$
is unique and assured by [Reference Clozel, Harris and TaylorCHT08, Proposition 1.1.4] (as
![]() $2+1=3$
is odd). More precisely,
$2+1=3$
is odd). More precisely,
where
![]() $g=zg_{\mathbb{Q}}g_{1}$
is written following the decomposition
$g=zg_{\mathbb{Q}}g_{1}$
is written following the decomposition
![]() $G(\mathbb{A})=T(\mathbb{A})G(\mathbb{Q})G_{1}(\mathbb{A})$
.
$G(\mathbb{A})=T(\mathbb{A})G(\mathbb{Q})G_{1}(\mathbb{A})$
.
Denote by
![]() $V_{p}$
the space of
$V_{p}$
the space of
![]() $\unicode[STIX]{x1D70B}_{p}^{n}$
(and thus of
$\unicode[STIX]{x1D70B}_{p}^{n}$
(and thus of
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{p}^{n}$
). Also,
$\widetilde{\unicode[STIX]{x1D70B}}_{p}^{n}$
). Also,
![]() $I\subset GU(2,1)(\mathbb{Q}_{p})$
the Iwahori subgroup, and
$I\subset GU(2,1)(\mathbb{Q}_{p})$
the Iwahori subgroup, and
![]() $I_{1}$
is its intersection with
$I_{1}$
is its intersection with
![]() $U(2,1)(\mathbb{Q}_{p})$
. Because if
$U(2,1)(\mathbb{Q}_{p})$
. Because if
![]() $M\in I$
, then
$M\in I$
, then
![]() $M\equiv B(\text{mod}~p)$
, up to multiplying by an element of
$M\equiv B(\text{mod}~p)$
, up to multiplying by an element of
![]() $T\in T({\mathcal{O}})$
, suppose that
$T\in T({\mathcal{O}})$
, suppose that
![]() $TM\equiv U~(\text{mod}~p)$
. In this case
$TM\equiv U~(\text{mod}~p)$
. In this case
![]() $c(TM)\equiv 1~(\text{mod}~p)$
; thus, as
$c(TM)\equiv 1~(\text{mod}~p)$
; thus, as
![]() $p$
is unramified in
$p$
is unramified in
![]() $E$
, there exist
$E$
, there exist
![]() $T^{\prime }\in T(\mathbb{Z}_{p})$
such that
$T^{\prime }\in T(\mathbb{Z}_{p})$
such that
![]() $c(T^{\prime }TM)=1$
and hence
$c(T^{\prime }TM)=1$
and hence
![]() $M=T^{-1}(T^{\prime }TM)\in T(\mathbb{Z}_{p})I_{1}$
. Thus, as we can write
$M=T^{-1}(T^{\prime }TM)\in T(\mathbb{Z}_{p})I_{1}$
. Thus, as we can write
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & N(e)\overline{a}^{-1}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}ae^{-1} & & \\ & 1 & \\ & & \overline{e}\overline{a}^{-1}\end{array}\right)\left(\begin{array}{@{}ccc@{}}e & & \\ & e & \\ & & e\end{array}\right)\in I_{1}T(\mathbb{Z}_{p}).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & N(e)\overline{a}^{-1}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}ae^{-1} & & \\ & 1 & \\ & & \overline{e}\overline{a}^{-1}\end{array}\right)\left(\begin{array}{@{}ccc@{}}e & & \\ & e & \\ & & e\end{array}\right)\in I_{1}T(\mathbb{Z}_{p}).\end{eqnarray}$$
We get that
but as
![]() $T(\mathbb{Q}_{p})\cap I={\mathcal{O}}_{E_{p}^{\times }}\text{Id}$
and
$T(\mathbb{Q}_{p})\cap I={\mathcal{O}}_{E_{p}^{\times }}\text{Id}$
and
![]() $\widetilde{w}_{p}$
is unramified,
$\widetilde{w}_{p}$
is unramified,
![]() $V_{p}^{I}=V_{p}^{I_{1}}$
. The assertion for
$V_{p}^{I}=V_{p}^{I_{1}}$
. The assertion for
![]() $K_{\ell }$
follows the same lines and is easier.◻
$K_{\ell }$
follows the same lines and is easier.◻
Remark 10.13. We could have lifted the central character of
![]() $\unicode[STIX]{x1D70B}^{n}$
simply by
$\unicode[STIX]{x1D70B}^{n}$
simply by
![]() $\unicode[STIX]{x1D712}$
, in which case the resulting representation would have been a twist of the previous one, but as we only used three variables on the weight space, which means that we do not allow families which are twists by power of the norm of the central character, only one choice of the lift of the central character gives a point in our eigenvariety. We can check that the Hecke eigenvalues of
$\unicode[STIX]{x1D712}$
, in which case the resulting representation would have been a twist of the previous one, but as we only used three variables on the weight space, which means that we do not allow families which are twists by power of the norm of the central character, only one choice of the lift of the central character gives a point in our eigenvariety. We can check that the Hecke eigenvalues of
![]() $\widetilde{\unicode[STIX]{x1D70B}^{n}}$
appears in
$\widetilde{\unicode[STIX]{x1D70B}^{n}}$
appears in
![]() $H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
, with
$H^{0}(X,\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
, with
How can we find the power of the norm and the coherent weight? First, as Hodge–Tate and coherent weights vary continuously on
![]() ${\mathcal{E}}$
, and
${\mathcal{E}}$
, and
![]() $\widetilde{\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})}$
appears as a classical form of
$\widetilde{\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})}$
appears as a classical form of
![]() ${\mathcal{E}}$
(Proposition D.2), according to Propositions 9.17 and 9.19, the polarized Galois representation associated to
${\mathcal{E}}$
(Proposition D.2), according to Propositions 9.17 and 9.19, the polarized Galois representation associated to
![]() $\widetilde{\unicode[STIX]{x1D70B}^{n}}(\unicode[STIX]{x1D712})$
is
$\widetilde{\unicode[STIX]{x1D70B}^{n}}(\unicode[STIX]{x1D712})$
is
and thus
![]() $(k_{1},k_{2}-1,1-k_{3})=(-a,0,1-a)$
up to order. This leaves us six possibilities for
$(k_{1},k_{2}-1,1-k_{3})=(-a,0,1-a)$
up to order. This leaves us six possibilities for
![]() $\unicode[STIX]{x1D705}$
:
$\unicode[STIX]{x1D705}$
:
(i)
 $(0,1-a,a)$
;
$(0,1-a,a)$
;(ii)
 $(0,2-a,a+1)$
;
$(0,2-a,a+1)$
;(iii)
 $(1-a,1-a,1)$
;
$(1-a,1-a,1)$
;(iv)
 $(-a,1-a,a)$
;
$(-a,1-a,a)$
;(v)
 $(-a,2-a,1+a)$
;
$(-a,2-a,1+a)$
;(vi)
 $(1-a,1,1+a)$
,
$(1-a,1,1+a)$
,
but as for classical points (as
![]() $\widetilde{\unicode[STIX]{x1D70B}^{n}}(\unicode[STIX]{x1D712})$
)
$\widetilde{\unicode[STIX]{x1D70B}^{n}}(\unicode[STIX]{x1D712})$
)
![]() $k_{1}\geqslant k_{2}$
, and
$k_{1}\geqslant k_{2}$
, and
![]() $a\geqslant 1$
, this eliminates the three last possibilities (and the second when
$a\geqslant 1$
, this eliminates the three last possibilities (and the second when
![]() $a=1$
). But then we know that the lowest
$a=1$
). But then we know that the lowest
![]() $K_{\infty }$
-type for
$K_{\infty }$
-type for
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
is of dimension
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
is of dimension
![]() $a$
by restriction to
$a$
by restriction to
![]() $U(2)$
and the calculation of Appendix D, Proposition D.2, which makes only the first coherent weight possible when
$U(2)$
and the calculation of Appendix D, Proposition D.2, which makes only the first coherent weight possible when
![]() $a>1$
. When
$a>1$
. When
![]() $a=1$
, the first and third weights are the same. Another possibility is also to find the infinitesimal character of
$a=1$
, the first and third weights are the same. Another possibility is also to find the infinitesimal character of
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
(using for example [Reference KnappKna16, Proposition 8.22]), and that
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
(using for example [Reference KnappKna16, Proposition 8.22]), and that
![]() $\unicode[STIX]{x1D702}=(-k_{3},k_{1},k_{2})$
is the highest weight character of
$\unicode[STIX]{x1D702}=(-k_{3},k_{1},k_{2})$
is the highest weight character of
![]() $V_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C}_{n}-\unicode[STIX]{x1D70C}_{c}}^{\vee }$
in the notations of [Reference GoldringGol14] (paying attention to the dual). Finally, if
$V_{\unicode[STIX]{x1D706}+\unicode[STIX]{x1D70C}_{n}-\unicode[STIX]{x1D70C}_{c}}^{\vee }$
in the notations of [Reference GoldringGol14] (paying attention to the dual). Finally, if
![]() $a>1$
, then the BGG decomposition tells us which weight
$a>1$
, then the BGG decomposition tells us which weight
![]() $\unicode[STIX]{x1D705}$
has to be. Then to find the corresponding power of the norm, note that
$\unicode[STIX]{x1D705}$
has to be. Then to find the corresponding power of the norm, note that
![]() $|\unicode[STIX]{x1D705}|$
must be equal to the opposite of the power of the norm of the central character of
$|\unicode[STIX]{x1D705}|$
must be equal to the opposite of the power of the norm of the central character of
![]() $\widetilde{\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})}$
by the calculation before Proposition 2.6 and conventions on weights (see § 9.6 about
$\widetilde{\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})}$
by the calculation before Proposition 2.6 and conventions on weights (see § 9.6 about
![]() $(c_{0},c_{0}^{\prime })$
).
$(c_{0},c_{0}^{\prime })$
).
10.5 Refinement of representations of
 $GU(2,1)(\mathbb{Q}_{p})$
$GU(2,1)(\mathbb{Q}_{p})$
Let
![]() $G=GU(2,1)(\mathbb{Q}_{p})$
. Consider in
$G=GU(2,1)(\mathbb{Q}_{p})$
. Consider in
![]() $C_{c}(I\backslash G/I,\mathbb{Z}[1/p])$
the double classes,
$C_{c}(I\backslash G/I,\mathbb{Z}[1/p])$
the double classes,
 $$\begin{eqnarray}U_{p}^{c}=\left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right)\quad \text{and}\quad S_{p}^{c}=\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & p\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}U_{p}^{c}=\left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right)\quad \text{and}\quad S_{p}^{c}=\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & p\end{array}\right).\end{eqnarray}$$
The characteristic functions of
![]() $S_{p}^{c}$
and
$S_{p}^{c}$
and
![]() $U_{p}^{c}$
are invertible in
$U_{p}^{c}$
are invertible in
![]() $C_{c}(I\backslash G/I,\mathbb{Z}[1/p])$
and denote by
$C_{c}(I\backslash G/I,\mathbb{Z}[1/p])$
and denote by
![]() ${\mathcal{A}}(p)$
the sub-algebra generated by the characteristic functions of
${\mathcal{A}}(p)$
the sub-algebra generated by the characteristic functions of
![]() $U_{p}^{c},S_{p}^{c}$
and their inverses.
$U_{p}^{c},S_{p}^{c}$
and their inverses.
Proposition 10.14. For
![]() $\unicode[STIX]{x1D70B}$
a smooth complex representation of
$\unicode[STIX]{x1D70B}$
a smooth complex representation of
![]() $G$
, we have a natural
$G$
, we have a natural
![]() $\mathbb{C}[{\mathcal{A}}(p)]$
-isomorphism,
$\mathbb{C}[{\mathcal{A}}(p)]$
-isomorphism,
Let
![]() $\unicode[STIX]{x1D70B}$
be a smooth admissible representation of
$\unicode[STIX]{x1D70B}$
be a smooth admissible representation of
![]() $G$
, such that
$G$
, such that
![]() $\unicode[STIX]{x1D70B}$
is a subquotient of the (normalized) induction of an unramified character
$\unicode[STIX]{x1D70B}$
is a subquotient of the (normalized) induction of an unramified character
![]() $\unicode[STIX]{x1D713}$
of the torus
$\unicode[STIX]{x1D713}$
of the torus
![]() $T$
of
$T$
of
![]() $G$
. For example, this is the case if
$G$
. For example, this is the case if
![]() $\unicode[STIX]{x1D70B}$
is unramified, or if
$\unicode[STIX]{x1D70B}$
is unramified, or if
![]() $\unicode[STIX]{x1D70B}^{I}\neq \{0\}$
(by the previous equality and adjunction between Jacquet functor and induction for example).
$\unicode[STIX]{x1D70B}^{I}\neq \{0\}$
(by the previous equality and adjunction between Jacquet functor and induction for example).
Definition 10.15. Following [Reference Bellaïche and ChenevierBC09], an accessible refinement of
![]() $\unicode[STIX]{x1D70B}$
is a
$\unicode[STIX]{x1D70B}$
is a
![]() $\unicode[STIX]{x1D70E}\in W$
such that
$\unicode[STIX]{x1D70E}\in W$
such that
![]() $\unicode[STIX]{x1D713}^{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D6FF}_{B}^{1/2}$
is a subrepresentation of
$\unicode[STIX]{x1D713}^{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D6FF}_{B}^{1/2}$
is a subrepresentation of
![]() $\unicode[STIX]{x1D70B}_{N}^{T^{0}}$
(equivalently if
$\unicode[STIX]{x1D70B}_{N}^{T^{0}}$
(equivalently if
![]() $\unicode[STIX]{x1D713}^{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D6FF}_{B}^{-1/2}$
appears in
$\unicode[STIX]{x1D713}^{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D6FF}_{B}^{-1/2}$
appears in
![]() $\unicode[STIX]{x1D70B}^{I}$
).
$\unicode[STIX]{x1D70B}^{I}$
).
Another way to see it is that a refinement is an ordering of the eigenvalues of the Frobenius class of
![]() $LL(\unicode[STIX]{x1D70B})$
, the Weil representation associated by local Langlands to
$LL(\unicode[STIX]{x1D70B})$
, the Weil representation associated by local Langlands to
![]() $\unicode[STIX]{x1D70B}$
, and it is accessible if it appears in the previous sense in
$\unicode[STIX]{x1D70B}$
, and it is accessible if it appears in the previous sense in
![]() $\unicode[STIX]{x1D70B}^{I}$
(or
$\unicode[STIX]{x1D70B}^{I}$
(or
![]() $\unicode[STIX]{x1D70B}_{N}^{T^{0}}$
).
$\unicode[STIX]{x1D70B}_{N}^{T^{0}}$
).
For
![]() $GU(2,1)$
when
$GU(2,1)$
when
![]() $p$
is split,
$p$
is split,
![]() $GU(2,1)(\mathbb{Q}_{p})\simeq \operatorname{GL}_{3}(\mathbb{Q}_{p})\times \mathbb{Q}_{p}^{\times }$
and
$GU(2,1)(\mathbb{Q}_{p})\simeq \operatorname{GL}_{3}(\mathbb{Q}_{p})\times \mathbb{Q}_{p}^{\times }$
and
![]() $\unicode[STIX]{x1D713}$
is an unramified character of
$\unicode[STIX]{x1D713}$
is an unramified character of
![]() $\mathbb{Q}_{p}^{4}$
. The local Langlands representation associated to
$\mathbb{Q}_{p}^{4}$
. The local Langlands representation associated to
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{1}\otimes \unicode[STIX]{x1D713}_{4}$
in this case is
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{1}\otimes \unicode[STIX]{x1D713}_{4}$
in this case is
![]() $LL(\unicode[STIX]{x1D70B}_{1})\otimes \overline{\unicode[STIX]{x1D713}_{4}}$
which has eigenvalues
$LL(\unicode[STIX]{x1D70B}_{1})\otimes \overline{\unicode[STIX]{x1D713}_{4}}$
which has eigenvalues
![]() $(\unicode[STIX]{x1D713}_{1}(p)\overline{\unicode[STIX]{x1D713}}_{4}(p),\unicode[STIX]{x1D713}_{2}(p)\overline{\unicode[STIX]{x1D713}}_{4}(p),\unicode[STIX]{x1D713}_{3}(p)\overline{\unicode[STIX]{x1D713}}_{4}(p))$
and an ordering of these eigenvalues is given by an element of
$(\unicode[STIX]{x1D713}_{1}(p)\overline{\unicode[STIX]{x1D713}}_{4}(p),\unicode[STIX]{x1D713}_{2}(p)\overline{\unicode[STIX]{x1D713}}_{4}(p),\unicode[STIX]{x1D713}_{3}(p)\overline{\unicode[STIX]{x1D713}}_{4}(p))$
and an ordering of these eigenvalues is given by an element of
![]() $\mathfrak{S}_{3}=W_{\operatorname{GL}_{3}}=W_{\operatorname{GL}_{3}\times \operatorname{GL}_{1}}$
. Of course, a priori, not all refinements are accessible (
$\mathfrak{S}_{3}=W_{\operatorname{GL}_{3}}=W_{\operatorname{GL}_{3}\times \operatorname{GL}_{1}}$
. Of course, a priori, not all refinements are accessible (
![]() $\unicode[STIX]{x1D70B}_{p}^{n}$
will be an example).
$\unicode[STIX]{x1D70B}_{p}^{n}$
will be an example).
When
![]() $p$
is inert,
$p$
is inert,
![]() $W_{G}\simeq \mathbb{Z}/2\mathbb{Z}$
, and a character of
$W_{G}\simeq \mathbb{Z}/2\mathbb{Z}$
, and a character of
![]() $T=(\operatorname{Res}_{\mathbb{Q}_{p^{2}}/\mathbb{Q}_{p}}\mathbb{G}_{m})^{2}$
is given by two characters
$T=(\operatorname{Res}_{\mathbb{Q}_{p^{2}}/\mathbb{Q}_{p}}\mathbb{G}_{m})^{2}$
is given by two characters
![]() $(\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2})$
, by
$(\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2})$
, by
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & N(e)\overline{a}^{-1}\end{array}\right),a,e\in \mathbb{Q}_{p^{2}}^{\times }\longmapsto \unicode[STIX]{x1D712}_{1}(a)\unicode[STIX]{x1D712}_{2}(e).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}a & & \\ & e & \\ & & N(e)\overline{a}^{-1}\end{array}\right),a,e\in \mathbb{Q}_{p^{2}}^{\times }\longmapsto \unicode[STIX]{x1D712}_{1}(a)\unicode[STIX]{x1D712}_{2}(e).\end{eqnarray}$$
The non-trivial element
![]() $w\in W_{G}$
acts on the character by
$w\in W_{G}$
acts on the character by
![]() $w\cdot (\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2})=(\unicode[STIX]{x1D712}_{1}^{\bot },\unicode[STIX]{x1D712}_{2}(\unicode[STIX]{x1D712}_{1}\circ N))$
. Thus a refinement in this case is simply given by
$w\cdot (\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2})=(\unicode[STIX]{x1D712}_{1}^{\bot },\unicode[STIX]{x1D712}_{2}(\unicode[STIX]{x1D712}_{1}\circ N))$
. Thus a refinement in this case is simply given by
![]() $1$
or
$1$
or
![]() $w$
.
$w$
.
Remark 10.16. In terms of Galois representation, the base change morphism from
![]() $GU(2,1)$
to
$GU(2,1)$
to
![]() $\operatorname{GL}_{3}\times \operatorname{GL}_{1}$
sends the (unramified) Satake parameter
$\operatorname{GL}_{3}\times \operatorname{GL}_{1}$
sends the (unramified) Satake parameter
![]() $\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}$
(if
$\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2}$
(if
![]() $\unicode[STIX]{x1D712}_{2}$
is unramified, it is trivial on
$\unicode[STIX]{x1D712}_{2}$
is unramified, it is trivial on
![]() $E^{1}$
) to the parameter
$E^{1}$
) to the parameter
![]() $((\unicode[STIX]{x1D712}_{1},1,\overline{\unicode[STIX]{x1D712}}_{1}^{-1}),\unicode[STIX]{x1D712}_{1}\unicode[STIX]{x1D712}_{2})$
(see [Reference Blasius and RogawskiBR92, Theorem 1.9.1] or [Reference SkinnerSki12, § 2]), whose semi-simple class in
$((\unicode[STIX]{x1D712}_{1},1,\overline{\unicode[STIX]{x1D712}}_{1}^{-1}),\unicode[STIX]{x1D712}_{1}\unicode[STIX]{x1D712}_{2})$
(see [Reference Blasius and RogawskiBR92, Theorem 1.9.1] or [Reference SkinnerSki12, § 2]), whose semi-simple class in
![]() $\operatorname{GL}_{3}$
associated by local Langlands has Frobenius class given by
$\operatorname{GL}_{3}$
associated by local Langlands has Frobenius class given by
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D712}_{2}(p) & & \\ & \unicode[STIX]{x1D712}_{1}(p)\unicode[STIX]{x1D712}_{2}(p) & \\ & & \unicode[STIX]{x1D712}_{2}(p)\unicode[STIX]{x1D712}_{1}^{2}(p)\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D712}_{2}(p) & & \\ & \unicode[STIX]{x1D712}_{1}(p)\unicode[STIX]{x1D712}_{2}(p) & \\ & & \unicode[STIX]{x1D712}_{2}(p)\unicode[STIX]{x1D712}_{1}^{2}(p)\end{array}\right).\end{eqnarray}$$
In the inert case, say
![]() $\unicode[STIX]{x1D70E}\in W_{G}$
is a refinement, then the action of
$\unicode[STIX]{x1D70E}\in W_{G}$
is a refinement, then the action of
![]() $U_{p}$
on the
$U_{p}$
on the
![]() $\unicode[STIX]{x1D70E}$
-part of
$\unicode[STIX]{x1D70E}$
-part of
![]() $\unicode[STIX]{x1D70B}_{N}^{T^{0}}$
is given by
$\unicode[STIX]{x1D70B}_{N}^{T^{0}}$
is given by
![]() $\unicode[STIX]{x1D712}_{1}^{\unicode[STIX]{x1D70E}}(p)^{2}\unicode[STIX]{x1D712}_{2}^{\unicode[STIX]{x1D70E}}(p)$
, and the action of
$\unicode[STIX]{x1D712}_{1}^{\unicode[STIX]{x1D70E}}(p)^{2}\unicode[STIX]{x1D712}_{2}^{\unicode[STIX]{x1D70E}}(p)$
, and the action of
![]() $s$
is given by
$s$
is given by
![]() $\unicode[STIX]{x1D712}_{1}^{\unicode[STIX]{x1D70E}}(p)\unicode[STIX]{x1D712}_{2}^{\unicode[STIX]{x1D70E}}(p)$
. In particular, the action of
$\unicode[STIX]{x1D712}_{1}^{\unicode[STIX]{x1D70E}}(p)\unicode[STIX]{x1D712}_{2}^{\unicode[STIX]{x1D70E}}(p)$
. In particular, the action of
![]() ${\mathcal{A}}(p)$
(through
${\mathcal{A}}(p)$
(through
![]() $T/T^{0}$
), and actually of
$T/T^{0}$
), and actually of
![]() $U_{p}$
or
$U_{p}$
or
![]() $u_{1}=U_{p}S_{p}^{-1}$
, on
$u_{1}=U_{p}S_{p}^{-1}$
, on
![]() $\unicode[STIX]{x1D70B}^{I}$
determines the refinement.
$\unicode[STIX]{x1D70B}^{I}$
determines the refinement.
This is also true (and easier) if
![]() $p$
splits.
$p$
splits.
As we normalized our Galois representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
so that they are polarized, i.e. forgetting the central character, the previous class does not directly relate to the Frobenius eigenvalues of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
so that they are polarized, i.e. forgetting the central character, the previous class does not directly relate to the Frobenius eigenvalues of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
but rather of the one of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
but rather of the one of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
. But as the link between both only differ through the central character of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
. But as the link between both only differ through the central character of
![]() $\unicode[STIX]{x1D70B}$
, it is straightforward that the Frobenius eigenvalues of (a crystalline)
$\unicode[STIX]{x1D70B}$
, it is straightforward that the Frobenius eigenvalues of (a crystalline)
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
are given by
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
are given by
![]() $(\unicode[STIX]{x1D713}_{1},1,\unicode[STIX]{x1D713}_{1}^{\bot })$
, when
$(\unicode[STIX]{x1D713}_{1},1,\unicode[STIX]{x1D713}_{1}^{\bot })$
, when
![]() $p$
is inert, and
$p$
is inert, and
![]() $\unicode[STIX]{x1D713}_{1}$
is given (if unramified) by the action of the Iwahori–Hecke double class
$\unicode[STIX]{x1D713}_{1}$
is given (if unramified) by the action of the Iwahori–Hecke double class
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & p^{-1}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & p^{-1}\end{array}\right)\end{eqnarray}$$
which corresponds to
![]() $U_{p}S_{p}^{-1}$
(see next subsection). In the split case, an unramified character of the torus of
$U_{p}S_{p}^{-1}$
(see next subsection). In the split case, an unramified character of the torus of
![]() $\operatorname{GL}_{3}\times \operatorname{GL}_{1}$
gives Frobenius eigenvalues
$\operatorname{GL}_{3}\times \operatorname{GL}_{1}$
gives Frobenius eigenvalues
![]() $(p\unicode[STIX]{x1D713}_{1}(p)\unicode[STIX]{x1D713}_{4}(p),p\unicode[STIX]{x1D713}_{2}(p)\unicode[STIX]{x1D713}_{4}(p),p\unicode[STIX]{x1D713}_{3}(p)\unicode[STIX]{x1D713}_{4}(p))$
for (crystalline)
$(p\unicode[STIX]{x1D713}_{1}(p)\unicode[STIX]{x1D713}_{4}(p),p\unicode[STIX]{x1D713}_{2}(p)\unicode[STIX]{x1D713}_{4}(p),p\unicode[STIX]{x1D713}_{3}(p)\unicode[STIX]{x1D713}_{4}(p))$
for (crystalline)
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
and
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},\text{Ski}}$
and
![]() $(\unicode[STIX]{x1D713}_{1}(p),\unicode[STIX]{x1D713}_{2}(p),\unicode[STIX]{x1D713}_{3}(p))$
for
$(\unicode[STIX]{x1D713}_{1}(p),\unicode[STIX]{x1D713}_{2}(p),\unicode[STIX]{x1D713}_{3}(p))$
for
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
, which relates to operators
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B}}$
, which relates to operators
![]() $U_{i-1}/U_{3}$
(see next subsection).
$U_{i-1}/U_{3}$
(see next subsection).
Thus, using the previous definition of refinement, local global compatibility at
![]() $p$
, we can associate to
$p$
, we can associate to
![]() $\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D70B}_{\infty }\otimes \bigotimes _{\ell }\unicode[STIX]{x1D70B}_{\ell }$
an algebraic regular cuspidal automorphic representation of
$\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D70B}_{\infty }\otimes \bigotimes _{\ell }\unicode[STIX]{x1D70B}_{\ell }$
an algebraic regular cuspidal automorphic representation of
![]() $GU(2,1)$
of level
$GU(2,1)$
of level
![]() $K^{Np}I$
a representation
$K^{Np}I$
a representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},p}$
together with an (accessible) ordering of its crystalline-Frobenius eigenvalues for each choice of a character in
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70B},p}$
together with an (accessible) ordering of its crystalline-Frobenius eigenvalues for each choice of a character in
![]() $\unicode[STIX]{x1D70B}_{p}^{I}$
under
$\unicode[STIX]{x1D70B}_{p}^{I}$
under
![]() ${\mathcal{A}}(p)$
, such that the following proposition holds.
${\mathcal{A}}(p)$
, such that the following proposition holds.
Proposition 10.17. The automorphic representation
![]() $\widetilde{\unicode[STIX]{x1D70B}}^{n}(\unicode[STIX]{x1D712})$
of
$\widetilde{\unicode[STIX]{x1D70B}}^{n}(\unicode[STIX]{x1D712})$
of
![]() $GU(2,1)$
constructed by Proposition 10.12 has only one accessible refinement at
$GU(2,1)$
constructed by Proposition 10.12 has only one accessible refinement at
![]() $p$
if
$p$
if
![]() $p$
is inert, it is given by
$p$
is inert, it is given by
which correspond to the ordering
![]() $((\unicode[STIX]{x1D712}^{\bot }(p),1,\unicode[STIX]{x1D712}(p)),\unicode[STIX]{x1D712}(p))$
or
$((\unicode[STIX]{x1D712}^{\bot }(p),1,\unicode[STIX]{x1D712}(p)),\unicode[STIX]{x1D712}(p))$
or
![]() $(1,\unicode[STIX]{x1D712}(p),|p|)$
. If
$(1,\unicode[STIX]{x1D712}(p),|p|)$
. If
![]() $p=\overline{v}v$
is split, there are three accessible refinements, given by:
$p=\overline{v}v$
is split, there are three accessible refinements, given by:
–
 $\unicode[STIX]{x1D70E}=1,((1,\unicode[STIX]{x1D712}_{v}^{\bot }(p),\unicode[STIX]{x1D712}_{v}(p)),\unicode[STIX]{x1D712}_{v}(p))$
which corresponds to
$\unicode[STIX]{x1D70E}=1,((1,\unicode[STIX]{x1D712}_{v}^{\bot }(p),\unicode[STIX]{x1D712}_{v}(p)),\unicode[STIX]{x1D712}_{v}(p))$
which corresponds to
 $(\unicode[STIX]{x1D712}_{v}(p),1,|p|)$
;
$(\unicode[STIX]{x1D712}_{v}(p),1,|p|)$
;–
 $\unicode[STIX]{x1D70E}=(3,2),((\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p)),\unicode[STIX]{x1D712}_{v}(p))$
which corresponds to
$\unicode[STIX]{x1D70E}=(3,2),((\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p)),\unicode[STIX]{x1D712}_{v}(p))$
which corresponds to
 $(1,\unicode[STIX]{x1D712}_{v}(p),|p|)$
;
$(1,\unicode[STIX]{x1D712}_{v}(p),|p|)$
;–
 $\unicode[STIX]{x1D70E}=(3,2,1),((\unicode[STIX]{x1D712}_{v}^{\bot }(p),\unicode[STIX]{x1D712}_{v}(p),1),\unicode[STIX]{x1D712}_{v}(p))$
which corresponds to
$\unicode[STIX]{x1D70E}=(3,2,1),((\unicode[STIX]{x1D712}_{v}^{\bot }(p),\unicode[STIX]{x1D712}_{v}(p),1),\unicode[STIX]{x1D712}_{v}(p))$
which corresponds to
 $(1,|p|,\unicode[STIX]{x1D712}_{v}(p))$
.
$(1,|p|,\unicode[STIX]{x1D712}_{v}(p))$
.
We denote by
![]() $\unicode[STIX]{x1D70E}$
the unique refinement in the inert case, and the refinement denoted by
$\unicode[STIX]{x1D70E}$
the unique refinement in the inert case, and the refinement denoted by
![]() $(3,2)$
in the split case.
$(3,2)$
in the split case.
Proof. The action of
![]() $u_{1}$
on
$u_{1}$
on
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})_{p}$
as been calculated in a previous section.◻
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})_{p}$
as been calculated in a previous section.◻
10.6 Modular and classical Hecke operators
In order to understand how the refinements vary on the eigenvariety, we need to make explicit the link between Hecke operators (at
![]() $p$
) constructed in § 8 and classical Hecke acting on automorphic forms, as above. Here we work at Iwahori level at
$p$
) constructed in § 8 and classical Hecke acting on automorphic forms, as above. Here we work at Iwahori level at
![]() $p$
and identify matrices with the corresponding Iwahori double classes. If
$p$
and identify matrices with the corresponding Iwahori double classes. If
![]() $p$
is inert in
$p$
is inert in
![]() $E$
, the Atkin–Lehner algebra we consider at
$E$
, the Atkin–Lehner algebra we consider at
![]() $p$
is generated by the two (so-called classical) operators
$p$
is generated by the two (so-called classical) operators
![]() $U_{p}^{c}$
and
$U_{p}^{c}$
and
![]() $S_{p}^{c}$
described above. If
$S_{p}^{c}$
described above. If
![]() $p$
is split in
$p$
is split in
![]() $E$
, we consider the Atkin–Lehner algebra
$E$
, we consider the Atkin–Lehner algebra
![]() ${\mathcal{A}}(p)$
of
${\mathcal{A}}(p)$
of
![]() $\operatorname{GL}_{3}(\mathbb{Q}_{p})\times \mathbb{Q}_{p}^{\times }$
(see [Reference Bellaïche and ChenevierBC09, § 6.4.1]); it is generated by the Hecke operators, up to identification of
$\operatorname{GL}_{3}(\mathbb{Q}_{p})\times \mathbb{Q}_{p}^{\times }$
(see [Reference Bellaïche and ChenevierBC09, § 6.4.1]); it is generated by the Hecke operators, up to identification of
![]() $E\otimes \mathbb{Q}_{p}\overset{i_{v}\times i_{\overline{v}}}{\simeq }\mathbb{Q}_{p}\times \mathbb{Q}_{p}$
,
$E\otimes \mathbb{Q}_{p}\overset{i_{v}\times i_{\overline{v}}}{\simeq }\mathbb{Q}_{p}\times \mathbb{Q}_{p}$
,
 $$\begin{eqnarray}(pI_{3},I_{3}),\quad \left(\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & 1\end{array}\right)\right),\left(\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & 1\end{array}\right)\right),\quad \left(\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & 1\end{array}\right),\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & 1\end{array}\right)\right),\quad (I_{3},pI_{3}),\end{eqnarray}$$
$$\begin{eqnarray}(pI_{3},I_{3}),\quad \left(\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & 1\end{array}\right)\right),\left(\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & 1\end{array}\right)\right),\quad \left(\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & 1\end{array}\right),\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & 1\end{array}\right)\right),\quad (I_{3},pI_{3}),\end{eqnarray}$$
that we denote respectively
![]() $U_{0}^{c},U_{1}^{c},U_{2}^{c}$
and
$U_{0}^{c},U_{1}^{c},U_{2}^{c}$
and
![]() $U_{3}^{c}$
(
$U_{3}^{c}$
(
![]() $c$
stands for classical in the sense ‘not normalized’). If we use
$c$
stands for classical in the sense ‘not normalized’). If we use
![]() $i_{v}$
to identify
$i_{v}$
to identify
![]() $GU(2,1)(\mathbb{Q}_{p})$
with
$GU(2,1)(\mathbb{Q}_{p})$
with
![]() $\operatorname{GL}_{3}\times \operatorname{GL}_{1}(\mathbb{Q}_{p})$
, then these operators are identified respectively with
$\operatorname{GL}_{3}\times \operatorname{GL}_{1}(\mathbb{Q}_{p})$
, then these operators are identified respectively with
 $$\begin{eqnarray}(pI_{3},p),\quad \left(\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & 1\end{array}\right),p\right),\quad \left(\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & 1\end{array}\right),p\right),\quad (I_{3},p).\end{eqnarray}$$
$$\begin{eqnarray}(pI_{3},p),\quad \left(\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & 1\end{array}\right),p\right),\quad \left(\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & 1\end{array}\right),p\right),\quad (I_{3},p).\end{eqnarray}$$
In § 8 we defined Hecke operators modularly,
![]() $U_{p}$
and
$U_{p}$
and
![]() $S_{p}$
in the inert case, and both Brasca [Reference BrascaBra16] and Bijakowski [Reference BijakowskiBij16] defined
$S_{p}$
in the inert case, and both Brasca [Reference BrascaBra16] and Bijakowski [Reference BijakowskiBij16] defined
![]() $U_{0},U_{1},U_{2},U_{3}$
in the split case (see remark in § 8.3). These Hecke operators have been normalized and correspond to the above Iwahori double classes, so that we have the following result.
$U_{0},U_{1},U_{2},U_{3}$
in the split case (see remark in § 8.3). These Hecke operators have been normalized and correspond to the above Iwahori double classes, so that we have the following result.
Let
![]() $\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D70B}_{\infty }\otimes \bigotimes _{\ell }\unicode[STIX]{x1D70B}_{\ell }$
be an algebraic, regular, cuspidal automorphic representation of
$\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D70B}_{\infty }\otimes \bigotimes _{\ell }\unicode[STIX]{x1D70B}_{\ell }$
be an algebraic, regular, cuspidal automorphic representation of
![]() $GU(2,1)$
of level
$GU(2,1)$
of level
![]() $K^{Np}I$
whose Hecke eigenvalues appear in the global sections of a coherent automorphic sheaf (of weight
$K^{Np}I$
whose Hecke eigenvalues appear in the global sections of a coherent automorphic sheaf (of weight
![]() $\unicode[STIX]{x1D705}$
) and
$\unicode[STIX]{x1D705}$
) and
![]() $f\in \unicode[STIX]{x1D6F1}\cap H^{0}(X_{I},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
an eigenform for
$f\in \unicode[STIX]{x1D6F1}\cap H^{0}(X_{I},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
an eigenform for
![]() ${\mathcal{H}}={\mathcal{H}}^{Np}\otimes {\mathcal{A}}(p)$
, such that, if
${\mathcal{H}}={\mathcal{H}}^{Np}\otimes {\mathcal{A}}(p)$
, such that, if
![]() $p$
is inert,
$p$
is inert,
and if
![]() $p$
splits,
$p$
splits,
where the action of the double classes
![]() $U_{p}^{c}$
,
$U_{p}^{c}$
,
![]() $S_{p}^{c}$
and
$S_{p}^{c}$
and
![]() $U_{i}^{c}$
is given by convolution on
$U_{i}^{c}$
is given by convolution on
![]() $\unicode[STIX]{x1D70B}_{p}$
.
$\unicode[STIX]{x1D70B}_{p}$
.
Proposition 10.18. Suppose
![]() $p$
is inert,
$p$
is inert,
![]() $f$
is a classical automorphic form of classical weight
$f$
is a classical automorphic form of classical weight
![]() $\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})$
of Iwahori level at p (i.e.
$\unicode[STIX]{x1D705}=(k_{1},k_{2},k_{3})$
of Iwahori level at p (i.e.
![]() $f\in H^{0}(X_{Iw},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
), which is an eigenform for the action of
$f\in H^{0}(X_{Iw},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
), which is an eigenform for the action of
![]() ${\mathcal{H}}\otimes {\mathcal{A}}(p)$
, and denote by
${\mathcal{H}}\otimes {\mathcal{A}}(p)$
, and denote by
![]() $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}$
the eigenvalues of
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}$
the eigenvalues of
![]() $f$
for
$f$
for
![]() $U_{p},S_{p}$
respectively.
$U_{p},S_{p}$
respectively.
Let
![]() $\unicode[STIX]{x1D6F1}$
be a irreducible factor of the associated automorphic representation (generated by
$\unicode[STIX]{x1D6F1}$
be a irreducible factor of the associated automorphic representation (generated by
![]() $\unicode[STIX]{x1D6F7}_{f}$
). Then
$\unicode[STIX]{x1D6F7}_{f}$
). Then
![]() $\unicode[STIX]{x1D6F1}_{p}^{I}\neq \{0\}$
and thus the algebra
$\unicode[STIX]{x1D6F1}_{p}^{I}\neq \{0\}$
and thus the algebra
![]() ${\mathcal{A}}(p)$
acts on
${\mathcal{A}}(p)$
acts on
![]() $\unicode[STIX]{x1D6F1}_{p}^{I}$
with
$\unicode[STIX]{x1D6F1}_{p}^{I}$
with
![]() $U_{p}^{c}$
of eigenvalue
$U_{p}^{c}$
of eigenvalue
![]() $p^{k_{2}}\unicode[STIX]{x1D706}$
and
$p^{k_{2}}\unicode[STIX]{x1D706}$
and
![]() $S_{p}^{c}$
of eigenvalue
$S_{p}^{c}$
of eigenvalue
![]() $p^{|k|}\unicode[STIX]{x1D707}$
.
$p^{|k|}\unicode[STIX]{x1D707}$
.
Proof. To prove the statement, we remark that the association
![]() $f\mapsto \unicode[STIX]{x1D6F7}_{f}$
is Hecke equivariant for the classical Hecke operators
$f\mapsto \unicode[STIX]{x1D6F7}_{f}$
is Hecke equivariant for the classical Hecke operators
![]() $U_{p}^{c},S_{p}^{c}$
acting on
$U_{p}^{c},S_{p}^{c}$
acting on
![]() $f$
. But we defined the Hecke operators
$f$
. But we defined the Hecke operators
![]() $U_{p},S_{p}$
geometrically by
$U_{p},S_{p}$
geometrically by
![]() $U_{p}=p^{-k_{2}}U_{p}^{c}$
and
$U_{p}=p^{-k_{2}}U_{p}^{c}$
and
![]() $S_{p}=p^{-|k|}S_{p}^{c}$
to make them vary p-adically. Thus we get the result.◻
$S_{p}=p^{-|k|}S_{p}^{c}$
to make them vary p-adically. Thus we get the result.◻
Using the previous refinements for representations of
![]() $GU(2,1)$
, we can prove the following result on density of crystalline points on the eigenvariety
$GU(2,1)$
, we can prove the following result on density of crystalline points on the eigenvariety
![]() ${\mathcal{E}}$
of Theorem 9.15,
${\mathcal{E}}$
of Theorem 9.15,
Proposition 10.19. Suppose
![]() $p$
is inert. Let
$p$
is inert. Let
![]() $x\in {\mathcal{E}}(F)$
. There exists a neighborhood
$x\in {\mathcal{E}}(F)$
. There exists a neighborhood
![]() $V$
of
$V$
of
![]() $x$
and a constant
$x$
and a constant
![]() $C>0$
such, that for all classical points
$C>0$
such, that for all classical points
![]() $y\in V$
, if
$y\in V$
, if
![]() $|w_{2}(y)+w_{3}(y)|>C$
, then
$|w_{2}(y)+w_{3}(y)|>C$
, then
![]() $\unicode[STIX]{x1D70C}_{y}$
is crystalline and of Hodge–Tate weights
$\unicode[STIX]{x1D70C}_{y}$
is crystalline and of Hodge–Tate weights
![]() $(1+w_{3}(y),-1-w_{1}(y),-w_{2}(y))$
.
$(1+w_{3}(y),-1-w_{1}(y),-w_{2}(y))$
.
In particular crystalline points are dense in
![]() ${\mathcal{E}}$
by classicity Proposition 8.16 (as we can also assume
${\mathcal{E}}$
by classicity Proposition 8.16 (as we can also assume
![]() $w_{1}(y)-w_{2}(y)>C$
) and Theorem 8.17 (as we can moreover assume
$w_{1}(y)-w_{2}(y)>C$
) and Theorem 8.17 (as we can moreover assume
![]() $-w_{1}(y)-w_{3}(y)>C$
).
$-w_{1}(y)-w_{3}(y)>C$
).
Proof. Denote by
![]() $F_{1},F_{2}$
the two invertible functions of
$F_{1},F_{2}$
the two invertible functions of
![]() ${\mathcal{E}}$
given by the eigenvalues under
${\mathcal{E}}$
given by the eigenvalues under
 $$\begin{eqnarray}U_{p}=\left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right)\quad \text{and}\quad S_{p}=\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & p\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}U_{p}=\left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right)\quad \text{and}\quad S_{p}=\left(\begin{array}{@{}ccc@{}}p & & \\ & p & \\ & & p\end{array}\right).\end{eqnarray}$$
The valuations of
![]() $F_{1},F_{2}$
are locally constant on
$F_{1},F_{2}$
are locally constant on
![]() ${\mathcal{E}}$
, and thus there exists
${\mathcal{E}}$
, and thus there exists
![]() $V$
a neighborhood of
$V$
a neighborhood of
![]() $x$
where these valuations are constant. As
$x$
where these valuations are constant. As
![]() $y$
corresponds to
$y$
corresponds to
![]() $f$
a classical form of (
$f$
a classical form of (
![]() $p$
-adic) weight
$p$
-adic) weight
![]() $w(y)$
and level
$w(y)$
and level
![]() $K$
proper under
$K$
proper under
![]() ${\mathcal{H}}\otimes {\mathcal{A}}(p)$
, we can look at
${\mathcal{H}}\otimes {\mathcal{A}}(p)$
, we can look at
![]() $\unicode[STIX]{x1D6F1}$
an irreducible component of the representation generated by
$\unicode[STIX]{x1D6F1}$
an irreducible component of the representation generated by
![]() $\unicode[STIX]{x1D6F7}_{f}$
, which is thus algebraic, regular, and its associated representation
$\unicode[STIX]{x1D6F7}_{f}$
, which is thus algebraic, regular, and its associated representation
![]() $\unicode[STIX]{x1D70C}_{y}$
does not depend on
$\unicode[STIX]{x1D70C}_{y}$
does not depend on
![]() $\unicode[STIX]{x1D6F1}$
as it only depends on the eigenvalues of
$\unicode[STIX]{x1D6F1}$
as it only depends on the eigenvalues of
![]() ${\mathcal{H}}$
on
${\mathcal{H}}$
on
![]() $f$
. As
$f$
. As
![]() $\unicode[STIX]{x1D6F1}_{p}$
, the
$\unicode[STIX]{x1D6F1}_{p}$
, the
![]() $p$
th component of
$p$
th component of
![]() $\unicode[STIX]{x1D6F1}$
, is generated by its
$\unicode[STIX]{x1D6F1}$
, is generated by its
![]() $I$
-invariants,
$I$
-invariants,
![]() $\unicode[STIX]{x1D6F1}_{p}$
is a subquotient of the induction
$\unicode[STIX]{x1D6F1}_{p}$
is a subquotient of the induction
![]() $\operatorname{ind}-n_{B}^{G}(\mathbb{Q}_{p})(\unicode[STIX]{x1D713})$
for some unramified character
$\operatorname{ind}-n_{B}^{G}(\mathbb{Q}_{p})(\unicode[STIX]{x1D713})$
for some unramified character
![]() $\unicode[STIX]{x1D713}$
([Reference Bellaïche and ChenevierBC09, Proposition 6.4.3] and the adjunction property of induction). We need to show that
$\unicode[STIX]{x1D713}$
([Reference Bellaïche and ChenevierBC09, Proposition 6.4.3] and the adjunction property of induction). We need to show that
![]() $\unicode[STIX]{x1D6F1}_{p}$
is unramified, but as
$\unicode[STIX]{x1D6F1}_{p}$
is unramified, but as
![]() $\unicode[STIX]{x1D6F1}_{p}$
appears as a subquotient of
$\unicode[STIX]{x1D6F1}_{p}$
appears as a subquotient of
![]() $\operatorname{ind}_{B}(\unicode[STIX]{x1D713})$
, which has a unique unramified subquotient, it suffices to prove that
$\operatorname{ind}_{B}(\unicode[STIX]{x1D713})$
, which has a unique unramified subquotient, it suffices to prove that
![]() $\operatorname{ind}_{B}(\unicode[STIX]{x1D713})$
is irreducible, which happens in particular when
$\operatorname{ind}_{B}(\unicode[STIX]{x1D713})$
is irreducible, which happens in particular when
![]() $|\unicode[STIX]{x1D713}_{1}(p)|\neq p^{\pm 1}$
when
$|\unicode[STIX]{x1D713}_{1}(p)|\neq p^{\pm 1}$
when
![]() $p$
is inert (cf. the key result of Keys, see [Reference RogawskiRog90, 12.2]).
$p$
is inert (cf. the key result of Keys, see [Reference RogawskiRog90, 12.2]).
In the inert case, we have that if
![]() $w=(-k_{2},-k_{1},-k_{3})$
i.e.
$w=(-k_{2},-k_{1},-k_{3})$
i.e.
![]() $f$
is of automorphic classical weight
$f$
is of automorphic classical weight
![]() $(k_{1},k_{2},k_{3})$
, then by Proposition 10.18
$(k_{1},k_{2},k_{3})$
, then by Proposition 10.18
for a certain choice
![]() $\unicode[STIX]{x1D70E}\in W_{GU}$
(see § 10.5 for example), but as the valuations of
$\unicode[STIX]{x1D70E}\in W_{GU}$
(see § 10.5 for example), but as the valuations of
![]() $F_{1},F_{2}$
are constant on
$F_{1},F_{2}$
are constant on
![]() $V$
, there is a constant
$V$
, there is a constant
![]() $C$
such that if
$C$
such that if
![]() $|k_{1}+k_{3}|>C$
,
$|k_{1}+k_{3}|>C$
,
![]() $\unicode[STIX]{x1D6F1}_{p}$
is unramified. Thus, by local–global compatibility at
$\unicode[STIX]{x1D6F1}_{p}$
is unramified. Thus, by local–global compatibility at
![]() $p$
for
$p$
for
![]() $\unicode[STIX]{x1D6F1}$
(cf. [Reference SkinnerSki12, Theorem B]),
$\unicode[STIX]{x1D6F1}$
(cf. [Reference SkinnerSki12, Theorem B]),
![]() $\unicode[STIX]{x1D70C}_{y}$
is crystalline.◻
$\unicode[STIX]{x1D70C}_{y}$
is crystalline.◻
Remark 10.20. In the split case, the same proposition is true under the assumption
![]() $\unicode[STIX]{x1D6FF}(w(y)):=\min _{i}(|w_{i}(y)-w_{i+1}(y)|)>C$
as the same proof of proposition 8.2 of [Reference Bellaïche and ChenevierBC04], together with classicity results of [Reference Bijakowski, Pilloni and StrohBPS16], and [Reference BrascaBra16, Proposition 6.6, Theorem 6.7] applies.
$\unicode[STIX]{x1D6FF}(w(y)):=\min _{i}(|w_{i}(y)-w_{i+1}(y)|)>C$
as the same proof of proposition 8.2 of [Reference Bellaïche and ChenevierBC04], together with classicity results of [Reference Bijakowski, Pilloni and StrohBPS16], and [Reference BrascaBra16, Proposition 6.6, Theorem 6.7] applies.
10.7 Types at ramified primes for
 $\unicode[STIX]{x1D712}$
$\unicode[STIX]{x1D712}$
In order to control the ramification at
![]() $\ell |\operatorname{Cond}(\unicode[STIX]{x1D712})$
, Bellaïche and Chenevier introduced a particular type
$\ell |\operatorname{Cond}(\unicode[STIX]{x1D712})$
, Bellaïche and Chenevier introduced a particular type
![]() $(K_{0},J_{0})$
, which we can slightly modify to suit our situation.
$(K_{0},J_{0})$
, which we can slightly modify to suit our situation.
Proposition 10.21. Let
![]() $\ell |\operatorname{Cond}(\unicode[STIX]{x1D712})$
a prime. There exists a compact subgroup
$\ell |\operatorname{Cond}(\unicode[STIX]{x1D712})$
a prime. There exists a compact subgroup
![]() $K_{\ell }$
of
$K_{\ell }$
of
![]() $GU$
$GU$
![]() $(2,1)(\mathbb{Q}_{\ell })$
and a representation
$(2,1)(\mathbb{Q}_{\ell })$
and a representation
![]() $J_{\ell }$
of
$J_{\ell }$
of
![]() $K_{\ell }$
such that the following hold:
$K_{\ell }$
such that the following hold:
(i)
 $\operatorname{Hom}_{K_{\ell }}(J_{\ell },\widetilde{\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})}\otimes (\unicode[STIX]{x1D712}_{0,\ell }\circ \det ))\neq 0$
;
$\operatorname{Hom}_{K_{\ell }}(J_{\ell },\widetilde{\unicode[STIX]{x1D70B}_{\ell }^{n}(\unicode[STIX]{x1D712})}\otimes (\unicode[STIX]{x1D712}_{0,\ell }\circ \det ))\neq 0$
;(ii) For all smooth admissible representation
 $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
 $GU(2,1)(\mathbb{Q}_{\ell })$
such that
$GU(2,1)(\mathbb{Q}_{\ell })$
such that
 $\operatorname{Hom}_{K_{\ell }}(J_{\ell },\unicode[STIX]{x1D70B})\neq 0$
and for all place
$\operatorname{Hom}_{K_{\ell }}(J_{\ell },\unicode[STIX]{x1D70B})\neq 0$
and for all place
 $v|\ell$
, there exist four unramified characters
$v|\ell$
, there exist four unramified characters
 $\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D719}_{3},\unicode[STIX]{x1D719}_{4}:E_{v}^{\times }\longrightarrow \mathbb{C}^{\times }$
such that the Langlands semi-simple class in
$\unicode[STIX]{x1D719}_{1},\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D719}_{3},\unicode[STIX]{x1D719}_{4}:E_{v}^{\times }\longrightarrow \mathbb{C}^{\times }$
such that the Langlands semi-simple class in
 $\operatorname{GL}_{3}\times \operatorname{GL}_{1}$
corresponds to or to the (unpolarized) Langlands class in
$\operatorname{GL}_{3}\times \operatorname{GL}_{1}$
corresponds to or to the (unpolarized) Langlands class in $$\begin{eqnarray}L(\unicode[STIX]{x1D70B}_{E_{v}})=(\unicode[STIX]{x1D719}_{1}\oplus \unicode[STIX]{x1D719}_{2}\oplus \unicode[STIX]{x1D719}_{3}\unicode[STIX]{x1D712}_{0}^{-1},\unicode[STIX]{x1D719}_{4}\unicode[STIX]{x1D712}_{0}^{-1})\end{eqnarray}$$
$$\begin{eqnarray}L(\unicode[STIX]{x1D70B}_{E_{v}})=(\unicode[STIX]{x1D719}_{1}\oplus \unicode[STIX]{x1D719}_{2}\oplus \unicode[STIX]{x1D719}_{3}\unicode[STIX]{x1D712}_{0}^{-1},\unicode[STIX]{x1D719}_{4}\unicode[STIX]{x1D712}_{0}^{-1})\end{eqnarray}$$
 $\operatorname{GL}_{3}$
,
$\operatorname{GL}_{3}$
,  $$\begin{eqnarray}L(\unicode[STIX]{x1D70B}_{E_{v}})=\unicode[STIX]{x1D719}_{1}\overline{\unicode[STIX]{x1D719}_{4}}\unicode[STIX]{x1D712}_{0}\oplus \unicode[STIX]{x1D719}_{1}\overline{\unicode[STIX]{x1D719}_{4}}\unicode[STIX]{x1D712}_{0}\oplus \unicode[STIX]{x1D719}_{3}\overline{\unicode[STIX]{x1D719}_{4}}.\end{eqnarray}$$
$$\begin{eqnarray}L(\unicode[STIX]{x1D70B}_{E_{v}})=\unicode[STIX]{x1D719}_{1}\overline{\unicode[STIX]{x1D719}_{4}}\unicode[STIX]{x1D712}_{0}\oplus \unicode[STIX]{x1D719}_{1}\overline{\unicode[STIX]{x1D719}_{4}}\unicode[STIX]{x1D712}_{0}\oplus \unicode[STIX]{x1D719}_{3}\overline{\unicode[STIX]{x1D719}_{4}}.\end{eqnarray}$$
Proof. Let
![]() $(K_{\ell }^{0},J_{\ell }^{0})$
be the type defined by Bellaïche and Chenevier in [Reference Bellaïche and ChenevierBC04]. If
$(K_{\ell }^{0},J_{\ell }^{0})$
be the type defined by Bellaïche and Chenevier in [Reference Bellaïche and ChenevierBC04]. If
![]() $\ell =v_{1}v_{2}$
is split, let
$\ell =v_{1}v_{2}$
is split, let
![]() $K_{\ell }$
be the subgroup of matrices congruent to
$K_{\ell }$
be the subgroup of matrices congruent to
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\star & \star & \star \\ \star & \star & \star \\ 0 & 0 & y\end{array}\right),e\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}\star & \star & \star \\ \star & \star & \star \\ 0 & 0 & y\end{array}\right),e\end{eqnarray}$$
modulo
![]() $\ell ^{m}$
, the
$\ell ^{m}$
, the
![]() $\ell$
-adic valuation of
$\ell$
-adic valuation of
![]() $\operatorname{Cond}(\unicode[STIX]{x1D712})$
. Let
$\operatorname{Cond}(\unicode[STIX]{x1D712})$
. Let
![]() $J_{\ell }$
be the representation that sends the matrices in
$J_{\ell }$
be the representation that sends the matrices in
![]() $K_{\ell }$
to
$K_{\ell }$
to
![]() $\unicode[STIX]{x1D712}_{0,v_{1}}^{-1}(y)\unicode[STIX]{x1D712}_{0,v_{1}}(\overline{e})$
. As every matrix in
$\unicode[STIX]{x1D712}_{0,v_{1}}^{-1}(y)\unicode[STIX]{x1D712}_{0,v_{1}}(\overline{e})$
. As every matrix in
![]() $GU(2,1)(\mathbb{Q}_{\ell })=\operatorname{GL}_{3}\times \operatorname{GL}_{1}(\mathbb{Q}_{\ell })$
can be written as
$GU(2,1)(\mathbb{Q}_{\ell })=\operatorname{GL}_{3}\times \operatorname{GL}_{1}(\mathbb{Q}_{\ell })$
can be written as
![]() $M=\unicode[STIX]{x1D706}U$
where
$M=\unicode[STIX]{x1D706}U$
where
![]() $U\in U(2,1)(\mathbb{Q}_{\ell })=\operatorname{GL}_{3}(\mathbb{Q}_{\ell })$
and
$U\in U(2,1)(\mathbb{Q}_{\ell })=\operatorname{GL}_{3}(\mathbb{Q}_{\ell })$
and
![]() $\unicode[STIX]{x1D706}=(1,\unicode[STIX]{x1D706})$
is in the center, we can check that
$\unicode[STIX]{x1D706}=(1,\unicode[STIX]{x1D706})$
is in the center, we can check that
![]() $\operatorname{Hom}_{K_{\ell }}(J_{\ell },\widetilde{\unicode[STIX]{x1D70B}}_{\ell }^{n}\otimes \unicode[STIX]{x1D712}_{0,v_{1}}\circ \det ^{-1})\neq 0$
.
$\operatorname{Hom}_{K_{\ell }}(J_{\ell },\widetilde{\unicode[STIX]{x1D70B}}_{\ell }^{n}\otimes \unicode[STIX]{x1D712}_{0,v_{1}}\circ \det ^{-1})\neq 0$
.
Now, if
![]() $\operatorname{Hom}_{K_{\ell }}(J_{\ell },\unicode[STIX]{x1D70B})\neq 0$
, then
$\operatorname{Hom}_{K_{\ell }}(J_{\ell },\unicode[STIX]{x1D70B})\neq 0$
, then
![]() $\operatorname{Hom}_{K_{\ell }^{0}}(J_{\ell }^{0},\unicode[STIX]{x1D70B}_{|U(2,1)})\neq 0$
when restricted to
$\operatorname{Hom}_{K_{\ell }^{0}}(J_{\ell }^{0},\unicode[STIX]{x1D70B}_{|U(2,1)})\neq 0$
when restricted to
![]() $U(2,1)=\operatorname{GL}_{3}$
, and thus by [Reference Bellaïche and ChenevierBC04] we have the conclusion up to a character. But, as
$U(2,1)=\operatorname{GL}_{3}$
, and thus by [Reference Bellaïche and ChenevierBC04] we have the conclusion up to a character. But, as
![]() $K^{\prime }=(\text{Id}\times \operatorname{GL}_{1})\cap K_{\ell }^{0}\simeq \mathbb{Z}_{\ell }^{\times }$
,
$K^{\prime }=(\text{Id}\times \operatorname{GL}_{1})\cap K_{\ell }^{0}\simeq \mathbb{Z}_{\ell }^{\times }$
,
![]() $\unicode[STIX]{x1D70B}_{|K^{\prime }}=\unicode[STIX]{x1D712}_{0,v_{1}}^{-1}\otimes \unicode[STIX]{x1D713}$
where
$\unicode[STIX]{x1D70B}_{|K^{\prime }}=\unicode[STIX]{x1D712}_{0,v_{1}}^{-1}\otimes \unicode[STIX]{x1D713}$
where
![]() $\unicode[STIX]{x1D713}$
is an unramified character, and thus
$\unicode[STIX]{x1D713}$
is an unramified character, and thus
If
![]() $\ell$
is prime, write
$\ell$
is prime, write
![]() $K_{\ell }={\mathcal{O}}_{E_{\ell }}^{\times }K_{\ell }^{0}$
and define
$K_{\ell }={\mathcal{O}}_{E_{\ell }}^{\times }K_{\ell }^{0}$
and define
![]() $J_{\ell }$
by
$J_{\ell }$
by
As
![]() ${\mathcal{O}}_{E_{\ell }}^{\times }\cap K^{0}\subset {\mathcal{O}}_{E_{\ell }}^{1}$
, this is well-defined because the central character of
${\mathcal{O}}_{E_{\ell }}^{\times }\cap K^{0}\subset {\mathcal{O}}_{E_{\ell }}^{1}$
, this is well-defined because the central character of
![]() $J_{\ell }^{0}$
is up to an unramified character equal to
$J_{\ell }^{0}$
is up to an unramified character equal to
![]() $\unicode[STIX]{x1D712}_{\ell }^{-2}$
. Moreover,
$\unicode[STIX]{x1D712}_{\ell }^{-2}$
. Moreover,
![]() $\operatorname{Hom}_{K_{\ell }}(J_{\ell },\widetilde{\unicode[STIX]{x1D70B}}_{\ell }^{n})(\unicode[STIX]{x1D712})\otimes (\unicode[STIX]{x1D712}_{0,\ell }\,\circ \,\det )\neq 0$
as it is the case for
$\operatorname{Hom}_{K_{\ell }}(J_{\ell },\widetilde{\unicode[STIX]{x1D70B}}_{\ell }^{n})(\unicode[STIX]{x1D712})\otimes (\unicode[STIX]{x1D712}_{0,\ell }\,\circ \,\det )\neq 0$
as it is the case for
![]() $(K_{\ell }^{0},J_{\ell }^{0})$
by [Reference Bellaïche and ChenevierBC04] which refers back to Blasco [Reference BlascoBla02], and the central character of
$(K_{\ell }^{0},J_{\ell }^{0})$
by [Reference Bellaïche and ChenevierBC04] which refers back to Blasco [Reference BlascoBla02], and the central character of
![]() $\widetilde{\unicode[STIX]{x1D70B}^{n}}_{\ell }(\unicode[STIX]{x1D712})$
is equal to
$\widetilde{\unicode[STIX]{x1D70B}^{n}}_{\ell }(\unicode[STIX]{x1D712})$
is equal to
![]() $\unicode[STIX]{x1D712}_{\ell }$
(up to a unramified character).
$\unicode[STIX]{x1D712}_{\ell }$
(up to a unramified character).
Conversely, if
![]() $\unicode[STIX]{x1D70B}$
is a representation of
$\unicode[STIX]{x1D70B}$
is a representation of
![]() $GU(3)(\mathbb{Q}_{\ell })$
such that
$GU(3)(\mathbb{Q}_{\ell })$
such that
![]() $\operatorname{Hom}_{K_{\ell }}(J_{\ell },\unicode[STIX]{x1D70B})\neq 0$
, then
$\operatorname{Hom}_{K_{\ell }}(J_{\ell },\unicode[STIX]{x1D70B})\neq 0$
, then
![]() $\operatorname{Hom}_{K_{\ell }^{0}}(J_{\ell }^{0},\unicode[STIX]{x1D70B}_{|U(3)(\mathbb{Q}_{\ell })})\neq 0$
and thus
$\operatorname{Hom}_{K_{\ell }^{0}}(J_{\ell }^{0},\unicode[STIX]{x1D70B}_{|U(3)(\mathbb{Q}_{\ell })})\neq 0$
and thus
![]() $L(\unicode[STIX]{x1D70B}_{|U(3)})=\unicode[STIX]{x1D719}_{1}\oplus \unicode[STIX]{x1D719}_{2}\oplus \unicode[STIX]{x1D719}_{3}\unicode[STIX]{x1D712}_{0}^{-1}$
by [Reference Bellaïche and ChenevierBC04], and its central character corresponds to
$L(\unicode[STIX]{x1D70B}_{|U(3)})=\unicode[STIX]{x1D719}_{1}\oplus \unicode[STIX]{x1D719}_{2}\oplus \unicode[STIX]{x1D719}_{3}\unicode[STIX]{x1D712}_{0}^{-1}$
by [Reference Bellaïche and ChenevierBC04], and its central character corresponds to
![]() $\unicode[STIX]{x1D712}_{\ell }$
up to an unramified character, and we thus get the result on the Langlands Base change of
$\unicode[STIX]{x1D712}_{\ell }$
up to an unramified character, and we thus get the result on the Langlands Base change of
![]() $\unicode[STIX]{x1D70B}$
.◻
$\unicode[STIX]{x1D70B}$
.◻
11 Deformation of
 $\widetilde{\unicode[STIX]{x1D70B}^{n}}$
$\widetilde{\unicode[STIX]{x1D70B}^{n}}$
By Proposition 10.21, we can find for every
![]() $\ell |\operatorname{Cond}(\unicode[STIX]{x1D712})$
$\ell |\operatorname{Cond}(\unicode[STIX]{x1D712})$
![]() $K_{\ell }$
a subgroup of
$K_{\ell }$
a subgroup of
![]() $GU(2,1)(\mathbb{Q}_{\ell })$
and an irreducible representation
$GU(2,1)(\mathbb{Q}_{\ell })$
and an irreducible representation
![]() $J_{\ell }$
such that
$J_{\ell }$
such that
and for all
![]() $\widetilde{\unicode[STIX]{x1D70B}}_{\ell }$
of type
$\widetilde{\unicode[STIX]{x1D70B}}_{\ell }$
of type
![]() $(K_{\ell },J_{\ell })$
its base change to
$(K_{\ell },J_{\ell })$
its base change to
![]() $\operatorname{GL}_{3}(E_{v})$
, for all
$\operatorname{GL}_{3}(E_{v})$
, for all
![]() $v|\ell$
, gives the representation (normalized as in Proposition 9.17, Theorem 9.19)
$v|\ell$
, gives the representation (normalized as in Proposition 9.17, Theorem 9.19)
where
![]() $\unicode[STIX]{x1D719}_{j}:E_{v}^{\times }\longrightarrow \mathbb{C}^{\times }$
are unramified characters.
$\unicode[STIX]{x1D719}_{j}:E_{v}^{\times }\longrightarrow \mathbb{C}^{\times }$
are unramified characters.
11.1 Choosing the level
Up to choosing compatibly places at
![]() $\infty$
and embeddings of
$\infty$
and embeddings of
![]() $\mathbb{Q}_{p^{2}}$
, we can make
$\mathbb{Q}_{p^{2}}$
, we can make
![]() $\unicode[STIX]{x1D712}:G_{E}\longrightarrow \overline{\mathbb{Q}_{p}}$
, the
$\unicode[STIX]{x1D712}:G_{E}\longrightarrow \overline{\mathbb{Q}_{p}}$
, the
![]() $p$
-adic realization of
$p$
-adic realization of
![]() $\unicode[STIX]{x1D712}$
at
$\unicode[STIX]{x1D712}$
at
![]() $p$
, have
$p$
, have
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weight
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weight
![]() $-a=-(k+1)/2$
and thus
$-a=-(k+1)/2$
and thus
![]() $\overline{\unicode[STIX]{x1D712}}$
$\overline{\unicode[STIX]{x1D712}}$
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weight
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weight
![]() $a-1=(k-1)/2$
.
$a-1=(k-1)/2$
.
Let
![]() $N=\operatorname{Cond}(\unicode[STIX]{x1D712})$
; suppose
$N=\operatorname{Cond}(\unicode[STIX]{x1D712})$
; suppose
![]() $p\neq 2$
if
$p\neq 2$
if
![]() $p$
is inert,
$p$
is inert,
![]() $p\mid N$
, and is unramified in
$p\mid N$
, and is unramified in
![]() $E$
. Define
$E$
. Define
![]() $K_{f}=\prod _{\ell }K_{\ell }$
by the following.
$K_{f}=\prod _{\ell }K_{\ell }$
by the following.
(i) If
 $\ell$
is prime to
$\ell$
is prime to
 $pN$
,
$pN$
,
 $K_{\ell }$
is the maximal compact subgroup defined previously such that
$K_{\ell }$
is the maximal compact subgroup defined previously such that
 $\widetilde{\unicode[STIX]{x1D70B}}^{n}$
as invariants by
$\widetilde{\unicode[STIX]{x1D70B}}^{n}$
as invariants by
 $K_{\ell }$
(hyperspecial at unramified
$K_{\ell }$
(hyperspecial at unramified
 $\ell$
, very special otherwise).
$\ell$
, very special otherwise).(ii) If
 $\ell =p$
,
$\ell =p$
,
 $K_{p}$
is the Iwahori subgroup of
$K_{p}$
is the Iwahori subgroup of
 $GU(2,1)(\mathbb{Q}_{p})$
.
$GU(2,1)(\mathbb{Q}_{p})$
.(iii) If
 $\ell |N$
,
$\ell |N$
,
 $K_{\ell }$
is the type as defined before.
$K_{\ell }$
is the type as defined before.
We then set
as representation of
![]() $K_{f}$
.
$K_{f}$
.
By construction of
![]() $K_{f}$
, there is
$K_{f}$
, there is
![]() $\unicode[STIX]{x1D719}\in \widetilde{\unicode[STIX]{x1D70B}^{n}}(\unicode[STIX]{x1D712})^{K_{f}}$
, an automorphic eigenform for
$\unicode[STIX]{x1D719}\in \widetilde{\unicode[STIX]{x1D70B}^{n}}(\unicode[STIX]{x1D712})^{K_{f}}$
, an automorphic eigenform for
![]() ${\mathcal{H}}^{Np}$
and of character under
${\mathcal{H}}^{Np}$
and of character under
![]() ${\mathcal{A}}(p)$
corresponding to the refinement
${\mathcal{A}}(p)$
corresponding to the refinement
![]() $\unicode[STIX]{x1D70E}$
of Proposition 10.17 and which is associated a classical Picard modular form
$\unicode[STIX]{x1D70E}$
of Proposition 10.17 and which is associated a classical Picard modular form
![]() $f\in H^{0}(X_{I},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
(by Proposition D.2 or Proposition 10.11 if
$f\in H^{0}(X_{I},\unicode[STIX]{x1D714}^{\unicode[STIX]{x1D705}})$
(by Proposition D.2 or Proposition 10.11 if
![]() $a>1$
) which is an eigenform for
$a>1$
) which is an eigenform for
![]() ${\mathcal{A}}(p)$
, whose eigenvalues for
${\mathcal{A}}(p)$
, whose eigenvalues for
![]() ${\mathcal{A}}(p)$
corresponds to the refinement
${\mathcal{A}}(p)$
corresponds to the refinement
![]() $\unicode[STIX]{x1D70E}$
too (with the normalization explained in Proposition 10.18), and
$\unicode[STIX]{x1D70E}$
too (with the normalization explained in Proposition 10.18), and
![]() $\unicode[STIX]{x1D705}=(0,1-a,a)$
.
$\unicode[STIX]{x1D705}=(0,1-a,a)$
.
Thus, setting
![]() $w_{0}=(a-1,0,-a)$
(corresponding to automorphic weight
$w_{0}=(a-1,0,-a)$
(corresponding to automorphic weight
![]() $(0,1-a,a)$
), to
$(0,1-a,a)$
), to
![]() $f$
is associated a point
$f$
is associated a point
![]() $x_{0}\in {\mathcal{E}}$
such that
$x_{0}\in {\mathcal{E}}$
such that
![]() $w(x_{0})=w_{0}$
and
$w(x_{0})=w_{0}$
and
![]() $\unicode[STIX]{x1D70C}_{x,\text{Ski}}^{ss}=\overline{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D700}^{-2}(1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot })$
, and, with normalization of Proposition 9.17,
$\unicode[STIX]{x1D70C}_{x,\text{Ski}}^{ss}=\overline{\unicode[STIX]{x1D712}}\unicode[STIX]{x1D700}^{-2}(1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot })$
, and, with normalization of Proposition 9.17,
which is of (ordered) Hodge–Tate weights
![]() $(1-a,-a,0)$
.
$(1-a,-a,0)$
.
11.2 A family passing through
 $f$
$f$
As we have normalized the pseudocharacter
![]() $T$
of Proposition 9.19 in order to have the ‘right’ representation at
$T$
of Proposition 9.19 in order to have the ‘right’ representation at
![]() $x_{0}$
(corresponding to
$x_{0}$
(corresponding to
![]() $1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
), the map
$1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
), the map
![]() $w$
from the eigenvariety gives the
$w$
from the eigenvariety gives the
![]() $p$
-adic (automorphic) weight, and neither the classical automorphic weight nor the Hodge–Tate weights of
$p$
-adic (automorphic) weight, and neither the classical automorphic weight nor the Hodge–Tate weights of
![]() $T$
; thus we will normalize this map accordingly.
$T$
; thus we will normalize this map accordingly.
The
![]() $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights of
![]() $1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
are given by
$1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
are given by
![]() $(1-a,-a,0)=:h_{0}$
. Let
$(1-a,-a,0)=:h_{0}$
. Let
![]() $F/\mathbb{Q}_{p}$
be a finite extension such that
$F/\mathbb{Q}_{p}$
be a finite extension such that
![]() $f$
is defined over
$f$
is defined over
![]() $F$
.
$F$
.
Proposition 11.1. If
![]() $p$
is inert, there exist:
$p$
is inert, there exist:
(i) a dimension-1 regular integral affinoid
 $Y$
over
$Y$
over
 $F$
, and
$F$
, and
 $y_{0}\in Y(F)$
;
$y_{0}\in Y(F)$
;(ii) a semi-simple continuous representation,
satisfying $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{K(Y)}:\operatorname{Gal}(\overline{E}/E)_{Np}\longrightarrow \operatorname{GL}_{3}(K(Y)),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{K(Y)}:\operatorname{Gal}(\overline{E}/E)_{Np}\longrightarrow \operatorname{GL}_{3}(K(Y)),\end{eqnarray}$$
 $\unicode[STIX]{x1D70C}_{K(Y)}^{\bot }\simeq \unicode[STIX]{x1D70C}_{K(Y)}$
, the property (ABS) of [Reference Bellaïche and ChenevierBC04], and
$\unicode[STIX]{x1D70C}_{K(Y)}^{\bot }\simeq \unicode[STIX]{x1D70C}_{K(Y)}$
, the property (ABS) of [Reference Bellaïche and ChenevierBC04], and
 $\operatorname{tr}(\unicode[STIX]{x1D70C}_{K(Y)})(\operatorname{Gal}(\overline{E}/E))\subset {\mathcal{O}}_{Y}$
;
$\operatorname{tr}(\unicode[STIX]{x1D70C}_{K(Y)})(\operatorname{Gal}(\overline{E}/E))\subset {\mathcal{O}}_{Y}$
;(iii) an
 $F$
-morphism,
$F$
-morphism,
 $h=(h_{1},h_{2},h_{3}):Y\longrightarrow \mathbb{A}^{3}$
such that
$h=(h_{1},h_{2},h_{3}):Y\longrightarrow \mathbb{A}^{3}$
such that
 $h_{3}=0$
,
$h_{3}=0$
,
 $h(y_{0})=h_{0}$
;
$h(y_{0})=h_{0}$
;(iv) a subset
 $Z\subset Y(F)$
such that
$Z\subset Y(F)$
such that
 $h(Z)\subset h_{0}+(p-1)(p+1)^{2}\mathbb{Z}_{\text{dom}}^{3}$
(i.e. the weights are regular);
$h(Z)\subset h_{0}+(p-1)(p+1)^{2}\mathbb{Z}_{\text{dom}}^{3}$
(i.e. the weights are regular);(v) a function
 $F_{1}$
in
$F_{1}$
in
 ${\mathcal{O}}(Y)^{\times }$
of constant valuation
${\mathcal{O}}(Y)^{\times }$
of constant valuation
such that we have the following.
(1) For every affinoid
 $\unicode[STIX]{x1D6FA}$
containing
$\unicode[STIX]{x1D6FA}$
containing
 $y_{0}$
,
$y_{0}$
,
 $\unicode[STIX]{x1D6FA}\cap Z$
is Zariski dense in
$\unicode[STIX]{x1D6FA}\cap Z$
is Zariski dense in
 $\unicode[STIX]{x1D6FA}$
.
$\unicode[STIX]{x1D6FA}$
.(2) For all
 $z\in Z\cup \{y_{0}\}$
$z\in Z\cup \{y_{0}\}$
 $\unicode[STIX]{x1D70C}_{z}^{ss}$
is the Galois representation associated to a cuspidal (algebraic) automorphic representation
$\unicode[STIX]{x1D70C}_{z}^{ss}$
is the Galois representation associated to a cuspidal (algebraic) automorphic representation
 $\unicode[STIX]{x1D6F1}$
of
$\unicode[STIX]{x1D6F1}$
of
 $GU(2,1)$
such that
$GU(2,1)$
such that  $$\begin{eqnarray}\operatorname{Hom}_{K_{f}}(J,\unicode[STIX]{x1D6F1})\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{K_{f}}(J,\unicode[STIX]{x1D6F1})\neq 0.\end{eqnarray}$$
(3)
 $\unicode[STIX]{x1D70C}_{y_{0}}^{ss}\simeq 1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
.
$\unicode[STIX]{x1D70C}_{y_{0}}^{ss}\simeq 1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
.(4) For
 $z\in Z$
,
$z\in Z$
,
 $(\unicode[STIX]{x1D70C}_{z}^{ss})_{G_{K}}$
is crystalline of
$(\unicode[STIX]{x1D70C}_{z}^{ss})_{G_{K}}$
is crystalline of
 $\unicode[STIX]{x1D70F}$
-Hodge–Tate weights
$\unicode[STIX]{x1D70F}$
-Hodge–Tate weights
 $h_{1}(z)<h_{2}(z)<h_{3}(z)$
, and its
$h_{1}(z)<h_{2}(z)<h_{3}(z)$
, and its
 $\unicode[STIX]{x1D70F}$
-refinement given by
$\unicode[STIX]{x1D70F}$
-refinement given by
 $F_{1}$
is In particular,
$F_{1}$
is In particular, $$\begin{eqnarray}(p^{h_{1}-h_{3}(z)}F_{1}(z),1,p^{h_{3}-h_{1}(z)}F_{1}^{-1}(z)).\end{eqnarray}$$
$$\begin{eqnarray}(p^{h_{1}-h_{3}(z)}F_{1}(z),1,p^{h_{3}-h_{1}(z)}F_{1}^{-1}(z)).\end{eqnarray}$$
 $$\begin{eqnarray}D_{\text{crys}}(\unicode[STIX]{x1D70C}_{z}^{ss})_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D711}^{2}=p^{h_{1}-h_{3}}F_{1}(z)}\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}D_{\text{crys}}(\unicode[STIX]{x1D70C}_{z}^{ss})_{\unicode[STIX]{x1D70F}}^{\unicode[STIX]{x1D711}^{2}=p^{h_{1}-h_{3}}F_{1}(z)}\neq 0.\end{eqnarray}$$
(5) At
 $y_{0}$
, the refinement is
$y_{0}$
, the refinement is
 $(\unicode[STIX]{x1D712}_{p}^{\bot }(p),1,\unicode[STIX]{x1D712}_{p}(p)).$
$(\unicode[STIX]{x1D712}_{p}^{\bot }(p),1,\unicode[STIX]{x1D712}_{p}(p)).$
Proof. Recall that
![]() $p$
is inert here. The modular form
$p$
is inert here. The modular form
![]() $f$
corresponds to a point
$f$
corresponds to a point
![]() $x_{0}\in {\mathcal{E}}$
, the eigenvariety defined in Theorem 9.15, associated to the type
$x_{0}\in {\mathcal{E}}$
, the eigenvariety defined in Theorem 9.15, associated to the type
![]() $(K_{f},J)$
. Let
$(K_{f},J)$
. Let
![]() $B\subset B(w_{0},r)\subset {\mathcal{W}}$
be the closed subset defined in the same fashion as in [Reference Bellaïche and ChenevierBC04] by,
$B\subset B(w_{0},r)\subset {\mathcal{W}}$
be the closed subset defined in the same fashion as in [Reference Bellaïche and ChenevierBC04] by,
Thus
![]() $w_{0}\in B$
. Define
$w_{0}\in B$
. Define
![]() $X$
to be an irreducible component of
$X$
to be an irreducible component of
![]() ${\mathcal{E}}\otimes _{{\mathcal{W}}}B$
containing
${\mathcal{E}}\otimes _{{\mathcal{W}}}B$
containing
![]() $x_{f}$
. We get
$x_{f}$
. We get
![]() $w_{B}:X\longrightarrow B$
which is finite (if
$w_{B}:X\longrightarrow B$
which is finite (if
![]() $r$
small enough) surjective. We can thus look at the universal pseudo-character
$r$
small enough) surjective. We can thus look at the universal pseudo-character
![]() $T$
on
$T$
on
![]() ${\mathcal{E}}$
and compose it with
${\mathcal{E}}$
and compose it with
![]() ${\mathcal{O}}_{{\mathcal{E}}}\longrightarrow {\mathcal{O}}(X)$
. Applying [Reference Bellaïche and ChenevierBC04, Lemma 7.2], we get an affinoid
${\mathcal{O}}_{{\mathcal{E}}}\longrightarrow {\mathcal{O}}(X)$
. Applying [Reference Bellaïche and ChenevierBC04, Lemma 7.2], we get an affinoid
![]() $Y$
, regular of dimension
$Y$
, regular of dimension
![]() $1$
,
$1$
,
![]() $y_{0}\in Y$
and a finite surjective morphism
$y_{0}\in Y$
and a finite surjective morphism
![]() $m:Y\longrightarrow X$
such that
$m:Y\longrightarrow X$
such that
![]() $m(y_{0})=x_{f}$
and there exist a representation
$m(y_{0})=x_{f}$
and there exist a representation
![]() $\unicode[STIX]{x1D70C}:G_{E}\longrightarrow \operatorname{GL}_{3}(K(Y))$
of trace
$\unicode[STIX]{x1D70C}:G_{E}\longrightarrow \operatorname{GL}_{3}(K(Y))$
of trace
![]() $G_{E}\overset{T}{\longrightarrow }{\mathcal{O}}_{X}\longrightarrow {\mathcal{O}}_{Y}$
satisfying (ABS). At
$G_{E}\overset{T}{\longrightarrow }{\mathcal{O}}_{X}\longrightarrow {\mathcal{O}}_{Y}$
satisfying (ABS). At
![]() $y_{0}$
, the representation
$y_{0}$
, the representation
![]() $\unicode[STIX]{x1D70C}_{y_{0}}^{ss}$
is given by
$\unicode[STIX]{x1D70C}_{y_{0}}^{ss}$
is given by
![]() $1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
. The map
$1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
. The map
![]() $h$
is given as follow. First, write
$h$
is given as follow. First, write
![]() $\unicode[STIX]{x1D708}=(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},\unicode[STIX]{x1D708}_{3})=(1+w_{3},-1-w_{1},-w_{2})$
. Then
$\unicode[STIX]{x1D708}=(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},\unicode[STIX]{x1D708}_{3})=(1+w_{3},-1-w_{1},-w_{2})$
. Then
![]() $h$
is given by composition of
$h$
is given by composition of
![]() $m$
with the map
$m$
with the map
![]() $\unicode[STIX]{x1D708}$
(the shift of
$\unicode[STIX]{x1D708}$
(the shift of
![]() $w$
) of
$w$
) of
![]() ${\mathcal{E}}$
; it is still finite and surjective on
${\mathcal{E}}$
; it is still finite and surjective on
![]() $B$
,Footnote
5
and for every
$B$
,Footnote
5
and for every
![]() $y\in Y$
such that
$y\in Y$
such that
![]() $m(y)=x_{f}$
, then
$m(y)=x_{f}$
, then
![]() $h(y)=h_{0}$
. In terms of automorphic weight
$h(y)=h_{0}$
. In terms of automorphic weight
![]() $(k_{1},k_{2},k_{3})$
the previous map is given by
$(k_{1},k_{2},k_{3})$
the previous map is given by
![]() $(1-k_{3},k_{2}-1,k_{1})$
, and thus gives the Hodge–Tate weights for regular discrete series. In terms of Hodge–Tate weights, the equations (1) giving rise to
$(1-k_{3},k_{2}-1,k_{1})$
, and thus gives the Hodge–Tate weights for regular discrete series. In terms of Hodge–Tate weights, the equations (1) giving rise to
![]() $B$
become
$B$
become
Write
where
![]() $C^{\prime \prime }>0$
is bigger than the bound given (up to reducing
$C^{\prime \prime }>0$
is bigger than the bound given (up to reducing
![]() $r$
and thus
$r$
and thus
![]() $B$
) in Proposition 10.19 for crystallinity,
$B$
) in Proposition 10.19 for crystallinity,
![]() $C^{\prime }$
is the bound given by classicity Theorem 8.17, and
$C^{\prime }$
is the bound given by classicity Theorem 8.17, and
![]() $C$
is the bound given in classicity at the level of sheaves, Proposition 8.16 (we remark that
$C$
is the bound given in classicity at the level of sheaves, Proposition 8.16 (we remark that
![]() $h_{3}$
is constant). Then
$h_{3}$
is constant). Then
![]() ${\mathcal{Z}}$
is strongly Zariski dense in
${\mathcal{Z}}$
is strongly Zariski dense in
![]() $B$
. Then
$B$
. Then
![]() $Z:=\unicode[STIX]{x1D705}^{-1}({\mathcal{Z}})\subset Y(F)$
contains only classical (and regular) points by Proposition 8.16 and the classicity result of Bijakowski (Theorem 8.17). Moreover they are all crystalline by Proposition 10.19. It is strongly Zariski dense by flatness (thus openness) of
$Z:=\unicode[STIX]{x1D705}^{-1}({\mathcal{Z}})\subset Y(F)$
contains only classical (and regular) points by Proposition 8.16 and the classicity result of Bijakowski (Theorem 8.17). Moreover they are all crystalline by Proposition 10.19. It is strongly Zariski dense by flatness (thus openness) of
![]() $\unicode[STIX]{x1D705}$
. Let us define
$\unicode[STIX]{x1D705}$
. Let us define
![]() $F_{1}$
. The action on a point
$F_{1}$
. The action on a point
![]() $x_{f}$
associated to modular form
$x_{f}$
associated to modular form
![]() $f$
– of (classical automorphic) weight
$f$
– of (classical automorphic) weight
![]() $(k_{1},k_{2},k_{3})$
associated to
$(k_{1},k_{2},k_{3})$
associated to
![]() $\unicode[STIX]{x1D70B}$
that is a quotient of
$\unicode[STIX]{x1D70B}$
that is a quotient of
![]() $\operatorname{ind}_{b}^{GU(3)}(\unicode[STIX]{x1D713})$
– of the operator
$\operatorname{ind}_{b}^{GU(3)}(\unicode[STIX]{x1D713})$
– of the operator
which corresponds up to a normalization by
![]() $1/p^{h_{1}-h_{3}-1}=p^{k_{1}+k_{3}}$
to the classical Iwahori double coset
$1/p^{h_{1}-h_{3}-1}=p^{k_{1}+k_{3}}$
to the classical Iwahori double coset
 $$\begin{eqnarray}p^{-1}\left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right)=\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & p^{-1}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}p^{-1}\left(\begin{array}{@{}ccc@{}}p^{2} & & \\ & p & \\ & & 1\end{array}\right)=\left(\begin{array}{@{}ccc@{}}p & & \\ & 1 & \\ & & p^{-1}\end{array}\right),\end{eqnarray}$$
and corresponds to
where
![]() $\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2})$
is a character of
$\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2})$
is a character of
![]() $({\mathcal{O}}^{\times })^{2}$
and
$({\mathcal{O}}^{\times })^{2}$
and
![]() $\unicode[STIX]{x1D70E}$
the refinement of
$\unicode[STIX]{x1D70E}$
the refinement of
![]() $f$
associated to the action of
$f$
associated to the action of
![]() ${\mathcal{A}}(p)$
. Indeed, the eigenvalue of
${\mathcal{A}}(p)$
. Indeed, the eigenvalue of
![]() $U_{p}$
coincide with
$U_{p}$
coincide with
![]() $p^{-k_{2}}\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)^{2}\unicode[STIX]{x1D713}_{2}^{\unicode[STIX]{x1D70E}}$
and the one of
$p^{-k_{2}}\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)^{2}\unicode[STIX]{x1D713}_{2}^{\unicode[STIX]{x1D70E}}$
and the one of
![]() $S_{p}$
with
$S_{p}$
with
![]() $p^{-k_{1}-k_{2}-k_{3}}\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)\unicode[STIX]{x1D713}_{2}^{\unicode[STIX]{x1D70E}}(p)$
. Thus,
$p^{-k_{1}-k_{2}-k_{3}}\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)\unicode[STIX]{x1D713}_{2}^{\unicode[STIX]{x1D70E}}(p)$
. Thus,
![]() $U_{p}S_{p}^{-1}$
has eigenvalue
$U_{p}S_{p}^{-1}$
has eigenvalue
![]() $p^{k_{1}+k_{3}}\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)=p^{h_{3}-h_{1}}p\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)$
. Thus, we set
$p^{k_{1}+k_{3}}\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)=p^{h_{3}-h_{1}}p\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)$
. Thus, we set
![]() $F_{1}$
the function on
$F_{1}$
the function on
![]() ${\mathcal{E}}$
given by
${\mathcal{E}}$
given by
![]() $p^{-1}U_{p}S_{p}^{-1}$
. We have that
$p^{-1}U_{p}S_{p}^{-1}$
. We have that
![]() $p^{h_{1}-h_{3}}F_{1}=\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)$
. Property (2) comes from the construction of the eigenvariety
$p^{h_{1}-h_{3}}F_{1}=\unicode[STIX]{x1D713}_{1}^{\unicode[STIX]{x1D70E}}(p)$
. Property (2) comes from the construction of the eigenvariety
![]() ${\mathcal{E}}$
. Part (3) is the calculation of the Galois representation associated to
${\mathcal{E}}$
. Part (3) is the calculation of the Galois representation associated to
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
. Part (4) is local–global compatibility at
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
. Part (4) is local–global compatibility at
![]() $\ell =p$
([Reference SkinnerSki12] as recalled in § 9.6) and Proposition 10.19 as the eigenvalues of the crystalline Frobenius class
$\ell =p$
([Reference SkinnerSki12] as recalled in § 9.6) and Proposition 10.19 as the eigenvalues of the crystalline Frobenius class
![]() $\unicode[STIX]{x1D711}^{2}$
coincide with
$\unicode[STIX]{x1D711}^{2}$
coincide with
![]() $\unicode[STIX]{x1D713}_{i}^{\unicode[STIX]{x1D70E}}(p)$
.
$\unicode[STIX]{x1D713}_{i}^{\unicode[STIX]{x1D70E}}(p)$
.
The last assertion is the calculation made in Proposition 10.17.◻
Proposition 11.2. If
![]() $p=v\overline{v}$
is split, there exist:
$p=v\overline{v}$
is split, there exist:
(i) a dimension-1 regular integral affinoid
 $Y$
over
$Y$
over
 $F$
, and
$F$
, and
 $y_{0}\in Y(F)$
;
$y_{0}\in Y(F)$
;(ii) a semi-simple continuous representation,
satisfying $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{K(Y)}:\operatorname{Gal}(\overline{E}/E)_{Np}\longrightarrow \operatorname{GL}_{3}(K(Y)),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{K(Y)}:\operatorname{Gal}(\overline{E}/E)_{Np}\longrightarrow \operatorname{GL}_{3}(K(Y)),\end{eqnarray}$$
 $\unicode[STIX]{x1D70C}_{K(Y)}^{\bot }\simeq \unicode[STIX]{x1D70C}_{K(Y)}$
, the property (ABS) of [Reference Bellaïche and ChenevierBC04], and
$\unicode[STIX]{x1D70C}_{K(Y)}^{\bot }\simeq \unicode[STIX]{x1D70C}_{K(Y)}$
, the property (ABS) of [Reference Bellaïche and ChenevierBC04], and
 $\operatorname{tr}(\unicode[STIX]{x1D70C}_{K(Y)})(\operatorname{Gal}(\overline{E}/E))\subset {\mathcal{O}}_{Y}$
;
$\operatorname{tr}(\unicode[STIX]{x1D70C}_{K(Y)})(\operatorname{Gal}(\overline{E}/E))\subset {\mathcal{O}}_{Y}$
;(iii) an
 $F$
-morphism,
$F$
-morphism,
 $h=(h_{1},h_{2},h_{3}):Y\longrightarrow \mathbb{A}^{3}$
such that
$h=(h_{1},h_{2},h_{3}):Y\longrightarrow \mathbb{A}^{3}$
such that
 $h_{3}=0$
,
$h_{3}=0$
,
 $h(y_{0})=h_{0}$
;
$h(y_{0})=h_{0}$
;(iv) a subset
 $Z\subset Y(F)$
such that
$Z\subset Y(F)$
such that
 $h(Z)\subset h_{0}+(p-1)\mathbb{Z}_{\text{dom}}^{3}$
;
$h(Z)\subset h_{0}+(p-1)\mathbb{Z}_{\text{dom}}^{3}$
;(v) three functions
 $F_{1},F_{2},F_{3}$
in
$F_{1},F_{2},F_{3}$
in
 ${\mathcal{O}}(Y)$
of constant valuation
${\mathcal{O}}(Y)$
of constant valuation
such that we have the following.
(1) For every affinoid
 $\unicode[STIX]{x1D6FA}$
containing
$\unicode[STIX]{x1D6FA}$
containing
 $y_{0}$
,
$y_{0}$
,
 $\unicode[STIX]{x1D6FA}\cap Z$
is Zariski dense in
$\unicode[STIX]{x1D6FA}\cap Z$
is Zariski dense in
 $\unicode[STIX]{x1D6FA}$
.
$\unicode[STIX]{x1D6FA}$
.(2) For all
 $z\in Z\cup \{y_{0}\}$
$z\in Z\cup \{y_{0}\}$
 $\unicode[STIX]{x1D70C}_{z}^{ss}$
is the Galois representation associated to a cuspidal (algebraic) automorphic representation
$\unicode[STIX]{x1D70C}_{z}^{ss}$
is the Galois representation associated to a cuspidal (algebraic) automorphic representation
 $\unicode[STIX]{x1D6F1}$
of
$\unicode[STIX]{x1D6F1}$
of
 $GU(2,1)$
such that
$GU(2,1)$
such that  $$\begin{eqnarray}Hom_{K_{f}}(J,\unicode[STIX]{x1D6F1})\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}Hom_{K_{f}}(J,\unicode[STIX]{x1D6F1})\neq 0.\end{eqnarray}$$
(3)
 $\unicode[STIX]{x1D70C}_{y_{0}}^{ss}\simeq 1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
.
$\unicode[STIX]{x1D70C}_{y_{0}}^{ss}\simeq 1\oplus \unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
.(4) For
 $z\in Z$
,
$z\in Z$
,
 $(\unicode[STIX]{x1D70C}_{z}^{ss})_{G_{v}}$
is crystalline of Hodge–Tate weights
$(\unicode[STIX]{x1D70C}_{z}^{ss})_{G_{v}}$
is crystalline of Hodge–Tate weights
 $h_{1}(z)<h_{2}(z)<h_{3}(z)$
, and is an accessible refinement of
$h_{1}(z)<h_{2}(z)<h_{3}(z)$
, and is an accessible refinement of $$\begin{eqnarray}(p^{h_{1}(z)}F_{1}(z),p^{h_{2}(z)}F_{2}(z),p^{h_{3}(z)}F_{3}(z))\end{eqnarray}$$
$$\begin{eqnarray}(p^{h_{1}(z)}F_{1}(z),p^{h_{2}(z)}F_{2}(z),p^{h_{3}(z)}F_{3}(z))\end{eqnarray}$$
 $\unicode[STIX]{x1D70C}_{z}^{ss}$
.
$\unicode[STIX]{x1D70C}_{z}^{ss}$
.(5) At
 $y_{0}$
, this refinement is
$y_{0}$
, this refinement is
 $(\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p))$
.
$(\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p))$
.
Proof. As the proof is almost the same as [Reference Bellaïche and ChenevierBC04] and we chose to detail the inert case, we will just sketch it. Choose
![]() $x_{f}$
the point in
$x_{f}$
the point in
![]() ${\mathcal{E}}$
associated to
${\mathcal{E}}$
associated to
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
and the accessible refinement
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
and the accessible refinement
![]() $(\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p))$
. Denote by
$(\unicode[STIX]{x1D712}_{v}^{\bot }(p),1,\unicode[STIX]{x1D712}_{v}(p))$
. Denote by
![]() $B\subset {\mathcal{W}}$
the closed subset defined as in the inert case by
$B\subset {\mathcal{W}}$
the closed subset defined as in the inert case by
and choose
![]() $X$
an irreducible component of
$X$
an irreducible component of
![]() ${\mathcal{E}}\times _{{\mathcal{W}}}B$
containing
${\mathcal{E}}\times _{{\mathcal{W}}}B$
containing
![]() $x_{f}$
. Apply [Reference Bellaïche and ChenevierBC04, Lemma 7.2], and get
$x_{f}$
. Apply [Reference Bellaïche and ChenevierBC04, Lemma 7.2], and get
![]() $Y$
regular and
$Y$
regular and
![]() $y_{0}$
and a representation,
$y_{0}$
and a representation,
such that
![]() $\unicode[STIX]{x1D70C}^{\bot }=\unicode[STIX]{x1D70C}$
. Denote
$\unicode[STIX]{x1D70C}^{\bot }=\unicode[STIX]{x1D70C}$
. Denote
![]() $h$
as in the inert case (
$h$
as in the inert case (
![]() $\unicode[STIX]{x1D708}=(1-k_{3},k_{2}-1,k_{1})$
), and idem for
$\unicode[STIX]{x1D708}=(1-k_{3},k_{2}-1,k_{1})$
), and idem for
![]() $Z$
(classicity at the level of sheaves is given by [Reference BrascaBra16, 6.2], and classicity by Pilloni and Stroh [Reference Pilloni and StrohPS12] or (in greater generality) [Reference Bijakowski, Pilloni and StrohBPS16].). The four Hecke operators living on
$Z$
(classicity at the level of sheaves is given by [Reference BrascaBra16, 6.2], and classicity by Pilloni and Stroh [Reference Pilloni and StrohPS12] or (in greater generality) [Reference Bijakowski, Pilloni and StrohBPS16].). The four Hecke operators living on
![]() ${\mathcal{E}}$
,
${\mathcal{E}}$
,
![]() $U_{i},i=0,\ldots ,3$
are normalized as in 8.3, then set, for
$U_{i},i=0,\ldots ,3$
are normalized as in 8.3, then set, for
![]() $i=1,2,3$
,
$i=1,2,3$
,
By § 10.6, and local–global compatibility at
![]() $v$
(with the fact that
$v$
(with the fact that
![]() $v$
coincide with
$v$
coincide with
![]() $\unicode[STIX]{x1D70F}_{\infty }$
),
$\unicode[STIX]{x1D70F}_{\infty }$
),
![]() $h_{i}$
are the Hodge–Tate weights of
$h_{i}$
are the Hodge–Tate weights of
![]() $(\unicode[STIX]{x1D70C}_{z})_{|G_{v}}$
, and the normalization of the Hecke Operators recalled in 10.6 assure that
$(\unicode[STIX]{x1D70C}_{z})_{|G_{v}}$
, and the normalization of the Hecke Operators recalled in 10.6 assure that
![]() $(p^{h_{i}}F_{i})_{i}$
is a refinement at
$(p^{h_{i}}F_{i})_{i}$
is a refinement at
![]() $v$
for all classical forms.◻
$v$
for all classical forms.◻
11.3 Constructing the extension
Proposition 11.3. We are in one of the following two cases:
(i)
 $\unicode[STIX]{x1D70C}_{K(Y)}$
is absolutely irreducible;
$\unicode[STIX]{x1D70C}_{K(Y)}$
is absolutely irreducible;(ii) there exists a two-dimensional representation
 $r\subset \unicode[STIX]{x1D70C}$
such that
$r\subset \unicode[STIX]{x1D70C}$
such that
 $r_{K(Y)}$
is absolutely irreducible and
$r_{K(Y)}$
is absolutely irreducible and  $$\begin{eqnarray}r_{y_{0}}^{ss}=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D712} & \\ & \unicode[STIX]{x1D712}^{\bot }\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}r_{y_{0}}^{ss}=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D712} & \\ & \unicode[STIX]{x1D712}^{\bot }\end{array}\right).\end{eqnarray}$$
Remark 11.4. As showed by the proof, the second case never happens if
![]() $a\geqslant 2$
and
$a\geqslant 2$
and
![]() $p$
is split.
$p$
is split.
Proof. The proof uses similar ideas as in [Reference Bellaïche and ChenevierBC04, Proposition 9.1], but unfortunately in our case the refinement authorizes a two-dimensional subrepresentation and a one-dimensional quotient. Let us first suppose
![]() $p$
splits, and suppose
$p$
splits, and suppose
![]() $\unicode[STIX]{x1D70C}_{K(Y)}$
is reducible. As
$\unicode[STIX]{x1D70C}_{K(Y)}$
is reducible. As
![]() $\unicode[STIX]{x1D70C}^{\bot }\simeq \unicode[STIX]{x1D70C}$
, we can suppose that there exists a character
$\unicode[STIX]{x1D70C}^{\bot }\simeq \unicode[STIX]{x1D70C}$
, we can suppose that there exists a character
![]() $\unicode[STIX]{x1D713}\subset \unicode[STIX]{x1D70C}$
and a two-dimensional representation
$\unicode[STIX]{x1D713}\subset \unicode[STIX]{x1D70C}$
and a two-dimensional representation
![]() $r$
such that
$r$
such that
Thus there exists
![]() $i$
such that the (generalized) Hodge–Tate weight of
$i$
such that the (generalized) Hodge–Tate weight of
![]() $\unicode[STIX]{x1D713}$
at
$\unicode[STIX]{x1D713}$
at
![]() $v$
is
$v$
is
![]() $h_{i}$
. Moreover, for all
$h_{i}$
. Moreover, for all
![]() $z\in Z$
, by weak admissibility of
$z\in Z$
, by weak admissibility of
![]() $\unicode[STIX]{x1D713}$
, we must have that there exists a
$\unicode[STIX]{x1D713}$
, we must have that there exists a
![]() $j$
such that
$j$
such that
![]() $v(p^{h_{j}}F_{j}(z))=h_{i}(z)$
. As the valuation of
$v(p^{h_{j}}F_{j}(z))=h_{i}(z)$
. As the valuation of
![]() $F_{j}$
is constant on
$F_{j}$
is constant on
![]() $Y$
, we can calculate it at
$Y$
, we can calculate it at
![]() $y_{0}$
and
$y_{0}$
and
In particular, at
![]() $z\in Z$
such that
$z\in Z$
such that
![]() $|h_{i}(z)-h_{j}(z)|>a$
for all
$|h_{i}(z)-h_{j}(z)|>a$
for all
![]() $i\neq j$
, we find
$i\neq j$
, we find
![]() $\unicode[STIX]{x1D6FC}_{j}=0$
and
$\unicode[STIX]{x1D6FC}_{j}=0$
and
![]() $i=j=1$
. Thus, by density
$i=j=1$
. Thus, by density
![]() $\unicode[STIX]{x1D713}$
is of Hodge–Tate weight
$\unicode[STIX]{x1D713}$
is of Hodge–Tate weight
![]() $h_{1}$
. In particular, at
$h_{1}$
. In particular, at
![]() $y_{0}$
,
$y_{0}$
,
![]() $\unicode[STIX]{x1D713}$
is of Hodge–Tate weight
$\unicode[STIX]{x1D713}$
is of Hodge–Tate weight
![]() $h_{1}(y_{0})=1-a$
. Now, if
$h_{1}(y_{0})=1-a$
. Now, if
![]() $a\neq 1$
,
$a\neq 1$
,
![]() $\unicode[STIX]{x1D713}_{y_{0}}=\unicode[STIX]{x1D712}$
, and if
$\unicode[STIX]{x1D713}_{y_{0}}=\unicode[STIX]{x1D712}$
, and if
![]() $r$
were reducible, then by weak admissibility we would find
$r$
were reducible, then by weak admissibility we would find
![]() $i,j\neq 1$
such that
$i,j\neq 1$
such that
![]() $h_{i}(z)=h_{j}(z)+\unicode[STIX]{x1D6FC}_{j}$
, for a Zariski dense subset of
$h_{i}(z)=h_{j}(z)+\unicode[STIX]{x1D6FC}_{j}$
, for a Zariski dense subset of
![]() $z\in Z$
, which is absurd. Thus there is a unique subquotient of
$z\in Z$
, which is absurd. Thus there is a unique subquotient of
![]() $\unicode[STIX]{x1D70C}$
which is of rank
$\unicode[STIX]{x1D70C}$
which is of rank
![]() $1$
, it is
$1$
, it is
![]() $\unicode[STIX]{x1D713}$
. As
$\unicode[STIX]{x1D713}$
. As
![]() $\unicode[STIX]{x1D70C}^{\bot }=\unicode[STIX]{x1D70C}$
, this means that
$\unicode[STIX]{x1D70C}^{\bot }=\unicode[STIX]{x1D70C}$
, this means that
![]() $\unicode[STIX]{x1D713}^{\bot }=\unicode[STIX]{x1D713}$
, which is impossible as
$\unicode[STIX]{x1D713}^{\bot }=\unicode[STIX]{x1D713}$
, which is impossible as
![]() $\unicode[STIX]{x1D713}_{y_{0}}=\unicode[STIX]{x1D712}$
. If
$\unicode[STIX]{x1D713}_{y_{0}}=\unicode[STIX]{x1D712}$
. If
![]() $a=1$
then
$a=1$
then
![]() $\unicode[STIX]{x1D713}_{y_{0}}$
has
$\unicode[STIX]{x1D713}_{y_{0}}$
has
![]() $v$
-Hodge–Tate weight
$v$
-Hodge–Tate weight
![]() $0$
, and if
$0$
, and if
![]() $\unicode[STIX]{x1D713}_{y_{0}}=\unicode[STIX]{x1D712}$
the same as previously happens; thus suppose that
$\unicode[STIX]{x1D713}_{y_{0}}=\unicode[STIX]{x1D712}$
the same as previously happens; thus suppose that
![]() $\unicode[STIX]{x1D713}_{y_{0}}=1$
. In this case,
$\unicode[STIX]{x1D713}_{y_{0}}=1$
. In this case,
![]() $r$
is still irreducible but
$r$
is still irreducible but
![]() $r_{y_{0}}^{ss}=\unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
.
$r_{y_{0}}^{ss}=\unicode[STIX]{x1D712}\oplus \unicode[STIX]{x1D712}^{\bot }$
.
Now, we focus on
![]() $p$
inert, which is similar. Suppose we are not in the case where
$p$
inert, which is similar. Suppose we are not in the case where
![]() $\unicode[STIX]{x1D70C}_{K(Y)}$
is irreducible. We can thus find a two-dimensional subrepresentation
$\unicode[STIX]{x1D70C}_{K(Y)}$
is irreducible. We can thus find a two-dimensional subrepresentation
![]() $r\subset \unicode[STIX]{x1D70C}$
(if
$r\subset \unicode[STIX]{x1D70C}$
(if
![]() $r$
is one-dimensional, take the quotient and apply
$r$
is one-dimensional, take the quotient and apply
![]() $(.)^{\bot }$
, as
$(.)^{\bot }$
, as
![]() $\unicode[STIX]{x1D70C}^{\bot }=\unicode[STIX]{x1D70C}$
). Suppose that
$\unicode[STIX]{x1D70C}^{\bot }=\unicode[STIX]{x1D70C}$
). Suppose that
![]() $r$
is reducible. Take
$r$
is reducible. Take
![]() $z\in {\mathcal{Z}}$
; as the valuation
$z\in {\mathcal{Z}}$
; as the valuation
![]() $\unicode[STIX]{x1D6FC}_{1}$
of
$\unicode[STIX]{x1D6FC}_{1}$
of
![]() $F_{1}$
is constant, we can calculate it at
$F_{1}$
is constant, we can calculate it at
![]() $y_{0}$
, and we get, from
$y_{0}$
, and we get, from
![]() $p^{h_{1}-h_{3}}F_{1}(y_{0})=\unicode[STIX]{x1D712}_{p}^{\bot }(p)$
,
$p^{h_{1}-h_{3}}F_{1}(y_{0})=\unicode[STIX]{x1D712}_{p}^{\bot }(p)$
,
But if
![]() $r_{z}^{ss}$
is not irreducible, this means, following Rogawski’s classification recalled in [Reference Bellaïche and ChenevierBC04, § 3.2.3], and the fact that the representations associated by Blasius and Rogawski [Reference Blasius and RogawskiBR92] are irreducible (but not necessarily three-dimensional), that
$r_{z}^{ss}$
is not irreducible, this means, following Rogawski’s classification recalled in [Reference Bellaïche and ChenevierBC04, § 3.2.3], and the fact that the representations associated by Blasius and Rogawski [Reference Blasius and RogawskiBR92] are irreducible (but not necessarily three-dimensional), that
![]() $z$
is either endoscopic-tempered of type
$z$
is either endoscopic-tempered of type
![]() $(1,1,1)$
, endoscopic non-tempered or stable non-tempered. In the case endoscopic non-tempered, looking at the Arthur parameter at infinity, the Hodge–Tate weights verifies
$(1,1,1)$
, endoscopic non-tempered or stable non-tempered. In the case endoscopic non-tempered, looking at the Arthur parameter at infinity, the Hodge–Tate weights verifies
![]() $h_{1}=h_{2}$
or
$h_{1}=h_{2}$
or
![]() $h_{2}=h_{3}$
, which is not possible by choice of
$h_{2}=h_{3}$
, which is not possible by choice of
![]() $Y$
and
$Y$
and
![]() $Z$
. In the stable non-tempered case, the Hodge–Tate weights are
$Z$
. In the stable non-tempered case, the Hodge–Tate weights are
![]() $(k,k,k)$
, which is not allowed in
$(k,k,k)$
, which is not allowed in
![]() ${\mathcal{Z}}$
. So we need to check that
${\mathcal{Z}}$
. So we need to check that
![]() $z$
is not endoscopic of type
$z$
is not endoscopic of type
![]() $(1,1,1)$
. But in this case, this would mean by weak admissibility for
$(1,1,1)$
. But in this case, this would mean by weak admissibility for
![]() $\unicode[STIX]{x1D70C}_{z}^{ss}$
(which would thus be a totally split sum of three characters) that
$\unicode[STIX]{x1D70C}_{z}^{ss}$
(which would thus be a totally split sum of three characters) that
but the previous equality is impossible for
![]() $-h_{1}<-a$
(which is the generic situation). Thus
$-h_{1}<-a$
(which is the generic situation). Thus
![]() $z\in {\mathcal{Z}}$
is endoscopic, tempered, of type
$z\in {\mathcal{Z}}$
is endoscopic, tempered, of type
![]() $(2,1)$
, and
$(2,1)$
, and
![]() $r$
is irreducible. By weak admissibility, and the previous calculations (or because
$r$
is irreducible. By weak admissibility, and the previous calculations (or because
![]() $\unicode[STIX]{x1D70C}^{\bot }=\unicode[STIX]{x1D70C}$
),
$\unicode[STIX]{x1D70C}^{\bot }=\unicode[STIX]{x1D70C}$
),
![]() $r_{y_{0}}^{ss}$
has to be
$r_{y_{0}}^{ss}$
has to be
![]() $\unicode[STIX]{x1D712}^{\bot }\oplus \unicode[STIX]{x1D712}$
.◻
$\unicode[STIX]{x1D712}^{\bot }\oplus \unicode[STIX]{x1D712}$
.◻
11.4 Good reduction outside
 $p$
$p$
Proposition 11.5. In the previous case (i) of Proposition 11.3, write
![]() $\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D70C}_{K(Y)}\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1}$
. Let
$\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D70C}_{K(Y)}\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1}$
. Let
![]() $v|\ell \neq p$
be a place of
$v|\ell \neq p$
be a place of
![]() $E$
. Then we have the following.
$E$
. Then we have the following.
(i) If
 $v\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
, then
$v\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
, then
 $\unicode[STIX]{x1D70C}_{K(Y)}$
and
$\unicode[STIX]{x1D70C}_{K(Y)}$
and
 $\unicode[STIX]{x1D70C}^{\prime }$
are unramified at
$\unicode[STIX]{x1D70C}^{\prime }$
are unramified at
 $v$
.
$v$
.(ii) If
 $v|\text{Cond}(\unicode[STIX]{x1D712})$
, then
$v|\text{Cond}(\unicode[STIX]{x1D712})$
, then
 $\dim _{K(Y)}(\unicode[STIX]{x1D70C}_{K(Y)}^{\prime })^{I_{v}}=2$
.
$\dim _{K(Y)}(\unicode[STIX]{x1D70C}_{K(Y)}^{\prime })^{I_{v}}=2$
.
In case (ii) of Proposition 11.3, write
![]() $r^{\prime }=r_{K(Y)}\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1}$
. Let
$r^{\prime }=r_{K(Y)}\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1}$
. Let
![]() $v|\ell \neq p$
be a place of
$v|\ell \neq p$
be a place of
![]() $E$
. Then we have the following.
$E$
. Then we have the following.
(i) If
 $v\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
, then
$v\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
, then
 $r_{K(Y)}$
and
$r_{K(Y)}$
and
 $r^{\prime }$
are unramified at
$r^{\prime }$
are unramified at
 $v$
.
$v$
.(ii) If
 $v|\text{Cond}(\unicode[STIX]{x1D712})$
, then
$v|\text{Cond}(\unicode[STIX]{x1D712})$
, then
 $\dim _{K(Y)}(r^{\prime })^{I_{v}}=1$
.
$\dim _{K(Y)}(r^{\prime })^{I_{v}}=1$
.
Proof. After all the constructions, this can be deduced as in [Reference Bellaïche and ChenevierBC04]. First there exists
![]() $g\in {\mathcal{O}}_{Y}$
such that
$g\in {\mathcal{O}}_{Y}$
such that
![]() $g(y_{0})\neq 0$
and
$g(y_{0})\neq 0$
and
![]() $\unicode[STIX]{x1D70C}_{K(Y)}$
has a
$\unicode[STIX]{x1D70C}_{K(Y)}$
has a
![]() ${\mathcal{O}}_{Y,(g)}$
stable lattice. Denote by
${\mathcal{O}}_{Y,(g)}$
stable lattice. Denote by
![]() $\unicode[STIX]{x1D70C}$
the representation valued in
$\unicode[STIX]{x1D70C}$
the representation valued in
![]() ${\mathcal{O}}_{Y,(g)}$
, and for all
${\mathcal{O}}_{Y,(g)}$
, and for all
![]() $y\in \operatorname{Spm}({\mathcal{O}}_{Y,(g)})=Y(g^{-1})$
,
$y\in \operatorname{Spm}({\mathcal{O}}_{Y,(g)})=Y(g^{-1})$
,
![]() $\unicode[STIX]{x1D70C}_{y}$
the reduction at
$\unicode[STIX]{x1D70C}_{y}$
the reduction at
![]() $y$
. In case (i) of Proposition 11.3, as
$y$
. In case (i) of Proposition 11.3, as
![]() $\unicode[STIX]{x1D70C}_{K(Y)}$
is semi-simple,
$\unicode[STIX]{x1D70C}_{K(Y)}$
is semi-simple,
![]() $\unicode[STIX]{x1D70C}_{z}$
is semi-simple for
$\unicode[STIX]{x1D70C}_{z}$
is semi-simple for
![]() $z\in Z^{\prime }$
, a cofinite subset of
$z\in Z^{\prime }$
, a cofinite subset of
![]() $Z\cap Y(g^{-1})$
. But now, for
$Z\cap Y(g^{-1})$
. But now, for
![]() $z\in Z^{\prime }$
,
$z\in Z^{\prime }$
,
![]() $\unicode[STIX]{x1D70C}_{z}=\unicode[STIX]{x1D70C}_{z}^{ss}$
is the Galois representation associated to a regular automorphic representation
$\unicode[STIX]{x1D70C}_{z}=\unicode[STIX]{x1D70C}_{z}^{ss}$
is the Galois representation associated to a regular automorphic representation
![]() $\unicode[STIX]{x1D6F1}_{z}$
of
$\unicode[STIX]{x1D6F1}_{z}$
of
![]() $GU(2,1)$
. In case (ii) of Proposition 11.3,
$GU(2,1)$
. In case (ii) of Proposition 11.3,
![]() $r_{K(Y)}$
is semi-simple, thus for all
$r_{K(Y)}$
is semi-simple, thus for all
![]() $z\in Z^{\prime }$
, still cofinite in
$z\in Z^{\prime }$
, still cofinite in
![]() $Z$
,
$Z$
,
![]() $r_{z}^{ss}=r_{z}\subset \unicode[STIX]{x1D70C}_{z}^{ss}$
, and
$r_{z}^{ss}=r_{z}\subset \unicode[STIX]{x1D70C}_{z}^{ss}$
, and
and
![]() $\dim _{K(Y)}(\unicode[STIX]{x1D70C}^{\prime })^{I_{v}}$
is related to the ramification of a (tempered endoscopic of type
$\dim _{K(Y)}(\unicode[STIX]{x1D70C}^{\prime })^{I_{v}}$
is related to the ramification of a (tempered endoscopic of type
![]() $(2,1)$
) automorphic representation of
$(2,1)$
) automorphic representation of
![]() $GU(2,1)$
. Thus, to show the result, we only need to control ramification at
$GU(2,1)$
. Thus, to show the result, we only need to control ramification at
![]() $v$
of (the base change of)
$v$
of (the base change of)
![]() $\unicode[STIX]{x1D6F1}_{z}$
.
$\unicode[STIX]{x1D6F1}_{z}$
.
If
![]() $v\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
, by construction of the eigenvariety and choice of the maximal compact,
$v\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
, by construction of the eigenvariety and choice of the maximal compact,
![]() $(\unicode[STIX]{x1D6F1}_{z})_{v}$
has a vector fixed by
$(\unicode[STIX]{x1D6F1}_{z})_{v}$
has a vector fixed by
![]() $K_{\ell }$
. We can thus finish because if
$K_{\ell }$
. We can thus finish because if
![]() $\ell$
is unramified, then
$\ell$
is unramified, then
![]() $K_{\ell }$
is hyperspecial, and if
$K_{\ell }$
is hyperspecial, and if
![]() $\ell$
ramifies, then
$\ell$
ramifies, then
![]() $K_{\ell }$
is chosen very special, and [Reference Bellaïche and ChenevierBC04, Proposition 3.1] gives the result for the base change. Now by local–global compatibility (for example [Reference SkinnerSki12]),
$K_{\ell }$
is chosen very special, and [Reference Bellaïche and ChenevierBC04, Proposition 3.1] gives the result for the base change. Now by local–global compatibility (for example [Reference SkinnerSki12]),
![]() $\unicode[STIX]{x1D70C}_{z}^{ss}$
(and thus
$\unicode[STIX]{x1D70C}_{z}^{ss}$
(and thus
![]() $r_{z}$
in case (ii) of Proposition 11.3) is unramified at
$r_{z}$
in case (ii) of Proposition 11.3) is unramified at
![]() $v$
.
$v$
.
If
![]() $v|\text{Cond}(\unicode[STIX]{x1D712})$
, by construction
$v|\text{Cond}(\unicode[STIX]{x1D712})$
, by construction
![]() $\unicode[STIX]{x1D6F1}_{z}$
has type
$\unicode[STIX]{x1D6F1}_{z}$
has type
![]() $(K_{\ell },J_{\ell }\otimes \unicode[STIX]{x1D712}_{0,\ell }^{-1}\circ \det )$
, and thus by Proposition 10.21 the local Langlands representation associated to
$(K_{\ell },J_{\ell }\otimes \unicode[STIX]{x1D712}_{0,\ell }^{-1}\circ \det )$
, and thus by Proposition 10.21 the local Langlands representation associated to
![]() $(\unicode[STIX]{x1D6F1}_{z})_{v}$
is
$(\unicode[STIX]{x1D6F1}_{z})_{v}$
is
![]() $\unicode[STIX]{x1D719}_{1}\oplus \unicode[STIX]{x1D719}_{2}\oplus \unicode[STIX]{x1D719}_{3}\unicode[STIX]{x1D712}_{0,\ell }$
for three unramified characters
$\unicode[STIX]{x1D719}_{1}\oplus \unicode[STIX]{x1D719}_{2}\oplus \unicode[STIX]{x1D719}_{3}\unicode[STIX]{x1D712}_{0,\ell }$
for three unramified characters
![]() $\unicode[STIX]{x1D719}_{i}$
. Thus, by local–global compatibility again, there exists
$\unicode[STIX]{x1D719}_{i}$
. Thus, by local–global compatibility again, there exists
![]() $I_{v}^{\prime }$
a finite index subgroup of
$I_{v}^{\prime }$
a finite index subgroup of
![]() $I_{v}$
such that
$I_{v}$
such that
![]() $\unicode[STIX]{x1D70C}_{z}^{\prime }(I_{v}^{\prime })=1$
. Thus,
$\unicode[STIX]{x1D70C}_{z}^{\prime }(I_{v}^{\prime })=1$
. Thus,
![]() $(\unicode[STIX]{x1D70C}^{\prime })(I_{v}^{\prime })=1$
. But up to extending scalars,
$(\unicode[STIX]{x1D70C}^{\prime })(I_{v}^{\prime })=1$
. But up to extending scalars,
![]() $\unicode[STIX]{x1D70C}_{|I_{v}}^{\prime }$
is a finite representation
$\unicode[STIX]{x1D70C}_{|I_{v}}^{\prime }$
is a finite representation
![]() $\unicode[STIX]{x1D703}$
of
$\unicode[STIX]{x1D703}$
of
![]() $I_{v}/I_{v}^{\prime }$
, defined on
$I_{v}/I_{v}^{\prime }$
, defined on
![]() $F^{\prime }$
a finite extension of
$F^{\prime }$
a finite extension of
![]() $F$
. Thus,
$F$
. Thus,
![]() $\unicode[STIX]{x1D70C}_{I_{v}}^{\prime }\otimes _{F}F^{\prime }$
is well-defined and semi-simple, and, evaluating the trace, we get
$\unicode[STIX]{x1D70C}_{I_{v}}^{\prime }\otimes _{F}F^{\prime }$
is well-defined and semi-simple, and, evaluating the trace, we get
We thus get the result.◻
11.5 Elimination of case (ii) of Proposition 11.3
We want to prove that
![]() $\unicode[STIX]{x1D70C}_{K(Y)}$
is always irreducible, and thus prove that case (ii) of Proposition 11.3 can never happen. Thus suppose we are in case (ii).
$\unicode[STIX]{x1D70C}_{K(Y)}$
is always irreducible, and thus prove that case (ii) of Proposition 11.3 can never happen. Thus suppose we are in case (ii).
Proposition 11.6. There exists a continuous representation
![]() $\overline{r}:G_{E}\longrightarrow \operatorname{GL}_{3}(F)$
such that
$\overline{r}:G_{E}\longrightarrow \operatorname{GL}_{3}(F)$
such that
![]() $\overline{r}$
is a non-split extension of
$\overline{r}$
is a non-split extension of
![]() $\unicode[STIX]{x1D712}^{\bot }$
by
$\unicode[STIX]{x1D712}^{\bot }$
by
![]() $\unicode[STIX]{x1D712}$
,
$\unicode[STIX]{x1D712}$
,
such that
![]() $\overline{r}=\overline{r}^{\bot }$
and verifying:
$\overline{r}=\overline{r}^{\bot }$
and verifying:
(i)
 $\dim _{F}(\overline{r}\otimes \overline{\unicode[STIX]{x1D712}})^{I_{v}}=2$
if
$\dim _{F}(\overline{r}\otimes \overline{\unicode[STIX]{x1D712}})^{I_{v}}=2$
if
 $v\!\not |~\text{Cond}(\unicode[STIX]{x1D712})$
;
$v\!\not |~\text{Cond}(\unicode[STIX]{x1D712})$
;(ii)
 $\dim _{F}(\overline{r}\otimes \overline{\unicode[STIX]{x1D712}})^{I_{v}}\geqslant 1$
if
$\dim _{F}(\overline{r}\otimes \overline{\unicode[STIX]{x1D712}})^{I_{v}}\geqslant 1$
if
 $v|\text{Cond}(\unicode[STIX]{x1D712})$
;
$v|\text{Cond}(\unicode[STIX]{x1D712})$
;(iii) if
 $p$
splits,
$p$
splits,
 $D_{\text{cris},\overline{v}}(\overline{r})^{\unicode[STIX]{x1D719}=\unicode[STIX]{x1D712}_{\overline{v}}^{\bot }(p)}\neq 0$
and
$D_{\text{cris},\overline{v}}(\overline{r})^{\unicode[STIX]{x1D719}=\unicode[STIX]{x1D712}_{\overline{v}}^{\bot }(p)}\neq 0$
and
 $D_{\text{cris},v}(\overline{r})^{\unicode[STIX]{x1D719}=\unicode[STIX]{x1D712}_{v}^{\bot }(p)}\neq 0$
;
$D_{\text{cris},v}(\overline{r})^{\unicode[STIX]{x1D719}=\unicode[STIX]{x1D712}_{v}^{\bot }(p)}\neq 0$
;(iv) if
 $p$
is inert,
$p$
is inert,
 $D_{\text{cris},\unicode[STIX]{x1D70F}}(\overline{r})^{\unicode[STIX]{x1D719}^{2}=\unicode[STIX]{x1D712}^{\bot }(p)}\neq 0$
.
$D_{\text{cris},\unicode[STIX]{x1D70F}}(\overline{r})^{\unicode[STIX]{x1D719}^{2}=\unicode[STIX]{x1D712}^{\bot }(p)}\neq 0$
.
Proof. We first sketch the proof in case
![]() $p$
inert we will detail a bit the argument in Proposition 11.8. First, by Ribet’s Lemma (see [Reference BellaïcheBel03, Corollaire 1] or [Reference ChenevierChe03, Appendice, Lemma 3.1] and [Reference Bellaïche and ChenevierBC04, Lemme 7.3]) there exists a
$p$
inert we will detail a bit the argument in Proposition 11.8. First, by Ribet’s Lemma (see [Reference BellaïcheBel03, Corollaire 1] or [Reference ChenevierChe03, Appendice, Lemma 3.1] and [Reference Bellaïche and ChenevierBC04, Lemme 7.3]) there exists a
![]() $g\neq 0\in {\mathcal{O}}_{Y}$
and a
$g\neq 0\in {\mathcal{O}}_{Y}$
and a
![]() ${\mathcal{O}}_{Y,(g)}$
-lattice
${\mathcal{O}}_{Y,(g)}$
-lattice
![]() $\unicode[STIX]{x1D6EC}$
stable by
$\unicode[STIX]{x1D6EC}$
stable by
![]() $r_{K(Y)}$
such that
$r_{K(Y)}$
such that
![]() $\overline{r}:=\overline{r_{\unicode[STIX]{x1D6EC}}}=\Bigl(\begin{smallmatrix}\unicode[STIX]{x1D712} & \star \\ & \unicode[STIX]{x1D712}^{\bot }\end{smallmatrix}\!\Bigr)$
is a non-split extension. We can moreover easily assure that this lattice is a direct factor of a lattice stable by
$\overline{r}:=\overline{r_{\unicode[STIX]{x1D6EC}}}=\Bigl(\begin{smallmatrix}\unicode[STIX]{x1D712} & \star \\ & \unicode[STIX]{x1D712}^{\bot }\end{smallmatrix}\!\Bigr)$
is a non-split extension. We can moreover easily assure that this lattice is a direct factor of a lattice stable by
![]() $\unicode[STIX]{x1D70C}_{K(Y)}$
. Then, conditions (i) and (ii) follow from the Proposition 11.5. For condition (iii), we can use the analog of Kisin’s argument as extended by Liu, see [Reference LiuLiu15], as in the proof of the next proposition, as for all
$\unicode[STIX]{x1D70C}_{K(Y)}$
. Then, conditions (i) and (ii) follow from the Proposition 11.5. For condition (iii), we can use the analog of Kisin’s argument as extended by Liu, see [Reference LiuLiu15], as in the proof of the next proposition, as for all
![]() $z\in Z$
,
$z\in Z$
,
as shown by Proposition 11.3. The split case is similar to [Reference Bellaïche and ChenevierBC04, Proposition 9.3 and Lemme 9.1] (see also Remarque 6.3.8 or apply the results to
![]() $\overline{r}_{\overline{v}}$
).◻
$\overline{r}_{\overline{v}}$
).◻
Write
![]() $r^{\prime }=r\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1}=r\otimes \overline{\unicode[STIX]{x1D712}_{p}}$
, which is an extension of
$r^{\prime }=r\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1}=r\otimes \overline{\unicode[STIX]{x1D712}_{p}}$
, which is an extension of
![]() $1$
by
$1$
by
![]() $\unicode[STIX]{x1D712}_{p}\overline{\unicode[STIX]{x1D712}_{p}}=\unicode[STIX]{x1D714}_{p}$
(the cyclotomic character).
$\unicode[STIX]{x1D712}_{p}\overline{\unicode[STIX]{x1D712}_{p}}=\unicode[STIX]{x1D714}_{p}$
(the cyclotomic character).
Lemma 11.7. The representation
![]() $r^{\prime }$
is crystalline at
$r^{\prime }$
is crystalline at
![]() $p$
.
$p$
.
Proof. As
![]() $\unicode[STIX]{x1D712}^{\bot }$
is crystalline (at
$\unicode[STIX]{x1D712}^{\bot }$
is crystalline (at
![]() $v$
and
$v$
and
![]() $\overline{v}$
if
$\overline{v}$
if
![]() $p$
splits, at
$p$
splits, at
![]() $p$
if
$p$
if
![]() $p$
is inert), it is enough to prove that
$p$
is inert), it is enough to prove that
![]() $r$
is crystalline. Suppose first
$r$
is crystalline. Suppose first
![]() $p$
is inert. As
$p$
is inert. As
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}$
is left-exact, because
$D_{\text{crys},\unicode[STIX]{x1D70F}}$
is left-exact, because
![]() $\overline{r}$
is extension of
$\overline{r}$
is extension of
![]() $\unicode[STIX]{x1D712}_{p}^{\bot }$
by
$\unicode[STIX]{x1D712}_{p}^{\bot }$
by
![]() $\unicode[STIX]{x1D712}_{p}$
we have
$\unicode[STIX]{x1D712}_{p}$
we have
but on
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D712}_{p})$
$D_{\text{crys},\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D712}_{p})$
![]() $\unicode[STIX]{x1D711}^{2}$
acts as
$\unicode[STIX]{x1D711}^{2}$
acts as
![]() $\unicode[STIX]{x1D712}_{p}(p)=\unicode[STIX]{x1D712}_{p}^{\bot }(p)p^{-2}$
, thus this line is distinct from
$\unicode[STIX]{x1D712}_{p}(p)=\unicode[STIX]{x1D712}_{p}^{\bot }(p)p^{-2}$
, thus this line is distinct from
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}(r)^{\unicode[STIX]{x1D711}^{2}=\unicode[STIX]{x1D712}^{\bot }(p)}$
, and thus
$D_{\text{crys},\unicode[STIX]{x1D70F}}(r)^{\unicode[STIX]{x1D711}^{2}=\unicode[STIX]{x1D712}^{\bot }(p)}$
, and thus
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}(r)$
is of dimension
$D_{\text{crys},\unicode[STIX]{x1D70F}}(r)$
is of dimension
![]() $2$
. But because of the action of
$2$
. But because of the action of
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
![]() $D_{\text{crys}}(r)$
is a
$D_{\text{crys}}(r)$
is a
![]() $K\otimes _{\mathbb{Z}_{p}}F$
-module of dimension
$K\otimes _{\mathbb{Z}_{p}}F$
-module of dimension
![]() $2$
, i.e.
$2$
, i.e.
![]() $r$
is crystalline. If
$r$
is crystalline. If
![]() $p$
splits, as
$p$
splits, as
![]() $\overline{r}^{\bot }\simeq r$
, it suffices to prove that
$\overline{r}^{\bot }\simeq r$
, it suffices to prove that
![]() $\overline{r}$
is crystalline at
$\overline{r}$
is crystalline at
![]() $\overline{v}$
. But we use
$\overline{v}$
. But we use
![]() $D_{\text{cris},\overline{v}}(\overline{r})^{\unicode[STIX]{x1D719}=\unicode[STIX]{x1D712}_{\overline{v}}^{\bot }(p)}$
as in the inert case to get the result.◻
$D_{\text{cris},\overline{v}}(\overline{r})^{\unicode[STIX]{x1D719}=\unicode[STIX]{x1D712}_{\overline{v}}^{\bot }(p)}$
as in the inert case to get the result.◻
Thus
![]() $r^{\prime }$
gives a non-zero element in
$r^{\prime }$
gives a non-zero element in
![]() $H_{f}^{1}(E,\unicode[STIX]{x1D714}_{p})$
, but by [Reference Bellaïche and ChenevierBC04, Lemme 9.3], which is a well-known result,
$H_{f}^{1}(E,\unicode[STIX]{x1D714}_{p})$
, but by [Reference Bellaïche and ChenevierBC04, Lemme 9.3], which is a well-known result,
![]() $H_{f}^{1}(E,\unicode[STIX]{x1D714}_{p})=\{0\}$
, and thus
$H_{f}^{1}(E,\unicode[STIX]{x1D714}_{p})=\{0\}$
, and thus
![]() $r^{\prime }$
must be trivial, which gives a contradiction. We are thus in the case where
$r^{\prime }$
must be trivial, which gives a contradiction. We are thus in the case where
![]() $\unicode[STIX]{x1D70C}_{K(Y)}$
is irreducible.
$\unicode[STIX]{x1D70C}_{K(Y)}$
is irreducible.
11.6 Good reduction at
 $p$
$p$
Suppose
![]() $p$
is inert. The result for
$p$
is inert. The result for
![]() $p$
split is analogous to [Reference Bellaïche and ChenevierBC04, Proposition 9.3]. Write
$p$
split is analogous to [Reference Bellaïche and ChenevierBC04, Proposition 9.3]. Write
![]() $u=\unicode[STIX]{x1D712}_{p}^{\bot }(p)$
.
$u=\unicode[STIX]{x1D712}_{p}^{\bot }(p)$
.
Proposition 11.8. There exists a continuous representation
![]() $\overline{\unicode[STIX]{x1D70C}}:G_{E}\longrightarrow \operatorname{GL}_{3}(F)$
such that we have the following.
$\overline{\unicode[STIX]{x1D70C}}:G_{E}\longrightarrow \operatorname{GL}_{3}(F)$
such that we have the following.
(i) For every place
 $v$
of
$v$
of
 $E$
not dividing
$E$
not dividing
 $p$
, we have:
$p$
, we have:(a)
 $\dim _{F}(\overline{\unicode[STIX]{x1D70C}}\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1})^{I_{v}}\geqslant 2$
if
$\dim _{F}(\overline{\unicode[STIX]{x1D70C}}\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1})^{I_{v}}\geqslant 2$
if
 $v|\text{Cond}(\unicode[STIX]{x1D712})$
;
$v|\text{Cond}(\unicode[STIX]{x1D712})$
;(b)
 $\dim _{F}(\overline{\unicode[STIX]{x1D70C}}\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1})^{I_{v}}=3$
if
$\dim _{F}(\overline{\unicode[STIX]{x1D70C}}\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1})^{I_{v}}=3$
if
 $v\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
.
$v\!\not |~\operatorname{Cond}(\unicode[STIX]{x1D712})$
.
(ii)
 $D_{\text{cris},\unicode[STIX]{x1D70F}}(\overline{\unicode[STIX]{x1D70C}})^{\unicode[STIX]{x1D711}^{2}=u}$
is non-zero.
$D_{\text{cris},\unicode[STIX]{x1D70F}}(\overline{\unicode[STIX]{x1D70C}})^{\unicode[STIX]{x1D711}^{2}=u}$
is non-zero.(iii)
 $\overline{\unicode[STIX]{x1D70C}}^{ss}\simeq \unicode[STIX]{x1D712}_{p}\oplus \unicode[STIX]{x1D712}_{p}^{\bot }\oplus 1$
and one of the two following assertions is true.
$\overline{\unicode[STIX]{x1D70C}}^{ss}\simeq \unicode[STIX]{x1D712}_{p}\oplus \unicode[STIX]{x1D712}_{p}^{\bot }\oplus 1$
and one of the two following assertions is true.(a) Either
 $\overline{\unicode[STIX]{x1D70C}}$
has a subquotient
$\overline{\unicode[STIX]{x1D70C}}$
has a subquotient
 $r$
of dimension 2, such that
$r$
of dimension 2, such that
 $r^{\bot }\simeq r$
and
$r^{\bot }\simeq r$
and
 $r$
is a non-trivial extension of
$r$
is a non-trivial extension of
 $\unicode[STIX]{x1D712}_{p}^{\bot }$
by
$\unicode[STIX]{x1D712}_{p}^{\bot }$
by
 $\unicode[STIX]{x1D712}_{p}$
.
$\unicode[STIX]{x1D712}_{p}$
.(b) Either
 $\overline{\unicode[STIX]{x1D70C}}\simeq \overline{\unicode[STIX]{x1D70C}}^{\bot }$
;
$\overline{\unicode[STIX]{x1D70C}}\simeq \overline{\unicode[STIX]{x1D70C}}^{\bot }$
;
 $\overline{\unicode[STIX]{x1D70C}}$
has a unique subrepresentation
$\overline{\unicode[STIX]{x1D70C}}$
has a unique subrepresentation
 $r_{1}$
of dimension 2 and a unique subquotient
$r_{1}$
of dimension 2 and a unique subquotient
 $r_{2}$
of dimension 2, with
$r_{2}$
of dimension 2, with
 $r_{1}$
a non-trivial extension of 1 by
$r_{1}$
a non-trivial extension of 1 by
 $\unicode[STIX]{x1D712}_{p}$
and
$\unicode[STIX]{x1D712}_{p}$
and
 $r_{2}$
a non-trivial extension of
$r_{2}$
a non-trivial extension of
 $\unicode[STIX]{x1D712}_{p}^{\bot }$
by 1, and
$\unicode[STIX]{x1D712}_{p}^{\bot }$
by 1, and
 $r_{1}^{\bot }\simeq r_{2}$
.
$r_{1}^{\bot }\simeq r_{2}$
.
Proof. Denote by
![]() ${\mathcal{O}}$
the rigid local ring of
${\mathcal{O}}$
the rigid local ring of
![]() $Y$
at
$Y$
at
![]() $y_{0}$
, a discrete valuation ring of residual field
$y_{0}$
, a discrete valuation ring of residual field
![]() $F$
, denote by
$F$
, denote by
![]() $L$
its fraction field, and
$L$
its fraction field, and
![]() $\unicode[STIX]{x1D70C}_{L}$
the representation which is the scalar extension of
$\unicode[STIX]{x1D70C}_{L}$
the representation which is the scalar extension of
![]() $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
![]() $L$
. As
$L$
. As
![]() $\overline{\unicode[STIX]{x1D70C}_{L}}^{ss}=1\oplus \unicode[STIX]{x1D712}_{p}\oplus \unicode[STIX]{x1D712}_{p}^{\bot }$
which are pairwise distinct characters, we can also use [Reference Bellaïche and ChenevierBC04, Proposition 7.1], the analog to Ribet’s theorem, to find
$\overline{\unicode[STIX]{x1D70C}_{L}}^{ss}=1\oplus \unicode[STIX]{x1D712}_{p}\oplus \unicode[STIX]{x1D712}_{p}^{\bot }$
which are pairwise distinct characters, we can also use [Reference Bellaïche and ChenevierBC04, Proposition 7.1], the analog to Ribet’s theorem, to find
![]() $\unicode[STIX]{x1D6EC}\subset L^{3}$
a lattice stable by
$\unicode[STIX]{x1D6EC}\subset L^{3}$
a lattice stable by
![]() $\unicode[STIX]{x1D70C}_{L}$
such that the reduced representation
$\unicode[STIX]{x1D70C}_{L}$
such that the reduced representation
![]() $\overline{\unicode[STIX]{x1D70C}}=\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}}}$
satisfies condition (iii)(a) or (iii)(b). Condition (i) is true by Proposition 11.5. We can argue as in [Reference Bellaïche and ChenevierBC04] to get condition (ii), but we will need a generalization to
$\overline{\unicode[STIX]{x1D70C}}=\overline{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}}}$
satisfies condition (iii)(a) or (iii)(b). Condition (i) is true by Proposition 11.5. We can argue as in [Reference Bellaïche and ChenevierBC04] to get condition (ii), but we will need a generalization to
![]() $G_{K}$
if
$G_{K}$
if
![]() $p$
is inert. Fortunately what we need is in [Reference LiuLiu15]. As in [Reference Bellaïche and ChenevierBC04, Lemma 7.3] there is an affinoid
$p$
is inert. Fortunately what we need is in [Reference LiuLiu15]. As in [Reference Bellaïche and ChenevierBC04, Lemma 7.3] there is an affinoid
![]() $Y\supset \unicode[STIX]{x1D6FA}\ni y_{0}$
such that
$Y\supset \unicode[STIX]{x1D6FA}\ni y_{0}$
such that
![]() $\unicode[STIX]{x1D70C}_{L}$
as a
$\unicode[STIX]{x1D70C}_{L}$
as a
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6FA}}$
-stable lattice
${\mathcal{O}}_{\unicode[STIX]{x1D6FA}}$
-stable lattice
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FA}}$
such that
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FA}}$
such that
![]() $\overline{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FA}},y_{0}}=\overline{\unicode[STIX]{x1D70C}}$
. Write
$\overline{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FA}},y_{0}}=\overline{\unicode[STIX]{x1D70C}}$
. Write
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FA}}}$
. Let thus
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FA}}}$
. Let thus
![]() $Z^{\prime }\subset \unicode[STIX]{x1D6FA}$
the points that are in
$Z^{\prime }\subset \unicode[STIX]{x1D6FA}$
the points that are in
![]() $Z\subset Y$
, in
$Z\subset Y$
, in
![]() $\unicode[STIX]{x1D6FA}$
, and such that
$\unicode[STIX]{x1D6FA}$
, and such that
![]() $\overline{\unicode[STIX]{x1D70C}_{z}}$
is semi-simple (it is a cofinite subset of
$\overline{\unicode[STIX]{x1D70C}_{z}}$
is semi-simple (it is a cofinite subset of
![]() $Z\cap \unicode[STIX]{x1D6FA}$
as
$Z\cap \unicode[STIX]{x1D6FA}$
as
![]() $\unicode[STIX]{x1D70C}_{K(\unicode[STIX]{x1D6FA})}$
is semi-simple (irreducible)). By choice of
$\unicode[STIX]{x1D70C}_{K(\unicode[STIX]{x1D6FA})}$
is semi-simple (irreducible)). By choice of
![]() $Z$
, we have that for all
$Z$
, we have that for all
![]() $z\in Z^{\prime }$
$z\in Z^{\prime }$
As
![]() $\unicode[STIX]{x1D70C}$
is polarized, its
$\unicode[STIX]{x1D70C}$
is polarized, its
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-Hodge–Tate weights are
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
-Hodge–Tate weights are
![]() $h^{\unicode[STIX]{x1D70E}}(z)=(-h_{3},-h_{2},-h_{1})$
. Set
$h^{\unicode[STIX]{x1D70E}}(z)=(-h_{3},-h_{2},-h_{1})$
. Set
![]() $h_{i}^{K}=(h_{i},h_{4-i})\in F_{\unicode[STIX]{x1D70F}}\times F_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=K\otimes _{\mathbb{Q}_{p}}F$
. Thus
$h_{i}^{K}=(h_{i},h_{4-i})\in F_{\unicode[STIX]{x1D70F}}\times F_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=K\otimes _{\mathbb{Q}_{p}}F$
. Thus
![]() $(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D70C},(h_{i}^{K})_{i},F_{1},Z)$
is a weakly refined (polarized)
$(\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D70C},(h_{i}^{K})_{i},F_{1},Z)$
is a weakly refined (polarized)
![]() $p$
-adic representation of
$p$
-adic representation of
![]() $G_{K}$
of dimension
$G_{K}$
of dimension
![]() $3$
in the sense of [Reference LiuLiu15, Definition 0.3.1]. To verify property (f) of [Reference LiuLiu15, Definition 0.3.1], recall that over the weight space
$3$
in the sense of [Reference LiuLiu15, Definition 0.3.1]. To verify property (f) of [Reference LiuLiu15, Definition 0.3.1], recall that over the weight space
![]() ${\mathcal{W}}$
we had a universal character
${\mathcal{W}}$
we had a universal character
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{1}\times \unicode[STIX]{x1D712}_{2}:{\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}\longrightarrow {\mathcal{O}}({\mathcal{W}})^{\times }$
, and, as
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{1}\times \unicode[STIX]{x1D712}_{2}:{\mathcal{O}}^{\times }\times {\mathcal{O}}^{1}\longrightarrow {\mathcal{O}}({\mathcal{W}})^{\times }$
, and, as
![]() ${\mathcal{W}}$
is regarded over
${\mathcal{W}}$
is regarded over
![]() $K$
, we can split
$K$
, we can split
![]() ${\mathcal{O}}({\mathcal{W}})\otimes _{\mathbb{Q}_{p}}K={\mathcal{O}}(W)_{\unicode[STIX]{x1D70F}}\times {\mathcal{O}}(W)_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. Under this isomorphism, the derivative at
${\mathcal{O}}({\mathcal{W}})\otimes _{\mathbb{Q}_{p}}K={\mathcal{O}}(W)_{\unicode[STIX]{x1D70F}}\times {\mathcal{O}}(W)_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
. Under this isomorphism, the derivative at
![]() $1$
of
$1$
of
![]() $\unicode[STIX]{x1D712}_{1}$
, denoted
$\unicode[STIX]{x1D712}_{1}$
, denoted
![]() $(wt_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D712}_{1}),wt_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D712}_{1}))$
, is at every
$(wt_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D712}_{1}),wt_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D712}_{1}))$
, is at every
![]() $\unicode[STIX]{x1D705}\in \mathbb{Z}^{3}\subset {\mathcal{W}}$
given by
$\unicode[STIX]{x1D705}\in \mathbb{Z}^{3}\subset {\mathcal{W}}$
given by
Thus set
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D70F}^{-1}(\unicode[STIX]{x1D712}_{1}\circ c)$
. Its derivative at
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D70F}^{-1}(\unicode[STIX]{x1D712}_{1}\circ c)$
. Its derivative at
![]() $1$
is given by
$1$
is given by
![]() $(k_{3}-1,k_{1})=(-h_{1},h_{3})$
at classical points
$(k_{3}-1,k_{1})=(-h_{1},h_{3})$
at classical points
![]() $\unicode[STIX]{x1D705}\in \mathbb{Z}^{3}$
. Thus, the character,
$\unicode[STIX]{x1D705}\in \mathbb{Z}^{3}$
. Thus, the character,
has the desired property (f).
Write
![]() $\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D713}$
(where
$\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D713}$
(where
![]() $\unicode[STIX]{x1D713}$
is precomposed by product of the two Lubin–Tate characters of
$\unicode[STIX]{x1D713}$
is precomposed by product of the two Lubin–Tate characters of
![]() $K$
,
$K$
,
![]() $G_{K}\longrightarrow O^{\times }$
). Thus
$G_{K}\longrightarrow O^{\times }$
). Thus
![]() $\unicode[STIX]{x1D70C}^{\prime }$
has
$\unicode[STIX]{x1D70C}^{\prime }$
has
![]() $\unicode[STIX]{x1D705}_{1}^{K^{\prime }}=(0,0)$
as smallest Hodge–Tate weight. In particular, by [Reference LiuLiu15, Theorem 0.3.2],
$\unicode[STIX]{x1D705}_{1}^{K^{\prime }}=(0,0)$
as smallest Hodge–Tate weight. In particular, by [Reference LiuLiu15, Theorem 0.3.2],
![]() $\unicode[STIX]{x1D6FA}_{fs}=\unicode[STIX]{x1D6FA}$
. But then by Theorem 0.1.2 applied to
$\unicode[STIX]{x1D6FA}_{fs}=\unicode[STIX]{x1D6FA}$
. But then by Theorem 0.1.2 applied to
![]() $S=\unicode[STIX]{x1D6FA}$
,
$S=\unicode[STIX]{x1D6FA}$
,
![]() $k,n$
big enough, and
$k,n$
big enough, and
![]() $\unicode[STIX]{x1D70C}^{\prime }$
, we have that
$\unicode[STIX]{x1D70C}^{\prime }$
, we have that
(see [Reference LiuLiu15, Remark 3.3.5 and Corollary 1.5.4]; as
![]() $0$
is the only non-positive Hodge–Tate weightFootnote
6
of
$0$
is the only non-positive Hodge–Tate weightFootnote
6
of
![]() $\unicode[STIX]{x1D70C}^{\prime }$
, [Reference LiuLiu15, Corollary 1.5.4] applies), and
$\unicode[STIX]{x1D70C}^{\prime }$
, [Reference LiuLiu15, Corollary 1.5.4] applies), and
![]() $D_{\text{Sen}}^{+}(\unicode[STIX]{x1D70C}_{y_{0}}^{\prime })^{\unicode[STIX]{x1D6E4}}\neq 0$
.
$D_{\text{Sen}}^{+}(\unicode[STIX]{x1D70C}_{y_{0}}^{\prime })^{\unicode[STIX]{x1D6E4}}\neq 0$
.
Thus
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70C}_{y_{0}}^{\prime })^{\unicode[STIX]{x1D711}^{2}=F_{1}}\neq 0$
, which means
$D_{\text{crys},\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D70C}_{y_{0}}^{\prime })^{\unicode[STIX]{x1D711}^{2}=F_{1}}\neq 0$
, which means
11.7 Elimination of case (iii)(a) of Proposition 11.8
We can do as in [Reference Bellaïche and ChenevierBC04], and as we eliminated case (ii) of Proposition 11.3, to eliminate case (iii)(a) of Proposition 11.8. Suppose we are in case (iii)(a); there is thus a subquotient
![]() $r$
of
$r$
of
![]() $\overline{\unicode[STIX]{x1D70C}}$
such that
$\overline{\unicode[STIX]{x1D70C}}$
such that
![]() $r^{\bot }\simeq r$
and
$r^{\bot }\simeq r$
and
![]() $r$
is an extension of
$r$
is an extension of
![]() $\unicode[STIX]{x1D712}_{p}^{\bot }$
by
$\unicode[STIX]{x1D712}_{p}^{\bot }$
by
![]() $\unicode[STIX]{x1D712}_{p}$
. Write
$\unicode[STIX]{x1D712}_{p}$
. Write
![]() $r^{\prime }=r\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1}=r\otimes \overline{\unicode[STIX]{x1D712}_{p}}$
, which is an extension of
$r^{\prime }=r\otimes (\unicode[STIX]{x1D712}_{p}^{\bot })^{-1}=r\otimes \overline{\unicode[STIX]{x1D712}_{p}}$
, which is an extension of
![]() $1$
by
$1$
by
![]() $\unicode[STIX]{x1D712}_{p}\overline{\unicode[STIX]{x1D712}_{p}}=\unicode[STIX]{x1D714}_{p}$
(the cyclotomic character).
$\unicode[STIX]{x1D712}_{p}\overline{\unicode[STIX]{x1D712}_{p}}=\unicode[STIX]{x1D714}_{p}$
(the cyclotomic character).
Lemma 11.9. The representation
![]() $r^{\prime }$
is crystalline at
$r^{\prime }$
is crystalline at
![]() $p$
(at
$p$
(at
![]() $v_{1},v_{2}|p$
is
$v_{1},v_{2}|p$
is
![]() $p$
is split).
$p$
is split).
Proof. The split case is identical to [Reference Bellaïche and ChenevierBC04, Lemma 9.1] and Lemma 11.7. Suppose
![]() $p$
is inert. As
$p$
is inert. As
![]() $\unicode[STIX]{x1D712}_{p}^{\bot }$
is crystalline, it is enough to prove that
$\unicode[STIX]{x1D712}_{p}^{\bot }$
is crystalline, it is enough to prove that
![]() $r$
is crystalline. But
$r$
is crystalline. But
![]() $V\mapsto D_{\text{crys},\unicode[STIX]{x1D70F}}(V)^{\unicode[STIX]{x1D711}^{2}=u}$
is left-exact, thus, if we write
$V\mapsto D_{\text{crys},\unicode[STIX]{x1D70F}}(V)^{\unicode[STIX]{x1D711}^{2}=u}$
is left-exact, thus, if we write
![]() $u=\unicode[STIX]{x1D712}^{\bot }(p)$
,
$u=\unicode[STIX]{x1D712}^{\bot }(p)$
,
But
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}(1)^{\unicode[STIX]{x1D711}^{2}=u}=0$
, and thus
$D_{\text{crys},\unicode[STIX]{x1D70F}}(1)^{\unicode[STIX]{x1D711}^{2}=u}=0$
, and thus
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}(r)^{\unicode[STIX]{x1D711}^{2}=u}\neq 0$
. The end of the proof is identical to Lemma 11.7.◻
$D_{\text{crys},\unicode[STIX]{x1D70F}}(r)^{\unicode[STIX]{x1D711}^{2}=u}\neq 0$
. The end of the proof is identical to Lemma 11.7.◻
Lemma 11.10. The representation
![]() $r^{\prime }$
is unramified at every place
$r^{\prime }$
is unramified at every place
![]() $w\!\not |~p$
.
$w\!\not |~p$
.
Proof. This is exactly identical to [Reference Bellaïche and ChenevierBC04, Lemme 9.2].◻
Thus by [Reference Bellaïche and ChenevierBC04, Lemme 9.3],
![]() $r$
must be trivial, which contradicts Proposition 11.8(iii)(a).
$r$
must be trivial, which contradicts Proposition 11.8(iii)(a).
11.8 Conclusion
We are thus in case (iii)(b) of Proposition 11.8, with
![]() $r_{1}$
a non-trivial extension of
$r_{1}$
a non-trivial extension of
![]() $1$
by
$1$
by
![]() $\unicode[STIX]{x1D712}_{p}$
.
$\unicode[STIX]{x1D712}_{p}$
.
Lemma 11.11. The representation
![]() $r_{1}$
is crystalline at
$r_{1}$
is crystalline at
![]() $p$
if
$p$
if
![]() $p$
is inert, and at
$p$
is inert, and at
![]() $v_{1},v_{2}|p$
if
$v_{1},v_{2}|p$
if
![]() $p$
splits.
$p$
splits.
Proof. Suppose
![]() $p$
inert. As
$p$
inert. As
![]() $r_{1}\simeq r_{2}^{\bot }$
, we only need to prove that
$r_{1}\simeq r_{2}^{\bot }$
, we only need to prove that
![]() $r_{2}$
is crystalline. Because
$r_{2}$
is crystalline. Because
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}(\cdot )^{\unicode[STIX]{x1D711}^{2}=u}$
is left-exact, we again have
$D_{\text{crys},\unicode[STIX]{x1D70F}}(\cdot )^{\unicode[STIX]{x1D711}^{2}=u}$
is left-exact, we again have
As
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D712}_{p})^{\unicode[STIX]{x1D711}^{2}=u}=\{0\}$
and
$D_{\text{crys},\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D712}_{p})^{\unicode[STIX]{x1D711}^{2}=u}=\{0\}$
and
![]() $\dim _{F}D_{\text{crys},\unicode[STIX]{x1D70F}}(\overline{\unicode[STIX]{x1D70C}})^{\unicode[STIX]{x1D711}^{2}=u}\neq 0$
, we have
$\dim _{F}D_{\text{crys},\unicode[STIX]{x1D70F}}(\overline{\unicode[STIX]{x1D70C}})^{\unicode[STIX]{x1D711}^{2}=u}\neq 0$
, we have
![]() $\dim _{F}D_{\text{crys},\unicode[STIX]{x1D70F}}(r_{2})^{\unicode[STIX]{x1D711}^{2}=u}\neq \{0\}$
. Moreover,
$\dim _{F}D_{\text{crys},\unicode[STIX]{x1D70F}}(r_{2})^{\unicode[STIX]{x1D711}^{2}=u}\neq \{0\}$
. Moreover,
by left-exactness of
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}$
, which gives a line where
$D_{\text{crys},\unicode[STIX]{x1D70F}}$
, which gives a line where
![]() $\unicode[STIX]{x1D711}^{2}$
acts as
$\unicode[STIX]{x1D711}^{2}$
acts as
![]() $1\neq u$
. Thus there are at least two different lines in
$1\neq u$
. Thus there are at least two different lines in
![]() $D_{\text{crys},\unicode[STIX]{x1D70F}}(r_{2})$
which means this is two-dimensional and, by existence of
$D_{\text{crys},\unicode[STIX]{x1D70F}}(r_{2})$
which means this is two-dimensional and, by existence of
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
![]() $r_{2}$
(thus
$r_{2}$
(thus
![]() $r_{1}$
) is crystalline.
$r_{1}$
) is crystalline.
Now suppose
![]() $p$
splits. Then the proof is identical to [Reference Bellaïche and ChenevierBC04, Lemme 9.4], as
$p$
splits. Then the proof is identical to [Reference Bellaïche and ChenevierBC04, Lemme 9.4], as
![]() $1\neq \unicode[STIX]{x1D712}_{v}(p)\neq \unicode[STIX]{x1D712}_{v}^{\bot }(p)\neq 1$
(recall
$1\neq \unicode[STIX]{x1D712}_{v}(p)\neq \unicode[STIX]{x1D712}_{v}^{\bot }(p)\neq 1$
(recall
![]() $|\unicode[STIX]{x1D712}_{v}(p)|_{\mathbb{C}}=|\unicode[STIX]{x1D712}_{\overline{v}}(p)|_{\mathbb{C}}=p^{-1/2}$
).◻
$|\unicode[STIX]{x1D712}_{v}(p)|_{\mathbb{C}}=|\unicode[STIX]{x1D712}_{\overline{v}}(p)|_{\mathbb{C}}=p^{-1/2}$
).◻
Theorem 11.12. The representation
![]() $r_{1}$
gives a non-zero element of
$r_{1}$
gives a non-zero element of
![]() $H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
.
$H_{f}^{1}(E,\unicode[STIX]{x1D712}_{p})$
.
Proof. We only need to prove that
![]() $r_{1}$
has good reduction outside
$r_{1}$
has good reduction outside
![]() $p$
. But then as
$p$
. But then as
![]() $\unicode[STIX]{x1D70C}$
is unramified outside
$\unicode[STIX]{x1D70C}$
is unramified outside
![]() $p\operatorname{Cond}(\unicode[STIX]{x1D712})$
, by Proposition 11.8, we only need to check for
$p\operatorname{Cond}(\unicode[STIX]{x1D712})$
, by Proposition 11.8, we only need to check for
![]() $v|\text{Cond}(\unicode[STIX]{x1D712})$
. We have shown in the proof of Proposition 11.5 that there exists an open subgroup
$v|\text{Cond}(\unicode[STIX]{x1D712})$
. We have shown in the proof of Proposition 11.5 that there exists an open subgroup
![]() $I_{w}^{\prime }\subset I_{w}$
such that
$I_{w}^{\prime }\subset I_{w}$
such that
![]() $\unicode[STIX]{x1D70C}_{|I_{w}}^{\prime }$
factors through
$\unicode[STIX]{x1D70C}_{|I_{w}}^{\prime }$
factors through
![]() $I_{w}/I_{w}^{\prime }$
and
$I_{w}/I_{w}^{\prime }$
and
![]() $\unicode[STIX]{x1D70C}_{|I_{w}}^{\prime }=1\oplus 1\oplus (\unicode[STIX]{x1D712}_{p}^{\bot })_{|I_{w}}^{-1}$
. Thus
$\unicode[STIX]{x1D70C}_{|I_{w}}^{\prime }=1\oplus 1\oplus (\unicode[STIX]{x1D712}_{p}^{\bot })_{|I_{w}}^{-1}$
. Thus
![]() $r_{1}^{I_{w}}$
is then of dimension
$r_{1}^{I_{w}}$
is then of dimension
![]() $1$
.◻
$1$
.◻
Acknowledgements
I would like to warmly thank my PhD advisors Laurent Fargues, and even more Vincent Pilloni for explaining carefully to me his previous work and suggesting this subject. I would also like to thank Fabrizio Andreatta and Adrian Iovita for their support, remarks and interesting discussions on this subject. It should be clear that this work is a continuations of theirs. I would like to particularly thank Joël Bellaïche and Gaëtan Chenevier for their perfectly written article and book on extensions in Selmer groups (from which my inspiration is easy to feel) but also for very inspiring discussions, encouragement and remarks. I would also like to thank Nicolas Bergeron, Stéphane Bijakowski, Jean-François Dat, Guy Henniart, Bruno Klingler, Arthur-César Le Bras, Alberto Minguez, Benoit Stroh, and Éric Urban for very interesting discussions on the subject. I would also like to thank the referees for their remarks which helped improve the exposition.
Appendix A Calculations on the weight space
In this appendix we explain a bit more the structure of the weight space
![]() ${\mathcal{W}}$
defined in § 3.
${\mathcal{W}}$
defined in § 3.
![]() ${\mathcal{W}}$
is represented by a disjoint union of (
${\mathcal{W}}$
is represented by a disjoint union of (
![]() $(p+1)(p^{2}-1)$
) three-dimensional open balls over
$(p+1)(p^{2}-1)$
) three-dimensional open balls over
![]() ${\mathcal{O}}$
. Indeed (if
${\mathcal{O}}$
. Indeed (if
![]() $p\neq 2$
)
$p\neq 2$
)
which induced, up to the choice of a basis of
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $\mathbb{Z}_{p}$
, an isomorphism,
$\mathbb{Z}_{p}$
, an isomorphism,
where
![]() $B_{2}(1,1^{-})$
is the open two-dimensional ball centered in
$B_{2}(1,1^{-})$
is the open two-dimensional ball centered in
![]() $1$
, of radius
$1$
, of radius
![]() $1$
. Also, as a
$1$
. Also, as a
![]() $\mathbb{Z}_{p}$
-module,
$\mathbb{Z}_{p}$
-module,
where
![]() $S$
is a finite group of cardinal
$S$
is a finite group of cardinal
![]() $p+1$
.
$p+1$
.
Proof. We have the exact sequence,
(surjectivity is given by local class field theory for example). Reducing modulo
![]() $p$
, we have the surjectivity of
$p$
, we have the surjectivity of
![]() $\mathbb{F}_{p^{2}}\overset{\overline{Nm}}{\longrightarrow }\mathbb{F}_{p}$
. We thus have the following diagram.
$\mathbb{F}_{p^{2}}\overset{\overline{Nm}}{\longrightarrow }\mathbb{F}_{p}$
. We thus have the following diagram.

The application
![]() $Nm^{1}=1+p{\mathcal{O}}\longrightarrow 1+p\mathbb{Z}_{p}$
is surjective; indeed, for all
$Nm^{1}=1+p{\mathcal{O}}\longrightarrow 1+p\mathbb{Z}_{p}$
is surjective; indeed, for all
![]() $z$
inside
$z$
inside
![]() $1+p\mathbb{Z}_{p}$
, because
$1+p\mathbb{Z}_{p}$
, because
![]() $Nm$
is surjective, there exists
$Nm$
is surjective, there exists
![]() $u\in {\mathcal{O}}^{\times }$
such that
$u\in {\mathcal{O}}^{\times }$
such that
![]() $uu^{\unicode[STIX]{x1D70E}}=1+pz$
(denote by
$uu^{\unicode[STIX]{x1D70E}}=1+pz$
(denote by
![]() $\unicode[STIX]{x1D70E}$
the conjugation, and
$\unicode[STIX]{x1D70E}$
the conjugation, and
![]() $\overline{\bullet }$
reduction modulo
$\overline{\bullet }$
reduction modulo
![]() $p$
). We deduce that
$p$
). We deduce that
![]() $\overline{u}\in \{x\in \mathbb{F}_{p^{2}}:x^{p+1}=1\}$
. We then set
$\overline{u}\in \{x\in \mathbb{F}_{p^{2}}:x^{p+1}=1\}$
. We then set
![]() $u^{\prime }=u/[\overline{u}]$
, where
$u^{\prime }=u/[\overline{u}]$
, where
![]() $[.]$
denotes the Teichmuller lift. Then
$[.]$
denotes the Teichmuller lift. Then
![]() $u^{\prime }\in 1+p{\mathcal{O}}$
and
$u^{\prime }\in 1+p{\mathcal{O}}$
and
![]() $(u^{\prime })(u^{\prime })^{\unicode[STIX]{x1D70E}}=uu^{\unicode[STIX]{x1D70E}}/([\overline{u}][\overline{u}]^{\unicode[STIX]{x1D70E}})=uu^{\unicode[STIX]{x1D70E}}/([\overline{u}^{p+1}])=1+pz$
. The second equality is because
$(u^{\prime })(u^{\prime })^{\unicode[STIX]{x1D70E}}=uu^{\unicode[STIX]{x1D70E}}/([\overline{u}][\overline{u}]^{\unicode[STIX]{x1D70E}})=uu^{\unicode[STIX]{x1D70E}}/([\overline{u}^{p+1}])=1+pz$
. The second equality is because
![]() $[.]$
commutes with Frobenius morphisms. (We could also prove the surjectivity by a method of successive approximations.) The map
$[.]$
commutes with Frobenius morphisms. (We could also prove the surjectivity by a method of successive approximations.) The map
![]() ${\mathcal{O}}^{1}\longrightarrow \{x\in \mathbb{F}_{p^{2}}:x^{p+1}=1\}$
is also surjective: for all
${\mathcal{O}}^{1}\longrightarrow \{x\in \mathbb{F}_{p^{2}}:x^{p+1}=1\}$
is also surjective: for all
![]() $x\in \{x\in \mathbb{F}_{p^{2}}:x^{p+1}=1\}$
,
$x\in \{x\in \mathbb{F}_{p^{2}}:x^{p+1}=1\}$
,
![]() $[x][x]^{\unicode[STIX]{x1D70E}}=[x^{p+1}]=[1]=1$
. Thus, up to choosing a base of
$[x][x]^{\unicode[STIX]{x1D70E}}=[x^{p+1}]=[1]=1$
. Thus, up to choosing a base of
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $\mathbb{Z}_{p}$
, we can with the logarithm identify
$\mathbb{Z}_{p}$
, we can with the logarithm identify
![]() $1+p{\mathcal{O}}$
to
$1+p{\mathcal{O}}$
to
![]() $\mathbb{Z}_{p}^{2}$
; this assures that
$\mathbb{Z}_{p}^{2}$
; this assures that
![]() $\{x\in {\mathcal{O}}^{1}:x\equiv 1(\text{mod}~p)\}\simeq \mathbb{Z}_{p}$
(because logarithm exchanges trace and
$\{x\in {\mathcal{O}}^{1}:x\equiv 1(\text{mod}~p)\}\simeq \mathbb{Z}_{p}$
(because logarithm exchanges trace and
![]() $Nm$
).◻
$Nm$
).◻
In particular,
Thus,
![]() ${\mathcal{W}}$
is isomorphic to a union of
${\mathcal{W}}$
is isomorphic to a union of
![]() $(p+1)(p^{2}-1)$
open balls of dimension
$(p+1)(p^{2}-1)$
open balls of dimension
![]() $3$
. There is also a universal character,
$3$
. There is also a universal character,
The following lemma is essential.
Lemma A.1. Every weight
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}(K)$
is automatically locally (
$\unicode[STIX]{x1D705}\in {\mathcal{W}}(K)$
is automatically locally (
![]() $\mathbb{Q}_{p}$
-) analytic.
$\mathbb{Q}_{p}$
-) analytic.
Actually we can be more precise.
Lemma A.2. Let
![]() ${\mathcal{U}}\subset {\mathcal{W}}$
a quasi-compact open; then there exists
${\mathcal{U}}\subset {\mathcal{W}}$
a quasi-compact open; then there exists
![]() $w_{{\mathcal{U}}}$
such that
$w_{{\mathcal{U}}}$
such that
![]() $\unicode[STIX]{x1D705}_{|{\mathcal{U}}}^{\text{un}}$
is
$\unicode[STIX]{x1D705}_{|{\mathcal{U}}}^{\text{un}}$
is
![]() $w_{{\mathcal{U}}}$
-analytic.
$w_{{\mathcal{U}}}$
-analytic.
Proof. It is [Reference UrbanUrb11, Lemma 3.4.6].◻
We will construct
![]() ${\mathcal{W}}(w)$
, an open subset of
${\mathcal{W}}(w)$
, an open subset of
![]() ${\mathcal{W}}$
containing the
${\mathcal{W}}$
containing the
![]() $w$
-analytic
$w$
-analytic
![]() $\unicode[STIX]{x1D705}$
(it is an affinoid). Set
$\unicode[STIX]{x1D705}$
(it is an affinoid). Set
![]() $w\in ]n-1,n]\cap \,v(\overline{\mathbb{Q}}_{p})$
. We define it this way, following [Reference Andreatta, Iovita and PilloniAIP15]. First set
$w\in ]n-1,n]\cap \,v(\overline{\mathbb{Q}}_{p})$
. We define it this way, following [Reference Andreatta, Iovita and PilloniAIP15]. First set
![]() $\mathfrak{W}(w)^{0}$
to be
$\mathfrak{W}(w)^{0}$
to be
![]() $\operatorname{Spf}{\mathcal{O}}_{K}\langle \langle S_{1},S_{2},S_{3}\rangle \rangle$
where
$\operatorname{Spf}{\mathcal{O}}_{K}\langle \langle S_{1},S_{2},S_{3}\rangle \rangle$
where
![]() $K$
is a finite extension of
$K$
is a finite extension of
![]() $\mathbb{Q}_{p}$
containing an element
$\mathbb{Q}_{p}$
containing an element
![]() $p^{w}$
of valuation
$p^{w}$
of valuation
![]() $w$
. Define
$w$
. Define
![]() $\mathfrak{T}_{w}$
the subtorus of
$\mathfrak{T}_{w}$
the subtorus of
![]() $\mathfrak{T}$
the formal torus associated to
$\mathfrak{T}$
the formal torus associated to
![]() $T^{0}$
, given by
$T^{0}$
, given by
for any flat,
![]() $p$
-adically complete
$p$
-adically complete
![]() ${\mathcal{O}}_{K}$
-algebra
${\mathcal{O}}_{K}$
-algebra
![]() $R$
. Denote by
$R$
. Denote by
![]() $X_{i}^{\prime }$
the coordinates on
$X_{i}^{\prime }$
the coordinates on
![]() $\mathfrak{T}_{w}$
, so that
$\mathfrak{T}_{w}$
, so that
![]() $1+p^{w}X_{i}^{\prime }=1+X_{i}$
on
$1+p^{w}X_{i}^{\prime }=1+X_{i}$
on
![]() $\mathfrak{T}$
, and define the universal character,
$\mathfrak{T}$
, and define the universal character,
 $$\begin{eqnarray}\unicode[STIX]{x1D705}^{0,\text{un}}:\begin{array}{@{}ccc@{}}\mathfrak{T}_{w}\times \mathfrak{W}(w)^{0} & \longrightarrow & \widehat{\mathbb{G}_{m}}\\ (1+p^{w}X_{1}^{\prime },1+p^{w}X_{2}^{\prime },1+p^{w}X_{3}^{\prime },S_{1},S_{2},S_{3}) & \longmapsto & \displaystyle \mathop{\prod }_{i=1}^{3}(1+p^{w}X_{i})^{S_{i}p^{-w+2/p-1}}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}^{0,\text{un}}:\begin{array}{@{}ccc@{}}\mathfrak{T}_{w}\times \mathfrak{W}(w)^{0} & \longrightarrow & \widehat{\mathbb{G}_{m}}\\ (1+p^{w}X_{1}^{\prime },1+p^{w}X_{2}^{\prime },1+p^{w}X_{3}^{\prime },S_{1},S_{2},S_{3}) & \longmapsto & \displaystyle \mathop{\prod }_{i=1}^{3}(1+p^{w}X_{i})^{S_{i}p^{-w+2/p-1}}.\end{array}\end{eqnarray}$$
Then define
![]() ${\mathcal{W}}(w)^{0}$
to be the rigid fiber of
${\mathcal{W}}(w)^{0}$
to be the rigid fiber of
![]() $\mathfrak{W}(w)^{0}$
and finally,
$\mathfrak{W}(w)^{0}$
and finally,
![]() $W(w)$
to be the fiber product,
$W(w)$
to be the fiber product,
where the map
![]() ${\mathcal{W}}(w)^{0}\longrightarrow \operatorname{Hom}_{\text{cont}}(1+p{\mathcal{O}})\times (1+p{\mathcal{O}})^{1},(\mathbb{C}_{p}^{\times })$
is given by
${\mathcal{W}}(w)^{0}\longrightarrow \operatorname{Hom}_{\text{cont}}(1+p{\mathcal{O}})\times (1+p{\mathcal{O}})^{1},(\mathbb{C}_{p}^{\times })$
is given by
Then we can write
![]() ${\mathcal{W}}=\bigcup _{w\geqslant 0}{\mathcal{W}}(w)$
as an increasing union of affinoids.
${\mathcal{W}}=\bigcup _{w\geqslant 0}{\mathcal{W}}(w)$
as an increasing union of affinoids.
Appendix B Kernel of Frobenius
Proposition B.1. On the stack
![]() ${\mathcal{B}}{\mathcal{T}}_{(2,1),\text{pol}}^{{\mathcal{O}}}$
and
${\mathcal{B}}{\mathcal{T}}_{(2,1),\text{pol}}^{{\mathcal{O}}}$
and
![]() $\overline{X}$
, the Cartier divisor
$\overline{X}$
, the Cartier divisor
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
is reduced.
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
is reduced.
Proof. This is [Reference de Shalit and GorendSG16, Theorem 2.8], which can be proved by considering the deformation space at a point. Unfortunately we cannot use the result of [Reference HernandezHer18] because of the polarization (but a similar proof works).◻
Proposition B.2. Let
![]() $G/\operatorname{Spec}({\mathcal{O}}_{C})$
be a
$G/\operatorname{Spec}({\mathcal{O}}_{C})$
be a
![]() $p$
-divisible
$p$
-divisible
![]() ${\mathcal{O}}$
-module. Suppose
${\mathcal{O}}$
-module. Suppose
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<1/2p^{2}$
, and let
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<1/2p^{2}$
, and let
![]() $K_{1}$
the first Frobenius-subgroup of
$K_{1}$
the first Frobenius-subgroup of
![]() $G$
(see Theorem 5.8). Then
$G$
(see Theorem 5.8). Then
Denote, for
![]() $K/\mathbb{Q}_{p^{2}}$
, by
$K/\mathbb{Q}_{p^{2}}$
, by
![]() $\mathfrak{X}/\operatorname{Spf}({\mathcal{O}}_{K})$
a (smooth) presentation of
$\mathfrak{X}/\operatorname{Spf}({\mathcal{O}}_{K})$
a (smooth) presentation of
![]() ${\mathcal{B}}{\mathcal{T}}_{r,(2,1),\text{pol}}^{{\mathcal{O}}}/\text{Spf}({\mathcal{O}}_{K})$
(which is smooth, see for example [Reference WedhornWed01]), and, for
${\mathcal{B}}{\mathcal{T}}_{r,(2,1),\text{pol}}^{{\mathcal{O}}}/\text{Spf}({\mathcal{O}}_{K})$
(which is smooth, see for example [Reference WedhornWed01]), and, for
![]() $v\in v(K)$
,
$v\in v(K)$
,
![]() $\mathfrak{X}(v)$
is the open subset of the blow-up along
$\mathfrak{X}(v)$
is the open subset of the blow-up along
![]() $I_{v}=(p^{v},\operatorname{ha}_{\unicode[STIX]{x1D70F}})$
where
$I_{v}=(p^{v},\operatorname{ha}_{\unicode[STIX]{x1D70F}})$
where
![]() $I_{v}$
is generated by
$I_{v}$
is generated by
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
. As
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
. As
![]() $\mathfrak{X}$
is smooth and
$\mathfrak{X}$
is smooth and
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
is reduced,
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
is reduced,
![]() $\mathfrak{X}(v)$
is normal and its special fiber (modulo
$\mathfrak{X}(v)$
is normal and its special fiber (modulo
![]() $\unicode[STIX]{x1D70B}_{K}$
) is reduced.
$\unicode[STIX]{x1D70B}_{K}$
) is reduced.
Take
![]() $v=1/2p^{2}$
and
$v=1/2p^{2}$
and
![]() $K$
a totally ramified extension of
$K$
a totally ramified extension of
![]() $\mathbb{Q}_{p}$
of degree
$\mathbb{Q}_{p}$
of degree
![]() $1/2p^{2}$
(so that
$1/2p^{2}$
(so that
![]() $v(\unicode[STIX]{x1D70B}_{K})=1/2p^{2}$
).
$v(\unicode[STIX]{x1D70B}_{K})=1/2p^{2}$
).
Then over
![]() $X(v)$
, the rigid fiber over
$X(v)$
, the rigid fiber over
![]() $K$
of
$K$
of
![]() $\mathfrak{X}(v)$
, we have a subgroup
$\mathfrak{X}(v)$
, we have a subgroup
![]() $K_{1}\subset G[p^{2}]$
, and by the Proposition 5.11 this subgroup extend to a subgroup over
$K_{1}\subset G[p^{2}]$
, and by the Proposition 5.11 this subgroup extend to a subgroup over
![]() $\mathfrak{X}(v)$
. Now, over
$\mathfrak{X}(v)$
. Now, over
![]() $\mathfrak{X}(v)\otimes {\mathcal{O}}_{K}/\unicode[STIX]{x1D70B}_{K}=\mathfrak{X}(v)\otimes \unicode[STIX]{x1D705}_{K}$
the rigid fiber of
$\mathfrak{X}(v)\otimes {\mathcal{O}}_{K}/\unicode[STIX]{x1D70B}_{K}=\mathfrak{X}(v)\otimes \unicode[STIX]{x1D705}_{K}$
the rigid fiber of
![]() $\mathfrak{X}(v)$
, we have two subgroups,
$\mathfrak{X}(v)$
, we have two subgroups,
![]() $K_{1}$
and
$K_{1}$
and
![]() $\operatorname{Ker}F^{2}$
, which coincide on every point (by [Reference HernandezHer19, § 9] or the very proof of the Proposition 5.11) but as
$\operatorname{Ker}F^{2}$
, which coincide on every point (by [Reference HernandezHer19, § 9] or the very proof of the Proposition 5.11) but as
![]() $\mathfrak{X}(v)\otimes {\mathcal{O}}_{K}/\unicode[STIX]{x1D70B}_{K}$
is reduced,
$\mathfrak{X}(v)\otimes {\mathcal{O}}_{K}/\unicode[STIX]{x1D70B}_{K}$
is reduced,
![]() $K_{1}=\operatorname{Ker}F^{2}$
over
$K_{1}=\operatorname{Ker}F^{2}$
over
![]() $X(v)\otimes {\mathcal{O}}_{K}/\unicode[STIX]{x1D70B}_{K}$
. As every
$X(v)\otimes {\mathcal{O}}_{K}/\unicode[STIX]{x1D70B}_{K}$
. As every
![]() ${\mathcal{O}}_{C}$
-point of
${\mathcal{O}}_{C}$
-point of
![]() ${\mathcal{B}}{\mathcal{T}}_{(2,1),\text{pol}}^{{\mathcal{O}}}$
gives a point of
${\mathcal{B}}{\mathcal{T}}_{(2,1),\text{pol}}^{{\mathcal{O}}}$
gives a point of
![]() $\mathfrak{X}$
, we have the result using
$\mathfrak{X}$
, we have the result using
![]() $G[p^{r}]$
for
$G[p^{r}]$
for
![]() $r$
big enough (bigger than
$r$
big enough (bigger than
![]() $3$
is enough).
$3$
is enough).
Corollary B.3. Let
![]() $G$
as in the previous proposition, but suppose
$G$
as in the previous proposition, but suppose
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<1/2p^{4}$
. Then
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<1/2p^{4}$
. Then
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G/K_{1})=p^{2}\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)$
.
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G/K_{1})=p^{2}\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)$
.
Proof. Recall that
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}=\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}=\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
and
![]() $\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
is given by
$\operatorname{ha}_{\unicode[STIX]{x1D70F}}$
is given by
![]() $\det (V^{2})$
without any division. By the previous proposition, the map
$\det (V^{2})$
without any division. By the previous proposition, the map
![]() $G[p^{2}]\longrightarrow G[p^{2}]/K_{1}$
coincide modulo
$G[p^{2}]\longrightarrow G[p^{2}]/K_{1}$
coincide modulo
![]() $\unicode[STIX]{x1D70B}_{K}$
with the map
$\unicode[STIX]{x1D70B}_{K}$
with the map
![]() $G[p^{2}]\overset{F^{2}}{\longrightarrow }G[p^{2}]^{(p^{2})}$
. Thus, there is an isomorphism modulo
$G[p^{2}]\overset{F^{2}}{\longrightarrow }G[p^{2}]^{(p^{2})}$
. Thus, there is an isomorphism modulo
![]() $\unicode[STIX]{x1D70B}_{K}$
:
$\unicode[STIX]{x1D70B}_{K}$
:
![]() $\det (\unicode[STIX]{x1D714}_{(G/K_{1})^{D},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}})\simeq \det (\unicode[STIX]{x1D714}_{G^{D},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{\otimes p^{2}})$
which identifies (modulo
$\det (\unicode[STIX]{x1D714}_{(G/K_{1})^{D},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}})\simeq \det (\unicode[STIX]{x1D714}_{G^{D},\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}^{\otimes p^{2}})$
which identifies (modulo
![]() $\unicode[STIX]{x1D70B}_{K}$
)
$\unicode[STIX]{x1D70B}_{K}$
)
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}(G/K_{1})$
with
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}(G/K_{1})$
with
![]() $\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}(G)^{\otimes p^{2}}$
. Thus we get
$\widetilde{\operatorname{ha}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}}(G)^{\otimes p^{2}}$
. Thus we get
As
![]() $p^{2}\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<1/2p^{2}$
, we get the result.◻
$p^{2}\operatorname{ha}_{\unicode[STIX]{x1D70F}}(G)<1/2p^{2}$
, we get the result.◻
Appendix C Dévissage of the formal coherent locally analytic sheaves
Let
![]() $\unicode[STIX]{x1D705}\in {\mathcal{W}}(w)$
a character and
$\unicode[STIX]{x1D705}\in {\mathcal{W}}(w)$
a character and
![]() $\unicode[STIX]{x1D705}^{0}$
its restriction to
$\unicode[STIX]{x1D705}^{0}$
its restriction to
![]() ${\mathcal{W}}(w)^{0}$
, and
${\mathcal{W}}(w)^{0}$
, and
![]() $w<m-(p^{2}m-1)/(p^{2}-1)$
. Denote on
$w<m-(p^{2}m-1)/(p^{2}-1)$
. Denote on
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
the sheaf
$\mathfrak{X}_{1}(p^{2m})(v)$
the sheaf
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0}\dagger }$
defined as
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0}\dagger }$
defined as
If we set
![]() $\unicode[STIX]{x1D70B}:\mathfrak{X}_{1}(p^{2m})(v)\longrightarrow \mathfrak{X}(v)$
, then the sheaf
$\unicode[STIX]{x1D70B}:\mathfrak{X}_{1}(p^{2m})(v)\longrightarrow \mathfrak{X}(v)$
, then the sheaf
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }$
of overconvergent forms is given by
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}\dagger }$
of overconvergent forms is given by
where
![]() $(-)(-\unicode[STIX]{x1D705}^{\prime })$
denotes a twist of the action of
$(-)(-\unicode[STIX]{x1D705}^{\prime })$
denotes a twist of the action of
![]() $B(\mathbb{Z}_{p})\mathfrak{B}_{w}$
and
$B(\mathbb{Z}_{p})\mathfrak{B}_{w}$
and
![]() $(-)^{B(\mathbb{Z}_{p})\mathfrak{B}_{w}}$
means taking invariants. Remark that after the twist, the action of
$(-)^{B(\mathbb{Z}_{p})\mathfrak{B}_{w}}$
means taking invariants. Remark that after the twist, the action of
![]() $B(\mathbb{Z}_{p})\mathfrak{B}_{w}$
factors through
$B(\mathbb{Z}_{p})\mathfrak{B}_{w}$
factors through
![]() $B_{n}$
.
$B_{n}$
.
Consider the projection ‘in family’
and denote by
the family of sheaves over
![]() $\mathfrak{X}_{1}(p^{2m})(v)\times \mathfrak{W}(w)^{0}$
.
$\mathfrak{X}_{1}(p^{2m})(v)\times \mathfrak{W}(w)^{0}$
.
Let
![]() $\operatorname{Spf}(R)$
a small enough open in
$\operatorname{Spf}(R)$
a small enough open in
![]() $\mathfrak{X}_{1}(p^{2m})(v)$
. Recall that we denote by
$\mathfrak{X}_{1}(p^{2m})(v)$
. Recall that we denote by
![]() $\unicode[STIX]{x1D713}$
the universal polarized trivialization of
$\unicode[STIX]{x1D713}$
the universal polarized trivialization of
![]() $K_{m}^{D}$
, denote by
$K_{m}^{D}$
, denote by
![]() $e_{1},e_{2}$
a basis of
$e_{1},e_{2}$
a basis of
![]() ${\mathcal{O}}/p^{m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}}$
,
${\mathcal{O}}/p^{m}{\mathcal{O}}\oplus {\mathcal{O}}/p^{2m}{\mathcal{O}}$
,
![]() $e_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}(e_{1}),e_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}(e_{2}),e^{\unicode[STIX]{x1D70F}}=\operatorname{HT}_{\unicode[STIX]{x1D70F},w}(e_{2})$
the images of this basis in
$e_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}(e_{1}),e_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}=\operatorname{HT}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F},w}(e_{2}),e^{\unicode[STIX]{x1D70F}}=\operatorname{HT}_{\unicode[STIX]{x1D70F},w}(e_{2})$
the images of this basis in
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}/p^{w},{\mathcal{F}}_{\unicode[STIX]{x1D70F}}/p^{w}$
. Denote by
${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}/p^{w},{\mathcal{F}}_{\unicode[STIX]{x1D70F}}/p^{w}$
. Denote by
![]() $f_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},f_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},f^{\unicode[STIX]{x1D70F}}$
a lift of this basis in
$f_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},f_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},f^{\unicode[STIX]{x1D70F}}$
a lift of this basis in
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},{\mathcal{F}}_{\unicode[STIX]{x1D70F}}$
.
${\mathcal{F}}_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}},{\mathcal{F}}_{\unicode[STIX]{x1D70F}}$
.
With these choices we can identify
![]() $\mathfrak{I}\mathfrak{W}_{w|\operatorname{Spf}(R)}^{+}$
with matrices,
$\mathfrak{I}\mathfrak{W}_{w|\operatorname{Spf}(R)}^{+}$
with matrices,
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}1 & & \\ p^{w}\mathfrak{B}(0,1) & 1 & \\ & & 1\end{array}\right)\times \left(\begin{array}{@{}c@{}}1+p^{w}\mathfrak{B}(0,1)\\ 1+p^{w}\mathfrak{B}(0,1)\\ 1+p^{w}\mathfrak{B}(0,1)\end{array}\right)\times _{\operatorname{Spf}({\mathcal{O}}_{K})}\operatorname{Spf}(R).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}1 & & \\ p^{w}\mathfrak{B}(0,1) & 1 & \\ & & 1\end{array}\right)\times \left(\begin{array}{@{}c@{}}1+p^{w}\mathfrak{B}(0,1)\\ 1+p^{w}\mathfrak{B}(0,1)\\ 1+p^{w}\mathfrak{B}(0,1)\end{array}\right)\times _{\operatorname{Spf}({\mathcal{O}}_{K})}\operatorname{Spf}(R).\end{eqnarray}$$
Denote by
![]() $X_{0}$
the coordinate in the
$X_{0}$
the coordinate in the
![]() $3\times 3$
matrix and by
$3\times 3$
matrix and by
![]() $X_{1},X_{2},X_{3}$
the coordinates of the balls inside the column. Thus, we can identify a function
$X_{1},X_{2},X_{3}$
the coordinates of the balls inside the column. Thus, we can identify a function
![]() $f$
on
$f$
on
![]() $\mathfrak{I}\mathfrak{W}_{w|\operatorname{Spf}(R)}^{+}$
to a formal series in
$\mathfrak{I}\mathfrak{W}_{w|\operatorname{Spf}(R)}^{+}$
to a formal series in
![]() $R\langle \langle X_{0},X_{1},X_{2},X_{3}\rangle \rangle$
.
$R\langle \langle X_{0},X_{1},X_{2},X_{3}\rangle \rangle$
.
Now, let
![]() $\unicode[STIX]{x1D705}^{0}\in \mathfrak{W}(w)^{0}$
; then
$\unicode[STIX]{x1D705}^{0}\in \mathfrak{W}(w)^{0}$
; then
![]() $f\in \mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0}\dagger }$
if it verifies
$f\in \mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0}\dagger }$
if it verifies
In particular, we deduce that there exists a unique
![]() $g\in R\langle \langle X_{0}\rangle \rangle$
such that
$g\in R\langle \langle X_{0}\rangle \rangle$
such that
and thus there is a bijection
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0}\dagger }\simeq R\langle \langle X_{0}\rangle \rangle$
. The same holds in family.
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0}\dagger }\simeq R\langle \langle X_{0}\rangle \rangle$
. The same holds in family.
Lemma C.1. For all
![]() $f\in \mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }(R\,\hat{\otimes }\,{\mathcal{O}}_{K}\langle \langle S_{1},S_{2},S_{3}\rangle \rangle )$
, there exists a unique
$f\in \mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }(R\,\hat{\otimes }\,{\mathcal{O}}_{K}\langle \langle S_{1},S_{2},S_{3}\rangle \rangle )$
, there exists a unique
![]() $g\in R\langle \langle S_{1},S_{2},S_{3},X_{0}\rangle \rangle$
such that
$g\in R\langle \langle S_{1},S_{2},S_{3},X_{0}\rangle \rangle$
such that
This decomposition induces a bijection
Lemma C.2. Let
![]() $\unicode[STIX]{x1D70B}$
be a uniformizer of
$\unicode[STIX]{x1D70B}$
be a uniformizer of
![]() ${\mathcal{O}}_{K}$
. Then
${\mathcal{O}}_{K}$
. Then
Proof. The calculation is made in [Reference Andreatta, Iovita and PilloniAIP15, Lemma 8.1.5.3].◻
Corollary C.3. Denote by
![]() $\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
the reduction modulo
$\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
the reduction modulo
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
. Then the sheaf
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
. Then the sheaf
![]() $\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is constant on
$\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is constant on
![]() $(\mathfrak{X}_{1}(p^{2n})\times \mathfrak{W}(w)^{0})\times \operatorname{Spec}({\mathcal{O}}_{K}/\unicode[STIX]{x1D70B})$
: it is the inverse image of a sheaf on
$(\mathfrak{X}_{1}(p^{2n})\times \mathfrak{W}(w)^{0})\times \operatorname{Spec}({\mathcal{O}}_{K}/\unicode[STIX]{x1D70B})$
: it is the inverse image of a sheaf on
![]() $\mathfrak{X}_{1}(p^{2n})\times \operatorname{Spf}({\mathcal{O}}_{K}/\unicode[STIX]{x1D70B})$
.
$\mathfrak{X}_{1}(p^{2n})\times \operatorname{Spf}({\mathcal{O}}_{K}/\unicode[STIX]{x1D70B})$
.
Let
![]() $f_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}^{\prime }},f_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}^{\prime }},f^{\unicode[STIX]{x1D70F}^{\prime }}$
be another lift of the basis image of
$f_{1}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}^{\prime }},f_{2}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}^{\prime }},f^{\unicode[STIX]{x1D70F}^{\prime }}$
be another lift of the basis image of
![]() $\operatorname{HT}_{\star ,w}$
. Let
$\operatorname{HT}_{\star ,w}$
. Let
 $$\begin{eqnarray}P=\left(\begin{array}{@{}ccc@{}}1+p^{w}a_{1} & p^{w}a_{2} & \\ p^{w}a_{3} & 1+p^{w}a_{4} & \\ & & 1+p^{w}a_{5}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}P=\left(\begin{array}{@{}ccc@{}}1+p^{w}a_{1} & p^{w}a_{2} & \\ p^{w}a_{3} & 1+p^{w}a_{4} & \\ & & 1+p^{w}a_{5}\end{array}\right)\end{eqnarray}$$
be the base change matrix from
![]() $\text{}\underline{f}$
to
$\text{}\underline{f}$
to
![]() $\text{}\underline{f}^{\prime }$
and
$\text{}\underline{f}^{\prime }$
and
![]() $\text{}\underline{X}^{\prime }$
the coordinates on
$\text{}\underline{X}^{\prime }$
the coordinates on
![]() $\mathfrak{I}\mathfrak{W}_{w|\operatorname{Spf}(R)}^{+}$
relatively to
$\mathfrak{I}\mathfrak{W}_{w|\operatorname{Spf}(R)}^{+}$
relatively to
![]() $\text{}\underline{f}^{\prime }$
.
$\text{}\underline{f}^{\prime }$
.
Lemma C.4. We have the following congruences:
 $$\begin{eqnarray}\displaystyle X_{0}\equiv X_{0}^{\prime }+a_{3}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w}); & & \displaystyle \nonumber\\ \displaystyle X_{1}\equiv X_{1}^{\prime }+a_{1}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w}); & & \displaystyle \nonumber\\ \displaystyle X_{2}\equiv X_{2}^{\prime }+a_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w}); & & \displaystyle \nonumber\\ \displaystyle X_{3}\equiv X_{3}^{\prime }+a_{5}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w}). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{0}\equiv X_{0}^{\prime }+a_{3}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w}); & & \displaystyle \nonumber\\ \displaystyle X_{1}\equiv X_{1}^{\prime }+a_{1}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w}); & & \displaystyle \nonumber\\ \displaystyle X_{2}\equiv X_{2}^{\prime }+a_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w}); & & \displaystyle \nonumber\\ \displaystyle X_{3}\equiv X_{3}^{\prime }+a_{5}\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{w}). & & \displaystyle \nonumber\end{eqnarray}$$
Proof. Indeed, as seen inside
![]() ${\mathcal{T}}_{a}^{\times }n/U_{a}n$
, we have that the two systems of coordinates verifies
${\mathcal{T}}_{a}^{\times }n/U_{a}n$
, we have that the two systems of coordinates verifies
where
![]() $U\in \operatorname{GL}_{2}\times \operatorname{GL}_{1}$
is a unipotent matrix of the form
$U\in \operatorname{GL}_{2}\times \operatorname{GL}_{1}$
is a unipotent matrix of the form
![]() $I_{3}+p^{w}N$
,
$I_{3}+p^{w}N$
,
![]() $N$
upper triangular nilpotent, and
$N$
upper triangular nilpotent, and
 $$\begin{eqnarray}\text{}\underline{X}=\left(\begin{array}{@{}ccc@{}}X_{1} & & \\ X_{0} & X_{2} & \\ & & X_{3}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{X}=\left(\begin{array}{@{}ccc@{}}X_{1} & & \\ X_{0} & X_{2} & \\ & & X_{3}\end{array}\right).\end{eqnarray}$$
Thus, write
![]() $P=I_{3}+p^{w}P_{0}$
; then
$P=I_{3}+p^{w}P_{0}$
; then
![]() $I_{3}+p^{w}(P_{0}+\text{}\underline{X}+N)\equiv I_{3}+p^{w}\text{}\underline{X}^{\prime }\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{2w})$
.◻
$I_{3}+p^{w}(P_{0}+\text{}\underline{X}+N)\equiv I_{3}+p^{w}\text{}\underline{X}^{\prime }\hspace{0.6em}({\rm mod}\hspace{0.2em}p^{2w})$
.◻
We can thus deduce the following corollary for the family of sheaves,
Corollary C.5. Let
![]() $\unicode[STIX]{x1D705}^{0}\in {\mathcal{W}}(w)(K)$
. The quasi-coherent sheaf
$\unicode[STIX]{x1D705}^{0}\in {\mathcal{W}}(w)(K)$
. The quasi-coherent sheaf
![]() $\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
on
$\mathfrak{w}_{w}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
on
![]() $\mathfrak{X}_{1}(p^{2m})\times \mathfrak{W}(w)^{0}$
is a small Banach sheaf.
$\mathfrak{X}_{1}(p^{2m})\times \mathfrak{W}(w)^{0}$
is a small Banach sheaf.
Proof. We just have to check that on
![]() $\mathfrak{X}_{1}(p^{2m})\times \mathfrak{W}(w)^{0}\times \operatorname{Spec}(O_{K}/\unicode[STIX]{x1D70B})$
the sheaf
$\mathfrak{X}_{1}(p^{2m})\times \mathfrak{W}(w)^{0}\times \operatorname{Spec}(O_{K}/\unicode[STIX]{x1D70B})$
the sheaf
![]() $\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is an inductive limit of coherent sheaves which are extensions of the trivial sheaf. Write
$\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is an inductive limit of coherent sheaves which are extensions of the trivial sheaf. Write
![]() $\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\geqslant r}$
the subsheaf of sections that are locally polynomials in
$\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\geqslant r}$
the subsheaf of sections that are locally polynomials in
![]() $X_{0}$
of total degree smaller than
$X_{0}$
of total degree smaller than
![]() $r$
. This makes sense globally by Lemma C.4, and moreover,
$r$
. This makes sense globally by Lemma C.4, and moreover,
![]() $\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is the inductive limit over
$\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger }$
is the inductive limit over
![]() $r$
of these sheaves. But then
$r$
of these sheaves. But then
![]() $\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\geqslant r}(\text{mod})\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\geqslant r-1}$
is isomorphic to the trivial sheaf.◻
$\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\geqslant r}(\text{mod})\mathfrak{w}_{w,1}^{\unicode[STIX]{x1D705}^{0,\text{un}}\dagger ,\geqslant r-1}$
is isomorphic to the trivial sheaf.◻
Appendix D Non-tempered representations and
 $(\mathfrak{q},K)$
-cohomology
$(\mathfrak{q},K)$
-cohomology
We are interested in calculating the
![]() $(\mathfrak{q},K)$
-cohomology of the representation
$(\mathfrak{q},K)$
-cohomology of the representation
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
defined in Proposition 10.12 to show it appears in the global sections of a coherent automorphic sheaf on the Picard modular surface.
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
defined in Proposition 10.12 to show it appears in the global sections of a coherent automorphic sheaf on the Picard modular surface.
We have the following theorem of Harris ([Reference HarrisHar90b, Lemma 5.2.3 and Proposition 5.4.2], [Reference GoldringGol14, Theorem 2.6.1])
Theorem D.1. Let
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
be an automorphic representation of
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
be an automorphic representation of
![]() $U(2,1)$
of Harish-Chandra parameter
$U(2,1)$
of Harish-Chandra parameter
![]() $\unicode[STIX]{x1D706}$
, and such that
$\unicode[STIX]{x1D706}$
, and such that
![]() $H^{0}(\mathfrak{q},K,\unicode[STIX]{x1D70B}_{\infty }\otimes V_{\unicode[STIX]{x1D70E}}^{\vee })\neq 0$
; then there is a
$H^{0}(\mathfrak{q},K,\unicode[STIX]{x1D70B}_{\infty }\otimes V_{\unicode[STIX]{x1D70E}}^{\vee })\neq 0$
; then there is a
![]() $U(2,1)(\mathbb{A}_{f})$
equivariant embedding,
$U(2,1)(\mathbb{A}_{f})$
equivariant embedding,
where
![]() ${\mathcal{V}}_{\unicode[STIX]{x1D70E}}^{\vee }$
is the automorphic vector bundle associated to the representation
${\mathcal{V}}_{\unicode[STIX]{x1D70E}}^{\vee }$
is the automorphic vector bundle associated to the representation
![]() $V_{\unicode[STIX]{x1D70E}}^{\vee }$
of
$V_{\unicode[STIX]{x1D70E}}^{\vee }$
of
![]() $K=K_{\infty }$
.
$K=K_{\infty }$
.
Thus we only need to calculate the
![]() $(\mathfrak{q},K)$
-cohomology of
$(\mathfrak{q},K)$
-cohomology of
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})_{\infty }$
, and even the one of the restriction of the representation to
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})_{\infty }$
, and even the one of the restriction of the representation to
![]() $SU(2,1)$
. Fortunately we can explicitly do so, rewriting the induction
$SU(2,1)$
. Fortunately we can explicitly do so, rewriting the induction
![]() $\operatorname{ind}-n_{B}^{SU(2,1)}(\mathbb{R})(\unicode[STIX]{x1D712}_{\infty })$
, as a space of functions, and determining the quotient corresponding to
$\operatorname{ind}-n_{B}^{SU(2,1)}(\mathbb{R})(\unicode[STIX]{x1D712}_{\infty })$
, as a space of functions, and determining the quotient corresponding to
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
. In [Reference WallachWal76], Wallach calculated all the representations of
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
. In [Reference WallachWal76], Wallach calculated all the representations of
![]() $SU(2,1)(\mathbb{R})$
using this description of the induction. As explained in [Reference WallachWal76, p. 181], the induction space
$SU(2,1)(\mathbb{R})$
using this description of the induction. As explained in [Reference WallachWal76, p. 181], the induction space
![]() $\operatorname{ind}-n_{B}^{SU(2,1)(\mathbb{R})}(\unicode[STIX]{x1D712})$
corresponds to
$\operatorname{ind}-n_{B}^{SU(2,1)(\mathbb{R})}(\unicode[STIX]{x1D712})$
corresponds to
![]() $X^{\unicode[STIX]{x1D6EC}}$
with
$X^{\unicode[STIX]{x1D6EC}}$
with
![]() $\unicode[STIX]{x1D6EC}=(a-1)\unicode[STIX]{x1D6EC}_{1}+(-a)\unicode[STIX]{x1D6EC}_{2}$
(which is thus reducible). The shift by
$\unicode[STIX]{x1D6EC}=(a-1)\unicode[STIX]{x1D6EC}_{1}+(-a)\unicode[STIX]{x1D6EC}_{2}$
(which is thus reducible). The shift by
![]() $-\unicode[STIX]{x1D6EC}_{1}-\unicode[STIX]{x1D6EC}_{2}$
is due to the normalization by the modulus character in the induction. Its discrete series subobject corresponds to one of the discrete series
$-\unicode[STIX]{x1D6EC}_{1}-\unicode[STIX]{x1D6EC}_{2}$
is due to the normalization by the modulus character in the induction. Its discrete series subobject corresponds to one of the discrete series
![]() $D_{\widetilde{\unicode[STIX]{x1D6EC}}}^{-}$
described in [Reference WallachWal76, p. 183], and its quotient corresponds to the non-tempered representation
$D_{\widetilde{\unicode[STIX]{x1D6EC}}}^{-}$
described in [Reference WallachWal76, p. 183], and its quotient corresponds to the non-tempered representation
![]() $(T_{a-2}^{-},Z_{a-2}^{-})$
(defined in [Reference WallachWal76, p. 184], and the fact that it appears in the said induction is [Reference WallachWal76, Lemma 7.12]). As the name does not suggest,
$(T_{a-2}^{-},Z_{a-2}^{-})$
(defined in [Reference WallachWal76, p. 184], and the fact that it appears in the said induction is [Reference WallachWal76, Lemma 7.12]). As the name does not suggest,
![]() $T_{a-2}^{-}$
, which coincides with the restriction of
$T_{a-2}^{-}$
, which coincides with the restriction of
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})_{\infty }$
to
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})_{\infty }$
to
![]() $SU(2,1)(\mathbb{R})$
, will be holomorphic (but we can exchange holomorphic and anti-holomorphic by changing the complex structure of the Picard surface).
$SU(2,1)(\mathbb{R})$
, will be holomorphic (but we can exchange holomorphic and anti-holomorphic by changing the complex structure of the Picard surface).
Proposition D.2. Let
![]() $(\unicode[STIX]{x1D70E},V_{\unicode[STIX]{x1D70E}})=\operatorname{Sym}^{a-1}\otimes \det ^{-a}:M\mapsto \operatorname{Sym}^{a-1}(\overline{M})\otimes \det (\overline{M})^{-a}$
the representation of
$(\unicode[STIX]{x1D70E},V_{\unicode[STIX]{x1D70E}})=\operatorname{Sym}^{a-1}\otimes \det ^{-a}:M\mapsto \operatorname{Sym}^{a-1}(\overline{M})\otimes \det (\overline{M})^{-a}$
the representation of
![]() $U(2)=SK_{\infty }\subset SU(2,1)(\mathbb{R})$
. Then
$U(2)=SK_{\infty }\subset SU(2,1)(\mathbb{R})$
. Then
To show the previous proposition, denote by
 $$\begin{eqnarray}J_{0}=\left(\begin{array}{@{}ccc@{}}1 & & \\ & 1 & \\ & & -1\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}J_{0}=\left(\begin{array}{@{}ccc@{}}1 & & \\ & 1 & \\ & & -1\end{array}\right)\end{eqnarray}$$
the hermitian form of signature
![]() $(2,1)$
used in [Reference WallachWal76]. Denote by
$(2,1)$
used in [Reference WallachWal76]. Denote by
 $$\begin{eqnarray}P=\left(\begin{array}{@{}ccc@{}}\frac{1}{\sqrt{2}} & & \frac{1}{\sqrt{2}}\\ & 1 & \\ \frac{1}{\sqrt{2}} & & -\frac{1}{\sqrt{2}}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}P=\left(\begin{array}{@{}ccc@{}}\frac{1}{\sqrt{2}} & & \frac{1}{\sqrt{2}}\\ & 1 & \\ \frac{1}{\sqrt{2}} & & -\frac{1}{\sqrt{2}}\end{array}\right)\end{eqnarray}$$
the base change matrix (so that
![]() $PJ_{0}P=J$
,
$PJ_{0}P=J$
,
![]() $\overline{P}=P^{-1}=P$
). In this new presentation, the complex structure is given by
$\overline{P}=P^{-1}=P$
). In this new presentation, the complex structure is given by
![]() $h^{\prime }=PhP$
, i.e.,
$h^{\prime }=PhP$
, i.e.,
 $$\begin{eqnarray}h^{\prime }:z\in \mathbb{C}\mapsto \left(\begin{array}{@{}ccc@{}}z & & \\ & z & \\ & & \overline{z}\end{array}\right)\in U_{J_{0}}(\mathbb{R}).\end{eqnarray}$$
$$\begin{eqnarray}h^{\prime }:z\in \mathbb{C}\mapsto \left(\begin{array}{@{}ccc@{}}z & & \\ & z & \\ & & \overline{z}\end{array}\right)\in U_{J_{0}}(\mathbb{R}).\end{eqnarray}$$
In this form, the Lie algebra of
![]() $U_{J_{0}}(\mathbb{R})$
is given by
$U_{J_{0}}(\mathbb{R})$
is given by
 $$\begin{eqnarray}\mathfrak{g}=\left\{\!\left(\begin{array}{@{}ccc@{}}ia_{0} & b & c\\ -\overline{b} & ie_{0} & f\\ \overline{c} & \overline{f} & il_{0}\end{array}\right),a_{0},e_{0},l_{0}\in \mathbb{R}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}=\left\{\!\left(\begin{array}{@{}ccc@{}}ia_{0} & b & c\\ -\overline{b} & ie_{0} & f\\ \overline{c} & \overline{f} & il_{0}\end{array}\right),a_{0},e_{0},l_{0}\in \mathbb{R}\right\}.\end{eqnarray}$$
Using the action of
![]() $h^{\prime }(i)$
we can decompose
$h^{\prime }(i)$
we can decompose
![]() $\mathfrak{g}=\mathfrak{k}+\mathfrak{p}$
with
$\mathfrak{g}=\mathfrak{k}+\mathfrak{p}$
with
 $$\begin{eqnarray}\mathfrak{p}=\left\{\!\left(\begin{array}{@{}ccc@{}}0 & 0 & c\\ & 0 & f\\ \overline{c} & \overline{f} & 0\end{array}\right),c_{0},a_{0}\in \mathbb{R}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}=\left\{\!\left(\begin{array}{@{}ccc@{}}0 & 0 & c\\ & 0 & f\\ \overline{c} & \overline{f} & 0\end{array}\right),c_{0},a_{0}\in \mathbb{R}\right\}.\end{eqnarray}$$
Extending scalars to
![]() $\mathbb{C}$
, we can further decompose,
$\mathbb{C}$
, we can further decompose,
![]() $\mathfrak{p}_{\mathbb{C}}=\mathfrak{p}^{+}\oplus \mathfrak{p}^{-}$
, where conjugacy by
$\mathfrak{p}_{\mathbb{C}}=\mathfrak{p}^{+}\oplus \mathfrak{p}^{-}$
, where conjugacy by
![]() $h^{\prime }(z)$
on
$h^{\prime }(z)$
on
![]() $\mathfrak{p}^{+}$
and
$\mathfrak{p}^{+}$
and
![]() $\mathfrak{p}^{-}$
is given by
$\mathfrak{p}^{-}$
is given by
![]() $z/\overline{z}$
and
$z/\overline{z}$
and
![]() $\overline{z}/z$
respectively. Explicitly,
$\overline{z}/z$
respectively. Explicitly,
![]() $\mathfrak{p}^{-}$
is generated by
$\mathfrak{p}^{-}$
is generated by
 $$\begin{eqnarray}\displaystyle & \displaystyle X^{-}=N^{+}\otimes i-N^{-}\otimes 1\quad \text{and}\quad Y^{-}=M^{+}\otimes i-M^{-}\otimes 1, & \displaystyle \nonumber\\ \displaystyle & \displaystyle N^{-}=\left(\begin{array}{@{}ccc@{}}0 & & i\\ & 0 & \\ -i & & 0\end{array}\right),\quad N^{+}=\left(\begin{array}{@{}ccc@{}}0 & & 1\\ & 0 & \\ 1 & & 0\end{array}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M^{-}=\left(\begin{array}{@{}ccc@{}}0 & & 0\\ & 0 & i\\ 0 & -i & 0\end{array}\right),\quad M^{+}=\left(\begin{array}{@{}ccc@{}}0 & & 0\\ & 0 & 1\\ 0 & 1 & 0\end{array}\right), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle X^{-}=N^{+}\otimes i-N^{-}\otimes 1\quad \text{and}\quad Y^{-}=M^{+}\otimes i-M^{-}\otimes 1, & \displaystyle \nonumber\\ \displaystyle & \displaystyle N^{-}=\left(\begin{array}{@{}ccc@{}}0 & & i\\ & 0 & \\ -i & & 0\end{array}\right),\quad N^{+}=\left(\begin{array}{@{}ccc@{}}0 & & 1\\ & 0 & \\ 1 & & 0\end{array}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle M^{-}=\left(\begin{array}{@{}ccc@{}}0 & & 0\\ & 0 & i\\ 0 & -i & 0\end{array}\right),\quad M^{+}=\left(\begin{array}{@{}ccc@{}}0 & & 0\\ & 0 & 1\\ 0 & 1 & 0\end{array}\right), & \displaystyle \nonumber\end{eqnarray}$$
and
![]() $\mathfrak{p}^{+}$
is generated
$\mathfrak{p}^{+}$
is generated
To calculate the action of
![]() $\mathfrak{p}^{-}$
on our representation, we use the following formula for a matrix
$\mathfrak{p}^{-}$
on our representation, we use the following formula for a matrix
![]() $X$
and
$X$
and
![]() $f\in \mathfrak{g}$
:
$f\in \mathfrak{g}$
:
As
![]() $Z_{a-2}^{-}$
is a space of holomorphic functions, we get the following exponentials for the matrices
$Z_{a-2}^{-}$
is a space of holomorphic functions, we get the following exponentials for the matrices
![]() $M^{\pm },N^{\pm }$
:
$M^{\pm },N^{\pm }$
:
 $$\begin{eqnarray}\displaystyle \exp (tM^{-})=\left(\begin{array}{@{}ccc@{}}1 & & 0\\ & \operatorname{ch}t & i\operatorname{sh}t\\ & -i\operatorname{sh}t & \operatorname{ch}t\end{array}\right),\quad \exp (tM^{+})=\left(\begin{array}{@{}ccc@{}}1 & & 0\\ & \operatorname{ch}t & \operatorname{sh}t\\ & \operatorname{sh}t & \operatorname{ch}t\end{array}\right), & & \displaystyle \nonumber\\ \displaystyle \exp (tN^{-})=\left(\begin{array}{@{}ccc@{}}\operatorname{ch}t & & i\operatorname{sh}t\\ & 1 & 0\\ -i\operatorname{sh}t & & \operatorname{ch}t\end{array}\right),\quad \exp (tN^{+})=\left(\begin{array}{@{}ccc@{}}\operatorname{ch}t & & \operatorname{sh}t\\ & 1 & 0\\ \operatorname{sh}t & & \operatorname{ch}t\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \exp (tM^{-})=\left(\begin{array}{@{}ccc@{}}1 & & 0\\ & \operatorname{ch}t & i\operatorname{sh}t\\ & -i\operatorname{sh}t & \operatorname{ch}t\end{array}\right),\quad \exp (tM^{+})=\left(\begin{array}{@{}ccc@{}}1 & & 0\\ & \operatorname{ch}t & \operatorname{sh}t\\ & \operatorname{sh}t & \operatorname{ch}t\end{array}\right), & & \displaystyle \nonumber\\ \displaystyle \exp (tN^{-})=\left(\begin{array}{@{}ccc@{}}\operatorname{ch}t & & i\operatorname{sh}t\\ & 1 & 0\\ -i\operatorname{sh}t & & \operatorname{ch}t\end{array}\right),\quad \exp (tN^{+})=\left(\begin{array}{@{}ccc@{}}\operatorname{ch}t & & \operatorname{sh}t\\ & 1 & 0\\ \operatorname{sh}t & & \operatorname{ch}t\end{array}\right), & & \displaystyle \nonumber\end{eqnarray}$$
and the actions of the matrices
![]() $M^{\pm },N^{\pm }$
is given by
$M^{\pm },N^{\pm }$
is given by
 $$\begin{eqnarray}\displaystyle N^{+}f & = & \displaystyle -(a-2)\overline{z_{1}}f+(\overline{z_{1}}^{2}-1)\frac{df}{d\overline{z_{1}}}+\overline{z_{1}z_{2}}\frac{df}{d\overline{z_{2}}},\nonumber\\ \displaystyle N^{-}f & = & \displaystyle -i(a-2)\overline{z_{1}}f+i(\overline{z_{1}}^{2}+1)\frac{df}{d\overline{z_{1}}}+i\overline{z_{1}z_{2}}\frac{df}{d\overline{z_{2}}},\nonumber\\ \displaystyle M^{+}f & = & \displaystyle -(a-2)\overline{z_{2}}f+\overline{z_{1}z_{2}}\frac{df}{d\overline{z_{1}}}+(\overline{z_{1}}^{2}-1)\frac{df}{d\overline{z_{2}}},\nonumber\\ \displaystyle M^{-}f & = & \displaystyle -i(a-2)\overline{z_{2}}f+i\overline{z_{1}z_{2}}\frac{df}{d\overline{z_{1}}}+i(\overline{z_{1}}^{2}+1)\frac{df}{d\overline{z_{2}}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N^{+}f & = & \displaystyle -(a-2)\overline{z_{1}}f+(\overline{z_{1}}^{2}-1)\frac{df}{d\overline{z_{1}}}+\overline{z_{1}z_{2}}\frac{df}{d\overline{z_{2}}},\nonumber\\ \displaystyle N^{-}f & = & \displaystyle -i(a-2)\overline{z_{1}}f+i(\overline{z_{1}}^{2}+1)\frac{df}{d\overline{z_{1}}}+i\overline{z_{1}z_{2}}\frac{df}{d\overline{z_{2}}},\nonumber\\ \displaystyle M^{+}f & = & \displaystyle -(a-2)\overline{z_{2}}f+\overline{z_{1}z_{2}}\frac{df}{d\overline{z_{1}}}+(\overline{z_{1}}^{2}-1)\frac{df}{d\overline{z_{2}}},\nonumber\\ \displaystyle M^{-}f & = & \displaystyle -i(a-2)\overline{z_{2}}f+i\overline{z_{1}z_{2}}\frac{df}{d\overline{z_{1}}}+i(\overline{z_{1}}^{2}+1)\frac{df}{d\overline{z_{2}}}.\nonumber\end{eqnarray}$$
We deduce that the action of
![]() $\mathfrak{p}^{-}$
is given by
$\mathfrak{p}^{-}$
is given by
and
and the action of
![]() $\mathfrak{p}^{+}$
by
$\mathfrak{p}^{+}$
by
and
As
![]() $Z_{a-2}^{-}$
is defined as a completion of the quotient of holomorphic polynomials in variables
$Z_{a-2}^{-}$
is defined as a completion of the quotient of holomorphic polynomials in variables
![]() $\overline{z_{1}},\overline{z_{2}}$
by the subspace of polynomials of degrees less or equal to
$\overline{z_{1}},\overline{z_{2}}$
by the subspace of polynomials of degrees less or equal to
![]() $(a-2)$
,
$(a-2)$
,
![]() $H^{0}(\mathfrak{p}^{-},Z_{a-2}^{-})=(Z_{a-2}^{+})^{\mathfrak{p}^{-}=0}$
is identified with homogeneous polynomials in
$H^{0}(\mathfrak{p}^{-},Z_{a-2}^{-})=(Z_{a-2}^{+})^{\mathfrak{p}^{-}=0}$
is identified with homogeneous polynomials in
![]() $\overline{z_{1}},\overline{z_{2}}$
of degree
$\overline{z_{1}},\overline{z_{2}}$
of degree
![]() $a-1$
.
$a-1$
.
As for a representation
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $K_{\infty }$
we have
$K_{\infty }$
we have
(cf. [Reference HarrisHar90b, 4.14]), we have that
![]() $H^{0}(\mathfrak{q},K,Z_{a-1}^{+}\otimes V_{\unicode[STIX]{x1D70E}}^{\vee })\neq 0$
.
$H^{0}(\mathfrak{q},K,Z_{a-1}^{+}\otimes V_{\unicode[STIX]{x1D70E}}^{\vee })\neq 0$
.
Remark D.3. Using a slightly more precise calculation for
![]() $U(2,1)$
instead of
$U(2,1)$
instead of
![]() $SU(2,1)$
, we could show for
$SU(2,1)$
, we could show for
![]() $U(2,1)$
that
$U(2,1)$
that
in particular, the Hecke eigenvalues of
![]() $\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appear in the global sections over
$\unicode[STIX]{x1D70B}^{n}(\unicode[STIX]{x1D712})$
appear in the global sections over
![]() $X$
, the Picard modular variety, of the automorphic sheaf
$X$
, the Picard modular variety, of the automorphic sheaf
![]() $\unicode[STIX]{x1D714}^{(0,1-a,a)}$
.
$\unicode[STIX]{x1D714}^{(0,1-a,a)}$
.