Article contents
The Brauer group and indecomposable 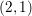 $(2,1)$-cycles
$(2,1)$-cycles
Published online by Cambridge University Press: 17 December 2015
Abstract
We show that the torsion in the group of indecomposable 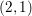 $(2,1)$-cycles on a smooth projective variety over an algebraically closed field is isomorphic to a twist of its Brauer group, away from the characteristic. In particular, this group is infinite as soon as
$(2,1)$-cycles on a smooth projective variety over an algebraically closed field is isomorphic to a twist of its Brauer group, away from the characteristic. In particular, this group is infinite as soon as 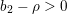 $b_{2}-{\it\rho}>0$. We derive a new insight into Roǐtman’s theorem on torsion
$b_{2}-{\it\rho}>0$. We derive a new insight into Roǐtman’s theorem on torsion 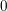 $0$-cycles over a surface.
$0$-cycles over a surface.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2015
References
- 3
- Cited by


