Article contents
K3 surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space IV: The structure of the invariant
Published online by Cambridge University Press: 19 November 2020
Abstract
Yoshikawa in [Invent. Math. 156 (2004), 53–117] introduces a holomorphic torsion invariant of 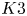 $K3$ surfaces with involution. In this paper we completely determine its structure as an automorphic function on the moduli space of such
$K3$ surfaces with involution. In this paper we completely determine its structure as an automorphic function on the moduli space of such 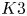 $K3$ surfaces. On every component of the moduli space, it is expressed as the product of an explicit Borcherds lift and a classical Siegel modular form. We also introduce its twisted version. We prove its modularity and a certain uniqueness of the modular form corresponding to the twisted holomorphic torsion invariant. This is used to study an equivariant analogue of Borcherds’ conjecture.
$K3$ surfaces. On every component of the moduli space, it is expressed as the product of an explicit Borcherds lift and a classical Siegel modular form. We also introduce its twisted version. We prove its modularity and a certain uniqueness of the modular form corresponding to the twisted holomorphic torsion invariant. This is used to study an equivariant analogue of Borcherds’ conjecture.
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2020
References
- 1
- Cited by



