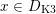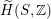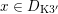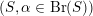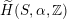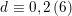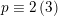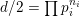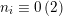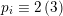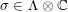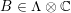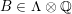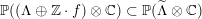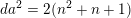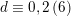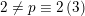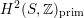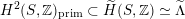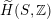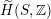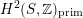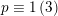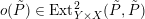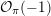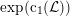1 Introduction
As shown by Kuznetsov [Reference KuznetsovKuz10, Reference KuznetsovKuz06], the bounded derived category
![]() $\text{D}^{\text{b}}(X)$
of coherent sheaves on a smooth cubic hypersurface
$\text{D}^{\text{b}}(X)$
of coherent sheaves on a smooth cubic hypersurface
![]() $X\subset \mathbb{P}^{5}$
contains, as the semi-orthogonal complement of three line bundles, a full triangulated subcategory
$X\subset \mathbb{P}^{5}$
contains, as the semi-orthogonal complement of three line bundles, a full triangulated subcategory
 $$\begin{eqnarray}{\mathcal{A}}_{X}:=\langle {\mathcal{O}},{\mathcal{O}}(1),{\mathcal{O}}(2)\rangle ^{\bot }\subset \text{D}^{\text{b}}(X)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{X}:=\langle {\mathcal{O}},{\mathcal{O}}(1),{\mathcal{O}}(2)\rangle ^{\bot }\subset \text{D}^{\text{b}}(X)\end{eqnarray}$$
that behaves in many respects like the bounded derived category
![]() $\text{D}^{\text{b}}(S)$
of coherent sheaves on a K3 surface
$\text{D}^{\text{b}}(S)$
of coherent sheaves on a K3 surface
![]() $S$
. In fact, for certain special cubics
$S$
. In fact, for certain special cubics
![]() ${\mathcal{A}}_{X}$
is equivalent to
${\mathcal{A}}_{X}$
is equivalent to
![]() $\text{D}^{\text{b}}(S)$
or, more generally, to the derived category
$\text{D}^{\text{b}}(S)$
or, more generally, to the derived category
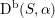 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
of
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
of
![]() $\unicode[STIX]{x1D6FC}$
-twisted sheaves on a K3 surface
$\unicode[STIX]{x1D6FC}$
-twisted sheaves on a K3 surface
![]() $S$
. Kuznetsov also conjectured that
$S$
. Kuznetsov also conjectured that
![]() ${\mathcal{A}}_{X}$
is of the form
${\mathcal{A}}_{X}$
is of the form
![]() $\text{D}^{\text{b}}(S)$
if and only if
$\text{D}^{\text{b}}(S)$
if and only if
![]() $X$
is rational. Neither of the two implications has been verified until now, although Addington and Thomas recently have shown in [Reference Addington and ThomasAT14] that the conjecture is (generically) equivalent to a conjecture attributed to Hassett [Reference HassettHas00] describing rational cubics in terms of their periods.
$X$
is rational. Neither of the two implications has been verified until now, although Addington and Thomas recently have shown in [Reference Addington and ThomasAT14] that the conjecture is (generically) equivalent to a conjecture attributed to Hassett [Reference HassettHas00] describing rational cubics in terms of their periods.
1.1
This paper is not concerned with the rationality of cubic fourfolds, but with basic results on
![]() ${\mathcal{A}}_{X}$
. Ideally, one would like to have a theory for
${\mathcal{A}}_{X}$
. Ideally, one would like to have a theory for
![]() ${\mathcal{A}}_{X}$
that parallels the theory for
${\mathcal{A}}_{X}$
that parallels the theory for
![]() $\text{D}^{\text{b}}(S)$
and
$\text{D}^{\text{b}}(S)$
and
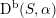 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
. In particular, one would like to have analogues of the following results and conjectures.
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
. In particular, one would like to have analogues of the following results and conjectures.
– For a given twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
there exist only finitely many isomorphism classes of twisted K3 surfaces
$(S,\unicode[STIX]{x1D6FC})$
there exist only finitely many isomorphism classes of twisted K3 surfaces
![]() $(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
with
$(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
with
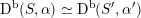 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})\simeq \text{D}^{\text{b}}(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
.
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})\simeq \text{D}^{\text{b}}(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
.
– Two twisted K3 surfaces
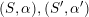 $(S,\unicode[STIX]{x1D6FC}),(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
are derived equivalent, i.e. there exists a
$(S,\unicode[STIX]{x1D6FC}),(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
are derived equivalent, i.e. there exists a
![]() $\mathbb{C}$
-linear exact equivalence
$\mathbb{C}$
-linear exact equivalence
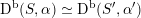 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})\simeq \text{D}^{\text{b}}(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
, if and only if there exists an orientation-preserving Hodge isometry
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})\simeq \text{D}^{\text{b}}(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
, if and only if there exists an orientation-preserving Hodge isometry
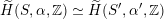 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})\simeq \widetilde{H}(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime },\mathbb{Z})$
.
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})\simeq \widetilde{H}(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime },\mathbb{Z})$
.
– The group of linear exact autoequivalences of
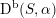 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
admits a natural representation
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
admits a natural representation
 which is surjective up to index two. Moreover, up to finite index
which is surjective up to index two. Moreover, up to finite index
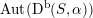 $\operatorname{Aut}(\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC}))$
is conjecturally described as a fundamental group of a certain Deligne–Mumford stack.
$\operatorname{Aut}(\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC}))$
is conjecturally described as a fundamental group of a certain Deligne–Mumford stack.
Most of the theory for untwisted K3 surfaces is due to Mukai [Reference MukaiMuk87] and Orlov [Reference OrlovOrl97], whereas the basic theory of twisted K3 surfaces was developed in [Reference Huybrechts and StellariHS05, Reference Huybrechts and StellariHS06]. See also [Reference HuybrechtsHuy06, Reference HuybrechtsHuy09] for surveys and further references. Originally, the generalization to twisted K3 surfaces was motivated by the existence of non-fine moduli spaces [Reference CăldăraruCăl00]. However, more recently it has become clear that allowing twists has quite unexpected applications, e.g. to the Tate conjecture [Reference CharlesCha16, Reference Lieblich, Maulik and SnowdenLMS14]. Crucial for the purpose of this article is the observation proved together with Macrì and Stellari [Reference Huybrechts, Macrì and StellariHMS08] that
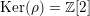 $\text{Ker}(\unicode[STIX]{x1D70C})=\mathbb{Z}[2]$
for many twisted K3 surfaces
$\text{Ker}(\unicode[STIX]{x1D70C})=\mathbb{Z}[2]$
for many twisted K3 surfaces
![]() $(S,\unicode[STIX]{x1D6FC})$
. Note that for untwisted projective K3 surfaces the kernel is always highly non-trivial and, in particular, not finitely generated. The conjectural description of
$(S,\unicode[STIX]{x1D6FC})$
. Note that for untwisted projective K3 surfaces the kernel is always highly non-trivial and, in particular, not finitely generated. The conjectural description of
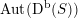 $\operatorname{Aut}(\text{D}^{\text{b}}(S))$
has in this case only been achieved for K3 surfaces of Picard rank one [Reference Bayer and BridgelandBB13].
$\operatorname{Aut}(\text{D}^{\text{b}}(S))$
has in this case only been achieved for K3 surfaces of Picard rank one [Reference Bayer and BridgelandBB13].
1.2
As a direct attack on
![]() ${\mathcal{A}}_{X}$
is difficult, we follow Addington and Thomas [Reference Addington and ThomasAT14] and reduce the study of
${\mathcal{A}}_{X}$
is difficult, we follow Addington and Thomas [Reference Addington and ThomasAT14] and reduce the study of
![]() ${\mathcal{A}}_{X}$
via deformation to the case of (twisted) K3 surfaces. Central to our discussion is the Hodge structure
${\mathcal{A}}_{X}$
via deformation to the case of (twisted) K3 surfaces. Central to our discussion is the Hodge structure
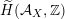 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
associated with
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
associated with
![]() ${\mathcal{A}}_{X}$
introduced in [Reference Addington and ThomasAT14] as the analogue of the Mukai–Hodge structure
${\mathcal{A}}_{X}$
introduced in [Reference Addington and ThomasAT14] as the analogue of the Mukai–Hodge structure
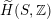 $\widetilde{H}(S,\mathbb{Z})$
of weight two on the full cohomology
$\widetilde{H}(S,\mathbb{Z})$
of weight two on the full cohomology
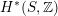 $H^{\ast }(S,\mathbb{Z})$
of a K3 surface
$H^{\ast }(S,\mathbb{Z})$
of a K3 surface
![]() $S$
or of the twisted version
$S$
or of the twisted version
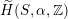 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
introduced in [Reference Huybrechts and StellariHS05]. For example, any FM-equivalence
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
introduced in [Reference Huybrechts and StellariHS05]. For example, any FM-equivalence
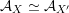 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
induces a Hodge isometry
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
induces a Hodge isometry
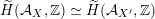 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
, cf. Proposition 3.4. This suffices to prove the following theorem.
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
, cf. Proposition 3.4. This suffices to prove the following theorem.
Theorem 1.1. For any given smooth cubic
![]() $X\subset \mathbb{P}^{5}$
there are only finitely many cubics
$X\subset \mathbb{P}^{5}$
there are only finitely many cubics
 $X^{\prime }\subset \mathbb{P}^{5}$
up to isomorphism for which there exists a FM-equivalence
$X^{\prime }\subset \mathbb{P}^{5}$
up to isomorphism for which there exists a FM-equivalence
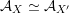 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
. See Corollary 3.5.
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
. See Corollary 3.5.
Recall that due to a result of Bondal and Orlov a smooth cubic
![]() $X\subset \mathbb{P}^{5}$
itself does not admit any non-isomorphic Fourier–Mukai partners. This is no longer true if
$X\subset \mathbb{P}^{5}$
itself does not admit any non-isomorphic Fourier–Mukai partners. This is no longer true if
![]() $\text{D}^{\text{b}}(X)$
is replaced by its K3 category
$\text{D}^{\text{b}}(X)$
is replaced by its K3 category
![]() ${\mathcal{A}}_{X}$
. In particular, there exist FM-equivalences
${\mathcal{A}}_{X}$
. In particular, there exist FM-equivalences
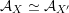 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
that do not extend to equivalences
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
that do not extend to equivalences
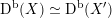 $\text{D}^{\text{b}}(X)\simeq \text{D}^{\text{b}}(X^{\prime })$
. However, we will also see that general cubics
$\text{D}^{\text{b}}(X)\simeq \text{D}^{\text{b}}(X^{\prime })$
. However, we will also see that general cubics
![]() $X$
and
$X$
and
![]() $X^{\prime }$
, i.e. those for which
$X^{\prime }$
, i.e. those for which
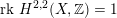 $\operatorname{rk}\,H^{2,2}(X,\mathbb{Z})=1$
, admit a FM-equivalence
$\operatorname{rk}\,H^{2,2}(X,\mathbb{Z})=1$
, admit a FM-equivalence
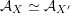 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if
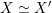 $X\simeq X^{\prime }$
, see Theorem 1.5 or Corollary 3.6.
$X\simeq X^{\prime }$
, see Theorem 1.5 or Corollary 3.6.
The following can be seen as an easy analogue of the result of Bayer and Bridgeland [Reference Bayer and BridgelandBB13] describing
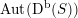 $\operatorname{Aut}(\text{D}^{\text{b}}(S))$
for general K3 surfaces
$\operatorname{Aut}(\text{D}^{\text{b}}(S))$
for general K3 surfaces
![]() $S$
(namely those with
$S$
(namely those with
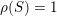 $\unicode[STIX]{x1D70C}(S)=1$
) or rather of [Reference Huybrechts, Macrì and StellariHMS09] describing this group for general non-projective K3 surfaces or twisted projective K3 surfaces
$\unicode[STIX]{x1D70C}(S)=1$
) or rather of [Reference Huybrechts, Macrì and StellariHMS09] describing this group for general non-projective K3 surfaces or twisted projective K3 surfaces
![]() $(S,\unicode[STIX]{x1D6FC})$
without
$(S,\unicode[STIX]{x1D6FC})$
without
![]() $(-2)$
classes (see § 6.1).
$(-2)$
classes (see § 6.1).
Theorem 1.2.
![]() $\text{(i)}$
For the very generalFootnote
1
smooth cubic
$\text{(i)}$
For the very generalFootnote
1
smooth cubic
![]() $X\subset \mathbb{P}^{5}$
the group
$X\subset \mathbb{P}^{5}$
the group
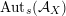 $\operatorname{Aut}_{s}({\mathcal{A}}_{X})$
of symplectic FM-autoequivalences is infinite cyclic with
$\operatorname{Aut}_{s}({\mathcal{A}}_{X})$
of symplectic FM-autoequivalences is infinite cyclic with
 $$\begin{eqnarray}\operatorname{Aut}_{s}({\mathcal{A}}_{X})/\mathbb{Z}\cdot [2]\simeq \mathbb{Z}/3\mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Aut}_{s}({\mathcal{A}}_{X})/\mathbb{Z}\cdot [2]\simeq \mathbb{Z}/3\mathbb{Z}.\end{eqnarray}$$
Alternatively, the group of all FM-autoequivalences
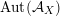 $\operatorname{Aut}({\mathcal{A}}_{X})$
is infinite cyclic containing
$\operatorname{Aut}({\mathcal{A}}_{X})$
is infinite cyclic containing
![]() $\mathbb{Z}\cdot [1]$
as a subgroup of index three.
$\mathbb{Z}\cdot [1]$
as a subgroup of index three.
-
(ii) Moreover, the induced action on
 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
of any FM-autoequivalence
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
of any FM-autoequivalence  of a non-special cubic preserves the natural orientation.
of a non-special cubic preserves the natural orientation.
In fact, for every smooth cubic
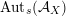 $\operatorname{Aut}_{s}({\mathcal{A}}_{X})$
contains an infinite cyclic group with
$\operatorname{Aut}_{s}({\mathcal{A}}_{X})$
contains an infinite cyclic group with
![]() $\mathbb{Z}\cdot [2]$
as a subgroup of index three, see Corollary 3.13. The theory of twisted K3 surfaces is crucial for the theorem, as eventually the problem is reduced to [Reference Huybrechts, Macrì and StellariHMS08] which deals with general twisted K3 surfaces.
$\mathbb{Z}\cdot [2]$
as a subgroup of index three, see Corollary 3.13. The theory of twisted K3 surfaces is crucial for the theorem, as eventually the problem is reduced to [Reference Huybrechts, Macrì and StellariHMS08] which deals with general twisted K3 surfaces.
The group
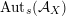 $\operatorname{Aut}_{s}({\mathcal{A}}_{X})$
of an arbitrary cubic is described by an analogue of Brigdeland’s conjecture, see Conjecture 3.15.
$\operatorname{Aut}_{s}({\mathcal{A}}_{X})$
of an arbitrary cubic is described by an analogue of Brigdeland’s conjecture, see Conjecture 3.15.
1.3
In [Reference HassettHas00] Hassett showed that in the moduli space
![]() ${\mathcal{C}}$
of smooth cubics, the set of those cubics
${\mathcal{C}}$
of smooth cubics, the set of those cubics
![]() $X$
for which there exists a primitive positive plane
$X$
for which there exists a primitive positive plane
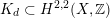 $K_{d}\subset H^{2,2}(X,\mathbb{Z})$
of discriminant
$K_{d}\subset H^{2,2}(X,\mathbb{Z})$
of discriminant
![]() $d$
containing the class
$d$
containing the class
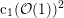 $\text{c}_{1}({\mathcal{O}}(1))^{2}$
is an irreducible divisor
$\text{c}_{1}({\mathcal{O}}(1))^{2}$
is an irreducible divisor
![]() ${\mathcal{C}}_{d}\subset {\mathcal{C}}$
. Moreover,
${\mathcal{C}}_{d}\subset {\mathcal{C}}$
. Moreover,
![]() ${\mathcal{C}}_{d}$
is not empty if and only if
${\mathcal{C}}_{d}$
is not empty if and only if
-
 $(\ast )$
$(\ast )$
-
 $d\equiv 0,2\,(6)$
and
$d\equiv 0,2\,(6)$
and
 $d>6$
.
$d>6$
.
Cubics parametrized by the divisors
![]() ${\mathcal{C}}_{d}$
are called special. Hassett also introduced the numerical condition
${\mathcal{C}}_{d}$
are called special. Hassett also introduced the numerical condition
-
 $(\ast \ast )$
$(\ast \ast )$
-
 $d$
is even and
$d$
is even and
 $d/2$
is not divisible by nine or any prime
$d/2$
is not divisible by nine or any prime
 $p\equiv 2\,(3)$
.Footnote
2
$p\equiv 2\,(3)$
.Footnote
2
Hassett then proved that (
![]() $\ast \ast$
) is equivalent to the orthogonal complement of the corresponding lattice
$\ast \ast$
) is equivalent to the orthogonal complement of the corresponding lattice
![]() $K_{d}$
in
$K_{d}$
in
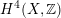 $H^{4}(X,\mathbb{Z})$
being (up to sign) Hodge isometric to the primitive Hodge structure
$H^{4}(X,\mathbb{Z})$
being (up to sign) Hodge isometric to the primitive Hodge structure
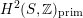 $H^{2}(S,\mathbb{Z})_{\text{prim}}$
of a polarized K3 surface. In [Reference Addington and ThomasAT14] the condition was shown to be equivalent to the existence of a Hodge isometry
$H^{2}(S,\mathbb{Z})_{\text{prim}}$
of a polarized K3 surface. In [Reference Addington and ThomasAT14] the condition was shown to be equivalent to the existence of a Hodge isometry
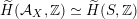 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}(S,\mathbb{Z})$
for some K3 surface
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}(S,\mathbb{Z})$
for some K3 surface
![]() $S$
. We prove the following twisted version of it (cf. Proposition 2.10).
$S$
. We prove the following twisted version of it (cf. Proposition 2.10).
Theorem 1.3. For a smooth cubic
![]() $X\subset \mathbb{P}^{5}$
the Hodge structure
$X\subset \mathbb{P}^{5}$
the Hodge structure
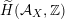 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
is Hodge isometric to the Hodge structure
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
is Hodge isometric to the Hodge structure
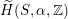 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
of a twisted K3 surface
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
of a twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
if and only if
$(S,\unicode[STIX]{x1D6FC})$
if and only if
![]() $X\in {\mathcal{C}}_{d}$
with
$X\in {\mathcal{C}}_{d}$
with
-
 $(\ast \ast ^{\prime })$
$(\ast \ast ^{\prime })$
-
 $d$
is even and in the prime factorization
$d$
is even and in the prime factorization
 $d/2=\prod p_{i}^{n_{i}}$
one has
$d/2=\prod p_{i}^{n_{i}}$
one has
 $n_{i}\equiv 0\,(2)$
for all primes
$n_{i}\equiv 0\,(2)$
for all primes
 $p_{i}\equiv 2\,(3)$
.
$p_{i}\equiv 2\,(3)$
.
Obviously, if
![]() $d$
satisfies
$d$
satisfies
![]() $(\ast \ast )$
, then
$(\ast \ast )$
, then
![]() $k^{2}d$
satisfies (
$k^{2}d$
satisfies (
![]() $\ast \ast ^{\prime }$
) for all integers
$\ast \ast ^{\prime }$
) for all integers
![]() $k$
. Conversely, any
$k$
. Conversely, any
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
) can be written (in general, non-uniquely) as
$\ast \ast ^{\prime }$
) can be written (in general, non-uniquely) as
![]() $k^{2}d_{0}$
with
$k^{2}d_{0}$
with
![]() $d_{0}$
satisfying (
$d_{0}$
satisfying (
![]() $\ast \ast$
).
$\ast \ast$
).
Also note that for
![]() $X\in {\mathcal{C}}_{d}$
with
$X\in {\mathcal{C}}_{d}$
with
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
) the transcendental part
$\ast \ast ^{\prime }$
) the transcendental part
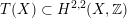 $T(X)\subset H^{2,2}(X,\mathbb{Z})$
is Hodge isometric (up to sign) to
$T(X)\subset H^{2,2}(X,\mathbb{Z})$
is Hodge isometric (up to sign) to
![]() $T(S,\unicode[STIX]{x1D6FC})$
of a twisted K3 surface
$T(S,\unicode[STIX]{x1D6FC})$
of a twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
(cf. [Reference Huybrechts and StellariHS05]):
$(S,\unicode[STIX]{x1D6FC})$
(cf. [Reference Huybrechts and StellariHS05]):

As the main result of [Reference Addington and ThomasAT14], Addington and Thomas proved that at least generically (
![]() $\ast \ast$
) is equivalent to
$\ast \ast$
) is equivalent to
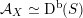 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
for some K3 surface
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
for some K3 surface
![]() $S$
. The following twisted version of it will be proved in § 6.2.
$S$
. The following twisted version of it will be proved in § 6.2.
Theorem 1.4.
![]() $\text{(i)}$
If
$\text{(i)}$
If
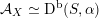 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
for some twisted K3 surface
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
for some twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
, then
$(S,\unicode[STIX]{x1D6FC})$
, then
![]() $X\in {\mathcal{C}}_{d}$
with
$X\in {\mathcal{C}}_{d}$
with
![]() $d$
satisfying
$d$
satisfying
![]() $(\ast \ast ^{\prime })$
.
$(\ast \ast ^{\prime })$
.
-
(ii) Conversely, if
 $d$
satisfies
$d$
satisfies
 $(\ast \ast ^{\prime })$
, then there exists a Zariski open dense set
$(\ast \ast ^{\prime })$
, then there exists a Zariski open dense set
 $\emptyset \neq U\subset {\mathcal{C}}_{d}$
such that for all
$\emptyset \neq U\subset {\mathcal{C}}_{d}$
such that for all
 $X\in {\mathcal{C}}_{d}$
there exists a twisted K3 surface
$X\in {\mathcal{C}}_{d}$
there exists a twisted K3 surface
 $(S,\unicode[STIX]{x1D6FC})$
and an equivalence
$(S,\unicode[STIX]{x1D6FC})$
and an equivalence
 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
.
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
.
Non-special cubics are determined by their associated K3 category
![]() ${\mathcal{A}}_{X}$
and for general special cubics
${\mathcal{A}}_{X}$
and for general special cubics
![]() ${\mathcal{A}}_{X}$
is determined by its Hodge structure (see Corollary 3.6 and § 6.3).
${\mathcal{A}}_{X}$
is determined by its Hodge structure (see Corollary 3.6 and § 6.3).
Theorem 1.5. Let
![]() $X$
and
$X$
and
![]() $X^{\prime }$
be two smooth cubics.
$X^{\prime }$
be two smooth cubics.
-
(i) Assume
 $X$
is not special, i.e. not contained in any
$X$
is not special, i.e. not contained in any
 ${\mathcal{C}}_{d}\subset {\mathcal{C}}$
. Then there exists a FM-equivalence
${\mathcal{C}}_{d}\subset {\mathcal{C}}$
. Then there exists a FM-equivalence
 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if
 $X\simeq X^{\prime }$
.
$X\simeq X^{\prime }$
. -
(ii) For
 $d$
satisfying
$d$
satisfying
 $(\ast \ast ^{\prime })$
and a Zariski dense open set of cubics
$(\ast \ast ^{\prime })$
and a Zariski dense open set of cubics
 $X\in {\mathcal{C}}_{d}$
, there exists a FM-equivalence
$X\in {\mathcal{C}}_{d}$
, there exists a FM-equivalence
 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if there exists a Hodge isometry
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if there exists a Hodge isometry
 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
.
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
. -
(iii) For arbitrary
 $d$
and very general
$d$
and very general
 $X\in {\mathcal{C}}_{d}$
there exists a FM-equivalence
$X\in {\mathcal{C}}_{d}$
there exists a FM-equivalence
 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if there exists a Hodge isometry
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if there exists a Hodge isometry
 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
.
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
.
We will also see that arguments of Addington [Reference AddingtonAdd16] can be adapted to show that (
![]() $\ast \ast ^{\prime }$
) is in fact equivalent to the Fano variety of lines on
$\ast \ast ^{\prime }$
) is in fact equivalent to the Fano variety of lines on
![]() $X$
being birational to a moduli space of twisted sheaves on some K3 surface, see Proposition 4.1.
$X$
being birational to a moduli space of twisted sheaves on some K3 surface, see Proposition 4.1.
1.4
There are a few fundamental issues concerning
![]() ${\mathcal{A}}_{X}$
that we do not know how to address and that prevent us from developing the theory in full. First, this paper only deals with FM-equivalences
${\mathcal{A}}_{X}$
that we do not know how to address and that prevent us from developing the theory in full. First, this paper only deals with FM-equivalences
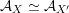 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
, i.e. those for which the composition
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
, i.e. those for which the composition  is a Fourier–Mukai transform. One would expect this to be the case for all equivalences, but the classical result of Orlov [Reference OrlovOrl97] and its generalization by Canonaco and Stellari [Reference Canonaco and StellariCS07] do not apply to this situation. Secondly, it is not known whether
is a Fourier–Mukai transform. One would expect this to be the case for all equivalences, but the classical result of Orlov [Reference OrlovOrl97] and its generalization by Canonaco and Stellari [Reference Canonaco and StellariCS07] do not apply to this situation. Secondly, it is not known whether
![]() ${\mathcal{A}}_{X}$
always admits bounded t-structures or stability conditions. This is problematic when one wants to study FM-partners of
${\mathcal{A}}_{X}$
always admits bounded t-structures or stability conditions. This is problematic when one wants to study FM-partners of
![]() ${\mathcal{A}}_{X}$
as moduli spaces of (stable) objects in
${\mathcal{A}}_{X}$
as moduli spaces of (stable) objects in
![]() ${\mathcal{A}}_{X}$
. As in [Reference Addington and ThomasAT14], the lack of stability is also the crucial stumbling block to use deformation theory to prove statements as in Theorem 1.4 for all cubics and not only for generic or very general ones.
${\mathcal{A}}_{X}$
. As in [Reference Addington and ThomasAT14], the lack of stability is also the crucial stumbling block to use deformation theory to prove statements as in Theorem 1.4 for all cubics and not only for generic or very general ones.
1.5
The plan of the paper is as follows. Section 2 deals with all issues related to the lattice theory and the abstract Hodge theory. In particular, natural (countable unions of) codimension-one subsets
 $D_{\text{K3}}\subset D_{\text{K3'}}$
of the period domain
$D_{\text{K3}}\subset D_{\text{K3'}}$
of the period domain
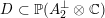 $D\subset \mathbb{P}(A_{2}^{\bot }\otimes \mathbb{C})$
are studied at great length. They parametrize periods that induce Hodge structures that are Hodge isometric to
$D\subset \mathbb{P}(A_{2}^{\bot }\otimes \mathbb{C})$
are studied at great length. They parametrize periods that induce Hodge structures that are Hodge isometric to
 $\widetilde{H}(S,\mathbb{Z})$
and
$\widetilde{H}(S,\mathbb{Z})$
and
 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
, respectively, and which are described in terms of the numerical conditions (
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
, respectively, and which are described in terms of the numerical conditions (
![]() $\ast \ast$
) and (
$\ast \ast$
) and (
![]() $\ast \ast ^{\prime }$
). In particular, Theorem 1.3 is proved. We also provide a geometric description of all periods
$\ast \ast ^{\prime }$
). In particular, Theorem 1.3 is proved. We also provide a geometric description of all periods
![]() $x\in D$
in terms of generalized K3 surfaces, see Proposition 2.17.
$x\in D$
in terms of generalized K3 surfaces, see Proposition 2.17.
In § 3 we extend results in [Reference Addington and ThomasAT14] from equivalences
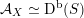 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
to the twisted case and prove the finiteness of FM-partners for
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
to the twisted case and prove the finiteness of FM-partners for
![]() ${\mathcal{A}}_{X}$
, see Theorem 1.1. Moreover, we produce an action of the universal cover of
${\mathcal{A}}_{X}$
, see Theorem 1.1. Moreover, we produce an action of the universal cover of
![]() $\text{SO}(A_{2})$
on
$\text{SO}(A_{2})$
on
![]() ${\mathcal{A}}_{X}$
for all cubics (Remark 3.14) and formulate an analogue of Bridgeland’s conjecture (cf. Conjecture 3.15).
${\mathcal{A}}_{X}$
for all cubics (Remark 3.14) and formulate an analogue of Bridgeland’s conjecture (cf. Conjecture 3.15).
The short § 4 shows that (
![]() $\ast \ast ^{\prime }$
) is equivalent to
$\ast \ast ^{\prime }$
) is equivalent to
![]() $F(X)$
being birational to a moduli space of stable twisted sheaves on a K3 surface. In § 5 we adapt the deformation theory of [Reference Addington and ThomasAT14] to the twisted case. Finally, in § 6 we conclude the proofs of Theorems 1.2, 1.4, and 1.5.
$F(X)$
being birational to a moduli space of stable twisted sheaves on a K3 surface. In § 5 we adapt the deformation theory of [Reference Addington and ThomasAT14] to the twisted case. Finally, in § 6 we conclude the proofs of Theorems 1.2, 1.4, and 1.5.
2 Lattice theory and period domains
We start by discussing the relevant lattice theory. To make the reading self-contained, we will also recall results due to Hassett and to Addington and Thomas on the way.
There are two kinds of lattices, those related to K3 surfaces,
![]() $\unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x1D6EC}$
,
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
, etc., and those attached to cubic fourfolds,
$\widetilde{\unicode[STIX]{x1D6EC}}$
, etc., and those attached to cubic fourfolds,
![]() $\text{I}_{21,2}$
,
$\text{I}_{21,2}$
,
![]() $K_{d}$
, etc. The two types are linked by a lattice
$K_{d}$
, etc. The two types are linked by a lattice
![]() $A_{2}^{\bot }$
of signature
$A_{2}^{\bot }$
of signature
![]() $(2,20)$
and two embeddings
$(2,20)$
and two embeddings

The induced maps between the associated period domains allows one to relate periods of cubic fourfolds to periods of (generalized) K3 surfaces.
2.1
By
![]() $U$
we shall denote the hyperbolic plane, i.e.
$U$
we shall denote the hyperbolic plane, i.e.
![]() $\mathbb{Z}^{2}$
with the intersection form
$\mathbb{Z}^{2}$
with the intersection form
![]() $(\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!)$
. The K3 lattice
$(\!\begin{smallmatrix}0 & 1\\ 1 & 0\end{smallmatrix}\!)$
. The K3 lattice
![]() $\unicode[STIX]{x1D6EC}$
and the extended K3 lattice
$\unicode[STIX]{x1D6EC}$
and the extended K3 lattice
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
are by definition the unique even, unimodular lattice of signature
$\widetilde{\unicode[STIX]{x1D6EC}}$
are by definition the unique even, unimodular lattice of signature
![]() $(3,19)$
and
$(3,19)$
and
![]() $(4,20)$
, respectively. So,
$(4,20)$
, respectively. So,
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\simeq E_{8}(-1)^{\oplus 2}\oplus U^{\oplus 3}\quad \text{and}\quad \widetilde{\unicode[STIX]{x1D6EC}}\simeq \unicode[STIX]{x1D6EC}\oplus U.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\simeq E_{8}(-1)^{\oplus 2}\oplus U^{\oplus 3}\quad \text{and}\quad \widetilde{\unicode[STIX]{x1D6EC}}\simeq \unicode[STIX]{x1D6EC}\oplus U.\end{eqnarray}$$
Next,
![]() $A_{2}$
denotes the standard root lattice of rank two, i.e. there exists a basis
$A_{2}$
denotes the standard root lattice of rank two, i.e. there exists a basis
![]() $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$
with respect to which the intersection matrix is given by
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$
with respect to which the intersection matrix is given by
![]() $(\!\begin{smallmatrix}2 & -1\\ -1 & 2\end{smallmatrix}\!)$
. The lattice
$(\!\begin{smallmatrix}2 & -1\\ -1 & 2\end{smallmatrix}\!)$
. The lattice
![]() $A_{2}$
is even and of signature
$A_{2}$
is even and of signature
![]() $(2,0)$
. Moreover, its discriminant group is
$(2,0)$
. Moreover, its discriminant group is
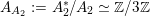 $A_{A_{2}}:=A_{2}^{\ast }/A_{2}\simeq \mathbb{Z}/3\mathbb{Z}$
and, in particular,
$A_{A_{2}}:=A_{2}^{\ast }/A_{2}\simeq \mathbb{Z}/3\mathbb{Z}$
and, in particular,
![]() $A_{2}$
is not unimodular.
$A_{2}$
is not unimodular.
Due to [Reference NikulinNik79, Theorem 1.14.4], there exist embeddings

which are both unique up to the action of
![]() $\text{O}(\unicode[STIX]{x1D6EC})$
and
$\text{O}(\unicode[STIX]{x1D6EC})$
and
![]() $\text{O}(\widetilde{\unicode[STIX]{x1D6EC}})$
, respectively. Note that all such embeddings are automatically primitive. In the following we will fix once and for all one such embedding
$\text{O}(\widetilde{\unicode[STIX]{x1D6EC}})$
, respectively. Note that all such embeddings are automatically primitive. In the following we will fix once and for all one such embedding  and consider the orthogonal complement of
and consider the orthogonal complement of
![]() $A_{2}\subset \widetilde{\unicode[STIX]{x1D6EC}}$
as a fixed primitive sublattice
$A_{2}\subset \widetilde{\unicode[STIX]{x1D6EC}}$
as a fixed primitive sublattice
 $$\begin{eqnarray}A_{2}^{\bot }\subset \widetilde{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
$$\begin{eqnarray}A_{2}^{\bot }\subset \widetilde{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
of signature
![]() $(2,20)$
. Its isomorphism type does not depend on the chosen embedding of
$(2,20)$
. Its isomorphism type does not depend on the chosen embedding of
![]() $A_{2}$
. It can be described explicitly as the orthogonal complement of the embedding
$A_{2}$
. It can be described explicitly as the orthogonal complement of the embedding  given by
given by

where
![]() $e,f$
and
$e,f$
and
![]() $e^{\prime },f^{\prime }$
denote the standard bases of the two copies of the hyperbolic plane. Thus,Footnote
3
$e^{\prime },f^{\prime }$
denote the standard bases of the two copies of the hyperbolic plane. Thus,Footnote
3
 $$\begin{eqnarray}A_{2}^{\bot }\simeq E_{8}(-1)^{\oplus 2}\oplus U^{\oplus 2}\oplus A_{2}(-1).\end{eqnarray}$$
$$\begin{eqnarray}A_{2}^{\bot }\simeq E_{8}(-1)^{\oplus 2}\oplus U^{\oplus 2}\oplus A_{2}(-1).\end{eqnarray}$$
Remark 2.1. For later use we recall that the group of isometries
![]() $\text{O}(A_{2})$
of the lattice
$\text{O}(A_{2})$
of the lattice
![]() $A_{2}$
is isomorphic to
$A_{2}$
is isomorphic to
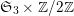 $\mathfrak{S}_{3}\times \mathbb{Z}/2\mathbb{Z}$
. Here, the Weyl group
$\mathfrak{S}_{3}\times \mathbb{Z}/2\mathbb{Z}$
. Here, the Weyl group
![]() $\mathfrak{S}_{3}$
permutes the unit vectors
$\mathfrak{S}_{3}$
permutes the unit vectors
![]() $e_{i}\in \mathbb{R}^{3}$
, where
$e_{i}\in \mathbb{R}^{3}$
, where  via
via
 $\unicode[STIX]{x1D706}_{1}=e_{1}-e_{2}$
and
$\unicode[STIX]{x1D706}_{1}=e_{1}-e_{2}$
and
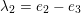 $\unicode[STIX]{x1D706}_{2}=e_{2}-e_{3}$
, and the generator of
$\unicode[STIX]{x1D706}_{2}=e_{2}-e_{3}$
, and the generator of
![]() $\mathbb{Z}/2\mathbb{Z}$
acts by
$\mathbb{Z}/2\mathbb{Z}$
acts by
![]() $-\text{id}$
. In fact,
$-\text{id}$
. In fact,
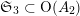 $\mathfrak{S}_{3}\subset \text{O}(A_{2})$
is the kernel of the natural map
$\mathfrak{S}_{3}\subset \text{O}(A_{2})$
is the kernel of the natural map  (use the aforementioned
(use the aforementioned
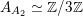 $A_{A_{2}}\simeq \mathbb{Z}/3\mathbb{Z}$
). The sign
$A_{A_{2}}\simeq \mathbb{Z}/3\mathbb{Z}$
). The sign  can be identified with the determinant
can be identified with the determinant  Thus, the group of orientation-preserving isometries of
Thus, the group of orientation-preserving isometries of
![]() $A_{2}$
acting trivially on
$A_{2}$
acting trivially on
![]() $A_{A_{2}}$
is just
$A_{A_{2}}$
is just
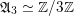 $\mathfrak{A}_{3}\simeq \mathbb{Z}/3\mathbb{Z}$
, where the generator can be chosen to act by
$\mathfrak{A}_{3}\simeq \mathbb{Z}/3\mathbb{Z}$
, where the generator can be chosen to act by 
2.2
Next, consider the unique odd, unimodular lattice
 $$\begin{eqnarray}\text{I}_{2,21}:=\mathbb{Z}^{\oplus 2}\oplus \mathbb{Z}(-1)^{\oplus 21}\simeq E_{8}(-1)^{\oplus 2}\oplus U^{\oplus 2}\oplus \mathbb{Z}(-1)^{\oplus 3}\end{eqnarray}$$
$$\begin{eqnarray}\text{I}_{2,21}:=\mathbb{Z}^{\oplus 2}\oplus \mathbb{Z}(-1)^{\oplus 21}\simeq E_{8}(-1)^{\oplus 2}\oplus U^{\oplus 2}\oplus \mathbb{Z}(-1)^{\oplus 3}\end{eqnarray}$$
of signature
![]() $(2,21)$
and an element
$(2,21)$
and an element
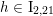 $h\in \text{I}_{2,21}$
with
$h\in \text{I}_{2,21}$
with
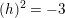 $(h)^{2}=-3$
, e.g.
$(h)^{2}=-3$
, e.g.
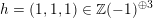 $h=(1,1,1)\in \mathbb{Z}(-1)^{\oplus 3}$
. Then the primitive sublattice
$h=(1,1,1)\in \mathbb{Z}(-1)^{\oplus 3}$
. Then the primitive sublattice
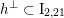 $h^{\bot }\subset \text{I}_{2,21}$
is of signature
$h^{\bot }\subset \text{I}_{2,21}$
is of signature
![]() $(2,20)$
and using (2.3) one finds
$(2,20)$
and using (2.3) one finds
 $$\begin{eqnarray}h^{\bot }\simeq A_{2}^{\bot }.\end{eqnarray}$$
$$\begin{eqnarray}h^{\bot }\simeq A_{2}^{\bot }.\end{eqnarray}$$
In the following, we will always consider
![]() $A_{2}^{\bot }$
with two fixed embeddings as above:
$A_{2}^{\bot }$
with two fixed embeddings as above:

Following Hassett [Reference HassettHas00], we now consider all primitive, negative-definite sublattices
 $$\begin{eqnarray}h\in K_{d}\subset \text{I}_{2,21}\end{eqnarray}$$
$$\begin{eqnarray}h\in K_{d}\subset \text{I}_{2,21}\end{eqnarray}$$
of rank two containing
![]() $h$
. Here, the index
$h$
. Here, the index
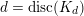 $d=\text{disc}(K_{d})$
denotes the discriminant of
$d=\text{disc}(K_{d})$
denotes the discriminant of
![]() $K_{d}$
, which is necessarily positive. Using [Reference NikulinNik79, § 1.5] one finds that up to the action of the subgroup of
$K_{d}$
, which is necessarily positive. Using [Reference NikulinNik79, § 1.5] one finds that up to the action of the subgroup of
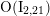 $\text{O}(\text{I}_{2,21})$
fixing
$\text{O}(\text{I}_{2,21})$
fixing
![]() $h$
the lattice
$h$
the lattice
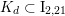 $K_{d}\subset \text{I}_{2,21}$
is uniquely determined by
$K_{d}\subset \text{I}_{2,21}$
is uniquely determined by
![]() $d$
, see [Reference HassettHas00, Proposition 3.2.4] for the details.
$d$
, see [Reference HassettHas00, Proposition 3.2.4] for the details.
Furthermore,
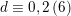 $d\equiv 0,2\,(6)$
and the generator
$d\equiv 0,2\,(6)$
and the generator
![]() $v$
of
$v$
of
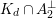 $K_{d}\cap A_{2}^{\bot }$
(unique up to sign) satisfies
$K_{d}\cap A_{2}^{\bot }$
(unique up to sign) satisfies
 $$\begin{eqnarray}-(v)^{2}=\left\{\begin{array}{@{}ll@{}}d/3\quad & \text{if}~d\equiv 0\,(6),\\ 3d\quad & \text{if}~d\equiv 2\,(6).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}-(v)^{2}=\left\{\begin{array}{@{}ll@{}}d/3\quad & \text{if}~d\equiv 0\,(6),\\ 3d\quad & \text{if}~d\equiv 2\,(6).\end{array}\right.\end{eqnarray}$$
More precisely, Hassett shows that up to isometry of
![]() $A_{2}^{\bot }$
the vector
$A_{2}^{\bot }$
the vector
![]() $v$
is given as
$v$
is given as
 $$\begin{eqnarray}v=e_{1}-(d/6)f_{1}\quad \text{and}\quad v=3(e_{1}-((d-2)/6)f_{1})+\unicode[STIX]{x1D707}_{1}-\unicode[STIX]{x1D707}_{2},\end{eqnarray}$$
$$\begin{eqnarray}v=e_{1}-(d/6)f_{1}\quad \text{and}\quad v=3(e_{1}-((d-2)/6)f_{1})+\unicode[STIX]{x1D707}_{1}-\unicode[STIX]{x1D707}_{2},\end{eqnarray}$$
respectively. Here,
![]() $e_{1},f_{1}$
is the standard basis of one of the copies of
$e_{1},f_{1}$
is the standard basis of one of the copies of
![]() $U$
in (2.3) and
$U$
in (2.3) and
![]() $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$
denotes the standard basis of
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}$
denotes the standard basis of
![]() $A_{2}(-1)$
. Viewing
$A_{2}(-1)$
. Viewing
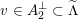 $v\in A_{2}^{\bot }\subset \widetilde{\unicode[STIX]{x1D6EC}}$
as an element of
$v\in A_{2}^{\bot }\subset \widetilde{\unicode[STIX]{x1D6EC}}$
as an element of
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
leads to a lattice
$\widetilde{\unicode[STIX]{x1D6EC}}$
leads to a lattice
 $$\begin{eqnarray}A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
$$\begin{eqnarray}A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
of rank three and signature
![]() $(2,1)$
. As it turns out, this is a primitive sublattice for
$(2,1)$
. As it turns out, this is a primitive sublattice for
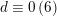 $d\equiv 0\,(6)$
and it is of index three in its saturation for
$d\equiv 0\,(6)$
and it is of index three in its saturation for
 $d\equiv 2\,(6)$
. This follows from [Reference HassettHas00, Proposition 3.2.2] asserting that in the two cases
$d\equiv 2\,(6)$
. This follows from [Reference HassettHas00, Proposition 3.2.2] asserting that in the two cases
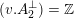 $(v.A_{2}^{\bot })=\mathbb{Z}$
and
$(v.A_{2}^{\bot })=\mathbb{Z}$
and
![]() $3\mathbb{Z}$
, respectively. Altogether this yields the following lemma.
$3\mathbb{Z}$
, respectively. Altogether this yields the following lemma.
Lemma 2.2. The saturation
![]() $\unicode[STIX]{x1D6E4}_{d}\subset \widetilde{\unicode[STIX]{x1D6EC}}$
of
$\unicode[STIX]{x1D6E4}_{d}\subset \widetilde{\unicode[STIX]{x1D6EC}}$
of
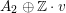 $A_{2}\oplus \mathbb{Z}\cdot v$
satisfies
$A_{2}\oplus \mathbb{Z}\cdot v$
satisfies
 $$\begin{eqnarray}\text{disc}(\unicode[STIX]{x1D6E4}_{d})=d.\end{eqnarray}$$
$$\begin{eqnarray}\text{disc}(\unicode[STIX]{x1D6E4}_{d})=d.\end{eqnarray}$$
Proof. This can either be proved by a direct computation or by observing that
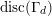 $\text{disc}(\unicode[STIX]{x1D6E4}_{d})$
equals the discriminant of
$\text{disc}(\unicode[STIX]{x1D6E4}_{d})$
equals the discriminant of
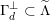 $\unicode[STIX]{x1D6E4}_{d}^{\bot }\subset \widetilde{\unicode[STIX]{x1D6EC}}$
, which is isomorphic to
$\unicode[STIX]{x1D6E4}_{d}^{\bot }\subset \widetilde{\unicode[STIX]{x1D6EC}}$
, which is isomorphic to
 $v^{\bot }\subset A_{2}^{\bot }$
. Similarly,
$v^{\bot }\subset A_{2}^{\bot }$
. Similarly,
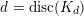 $d=\text{disc}(K_{d})$
equals the discriminant of the lattice
$d=\text{disc}(K_{d})$
equals the discriminant of the lattice
![]() $\langle v,h\rangle ^{\bot }$
, which again is just
$\langle v,h\rangle ^{\bot }$
, which again is just
 $v^{\bot }\subset A_{2}^{\bot }$
.◻
$v^{\bot }\subset A_{2}^{\bot }$
.◻
In our discussion, the lattices
![]() $K_{d}$
will take a back seat, as it will be more natural to work with the generator
$K_{d}$
will take a back seat, as it will be more natural to work with the generator
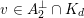 $v\in A_{2}^{\bot }\cap K_{d}$
directly.
$v\in A_{2}^{\bot }\cap K_{d}$
directly.
2.3
We shall be interested in the period domains
 $$\begin{eqnarray}D\subset \mathbb{P}(A_{2}^{\bot }\otimes \mathbb{C})\quad \text{and}\quad Q\subset \mathbb{P}(\widetilde{\unicode[STIX]{x1D6EC}}\otimes \mathbb{C}),\end{eqnarray}$$
$$\begin{eqnarray}D\subset \mathbb{P}(A_{2}^{\bot }\otimes \mathbb{C})\quad \text{and}\quad Q\subset \mathbb{P}(\widetilde{\unicode[STIX]{x1D6EC}}\otimes \mathbb{C}),\end{eqnarray}$$
defined by the two conditions
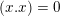 $(x.x)=0$
and
$(x.x)=0$
and
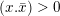 $(x.\bar{x})>0$
. Observe that
$(x.\bar{x})>0$
. Observe that
 $$\begin{eqnarray}\dim \,D=20\quad \text{and}\quad \dim \,Q=22\end{eqnarray}$$
$$\begin{eqnarray}\dim \,D=20\quad \text{and}\quad \dim \,Q=22\end{eqnarray}$$
and that
![]() $Q$
is connected while
$Q$
is connected while
![]() $D$
has two connected components. Using the embedding (2.1), we can write
$D$
has two connected components. Using the embedding (2.1), we can write
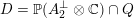 $D=\mathbb{P}(A_{2}^{\bot }\otimes \mathbb{C})\cap Q$
as part of the commutative diagram
$D=\mathbb{P}(A_{2}^{\bot }\otimes \mathbb{C})\cap Q$
as part of the commutative diagram

Thus, points
![]() $x\in D$
correspond to Hodge structures of weight two on the lattice
$x\in D$
correspond to Hodge structures of weight two on the lattice
![]() $A_{2}^{\bot }$
, but also to Hodge structures on
$A_{2}^{\bot }$
, but also to Hodge structures on
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
with
$\widetilde{\unicode[STIX]{x1D6EC}}$
with
![]() $A_{2}$
contained in the
$A_{2}$
contained in the
![]() $(1,1)$
part. In fact, for very general points
$(1,1)$
part. In fact, for very general points
![]() $x\in D$
the integral
$x\in D$
the integral
![]() $(1,1)$
part of the corresponding Hodge structure is the lattice
$(1,1)$
part of the corresponding Hodge structure is the lattice
![]() $A_{2}$
.
$A_{2}$
.
We shall refer to
![]() $D$
as the period domain of cubic fourfolds, although only an open subset really corresponds to smooth cubics. More concretely, for a smooth cubic
$D$
as the period domain of cubic fourfolds, although only an open subset really corresponds to smooth cubics. More concretely, for a smooth cubic
![]() $X\subset \mathbb{P}^{5}$
and any marking, i.e. an isometry,
$X\subset \mathbb{P}^{5}$
and any marking, i.e. an isometry,  (up to sign), one defines the associated period as the image
(up to sign), one defines the associated period as the image
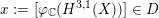 $x:=[\unicode[STIX]{x1D711}_{\mathbb{C}}(H^{3,1}(X))]\in D$
. A description of the image of the period map, allowing cubics with ADE singularities, has been given by Laza [Reference LazaLaz10] and Looijenga in [Reference LooijengaLoo09]. Points in
$x:=[\unicode[STIX]{x1D711}_{\mathbb{C}}(H^{3,1}(X))]\in D$
. A description of the image of the period map, allowing cubics with ADE singularities, has been given by Laza [Reference LazaLaz10] and Looijenga in [Reference LooijengaLoo09]. Points in
![]() $Q$
are thought of as periods of generalized K3 surfaces, cf. § 2.8.
$Q$
are thought of as periods of generalized K3 surfaces, cf. § 2.8.
For later use we state the following technical observation.
Lemma 2.3. The Hodge structure on
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
defined by an arbitrary
$\widetilde{\unicode[STIX]{x1D6EC}}$
defined by an arbitrary
![]() $x\in D$
admits a Hodge isometry that reverses any given orientation of the four positive directions.
$x\in D$
admits a Hodge isometry that reverses any given orientation of the four positive directions.
Proof. Consider a transposition
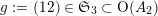 $g:=(12)\in \mathfrak{S}_{3}\subset \text{O}(A_{2})$
. Then
$g:=(12)\in \mathfrak{S}_{3}\subset \text{O}(A_{2})$
. Then
![]() $g$
acts trivially on the discriminant
$g$
acts trivially on the discriminant
![]() $A_{A_{2}}$
(see Remark 2.1) and can, therefore, be extended to
$A_{A_{2}}$
(see Remark 2.1) and can, therefore, be extended to
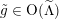 $\tilde{g}\in \text{O}(\widetilde{\unicode[STIX]{x1D6EC}})$
acting trivially on
$\tilde{g}\in \text{O}(\widetilde{\unicode[STIX]{x1D6EC}})$
acting trivially on
![]() $A_{2}^{\bot }$
. Thus, the Hodge structure defined by
$A_{2}^{\bot }$
. Thus, the Hodge structure defined by
![]() $x$
admits a Hodge isometry
$x$
admits a Hodge isometry
![]() $\tilde{g}$
, which preserves the orientation of the two positive directions given by the
$\tilde{g}$
, which preserves the orientation of the two positive directions given by the
![]() $(2,0)$
and
$(2,0)$
and
![]() $(0,2)$
parts. On the other hand, by construction, it reverses the orientation of the two positive directions in
$(0,2)$
parts. On the other hand, by construction, it reverses the orientation of the two positive directions in
![]() $A_{2}$
.◻
$A_{2}$
.◻
Remark 2.4. This result is the analogue of the observation that any Hodge structure on
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
containing a hyperbolic plane
$\widetilde{\unicode[STIX]{x1D6EC}}$
containing a hyperbolic plane
![]() $U$
in its
$U$
in its
![]() $(1,1)$
part admits an orientation-reversing Hodge isometry. This assertion applies to the Hodge structure
$(1,1)$
part admits an orientation-reversing Hodge isometry. This assertion applies to the Hodge structure
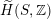 $\widetilde{H}(S,\mathbb{Z})$
of a K3 surface
$\widetilde{H}(S,\mathbb{Z})$
of a K3 surface
![]() $S$
, but it is not clear whether also
$S$
, but it is not clear whether also
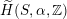 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
of a twisted K3 surface
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
of a twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
(see below) admits an orientation-reversing Hodge isometry. The latter would be important for adapting the arguments in [Reference Huybrechts, Macrì and StellariHMS09] to the description of the image of
$(S,\unicode[STIX]{x1D6FC})$
(see below) admits an orientation-reversing Hodge isometry. The latter would be important for adapting the arguments in [Reference Huybrechts, Macrì and StellariHMS09] to the description of the image of  see [Reference ReineckeRei14] for partial results.
see [Reference ReineckeRei14] for partial results.
2.4
Let us now turn to the geometric interpretation of certain periods in
![]() $Q$
. Recall that for a K3 surface
$Q$
. Recall that for a K3 surface
![]() $S$
the extended K3 (or Mukai) lattice
$S$
the extended K3 (or Mukai) lattice
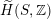 $\widetilde{H}(S,\mathbb{Z})$
is abstractly isomorphic to
$\widetilde{H}(S,\mathbb{Z})$
is abstractly isomorphic to
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
. Moreover,
$\widetilde{\unicode[STIX]{x1D6EC}}$
. Moreover,
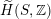 $\widetilde{H}(S,\mathbb{Z})$
comes with a natural Hodge structure of weight two defined by
$\widetilde{H}(S,\mathbb{Z})$
comes with a natural Hodge structure of weight two defined by
 $$\begin{eqnarray}\widetilde{H}^{2,0}(S):=H^{2,0}(S)\quad \text{and}\quad \widetilde{H}^{1,1}(S):=H^{1,1}(S)\oplus (H^{0}\oplus H^{4})(S,\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}^{2,0}(S):=H^{2,0}(S)\quad \text{and}\quad \widetilde{H}^{1,1}(S):=H^{1,1}(S)\oplus (H^{0}\oplus H^{4})(S,\mathbb{C}).\end{eqnarray}$$
For a Brauer class
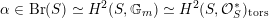 $\unicode[STIX]{x1D6FC}\in \text{Br}(S)\simeq H^{2}(S,\mathbb{G}_{m})\simeq H^{2}(S,{\mathcal{O}}_{S}^{\ast })_{\text{tors}}$
we have introduced in [Reference HuybrechtsHuy05] the weight-two Hodge structure
$\unicode[STIX]{x1D6FC}\in \text{Br}(S)\simeq H^{2}(S,\mathbb{G}_{m})\simeq H^{2}(S,{\mathcal{O}}_{S}^{\ast })_{\text{tors}}$
we have introduced in [Reference HuybrechtsHuy05] the weight-two Hodge structure
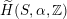 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
. As a lattice this is still isomorphic to
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
. As a lattice this is still isomorphic to
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
and its Hodge structure is determined by
$\widetilde{\unicode[STIX]{x1D6EC}}$
and its Hodge structure is determined by
 $$\begin{eqnarray}\widetilde{H}^{2,0}(S,\unicode[STIX]{x1D6FC}):=\mathbb{C}\cdot (\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E})\quad \text{and}\quad \widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC}):=\exp (B)\cdot \widetilde{H}^{1,1}(S).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}^{2,0}(S,\unicode[STIX]{x1D6FC}):=\mathbb{C}\cdot (\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E})\quad \text{and}\quad \widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC}):=\exp (B)\cdot \widetilde{H}^{1,1}(S).\end{eqnarray}$$
Here,
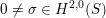 $0\neq \unicode[STIX]{x1D70E}\in H^{2,0}(S)$
and
$0\neq \unicode[STIX]{x1D70E}\in H^{2,0}(S)$
and
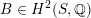 $B\in H^{2}(S,\mathbb{Q})$
maps to
$B\in H^{2}(S,\mathbb{Q})$
maps to
![]() $\unicode[STIX]{x1D6FC}$
under the exponential map
$\unicode[STIX]{x1D6FC}$
under the exponential map

The isomorphism type of the Hodge structure is independent of the choice of
![]() $B$
.
$B$
.
Definition 2.5. A period
![]() $x\in Q$
is of K3 type (respectively twisted K3 type) if there exists a K3 surface
$x\in Q$
is of K3 type (respectively twisted K3 type) if there exists a K3 surface
![]() $S$
(respectively a twisted K3 surface
$S$
(respectively a twisted K3 surface
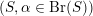 $(S,\unicode[STIX]{x1D6FC}\in \text{Br}(S))$
) such that the Hodge structure on
$(S,\unicode[STIX]{x1D6FC}\in \text{Br}(S))$
) such that the Hodge structure on
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
defined by
$\widetilde{\unicode[STIX]{x1D6EC}}$
defined by
![]() $x$
is Hodge isometric to
$x$
is Hodge isometric to
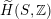 $\widetilde{H}(S,\mathbb{Z})$
(respectively
$\widetilde{H}(S,\mathbb{Z})$
(respectively
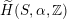 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
).
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
).
The sets of periods of K3 type and twisted K3 type will be denoted
 $$\begin{eqnarray}Q_{\text{K3}}\subset Q_{\text{K3'}}\subset Q.\end{eqnarray}$$
$$\begin{eqnarray}Q_{\text{K3}}\subset Q_{\text{K3'}}\subset Q.\end{eqnarray}$$
There is also a geometric interpretation for points outside
![]() $Q_{\text{K3'}}$
in terms of symplectic structures [Reference HuybrechtsHuy05], but those are a priori inaccessible by algebro-geometric techniques (see, however, § 2.8).
$Q_{\text{K3'}}$
in terms of symplectic structures [Reference HuybrechtsHuy05], but those are a priori inaccessible by algebro-geometric techniques (see, however, § 2.8).
For the following recall that the twisted hyperbolic plane
![]() $U(n)$
is the rank-two lattice with intersection matrix
$U(n)$
is the rank-two lattice with intersection matrix
![]() $(\!\begin{smallmatrix}0 & n\\ n & 0\end{smallmatrix}\!)$
. The standard isotropic generators will be denoted
$(\!\begin{smallmatrix}0 & n\\ n & 0\end{smallmatrix}\!)$
. The standard isotropic generators will be denoted
![]() $e_{n},f_{n}$
or simply
$e_{n},f_{n}$
or simply
![]() $e,f$
. Part (i) of the next lemma is well known.
$e,f$
. Part (i) of the next lemma is well known.
Lemma 2.6. Consider a period point
![]() $x\in Q$
. Then:
$x\in Q$
. Then:
-
(i)
 $x\in Q_{\text{K3}}$
if and only if there exists an embedding
$x\in Q_{\text{K3}}$
if and only if there exists an embedding  into the
into the
 $(1,1)$
part of the Hodge structure defined by
$(1,1)$
part of the Hodge structure defined by
 $x$
;
$x$
; -
(ii)
 $x\in Q_{\text{K3'}}$
if and only if there exists a (not necessarily primitive) embedding
$x\in Q_{\text{K3'}}$
if and only if there exists a (not necessarily primitive) embedding  for some
for some
 $n\neq 0$
into the
$n\neq 0$
into the
 $(1,1)$
part of the Hodge structure defined by
$(1,1)$
part of the Hodge structure defined by
 $x$
.
$x$
.
Proof. We prove the second assertion; the first one is even easier. Start with a twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
and pick a lift
$(S,\unicode[STIX]{x1D6FC})$
and pick a lift
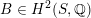 $B\in H^{2}(S,\mathbb{Q})$
of
$B\in H^{2}(S,\mathbb{Q})$
of
![]() $\unicode[STIX]{x1D6FC}$
. Then the algebraic part
$\unicode[STIX]{x1D6FC}$
. Then the algebraic part
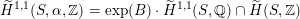 $\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})=\exp (B)\cdot \widetilde{H}^{1,1}(S,\mathbb{Q})\cap \widetilde{H}(S,\mathbb{Z})$
contains the lattice
$\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})=\exp (B)\cdot \widetilde{H}^{1,1}(S,\mathbb{Q})\cap \widetilde{H}(S,\mathbb{Z})$
contains the lattice
 $(\mathbb{Z}\cdot (1,B,B^{2}/2)\cap \widetilde{H}(S,\mathbb{Z}))\oplus H^{4}(S,\mathbb{Z})$
, which is isomorphic to
$(\mathbb{Z}\cdot (1,B,B^{2}/2)\cap \widetilde{H}(S,\mathbb{Z}))\oplus H^{4}(S,\mathbb{Z})$
, which is isomorphic to
![]() $U(n)$
for
$U(n)$
for
![]() $n$
minimal with
$n$
minimal with
 $n(1,B,B^{2}/2)\in \widetilde{H}(S,\mathbb{Z})$
.
$n(1,B,B^{2}/2)\in \widetilde{H}(S,\mathbb{Z})$
.
Conversely, assume
 $U(n)\subset \widetilde{\unicode[STIX]{x1D6EC}}$
is of type
$U(n)\subset \widetilde{\unicode[STIX]{x1D6EC}}$
is of type
![]() $(1,1)$
with respect to
$(1,1)$
with respect to
![]() $x$
. Choosing
$x$
. Choosing
![]() $n$
minimal, we can assume that the standard isotropic generator
$n$
minimal, we can assume that the standard isotropic generator
![]() $e_{n}=e$
is primitive in
$e_{n}=e$
is primitive in
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
. But then
$\widetilde{\unicode[STIX]{x1D6EC}}$
. But then
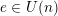 $e\in U(n)$
can be completed to a sublattice of
$e\in U(n)$
can be completed to a sublattice of
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
isomorphic to the hyperbolic plane
$\widetilde{\unicode[STIX]{x1D6EC}}$
isomorphic to the hyperbolic plane
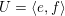 $U=\langle e,f\rangle$
, which therefore induces an orthogonal decomposition (usually different from that defining
$U=\langle e,f\rangle$
, which therefore induces an orthogonal decomposition (usually different from that defining
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
)
$\widetilde{\unicode[STIX]{x1D6EC}}$
)
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6EC}}\simeq \unicode[STIX]{x1D6EC}\oplus U.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6EC}}\simeq \unicode[STIX]{x1D6EC}\oplus U.\end{eqnarray}$$
With respect to (2.6) the second basis vector
 $f_{n}\in U(n)$
can be written as
$f_{n}\in U(n)$
can be written as
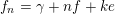 $f_{n}=\unicode[STIX]{x1D6FE}+nf+ke$
with
$f_{n}=\unicode[STIX]{x1D6FE}+nf+ke$
with
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6EC}$
. Similarly, a generator of the
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D6EC}$
. Similarly, a generator of the
![]() $(2,0)$
part of the Hodge structure determined by
$(2,0)$
part of the Hodge structure determined by
![]() $x$
is orthogonal to
$x$
is orthogonal to
![]() $e$
and hence of the form
$e$
and hence of the form
![]() $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e$
for some
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e$
for some
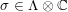 $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
and
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
and
![]() $\unicode[STIX]{x1D706}\in \mathbb{C}$
. However, it is also orthogonal to
$\unicode[STIX]{x1D706}\in \mathbb{C}$
. However, it is also orthogonal to
![]() $f_{n}$
and so
$f_{n}$
and so
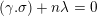 $(\unicode[STIX]{x1D6FE}.\unicode[STIX]{x1D70E})+n\unicode[STIX]{x1D706}=0$
. Now set
$(\unicode[STIX]{x1D6FE}.\unicode[STIX]{x1D70E})+n\unicode[STIX]{x1D706}=0$
. Now set
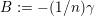 $B:=-(1/n)\unicode[STIX]{x1D6FE}$
. Then
$B:=-(1/n)\unicode[STIX]{x1D6FE}$
. Then
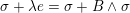 $\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e=\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E}$
, where
$\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e=\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E}$
, where
![]() $B\wedge \unicode[STIX]{x1D70E}$
stands for
$B\wedge \unicode[STIX]{x1D70E}$
stands for
![]() $(B.\unicode[STIX]{x1D70E})e$
.
$(B.\unicode[STIX]{x1D70E})e$
.
Eventually, the surjectivity of the period map implies that
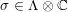 $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
can be realized as the period of some K3 surface
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
can be realized as the period of some K3 surface
![]() $S$
, i.e. there exists an isometry
$S$
, i.e. there exists an isometry
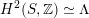 $H^{2}(S,\mathbb{Z})\simeq \unicode[STIX]{x1D6EC}$
identifying
$H^{2}(S,\mathbb{Z})\simeq \unicode[STIX]{x1D6EC}$
identifying
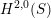 $H^{2,0}(S)$
with
$H^{2,0}(S)$
with
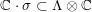 $\mathbb{C}\cdot \unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
. Here one uses
$\mathbb{C}\cdot \unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
. Here one uses
 $(\unicode[STIX]{x1D70E}.\unicode[STIX]{x1D70E})=(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e.\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e)=0$
and
$(\unicode[STIX]{x1D70E}.\unicode[STIX]{x1D70E})=(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e.\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e)=0$
and
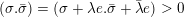 $(\unicode[STIX]{x1D70E}.\bar{\unicode[STIX]{x1D70E}})=(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e.\bar{\unicode[STIX]{x1D70E}}+\bar{\unicode[STIX]{x1D706}}e)>0$
. Mapping
$(\unicode[STIX]{x1D70E}.\bar{\unicode[STIX]{x1D70E}})=(\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D706}e.\bar{\unicode[STIX]{x1D70E}}+\bar{\unicode[STIX]{x1D706}}e)>0$
. Mapping
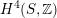 $H^{4}(S,\mathbb{Z})$
to
$H^{4}(S,\mathbb{Z})$
to
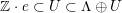 $\mathbb{Z}\cdot e\subset U\subset \unicode[STIX]{x1D6EC}\oplus U$
in (2.6) and defining
$\mathbb{Z}\cdot e\subset U\subset \unicode[STIX]{x1D6EC}\oplus U$
in (2.6) and defining
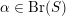 $\unicode[STIX]{x1D6FC}\in \text{Br}(S)$
as the Brauer class induced by
$\unicode[STIX]{x1D6FC}\in \text{Br}(S)$
as the Brauer class induced by
![]() $B$
under
$B$
under  yields a Hodge isometry between
yields a Hodge isometry between
 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
and the Hodge structure defined by
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
and the Hodge structure defined by
![]() $x$
on
$x$
on
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
.◻
$\widetilde{\unicode[STIX]{x1D6EC}}$
.◻
Corollary 2.7. The sets
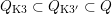 $Q_{\text{K3}}\subset Q_{\text{K3'}}\subset Q$
can be described as the intersections of
$Q_{\text{K3}}\subset Q_{\text{K3'}}\subset Q$
can be described as the intersections of
![]() $Q$
with countably many linear subspaces of codimension two:
$Q$
with countably many linear subspaces of codimension two:
 $$\begin{eqnarray}Q_{\text{K3}}=Q\cap \bigcup U^{\bot }\subset Q_{\text{K3'}}=Q\cap \bigcup U(n)^{\bot }\subset Q.\end{eqnarray}$$
$$\begin{eqnarray}Q_{\text{K3}}=Q\cap \bigcup U^{\bot }\subset Q_{\text{K3'}}=Q\cap \bigcup U(n)^{\bot }\subset Q.\end{eqnarray}$$
Here, the first union is over all embeddings  and the second over all
and the second over all  with arbitrary
with arbitrary
![]() $n\neq 0$
.
$n\neq 0$
.
2.5
However, it will turn out that the further intersection with
![]() $D$
yields countable unions of codimension-one subsets. These intersections are denoted by
$D$
yields countable unions of codimension-one subsets. These intersections are denoted by
 $$\begin{eqnarray}D_{\text{K3}}:=D\cap Q_{\text{K3}}\subset D_{\text{K3'}}:=D\cap Q_{\text{K3'}}\subset D\end{eqnarray}$$
$$\begin{eqnarray}D_{\text{K3}}:=D\cap Q_{\text{K3}}\subset D_{\text{K3'}}:=D\cap Q_{\text{K3'}}\subset D\end{eqnarray}$$
and will be viewed as the sets of cubic periods that define generalized K3 periods of K3 type and of twisted K3 type, respectively. So:
-
∙
 $x\in D_{\text{K3}}$
if and only if there exists a K3 surface
$x\in D_{\text{K3}}$
if and only if there exists a K3 surface
 $S$
such that the Hodge structure on
$S$
such that the Hodge structure on
 $\widetilde{\unicode[STIX]{x1D6EC}}$
defined by
$\widetilde{\unicode[STIX]{x1D6EC}}$
defined by
 $x$
is Hodge isometric to
$x$
is Hodge isometric to
 $\widetilde{H}(S,\mathbb{Z})$
;
$\widetilde{H}(S,\mathbb{Z})$
; -
∙
 $x\in D_{\text{K3'}}$
if and only if there exists a twisted K3 surface
$x\in D_{\text{K3'}}$
if and only if there exists a twisted K3 surface
 $(S,\unicode[STIX]{x1D6FC}\in \text{Br}(S))$
such that the Hodge structure on
$(S,\unicode[STIX]{x1D6FC}\in \text{Br}(S))$
such that the Hodge structure on
 $\widetilde{\unicode[STIX]{x1D6EC}}$
defined by
$\widetilde{\unicode[STIX]{x1D6EC}}$
defined by
 $x$
is Hodge isometric to
$x$
is Hodge isometric to
 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
.
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
.
We remark for later use that for very general
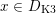 $x\in D_{\text{K3}}$
(or
$x\in D_{\text{K3}}$
(or
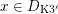 $x\in D_{\text{K3'}}$
) the algebraic part
$x\in D_{\text{K3'}}$
) the algebraic part
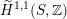 $\widetilde{H}^{1,1}(S,\mathbb{Z})$
(respectively
$\widetilde{H}^{1,1}(S,\mathbb{Z})$
(respectively
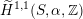 $\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
) is of rank three.
$\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
) is of rank three.
We will first explain that
![]() $D_{\text{K3'}}$
is a countable union of hyperplane sections. A second proof for the same assertion that also works for
$D_{\text{K3'}}$
is a countable union of hyperplane sections. A second proof for the same assertion that also works for
![]() $D_{\text{K3}}$
is provided in § 2.6.
$D_{\text{K3}}$
is provided in § 2.6.
Proposition 2.8. The set of twisted K3 periods in
![]() $D$
can also be described as the countable union of hyperplane sections:
$D$
can also be described as the countable union of hyperplane sections:
 $$\begin{eqnarray}D_{\text{K3'}}=D\cap \bigcup e^{\bot }.\end{eqnarray}$$
$$\begin{eqnarray}D_{\text{K3'}}=D\cap \bigcup e^{\bot }.\end{eqnarray}$$
Here, the union runs over all
 $0\neq e\in \widetilde{\unicode[STIX]{x1D6EC}}$
with
$0\neq e\in \widetilde{\unicode[STIX]{x1D6EC}}$
with
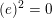 $(e)^{2}=0$
.
$(e)^{2}=0$
.
Proof. One inclusion follows from the fact that any
![]() $U(n)$
contains an isotropic vector. For the converse, assume
$U(n)$
contains an isotropic vector. For the converse, assume
![]() $x\in e^{\bot }$
for some primitive isotropic
$x\in e^{\bot }$
for some primitive isotropic
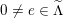 $0\neq e\in \widetilde{\unicode[STIX]{x1D6EC}}$
. Then
$0\neq e\in \widetilde{\unicode[STIX]{x1D6EC}}$
. Then
![]() $e\not \in A_{2}^{\bot }$
, as otherwise the positive plane corresponding to
$e\not \in A_{2}^{\bot }$
, as otherwise the positive plane corresponding to
![]() $x$
would be contained in the orthogonal complement of
$x$
would be contained in the orthogonal complement of
![]() $e$
in
$e$
in
![]() $A_{2}^{\bot }$
, which has only one positive direction left. Hence, there exists
$A_{2}^{\bot }$
, which has only one positive direction left. Hence, there exists
![]() $a\in A_{2}$
with
$a\in A_{2}$
with
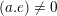 $(a.e)\neq 0$
. Let
$(a.e)\neq 0$
. Let
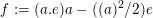 $f:=(a.e)a-((a)^{2}/2)e$
, which satisfies
$f:=(a.e)a-((a)^{2}/2)e$
, which satisfies
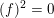 $(f)^{2}=0$
and
$(f)^{2}=0$
and
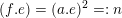 $(f.e)=(a.e)^{2}=:n$
. Hence,
$(f.e)=(a.e)^{2}=:n$
. Hence,
![]() $e,f$
span a twisted hyperbolic plane
$e,f$
span a twisted hyperbolic plane
![]() $U(n)$
in the
$U(n)$
in the
![]() $(1,1)$
part of the Hodge structure defined by
$(1,1)$
part of the Hodge structure defined by
![]() $x$
.◻
$x$
.◻
There is yet another class of hyperplane sections of
![]() $D$
that is of importance to us. We let
$D$
that is of importance to us. We let
 $$\begin{eqnarray}D_{\text{sph}}:=D\cap \bigcup \unicode[STIX]{x1D6FF}^{\bot },\end{eqnarray}$$
$$\begin{eqnarray}D_{\text{sph}}:=D\cap \bigcup \unicode[STIX]{x1D6FF}^{\bot },\end{eqnarray}$$
where the union is over all
![]() $\unicode[STIX]{x1D6FF}\in \widetilde{\unicode[STIX]{x1D6EC}}$
with
$\unicode[STIX]{x1D6FF}\in \widetilde{\unicode[STIX]{x1D6EC}}$
with
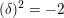 $(\unicode[STIX]{x1D6FF})^{2}=-2$
and call it the set of periods with spherical classes. Indeed,
$(\unicode[STIX]{x1D6FF})^{2}=-2$
and call it the set of periods with spherical classes. Indeed,
![]() $x\in D$
is contained in
$x\in D$
is contained in
![]() $D_{\text{sph}}$
if and only if the Hodge structure on
$D_{\text{sph}}$
if and only if the Hodge structure on
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
defined by
$\widetilde{\unicode[STIX]{x1D6EC}}$
defined by
![]() $x$
admits an integral
$x$
admits an integral
![]() $(1,1)$
class
$(1,1)$
class
![]() $\unicode[STIX]{x1D6FF}$
with
$\unicode[STIX]{x1D6FF}$
with
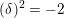 $(\unicode[STIX]{x1D6FF})^{2}=-2$
and those classes typically appear as Mukai vectors of spherical objects, see Example 3.11.
$(\unicode[STIX]{x1D6FF})^{2}=-2$
and those classes typically appear as Mukai vectors of spherical objects, see Example 3.11.
Note that there are natural inclusions
 $$\begin{eqnarray}D_{\text{K3}}\subset D_{\text{sph}}\subset D,\end{eqnarray}$$
$$\begin{eqnarray}D_{\text{K3}}\subset D_{\text{sph}}\subset D,\end{eqnarray}$$
for every hyperbolic plane
![]() $U$
contains a
$U$
contains a
![]() $(-2)$
class. However,
$(-2)$
class. However,
![]() $D_{\text{K3'}}$
is not contained in
$D_{\text{K3'}}$
is not contained in
![]() $D_{\text{sph}}$
and, more precisely, the inclusions
$D_{\text{sph}}$
and, more precisely, the inclusions
 $$\begin{eqnarray}D_{\text{K3}}\subsetneq D_{\text{K3'}}\cap D_{\text{sph}}\subsetneq D_{\text{K3'}},D_{\text{sph}}\end{eqnarray}$$
$$\begin{eqnarray}D_{\text{K3}}\subsetneq D_{\text{K3'}}\cap D_{\text{sph}}\subsetneq D_{\text{K3'}},D_{\text{sph}}\end{eqnarray}$$
2.6
It is instructive to study the sets
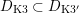 $D_{\text{K3}}\subset D_{\text{K3'}}$
and
$D_{\text{K3}}\subset D_{\text{K3'}}$
and
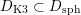 $D_{\text{K3}}\subset D_{\text{sph}}$
from a more cubic perspective, i.e. in terms of the lattices
$D_{\text{K3}}\subset D_{\text{sph}}$
from a more cubic perspective, i.e. in terms of the lattices
![]() $K_{d}$
.
$K_{d}$
.
For any
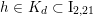 $h\in K_{d}\subset \text{I}_{2,21}$
as in § 2.2 one introduces the hyperplane section
$h\in K_{d}\subset \text{I}_{2,21}$
as in § 2.2 one introduces the hyperplane section
 $$\begin{eqnarray}D\cap K_{d}^{\bot }\subset \mathbb{P}(A_{2}^{\bot }\otimes \mathbb{C})\end{eqnarray}$$
$$\begin{eqnarray}D\cap K_{d}^{\bot }\subset \mathbb{P}(A_{2}^{\bot }\otimes \mathbb{C})\end{eqnarray}$$
of all cubic periods orthogonal to
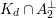 $K_{d}\cap A_{2}^{\bot }$
. In other words,
$K_{d}\cap A_{2}^{\bot }$
. In other words,
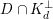 $D\cap K_{d}^{\bot }$
is the set of cubic periods for which the generator
$D\cap K_{d}^{\bot }$
is the set of cubic periods for which the generator
![]() $v$
of
$v$
of
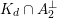 $K_{d}\cap A_{2}^{\bot }$
is of type
$K_{d}\cap A_{2}^{\bot }$
is of type
![]() $(1,1)$
, i.e.
$(1,1)$
, i.e.
 $D\cap K_{d}^{\bot }=D\cap v^{\bot }$
. Then one defines
$D\cap K_{d}^{\bot }=D\cap v^{\bot }$
. Then one defines
 $$\begin{eqnarray}D_{d}:=D\cap \,\bigcup \,K_{d}^{\bot },\end{eqnarray}$$
$$\begin{eqnarray}D_{d}:=D\cap \,\bigcup \,K_{d}^{\bot },\end{eqnarray}$$
where the union runs over all
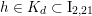 $h\in K_{d}\subset \text{I}_{2,21}$
as above. So, for each positive
$h\in K_{d}\subset \text{I}_{2,21}$
as above. So, for each positive
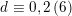 $d\equiv 0,2\,(6)$
the set
$d\equiv 0,2\,(6)$
the set
![]() $D_{d}$
is a countable union of hyperplane sections of
$D_{d}$
is a countable union of hyperplane sections of
![]() $D$
. Dividing
$D$
. Dividing
![]() $D_{d}$
by the subgroup
$D_{d}$
by the subgroup
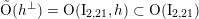 $\tilde{\text{O}}(h^{\bot })=\text{O}(\text{I}_{2,21},h)\subset \text{O}(\text{I}_{2,21})$
of elements fixing
$\tilde{\text{O}}(h^{\bot })=\text{O}(\text{I}_{2,21},h)\subset \text{O}(\text{I}_{2,21})$
of elements fixing
![]() $h$
yields Hassett’s irreducible divisor
$h$
yields Hassett’s irreducible divisor
 $$\begin{eqnarray}{\mathcal{C}}_{d}:=D_{d}/\tilde{\text{O}}(h^{\bot }).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}_{d}:=D_{d}/\tilde{\text{O}}(h^{\bot }).\end{eqnarray}$$
Consider the following conditions for an even integer
![]() $d>6$
:
$d>6$
:
-
 $(\ast )$
$(\ast )$
-
 $d\equiv 0,2\,(6)$
;
$d\equiv 0,2\,(6)$
; -
 $(\ast \ast )$
$(\ast \ast )$
-
 $d$
is even and
$d$
is even and
 $d/2$
is not divisible by
$d/2$
is not divisible by
 $9$
or any prime
$9$
or any prime
 $p\equiv 2\,(3)$
;
$p\equiv 2\,(3)$
; -
 $(\ast \ast ^{\prime })$
$(\ast \ast ^{\prime })$
-
 $d$
is even and in the prime factorization
$d$
is even and in the prime factorization
 $d/2=\prod p_{i}^{n_{i}}$
one has
$d/2=\prod p_{i}^{n_{i}}$
one has
 $n_{i}\equiv 0\,(2)$
for all primes
$n_{i}\equiv 0\,(2)$
for all primes
 $p_{i}\equiv 2\,(3)$
.
$p_{i}\equiv 2\,(3)$
.
Obviously, (
![]() $\ast \ast$
) implies (
$\ast \ast$
) implies (
![]() $\ast \ast ^{\prime }$
). More precisely, if
$\ast \ast ^{\prime }$
). More precisely, if
![]() $d$
satisfies (
$d$
satisfies (
![]() $\ast \ast$
), then (
$\ast \ast$
), then (
![]() $\ast \ast ^{\prime }$
) holds for all
$\ast \ast ^{\prime }$
) holds for all
![]() $k^{2}d$
.
$k^{2}d$
.
Remark 2.9. Conditions (
![]() $\ast$
) and (
$\ast$
) and (
![]() $\ast \ast$
) have first been introduced and studied by Hassett [Reference HassettHas00]. He shows that
$\ast \ast$
) have first been introduced and studied by Hassett [Reference HassettHas00]. He shows that
![]() $D_{d}$
is not empty if and only if (
$D_{d}$
is not empty if and only if (
![]() $\ast$
) is satisfied. Moreover,
$\ast$
) is satisfied. Moreover,
![]() $d$
satisfies (
$d$
satisfies (
![]() $\ast \ast$
) if and only if for all cubics
$\ast \ast$
) if and only if for all cubics
![]() $X$
with period
$X$
with period
![]() $x$
contained in
$x$
contained in
![]() $D_{d}$
there exists a polarized K3 surface
$D_{d}$
there exists a polarized K3 surface
![]() $(S,H)$
such that its primitive cohomology
$(S,H)$
such that its primitive cohomology
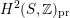 $H^{2}(S,\mathbb{Z})_{\text{pr}}$
is Hodge isometric to the Hodge structure on
$H^{2}(S,\mathbb{Z})_{\text{pr}}$
is Hodge isometric to the Hodge structure on
![]() $K_{d}^{\bot }$
defined by
$K_{d}^{\bot }$
defined by
![]() $x$
. To get polarized K3 surfaces and not only quasi-polarized ones, one has to use a result of Voisin [Reference VoisinVoi86, § 4, Proposition 1] saying that
$x$
. To get polarized K3 surfaces and not only quasi-polarized ones, one has to use a result of Voisin [Reference VoisinVoi86, § 4, Proposition 1] saying that
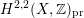 $H^{2,2}(X,\mathbb{Z})_{\text{pr}}$
does not contain any class of square two.
$H^{2,2}(X,\mathbb{Z})_{\text{pr}}$
does not contain any class of square two.
On the level of lattices this boils down to the observation that for
![]() $v\in A_{2}^{\bot }$
as in (2.5), say for
$v\in A_{2}^{\bot }$
as in (2.5), say for
 $d\equiv 0\,(6)$
, its orthogonal complement in
$d\equiv 0\,(6)$
, its orthogonal complement in
![]() $A_{2}^{\bot }$
is isometric to
$A_{2}^{\bot }$
is isometric to
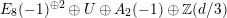 $E_{8}(-1)^{\oplus 2}\oplus U\oplus A_{2}(-1)\oplus \mathbb{Z}(d/3)$
. And indeed for
$E_{8}(-1)^{\oplus 2}\oplus U\oplus A_{2}(-1)\oplus \mathbb{Z}(d/3)$
. And indeed for
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
)
$\ast \ast ^{\prime }$
)
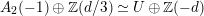 $A_{2}(-1)\oplus \mathbb{Z}(d/3)\simeq U\oplus \mathbb{Z}(-d)$
(see [Reference NikulinNik79, Corollary 1.10.2, 1.13.3] or [Reference HuybrechtsHuy16, Theorem 14.1.5]) and, therefore,
$A_{2}(-1)\oplus \mathbb{Z}(d/3)\simeq U\oplus \mathbb{Z}(-d)$
(see [Reference NikulinNik79, Corollary 1.10.2, 1.13.3] or [Reference HuybrechtsHuy16, Theorem 14.1.5]) and, therefore,
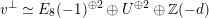 $v^{\bot }\simeq E_{8}(-1)^{\oplus 2}\oplus U^{\oplus 2}\oplus \mathbb{Z}(-d)$
, which is the transcendental lattice of a very general polarized K3 surface of degree
$v^{\bot }\simeq E_{8}(-1)^{\oplus 2}\oplus U^{\oplus 2}\oplus \mathbb{Z}(-d)$
, which is the transcendental lattice of a very general polarized K3 surface of degree
![]() $d$
. A similar argument holds for
$d$
. A similar argument holds for
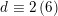 $d\equiv 2\,(6)$
.
$d\equiv 2\,(6)$
.
Proposition 2.10. With the above notation one has
 $$\begin{eqnarray}D_{\text{K3}}=\mathop{\bigcup }_{(\ast \ast )}D_{d}\quad \text{and}\quad D_{\text{K3'}}=\mathop{\bigcup }_{(\ast \ast ^{\prime })}D_{d},\end{eqnarray}$$
$$\begin{eqnarray}D_{\text{K3}}=\mathop{\bigcup }_{(\ast \ast )}D_{d}\quad \text{and}\quad D_{\text{K3'}}=\mathop{\bigcup }_{(\ast \ast ^{\prime })}D_{d},\end{eqnarray}$$
where
![]() $d$
runs through all
$d$
runs through all
![]() $d$
satisfying
$d$
satisfying
![]() $(\ast \ast )$
respectively
$(\ast \ast )$
respectively
![]() $(\ast \ast ^{\prime })$
.
$(\ast \ast ^{\prime })$
.
Proof. The first equality is due to Addington and Thomas [Reference Addington and ThomasAT14, Theorem 3.1]. Indeed, they show that
![]() $x\in D_{d}$
with
$x\in D_{d}$
with
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast$
) if and only if there exists a hyperbolic plane
$\ast \ast$
) if and only if there exists a hyperbolic plane
![]() $U\subset \widetilde{\unicode[STIX]{x1D6EC}}$
which is of type
$U\subset \widetilde{\unicode[STIX]{x1D6EC}}$
which is of type
![]() $(1,1)$
with respect to
$(1,1)$
with respect to
![]() $x$
. The latter is in turn equivalent to
$x$
. The latter is in turn equivalent to
 $x\in D_{\text{K3}}$
, see Lemma 2.6.Footnote
4
$x\in D_{\text{K3}}$
, see Lemma 2.6.Footnote
4
Maybe surprisingly, the second assertion is easier to prove. We include the elementary argument. Due to Corollary 2.8 we know
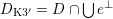 $D_{\text{K3'}}=D\cap \bigcup e^{\bot }$
with
$D_{\text{K3'}}=D\cap \bigcup e^{\bot }$
with
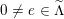 $0\neq e\in \widetilde{\unicode[STIX]{x1D6EC}}$
isotropic. So for one inclusion one has to show that each
$0\neq e\in \widetilde{\unicode[STIX]{x1D6EC}}$
isotropic. So for one inclusion one has to show that each
![]() $D\cap e^{\bot }$
is of the form
$D\cap e^{\bot }$
is of the form
![]() $D_{d}$
with
$D_{d}$
with
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
). Decompose
$\ast \ast ^{\prime }$
). Decompose
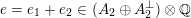 $e=e_{1}+e_{2}\in (A_{2}\oplus A_{2}^{\bot })\otimes \mathbb{Q}$
. Let then
$e=e_{1}+e_{2}\in (A_{2}\oplus A_{2}^{\bot })\otimes \mathbb{Q}$
. Let then
![]() $v\in A_{2}^{\bot }$
such that
$v\in A_{2}^{\bot }$
such that
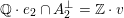 $\mathbb{Q}\cdot e_{2}\cap A_{2}^{\bot }=\mathbb{Z}\cdot v$
and define
$\mathbb{Q}\cdot e_{2}\cap A_{2}^{\bot }=\mathbb{Z}\cdot v$
and define
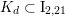 $K_{d}\subset \text{I}_{2,21}$
as the saturation of the sublattice spanned by
$K_{d}\subset \text{I}_{2,21}$
as the saturation of the sublattice spanned by
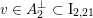 $v\in A_{2}^{\bot }\subset \text{I}_{2,21}$
and
$v\in A_{2}^{\bot }\subset \text{I}_{2,21}$
and
![]() $h$
. We have to show that the discriminant
$h$
. We have to show that the discriminant
![]() $d$
of
$d$
of
![]() $K_{d}$
satisfies (
$K_{d}$
satisfies (
![]() $\ast \ast ^{\prime }$
).
$\ast \ast ^{\prime }$
).
Assume first that
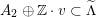 $A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{\unicode[STIX]{x1D6EC}}$
is primitive. Then
$A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{\unicode[STIX]{x1D6EC}}$
is primitive. Then
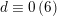 $d\equiv 0\,(6)$
and
$d\equiv 0\,(6)$
and
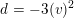 $d=-3(v)^{2}$
, see § 2.2. As
$d=-3(v)^{2}$
, see § 2.2. As
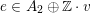 $e\in A_{2}\oplus \mathbb{Z}\cdot v$
in this case, the quadratic equation
$e\in A_{2}\oplus \mathbb{Z}\cdot v$
in this case, the quadratic equation
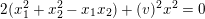 $2(x_{1}^{2}+x_{2}^{2}-x_{1}x_{2})+(v)^{2}x^{2}=0$
admits an integral solution. However, it is a classical result that
$2(x_{1}^{2}+x_{2}^{2}-x_{1}x_{2})+(v)^{2}x^{2}=0$
admits an integral solution. However, it is a classical result that
 $$\begin{eqnarray}2n=(w)^{2}\end{eqnarray}$$
$$\begin{eqnarray}2n=(w)^{2}\end{eqnarray}$$
for some
![]() $w\in A_{2}$
if and only if
$w\in A_{2}$
if and only if
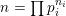 $n=\prod p_{i}^{n_{i}}$
with
$n=\prod p_{i}^{n_{i}}$
with
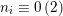 $n_{i}\equiv 0\,(2)$
for all
$n_{i}\equiv 0\,(2)$
for all
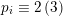 $p_{i}\equiv 2\,(3)$
, see [Reference KneserKne02].Footnote
5
But clearly this holds for
$p_{i}\equiv 2\,(3)$
, see [Reference KneserKne02].Footnote
5
But clearly this holds for
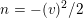 $n=-(v)^{2}/2$
if and only if
$n=-(v)^{2}/2$
if and only if
![]() $d=6n$
satisfies (
$d=6n$
satisfies (
![]() $\ast \ast ^{\prime }$
).
$\ast \ast ^{\prime }$
).
Next assume that
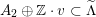 $A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{\unicode[STIX]{x1D6EC}}$
has index three in its saturation. Hence,
$A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{\unicode[STIX]{x1D6EC}}$
has index three in its saturation. Hence,
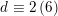 $d\equiv 2\,(6)$
and
$d\equiv 2\,(6)$
and
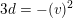 $3d=-(v)^{2}$
. Then argue as before, but now with the isotropic vector
$3d=-(v)^{2}$
. Then argue as before, but now with the isotropic vector
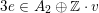 $3e\in A_{2}\oplus \mathbb{Z}\cdot v$
and with
$3e\in A_{2}\oplus \mathbb{Z}\cdot v$
and with
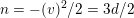 $n=-(v)^{2}/2=3d/2$
.
$n=-(v)^{2}/2=3d/2$
.
Running the argument backwards proves the reverse inclusion. ◻
So, in particular, although
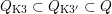 $Q_{\text{K3}}\subset Q_{\text{K3'}}\subset Q$
are countable unions of codimension-two subsets, their restrictions
$Q_{\text{K3}}\subset Q_{\text{K3'}}\subset Q$
are countable unions of codimension-two subsets, their restrictions
 $D_{\text{K3}}\subset D_{\text{K3'}}\subset D$
to
$D_{\text{K3}}\subset D_{\text{K3'}}\subset D$
to
![]() $D$
are countable unions of codimension-one subsets. For
$D$
are countable unions of codimension-one subsets. For
![]() $D_{\text{K3'}}$
we have observed this already in § 2.5.
$D_{\text{K3'}}$
we have observed this already in § 2.5.
Remark 2.11. As mentioned in [Reference Addington and ThomasAT14, Reference AddingtonAdd16] and explained to me by Addington, condition (
![]() $\ast \ast$
) is in fact equivalent to the existence of a primitive
$\ast \ast$
) is in fact equivalent to the existence of a primitive
![]() $w\in A_{2}$
with
$w\in A_{2}$
with
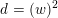 $d=(w)^{2}$
. And, as has become clear in the above proof, condition (
$d=(w)^{2}$
. And, as has become clear in the above proof, condition (
![]() $\ast \ast ^{\prime }$
) is equivalent to the existence of a (not necessarily primitive)
$\ast \ast ^{\prime }$
) is equivalent to the existence of a (not necessarily primitive)
![]() $w\in A_{2}$
with
$w\in A_{2}$
with
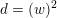 $d=(w)^{2}$
.
$d=(w)^{2}$
.
The first values of
![]() $d>6$
that satisfy the various conditions are
$d>6$
that satisfy the various conditions are

Example 2.12. For certain
![]() $d$
the condition that the period
$d$
the condition that the period
![]() $x\in D$
of a cubic
$x\in D$
of a cubic
![]() $X$
is contained in
$X$
is contained in
![]() $D_{d}$
has a geometric interpretation, see [Reference HassettHas00, § 4]. For example,
$D_{d}$
has a geometric interpretation, see [Reference HassettHas00, § 4]. For example,
![]() $x\in D_{8}$
if and only if
$x\in D_{8}$
if and only if
![]() $X$
contains a plane
$X$
contains a plane
![]() $\mathbb{P}^{2}\subset X$
, or if
$\mathbb{P}^{2}\subset X$
, or if
![]() $X$
is a Pfaffian cubic, then
$X$
is a Pfaffian cubic, then
 $x\in D_{14}$
.
$x\in D_{14}$
.
Let
![]() $x\in D_{d}$
with
$x\in D_{d}$
with
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
). Then there exists a twisted K3 surface
$\ast \ast ^{\prime }$
). Then there exists a twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
such that the Hodge structure defined by
$(S,\unicode[STIX]{x1D6FC})$
such that the Hodge structure defined by
![]() $x$
is Hodge isometric to
$x$
is Hodge isometric to
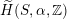 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
. If
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
. If
![]() $x\in D_{d}$
is a very general point of
$x\in D_{d}$
is a very general point of
![]() $D_{d}$
, then
$D_{d}$
, then
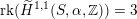 $\operatorname{rk}(\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z}))=3$
and
$\operatorname{rk}(\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z}))=3$
and
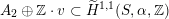 $A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
is of index one or three, respectively.
$A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
is of index one or three, respectively.
Lemma 2.13. For the order of the Brauer class
![]() $\unicode[STIX]{x1D6FC}$
one has
$\unicode[STIX]{x1D6FC}$
one has
 $$\begin{eqnarray}\text{ord}(\unicode[STIX]{x1D6FC})^{2}\mid d.\end{eqnarray}$$
$$\begin{eqnarray}\text{ord}(\unicode[STIX]{x1D6FC})^{2}\mid d.\end{eqnarray}$$
Proof. Let
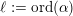 $\ell :=\text{ord}(\unicode[STIX]{x1D6FC})$
. As proved in [Reference HuybrechtsHuy05], the transcendental lattice
$\ell :=\text{ord}(\unicode[STIX]{x1D6FC})$
. As proved in [Reference HuybrechtsHuy05], the transcendental lattice
![]() $T(S,\unicode[STIX]{x1D6FC})$
is isometric to the kernel of the natural map
$T(S,\unicode[STIX]{x1D6FC})$
is isometric to the kernel of the natural map  defined by
defined by
![]() $\unicode[STIX]{x1D6FC}$
. Hence,
$\unicode[STIX]{x1D6FC}$
. Hence,
 $$\begin{eqnarray}|\text{disc}(T(S,\unicode[STIX]{x1D6FC}))|=|\text{disc}(T(S))|\cdot \text{ord}(\unicode[STIX]{x1D6FC})^{2}.\end{eqnarray}$$
$$\begin{eqnarray}|\text{disc}(T(S,\unicode[STIX]{x1D6FC}))|=|\text{disc}(T(S))|\cdot \text{ord}(\unicode[STIX]{x1D6FC})^{2}.\end{eqnarray}$$
On the other hand,
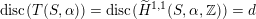 $\text{disc}(T(S,\unicode[STIX]{x1D6FC}))=\text{disc}(\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z}))=d$
by Lemma 2.2.◻
$\text{disc}(T(S,\unicode[STIX]{x1D6FC}))=\text{disc}(\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z}))=d$
by Lemma 2.2.◻
Clearly,
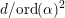 $d/\text{ord}(\unicode[STIX]{x1D6FC})^{2}$
still satisfies (
$d/\text{ord}(\unicode[STIX]{x1D6FC})^{2}$
still satisfies (
![]() $\ast \ast ^{\prime }$
) (but not necessarily (
$\ast \ast ^{\prime }$
) (but not necessarily (
![]() $\ast \ast$
)). As mentioned earlier, any
$\ast \ast$
)). As mentioned earlier, any
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
) can be written (not always uniquely) as
$\ast \ast ^{\prime }$
) can be written (not always uniquely) as
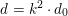 $d=k^{2}\cdot d_{0}$
with
$d=k^{2}\cdot d_{0}$
with
![]() $d_{0}$
satisfying (
$d_{0}$
satisfying (
![]() $\ast \ast$
). For any such factorization one can indeed choose
$\ast \ast$
). For any such factorization one can indeed choose
![]() $(S,\unicode[STIX]{x1D6FC})$
as above such that in addition
$(S,\unicode[STIX]{x1D6FC})$
as above such that in addition
 $\text{ord}(\unicode[STIX]{x1D6FC})=k$
. In particular, then the untwisted Hodge structure
$\text{ord}(\unicode[STIX]{x1D6FC})=k$
. In particular, then the untwisted Hodge structure
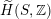 $\widetilde{H}(S,\mathbb{Z})$
defines a point in
$\widetilde{H}(S,\mathbb{Z})$
defines a point in
![]() $D_{d_{0}}$
. This is best seen by starting with
$D_{d_{0}}$
. This is best seen by starting with
![]() $D_{d_{0}}$
and then choosing globally a B-field which for the very general
$D_{d_{0}}$
and then choosing globally a B-field which for the very general
![]() $S$
in
$S$
in
![]() $D_{d_{0}}$
defines a Brauer class of order
$D_{d_{0}}$
defines a Brauer class of order
![]() $k$
.
$k$
.
2.7
We will need to say a few things about the spherical locus
![]() $D_{\text{sph}}$
, as this will be crucial later.
$D_{\text{sph}}$
, as this will be crucial later.
Example 2.14. (i) Consider
![]() $d=24$
which obviously satisfies (
$d=24$
which obviously satisfies (
![]() $\ast \ast ^{\prime }$
) but not (
$\ast \ast ^{\prime }$
) but not (
![]() $\ast \ast$
), i.e.
$\ast \ast$
), i.e.
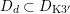 $D_{d}\subset D_{\text{K3'}}$
but
$D_{d}\subset D_{\text{K3'}}$
but
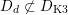 $D_{d}\not \subset D_{\text{K3}}$
. Also,
$D_{d}\not \subset D_{\text{K3}}$
. Also,
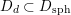 $D_{d}\subset D_{\text{sph}}$
. Indeed, if
$D_{d}\subset D_{\text{sph}}$
. Indeed, if
![]() $v$
generates
$v$
generates
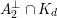 $A_{2}^{\bot }\cap K_{d}$
, then
$A_{2}^{\bot }\cap K_{d}$
, then
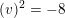 $(v)^{2}=-8$
and hence there exists
$(v)^{2}=-8$
and hence there exists
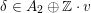 $\unicode[STIX]{x1D6FF}\in A_{2}\oplus \mathbb{Z}\cdot v$
with
$\unicode[STIX]{x1D6FF}\in A_{2}\oplus \mathbb{Z}\cdot v$
with
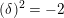 $(\unicode[STIX]{x1D6FF})^{2}=-2$
, e.g.
$(\unicode[STIX]{x1D6FF})^{2}=-2$
, e.g.
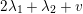 $2\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+v$
. So, as mentioned before, one has a proper inclusion
$2\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+v$
. So, as mentioned before, one has a proper inclusion
 $$\begin{eqnarray}D_{\text{K}3}\subsetneq D_{\text{K3'}}\cap D_{\text{sph}}.\end{eqnarray}$$
$$\begin{eqnarray}D_{\text{K}3}\subsetneq D_{\text{K3'}}\cap D_{\text{sph}}.\end{eqnarray}$$
(ii) Consider
![]() $d=12$
which does not satisfy (
$d=12$
which does not satisfy (
![]() $\ast \ast ^{\prime }$
). So,
$\ast \ast ^{\prime }$
). So,
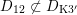 $D_{12}\not \subset D_{\text{K3'}}$
, but
$D_{12}\not \subset D_{\text{K3'}}$
, but
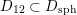 $D_{12}\subset D_{\text{sph}}$
. Indeed, in this case
$D_{12}\subset D_{\text{sph}}$
. Indeed, in this case
![]() $v$
in (2.4) satisfies
$v$
in (2.4) satisfies
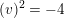 $(v)^{2}=-4$
and, therefore,
$(v)^{2}=-4$
and, therefore,
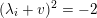 $(\unicode[STIX]{x1D706}_{i}+v)^{2}=-2$
. Hence,
$(\unicode[STIX]{x1D706}_{i}+v)^{2}=-2$
. Hence,
 $$\begin{eqnarray}D_{\text{sph}}\not \subset D_{\text{K3'}}.\end{eqnarray}$$
$$\begin{eqnarray}D_{\text{sph}}\not \subset D_{\text{K3'}}.\end{eqnarray}$$
It would be interesting to find a numerical condition (
![]() $\dagger$
) such that
$\dagger$
) such that
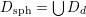 $D_{\text{sph}}=\bigcup D_{d}$
with the union over all
$D_{\text{sph}}=\bigcup D_{d}$
with the union over all
![]() $d$
satisfying (
$d$
satisfying (
![]() $\dagger$
). The best we have to offer at this time is the following proposition.
$\dagger$
). The best we have to offer at this time is the following proposition.
Proposition 2.15. Assume
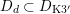 $D_{d}\subset D_{\text{K3'}}$
and
$D_{d}\subset D_{\text{K3'}}$
and
![]() $9|d$
. Then
$9|d$
. Then
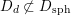 $D_{d}\not \subset D_{\text{sph}}$
.
$D_{d}\not \subset D_{\text{sph}}$
.
Proof. Consider a fixed
![]() $K_{d}$
and the corresponding generator
$K_{d}$
and the corresponding generator
![]() $v$
of
$v$
of
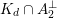 $K_{d}\cap A_{2}^{\bot }$
. As
$K_{d}\cap A_{2}^{\bot }$
. As
![]() $9|d$
, clearly
$9|d$
, clearly
 $d\equiv 0\,(6)$
and so
$d\equiv 0\,(6)$
and so
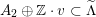 $A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{\unicode[STIX]{x1D6EC}}$
is primitive. If there were a
$A_{2}\oplus \mathbb{Z}\cdot v\subset \widetilde{\unicode[STIX]{x1D6EC}}$
is primitive. If there were a
![]() $(-2)$
-class
$(-2)$
-class
![]() $\unicode[STIX]{x1D6FF}\in \widetilde{\unicode[STIX]{x1D6EC}}$
with
$\unicode[STIX]{x1D6FF}\in \widetilde{\unicode[STIX]{x1D6EC}}$
with
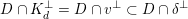 $D\cap K_{d}^{\bot }=D\cap v^{\bot }\subset D\cap \unicode[STIX]{x1D6FF}^{\bot }$
, then
$D\cap K_{d}^{\bot }=D\cap v^{\bot }\subset D\cap \unicode[STIX]{x1D6FF}^{\bot }$
, then
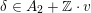 $\unicode[STIX]{x1D6FF}\in A_{2}+\mathbb{Z}\cdot v$
and so
$\unicode[STIX]{x1D6FF}\in A_{2}+\mathbb{Z}\cdot v$
and so
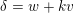 $\unicode[STIX]{x1D6FF}=w+kv$
for some
$\unicode[STIX]{x1D6FF}=w+kv$
for some
![]() $w\in A_{2}$
and
$w\in A_{2}$
and
![]() $k\in \mathbb{Z}$
. But then
$k\in \mathbb{Z}$
. But then
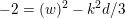 $-2=(w)^{2}-k^{2}d/3$
. However, if
$-2=(w)^{2}-k^{2}d/3$
. However, if
![]() $9|d$
, then
$9|d$
, then
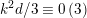 $k^{2}d/3\equiv 0\,(3)$
and hence
$k^{2}d/3\equiv 0\,(3)$
and hence
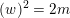 $(w)^{2}=2m$
with
$(w)^{2}=2m$
with
 $m\equiv 2\,(3)$
, which contradicts (2.7).◻
$m\equiv 2\,(3)$
, which contradicts (2.7).◻
The following immediate consequence is crucial for the proof of Theorem 1.2, see § 6.1.
Corollary 2.16. The locus of twisted K3 periods
![]() $D_{\text{K3'}}$
contains infinitely many hyperplane sections
$D_{\text{K3'}}$
contains infinitely many hyperplane sections
![]() $D_{d}$
with
$D_{d}$
with
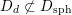 $D_{d}\not \subset D_{\text{sph}}$
.
$D_{d}\not \subset D_{\text{sph}}$
.
2.8
In [Reference HuybrechtsHuy05] we have shown that points in
![]() $Q$
can be understood as periods of generalized K3 surfaces. It is useful to distinguish three types.Footnote
6
$Q$
can be understood as periods of generalized K3 surfaces. It is useful to distinguish three types.Footnote
6
-
(i) Periods of ordinary K3 surfaces are parametrized by
 $Q_{\text{K3}}$
. Up to the action of
$Q_{\text{K3}}$
. Up to the action of
 $\text{O}(\widetilde{\unicode[STIX]{x1D6EC}})$
, the set of these periods is the intersection of
$\text{O}(\widetilde{\unicode[STIX]{x1D6EC}})$
, the set of these periods is the intersection of
 $Q$
with the linear codimension-two subspace
$Q$
with the linear codimension-two subspace
 $\mathbb{P}(\unicode[STIX]{x1D6EC}\otimes \mathbb{C})\subset \mathbb{P}(\widetilde{\unicode[STIX]{x1D6EC}}\otimes \mathbb{C})$
.
$\mathbb{P}(\unicode[STIX]{x1D6EC}\otimes \mathbb{C})\subset \mathbb{P}(\widetilde{\unicode[STIX]{x1D6EC}}\otimes \mathbb{C})$
. -
(ii) More generally, one can consider periods of the form
 $\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E}$
, where
$\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E}$
, where
 $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
is an ordinary period and
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
is an ordinary period and
 $B\in \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
(but not necessarily
$B\in \unicode[STIX]{x1D6EC}\otimes \mathbb{C}$
(but not necessarily
 $B\in \unicode[STIX]{x1D6EC}\otimes \mathbb{Q}$
). Up to the action of
$B\in \unicode[STIX]{x1D6EC}\otimes \mathbb{Q}$
). Up to the action of
 $\text{O}(\widetilde{\unicode[STIX]{x1D6EC}})$
, these periods are parametrized by the intersection of
$\text{O}(\widetilde{\unicode[STIX]{x1D6EC}})$
, these periods are parametrized by the intersection of
 $Q$
with the linear subspace of codimension one
$Q$
with the linear subspace of codimension one
 $\mathbb{P}((\unicode[STIX]{x1D6EC}\oplus \mathbb{Z}\cdot f)\otimes \mathbb{C})\subset \mathbb{P}(\widetilde{\unicode[STIX]{x1D6EC}}\otimes \mathbb{C})$
. Here,
$\mathbb{P}((\unicode[STIX]{x1D6EC}\oplus \mathbb{Z}\cdot f)\otimes \mathbb{C})\subset \mathbb{P}(\widetilde{\unicode[STIX]{x1D6EC}}\otimes \mathbb{C})$
. Here,
 $f$
is viewed as the generator of
$f$
is viewed as the generator of
 $H^{4}$
. Note that, by definition,
$H^{4}$
. Note that, by definition,
 $Q_{\text{K3'}}$
is the subset of periods for which
$Q_{\text{K3'}}$
is the subset of periods for which
 $B$
can be chosen in
$B$
can be chosen in
 $\unicode[STIX]{x1D6EC}\otimes \mathbb{Q}$
.
$\unicode[STIX]{x1D6EC}\otimes \mathbb{Q}$
. -
(iii) Periods of the form
 $\exp (B+i\unicode[STIX]{x1D714})=1+(B+i\unicode[STIX]{x1D714})+((B^{2}-\unicode[STIX]{x1D714}^{2})/2+(B.\unicode[STIX]{x1D714})i)$
are geometrically interpreted as periods associated with complexified symplectic forms. Here, the first and third summands are considered in
$\exp (B+i\unicode[STIX]{x1D714})=1+(B+i\unicode[STIX]{x1D714})+((B^{2}-\unicode[STIX]{x1D714}^{2})/2+(B.\unicode[STIX]{x1D714})i)$
are geometrically interpreted as periods associated with complexified symplectic forms. Here, the first and third summands are considered in
 $U\simeq H^{0}\oplus H^{4}$
. Periods of this type are parametrized by an open dense subset of
$U\simeq H^{0}\oplus H^{4}$
. Periods of this type are parametrized by an open dense subset of
 $Q$
.
$Q$
.
In particular, all cubic periods parametrized by
![]() $D\subset Q$
should have an interpretation in terms of these three types. This has been discussed above for type (i) and has led to consider the intersection
$D\subset Q$
should have an interpretation in terms of these three types. This has been discussed above for type (i) and has led to consider the intersection
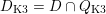 $D_{\text{K3}}=D\cap Q_{\text{K3}}$
. For type (ii) with
$D_{\text{K3}}=D\cap Q_{\text{K3}}$
. For type (ii) with
![]() $B$
rational the intersection with the cubic period domain gives
$B$
rational the intersection with the cubic period domain gives
![]() $D_{\text{K3'}}$
. It is now natural to ask whether the remaining periods, so the periods in
$D_{\text{K3'}}$
. It is now natural to ask whether the remaining periods, so the periods in
 $D\setminus D_{\text{K3'}}$
, are of type (ii) with
$D\setminus D_{\text{K3'}}$
, are of type (ii) with
![]() $B$
not rational or rather of type (iii), i.e. related to complexified symplectic forms. It is the latter, as shown by the following proposition.
$B$
not rational or rather of type (iii), i.e. related to complexified symplectic forms. It is the latter, as shown by the following proposition.
Proposition 2.17. The Hodge structure of a cubic period
![]() $x\in D$
is Hodge isometric to the Hodge structure of a twisted projective K3 surface
$x\in D$
is Hodge isometric to the Hodge structure of a twisted projective K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
, i.e.
$(S,\unicode[STIX]{x1D6FC})$
, i.e.
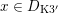 $x\in D_{\text{K3'}}$
, or to the Hodge structure associated with
$x\in D_{\text{K3'}}$
, or to the Hodge structure associated with
 $\exp (B+i\unicode[STIX]{x1D714})$
. Furthermore, if the Hodge structure of
$\exp (B+i\unicode[STIX]{x1D714})$
. Furthermore, if the Hodge structure of
![]() $x$
is Hodge isometric to a Hodge structure of the type
$x$
is Hodge isometric to a Hodge structure of the type
 $\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E}$
, then
$\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E}$
, then
![]() $B$
can be chosen rational.
$B$
can be chosen rational.
Proof. One first observes that, analogously to Lemma 2.6(ii), a period
![]() $x\in Q$
is of the type (ii) if and only if the integral
$x\in Q$
is of the type (ii) if and only if the integral
![]() $(1,1)$
part of the Hodge structure associated with
$(1,1)$
part of the Hodge structure associated with
![]() $x$
contains an isotropic direction. Indeed, if
$x$
contains an isotropic direction. Indeed, if
![]() $x$
is of type (ii), i.e. of the form
$x$
is of type (ii), i.e. of the form
 $\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E}$
, then
$\unicode[STIX]{x1D70E}+B\wedge \unicode[STIX]{x1D70E}$
, then
![]() $H^{4}$
provides an isotropic direction of type
$H^{4}$
provides an isotropic direction of type
![]() $(1,1)$
. For the converse use that any isotropic direction can be completed to a hyperbolic plane
$(1,1)$
. For the converse use that any isotropic direction can be completed to a hyperbolic plane
![]() $U$
as a direct summand of
$U$
as a direct summand of
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
. Now regard
$\widetilde{\unicode[STIX]{x1D6EC}}$
. Now regard
![]() $U$
as
$U$
as
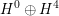 $H^{0}\oplus H^{4}$
with
$H^{0}\oplus H^{4}$
with
![]() $H^{4}$
as the given isotropic direction, which is of type
$H^{4}$
as the given isotropic direction, which is of type
![]() $(1,1)$
. Hence,
$(1,1)$
. Hence,
![]() $x$
is indeed of type (ii).
$x$
is indeed of type (ii).
Now let
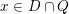 $x\in D\cap Q$
be of type (ii). It is enough to show that then
$x\in D\cap Q$
be of type (ii). It is enough to show that then
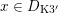 $x\in D_{\text{K3'}}$
. The integral
$x\in D_{\text{K3'}}$
. The integral
![]() $(1,1)$
-part of the Hodge structure associated with
$(1,1)$
-part of the Hodge structure associated with
![]() $x$
contains
$x$
contains
![]() $A_{2}$
and an isotropic direction, say
$A_{2}$
and an isotropic direction, say
![]() $\mathbb{Z}\cdot f$
. Then conclude by Proposition 2.8.◻
$\mathbb{Z}\cdot f$
. Then conclude by Proposition 2.8.◻
Note that both subsets,
 $$\begin{eqnarray}D\subset Q\quad \text{and}\quad Q_{\text{K3}}\subset Q,\end{eqnarray}$$
$$\begin{eqnarray}D\subset Q\quad \text{and}\quad Q_{\text{K3}}\subset Q,\end{eqnarray}$$
are of codimension two and that they both parametrize periods that can be interpreted in complex geometric terms (in contrast to the ‘symplectic periods’ of the form
 $\exp (B+i\unicode[STIX]{x1D714})$
). In fact, periods in
$\exp (B+i\unicode[STIX]{x1D714})$
). In fact, periods in
![]() $D$
are even algebro-geometric in the sense that essentially all of them are associated with cubic fourfolds
$D$
are even algebro-geometric in the sense that essentially all of them are associated with cubic fourfolds
![]() $X\subset \mathbb{P}^{5}$
, whereas most K3 surfaces are of course not projective.
$X\subset \mathbb{P}^{5}$
, whereas most K3 surfaces are of course not projective.
In categorical language one would want to interpret the inclusion
![]() $D\subset Q$
for points in the complement of
$D\subset Q$
for points in the complement of
![]() $D_{\text{K3'}}$
as saying that the cubic K3 category
$D_{\text{K3'}}$
as saying that the cubic K3 category
![]() ${\mathcal{A}}_{X}$
associated with the cubic fourfold
${\mathcal{A}}_{X}$
associated with the cubic fourfold
![]() $X\subset \mathbb{P}^{5}$
corresponding to
$X\subset \mathbb{P}^{5}$
corresponding to
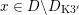 $x\in D\setminus D_{\text{K3'}}$
is equivalent to the derived Fukaya category
$x\in D\setminus D_{\text{K3'}}$
is equivalent to the derived Fukaya category
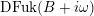 $\text{D}\text{Fuk}(B+i\unicode[STIX]{x1D714})$
associated with a complexified symplectic form
$\text{D}\text{Fuk}(B+i\unicode[STIX]{x1D714})$
associated with a complexified symplectic form
![]() $B+i\unicode[STIX]{x1D714}$
. Deciding which symplectic structures occur here is in principle possible, but establishing an equivalence
$B+i\unicode[STIX]{x1D714}$
. Deciding which symplectic structures occur here is in principle possible, but establishing an equivalence
 $$\begin{eqnarray}{\mathcal{A}}_{X}\simeq \text{D}\text{Fuk}(B+i\unicode[STIX]{x1D714})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{X}\simeq \text{D}\text{Fuk}(B+i\unicode[STIX]{x1D714})\end{eqnarray}$$
will be difficult even in special cases.
The categorical interpretation of
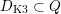 $D_{\text{K3}}\subset Q$
is the content of [Reference Addington and ThomasAT14], where it is proved that at least for a Zariski open dense set of periods
$D_{\text{K3}}\subset Q$
is the content of [Reference Addington and ThomasAT14], where it is proved that at least for a Zariski open dense set of periods
 $x\in D_{\text{K3}}$
the cubic K3 category
$x\in D_{\text{K3}}$
the cubic K3 category
![]() ${\mathcal{A}}_{X}$
really is equivalent to
${\mathcal{A}}_{X}$
really is equivalent to
![]() $\text{D}^{\text{b}}(S)$
of the K3 surface
$\text{D}^{\text{b}}(S)$
of the K3 surface
![]() $S$
realizing the Hodge structure associated with
$S$
realizing the Hodge structure associated with
![]() $x$
. This paper deals with the categorical interpretation of
$x$
. This paper deals with the categorical interpretation of
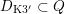 $D_{\text{K3'}}\subset Q$
.
$D_{\text{K3'}}\subset Q$
.
Remark 2.18. The period domain
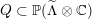 $Q\subset \mathbb{P}(\widetilde{\unicode[STIX]{x1D6EC}}\otimes \mathbb{C})$
contains
$Q\subset \mathbb{P}(\widetilde{\unicode[STIX]{x1D6EC}}\otimes \mathbb{C})$
contains
![]() $D\subset Q$
as a codimension two subset, but it also contains natural codimension one subspaces. For example, for a K3 surface
$D\subset Q$
as a codimension two subset, but it also contains natural codimension one subspaces. For example, for a K3 surface
![]() $S$
and the Mukai vector
$S$
and the Mukai vector
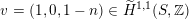 $v=(1,0,1-n)\in \widetilde{H}^{1,1}(S,\mathbb{Z})$
the hyperplane section
$v=(1,0,1-n)\in \widetilde{H}^{1,1}(S,\mathbb{Z})$
the hyperplane section
![]() $Q\cap v^{\bot }$
can be seen as the period domain for deformations of the Hilbert scheme
$Q\cap v^{\bot }$
can be seen as the period domain for deformations of the Hilbert scheme
![]() $S^{[n]}$
. Note, however, that from a categorical point of view the situation is different, even when one restricts to the codimension-two part that corresponds to projective deformations of the Hilbert scheme. In [Reference Markman and MehrotraMM15] it is explained how the non-full subcategory
$S^{[n]}$
. Note, however, that from a categorical point of view the situation is different, even when one restricts to the codimension-two part that corresponds to projective deformations of the Hilbert scheme. In [Reference Markman and MehrotraMM15] it is explained how the non-full subcategory
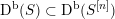 $\text{D}^{\text{b}}(S)\subset \text{D}^{\text{b}}(S^{[n]})$
deforms sideways.
$\text{D}^{\text{b}}(S)\subset \text{D}^{\text{b}}(S^{[n]})$
deforms sideways.
3 The cubic K3 category
Let
![]() $X\subset \mathbb{P}^{5}$
be a smooth cubic hypersurface. The cubic K3 category associated with
$X\subset \mathbb{P}^{5}$
be a smooth cubic hypersurface. The cubic K3 category associated with
![]() $X$
is the category
$X$
is the category
 $$\begin{eqnarray}{\mathcal{A}}_{X}:=\langle {\mathcal{O}}_{X},{\mathcal{O}}_{X}(1),{\mathcal{O}}_{X}(2)\rangle ^{\bot }:=\{E\in \text{D}^{\text{b}}(X)\mid \operatorname{Hom}({\mathcal{O}}_{X}(i),E[\ast ])=0\text{ for }i=0,1,2\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{X}:=\langle {\mathcal{O}}_{X},{\mathcal{O}}_{X}(1),{\mathcal{O}}_{X}(2)\rangle ^{\bot }:=\{E\in \text{D}^{\text{b}}(X)\mid \operatorname{Hom}({\mathcal{O}}_{X}(i),E[\ast ])=0\text{ for }i=0,1,2\}.\end{eqnarray}$$
The category has first been studied by Kuznetsov in [Reference KuznetsovKuz10], see also the more recent [Reference KuznetsovKuz15]. It behaves in many respects like the derived category
![]() $\text{D}^{\text{b}}(S)$
of a K3 surface
$\text{D}^{\text{b}}(S)$
of a K3 surface
![]() $S$
. In particular, the double shift
$S$
. In particular, the double shift  defines a Serre functor of
defines a Serre functor of
![]() ${\mathcal{A}}_{X}$
(see [Reference KuznetsovKuz09], [Reference KuznetsovKuz04, Corollary 4.3] and [Reference Kuznetsov and MarkushevichKM09, Remark 4.2]) and the dimension of Hochschild homology of
${\mathcal{A}}_{X}$
(see [Reference KuznetsovKuz09], [Reference KuznetsovKuz04, Corollary 4.3] and [Reference Kuznetsov and MarkushevichKM09, Remark 4.2]) and the dimension of Hochschild homology of
![]() ${\mathcal{A}}_{X}$
and of
${\mathcal{A}}_{X}$
and of
![]() $\text{D}^{\text{b}}(S)$
coincide, see [Reference KuznetsovKuz10, Reference KuznetsovKuz09].
$\text{D}^{\text{b}}(S)$
coincide, see [Reference KuznetsovKuz10, Reference KuznetsovKuz09].
Example 3.1. Due to the work of Kuznetsov [Reference KuznetsovKuz10, Reference KuznetsovKuz06], certain cubic K3 categories
![]() ${\mathcal{A}}_{X}$
are known to be equivalent to bounded derived categories
${\mathcal{A}}_{X}$
are known to be equivalent to bounded derived categories
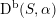 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
of twisted K3 surfaces
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
of twisted K3 surfaces
![]() $(S,\unicode[STIX]{x1D6FC})$
. For example, if the period
$(S,\unicode[STIX]{x1D6FC})$
. For example, if the period
![]() $x\in D$
of a cubic
$x\in D$
of a cubic
![]() $X$
is contained in
$X$
is contained in
![]() $D_{8}$
, then
$D_{8}$
, then
![]() $X$
contains a plane and for generic choices there exists a twisted K3 surface
$X$
contains a plane and for generic choices there exists a twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
with
$(S,\unicode[STIX]{x1D6FC})$
with
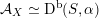 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
. Similarly, if
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
. Similarly, if
![]() $X$
is a Pfaffian cubic and hence
$X$
is a Pfaffian cubic and hence
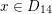 $x\in D_{14}$
, then
$x\in D_{14}$
, then
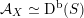 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
for the K3 surface
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
for the K3 surface
![]() $S$
naturally associated with the Pfaffian
$S$
naturally associated with the Pfaffian
![]() $X$
.
$X$
.
Remark 3.2. Despite the almost perfect analogy between the cubic K3 category
![]() ${\mathcal{A}}_{X}$
and the derived category
${\mathcal{A}}_{X}$
and the derived category
![]() $\text{D}^{\text{b}}(S)$
of K3 surfaces, certain fundamental issues are more difficult for
$\text{D}^{\text{b}}(S)$
of K3 surfaces, certain fundamental issues are more difficult for
![]() ${\mathcal{A}}_{X}$
. For example, to the best of my knowledge no
${\mathcal{A}}_{X}$
. For example, to the best of my knowledge no
![]() ${\mathcal{A}}_{X}$
, which is not equivalent to the derived category
${\mathcal{A}}_{X}$
, which is not equivalent to the derived category
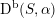 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
of some twisted K3 surface
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
of some twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
, has yet been endowed with a bounded t-structure, let alone a stability condition. See [Reference TodaTod14, Reference TodaTod13] for a discussion of special stability conditions on certain
$(S,\unicode[STIX]{x1D6FC})$
, has yet been endowed with a bounded t-structure, let alone a stability condition. See [Reference TodaTod14, Reference TodaTod13] for a discussion of special stability conditions on certain
![]() ${\mathcal{A}}_{X}$
of the form
${\mathcal{A}}_{X}$
of the form
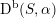 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
.
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
.
The semi-orthogonal decomposition
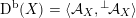 $\text{D}^{\text{b}}(X)=\langle {\mathcal{A}}_{X},^{\bot }\!{\mathcal{A}}_{X}\rangle$
with
$\text{D}^{\text{b}}(X)=\langle {\mathcal{A}}_{X},^{\bot }\!{\mathcal{A}}_{X}\rangle$
with
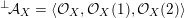 $^{\bot }\!{\mathcal{A}}_{X}=\langle {\mathcal{O}}_{X},{\mathcal{O}}_{X}(1),{\mathcal{O}}_{X}(2)\rangle$
comes with the full embedding
$^{\bot }\!{\mathcal{A}}_{X}=\langle {\mathcal{O}}_{X},{\mathcal{O}}_{X}(1),{\mathcal{O}}_{X}(2)\rangle$
comes with the full embedding  (which is often suppressed in the notation) and the left and right adjoint functors
(which is often suppressed in the notation) and the left and right adjoint functors  see [Reference KuznetsovKuz09, § 3] for a survey.
see [Reference KuznetsovKuz09, § 3] for a survey.
3.1
For a K3 surface
![]() $S$
the Mukai lattice
$S$
the Mukai lattice
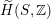 $\widetilde{H}(S,\mathbb{Z})$
is endowed with the Hodge structure determined by
$\widetilde{H}(S,\mathbb{Z})$
is endowed with the Hodge structure determined by
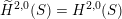 $\widetilde{H}^{2,0}(S)=H^{2,0}(S)$
and by requiring
$\widetilde{H}^{2,0}(S)=H^{2,0}(S)$
and by requiring
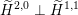 $\widetilde{H}^{2,0}\bot \widetilde{H}^{1,1}$
. Using the natural isomorphism
$\widetilde{H}^{2,0}\bot \widetilde{H}^{1,1}$
. Using the natural isomorphism
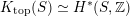 $K_{\text{top}}(S)\simeq H^{\ast }(S,\mathbb{Z})$
this Hodge structure can also be regarded as a Hodge structure on
$K_{\text{top}}(S)\simeq H^{\ast }(S,\mathbb{Z})$
this Hodge structure can also be regarded as a Hodge structure on
 $K_{\text{top}}(S)$
.
$K_{\text{top}}(S)$
.
In [Reference Addington and ThomasAT14] Addington and Thomas introduce a similar Hodge structure associated with the category
![]() ${\mathcal{A}}_{X}$
, defined on
${\mathcal{A}}_{X}$
, defined on
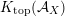 $K_{\text{top}}({\mathcal{A}}_{X})$
and denoted by
$K_{\text{top}}({\mathcal{A}}_{X})$
and denoted by
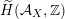 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
. Here,
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
. Here,
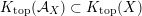 $K_{\text{top}}({\mathcal{A}}_{X})\subset K_{\text{top}}(X)$
is the orthogonal complement of
$K_{\text{top}}({\mathcal{A}}_{X})\subset K_{\text{top}}(X)$
is the orthogonal complement of
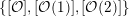 $\{[{\mathcal{O}}],[{\mathcal{O}}(1)],[{\mathcal{O}}(2)]\}$
with respect to the pairing
$\{[{\mathcal{O}}],[{\mathcal{O}}(1)],[{\mathcal{O}}(2)]\}$
with respect to the pairing
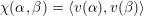 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=\langle v(\unicode[STIX]{x1D6FC}),v(\unicode[STIX]{x1D6FD})\rangle$
defined in terms of the Mukai vector
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=\langle v(\unicode[STIX]{x1D6FC}),v(\unicode[STIX]{x1D6FD})\rangle$
defined in terms of the Mukai vector  and the Mukai pairing on
and the Mukai pairing on
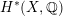 $H^{\ast }(X,\mathbb{Q})$
. It is not difficult to see that one has in fact a semi-orthogonal direct sum decomposition
$H^{\ast }(X,\mathbb{Q})$
. It is not difficult to see that one has in fact a semi-orthogonal direct sum decomposition
 $$\begin{eqnarray}K_{\text{top}}(X)=K_{\text{top}}({\mathcal{A}}_{X})\oplus \langle [{\mathcal{O}}_{X}],[{\mathcal{O}}_{X}(1)],[{\mathcal{O}}_{X}(2)]\rangle .\end{eqnarray}$$
$$\begin{eqnarray}K_{\text{top}}(X)=K_{\text{top}}({\mathcal{A}}_{X})\oplus \langle [{\mathcal{O}}_{X}],[{\mathcal{O}}_{X}(1)],[{\mathcal{O}}_{X}(2)]\rangle .\end{eqnarray}$$
As
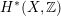 $H^{\ast }(X,\mathbb{Z})$
is torsion free,
$H^{\ast }(X,\mathbb{Z})$
is torsion free,
 $K_{\text{top}}(X)$
and
$K_{\text{top}}(X)$
and
 $$\begin{eqnarray}\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}):=K_{\text{top}}({\mathcal{A}}_{X})\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}):=K_{\text{top}}({\mathcal{A}}_{X})\end{eqnarray}$$
are as well. The Hodge structure is then defined by
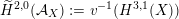 $\widetilde{H}^{2,0}({\mathcal{A}}_{X}):=v^{-1}(H^{3,1}(X))$
and the condition
$\widetilde{H}^{2,0}({\mathcal{A}}_{X}):=v^{-1}(H^{3,1}(X))$
and the condition
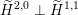 $\widetilde{H}^{2,0}\bot \widetilde{H}^{1,1}$
. Furthermore,
$\widetilde{H}^{2,0}\bot \widetilde{H}^{1,1}$
. Furthermore,
![]() $N({\mathcal{A}}_{X})$
and the transcendental lattice
$N({\mathcal{A}}_{X})$
and the transcendental lattice
![]() $T({\mathcal{A}}_{X})$
of
$T({\mathcal{A}}_{X})$
of
![]() ${\mathcal{A}}_{X}$
are introduced in terms of this Hodge structure as
${\mathcal{A}}_{X}$
are introduced in terms of this Hodge structure as
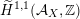 $\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
and its orthogonal complement
$\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
and its orthogonal complement
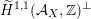 $\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})^{\bot }$
, respectively. As a lattice
$\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})^{\bot }$
, respectively. As a lattice
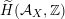 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
is independent of
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
is independent of
![]() $X$
and by [Reference Addington and ThomasAT14] any equivalence
$X$
and by [Reference Addington and ThomasAT14] any equivalence
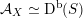 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
(see Example 3.1) induces a Hodge isometry
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
(see Example 3.1) induces a Hodge isometry
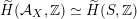 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}(S,\mathbb{Z})$
(cf. Proposition 3.3). In particular,
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}(S,\mathbb{Z})$
(cf. Proposition 3.3). In particular,
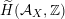 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
for all smooth cubics is abstractly isomorphic to
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
for all smooth cubics is abstractly isomorphic to
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
.
$\widetilde{\unicode[STIX]{x1D6EC}}$
.
As explained in [Reference Addington and ThomasAT14, Proposition 2.3], the classes
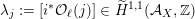 $\unicode[STIX]{x1D706}_{j}:=[i^{\ast }{\mathcal{O}}_{\ell }(j)]\in \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
, for a line
$\unicode[STIX]{x1D706}_{j}:=[i^{\ast }{\mathcal{O}}_{\ell }(j)]\in \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
, for a line
![]() $\ell \subset X$
and
$\ell \subset X$
and
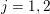 $j=1,2$
, can be viewed as the standard generators of a lattice
$j=1,2$
, can be viewed as the standard generators of a lattice
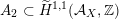 $A_{2}\subset \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
. Moreover, the Mukai vector
$A_{2}\subset \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
. Moreover, the Mukai vector  induces an isometry (up to sign)
induces an isometry (up to sign)

In particular, any marking  induces a marking
induces a marking  and further a marking
and further a marking

Conversely, any marking (3.1) inducing the standard identification  yields a marking
yields a marking  In this sense, (an open set of) points
In this sense, (an open set of) points
![]() $x\in D$
will be considered as periods of cubic K3 categories
$x\in D$
will be considered as periods of cubic K3 categories
![]() ${\mathcal{A}}_{X}$
via their Hodge structures
${\mathcal{A}}_{X}$
via their Hodge structures
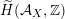 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
.
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
.
Note that the positive directions of
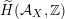 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
come with a natural orientation, given by the real and imaginary parts of
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
come with a natural orientation, given by the real and imaginary parts of
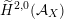 $\widetilde{H}^{2,0}({\mathcal{A}}_{X})$
and the oriented basis
$\widetilde{H}^{2,0}({\mathcal{A}}_{X})$
and the oriented basis
![]() $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$
of
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$
of
 $A_{2}\subset \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
.
$A_{2}\subset \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
.
3.2
As we are also interested in equivalences  we collect a few relevant facts dealing with the topological K-theory of twisted K3 surfaces
we collect a few relevant facts dealing with the topological K-theory of twisted K3 surfaces
![]() $(S,\unicode[STIX]{x1D6FC})$
. As it turns out, the topological setting does not require any substantially new arguments. In order to speak of twisted sheaves or bundles, let us fix a class
$(S,\unicode[STIX]{x1D6FC})$
. As it turns out, the topological setting does not require any substantially new arguments. In order to speak of twisted sheaves or bundles, let us fix a class
 $B\in H^{2}(S,\mathbb{Q})$
which under the exponential map
$B\in H^{2}(S,\mathbb{Q})$
which under the exponential map  is mapped to
is mapped to
![]() $\unicode[STIX]{x1D6FC}$
. Next choose a Čech representative
$\unicode[STIX]{x1D6FC}$
. Next choose a Čech representative
![]() $\{B_{ijk}\}$
of
$\{B_{ijk}\}$
of
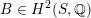 $B\in H^{2}(S,\mathbb{Q})$
and consider the associated Čech representative
$B\in H^{2}(S,\mathbb{Q})$
and consider the associated Čech representative
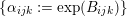 $\{\unicode[STIX]{x1D6FC}_{ijk}:=\exp (B_{ijk})\}$
of
$\{\unicode[STIX]{x1D6FC}_{ijk}:=\exp (B_{ijk})\}$
of
![]() $\unicode[STIX]{x1D6FC}$
. This allows one to speak of
$\unicode[STIX]{x1D6FC}$
. This allows one to speak of
![]() $\{\unicode[STIX]{x1D6FC}_{ijk}\}$
-twisted sheaves and bundles, in the holomorphic as well as in the topological setting.
$\{\unicode[STIX]{x1D6FC}_{ijk}\}$
-twisted sheaves and bundles, in the holomorphic as well as in the topological setting.
As explained in [Reference Huybrechts and StellariHS05, Proposition 1.2], any
![]() $\{\unicode[STIX]{x1D6FC}_{ijk}\}$
-twisted bundle
$\{\unicode[STIX]{x1D6FC}_{ijk}\}$
-twisted bundle
![]() $E$
can be ‘untwisted’ to a bundle
$E$
can be ‘untwisted’ to a bundle
![]() $E_{B}$
by changing the transition functions
$E_{B}$
by changing the transition functions
![]() $\unicode[STIX]{x1D711}_{ij}$
of
$\unicode[STIX]{x1D711}_{ij}$
of
![]() $E$
to
$E$
to
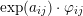 $\exp (a_{ij})\cdot \unicode[STIX]{x1D711}_{ij}$
, where the continuous functions
$\exp (a_{ij})\cdot \unicode[STIX]{x1D711}_{ij}$
, where the continuous functions
![]() $a_{ij}$
satisfy
$a_{ij}$
satisfy
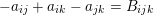 $-a_{ij}+a_{ik}-a_{jk}=B_{ijk}$
. The process can be reversed and so the categories of
$-a_{ij}+a_{ik}-a_{jk}=B_{ijk}$
. The process can be reversed and so the categories of
![]() $\{\unicode[STIX]{x1D6FC}_{ijk}\}$
-twisted topological bundles is equivalent to the category of untwisted topological bundles. In particular,
$\{\unicode[STIX]{x1D6FC}_{ijk}\}$
-twisted topological bundles is equivalent to the category of untwisted topological bundles. In particular,
 $$\begin{eqnarray}K_{\text{top}}(S,\unicode[STIX]{x1D6FC})\simeq K_{\text{top}}(S)\end{eqnarray}$$
$$\begin{eqnarray}K_{\text{top}}(S,\unicode[STIX]{x1D6FC})\simeq K_{\text{top}}(S)\end{eqnarray}$$
which composed with the Mukai vector yields an isomorphism
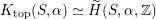 $K_{\text{top}}(S,\unicode[STIX]{x1D6FC})\simeq \widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
that identifies the image of
$K_{\text{top}}(S,\unicode[STIX]{x1D6FC})\simeq \widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
that identifies the image of  with
with
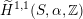 $\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
.
$\widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
.
The next result is the twisted version of the observation by Addington and Thomas mentioned earlier.
Proposition 3.3. Any linear, exact equivalence
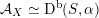 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
induces a Hodge isometry
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
induces a Hodge isometry
 $$\begin{eqnarray}\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z}).\end{eqnarray}$$
Proof. By results due to Orlov in the untwisted case and to Canonaco and Stellari [Reference Canonaco and StellariCS07] in the twisted case, any fully faithful functor  is of Fourier–Mukai type, i.e.
is of Fourier–Mukai type, i.e.
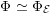 $\unicode[STIX]{x1D6F7}\simeq \unicode[STIX]{x1D6F7}_{{\mathcal{E}}}$
for some
$\unicode[STIX]{x1D6F7}\simeq \unicode[STIX]{x1D6F7}_{{\mathcal{E}}}$
for some
 ${\mathcal{E}}\in \text{D}^{\text{b}}(S\times X,\unicode[STIX]{x1D6FC}^{-1}\boxtimes 1)$
. Therefore,
${\mathcal{E}}\in \text{D}^{\text{b}}(S\times X,\unicode[STIX]{x1D6FC}^{-1}\boxtimes 1)$
. Therefore,
![]() $\unicode[STIX]{x1D6F7}$
induces a homomorphism
$\unicode[STIX]{x1D6F7}$
induces a homomorphism  see [Reference Hille and van den BerghHvdB07, Remark 3.4].
see [Reference Hille and van den BerghHvdB07, Remark 3.4].
If
![]() $\unicode[STIX]{x1D6F7}$
is induced by an equivalence
$\unicode[STIX]{x1D6F7}$
is induced by an equivalence  then
then  is an isomorphism and in fact a Hodge isometry
is an isomorphism and in fact a Hodge isometry  The compatibility with the Hodge structure follows from the twisted Chern character
The compatibility with the Hodge structure follows from the twisted Chern character
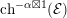 $\text{ch}^{-\unicode[STIX]{x1D6FC}\boxtimes 1}({\mathcal{E}})$
of the Mukai kernel being of Hodge type. See [Reference Huybrechts and StellariHS05, § 1] for the notion of twisted Chern characters. That the quadratic form is respected as well is proved by mimicking the argument for FM-equivalences, see e.g. [Reference HuybrechtsHuy06, § 5.2].
$\text{ch}^{-\unicode[STIX]{x1D6FC}\boxtimes 1}({\mathcal{E}})$
of the Mukai kernel being of Hodge type. See [Reference Huybrechts and StellariHS05, § 1] for the notion of twisted Chern characters. That the quadratic form is respected as well is proved by mimicking the argument for FM-equivalences, see e.g. [Reference HuybrechtsHuy06, § 5.2].
(We are suppressing a number of technical details here. As explained before, the actual realization of the Hodge structure
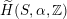 $\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
depends on the choice of a
$\widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
depends on the choice of a
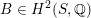 $B\in H^{2}(S,\mathbb{Q})$
lifting
$B\in H^{2}(S,\mathbb{Q})$
lifting
![]() $\unicode[STIX]{x1D6FC}$
. Similarly, the Chern character
$\unicode[STIX]{x1D6FC}$
. Similarly, the Chern character
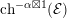 $\text{ch}^{-\unicode[STIX]{x1D6FC}\boxtimes 1}({\mathcal{E}})$
also actually depends on
$\text{ch}^{-\unicode[STIX]{x1D6FC}\boxtimes 1}({\mathcal{E}})$
also actually depends on
![]() $B$
.)◻
$B$
.)◻
3.3
The above result generalizes to FM-equivalences  i.e. to equivalences for which the composition
i.e. to equivalences for which the composition  admits a Fourier–Mukai kernel. It has been conjectured that in fact any linear exact equivalence is a FM-equivalence, but the existing results do not cover our case.
admits a Fourier–Mukai kernel. It has been conjectured that in fact any linear exact equivalence is a FM-equivalence, but the existing results do not cover our case.
Proposition 3.4. Any FM-equivalence  induces a Hodge isometry
induces a Hodge isometry

Proof. The argument is an easy modification of the above. ◻
The following improves upon a result in [Reference Bernardara, Macrì, Mehrotra and StellariBMMS12, Proposition 6.3] where it is shown that for a cubic
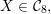 $X\in {\mathcal{C}}_{8},$
so containing a plane, there exist at most finitely many (up to isomorphism) cubics
$X\in {\mathcal{C}}_{8},$
so containing a plane, there exist at most finitely many (up to isomorphism) cubics
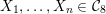 $X_{1},\ldots ,X_{n}\in {\mathcal{C}}_{8}$
with
$X_{1},\ldots ,X_{n}\in {\mathcal{C}}_{8}$
with
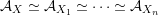 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X_{1}}\simeq \cdots \simeq {\mathcal{A}}_{X_{n}}$
.
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X_{1}}\simeq \cdots \simeq {\mathcal{A}}_{X_{n}}$
.
Corollary 3.5. For any given smooth cubic
![]() $X\subset \mathbb{P}^{5}$
there exist up to isomorphism only finitely many smooth cubics
$X\subset \mathbb{P}^{5}$
there exist up to isomorphism only finitely many smooth cubics
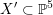 $X^{\prime }\subset \mathbb{P}^{5}$
admitting a FM-equivalence
$X^{\prime }\subset \mathbb{P}^{5}$
admitting a FM-equivalence 
Proof. The proof follows the argument for the analogous statement for K3 surfaces [Reference Bridgeland and MaciociaBM01] closely, but needs a modification at one point that shall be explained.
Due to the proposition, it suffices to prove that up to isomorphism there are only finitely many cubics
![]() $X^{\prime }$
such that there exists a Hodge isometry
$X^{\prime }$
such that there exists a Hodge isometry  Any such Hodge isometry induces a Hodge isometry
Any such Hodge isometry induces a Hodge isometry  and an isometry of lattices
and an isometry of lattices  We may assume
We may assume
 $$\begin{eqnarray}T({\mathcal{A}}_{X})\subset A_{2}^{\bot }\subset \widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\quad \text{and}\quad A_{2}\subset N({\mathcal{A}}_{X})\end{eqnarray}$$
$$\begin{eqnarray}T({\mathcal{A}}_{X})\subset A_{2}^{\bot }\subset \widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\quad \text{and}\quad A_{2}\subset N({\mathcal{A}}_{X})\end{eqnarray}$$
and similarly for
![]() $X^{\prime }$
. Note however that these inclusions need not be respected by
$X^{\prime }$
. Note however that these inclusions need not be respected by
![]() $\unicode[STIX]{x1D711}$
. The orthogonal complement of
$\unicode[STIX]{x1D711}$
. The orthogonal complement of
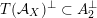 $T({\mathcal{A}}_{X})^{\bot }\subset A_{2}^{\bot }$
is just
$T({\mathcal{A}}_{X})^{\bot }\subset A_{2}^{\bot }$
is just
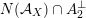 $N({\mathcal{A}}_{X})\cap A_{2}^{\bot }$
and the two inclusions of
$N({\mathcal{A}}_{X})\cap A_{2}^{\bot }$
and the two inclusions of
![]() $A_{2}^{\bot }$
induce two Hodge structures on
$A_{2}^{\bot }$
induce two Hodge structures on
![]() $A_{2}^{\bot }$
. Note that if the Hodge isometry
$A_{2}^{\bot }$
. Note that if the Hodge isometry
![]() $\unicode[STIX]{x1D711}_{T}$
can be extended to a Hodge isometry
$\unicode[STIX]{x1D711}_{T}$
can be extended to a Hodge isometry  which can be interpreted as a Hodge isometry
which can be interpreted as a Hodge isometry
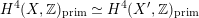 $H^{4}(X,\mathbb{Z})_{\text{prim}}\simeq H^{4}(X^{\prime },\mathbb{Z})_{\text{prim}}$
, then the global Torelli theorem [Reference VoisinVoi86, Reference VoisinVoi08] implies that
$H^{4}(X,\mathbb{Z})_{\text{prim}}\simeq H^{4}(X^{\prime },\mathbb{Z})_{\text{prim}}$
, then the global Torelli theorem [Reference VoisinVoi86, Reference VoisinVoi08] implies that
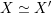 $X\simeq X^{\prime }$
.
$X\simeq X^{\prime }$
.
We first show that the set of isomorphism classes of lattices
![]() $\unicode[STIX]{x1D6E4}$
occurring as
$\unicode[STIX]{x1D6E4}$
occurring as
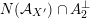 $N({\mathcal{A}}_{X^{\prime }})\cap A_{2}^{\bot }$
is finite. The required lattice theory is slightly more involved than the original in [Reference Bridgeland and MaciociaBM01]. Let us fix two even lattices
$N({\mathcal{A}}_{X^{\prime }})\cap A_{2}^{\bot }$
is finite. The required lattice theory is slightly more involved than the original in [Reference Bridgeland and MaciociaBM01]. Let us fix two even lattices
![]() $\unicode[STIX]{x1D6EC}_{1}$
and
$\unicode[STIX]{x1D6EC}_{1}$
and
![]() $\unicode[STIX]{x1D6EC}$
(in our situation,
$\unicode[STIX]{x1D6EC}$
(in our situation,
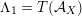 $\unicode[STIX]{x1D6EC}_{1}=T({\mathcal{A}}_{X})$
and
$\unicode[STIX]{x1D6EC}_{1}=T({\mathcal{A}}_{X})$
and
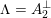 $\unicode[STIX]{x1D6EC}=A_{2}^{\bot }$
). We show that up to isomorphisms there exist only finitely many lattices
$\unicode[STIX]{x1D6EC}=A_{2}^{\bot }$
). We show that up to isomorphisms there exist only finitely many lattices
![]() $\unicode[STIX]{x1D6EC}_{2}$
occurring as the orthogonal complement of some primitive embedding
$\unicode[STIX]{x1D6EC}_{2}$
occurring as the orthogonal complement of some primitive embedding  For unimodular
For unimodular
![]() $\unicode[STIX]{x1D6EC}$
this is standard, but the proof can be tweaked to cover the more general statement. Of course, it suffices to show that only finitely many discriminant forms
$\unicode[STIX]{x1D6EC}$
this is standard, but the proof can be tweaked to cover the more general statement. Of course, it suffices to show that only finitely many discriminant forms
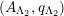 $(A_{\unicode[STIX]{x1D6EC}_{2}},q_{\unicode[STIX]{x1D6EC}_{2}})$
can occur. Now
$(A_{\unicode[STIX]{x1D6EC}_{2}},q_{\unicode[STIX]{x1D6EC}_{2}})$
can occur. Now
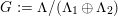 $G:=\unicode[STIX]{x1D6EC}/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
is naturally a finite subgroup of
$G:=\unicode[STIX]{x1D6EC}/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
is naturally a finite subgroup of
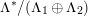 $\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
of index
$\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
of index
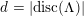 $d=|\text{disc}(\unicode[STIX]{x1D6EC})|$
. The first projection from
$d=|\text{disc}(\unicode[STIX]{x1D6EC})|$
. The first projection from
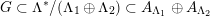 $G\subset \unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})\subset A_{\unicode[STIX]{x1D6EC}_{1}}\oplus A_{\unicode[STIX]{x1D6EC}_{2}}$
defines an isomorphism of
$G\subset \unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})\subset A_{\unicode[STIX]{x1D6EC}_{1}}\oplus A_{\unicode[STIX]{x1D6EC}_{2}}$
defines an isomorphism of
![]() $G$
with a finite subgroup of
$G$
with a finite subgroup of
![]() $A_{\unicode[STIX]{x1D6EC}_{1}}$
. This leaves only finitely many possibilities for the finite groups
$A_{\unicode[STIX]{x1D6EC}_{1}}$
. This leaves only finitely many possibilities for the finite groups
![]() $G$
and
$G$
and
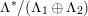 $\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
. Note that
$\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
. Note that
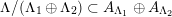 $\unicode[STIX]{x1D6EC}/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})\subset A_{\unicode[STIX]{x1D6EC}_{1}}\oplus A_{\unicode[STIX]{x1D6EC}_{2}}$
is isotropic but not necessarily the bigger
$\unicode[STIX]{x1D6EC}/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})\subset A_{\unicode[STIX]{x1D6EC}_{1}}\oplus A_{\unicode[STIX]{x1D6EC}_{2}}$
is isotropic but not necessarily the bigger
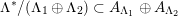 $\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})\subset A_{\unicode[STIX]{x1D6EC}_{1}}\oplus A_{\unicode[STIX]{x1D6EC}_{2}}$
. However, the restriction of the quadratic form to
$\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})\subset A_{\unicode[STIX]{x1D6EC}_{1}}\oplus A_{\unicode[STIX]{x1D6EC}_{2}}$
. However, the restriction of the quadratic form to
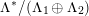 $\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
takes values only in
$\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
takes values only in
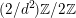 $(2/d^{2})\mathbb{Z}/2\mathbb{Z}$
. For fixed
$(2/d^{2})\mathbb{Z}/2\mathbb{Z}$
. For fixed
 $G\subset A_{\unicode[STIX]{x1D6EC}_{1}}$
the restriction of
$G\subset A_{\unicode[STIX]{x1D6EC}_{1}}$
the restriction of
![]() $q_{\unicode[STIX]{x1D6EC}_{1}}$
to
$q_{\unicode[STIX]{x1D6EC}_{1}}$
to
![]() $G$
can be extended in at most finitely many ways to a quadratic form on
$G$
can be extended in at most finitely many ways to a quadratic form on
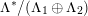 $\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
with values in
$\unicode[STIX]{x1D6EC}^{\ast }/(\unicode[STIX]{x1D6EC}_{1}\oplus \unicode[STIX]{x1D6EC}_{2})$
with values in
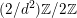 $(2/d^{2})\mathbb{Z}/2\mathbb{Z}$
. Now use the other projection
$(2/d^{2})\mathbb{Z}/2\mathbb{Z}$
. Now use the other projection  to see that there are only finitely many possibilities for the group
to see that there are only finitely many possibilities for the group
![]() $A_{\unicode[STIX]{x1D6EC}_{2}}$
and also for the quadratic form
$A_{\unicode[STIX]{x1D6EC}_{2}}$
and also for the quadratic form
![]() $q_{\unicode[STIX]{x1D6EC}_{2}}$
.
$q_{\unicode[STIX]{x1D6EC}_{2}}$
.
To conclude the proof, we can assume that
![]() $\unicode[STIX]{x1D6E4}$
is fixed. For two Fourier–Mukai partners realizing the fixed
$\unicode[STIX]{x1D6E4}$
is fixed. For two Fourier–Mukai partners realizing the fixed
![]() $\unicode[STIX]{x1D6E4}$
, any Hodge isometry
$\unicode[STIX]{x1D6E4}$
, any Hodge isometry
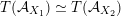 $T({\mathcal{A}}_{X_{1}})\simeq T({\mathcal{A}}_{X_{2}})$
can be extended to a Hodge isometry
$T({\mathcal{A}}_{X_{1}})\simeq T({\mathcal{A}}_{X_{2}})$
can be extended to a Hodge isometry
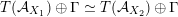 $T({\mathcal{A}}_{X_{1}})\oplus \unicode[STIX]{x1D6E4}\simeq T({\mathcal{A}}_{X_{2}})\oplus \unicode[STIX]{x1D6E4}$
. As the finite index overlattices
$T({\mathcal{A}}_{X_{1}})\oplus \unicode[STIX]{x1D6E4}\simeq T({\mathcal{A}}_{X_{2}})\oplus \unicode[STIX]{x1D6E4}$
. As the finite index overlattices
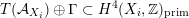 $T({\mathcal{A}}_{X_{i}})\oplus \unicode[STIX]{x1D6E4}\subset H^{4}(X_{i},\mathbb{Z})_{\text{prim}}$
are all contained in
$T({\mathcal{A}}_{X_{i}})\oplus \unicode[STIX]{x1D6E4}\subset H^{4}(X_{i},\mathbb{Z})_{\text{prim}}$
are all contained in
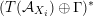 $(T({\mathcal{A}}_{X_{i}})\oplus \unicode[STIX]{x1D6E4})^{\ast }$
, there are only finitely many choices for them, which allows one to reduce to the case that the Hodge isometry extends to a Hodge isometry
$(T({\mathcal{A}}_{X_{i}})\oplus \unicode[STIX]{x1D6E4})^{\ast }$
, there are only finitely many choices for them, which allows one to reduce to the case that the Hodge isometry extends to a Hodge isometry
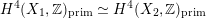 $H^{4}(X_{1},\mathbb{Z})_{\text{prim}}\simeq H^{4}(X_{2},\mathbb{Z})_{\text{prim}}$
.◻
$H^{4}(X_{1},\mathbb{Z})_{\text{prim}}\simeq H^{4}(X_{2},\mathbb{Z})_{\text{prim}}$
.◻
Two very general cubics have FM-equivalent K3 categories only if they are isomorphic.
Corollary 3.6. Let
![]() $X$
be a smooth cubic with
$X$
be a smooth cubic with
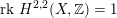 $\operatorname{rk}\,H^{2,2}(X,\mathbb{Z})=1$
. For a smooth cubic
$\operatorname{rk}\,H^{2,2}(X,\mathbb{Z})=1$
. For a smooth cubic
![]() $X^{\prime }$
there exists a FM-equivalence
$X^{\prime }$
there exists a FM-equivalence
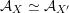 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
if and only if
 $X\simeq X^{\prime }$
.
$X\simeq X^{\prime }$
.
Proof. The assumption implies that
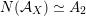 $N({\mathcal{A}}_{X})\simeq A_{2}$
. As any FM-equivalence
$N({\mathcal{A}}_{X})\simeq A_{2}$
. As any FM-equivalence
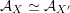 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
induces a Hodge isometry
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
induces a Hodge isometry
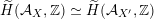 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
, also
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
, also
 $N({\mathcal{A}}_{X^{\prime }})\simeq A_{2}$
. Moreover, the natural inclusions of the transcendental lattices
$N({\mathcal{A}}_{X^{\prime }})\simeq A_{2}$
. Moreover, the natural inclusions of the transcendental lattices
 $T({\mathcal{A}}_{X})\subset A_{2}^{\bot }$
and
$T({\mathcal{A}}_{X})\subset A_{2}^{\bot }$
and
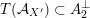 $T({\mathcal{A}}_{X^{\prime }})\subset A_{2}^{\bot }$
are in fact equalities and the induced Hodge isometry
$T({\mathcal{A}}_{X^{\prime }})\subset A_{2}^{\bot }$
are in fact equalities and the induced Hodge isometry
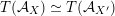 $T({\mathcal{A}}_{X})\simeq T({\mathcal{A}}_{X^{\prime }})$
can therefore be read as a Hodge isometry
$T({\mathcal{A}}_{X})\simeq T({\mathcal{A}}_{X^{\prime }})$
can therefore be read as a Hodge isometry
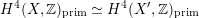 $H^{4}(X,\mathbb{Z})_{\text{prim}}\simeq H^{4}(X^{\prime },\mathbb{Z})_{\text{prim}}$
, which by the global Torelli theorem [Reference VoisinVoi86] implies that
$H^{4}(X,\mathbb{Z})_{\text{prim}}\simeq H^{4}(X^{\prime },\mathbb{Z})_{\text{prim}}$
, which by the global Torelli theorem [Reference VoisinVoi86] implies that
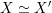 $X\simeq X^{\prime }$
.◻
$X\simeq X^{\prime }$
.◻
Note that, in contrast, very general projective K3 surfaces
![]() $S$
, i.e. such that
$S$
, i.e. such that
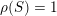 $\unicode[STIX]{x1D70C}(S)=1$
, usually have non-isomorphic FM-partners, see [Reference OguisoOgu02, Reference StellariSte04]. The result may also be compared to the main result of [Reference Bernardara, Macrì, Mehrotra and StellariBMMS12] showing that for all cubic threefolds
$\unicode[STIX]{x1D70C}(S)=1$
, usually have non-isomorphic FM-partners, see [Reference OguisoOgu02, Reference StellariSte04]. The result may also be compared to the main result of [Reference Bernardara, Macrì, Mehrotra and StellariBMMS12] showing that for all cubic threefolds
![]() $Y\subset \mathbb{P}^{4}$
the full subcategory
$Y\subset \mathbb{P}^{4}$
the full subcategory
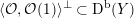 $\langle {\mathcal{O}},{\mathcal{O}}(1)\rangle ^{\bot }\subset \text{D}^{\text{b}}(Y)$
determines
$\langle {\mathcal{O}},{\mathcal{O}}(1)\rangle ^{\bot }\subset \text{D}^{\text{b}}(Y)$
determines
![]() $Y$
.
$Y$
.
Remark 3.7. In principle, it should be possible to count FM-partners of
![]() ${\mathcal{A}}_{X}$
for very general special cubics
${\mathcal{A}}_{X}$
for very general special cubics
![]() $X\in {\mathcal{C}}_{d}$
(i.e.
$X\in {\mathcal{C}}_{d}$
(i.e.
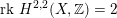 $\operatorname{rk}\,H^{2,2}(X,\mathbb{Z})=2$
). On the level of Hodge theory, this amounts to counting the number of Hodge structures on
$\operatorname{rk}\,H^{2,2}(X,\mathbb{Z})=2$
). On the level of Hodge theory, this amounts to counting the number of Hodge structures on
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
parametrized by
$\widetilde{\unicode[STIX]{x1D6EC}}$
parametrized by
![]() $D$
which are Hodge isometric to
$D$
which are Hodge isometric to
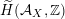 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
up to those that are Hodge isometric on
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
up to those that are Hodge isometric on
![]() $A_{2}^{\bot }$
. The arguments should follow [Reference Hosono, Lian, Oguiso and YauHLOY04, Theorem 1.4], see also [Reference StellariSte04], with the additional problem that
$A_{2}^{\bot }$
. The arguments should follow [Reference Hosono, Lian, Oguiso and YauHLOY04, Theorem 1.4], see also [Reference StellariSte04], with the additional problem that
![]() $A_{2}^{\bot }$
is not unimodular.
$A_{2}^{\bot }$
is not unimodular.
As an immediate consequence of Lemma 2.2 we also note the following.
Corollary 3.8. Let
![]() $X$
be a special cubic defining a very general point in
$X$
be a special cubic defining a very general point in
![]() ${\mathcal{C}}_{d}$
. Then
${\mathcal{C}}_{d}$
. Then
 $$\begin{eqnarray}\operatorname{rk}(\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z}))=3\quad \text{and}\quad \text{disc}(\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z}))=d.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{rk}(\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z}))=3\quad \text{and}\quad \text{disc}(\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z}))=d.\end{eqnarray}$$
Remark 3.9. Suppose
![]() $d$
satisfies (
$d$
satisfies (
![]() $\ast \ast ^{\prime }$
) and is written as
$\ast \ast ^{\prime }$
) and is written as
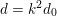 $d=k^{2}d_{0}$
. Then
$d=k^{2}d_{0}$
. Then
![]() $d_{0}$
also satisfies (
$d_{0}$
also satisfies (
![]() $\ast \ast ^{\prime }$
). The most interesting case is when in fact
$\ast \ast ^{\prime }$
). The most interesting case is when in fact
![]() $d_{0}$
satisfies (
$d_{0}$
satisfies (
![]() $\ast \ast$
). Then for very general
$\ast \ast$
). Then for very general
![]() $X\in {\mathcal{C}}_{d}$
, there exists a twisted K3 surface
$X\in {\mathcal{C}}_{d}$
, there exists a twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
with
$(S,\unicode[STIX]{x1D6FC})$
with
![]() $\unicode[STIX]{x1D6FC}$
of order
$\unicode[STIX]{x1D6FC}$
of order
![]() $k$
and such that
$k$
and such that
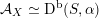 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
, see Lemma 2.13. Moreover, there also exists a cubic
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
, see Lemma 2.13. Moreover, there also exists a cubic
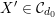 $X^{\prime }\in {\mathcal{C}}_{d_{0}}$
such that
$X^{\prime }\in {\mathcal{C}}_{d_{0}}$
such that
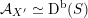 ${\mathcal{A}}_{X^{\prime }}\simeq \text{D}^{\text{b}}(S)$
. So, a K3 surface
${\mathcal{A}}_{X^{\prime }}\simeq \text{D}^{\text{b}}(S)$
. So, a K3 surface
![]() $S$
of the proper degree, with its various Brauer classes, is often related to more than one smooth cubic
$S$
of the proper degree, with its various Brauer classes, is often related to more than one smooth cubic
![]() $X$
.
$X$
.
3.4
We are interested in the group
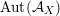 $\operatorname{Aut}({\mathcal{A}}_{X})$
of isomorphism classes of FM-equivalences
$\operatorname{Aut}({\mathcal{A}}_{X})$
of isomorphism classes of FM-equivalences  As any FM-equivalence
As any FM-equivalence
![]() $\unicode[STIX]{x1D6F7}$
induces a Hodge isometry
$\unicode[STIX]{x1D6F7}$
induces a Hodge isometry

there is a natural homomorphism

Here,
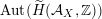 $\operatorname{Aut}(\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}))$
denotes the group of Hodge isometries. We say that
$\operatorname{Aut}(\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}))$
denotes the group of Hodge isometries. We say that
![]() $\unicode[STIX]{x1D6F7}$
is symplectic if the induced action on
$\unicode[STIX]{x1D6F7}$
is symplectic if the induced action on
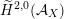 $\widetilde{H}^{2,0}({\mathcal{A}}_{X})$
, or equivalently on
$\widetilde{H}^{2,0}({\mathcal{A}}_{X})$
, or equivalently on
![]() $T({\mathcal{A}}_{X})$
, is the identity. The subgroup of symplectic autoequivalences shall be denoted by
$T({\mathcal{A}}_{X})$
, is the identity. The subgroup of symplectic autoequivalences shall be denoted by
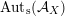 $\operatorname{Aut}_{\text{s}}({\mathcal{A}}_{X})$
. Thus, (3.2) induces
$\operatorname{Aut}_{\text{s}}({\mathcal{A}}_{X})$
. Thus, (3.2) induces

Remark 3.10. By
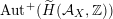 $\operatorname{Aut}^{+}(\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}))$
one denotes the subgroup of Hodge isometries preserving a given orientation of the four positive directions. We expect that
$\operatorname{Aut}^{+}(\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}))$
one denotes the subgroup of Hodge isometries preserving a given orientation of the four positive directions. We expect that
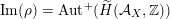 $\text{Im}(\unicode[STIX]{x1D70C})=\operatorname{Aut}^{+}(\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}))$
. This is known if
$\text{Im}(\unicode[STIX]{x1D70C})=\operatorname{Aut}^{+}(\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}))$
. This is known if
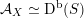 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
, see [Reference Huybrechts, Macrì and StellariHMS09], and one inclusion can be proved for non-special cubics, see Theorem 1.2.
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
, see [Reference Huybrechts, Macrì and StellariHMS09], and one inclusion can be proved for non-special cubics, see Theorem 1.2.
Example 3.11. The most important autoequivalences of K3 categories, responsible for the complexity of the groups
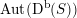 $\operatorname{Aut}(\text{D}^{\text{b}}(S))$
and
$\operatorname{Aut}(\text{D}^{\text{b}}(S))$
and
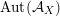 $\operatorname{Aut}({\mathcal{A}}_{X})$
, are spherical twists. Associated with any spherical object
$\operatorname{Aut}({\mathcal{A}}_{X})$
, are spherical twists. Associated with any spherical object
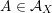 $A\in {\mathcal{A}}_{X}$
, i.e.
$A\in {\mathcal{A}}_{X}$
, i.e.
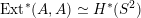 $\operatorname{Ext}^{\ast }(A,A)\simeq H^{\ast }(S^{2})$
, there exists a FM-equivalence
$\operatorname{Ext}^{\ast }(A,A)\simeq H^{\ast }(S^{2})$
, there exists a FM-equivalence

that sends
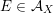 $E\in {\mathcal{A}}_{X}$
to the cone
$E\in {\mathcal{A}}_{X}$
to the cone
![]() $T_{A}(E)$
of the evaluation map
$T_{A}(E)$
of the evaluation map  This is indeed a FM-equivalence: its kernel can be described as the cone of the composition
This is indeed a FM-equivalence: its kernel can be described as the cone of the composition  Here,
Here,
![]() $(\text{id},i)^{\ast }$
is the left adjoint
$(\text{id},i)^{\ast }$
is the left adjoint  and
and
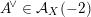 $A\!^{\vee }\in {\mathcal{A}}_{X}(-2)$
is the image of the classical dual of
$A\!^{\vee }\in {\mathcal{A}}_{X}(-2)$
is the image of the classical dual of
![]() $A$
in
$A$
in
![]() $\text{D}^{\text{b}}(X)$
under the left adjoint of
$\text{D}^{\text{b}}(X)$
under the left adjoint of
 ${\mathcal{A}}_{X}(-2)\subset \text{D}^{\text{b}}(X)$
. (With these choices the cone is contained in
${\mathcal{A}}_{X}(-2)\subset \text{D}^{\text{b}}(X)$
. (With these choices the cone is contained in
 ${\mathcal{A}}_{X}(-2)\boxtimes {\mathcal{A}}_{X}$
and would indeed induce a functor
${\mathcal{A}}_{X}(-2)\boxtimes {\mathcal{A}}_{X}$
and would indeed induce a functor  that is trivial on
that is trivial on
![]() $^{\bot }\!{\mathcal{A}}_{X}$
.)
$^{\bot }\!{\mathcal{A}}_{X}$
.)
The action of the spherical twist  on
on
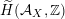 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
is given by the reflection
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
is given by the reflection  where
where
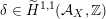 $\unicode[STIX]{x1D6FF}\in \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
is the Mukai vector of
$\unicode[STIX]{x1D6FF}\in \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
is the Mukai vector of
![]() $A$
.
$A$
.
In [Reference KuznetsovKuz04, § 4] Kuznetsov considers the functor

which turns out to be an equivalence satisfying
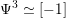 $\unicode[STIX]{x1D6F9}^{3}\simeq [-1]$
. Clearly, by construction
$\unicode[STIX]{x1D6F9}^{3}\simeq [-1]$
. Clearly, by construction
![]() $\unicode[STIX]{x1D6F9}$
is a FM-equivalence. In fact, for the proof that
$\unicode[STIX]{x1D6F9}$
is a FM-equivalence. In fact, for the proof that
![]() ${\mathcal{A}}_{X}$
is a K3 category this functor is crucial. Define
${\mathcal{A}}_{X}$
is a K3 category this functor is crucial. Define
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{0}:=\unicode[STIX]{x1D6F9}[1],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{0}:=\unicode[STIX]{x1D6F9}[1],\end{eqnarray}$$
which satisfies
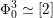 $\unicode[STIX]{x1D6F7}_{0}^{3}\simeq [2]$
.
$\unicode[STIX]{x1D6F7}_{0}^{3}\simeq [2]$
.
Proposition 3.12. The autoequivalence  is symplectic and the induced action
is symplectic and the induced action  corresponds to the element in
corresponds to the element in
![]() $\text{O}(A_{2})$
that is given by the cyclic permutation of the roots
$\text{O}(A_{2})$
that is given by the cyclic permutation of the roots
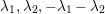 $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},-\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
.
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},-\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
.
Proof. As the action on cohomology is independent of the specific cubic
![]() $X\subset \mathbb{P}^{5}$
, we can assume that the transcendental lattice
$X\subset \mathbb{P}^{5}$
, we can assume that the transcendental lattice
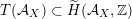 $T({\mathcal{A}}_{X})\subset \widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
is of odd rank. However,
$T({\mathcal{A}}_{X})\subset \widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
is of odd rank. However,
![]() $\pm \text{id}$
are the only Hodge isometries of an irreducible Hodge structure of weight two of K3 type of odd rank, cf. [Reference HuybrechtsHuy16, Corollary 3.3.5], and, as
$\pm \text{id}$
are the only Hodge isometries of an irreducible Hodge structure of weight two of K3 type of odd rank, cf. [Reference HuybrechtsHuy16, Corollary 3.3.5], and, as
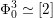 $\unicode[STIX]{x1D6F7}_{0}^{3}\simeq [2]$
acts trivially on
$\unicode[STIX]{x1D6F7}_{0}^{3}\simeq [2]$
acts trivially on
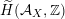 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
, we must have
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
, we must have
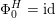 $\unicode[STIX]{x1D6F7}_{0}^{H}=\text{id}$
on
$\unicode[STIX]{x1D6F7}_{0}^{H}=\text{id}$
on
![]() $T({\mathcal{A}}_{X})$
, i.e.
$T({\mathcal{A}}_{X})$
, i.e.
![]() $\unicode[STIX]{x1D6F7}_{0}$
is symplectic.
$\unicode[STIX]{x1D6F7}_{0}$
is symplectic.
If
![]() $X$
is a cubic with
$X$
is a cubic with
 $A_{2}\simeq \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
, then
$A_{2}\simeq \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
, then
![]() $\unicode[STIX]{x1D6F7}_{0}^{H}$
corresponds to an element in
$\unicode[STIX]{x1D6F7}_{0}^{H}$
corresponds to an element in
![]() $\text{O}(A_{2})$
. As
$\text{O}(A_{2})$
. As
![]() $\unicode[STIX]{x1D6F7}_{0}$
is symplectic,
$\unicode[STIX]{x1D6F7}_{0}$
is symplectic,
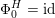 $\unicode[STIX]{x1D6F7}_{0}^{H}=\text{id}$
on
$\unicode[STIX]{x1D6F7}_{0}^{H}=\text{id}$
on
![]() $A_{2}^{\bot }$
and hence
$A_{2}^{\bot }$
and hence
 $\unicode[STIX]{x1D6F7}_{0}^{H}=\text{id}$
on the discriminant group
$\unicode[STIX]{x1D6F7}_{0}^{H}=\text{id}$
on the discriminant group
![]() $A_{A_{2}}$
. Therefore,
$A_{A_{2}}$
. Therefore,
 $\unicode[STIX]{x1D6F7}_{0}^{H}\in \mathfrak{S}_{3}$
, see Remark 2.1. For a cubic
$\unicode[STIX]{x1D6F7}_{0}^{H}\in \mathfrak{S}_{3}$
, see Remark 2.1. For a cubic
![]() $X$
such that
$X$
such that
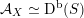 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
, we know that
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S)$
, we know that
![]() $\unicode[STIX]{x1D6F7}_{0}^{H}$
must be orientation preserving by [Reference Huybrechts, Macrì and StellariHMS09] and thus
$\unicode[STIX]{x1D6F7}_{0}^{H}$
must be orientation preserving by [Reference Huybrechts, Macrì and StellariHMS09] and thus
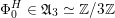 $\unicode[STIX]{x1D6F7}_{0}^{H}\in \mathfrak{A}_{3}\simeq \mathbb{Z}/3\mathbb{Z}$
in general.
$\unicode[STIX]{x1D6F7}_{0}^{H}\in \mathfrak{A}_{3}\simeq \mathbb{Z}/3\mathbb{Z}$
in general.
It remains to show that
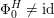 $\unicode[STIX]{x1D6F7}_{0}^{H}\neq \text{id}$
. One way to see this relies on a direct computation. Another possibility is to use the recent result of Bayer and Bridgeland [Reference Bayer and BridgelandBB13] confirming Bridgeland’s conjecture in [Reference BridgelandBri08] in the case of a K3 surface
$\unicode[STIX]{x1D6F7}_{0}^{H}\neq \text{id}$
. One way to see this relies on a direct computation. Another possibility is to use the recent result of Bayer and Bridgeland [Reference Bayer and BridgelandBB13] confirming Bridgeland’s conjecture in [Reference BridgelandBri08] in the case of a K3 surface
![]() $S$
of Picard rank one. More precisely, due to [Reference Bayer and BridgelandBB13, Theorem 1.4] for a K3 surface
$S$
of Picard rank one. More precisely, due to [Reference Bayer and BridgelandBB13, Theorem 1.4] for a K3 surface
![]() $S$
with
$S$
with
 $\unicode[STIX]{x1D70C}(S)=1$
the subgroup of
$\unicode[STIX]{x1D70C}(S)=1$
the subgroup of
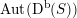 $\operatorname{Aut}(\text{D}^{\text{b}}(S))$
of autoequivalences acting trivially on
$\operatorname{Aut}(\text{D}^{\text{b}}(S))$
of autoequivalences acting trivially on
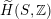 $\widetilde{H}(S,\mathbb{Z})$
is the product of
$\widetilde{H}(S,\mathbb{Z})$
is the product of
![]() $\mathbb{Z}[2]$
and the free group generated by squares of spherical twists
$\mathbb{Z}[2]$
and the free group generated by squares of spherical twists
![]() $T_{E}^{2}$
associated with spherical vector bundles
$T_{E}^{2}$
associated with spherical vector bundles
![]() $E$
on
$E$
on
![]() $S$
. (That this is a reformulation of Bridgeland’s original conjecture for
$S$
. (That this is a reformulation of Bridgeland’s original conjecture for
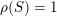 $\unicode[STIX]{x1D70C}(S)=1$
had also been observed by Kawatani [Reference KawataniKaw12].) Hence, if
$\unicode[STIX]{x1D70C}(S)=1$
had also been observed by Kawatani [Reference KawataniKaw12].) Hence, if
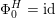 $\unicode[STIX]{x1D6F7}_{0}^{H}=\text{id}$
, then
$\unicode[STIX]{x1D6F7}_{0}^{H}=\text{id}$
, then  but then clearly
but then clearly
![]() $\unicode[STIX]{x1D6F7}_{0}^{3}$
could not be isomorphic to the double shift
$\unicode[STIX]{x1D6F7}_{0}^{3}$
could not be isomorphic to the double shift
![]() $[2]$
.◻
$[2]$
.◻
Corollary 3.13. For every smooth cubic
![]() $X\subset \mathbb{P}^{5}$
the group of symplectic FM-autoequivalences
$X\subset \mathbb{P}^{5}$
the group of symplectic FM-autoequivalences
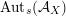 $\operatorname{Aut}_{s}({\mathcal{A}}_{X})$
contains an infinite cyclic group
$\operatorname{Aut}_{s}({\mathcal{A}}_{X})$
contains an infinite cyclic group
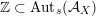 $\mathbb{Z}\subset \operatorname{Aut}_{s}({\mathcal{A}}_{X})$
generated by
$\mathbb{Z}\subset \operatorname{Aut}_{s}({\mathcal{A}}_{X})$
generated by
![]() $\unicode[STIX]{x1D6F7}_{0}$
such that
$\unicode[STIX]{x1D6F7}_{0}$
such that
 $$\begin{eqnarray}\mathbb{Z}\cdot [2]\subset \mathbb{Z}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Z}\cdot [2]\subset \mathbb{Z}\end{eqnarray}$$
is a subgroup of index three and such that the natural map  defines an isomorphism of the quotient
defines an isomorphism of the quotient
 $\mathbb{Z}/\mathbb{Z}\cdot [2]$
with the subgroup
$\mathbb{Z}/\mathbb{Z}\cdot [2]$
with the subgroup
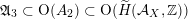 $\mathfrak{A}_{3}\subset \text{O}(A_{2})\subset \text{O}(\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}))$
of alternating permutations of the roots
$\mathfrak{A}_{3}\subset \text{O}(A_{2})\subset \text{O}(\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z}))$
of alternating permutations of the roots
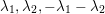 $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},-\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
of
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2},-\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
of
![]() $A_{2}$
.
$A_{2}$
.
Remark 3.14. The subgroup
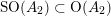 $\text{SO}(A_{2})\subset \text{O}(A_{2})$
of orientation-preserving isometries of
$\text{SO}(A_{2})\subset \text{O}(A_{2})$
of orientation-preserving isometries of
![]() $A_{2}$
is
$A_{2}$
is
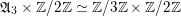 $\mathfrak{A}_{3}\times \mathbb{Z}/2\mathbb{Z}\simeq \mathbb{Z}/3\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
, see Remark 2.1. Its action can be ‘lifted’ to an action on
$\mathfrak{A}_{3}\times \mathbb{Z}/2\mathbb{Z}\simeq \mathbb{Z}/3\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z}$
, see Remark 2.1. Its action can be ‘lifted’ to an action on
![]() ${\mathcal{A}}_{X}$
via the natural extension
${\mathcal{A}}_{X}$
via the natural extension

which can be seen as induced by the universal cover of
 $\text{SO}(A_{2}\otimes \mathbb{R})$
. Clearly, the group in the middle is still infinite cyclic.
$\text{SO}(A_{2}\otimes \mathbb{R})$
. Clearly, the group in the middle is still infinite cyclic.
Inspired by Bridgeland’s conjecture for K3 surfaces in [Reference BridgelandBri08], we state the following conjecture (see [Reference HuybrechtsHuy14, § 5.4] explaining this reformulation).
Conjecture 3.15. There exists an isomorphism
 $$\begin{eqnarray}\operatorname{Aut}_{\text{s}}({\mathcal{A}}_{X})\simeq \unicode[STIX]{x1D70B}_{1}^{\text{st}}[P_{0}/\text{O}].\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Aut}_{\text{s}}({\mathcal{A}}_{X})\simeq \unicode[STIX]{x1D70B}_{1}^{\text{st}}[P_{0}/\text{O}].\end{eqnarray}$$
Here,
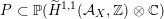 $P\subset \mathbb{P}(\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})\otimes \mathbb{C})$
is the period domain defined analogously to
$P\subset \mathbb{P}(\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})\otimes \mathbb{C})$
is the period domain defined analogously to
![]() $D$
and
$D$
and
![]() $Q$
in § 2.3 and
$Q$
in § 2.3 and
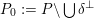 $P_{0}:=P\setminus \bigcup \unicode[STIX]{x1D6FF}^{\bot }$
, with the union over all
$P_{0}:=P\setminus \bigcup \unicode[STIX]{x1D6FF}^{\bot }$
, with the union over all
![]() $(-2)$
classes
$(-2)$
classes
 $\unicode[STIX]{x1D6FF}\in \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
. Moreover,
$\unicode[STIX]{x1D6FF}\in \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
. Moreover,
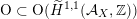 $\text{O}\subset \text{O}(\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z}))$
is the subgroup of all isometries acting trivially on the discriminant. However, contrary to the case of untwisted K3 surfaces we do not even have a natural map between these two groups at the moment.
$\text{O}\subset \text{O}(\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z}))$
is the subgroup of all isometries acting trivially on the discriminant. However, contrary to the case of untwisted K3 surfaces we do not even have a natural map between these two groups at the moment.
3.5
The cubic K3 category
![]() ${\mathcal{A}}_{X}$
can also be described as a category of graded matrix factorizations, see [Reference OrlovOrl09]. More precisely, there exists an exact linear equivalence
${\mathcal{A}}_{X}$
can also be described as a category of graded matrix factorizations, see [Reference OrlovOrl09]. More precisely, there exists an exact linear equivalence
 $$\begin{eqnarray}{\mathcal{A}}_{X}\simeq \text{MF}(W,\mathbb{Z}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{X}\simeq \text{MF}(W,\mathbb{Z}).\end{eqnarray}$$
Here,
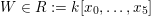 $W\in R:=k[x_{0},\ldots ,x_{5}]$
is a cubic polynomial defining
$W\in R:=k[x_{0},\ldots ,x_{5}]$
is a cubic polynomial defining
![]() $X$
. The objects of
$X$
. The objects of
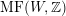 $\text{MF}(W,\mathbb{Z})$
are pairs
$\text{MF}(W,\mathbb{Z})$
are pairs 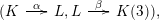 where
where
![]() $K$
and
$K$
and
![]() $L$
are finitely generated, free, graded
$L$
are finitely generated, free, graded
![]() $R$
-modules and
$R$
-modules and
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
are graded
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
are graded
![]() $R$
-module homomorphisms with
$R$
-module homomorphisms with
 $\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}=W\cdot \text{id}=\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D6FD}$
. Recall that
$\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}=W\cdot \text{id}=\unicode[STIX]{x1D6FC}\circ \unicode[STIX]{x1D6FD}$
. Recall that
![]() $K(n)$
for a graded
$K(n)$
for a graded
![]() $R$
-module
$R$
-module
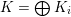 $K=\bigoplus K_{i}$
is the graded module with
$K=\bigoplus K_{i}$
is the graded module with
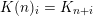 $K(n)_{i}=K_{n+i}$
. Homomorphisms in
$K(n)_{i}=K_{n+i}$
. Homomorphisms in
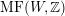 $\text{MF}(W,\mathbb{Z})$
are the obvious ones modulo those that are homotopic to zero (everything
$\text{MF}(W,\mathbb{Z})$
are the obvious ones modulo those that are homotopic to zero (everything
![]() $\mathbb{Z}/2\mathbb{Z}$
-periodic).
$\mathbb{Z}/2\mathbb{Z}$
-periodic).
The shift functor that makes
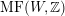 $\text{MF}(W,\mathbb{Z})$
a triangulated category is given by
$\text{MF}(W,\mathbb{Z})$
a triangulated category is given by

Viewing
![]() ${\mathcal{A}}_{X}$
as the category of graded matrix factorizations allows one to describe
${\mathcal{A}}_{X}$
as the category of graded matrix factorizations allows one to describe
![]() $\unicode[STIX]{x1D6F7}_{0}$
in Proposition 3.12 alternatively as follows. Consider the grade shift functor
$\unicode[STIX]{x1D6F7}_{0}$
in Proposition 3.12 alternatively as follows. Consider the grade shift functor

Then, obviously,
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{0}^{3}\simeq [2].\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{0}^{3}\simeq [2].\end{eqnarray}$$
Note that
![]() $\unicode[STIX]{x1D6F7}_{0}$
constructed in this way coincides with the FM-equivalence of Proposition 3.12, see [Reference Ballard, Favero and KatzarkovBFK12, Proposition 5.8].
$\unicode[STIX]{x1D6F7}_{0}$
constructed in this way coincides with the FM-equivalence of Proposition 3.12, see [Reference Ballard, Favero and KatzarkovBFK12, Proposition 5.8].
4 The Fano variety
For the sake of completeness, let us also mention the recent results of Addington [Reference AddingtonAdd16] building upon an observation of Hassett [Reference HassettHas00], see also [Reference Macrì and StellariMS12]. For this consider the Fano variety of lines
![]() $F(X)$
, which, due to work of Beauville and Donagi [Reference Beauville and DonagiBD85], is a four-dimensional irreducible holomorphic symplectic variety deformation equivalent to
$F(X)$
, which, due to work of Beauville and Donagi [Reference Beauville and DonagiBD85], is a four-dimensional irreducible holomorphic symplectic variety deformation equivalent to
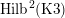 $\text{Hilb}^{2}(\text{K3})$
.
$\text{Hilb}^{2}(\text{K3})$
.
-
∙ For a smooth cubic
 $X$
and its period
$X$
and its period
 $x\in D$
the following two conditions are equivalent:
$x\in D$
the following two conditions are equivalent:-
(i)
 $x\in D_{d}$
such that
$x\in D_{d}$
such that
 $d$
satisfies (
$d$
satisfies (
 $\ast \ast$
);
$\ast \ast$
); -
(ii)
 $F(X)$
is birational to a moduli space of stable sheaves
$F(X)$
is birational to a moduli space of stable sheaves
 $M(v)$
on some K3 surface
$M(v)$
on some K3 surface
 $S$
.
$S$
.
-
-
∙ For a smooth cubic
 $X$
and its period
$X$
and its period
 $x\in D$
the following two conditions are equivalent:
$x\in D$
the following two conditions are equivalent:-
(iii)
 $x\in D_{d}$
such that there exist integers
$x\in D_{d}$
such that there exist integers
 $n$
and
$n$
and
 $a$
with
$a$
with
 $da^{2}=2(n^{2}+n+1)$
;
$da^{2}=2(n^{2}+n+1)$
;
-
(iv)
 $F(X)$
is birational to the Hilbert scheme
$F(X)$
is birational to the Hilbert scheme
 $\text{Hilb}^{2}(S)$
of some K3 surface
$\text{Hilb}^{2}(S)$
of some K3 surface
 $S$
.
$S$
.
-
Obviously, condition (iv) implies condition (ii) or, equivalently and after a moment’s thought, condition (iii) implies condition (i). See [Reference Galkin and ShinderGS14] for a discussion of the relation between rationality of the cubic
![]() $X$
and condition (iii) (or, equivalently, condition (iv)).
$X$
and condition (iii) (or, equivalently, condition (iv)).
Proposition 4.1. For the period
![]() $x$
of a smooth cubic
$x$
of a smooth cubic
![]() $X$
the following two conditions are equivalent:
$X$
the following two conditions are equivalent:
-
(i)
 $x\in D_{d}$
with
$x\in D_{d}$
with
 $d$
satisfying
$d$
satisfying
 $(\ast \ast ^{\prime })$
;
$(\ast \ast ^{\prime })$
; -
(ii)
 $F(X)$
is birational to a moduli space of stable twisted sheaves on some K3 surface.
$F(X)$
is birational to a moduli space of stable twisted sheaves on some K3 surface.
Proof. The argument is an adaptation of Addington’s proof [Reference AddingtonAdd16]. Note however that in the twisted case the transcendental lattice cannot play the same role as in the untwisted case. This was observed in [Reference Huybrechts and StellariHS05], where it was shown that twisted K3 surfaces
![]() $(S,\unicode[STIX]{x1D6FC})$
,
$(S,\unicode[STIX]{x1D6FC})$
,
![]() $(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
with Hodge isometric transcendental lattices,
$(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
with Hodge isometric transcendental lattices,
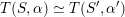 $T(S,\unicode[STIX]{x1D6FC})\simeq T(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
, need not be derived equivalent.
$T(S,\unicode[STIX]{x1D6FC})\simeq T(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
, need not be derived equivalent.
Following Markman [Reference MarkmanMar11] for every hyperkähler manifold
![]() $Y$
deformation equivalent to
$Y$
deformation equivalent to
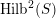 $\text{Hilb}^{2}(S)$
of a K3 surface
$\text{Hilb}^{2}(S)$
of a K3 surface
![]() $S$
there exists a distinguished primitive embedding
$S$
there exists a distinguished primitive embedding
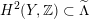 $H^{2}(Y,\mathbb{Z})\subset \widetilde{\unicode[STIX]{x1D6EC}}$
orthogonal to a vector
$H^{2}(Y,\mathbb{Z})\subset \widetilde{\unicode[STIX]{x1D6EC}}$
orthogonal to a vector
![]() $v\in \widetilde{\unicode[STIX]{x1D6EC}}$
with
$v\in \widetilde{\unicode[STIX]{x1D6EC}}$
with
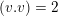 $(v.v)=2$
. The Hodge structure of
$(v.v)=2$
. The Hodge structure of
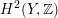 $H^{2}(Y,\mathbb{Z})$
extends to a Hodge structure on
$H^{2}(Y,\mathbb{Z})$
extends to a Hodge structure on
![]() $\widetilde{\unicode[STIX]{x1D6EC}}$
such that
$\widetilde{\unicode[STIX]{x1D6EC}}$
such that
![]() $v$
is of type
$v$
is of type
![]() $(1,1)$
. Moreover,
$(1,1)$
. Moreover,
![]() $Y$
and
$Y$
and
![]() $Y^{\prime }$
are birational if and only if there exists a Hodge isometry
$Y^{\prime }$
are birational if and only if there exists a Hodge isometry
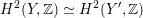 $H^{2}(Y,\mathbb{Z})\simeq H^{2}(Y^{\prime },\mathbb{Z})$
that extends to a Hodge isometry
$H^{2}(Y,\mathbb{Z})\simeq H^{2}(Y^{\prime },\mathbb{Z})$
that extends to a Hodge isometry
![]() $\widetilde{\unicode[STIX]{x1D6EC}}\simeq \widetilde{\unicode[STIX]{x1D6EC}}$
. For a moduli space
$\widetilde{\unicode[STIX]{x1D6EC}}\simeq \widetilde{\unicode[STIX]{x1D6EC}}$
. For a moduli space
![]() $M(v)$
of
$M(v)$
of
![]() $\unicode[STIX]{x1D6FC}$
-twisted stable sheaves on a K3 surface
$\unicode[STIX]{x1D6FC}$
-twisted stable sheaves on a K3 surface
![]() $S$
with primitive
$S$
with primitive
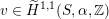 $v\in \widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
such that
$v\in \widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
such that
 $(v.v)=2$
the universal family induces the distinguished embedding (see [Reference YoshiokaYos06, Theorem 3.19])
$(v.v)=2$
the universal family induces the distinguished embedding (see [Reference YoshiokaYos06, Theorem 3.19])

Similarly, and this is the other crucial input, Addington shows in [Reference AddingtonAdd16, Corollary 8] that for the Fano variety of lines the universal family of lines induces this distinguished embedding

Hence,
![]() $F(X)$
and
$F(X)$
and
![]() $M(v)$
are birational if and only if there exists a Hodge isometry
$M(v)$
are birational if and only if there exists a Hodge isometry
 $$\begin{eqnarray}\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})\end{eqnarray}$$
for some twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
that restricts to
$(S,\unicode[STIX]{x1D6FC})$
that restricts to
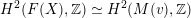 $H^{2}(F(X),\mathbb{Z})\simeq H^{2}(M(v),\mathbb{Z})$
. Due to Proposition 2.10, the existence of a Hodge isometry (4.1) is equivalent to
$H^{2}(F(X),\mathbb{Z})\simeq H^{2}(M(v),\mathbb{Z})$
. Due to Proposition 2.10, the existence of a Hodge isometry (4.1) is equivalent to
![]() $x\in D_{d}$
with
$x\in D_{d}$
with
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
). This proves that condition (ii) implies condition (i).
$\ast \ast ^{\prime }$
). This proves that condition (ii) implies condition (i).
Conversely, for a Hodge isometry (4.1) consider a primitive vector
 $v\in \widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
(the image of
$v\in \widetilde{H}^{1,1}(S,\unicode[STIX]{x1D6FC},\mathbb{Z})$
(the image of
![]() $\unicode[STIX]{x1D706}_{1}$
) in the orthogonal complement of
$\unicode[STIX]{x1D706}_{1}$
) in the orthogonal complement of  and the induced moduli space
and the induced moduli space
![]() $M(v)$
of stable
$M(v)$
of stable
![]() $\unicode[STIX]{x1D6FC}$
-twisted sheaves. Write
$\unicode[STIX]{x1D6FC}$
-twisted sheaves. Write
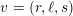 $v=(r,\ell ,s)$
. If
$v=(r,\ell ,s)$
. If
![]() $r\neq 0$
, then for
$r\neq 0$
, then for
![]() $v$
or
$v$
or
![]() $-v$
the moduli space
$-v$
the moduli space
![]() $M(v)$
is indeed non-empty. For
$M(v)$
is indeed non-empty. For
![]() $r=0$
observe that
$r=0$
observe that
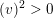 $(v)^{2}>0$
and, hence,
$(v)^{2}>0$
and, hence,
 $(\ell )^{2}>0$
. Again by passing to
$(\ell )^{2}>0$
. Again by passing to
![]() $-v$
if necessary, one can assume that
$-v$
if necessary, one can assume that
 $(\ell .H)>0$
for the polarization
$(\ell .H)>0$
for the polarization
![]() $H$
. That the moduli space is non-empty in this case was shown in [Reference YoshiokaYos09, Corollary 3.5]. (Note that for
$H$
. That the moduli space is non-empty in this case was shown in [Reference YoshiokaYos09, Corollary 3.5]. (Note that for
![]() $r=0$
twisted sheaves can also be considered as untwisted ones.) In [Reference AddingtonAdd16] the case
$r=0$
twisted sheaves can also be considered as untwisted ones.) In [Reference AddingtonAdd16] the case
![]() $r=0$
is dealt with by a reflection associated with
$r=0$
is dealt with by a reflection associated with
![]() ${\mathcal{O}}$
, which does not work in the twisted situation.
${\mathcal{O}}$
, which does not work in the twisted situation.
To conclude, compose the Hodge isometry
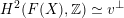 $H^{2}(F(X),\mathbb{Z})\simeq v^{\bot }$
, given by the choice of
$H^{2}(F(X),\mathbb{Z})\simeq v^{\bot }$
, given by the choice of
![]() $v$
, with
$v$
, with
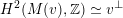 $H^{2}(M(v),\mathbb{Z})\simeq v^{\bot }$
, induced by the universal family as above. By construction, it extends to a Hodge isometry
$H^{2}(M(v),\mathbb{Z})\simeq v^{\bot }$
, induced by the universal family as above. By construction, it extends to a Hodge isometry
![]() $\widetilde{\unicode[STIX]{x1D6EC}}\simeq \widetilde{\unicode[STIX]{x1D6EC}}$
and, therefore,
$\widetilde{\unicode[STIX]{x1D6EC}}\simeq \widetilde{\unicode[STIX]{x1D6EC}}$
and, therefore,
![]() $F(X)$
and
$F(X)$
and
![]() $M(v)$
are birational.◻
$M(v)$
are birational.◻
5 Deformation theory
This section contains two results on the deformation theory of equivalences
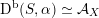 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})\simeq {\mathcal{A}}_{X}$
respectively
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})\simeq {\mathcal{A}}_{X}$
respectively
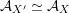 ${\mathcal{A}}_{X^{\prime }}\simeq {\mathcal{A}}_{X}$
that are crucial for the main results of the paper. The techniques have been developed by Toda [Reference TodaTod09], Huybrechts et al. [Reference Huybrechts, Macrì and StellariHMS09], Huybrechts and Thomas [Reference Huybrechts and ThomasHT10], and in the present setting by Addington and Thomas [Reference Addington and ThomasAT14]. We follow [Reference Addington and ThomasAT14] quite closely and often only indicate the additional difficulties and how to deal with them.
${\mathcal{A}}_{X^{\prime }}\simeq {\mathcal{A}}_{X}$
that are crucial for the main results of the paper. The techniques have been developed by Toda [Reference TodaTod09], Huybrechts et al. [Reference Huybrechts, Macrì and StellariHMS09], Huybrechts and Thomas [Reference Huybrechts and ThomasHT10], and in the present setting by Addington and Thomas [Reference Addington and ThomasAT14]. We follow [Reference Addington and ThomasAT14] quite closely and often only indicate the additional difficulties and how to deal with them.
5.1
We first consider FM-equivalences
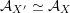 ${\mathcal{A}}_{X^{\prime }}\simeq {\mathcal{A}}_{X}$
between the K3 categories of two cubics
${\mathcal{A}}_{X^{\prime }}\simeq {\mathcal{A}}_{X}$
between the K3 categories of two cubics
![]() $X$
and
$X$
and
![]() $X^{\prime }$
and study under which condition they deform sideways with
$X^{\prime }$
and study under which condition they deform sideways with
![]() $X$
and
$X$
and
![]() $X^{\prime }$
.
$X^{\prime }$
.
Theorem 5.1. Consider two families of smooth cubics  over a smooth base
over a smooth base
![]() $T$
and with distinguished fibres
$T$
and with distinguished fibres
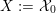 $X:={\mathcal{X}}_{0}$
and
$X:={\mathcal{X}}_{0}$
and
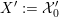 $X^{\prime }:={\mathcal{X}}_{0}^{\prime }$
, respectively. Assume
$X^{\prime }:={\mathcal{X}}_{0}^{\prime }$
, respectively. Assume  is a FM-equivalence inducing a Hodge isometry
is a FM-equivalence inducing a Hodge isometry  that remains a Hodge isometry
that remains a Hodge isometry  under parallel transport for all
under parallel transport for all
![]() $t\in T$
.
$t\in T$
.
Then
![]() $\unicode[STIX]{x1D6F7}$
deforms sideways to FM-equivalences
$\unicode[STIX]{x1D6F7}$
deforms sideways to FM-equivalences  for all
for all
![]() $t$
in a Zariski open neighbourhood
$t$
in a Zariski open neighbourhood
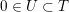 $0\in U\subset T$
.
$0\in U\subset T$
.
Proof. The argument is a variant of the deformation theory in [Reference Addington and ThomasAT14]. We only indicate the necessary modifications.
As, by assumption,
![]() $\unicode[STIX]{x1D6F7}$
is a FM-equivalence, the composition
$\unicode[STIX]{x1D6F7}$
is a FM-equivalence, the composition

is a FM-functor with some kernel
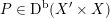 $P\in \text{D}^{\text{b}}(X^{\prime }\times X)$
contained in
$P\in \text{D}^{\text{b}}(X^{\prime }\times X)$
contained in
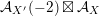 ${\mathcal{A}}_{X^{\prime }}(-2)\boxtimes {\mathcal{A}}_{X}$
. It suffices to show that
${\mathcal{A}}_{X^{\prime }}(-2)\boxtimes {\mathcal{A}}_{X}$
. It suffices to show that
![]() $P$
deforms to
$P$
deforms to
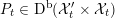 $P_{t}\in \text{D}^{\text{b}}({\mathcal{X}}_{t}^{\prime }\times {\mathcal{X}}_{t})$
for
$P_{t}\in \text{D}^{\text{b}}({\mathcal{X}}_{t}^{\prime }\times {\mathcal{X}}_{t})$
for
![]() $t$
in some open neighbourhood
$t$
in some open neighbourhood
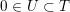 $0\in U\subset T$
, because the conditions for
$0\in U\subset T$
, because the conditions for
![]() $\unicode[STIX]{x1D6F7}_{P_{t}}$
to factorize via a functor
$\unicode[STIX]{x1D6F7}_{P_{t}}$
to factorize via a functor  and for this functor
and for this functor
![]() $\unicode[STIX]{x1D6F7}_{t}$
to define an equivalence are both Zariski open. Indeed,
$\unicode[STIX]{x1D6F7}_{t}$
to define an equivalence are both Zariski open. Indeed,
![]() $\unicode[STIX]{x1D6F7}_{t}$
takes values in
$\unicode[STIX]{x1D6F7}_{t}$
takes values in
![]() ${\mathcal{A}}_{{\mathcal{X}}_{t}}$
if and only if its composition with the projection
${\mathcal{A}}_{{\mathcal{X}}_{t}}$
if and only if its composition with the projection  is trivial. The composition, however, is again of FM-type and the vanishing of a FM-kernel is a Zariski open condition. Similarly, whether
is trivial. The composition, however, is again of FM-type and the vanishing of a FM-kernel is a Zariski open condition. Similarly, whether
![]() $\unicode[STIX]{x1D6F7}_{t}$
is an equivalence can be detected by composing it with its adjoints and then checking whether the natural map to the kernel of the identity is an isomorphism, again a Zariski open condition.
$\unicode[STIX]{x1D6F7}_{t}$
is an equivalence can be detected by composing it with its adjoints and then checking whether the natural map to the kernel of the identity is an isomorphism, again a Zariski open condition.
The crucial part is to understand the first-order deformations, the higher-order obstructions are dealt with by the
![]() $T^{1}$
-lifting property, see [Reference Addington and ThomasAT14, § 7.2] and [Reference Huybrechts, Macrì and StellariHMS09, § 3.2]. First note that by results of Kuznetsov [Reference KuznetsovKuz09] one has
$T^{1}$
-lifting property, see [Reference Addington and ThomasAT14, § 7.2] and [Reference Huybrechts, Macrì and StellariHMS09, § 3.2]. First note that by results of Kuznetsov [Reference KuznetsovKuz09] one has
 $$\begin{eqnarray}\mathit{HH}^{\ast }({\mathcal{A}}_{X^{\prime }})\simeq \operatorname{Ext}_{X^{\prime }\times X}^{\ast }(P,P)\simeq \mathit{HH}^{\ast }({\mathcal{A}}_{X}).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{HH}^{\ast }({\mathcal{A}}_{X^{\prime }})\simeq \operatorname{Ext}_{X^{\prime }\times X}^{\ast }(P,P)\simeq \mathit{HH}^{\ast }({\mathcal{A}}_{X}).\end{eqnarray}$$
This allows one to compare the first-order deformations
 $$\begin{eqnarray}\unicode[STIX]{x1D705}_{X^{\prime }}\in H^{1}(T_{X^{\prime }})\subset \mathit{HH}^{2}(X^{\prime })\quad \text{and}\quad \unicode[STIX]{x1D705}_{X}\in H^{1}(T_{X})\subset \mathit{HH}^{2}(X)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}_{X^{\prime }}\in H^{1}(T_{X^{\prime }})\subset \mathit{HH}^{2}(X^{\prime })\quad \text{and}\quad \unicode[STIX]{x1D705}_{X}\in H^{1}(T_{X})\subset \mathit{HH}^{2}(X)\end{eqnarray}$$
corresponding to some tangent vector
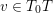 $v\in T_{0}T$
of
$v\in T_{0}T$
of
![]() $T$
at
$T$
at
![]() $0$
. Due to a result of Toda [Reference TodaTod09] (cf. [Reference Addington and ThomasAT14, Theorem 7.1]) it suffices to show that under
$0$
. Due to a result of Toda [Reference TodaTod09] (cf. [Reference Addington and ThomasAT14, Theorem 7.1]) it suffices to show that under  respectively
respectively  the classes
the classes
![]() $\unicode[STIX]{x1D705}_{X^{\prime }}$
and
$\unicode[STIX]{x1D705}_{X^{\prime }}$
and
![]() $\unicode[STIX]{x1D705}_{X}$
are mapped to the same class. For this consider the following diagram (cf. [Reference Addington and ThomasAT14, Proposition 6.2]).
$\unicode[STIX]{x1D705}_{X}$
are mapped to the same class. For this consider the following diagram (cf. [Reference Addington and ThomasAT14, Proposition 6.2]).

By
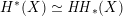 $H^{\ast }(X)\simeq \mathit{HH}_{\ast }(X)$
we denote the HKR isomorphism (see [Reference CăldăraruCăl05]) post-composed with
$H^{\ast }(X)\simeq \mathit{HH}_{\ast }(X)$
we denote the HKR isomorphism (see [Reference CăldăraruCăl05]) post-composed with
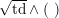 $\sqrt{\text{td}}\wedge (~)$
and so, in particular,
$\sqrt{\text{td}}\wedge (~)$
and so, in particular,
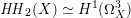 $\mathit{HH}_{2}(X)\simeq H^{1}(\unicode[STIX]{x1D6FA}_{X}^{3})$
with chosen generator
$\mathit{HH}_{2}(X)\simeq H^{1}(\unicode[STIX]{x1D6FA}_{X}^{3})$
with chosen generator
![]() $\unicode[STIX]{x1D70E}_{X}$
. Similarly for
$\unicode[STIX]{x1D70E}_{X}$
. Similarly for
![]() $X^{\prime }$
, where we choose the generator
$X^{\prime }$
, where we choose the generator
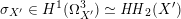 $\unicode[STIX]{x1D70E}_{X^{\prime }}\in H^{1}(\unicode[STIX]{x1D6FA}_{X^{\prime }}^{3})\simeq \mathit{HH}_{2}(X^{\prime })$
such that its image yields
$\unicode[STIX]{x1D70E}_{X^{\prime }}\in H^{1}(\unicode[STIX]{x1D6FA}_{X^{\prime }}^{3})\simeq \mathit{HH}_{2}(X^{\prime })$
such that its image yields
![]() $\unicode[STIX]{x1D70E}_{X}$
. Furthermore,
$\unicode[STIX]{x1D70E}_{X}$
. Furthermore,
![]() $\bar{\unicode[STIX]{x1D705}}_{X}$
denotes the image of
$\bar{\unicode[STIX]{x1D705}}_{X}$
denotes the image of
![]() $\unicode[STIX]{x1D705}_{X}$
under the projection
$\unicode[STIX]{x1D705}_{X}$
under the projection  see [Reference KuznetsovKuz09], and
see [Reference KuznetsovKuz09], and
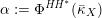 $\unicode[STIX]{x1D6FC}:=\unicode[STIX]{x1D6F7}^{\mathit{HH}^{\ast }}(\bar{\unicode[STIX]{x1D705}}_{X})$
.
$\unicode[STIX]{x1D6FC}:=\unicode[STIX]{x1D6F7}^{\mathit{HH}^{\ast }}(\bar{\unicode[STIX]{x1D705}}_{X})$
.
We aim at showing that (1) is commutative. For this note first that (4) is induced by the FM-transform  and hence commutative due to [Reference Macrì and StellariMS09]. The commutativity of (2) is obvious, as Hochschild (co)homology is respected by equivalences, and commutativity of (3) is the analogue of [Reference Addington and ThomasAT14, Proposition 6.1]. (Recall that
and hence commutative due to [Reference Macrì and StellariMS09]. The commutativity of (2) is obvious, as Hochschild (co)homology is respected by equivalences, and commutativity of (3) is the analogue of [Reference Addington and ThomasAT14, Proposition 6.1]. (Recall that
![]() $\unicode[STIX]{x1D6F7}_{P}$
does not necessarily induce a map
$\unicode[STIX]{x1D6F7}_{P}$
does not necessarily induce a map
![]() $\unicode[STIX]{x1D6F7}_{P}^{\mathit{HH}^{\ast }}$
, as it is not fully faithful.)
$\unicode[STIX]{x1D6F7}_{P}^{\mathit{HH}^{\ast }}$
, as it is not fully faithful.)
The first-order version of the assumption on the Hodge isometry
![]() $\unicode[STIX]{x1D711}$
is the statement that the diagram
$\unicode[STIX]{x1D711}$
is the statement that the diagram

is commutative. Using the ring-module isomorphism
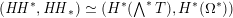 $(\mathit{HH}^{\ast },\mathit{HH}_{\ast })\simeq (H^{\ast }(\bigwedge ^{\ast }T),H^{\ast }(\unicode[STIX]{x1D6FA}^{\ast }))$
for
$(\mathit{HH}^{\ast },\mathit{HH}_{\ast })\simeq (H^{\ast }(\bigwedge ^{\ast }T),H^{\ast }(\unicode[STIX]{x1D6FA}^{\ast }))$
for
![]() $X^{\prime }$
, this implies that the image in
$X^{\prime }$
, this implies that the image in
![]() $H^{\ast }(X^{\prime })$
of
$H^{\ast }(X^{\prime })$
of
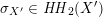 $\unicode[STIX]{x1D70E}_{X^{\prime }}\in \mathit{HH}_{2}(X^{\prime })$
under contraction with
$\unicode[STIX]{x1D70E}_{X^{\prime }}\in \mathit{HH}_{2}(X^{\prime })$
under contraction with
![]() $\unicode[STIX]{x1D705}_{X^{\prime }}$
is mapped to the image of
$\unicode[STIX]{x1D705}_{X^{\prime }}$
is mapped to the image of
![]() $\unicode[STIX]{x1D70E}_{X}$
under contraction with
$\unicode[STIX]{x1D70E}_{X}$
under contraction with
![]() $\unicode[STIX]{x1D705}_{X}$
. As
$\unicode[STIX]{x1D705}_{X}$
. As
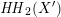 $\mathit{HH}_{2}(X^{\prime })$
is one-dimensional, this shows that also (1) is commutative.
$\mathit{HH}_{2}(X^{\prime })$
is one-dimensional, this shows that also (1) is commutative.
Therefore, in the diagram

the image of
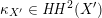 $\unicode[STIX]{x1D705}_{X^{\prime }}\in \mathit{HH}^{2}(X^{\prime })$
under the two compositions
$\unicode[STIX]{x1D705}_{X^{\prime }}\in \mathit{HH}^{2}(X^{\prime })$
under the two compositions  coincide. As the contraction
coincide. As the contraction  is injective (as for K3 surfaces), this implies that the image of
is injective (as for K3 surfaces), this implies that the image of
![]() $\unicode[STIX]{x1D705}_{X^{\prime }}$
under
$\unicode[STIX]{x1D705}_{X^{\prime }}$
under  is indeed
is indeed
![]() $\bar{\unicode[STIX]{x1D705}}_{X}$
as claimed.
$\bar{\unicode[STIX]{x1D705}}_{X}$
as claimed.
As in [Reference Addington and ThomasAT14], the deformation of
![]() $P$
to first and then, by
$P$
to first and then, by
![]() $T^{1}$
-lifting property, to higher order is unique, for
$T^{1}$
-lifting property, to higher order is unique, for
 $\operatorname{Ext}_{X^{\prime }\times X}^{1}(P,P)\simeq \mathit{HH}^{1}({\mathcal{A}}_{X})=0$
by [Reference KuznetsovKuz09].◻
$\operatorname{Ext}_{X^{\prime }\times X}^{1}(P,P)\simeq \mathit{HH}^{1}({\mathcal{A}}_{X})=0$
by [Reference KuznetsovKuz09].◻
5.2
We now come to the more involved situation of equivalences
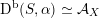 $\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})\simeq {\mathcal{A}}_{X}$
and their deformations.
$\text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})\simeq {\mathcal{A}}_{X}$
and their deformations.
Theorem 5.2. Consider two families  of smooth cubics and K3 surfaces, respectively, over a smooth base
of smooth cubics and K3 surfaces, respectively, over a smooth base
![]() $T$
. Denote the distinguished fibres by
$T$
. Denote the distinguished fibres by
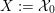 $X:={\mathcal{X}}_{0}$
,
$X:={\mathcal{X}}_{0}$
,
 $S:={\mathcal{S}}_{0}$
and let
$S:={\mathcal{S}}_{0}$
and let
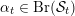 $\unicode[STIX]{x1D6FC}_{t}\in \operatorname{Br}({\mathcal{S}}_{t})$
be a deformation of a Brauer class
$\unicode[STIX]{x1D6FC}_{t}\in \operatorname{Br}({\mathcal{S}}_{t})$
be a deformation of a Brauer class
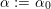 $\unicode[STIX]{x1D6FC}:=\unicode[STIX]{x1D6FC}_{0}$
on
$\unicode[STIX]{x1D6FC}:=\unicode[STIX]{x1D6FC}_{0}$
on
![]() $S$
. Assume
$S$
. Assume  is an equivalence inducing a Hodge isometry
is an equivalence inducing a Hodge isometry  that remains a Hodge isometry
that remains a Hodge isometry  under parallel transport for all
under parallel transport for all
![]() $t\in T$
.
$t\in T$
.
Then
![]() $\unicode[STIX]{x1D6F7}$
deforms sideways to equivalences
$\unicode[STIX]{x1D6F7}$
deforms sideways to equivalences  for all
for all
![]() $t$
in a Zariski open neighbourhood
$t$
in a Zariski open neighbourhood
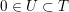 $0\in U\subset T$
.
$0\in U\subset T$
.
Proof. Let us fix representatives
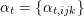 $\unicode[STIX]{x1D6FC}_{t}=\{\unicode[STIX]{x1D6FC}_{t,ijk}\}$
for the Brauer classes on
$\unicode[STIX]{x1D6FC}_{t}=\{\unicode[STIX]{x1D6FC}_{t,ijk}\}$
for the Brauer classes on
![]() ${\mathcal{S}}_{t}$
and a family
${\mathcal{S}}_{t}$
and a family
![]() $E_{t}$
of locally free
$E_{t}$
of locally free
![]() $\{\unicode[STIX]{x1D6FC}_{t,ijk}\}$
-twisted sheaves on the fibres
$\{\unicode[STIX]{x1D6FC}_{t,ijk}\}$
-twisted sheaves on the fibres
![]() ${\mathcal{S}}_{t}$
in a Zariski open neighbourhood of
${\mathcal{S}}_{t}$
in a Zariski open neighbourhood of
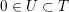 $0\in U\subset T$
.
$0\in U\subset T$
.
The proof now consists of copying [Reference Addington and ThomasAT14, §§ 6, 7]. However, the techniques have to be adapted to the twisted case, which sometimes causes additional problems as certain fundamental issues related to Hochschild (co)homology have not been addressed in the twisted setting. For certain parts we choose ad hoc arguments to reduce to the untwisted case, for others we rely on Reinecke [Reference ReineckeRei14].
Section 6 in [Reference Addington and ThomasAT14] deals with Hochschild (co)homology. For a twisted variety
![]() $(Z,\unicode[STIX]{x1D6FC})$
one defines
$(Z,\unicode[STIX]{x1D6FC})$
one defines
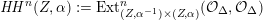 $\mathit{HH}^{n}(Z,\unicode[STIX]{x1D6FC}):=\operatorname{Ext}_{(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})$
. Here,
$\mathit{HH}^{n}(Z,\unicode[STIX]{x1D6FC}):=\operatorname{Ext}_{(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})$
. Here,
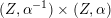 $(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})$
denotes the twisted variety
$(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})$
denotes the twisted variety
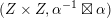 $(Z\times Z,\unicode[STIX]{x1D6FC}^{-1}\boxtimes \unicode[STIX]{x1D6FC})$
. Note that
$(Z\times Z,\unicode[STIX]{x1D6FC}^{-1}\boxtimes \unicode[STIX]{x1D6FC})$
. Note that
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6E5}}$
is indeed an
${\mathcal{O}}_{\unicode[STIX]{x1D6E5}}$
is indeed an
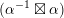 $(\unicode[STIX]{x1D6FC}^{-1}\boxtimes \unicode[STIX]{x1D6FC})$
-twisted sheaf. Similarly, one defines
$(\unicode[STIX]{x1D6FC}^{-1}\boxtimes \unicode[STIX]{x1D6FC})$
-twisted sheaf. Similarly, one defines
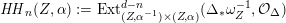 $\mathit{HH}_{n}(Z,\unicode[STIX]{x1D6FC}):=\operatorname{Ext}_{(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})}^{d-n}(\unicode[STIX]{x1D6E5}_{\ast }\unicode[STIX]{x1D714}_{Z}^{-1},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})$
, where
$\mathit{HH}_{n}(Z,\unicode[STIX]{x1D6FC}):=\operatorname{Ext}_{(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})}^{d-n}(\unicode[STIX]{x1D6E5}_{\ast }\unicode[STIX]{x1D714}_{Z}^{-1},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})$
, where
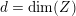 $d=\dim (Z)$
. Composition makes
$d=\dim (Z)$
. Composition makes
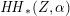 $\mathit{HH}_{\ast }(Z,\unicode[STIX]{x1D6FC})$
a right
$\mathit{HH}_{\ast }(Z,\unicode[STIX]{x1D6FC})$
a right
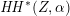 $\mathit{HH}^{\ast }(Z,\unicode[STIX]{x1D6FC})$
-module. Moreover, there are natural isomorphisms
$\mathit{HH}^{\ast }(Z,\unicode[STIX]{x1D6FC})$
-module. Moreover, there are natural isomorphisms
 $$\begin{eqnarray}\displaystyle \mathit{HH}^{n}(Z,\unicode[STIX]{x1D6FC}) & = & \displaystyle \operatorname{Ext}_{(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})\simeq \operatorname{Ext}_{Z}^{n}(\unicode[STIX]{x1D6E5}^{\ast }{\mathcal{O}}_{\unicode[STIX]{x1D6E5}},{\mathcal{O}}_{Z})\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{Ext}_{Z\times Z}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})=\mathit{HH}^{n}(Z)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{HH}^{n}(Z,\unicode[STIX]{x1D6FC}) & = & \displaystyle \operatorname{Ext}_{(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})\simeq \operatorname{Ext}_{Z}^{n}(\unicode[STIX]{x1D6E5}^{\ast }{\mathcal{O}}_{\unicode[STIX]{x1D6E5}},{\mathcal{O}}_{Z})\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{Ext}_{Z\times Z}^{n}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})=\mathit{HH}^{n}(Z)\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle \mathit{HH}_{n}(Z,\unicode[STIX]{x1D6FC}) & = & \displaystyle \operatorname{Ext}_{(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})}^{d-n}(\unicode[STIX]{x1D6E5}_{\ast }\unicode[STIX]{x1D714}_{Z}^{-1},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})\simeq \operatorname{Ext}_{Z}^{d-n}({\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}^{\ast }{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{Ext}_{Z\times Z}^{d-n}(\unicode[STIX]{x1D6E5}_{\ast }\unicode[STIX]{x1D714}_{Z}^{-1},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})=\mathit{HH}_{n}(Z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{HH}_{n}(Z,\unicode[STIX]{x1D6FC}) & = & \displaystyle \operatorname{Ext}_{(Z,\unicode[STIX]{x1D6FC}^{-1})\times (Z,\unicode[STIX]{x1D6FC})}^{d-n}(\unicode[STIX]{x1D6E5}_{\ast }\unicode[STIX]{x1D714}_{Z}^{-1},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})\simeq \operatorname{Ext}_{Z}^{d-n}({\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}^{\ast }{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{Ext}_{Z\times Z}^{d-n}(\unicode[STIX]{x1D6E5}_{\ast }\unicode[STIX]{x1D714}_{Z}^{-1},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}})=\mathit{HH}_{n}(Z).\nonumber\end{eqnarray}$$
In particular, the HKR isomorphisms post-composed with
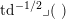 $\text{td}^{-1/2}\lrcorner (~)$
respectively
$\text{td}^{-1/2}\lrcorner (~)$
respectively
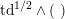 $\text{td}^{1/2}\wedge (~)$
yield isomorphisms
$\text{td}^{1/2}\wedge (~)$
yield isomorphisms

Note that these isomorphisms are again compatible with the ring and module structures on both sides, which follows from the fact that the isomorphisms
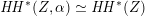 $\mathit{HH}^{\ast }(Z,\unicode[STIX]{x1D6FC})\simeq \mathit{HH}^{\ast }(Z)$
and
$\mathit{HH}^{\ast }(Z,\unicode[STIX]{x1D6FC})\simeq \mathit{HH}^{\ast }(Z)$
and
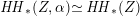 $\mathit{HH}_{\ast }(Z,\unicode[STIX]{x1D6FC})\simeq \mathit{HH}_{\ast }(Z)$
are. The latter is a consequence of the functoriality properties of
$\mathit{HH}_{\ast }(Z,\unicode[STIX]{x1D6FC})\simeq \mathit{HH}_{\ast }(Z)$
are. The latter is a consequence of the functoriality properties of
![]() $\unicode[STIX]{x1D6E5}_{!}$
,
$\unicode[STIX]{x1D6E5}_{!}$
,
![]() $\unicode[STIX]{x1D6E5}_{\ast }$
and
$\unicode[STIX]{x1D6E5}_{\ast }$
and
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
.
$\unicode[STIX]{x1D6E5}^{\ast }$
.
For a twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
one has
$(S,\unicode[STIX]{x1D6FC})$
one has
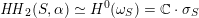 $\mathit{HH}_{2}(S,\unicode[STIX]{x1D6FC})\simeq H^{0}(\unicode[STIX]{x1D714}_{S})=\mathbb{C}\cdot \unicode[STIX]{x1D70E}_{S}$
and the following diagram commutes.
$\mathit{HH}_{2}(S,\unicode[STIX]{x1D6FC})\simeq H^{0}(\unicode[STIX]{x1D714}_{S})=\mathbb{C}\cdot \unicode[STIX]{x1D70E}_{S}$
and the following diagram commutes.

Let us now consider the fully faithful functor  between the twisted K3 surface
between the twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
and the smooth cubic
$(S,\unicode[STIX]{x1D6FC})$
and the smooth cubic
![]() $X$
, where
$X$
, where
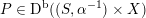 $P\in \text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)$
. Then as in [Reference Addington and ThomasAT14, § 6.1] one obtains natural maps
$P\in \text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)$
. Then as in [Reference Addington and ThomasAT14, § 6.1] one obtains natural maps

compatible with the module structures, i.e.
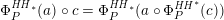 $\unicode[STIX]{x1D6F7}_{P}^{\mathit{HH}_{\ast }}(a)\circ c=\unicode[STIX]{x1D6F7}_{P}^{\mathit{HH}_{\ast }}(a\circ \unicode[STIX]{x1D6F7}_{P}^{\mathit{HH}^{\ast }}(c))$
for all
$\unicode[STIX]{x1D6F7}_{P}^{\mathit{HH}_{\ast }}(a)\circ c=\unicode[STIX]{x1D6F7}_{P}^{\mathit{HH}_{\ast }}(a\circ \unicode[STIX]{x1D6F7}_{P}^{\mathit{HH}^{\ast }}(c))$
for all
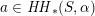 $a\in \mathit{HH}_{\ast }(S,\unicode[STIX]{x1D6FC})$
and
$a\in \mathit{HH}_{\ast }(S,\unicode[STIX]{x1D6FC})$
and
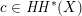 $c\in \mathit{HH}^{\ast }(X)$
. This has been checked by Reinecke in [Reference ReineckeRei14, § 4].
$c\in \mathit{HH}^{\ast }(X)$
. This has been checked by Reinecke in [Reference ReineckeRei14, § 4].
The remaining input in the proof of [Reference Addington and ThomasAT14, Proposition 6.2] is the commutativity of the untwisted version of the following diagram.

Note that defining the induced action on cohomology requires the lift of
![]() $\unicode[STIX]{x1D6FC}$
to a class
$\unicode[STIX]{x1D6FC}$
to a class
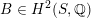 $B\in H^{2}(S,\mathbb{Q})$
, see [Reference HuybrechtsHuy05, Reference Huybrechts and StellariHS05]. Moreover, the usual HKR isomorphism
$B\in H^{2}(S,\mathbb{Q})$
, see [Reference HuybrechtsHuy05, Reference Huybrechts and StellariHS05]. Moreover, the usual HKR isomorphism
![]() $I$
post-composed with
$I$
post-composed with
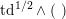 $\text{td}^{1/2}\wedge (~)$
needs to be twisted further to
$\text{td}^{1/2}\wedge (~)$
needs to be twisted further to
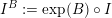 $I^{B}:=\exp (B)\circ I$
.
$I^{B}:=\exp (B)\circ I$
.
In principle, one could try to prove the commutativity of (5.1) by rewriting the existing untwisted theory, in particular [Reference CăldăraruCăl05, Reference Macrì and StellariMS09], for the twisted situation. Instead, we follow Yoshioka [Reference YoshiokaYos06] and reduce everything to the untwisted case by pulling back to a Brauer–Severi variety. We briefly review his approach and explain how to apply it to our situation.
Following [Reference YoshiokaYos06] we pick a locally free
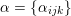 $\unicode[STIX]{x1D6FC}=\{\unicode[STIX]{x1D6FC}_{ijk}\}$
-twisted sheaf
$\unicode[STIX]{x1D6FC}=\{\unicode[STIX]{x1D6FC}_{ijk}\}$
-twisted sheaf
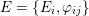 $E=\{E_{i},\unicode[STIX]{x1D711}_{ij}\}$
on a twisted variety
$E=\{E_{i},\unicode[STIX]{x1D711}_{ij}\}$
on a twisted variety
![]() $(Z,\unicode[STIX]{x1D6FC})$
and associate to it the projective bundle
$(Z,\unicode[STIX]{x1D6FC})$
and associate to it the projective bundle  which naturally comes with a
which naturally comes with a
![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FC}^{-1}$
-twisted line bundle
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FC}^{-1}$
-twisted line bundle
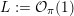 $L:={\mathcal{O}}_{\unicode[STIX]{x1D70B}}(1)$
. The pull-back of any
$L:={\mathcal{O}}_{\unicode[STIX]{x1D70B}}(1)$
. The pull-back of any
![]() $\unicode[STIX]{x1D6FC}$
-twisted sheaf
$\unicode[STIX]{x1D6FC}$
-twisted sheaf
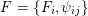 $F=\{F_{i},\unicode[STIX]{x1D713}_{ij}\}$
tensored with
$F=\{F_{i},\unicode[STIX]{x1D713}_{ij}\}$
tensored with
![]() $L$
then naturally leads to the untwisted sheaf
$L$
then naturally leads to the untwisted sheaf
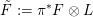 $\tilde{F}:=\unicode[STIX]{x1D70B}^{\ast }F\otimes L$
. Analogously, any
$\tilde{F}:=\unicode[STIX]{x1D70B}^{\ast }F\otimes L$
. Analogously, any
![]() $\unicode[STIX]{x1D6FC}^{-1}$
-twisted sheaf
$\unicode[STIX]{x1D6FC}^{-1}$
-twisted sheaf
![]() $F$
can be turned into the untwisted sheaf
$F$
can be turned into the untwisted sheaf
 $\unicode[STIX]{x1D70B}^{\ast }F\otimes L^{\ast }$
. The construction yields a functor
$\unicode[STIX]{x1D70B}^{\ast }F\otimes L^{\ast }$
. The construction yields a functor  which, in fact, defines an equivalence of
which, in fact, defines an equivalence of
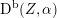 $\text{D}^{\text{b}}(Z,\unicode[STIX]{x1D6FC})$
with a full subcategory
$\text{D}^{\text{b}}(Z,\unicode[STIX]{x1D6FC})$
with a full subcategory

The construction applied to
![]() $E$
itself yields the sheaf
$E$
itself yields the sheaf
![]() $G:=\tilde{E}$
that corresponds to the unique non-trivial extension class in
$G:=\tilde{E}$
that corresponds to the unique non-trivial extension class in
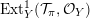 $\operatorname{Ext}_{Y}^{1}({\mathcal{T}}_{\unicode[STIX]{x1D70B}},{\mathcal{O}}_{Y})$
and
$\operatorname{Ext}_{Y}^{1}({\mathcal{T}}_{\unicode[STIX]{x1D70B}},{\mathcal{O}}_{Y})$
and
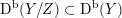 $\text{D}^{\text{b}}(Y/Z)\subset \text{D}^{\text{b}}(Y)$
can alternatively be described as the full subcategory of all objects
$\text{D}^{\text{b}}(Y/Z)\subset \text{D}^{\text{b}}(Y)$
can alternatively be described as the full subcategory of all objects
![]() $H$
for which the adjunction map
$H$
for which the adjunction map  is an isomorphism. Analogously,
is an isomorphism. Analogously,
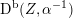 $\text{D}^{\text{b}}(Z,\unicode[STIX]{x1D6FC}^{-1})$
is equivalent to the full subcategory of objects
$\text{D}^{\text{b}}(Z,\unicode[STIX]{x1D6FC}^{-1})$
is equivalent to the full subcategory of objects
![]() $H$
for which
$H$
for which 
We apply this construction to the twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
and consider
$(S,\unicode[STIX]{x1D6FC})$
and consider  as above. Assume
as above. Assume
![]() $\unicode[STIX]{x1D6FC}$
is of order
$\unicode[STIX]{x1D6FC}$
is of order
![]() $r$
and choose a lift
$r$
and choose a lift
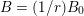 $B=(1/r)B_{0}$
with
$B=(1/r)B_{0}$
with
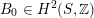 $B_{0}\in H^{2}(S,\mathbb{Z})$
of it. The FM-kernel of our given equivalence
$B_{0}\in H^{2}(S,\mathbb{Z})$
of it. The FM-kernel of our given equivalence  which is an object in
which is an object in
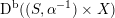 $\text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)$
, is turned into the untwisted sheaf
$\text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)$
, is turned into the untwisted sheaf
 $\tilde{P}:=\unicode[STIX]{x1D70B}^{\ast }P\otimes (L^{\ast }\boxtimes {\mathcal{O}})$
on
$\tilde{P}:=\unicode[STIX]{x1D70B}^{\ast }P\otimes (L^{\ast }\boxtimes {\mathcal{O}})$
on
![]() $Y\times X$
. This leads to the following commutative diagram.
$Y\times X$
. This leads to the following commutative diagram.

Therefore, the FM-functor  can be written as the composition
can be written as the composition
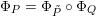 $\unicode[STIX]{x1D6F7}_{P}=\unicode[STIX]{x1D6F7}_{\tilde{P}}\circ \unicode[STIX]{x1D6F7}_{Q}$
of a twisted FM-functor
$\unicode[STIX]{x1D6F7}_{P}=\unicode[STIX]{x1D6F7}_{\tilde{P}}\circ \unicode[STIX]{x1D6F7}_{Q}$
of a twisted FM-functor
 $\unicode[STIX]{x1D6F7}_{Q}:=\tilde{(~)}$
, with
$\unicode[STIX]{x1D6F7}_{Q}:=\tilde{(~)}$
, with
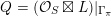 $Q=({\mathcal{O}}_{S}\boxtimes L)|_{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70B}}}$
, and an untwisted FM-functor
$Q=({\mathcal{O}}_{S}\boxtimes L)|_{\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D70B}}}$
, and an untwisted FM-functor
![]() $\unicode[STIX]{x1D6F7}_{\tilde{P}}$
:
$\unicode[STIX]{x1D6F7}_{\tilde{P}}$
:

This allows one to decompose the diagram (5.1) as

The right-hand square is induced by the usual untwisted FM-functor
![]() $\unicode[STIX]{x1D6F7}_{\tilde{P}}$
and its commutativity therefore follows from the result of Macrì and Stellari [Reference Macrì and StellariMS09, Theorem 1.2]. Hence, it suffices to prove the commutativity of the left-hand square (which does not involve the cubic
$\unicode[STIX]{x1D6F7}_{\tilde{P}}$
and its commutativity therefore follows from the result of Macrì and Stellari [Reference Macrì and StellariMS09, Theorem 1.2]. Hence, it suffices to prove the commutativity of the left-hand square (which does not involve the cubic
![]() $X$
anymore). For greater clarity we split this further by decomposing
$X$
anymore). For greater clarity we split this further by decomposing
![]() $\unicode[STIX]{x1D6F7}_{Q}$
as
$\unicode[STIX]{x1D6F7}_{Q}$
as

Let us first consider  and the induced diagram
and the induced diagram

Note that the usual
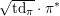 $\sqrt{\text{td}_{\unicode[STIX]{x1D70B}}}\cdot \unicode[STIX]{x1D70B}^{\ast }$
on the bottom is indeed the map on cohomology induced by the functor
$\sqrt{\text{td}_{\unicode[STIX]{x1D70B}}}\cdot \unicode[STIX]{x1D70B}^{\ast }$
on the bottom is indeed the map on cohomology induced by the functor  which a priori depends on the choice of the lifts of
which a priori depends on the choice of the lifts of
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FC}$
to classes in
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FC}$
to classes in
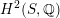 $H^{2}(S,\mathbb{Q})$
and
$H^{2}(S,\mathbb{Q})$
and
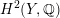 $H^{2}(Y,\mathbb{Q})$
, respectively, for which we choose
$H^{2}(Y,\mathbb{Q})$
, respectively, for which we choose
![]() $B$
and
$B$
and
![]() $\unicode[STIX]{x1D70B}^{\ast }B$
. The commutativity of the upper and the lower squares is trivial. The commutativity of the middle square is an easy case of [Reference Macrì and StellariMS09, Theorem 1.2]. Next consider
$\unicode[STIX]{x1D70B}^{\ast }B$
. The commutativity of the upper and the lower squares is trivial. The commutativity of the middle square is an easy case of [Reference Macrì and StellariMS09, Theorem 1.2]. Next consider  and the following induced diagram (where
and the following induced diagram (where
![]() $\unicode[STIX]{x1D713}$
is defined by the requirement of commutativity).
$\unicode[STIX]{x1D713}$
is defined by the requirement of commutativity).

By definition,
![]() $\unicode[STIX]{x1D6F9}^{H,\unicode[STIX]{x1D70B}^{\ast }B}$
is given by multiplication with
$\unicode[STIX]{x1D6F9}^{H,\unicode[STIX]{x1D70B}^{\ast }B}$
is given by multiplication with
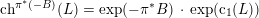 $\text{ch}^{\unicode[STIX]{x1D70B}^{\ast }(-B)}(L)=\exp (-\unicode[STIX]{x1D70B}^{\ast }B)\,\cdot \,\exp (\text{c}_{1}(L))$
. Here, use that
$\text{ch}^{\unicode[STIX]{x1D70B}^{\ast }(-B)}(L)=\exp (-\unicode[STIX]{x1D70B}^{\ast }B)\,\cdot \,\exp (\text{c}_{1}(L))$
. Here, use that
![]() $L^{r}$
is an untwisted line bundle and define
$L^{r}$
is an untwisted line bundle and define
 $\text{c}_{1}(L):=(1/r)\text{c}_{1}(L^{r})\in H^{1,1}(Y,\mathbb{Q})$
. See [Reference Huybrechts and StellariHS05, § 1] for the conventions concerning twisted Chern classes. In particular,
$\text{c}_{1}(L):=(1/r)\text{c}_{1}(L^{r})\in H^{1,1}(Y,\mathbb{Q})$
. See [Reference Huybrechts and StellariHS05, § 1] for the conventions concerning twisted Chern classes. In particular,
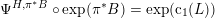 $\unicode[STIX]{x1D6F9}^{H,\unicode[STIX]{x1D70B}^{\ast }B}\circ \exp (\unicode[STIX]{x1D70B}^{\ast }B)=\exp (\text{c}_{1}(L))$
and, therefore, it suffices to prove the commutativity of the diagram
$\unicode[STIX]{x1D6F9}^{H,\unicode[STIX]{x1D70B}^{\ast }B}\circ \exp (\unicode[STIX]{x1D70B}^{\ast }B)=\exp (\text{c}_{1}(L))$
and, therefore, it suffices to prove the commutativity of the diagram

which no longer depends on
![]() $B$
and is a special case of Lemma 5.3 below.
$B$
and is a special case of Lemma 5.3 below.
This concludes the proof of the commutativity of the diagram (5.1) and hence of [Reference Addington and ThomasAT14, Proposition 6.2] in our twisted setting. More precisely, if a first-order deformation of
![]() $X$
in
$X$
in
![]() $D_{d}$
given by a class
$D_{d}$
given by a class
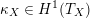 $\unicode[STIX]{x1D705}_{X}\in H^{1}(T_{X})$
corresponds via the interpretation of
$\unicode[STIX]{x1D705}_{X}\in H^{1}(T_{X})$
corresponds via the interpretation of
![]() $D_{d}$
as period domain for
$D_{d}$
as period domain for
![]() $X$
and
$X$
and
![]() $S$
to a first-order deformation
$S$
to a first-order deformation
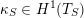 $\unicode[STIX]{x1D705}_{S}\in H^{1}(T_{S})$
, then
$\unicode[STIX]{x1D705}_{S}\in H^{1}(T_{S})$
, then  sends
sends
![]() $\unicode[STIX]{x1D705}_{X}$
to
$\unicode[STIX]{x1D705}_{X}$
to
![]() $\unicode[STIX]{x1D705}_{S}$
.
$\unicode[STIX]{x1D705}_{S}$
.
To conclude the proof one has to prove that the kernel
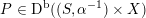 $P\in \text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)$
deforms sideways, for which we again apply Yoshioka’s untwisting technique. Instead of attempting to deform the twisted
$P\in \text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)$
deforms sideways, for which we again apply Yoshioka’s untwisting technique. Instead of attempting to deform the twisted
![]() $P$
sideways with
$P$
sideways with
 $(S,\unicode[STIX]{x1D6FC})\times X$
we deform the untwisted
$(S,\unicode[STIX]{x1D6FC})\times X$
we deform the untwisted
![]() $\tilde{P}$
. As the condition describing the full subcategory
$\tilde{P}$
. As the condition describing the full subcategory
 $\text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)\simeq \text{D}^{\text{b}}((Y\times X)/(S\times X))\subset \text{D}^{\text{b}}(Y\times X)$
is open, any deformation of
$\text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)\simeq \text{D}^{\text{b}}((Y\times X)/(S\times X))\subset \text{D}^{\text{b}}(Y\times X)$
is open, any deformation of
![]() $\tilde{P}$
will automatically induce a deformation of
$\tilde{P}$
will automatically induce a deformation of
![]() $P$
.Footnote
7
The decomposition (5.2) leads to a diagram
$P$
.Footnote
7
The decomposition (5.2) leads to a diagram

Recall that
![]() $\unicode[STIX]{x1D6F7}_{R}^{\mathit{HH}_{\ast }}$
is defined for any FM-functor
$\unicode[STIX]{x1D6F7}_{R}^{\mathit{HH}_{\ast }}$
is defined for any FM-functor
![]() $\unicode[STIX]{x1D6F7}_{R}$
, whereas in order to define
$\unicode[STIX]{x1D6F7}_{R}$
, whereas in order to define
![]() $\unicode[STIX]{x1D6F7}_{R}^{\mathit{HH}^{\ast }}$
one needs
$\unicode[STIX]{x1D6F7}_{R}^{\mathit{HH}^{\ast }}$
one needs
![]() $\unicode[STIX]{x1D6F7}_{R}$
to be fully faithful, which is the case for
$\unicode[STIX]{x1D6F7}_{R}$
to be fully faithful, which is the case for
![]() $\unicode[STIX]{x1D6F7}_{P}$
and
$\unicode[STIX]{x1D6F7}_{P}$
and
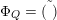 $\unicode[STIX]{x1D6F7}_{Q}=\tilde{(~)}$
. So, both maps in
$\unicode[STIX]{x1D6F7}_{Q}=\tilde{(~)}$
. So, both maps in

are well defined, where as above
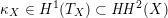 $\unicode[STIX]{x1D705}_{X}\in H^{1}(T_{X})\subset \mathit{HH}^{2}(X)$
corresponds to
$\unicode[STIX]{x1D705}_{X}\in H^{1}(T_{X})\subset \mathit{HH}^{2}(X)$
corresponds to
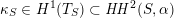 $\unicode[STIX]{x1D705}_{S}\in H^{1}(T_{S})\subset \mathit{HH}^{2}(S,\unicode[STIX]{x1D6FC})$
(via their periods or, equivalently, via
$\unicode[STIX]{x1D705}_{S}\in H^{1}(T_{S})\subset \mathit{HH}^{2}(S,\unicode[STIX]{x1D6FC})$
(via their periods or, equivalently, via
![]() $\unicode[STIX]{x1D6F7}^{\mathit{HH}^{2}}$
) and
$\unicode[STIX]{x1D6F7}^{\mathit{HH}^{2}}$
) and
![]() $\unicode[STIX]{x1D705}_{Y}$
is determined by our pre-chosen deformation
$\unicode[STIX]{x1D705}_{Y}$
is determined by our pre-chosen deformation
![]() $E_{t}$
of
$E_{t}$
of
![]() $E$
.
$E$
.
Now by [Reference Huybrechts and ThomasHT10] the obstruction
![]() $o(\tilde{P})$
can be expressed as
$o(\tilde{P})$
can be expressed as
 $$\begin{eqnarray}o(\tilde{P})=(\unicode[STIX]{x1D705}_{Y},\unicode[STIX]{x1D705}_{X})\circ \text{At}(\tilde{P}).\end{eqnarray}$$
$$\begin{eqnarray}o(\tilde{P})=(\unicode[STIX]{x1D705}_{Y},\unicode[STIX]{x1D705}_{X})\circ \text{At}(\tilde{P}).\end{eqnarray}$$
(Unfortunately, an analogous formula in the twisted case is not available.) The crucial [Reference Addington and ThomasAT14, Theorem 7.1], which goes back to Toda [Reference TodaTod09], proves that in the untwisted case
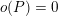 $o(P)=0$
if
$o(P)=0$
if
![]() $\unicode[STIX]{x1D705}_{X}$
is mapped to
$\unicode[STIX]{x1D705}_{X}$
is mapped to
![]() $\unicode[STIX]{x1D705}_{S}$
under
$\unicode[STIX]{x1D705}_{S}$
under  However, in the twisted situation one has to face the additional problem that there is no natural map
However, in the twisted situation one has to face the additional problem that there is no natural map  Nevertheless, the argument in [Reference Addington and ThomasAT14] goes through essentially unchanged as follows. Using the same notation, one writes
Nevertheless, the argument in [Reference Addington and ThomasAT14] goes through essentially unchanged as follows. Using the same notation, one writes
 $$\begin{eqnarray}o(\tilde{P})=\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D705}_{Y}\circ \text{At}_{Y}(\tilde{P})+\unicode[STIX]{x1D70B}_{2}^{\ast }\unicode[STIX]{x1D705}_{X}\circ \text{At}_{X}(\tilde{P})\in \operatorname{Ext}^{2}(\tilde{P},\tilde{P}).\end{eqnarray}$$
$$\begin{eqnarray}o(\tilde{P})=\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D705}_{Y}\circ \text{At}_{Y}(\tilde{P})+\unicode[STIX]{x1D70B}_{2}^{\ast }\unicode[STIX]{x1D705}_{X}\circ \text{At}_{X}(\tilde{P})\in \operatorname{Ext}^{2}(\tilde{P},\tilde{P}).\end{eqnarray}$$
The first term is the image of
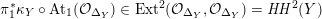 $\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D705}_{Y}\circ \text{At}_{1}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{Y}})\in \operatorname{Ext}^{2}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{Y}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{Y}})=\mathit{HH}^{2}(Y)$
which is just
$\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D705}_{Y}\circ \text{At}_{1}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{Y}})\in \operatorname{Ext}^{2}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{Y}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{Y}})=\mathit{HH}^{2}(Y)$
which is just
![]() $\unicode[STIX]{x1D705}_{Y}$
, whereas the second one is the image of
$\unicode[STIX]{x1D705}_{Y}$
, whereas the second one is the image of
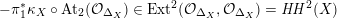 $-\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D705}_{X}\circ \text{At}_{2}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{X}})\in \operatorname{Ext}^{2}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{X}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{X}})=\mathit{HH}^{2}(X)$
which is just
$-\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D705}_{X}\circ \text{At}_{2}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{X}})\in \operatorname{Ext}^{2}({\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{X}},{\mathcal{O}}_{\unicode[STIX]{x1D6E5}_{X}})=\mathit{HH}^{2}(X)$
which is just
![]() $-\unicode[STIX]{x1D705}_{X}$
. Hence, to compare
$-\unicode[STIX]{x1D705}_{X}$
. Hence, to compare
![]() $\unicode[STIX]{x1D705}_{X}$
and
$\unicode[STIX]{x1D705}_{X}$
and
![]() $\unicode[STIX]{x1D705}_{Y}$
we do not need a map
$\unicode[STIX]{x1D705}_{Y}$
we do not need a map  (which simply does not exist naturally), as we only need to compare their images in
(which simply does not exist naturally), as we only need to compare their images in
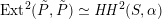 $\operatorname{Ext}^{2}(\tilde{P},\tilde{P})\simeq \mathit{HH}^{2}(S,\unicode[STIX]{x1D6FC})$
. Therefore, it suffices to ensure that under
$\operatorname{Ext}^{2}(\tilde{P},\tilde{P})\simeq \mathit{HH}^{2}(S,\unicode[STIX]{x1D6FC})$
. Therefore, it suffices to ensure that under  the class
the class
![]() $\unicode[STIX]{x1D705}_{X}$
is mapped to
$\unicode[STIX]{x1D705}_{X}$
is mapped to
![]() $\unicode[STIX]{x1D705}_{S}$
, which was verified above.
$\unicode[STIX]{x1D705}_{S}$
, which was verified above.
This concludes the argument proving that the FM-kernel
![]() $P$
deforms to first order with
$P$
deforms to first order with
 $(S,\unicode[STIX]{x1D6FC})\times X$
. The arguments in [Reference Addington and ThomasAT14, § 7.2] proving the existence of deformations of
$(S,\unicode[STIX]{x1D6FC})\times X$
. The arguments in [Reference Addington and ThomasAT14, § 7.2] proving the existence of deformations of
![]() $P$
to all orders apply verbatim. Note that at the very end of the argument one needs to apply a result of Lieblich [Reference LieblichLie06] saying that the space of objects with no negative self-Exts in the derived category is an Artin stack of locally finite presentation. Again, the result as such does not seem to be in the literature for the twisted situation, but once again it can be deduced from the untwisted case by Yoshioka’s trick. ◻
$P$
to all orders apply verbatim. Note that at the very end of the argument one needs to apply a result of Lieblich [Reference LieblichLie06] saying that the space of objects with no negative self-Exts in the derived category is an Artin stack of locally finite presentation. Again, the result as such does not seem to be in the literature for the twisted situation, but once again it can be deduced from the untwisted case by Yoshioka’s trick. ◻
It remains to check the commutativity of (5.4) which is a general fact. Consider a smooth variety
![]() $Z$
and
$Z$
and
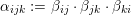 $\unicode[STIX]{x1D6FC}_{ijk}:=\unicode[STIX]{x1D6FD}_{ij}\cdot \unicode[STIX]{x1D6FD}_{jk}\cdot \unicode[STIX]{x1D6FD}_{ki}$
with
$\unicode[STIX]{x1D6FC}_{ijk}:=\unicode[STIX]{x1D6FD}_{ij}\cdot \unicode[STIX]{x1D6FD}_{jk}\cdot \unicode[STIX]{x1D6FD}_{ki}$
with
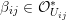 $\unicode[STIX]{x1D6FD}_{ij}\in {\mathcal{O}}_{U_{ij}}^{\ast }$
. The associated Brauer class
$\unicode[STIX]{x1D6FD}_{ij}\in {\mathcal{O}}_{U_{ij}}^{\ast }$
. The associated Brauer class
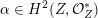 $\unicode[STIX]{x1D6FC}\in H^{2}(Z,{\mathcal{O}}_{Z}^{\ast })$
is of course trivial and hence
$\unicode[STIX]{x1D6FC}\in H^{2}(Z,{\mathcal{O}}_{Z}^{\ast })$
is of course trivial and hence
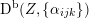 $\text{D}^{\text{b}}(Z,\{\unicode[STIX]{x1D6FC}_{ijk}\})$
and
$\text{D}^{\text{b}}(Z,\{\unicode[STIX]{x1D6FC}_{ijk}\})$
and
![]() $\text{D}^{\text{b}}(Z)$
are equivalent categories and an explicit equivalence can be given by ‘untwisting by
$\text{D}^{\text{b}}(Z)$
are equivalent categories and an explicit equivalence can be given by ‘untwisting by
![]() $\{\unicode[STIX]{x1D6FD}_{ij}\}$
’, i.e. by
$\{\unicode[STIX]{x1D6FD}_{ij}\}$
’, i.e. by  Note that changing
Note that changing
![]() $\unicode[STIX]{x1D6FD}_{ij}$
by a cocycle
$\unicode[STIX]{x1D6FD}_{ij}$
by a cocycle
![]() $\{\unicode[STIX]{x1D6FF}_{ij}\}$
, which would correspond to an untwisted line bundle say
$\{\unicode[STIX]{x1D6FF}_{ij}\}$
, which would correspond to an untwisted line bundle say
![]() $M$
, the equivalence would be modified by
$M$
, the equivalence would be modified by
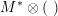 $M^{\ast }\otimes (~)$
.
$M^{\ast }\otimes (~)$
.
Assume furthermore that
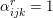 $\unicode[STIX]{x1D6FC}_{ijk}^{r}=1$
. Then
$\unicode[STIX]{x1D6FC}_{ijk}^{r}=1$
. Then
![]() $\{\unicode[STIX]{x1D6FD}_{ij}^{r}\}$
is a cocycle defining a line bundle
$\{\unicode[STIX]{x1D6FD}_{ij}^{r}\}$
is a cocycle defining a line bundle
![]() $H$
and we define
$H$
and we define
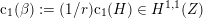 $\text{c}_{1}(\unicode[STIX]{x1D6FD}):=(1/r)\text{c}_{1}(H)\in H^{1,1}(Z)$
. Explicitly,
$\text{c}_{1}(\unicode[STIX]{x1D6FD}):=(1/r)\text{c}_{1}(H)\in H^{1,1}(Z)$
. Explicitly,
 $\text{c}_{1}(\unicode[STIX]{x1D6FD})=\{d\log \unicode[STIX]{x1D6FD}_{ij}\}$
.
$\text{c}_{1}(\unicode[STIX]{x1D6FD})=\{d\log \unicode[STIX]{x1D6FD}_{ij}\}$
.
Lemma 5.3. The ‘untwisting by
![]() $\{\unicode[STIX]{x1D6FD}_{ij}\}$
’, i.e. the equivalence
$\{\unicode[STIX]{x1D6FD}_{ij}\}$
’, i.e. the equivalence

induces a commutative diagram

The commutativity of (5.4) then follows from the observation that
![]() $L\otimes (~)$
can be written as the composition of the ‘untwisting by
$L\otimes (~)$
can be written as the composition of the ‘untwisting by
![]() $\{\unicode[STIX]{x1D6FD}_{ij}\}$
’ as above with the equivalence
$\{\unicode[STIX]{x1D6FD}_{ij}\}$
’ as above with the equivalence
![]() ${\mathcal{L}}\otimes (~)$
. Here,
${\mathcal{L}}\otimes (~)$
. Here,
![]() ${\mathcal{L}}$
is the untwisted line bundle given by
${\mathcal{L}}$
is the untwisted line bundle given by
 $\{\unicode[STIX]{x1D713}_{ij}\cdot \unicode[STIX]{x1D6FD}_{ij}\}$
, where
$\{\unicode[STIX]{x1D713}_{ij}\cdot \unicode[STIX]{x1D6FD}_{ij}\}$
, where
![]() $L$
itself is the
$L$
itself is the
![]() $\{\unicode[STIX]{x1D6FC}_{ijk}^{-1}\}$
-twisted line bundle given by
$\{\unicode[STIX]{x1D6FC}_{ijk}^{-1}\}$
-twisted line bundle given by
![]() $\{\unicode[STIX]{x1D713}_{ij}\}$
.
$\{\unicode[STIX]{x1D713}_{ij}\}$
.
Indeed, for  the commutativity of
the commutativity of

is an easy special case ofFootnote 8 [Reference Macrì and StellariMS09, Theorem 1.2], which can be proved by a direct calculation. The proof of the lemma is a variant of this computation.
Proof. Consider the universal Atiyah class  Twisted with a line bundle of the form
Twisted with a line bundle of the form
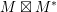 $M\boxtimes M^{\ast }$
it yields a map
$M\boxtimes M^{\ast }$
it yields a map  The usual formula
The usual formula
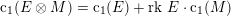 $\text{c}_{1}(E\otimes M)=\text{c}_{1}(E)+\operatorname{rk}\,E\cdot \text{c}_{1}(M)$
corresponds to the universal formula
$\text{c}_{1}(E\otimes M)=\text{c}_{1}(E)+\operatorname{rk}\,E\cdot \text{c}_{1}(M)$
corresponds to the universal formula
 $\text{At}_{M}=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6E5}_{\ast }\text{c}_{1}(M)$
, which can be checked by using arguments of [Reference Buchweitz and FlennerBF08, Reference Buchweitz and FlennerBF03] or a direct cocycle computation. Here,
$\text{At}_{M}=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6E5}_{\ast }\text{c}_{1}(M)$
, which can be checked by using arguments of [Reference Buchweitz and FlennerBF08, Reference Buchweitz and FlennerBF03] or a direct cocycle computation. Here,
![]() $\text{c}_{1}(M)$
is viewed as a map
$\text{c}_{1}(M)$
is viewed as a map  which can be pushed forward via
which can be pushed forward via
![]() $\unicode[STIX]{x1D6E5}$
. Similarly, the exponential
$\unicode[STIX]{x1D6E5}$
. Similarly, the exponential  (see [Reference CăldăraruCăl05]) twisted with
(see [Reference CăldăraruCăl05]) twisted with
 $M\boxtimes M^{\ast }$
is given by
$M\boxtimes M^{\ast }$
is given by
 $\exp (\text{At})_{M}=\unicode[STIX]{x1D6E5}_{\ast }\exp (\text{c}_{1}(M))\circ \exp (\text{At})$
.
$\exp (\text{At})_{M}=\unicode[STIX]{x1D6E5}_{\ast }\exp (\text{c}_{1}(M))\circ \exp (\text{At})$
.
Let now
 $f\in \mathit{HH}_{j}(Z)=\operatorname{Ext}_{Z\times Z}^{j}(\unicode[STIX]{x1D6E5}_{!}{\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}_{\ast }{\mathcal{O}}_{Z})$
and denote by
$f\in \mathit{HH}_{j}(Z)=\operatorname{Ext}_{Z\times Z}^{j}(\unicode[STIX]{x1D6E5}_{!}{\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}_{\ast }{\mathcal{O}}_{Z})$
and denote by
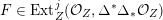 $F\in \operatorname{Ext}_{Z}^{j}({\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}^{\ast }\unicode[STIX]{x1D6E5}_{\ast }{\mathcal{O}}_{Z})$
its image under
$F\in \operatorname{Ext}_{Z}^{j}({\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}^{\ast }\unicode[STIX]{x1D6E5}_{\ast }{\mathcal{O}}_{Z})$
its image under
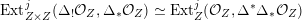 $\operatorname{Ext}_{Z\times Z}^{j}(\unicode[STIX]{x1D6E5}_{!}{\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}_{\ast }{\mathcal{O}}_{Z})\simeq \operatorname{Ext}_{Z}^{j}({\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}^{\ast }\unicode[STIX]{x1D6E5}_{\ast }{\mathcal{O}}_{Z})$
. So if
$\operatorname{Ext}_{Z\times Z}^{j}(\unicode[STIX]{x1D6E5}_{!}{\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}_{\ast }{\mathcal{O}}_{Z})\simeq \operatorname{Ext}_{Z}^{j}({\mathcal{O}}_{Z},\unicode[STIX]{x1D6E5}^{\ast }\unicode[STIX]{x1D6E5}_{\ast }{\mathcal{O}}_{Z})$
. So if  denotes adjunction, then
denotes adjunction, then
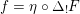 $f=\unicode[STIX]{x1D702}\circ \unicode[STIX]{x1D6E5}_{!}F$
. Due to [Reference CăldăraruCăl05, Proposition 4.4], the latter is under the HKR isomorphism given by
$f=\unicode[STIX]{x1D702}\circ \unicode[STIX]{x1D6E5}_{!}F$
. Due to [Reference CăldăraruCăl05, Proposition 4.4], the latter is under the HKR isomorphism given by
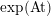 $\exp (\text{At})$
, so
$\exp (\text{At})$
, so

The image of
![]() $f$
under
$f$
under
![]() ${\mathcal{L}}\otimes (~)$
is given by tensoring with
${\mathcal{L}}\otimes (~)$
is given by tensoring with
![]() ${\mathcal{L}}\boxtimes {\mathcal{L}}^{\ast }$
. The push-forward
${\mathcal{L}}\boxtimes {\mathcal{L}}^{\ast }$
. The push-forward
![]() $\unicode[STIX]{x1D6E5}_{!}F$
remains unchanged by tensoring with
$\unicode[STIX]{x1D6E5}_{!}F$
remains unchanged by tensoring with
![]() ${\mathcal{L}}\boxtimes {\mathcal{L}}^{\ast }$
and by the above
${\mathcal{L}}\boxtimes {\mathcal{L}}^{\ast }$
and by the above
![]() $\unicode[STIX]{x1D702}$
changes by composing with
$\unicode[STIX]{x1D702}$
changes by composing with
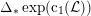 $\unicode[STIX]{x1D6E5}_{\ast }\exp (\text{c}_{1}({\mathcal{L}}))$
.
$\unicode[STIX]{x1D6E5}_{\ast }\exp (\text{c}_{1}({\mathcal{L}}))$
.
Literally the same argument applies to the untwisting by
![]() $\{\unicode[STIX]{x1D6FD}_{ij}\}$
for which one has to observe that the universal Atiyah class
$\{\unicode[STIX]{x1D6FD}_{ij}\}$
for which one has to observe that the universal Atiyah class  on
on
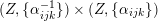 $(Z,\{\unicode[STIX]{x1D6FC}_{ijk}^{-1}\})\times (Z,\{\unicode[STIX]{x1D6FC}_{ijk}\})$
under untwisting by
$(Z,\{\unicode[STIX]{x1D6FC}_{ijk}^{-1}\})\times (Z,\{\unicode[STIX]{x1D6FC}_{ijk}\})$
under untwisting by
![]() $\{\unicode[STIX]{x1D6FD}_{ij}\}$
becomes
$\{\unicode[STIX]{x1D6FD}_{ij}\}$
becomes  on
on
![]() $Z\times Z$
.◻
$Z\times Z$
.◻
6 Proofs
6.1 Proof of Theorem 1.2
(i) According to Corollary 3.13, for every smooth cubic
![]() $X\subset \mathbb{P}^{5}$
there exists a distinguished FM-autoequivalence
$X\subset \mathbb{P}^{5}$
there exists a distinguished FM-autoequivalence  of infinite order which acts as the identity on
of infinite order which acts as the identity on
![]() $T({\mathcal{A}}_{X})$
, so it is symplectic, and such that
$T({\mathcal{A}}_{X})$
, so it is symplectic, and such that
![]() $\unicode[STIX]{x1D6F7}_{0}^{3}$
is the double shift
$\unicode[STIX]{x1D6F7}_{0}^{3}$
is the double shift  We have to show that for the very general cubic every symplectic FM-equivalence
We have to show that for the very general cubic every symplectic FM-equivalence
![]() $\unicode[STIX]{x1D6F7}$
is a power of
$\unicode[STIX]{x1D6F7}$
is a power of
![]() $\unicode[STIX]{x1D6F7}_{0}$
.
$\unicode[STIX]{x1D6F7}_{0}$
.
As
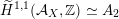 $\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})\simeq A_{2}$
for very general
$\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})\simeq A_{2}$
for very general
![]() $X$
and
$X$
and
 $\unicode[STIX]{x1D6F7}^{H}=\text{id}$
on
$\unicode[STIX]{x1D6F7}^{H}=\text{id}$
on
 $T({\mathcal{A}}_{X})=A_{2}^{\bot }$
, the induced action
$T({\mathcal{A}}_{X})=A_{2}^{\bot }$
, the induced action
![]() $\unicode[STIX]{x1D6F7}^{H}$
is contained in
$\unicode[STIX]{x1D6F7}^{H}$
is contained in
![]() $\text{O}(A_{2})$
. Clearly, any Hodge isometry of
$\text{O}(A_{2})$
. Clearly, any Hodge isometry of
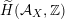 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
that is the identity on
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
that is the identity on
![]() $A_{2}^{\bot }$
stays a Hodge isometry for all deformations of
$A_{2}^{\bot }$
stays a Hodge isometry for all deformations of
![]() $X$
. Therefore, applying Theorem 5.1,
$X$
. Therefore, applying Theorem 5.1,
![]() $\unicode[STIX]{x1D6F7}$
deforms to FM-autoequivalences
$\unicode[STIX]{x1D6F7}$
deforms to FM-autoequivalences
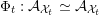 $\unicode[STIX]{x1D6F7}_{t}:{\mathcal{A}}_{{\mathcal{X}}_{t}}\simeq {\mathcal{A}}_{{\mathcal{X}}_{t}}$
for cubics
$\unicode[STIX]{x1D6F7}_{t}:{\mathcal{A}}_{{\mathcal{X}}_{t}}\simeq {\mathcal{A}}_{{\mathcal{X}}_{t}}$
for cubics
![]() ${\mathcal{X}}_{t}$
in a Zariski open neighbourhood
${\mathcal{X}}_{t}$
in a Zariski open neighbourhood
![]() $U\subset {\mathcal{C}}$
of
$U\subset {\mathcal{C}}$
of
![]() $X$
inside the moduli space of smooth cubics.
$X$
inside the moduli space of smooth cubics.
Then for all but finitely many
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast$
) the intersection
$\ast \ast$
) the intersection
![]() $U\cap {\mathcal{C}}_{d}$
is non-empty (and open) and, therefore, by [Reference Addington and ThomasAT14, Theorem 1.1] there exists
$U\cap {\mathcal{C}}_{d}$
is non-empty (and open) and, therefore, by [Reference Addington and ThomasAT14, Theorem 1.1] there exists
![]() $t\in U$
such that
$t\in U$
such that
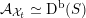 ${\mathcal{A}}_{{\mathcal{X}}_{t}}\simeq \text{D}^{\text{b}}(S)$
for some K3 surface
${\mathcal{A}}_{{\mathcal{X}}_{t}}\simeq \text{D}^{\text{b}}(S)$
for some K3 surface
![]() $S$
. Due to [Reference Huybrechts, Macrì and StellariHMS09, Theorem 2], autoequivalences of
$S$
. Due to [Reference Huybrechts, Macrì and StellariHMS09, Theorem 2], autoequivalences of
![]() $\text{D}^{\text{b}}(S)$
are orientation preserving and hence
$\text{D}^{\text{b}}(S)$
are orientation preserving and hence
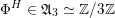 $\unicode[STIX]{x1D6F7}^{H}\in \mathfrak{A}_{3}\simeq \mathbb{Z}/3\mathbb{Z}$
, cf. Remark 2.1. Thus, by composing with some power of
$\unicode[STIX]{x1D6F7}^{H}\in \mathfrak{A}_{3}\simeq \mathbb{Z}/3\mathbb{Z}$
, cf. Remark 2.1. Thus, by composing with some power of
![]() $\unicode[STIX]{x1D6F7}_{0}$
, we may assume that
$\unicode[STIX]{x1D6F7}_{0}$
, we may assume that
 $\unicode[STIX]{x1D6F7}^{H}=\text{id}$
.
$\unicode[STIX]{x1D6F7}^{H}=\text{id}$
.
Now apply Corollary 2.16 and Theorem 1.4, to be proved below, to conclude that there exists
![]() $t\in U$
such that
$t\in U$
such that
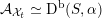 ${\mathcal{A}}_{{\mathcal{X}}_{t}}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
for a twisted K3 surface
${\mathcal{A}}_{{\mathcal{X}}_{t}}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
for a twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
not admitting any
$(S,\unicode[STIX]{x1D6FC})$
not admitting any
![]() $(-2)$
class. Indeed,
$(-2)$
class. Indeed,
 $$\begin{eqnarray}({\mathcal{C}}_{\text{K3'}}\cap U)\setminus {\mathcal{C}}_{\text{sph}}\neq \emptyset ,\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{C}}_{\text{K3'}}\cap U)\setminus {\mathcal{C}}_{\text{sph}}\neq \emptyset ,\end{eqnarray}$$
where
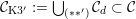 ${\mathcal{C}}_{\text{K3'}}:=\bigcup _{(\ast \ast ^{\prime })}{\mathcal{C}}_{d}\subset {\mathcal{C}}$
and
${\mathcal{C}}_{\text{K3'}}:=\bigcup _{(\ast \ast ^{\prime })}{\mathcal{C}}_{d}\subset {\mathcal{C}}$
and
 ${\mathcal{C}}_{\text{sph}}\subset {\mathcal{C}}$
is the image of
${\mathcal{C}}_{\text{sph}}\subset {\mathcal{C}}$
is the image of
![]() $D_{\text{sph}}$
. By [Reference Huybrechts, Macrì and StellariHMS08, Theorem 2], we know that then
$D_{\text{sph}}$
. By [Reference Huybrechts, Macrì and StellariHMS08, Theorem 2], we know that then
![]() $\unicode[STIX]{x1D6F7}_{t}$
is isomorphic to an even shift
$\unicode[STIX]{x1D6F7}_{t}$
is isomorphic to an even shift  It is easy to see that
It is easy to see that
![]() $k$
is independent of
$k$
is independent of
![]() $t$
.
$t$
.
The locus of points
![]() $U_{0}\subset U$
such that
$U_{0}\subset U$
such that
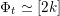 $\unicode[STIX]{x1D6F7}_{t}\simeq [2k]$
for
$\unicode[STIX]{x1D6F7}_{t}\simeq [2k]$
for
![]() $t\in U_{0}$
is Zariski open and by the above non-empty. Therefore, for every
$t\in U_{0}$
is Zariski open and by the above non-empty. Therefore, for every
![]() $X\in {\mathcal{C}}$
in the intersection of all
$X\in {\mathcal{C}}$
in the intersection of all
![]() $U_{0}\subset {\mathcal{C}}$
the assertion holds. But this intersection is certainly countable, as FM-kernels are parametrized by countably many products of Quot schemes.
$U_{0}\subset {\mathcal{C}}$
the assertion holds. But this intersection is certainly countable, as FM-kernels are parametrized by countably many products of Quot schemes.
(ii) Now consider a non-special cubic
![]() $X$
, i.e.
$X$
, i.e.
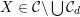 $X\in {\mathcal{C}}\setminus \bigcup {\mathcal{C}}_{d}$
, and an arbitrary
$X\in {\mathcal{C}}\setminus \bigcup {\mathcal{C}}_{d}$
, and an arbitrary
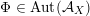 $\unicode[STIX]{x1D6F7}\in \operatorname{Aut}({\mathcal{A}}_{X})$
. By composing with the shift functor
$\unicode[STIX]{x1D6F7}\in \operatorname{Aut}({\mathcal{A}}_{X})$
. By composing with the shift functor
![]() $[1]$
if necessary, we may assume that
$[1]$
if necessary, we may assume that
![]() $\unicode[STIX]{x1D6F7}^{H}$
acts trivially on the discriminant group
$\unicode[STIX]{x1D6F7}^{H}$
acts trivially on the discriminant group
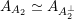 $A_{A_{2}}\simeq A_{A_{2}^{\bot }}$
. But then the induced Hodge isometry of
$A_{A_{2}}\simeq A_{A_{2}^{\bot }}$
. But then the induced Hodge isometry of
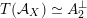 $T({\mathcal{A}}_{X})\simeq A_{2}^{\bot }$
extends to a Hodge isometry of
$T({\mathcal{A}}_{X})\simeq A_{2}^{\bot }$
extends to a Hodge isometry of
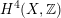 $H^{4}(X,\mathbb{Z})$
that respects
$H^{4}(X,\mathbb{Z})$
that respects
![]() $h$
. By the global Torelli theorem [Reference VoisinVoi86, Reference LooijengaLoo09, Reference CharlesCha12] it is therefore induced by an automorphism
$h$
. By the global Torelli theorem [Reference VoisinVoi86, Reference LooijengaLoo09, Reference CharlesCha12] it is therefore induced by an automorphism
 $f\in \operatorname{Aut}(X)$
, which clearly acts trivially on the orthogonal complement of
$f\in \operatorname{Aut}(X)$
, which clearly acts trivially on the orthogonal complement of
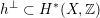 $h^{\bot }\subset H^{\ast }(X,\mathbb{Z})$
and hence as the identity on
$h^{\bot }\subset H^{\ast }(X,\mathbb{Z})$
and hence as the identity on
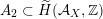 $A_{2}\subset \widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
. Moreover, since
$A_{2}\subset \widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
. Moreover, since
![]() $f$
respects
$f$
respects
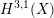 $H^{3,1}(X)$
, the action of
$H^{3,1}(X)$
, the action of
![]() $f$
in
$f$
in
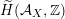 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
preserves the orientation.
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})$
preserves the orientation.
So, composing, if necessary,
![]() $\unicode[STIX]{x1D6F7}$
with the shift functor and an automorphism, we reduce to the case
$\unicode[STIX]{x1D6F7}$
with the shift functor and an automorphism, we reduce to the case
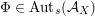 $\unicode[STIX]{x1D6F7}\in \operatorname{Aut}_{s}({\mathcal{A}}_{X})$
. As
$\unicode[STIX]{x1D6F7}\in \operatorname{Aut}_{s}({\mathcal{A}}_{X})$
. As
![]() $X$
is non-special, i.e.
$X$
is non-special, i.e.
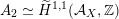 $A_{2}\simeq \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
, we can deform
$A_{2}\simeq \widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})$
, we can deform
![]() $\unicode[STIX]{x1D6F7}$
sideways as above until it can be interpreted as an autoequivalence of a category of the form
$\unicode[STIX]{x1D6F7}$
sideways as above until it can be interpreted as an autoequivalence of a category of the form
![]() $\text{D}^{\text{b}}(S)$
, which implies that it is orientation preserving. This eventually proves that for every non-special cubic the image of
$\text{D}^{\text{b}}(S)$
, which implies that it is orientation preserving. This eventually proves that for every non-special cubic the image of  is the subgroup of orientation-preserving Hodge isometries.
is the subgroup of orientation-preserving Hodge isometries.
Remark 6.1. We expect the first assertion in Theorem 1.2 to hold for every non-special cubic, i.e. for all
 $X\in {\mathcal{C}}\setminus \bigcup {\mathcal{C}}_{d}$
, but this would require to show that if
$X\in {\mathcal{C}}\setminus \bigcup {\mathcal{C}}_{d}$
, but this would require to show that if
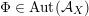 $\unicode[STIX]{x1D6F7}\in \operatorname{Aut}({\mathcal{A}}_{X})$
deforms to the identity functor and
$\unicode[STIX]{x1D6F7}\in \operatorname{Aut}({\mathcal{A}}_{X})$
deforms to the identity functor and
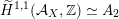 $\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})\simeq A_{2}$
, then
$\widetilde{H}^{1,1}({\mathcal{A}}_{X},\mathbb{Z})\simeq A_{2}$
, then
![]() $\unicode[STIX]{x1D6F7}\simeq \text{id}$
. The techniques of [Reference Huybrechts, Macrì and StellariHMS08] should be useful here, but they require the existence of stability conditions.
$\unicode[STIX]{x1D6F7}\simeq \text{id}$
. The techniques of [Reference Huybrechts, Macrì and StellariHMS08] should be useful here, but they require the existence of stability conditions.
Furthermore, one would also expect that any
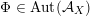 $\unicode[STIX]{x1D6F7}\in \operatorname{Aut}({\mathcal{A}}_{X})$
of any cubic preserves the natural orientation.
$\unicode[STIX]{x1D6F7}\in \operatorname{Aut}({\mathcal{A}}_{X})$
of any cubic preserves the natural orientation.
6.2 Proof of Theorem 1.4
Assertion (i) follows from Theorem 1.3 and Proposition 3.3. For the converse, fix
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
). Then for any smooth cubic
$\ast \ast ^{\prime }$
). Then for any smooth cubic
![]() $X\in {\mathcal{C}}_{d}$
there exists a Hodge isometry
$X\in {\mathcal{C}}_{d}$
there exists a Hodge isometry

for some twisted K3 surface
![]() $(S,\unicode[STIX]{x1D6FC})$
. In fact, this Hodge isometry can be chosen globally over the period domain
$(S,\unicode[STIX]{x1D6FC})$
. In fact, this Hodge isometry can be chosen globally over the period domain
![]() $D_{d}$
(or some appropriately constructed covering
$D_{d}$
(or some appropriately constructed covering
![]() $\tilde{{\mathcal{C}}}_{d}$
of
$\tilde{{\mathcal{C}}}_{d}$
of
![]() ${\mathcal{C}}_{d}$
, see [Reference Addington and ThomasAT14]). The aim is to show that generically this Hodge isometry is induced by an equivalence
${\mathcal{C}}_{d}$
, see [Reference Addington and ThomasAT14]). The aim is to show that generically this Hodge isometry is induced by an equivalence
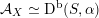 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
(up to changing the orientation).
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
(up to changing the orientation).
The starting point for the argument is [Reference Addington and ThomasAT14, Theorem 4.1], which is based on Kuznetsov’s work [Reference KuznetsovKuz10] and on the description of the image of the period map for cubic fourfolds due to Laza [Reference LazaLaz10] and Looijenga [Reference LooijengaLoo09]. Combined, these results show that for every
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
) (but in fact (
$\ast \ast ^{\prime }$
) (but in fact (
![]() $\ast$
) is enough) there exists a smooth cubic
$\ast$
) is enough) there exists a smooth cubic
 $X\in {\mathcal{C}}_{8}\cap {\mathcal{C}}_{d}$
, a K3 surface
$X\in {\mathcal{C}}_{8}\cap {\mathcal{C}}_{d}$
, a K3 surface
![]() $S_{0}$
and an equivalence
$S_{0}$
and an equivalence

By [Reference Addington and ThomasAT14] or Proposition 3.3, any such
![]() $\unicode[STIX]{x1D6F7}_{0}$
induces a Hodge isometry
$\unicode[STIX]{x1D6F7}_{0}$
induces a Hodge isometry  (usually completely unrelated to (6.1)). Consider now the composition
(usually completely unrelated to (6.1)). Consider now the composition

By modifying
![]() $\unicode[STIX]{x1D711}$
(globally over
$\unicode[STIX]{x1D711}$
(globally over
![]() $D_{d}$
) if necessary (use Lemma 2.3), we may assume that
$D_{d}$
) if necessary (use Lemma 2.3), we may assume that
![]() $\unicode[STIX]{x1D713}$
preserves the orientation and then [Reference Huybrechts and StellariHS06] applies and shows that there exists an equivalence
$\unicode[STIX]{x1D713}$
preserves the orientation and then [Reference Huybrechts and StellariHS06] applies and shows that there exists an equivalence with
with
 $\unicode[STIX]{x1D6F9}^{H}=\unicode[STIX]{x1D713}$
. Then the equivalence
$\unicode[STIX]{x1D6F9}^{H}=\unicode[STIX]{x1D713}$
. Then the equivalence

satisfies
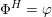 $\unicode[STIX]{x1D6F7}^{H}=\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D6F7}^{H}=\unicode[STIX]{x1D711}$
.
We can now forget about
![]() $S_{0}$
and only keep
$S_{0}$
and only keep
![]() $X$
and
$X$
and
![]() $S$
and the equivalence
$S$
and the equivalence
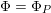 $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{P}$
with
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{P}$
with
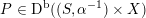 $P\in \text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)$
. Then consider the two families
$P\in \text{D}^{\text{b}}((S,\unicode[STIX]{x1D6FC}^{-1})\times X)$
. Then consider the two families
![]() ${\mathcal{X}}_{t}$
and
${\mathcal{X}}_{t}$
and
![]() $({\mathcal{S}}_{t},\unicode[STIX]{x1D6FC}_{t})$
over
$({\mathcal{S}}_{t},\unicode[STIX]{x1D6FC}_{t})$
over
![]() $D_{d}$
(or rather
$D_{d}$
(or rather
![]() $\tilde{{\mathcal{C}}}_{d}$
in order to use the Zariski topology) of cubics respectively twisted K3 surfaces with
$\tilde{{\mathcal{C}}}_{d}$
in order to use the Zariski topology) of cubics respectively twisted K3 surfaces with
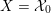 $X={\mathcal{X}}_{0}$
,
$X={\mathcal{X}}_{0}$
,
![]() $S={\mathcal{S}}_{0}$
, for which
$S={\mathcal{S}}_{0}$
, for which
![]() $\unicode[STIX]{x1D711}$
defines Hodge isometries
$\unicode[STIX]{x1D711}$
defines Hodge isometries  for all
for all
![]() $t$
. As
$t$
. As induces
induces
![]() $\unicode[STIX]{x1D711}$
, Theorem 5.2 applies and shows that
$\unicode[STIX]{x1D711}$
, Theorem 5.2 applies and shows that
![]() $\unicode[STIX]{x1D6F7}$
can be deformed to equivalences
$\unicode[STIX]{x1D6F7}$
can be deformed to equivalences  for all
for all
![]() $t$
in a Zariski open neighbourhood of
$t$
in a Zariski open neighbourhood of
![]() $0\in \tilde{{\mathcal{C}}}_{d}$
.
$0\in \tilde{{\mathcal{C}}}_{d}$
.
6.3 Proof of Theorem 1.5
The first assertion of the theorem has been proved already as Corollary 3.6. For assertions (ii) and (iii) recall that any FM-equivalence
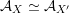 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
induces a Hodge isometry
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
induces a Hodge isometry
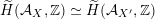 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
, cf. Proposition 3.4. So it remains to prove the converse for generic
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
, cf. Proposition 3.4. So it remains to prove the converse for generic
![]() $X\in {\mathcal{C}}_{d}$
with
$X\in {\mathcal{C}}_{d}$
with
![]() $d$
satisfying (
$d$
satisfying (
![]() $\ast \ast ^{\prime }$
) respectively very general
$\ast \ast ^{\prime }$
) respectively very general
![]() $X\in {\mathcal{C}}_{d}$
for arbitrary
$X\in {\mathcal{C}}_{d}$
for arbitrary
![]() $d$
. The first case is easy, as then, by Theorem 1.4,
$d$
. The first case is easy, as then, by Theorem 1.4,
 ${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
and
${\mathcal{A}}_{X}\simeq \text{D}^{\text{b}}(S,\unicode[STIX]{x1D6FC})$
and
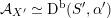 ${\mathcal{A}}_{X^{\prime }}\simeq \text{D}^{\text{b}}(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
for twisted K3 surfaces
${\mathcal{A}}_{X^{\prime }}\simeq \text{D}^{\text{b}}(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
for twisted K3 surfaces
![]() $(S,\unicode[STIX]{x1D6FC})$
respectively
$(S,\unicode[STIX]{x1D6FC})$
respectively
![]() $(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
. The assertion then follows from [Reference Huybrechts and StellariHS06] and Lemma 2.3.
$(S^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
. The assertion then follows from [Reference Huybrechts and StellariHS06] and Lemma 2.3.
For the second case consider the correspondence

of smooth cubics
![]() $X,X^{\prime }$
with
$X,X^{\prime }$
with
![]() $X\in {\mathcal{C}}_{d}$
and a Hodge isometry
$X\in {\mathcal{C}}_{d}$
and a Hodge isometry
![]() $\unicode[STIX]{x1D711}$
. (Note that with
$\unicode[STIX]{x1D711}$
. (Note that with
![]() $X$
also
$X$
also
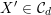 $X^{\prime }\in {\mathcal{C}}_{d}$
.) This correspondence consists of countably many components
$X^{\prime }\in {\mathcal{C}}_{d}$
.) This correspondence consists of countably many components
![]() $Z_{i}\subset Z$
and for the image of a component
$Z_{i}\subset Z$
and for the image of a component
![]() $Z_{0}\subset Z$
under the first projection
$Z_{0}\subset Z$
under the first projection 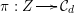 one either has
one either has
 $\unicode[STIX]{x1D70B}(Z_{0})\subset {\mathcal{C}}_{d}\cap \bigcup _{d^{\prime }\neq d}{\mathcal{C}}_{d^{\prime }}$
or
$\unicode[STIX]{x1D70B}(Z_{0})\subset {\mathcal{C}}_{d}\cap \bigcup _{d^{\prime }\neq d}{\mathcal{C}}_{d^{\prime }}$
or
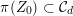 $\unicode[STIX]{x1D70B}(Z_{0})\subset {\mathcal{C}}_{d}$
is dense.
$\unicode[STIX]{x1D70B}(Z_{0})\subset {\mathcal{C}}_{d}$
is dense.
As we are interested in very general
![]() $X\in {\mathcal{C}}_{d}$
only, we may assume that we are in the latter situation. Then by [Reference Addington and ThomasAT14, Theorem 1.1], cf. § 6.1, one finds a
$X\in {\mathcal{C}}_{d}$
only, we may assume that we are in the latter situation. Then by [Reference Addington and ThomasAT14, Theorem 1.1], cf. § 6.1, one finds a
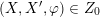 $(X,X^{\prime },\unicode[STIX]{x1D711})\in Z_{0}$
for which there exist K3 surfaces
$(X,X^{\prime },\unicode[STIX]{x1D711})\in Z_{0}$
for which there exist K3 surfaces
![]() $S$
and
$S$
and
![]() $S^{\prime }$
and FM-equivalences
$S^{\prime }$
and FM-equivalences

By Proposition 3.3,
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6F9}^{\prime }$
induce Hodge isometries
$\unicode[STIX]{x1D6F9}^{\prime }$
induce Hodge isometries
![]() $\unicode[STIX]{x1D6F9}^{H}$
respectively
$\unicode[STIX]{x1D6F9}^{H}$
respectively
![]() ${\unicode[STIX]{x1D6F9}^{\prime }}^{H}$
, which composed with
${\unicode[STIX]{x1D6F9}^{\prime }}^{H}$
, which composed with
![]() $\unicode[STIX]{x1D711}$
yield a Hodge isometry
$\unicode[STIX]{x1D711}$
yield a Hodge isometry

We may assume that
![]() $\unicode[STIX]{x1D711}_{0}$
is orientation preserving and, thus, induced by a FM-equivalence
$\unicode[STIX]{x1D711}_{0}$
is orientation preserving and, thus, induced by a FM-equivalence  Composing the latter with the equivalences (6.2) yields a FM-equivalence
Composing the latter with the equivalences (6.2) yields a FM-equivalence
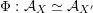 $\unicode[STIX]{x1D6F7}:{\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
inducing
$\unicode[STIX]{x1D6F7}:{\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
inducing
![]() $\unicode[STIX]{x1D711}$
. Now use Theorem 5.1 to deform
$\unicode[STIX]{x1D711}$
. Now use Theorem 5.1 to deform
![]() $\unicode[STIX]{x1D6F7}$
sideways to FM-equivalences
$\unicode[STIX]{x1D6F7}$
sideways to FM-equivalences  for all points
for all points
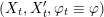 $(X_{t},X_{t}^{\prime },\unicode[STIX]{x1D711}_{t}\equiv \unicode[STIX]{x1D711})$
in a Zariski dense open subset
$(X_{t},X_{t}^{\prime },\unicode[STIX]{x1D711}_{t}\equiv \unicode[STIX]{x1D711})$
in a Zariski dense open subset
 $U_{0}\subset Z_{0}$
.
$U_{0}\subset Z_{0}$
.
Hence, for all
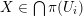 $X\in \bigcap \unicode[STIX]{x1D70B}(U_{i})$
, with the intersection over all components
$X\in \bigcap \unicode[STIX]{x1D70B}(U_{i})$
, with the intersection over all components
![]() $Z_{i}\subset Z$
(dominating
$Z_{i}\subset Z$
(dominating
![]() ${\mathcal{C}}_{d}$
), the existence of a Hodge isometry
${\mathcal{C}}_{d}$
), the existence of a Hodge isometry
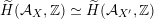 $\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
implies the existence of a FM-equivalence
$\widetilde{H}({\mathcal{A}}_{X},\mathbb{Z})\simeq \widetilde{H}({\mathcal{A}}_{X^{\prime }},\mathbb{Z})$
implies the existence of a FM-equivalence
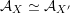 ${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
.
${\mathcal{A}}_{X}\simeq {\mathcal{A}}_{X^{\prime }}$
.
Acknowledgements
I would like to thank Nick Addington and Sasha Kuznetsov for very helpful discussions during the preparation of the paper. I am also grateful to Ben Bakker, Daniel Halpern-Leistner, Jørgen Rennemo, Paolo Stellari, Andrey Soldatenkov, and Richard Thomas for comments and suggestions. I enjoyed several discussions with Alex Perry, in particular on the possibility of proving a result like Theorem 1.1, for which he has also found a proof. Thanks to Emanuel Reinecke and Pawel Sosna for a long list of comments on the first version and to the referee for a very careful reading and innumerable suggestions.


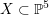
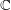
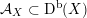
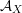
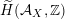
 of a non-special cubic preserves the natural orientation.
of a non-special cubic preserves the natural orientation.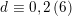
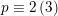
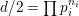


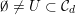
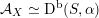
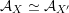
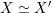
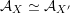
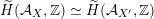
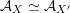
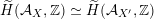

 into the
into the 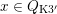
 for some
for some