Article contents
Resolution of T. Ward's Question and the Israel–Finch Conjecture: Precise Analysis of an Integer Sequence Arising in Dynamics
Published online by Cambridge University Press: 02 October 2014
Abstract
We analyse the first-order asymptotic growth of
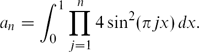 \[
a_{n}=\int_{0}^{1}\prod_{j=1}^{n}4\sin^{2}(\pi jx)\, dx.
\]
\[
a_{n}=\int_{0}^{1}\prod_{j=1}^{n}4\sin^{2}(\pi jx)\, dx.
\]
Keywords
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 24 , Special Issue 1: Honouring the Memory of Philippe Flajolet - Part 3 , January 2015 , pp. 195 - 215
- Copyright
- Copyright © Cambridge University Press 2014
References
- 1
- Cited by


