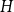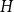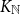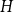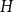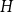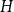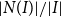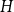1. Introduction
Let
![]() $K_{\mathbb{N}}$
be the complete graph on the natural numbers. Let
$K_{\mathbb{N}}$
be the complete graph on the natural numbers. Let
![]() $H$
be a countably infinite graph (meaning that the vertex set has the same cardinality as
$H$
be a countably infinite graph (meaning that the vertex set has the same cardinality as
![]() $\mathbb{N}$
). Suppose that the edges of
$\mathbb{N}$
). Suppose that the edges of
![]() $K_{\mathbb{N}}$
are coloured red or blue. We can find a monochromatic subgraph
$K_{\mathbb{N}}$
are coloured red or blue. We can find a monochromatic subgraph
![]() $H'\subseteq K_{\mathbb{N}}$
isomorphic to
$H'\subseteq K_{\mathbb{N}}$
isomorphic to
![]() $H$
. For example, using Ramsey’s Theorem, we can produce
$H$
. For example, using Ramsey’s Theorem, we can produce
![]() $H'$
by finding a bijection between
$H'$
by finding a bijection between
![]() $V(H)$
and the vertices of a monochromatic infinite clique. Out of all possible subgraphs
$V(H)$
and the vertices of a monochromatic infinite clique. Out of all possible subgraphs
![]() $H'$
, we want to find one which maximises its density. To measure the density, we use the following definition:
$H'$
, we want to find one which maximises its density. To measure the density, we use the following definition:
Definition 1.1. Let
![]() $S\subseteq{\mathbb{N}}$
. We define the upper density of
$S\subseteq{\mathbb{N}}$
. We define the upper density of
![]() $S$
(in this paper shortened to density) as
$S$
(in this paper shortened to density) as
If
![]() $H'\subseteq K_{\mathbb{N}}$
, we define
$H'\subseteq K_{\mathbb{N}}$
, we define
![]() $\bar d(H')=\bar d(V(H'))$
.
$\bar d(H')=\bar d(V(H'))$
.
We are interested in an extremal question: if
![]() $H$
is a fixed graph, what is the maximum density of
$H$
is a fixed graph, what is the maximum density of
![]() $H'$
that we can find in every red-blue colouring of
$H'$
that we can find in every red-blue colouring of
![]() $K_{\mathbb{N}}$
? We call this value the Ramsey upper density of
$K_{\mathbb{N}}$
? We call this value the Ramsey upper density of
![]() $H$
.
$H$
.
Definition 1.2. Let
![]() $H$
be a countably infinite graph. We define its Ramsey upper density
$H$
be a countably infinite graph. We define its Ramsey upper density
![]() $\rho (H)$
as the supremum of the values of
$\rho (H)$
as the supremum of the values of
![]() $\lambda$
for which, for every two-colouring of
$\lambda$
for which, for every two-colouring of
![]() $E(K_{\mathbb{N}})$
, there exists a monochromatic subgraph
$E(K_{\mathbb{N}})$
, there exists a monochromatic subgraph
![]() $H'\subseteq K_{\mathbb{N}}$
, isomorphic to
$H'\subseteq K_{\mathbb{N}}$
, isomorphic to
![]() $H$
, with
$H$
, with
![]() $\bar d(H')\geq \lambda$
.
$\bar d(H')\geq \lambda$
.
The study of this parameter was initiated by Erdős and Galvin [Reference Erdős and Galvin8] for the particular case
![]() $H=P_\infty$
, the one-way infinite path. They proved that
$H=P_\infty$
, the one-way infinite path. They proved that
![]() $2/3\leq \rho (P_\infty )\leq 8/9$
. After some improvements on these bounds in [Reference DeBiasio and McKenney6, Reference Lo, Sanhueza-Matamala and Wang10], the exact value
$2/3\leq \rho (P_\infty )\leq 8/9$
. After some improvements on these bounds in [Reference DeBiasio and McKenney6, Reference Lo, Sanhueza-Matamala and Wang10], the exact value
was determined by Corsten, DeBiasio, Lamaison and Lang [Reference Corsten, DeBiasio, Lamaison and Lang4]. The parameter
![]() $\rho (H)$
for general
$\rho (H)$
for general
![]() $H$
was first introduced by DeBiasio and McKenney [Reference DeBiasio and McKenney6].
$H$
was first introduced by DeBiasio and McKenney [Reference DeBiasio and McKenney6].
Our aim in this paper is to give bounds on
![]() $\rho (H)$
for a wider family of graphs
$\rho (H)$
for a wider family of graphs
![]() $H$
. These results can be found further down in the introduction, although some of the more general bounds, with a more involved statement, are left for later. As it will turn out, three parameters play an important role in the value of
$H$
. These results can be found further down in the introduction, although some of the more general bounds, with a more involved statement, are left for later. As it will turn out, three parameters play an important role in the value of
![]() $\rho (H)$
: its chromatic number, the number of components and the expansion properties of its independent sets.
$\rho (H)$
: its chromatic number, the number of components and the expansion properties of its independent sets.
1.1 Notation
An infinite graph is locally finite if every vertex has finite degree. The bounds that we will show in this paper apply only to locally finite graphs
![]() $H$
.
$H$
.
Given
![]() $S\subseteq V(H)$
, we will denote by
$S\subseteq V(H)$
, we will denote by
![]() $N(S)= (\cup _{v\in S} N(v) )\setminus S$
the set of vertices outside
$N(S)= (\cup _{v\in S} N(v) )\setminus S$
the set of vertices outside
![]() $S$
with a neighbour in
$S$
with a neighbour in
![]() $S$
. We let
$S$
. We let
![]() $\mu (H,n)$
be the minimum value of
$\mu (H,n)$
be the minimum value of
![]() $|N(I)|$
, where
$|N(I)|$
, where
![]() $I$
is an independent set in
$I$
is an independent set in
![]() $H$
of size
$H$
of size
![]() $n$
. We say that a set
$n$
. We say that a set
![]() $I$
is doubly independent if both
$I$
is doubly independent if both
![]() $I$
and
$I$
and
![]() $N(I)$
are independent.
$N(I)$
are independent.
We say that a family
![]() $\{S_1, S_2, \dots \}$
of subsets of
$\{S_1, S_2, \dots \}$
of subsets of
![]() $V(H)$
is concentrated in at most
$V(H)$
is concentrated in at most
![]() $k$
components if there are components
$k$
components if there are components
![]() $C_1, C_2, \dots, C_s$
of
$C_1, C_2, \dots, C_s$
of
![]() $H$
, with
$H$
, with
![]() $s\leq k$
, such that all but finitely many sets
$s\leq k$
, such that all but finitely many sets
![]() $S_i$
intersect some component
$S_i$
intersect some component
![]() $C_j$
. We say that
$C_j$
. We say that
![]() $V(H)$
is concentrated in at most
$V(H)$
is concentrated in at most
![]() $k$
components if
$k$
components if
![]() $\{\{v\}\;:\;v\in V(H)\}$
is concentrated in at most
$\{\{v\}\;:\;v\in V(H)\}$
is concentrated in at most
![]() $k$
components.
$k$
components.
On some occasions we will use
![]() $C\in \{R,B\}$
to designate a colour (red or blue). When this happens,
$C\in \{R,B\}$
to designate a colour (red or blue). When this happens,
![]() $\bar C$
will denote the other colour. In a graph
$\bar C$
will denote the other colour. In a graph
![]() $G$
with coloured vertices, we will use
$G$
with coloured vertices, we will use
![]() $C_G$
to refer to the set of vertices of colour
$C_G$
to refer to the set of vertices of colour
![]() $C$
. If there is no ambiguity, we will omit the subindex
$C$
. If there is no ambiguity, we will omit the subindex
![]() $G$
.
$G$
.
If
![]() $F$
is a finite graph, we denote by
$F$
is a finite graph, we denote by
![]() $\omega \cdot F$
the graph obtained by taking the disjoint union of a countably infinite number of copies of
$\omega \cdot F$
the graph obtained by taking the disjoint union of a countably infinite number of copies of
![]() $F$
.
$F$
.
Finally, we define a function
![]() $f(x)$
which will be crucial in relating the values of
$f(x)$
which will be crucial in relating the values of
![]() $\rho (H)$
and
$\rho (H)$
and
![]() $|N(I)|/|I|$
, where
$|N(I)|/|I|$
, where
![]() $I$
is an independent or a doubly independent set of
$I$
is an independent or a doubly independent set of
![]() $H$
. Unfortunately, there is no satisfying intuition for why this particular choice of
$H$
. Unfortunately, there is no satisfying intuition for why this particular choice of
![]() $f(x)$
, and not another, is behind the relation between these two parameters. It is interesting however that the same function
$f(x)$
, and not another, is behind the relation between these two parameters. It is interesting however that the same function
![]() $f(x)$
arises from the study of upper bounds and lower bounds for
$f(x)$
arises from the study of upper bounds and lower bounds for
![]() $\rho (H)$
.
$\rho (H)$
.
Since the definition of
![]() $f(x)$
is quite complicated and its comprehension is not essential to the appreciation of our results, we encourage the reader to skip it for now. For the reading of the introduction, knowing that such a function exists is enough. Of course, for the reading of the proofs, the precise definition becomes necessary.
$f(x)$
is quite complicated and its comprehension is not essential to the appreciation of our results, we encourage the reader to skip it for now. For the reading of the introduction, knowing that such a function exists is enough. Of course, for the reading of the proofs, the precise definition becomes necessary.
Definition 1.3. Let
![]() $\gamma \in (\!-\!1,1)$
. For a continuous function
$\gamma \in (\!-\!1,1)$
. For a continuous function
![]() $g(x)\;:\;[0,+\infty )\rightarrow \mathbb{R}$
, define
$g(x)\;:\;[0,+\infty )\rightarrow \mathbb{R}$
, define
where we take the minimum of the empty set to be
![]() $+\infty$
. We define
$+\infty$
. We define
![]() $h(\gamma )$
to be the infimum, over all 1-LipschitzFootnote
1
functions
$h(\gamma )$
to be the infimum, over all 1-LipschitzFootnote
1
functions
![]() $g$
with
$g$
with
![]() $g(0)=0$
, of
$g(0)=0$
, of
Define
![]() $f\;:\;(0,+\infty )\rightarrow \mathbb{R}$
as
$f\;:\;(0,+\infty )\rightarrow \mathbb{R}$
as
 \begin{equation*}f(\lambda )=1-\frac {1}{\frac {2\lambda }{(1+\lambda )^2}h\left (\frac {\lambda -1}{\lambda +1}\right )+\frac {2\lambda }{1+\lambda }}.\end{equation*}
\begin{equation*}f(\lambda )=1-\frac {1}{\frac {2\lambda }{(1+\lambda )^2}h\left (\frac {\lambda -1}{\lambda +1}\right )+\frac {2\lambda }{1+\lambda }}.\end{equation*}
We define
![]() $f(0)=1$
and
$f(0)=1$
and
![]() $f(\!+\!\infty )=1/2$
(by (2) below, we have
$f(\!+\!\infty )=1/2$
(by (2) below, we have
![]() $\lim \limits _{t\rightarrow 0}f(t)=1$
and
$\lim \limits _{t\rightarrow 0}f(t)=1$
and
![]() $\lim \limits _{t\rightarrow +\infty }f(t)=1/2$
.)
$\lim \limits _{t\rightarrow +\infty }f(t)=1/2$
.)
In an appendix to this paper, which can be found in the arXiv version (arXiv:2003.06329), we prove some properties of
![]() $f(x)$
, including the following bounds:
$f(x)$
, including the following bounds:
 \begin{equation} \frac{x+1}{2x+1}\leq f(x) \leq \left \{ \begin{array}{l@{\quad}l@{\quad}l} \dfrac{2x^2+3x+7+2\sqrt{x+1}}{4x^2+4x+9} & \text{for} & 0\leq x\lt 3,\\[12pt] \dfrac{x+1}{2x} & \text{for} & x \geq 3. \end{array} \right . \end{equation}
\begin{equation} \frac{x+1}{2x+1}\leq f(x) \leq \left \{ \begin{array}{l@{\quad}l@{\quad}l} \dfrac{2x^2+3x+7+2\sqrt{x+1}}{4x^2+4x+9} & \text{for} & 0\leq x\lt 3,\\[12pt] \dfrac{x+1}{2x} & \text{for} & x \geq 3. \end{array} \right . \end{equation}
The upper bound is sharp for
![]() $x\in [0,1]$
, and we conjectureFootnote
2
that it is sharp everywhere. Observe that
$x\in [0,1]$
, and we conjectureFootnote
2
that it is sharp everywhere. Observe that
![]() $f(1)=(12+\sqrt{8})/17=\rho (P_\infty )$
.
$f(1)=(12+\sqrt{8})/17=\rho (P_\infty )$
.
1.2 Results
We will now give a few bounds on
![]() $\rho (H)$
, some of which apply for all locally finite graphs and some of which apply only for particular families. In many cases the specific results follow from other results which are more general, but which have more involved statements. These will be stated in later sections.
$\rho (H)$
, some of which apply for all locally finite graphs and some of which apply only for particular families. In many cases the specific results follow from other results which are more general, but which have more involved statements. These will be stated in later sections.
For locally finite graphs, knowing the chromatic number and the number of components is enough to determine
![]() $\rho (H)$
up to a factor of 2.
$\rho (H)$
up to a factor of 2.
Theorem 1.4.
Let
![]() $H$
be a locally finite graph.
$H$
be a locally finite graph.
-
1. If
 $H$
has infinitely many components, then
$H$
has infinitely many components, then
 $\rho (H)\geq 1/2$
.
$\rho (H)\geq 1/2$
. -
2. If
 $H$
has finitely many components:
$H$
has finitely many components:
-
(a) If
 $H$
has infinite chromatic number, then
$H$
has infinite chromatic number, then
 $\rho (H)=0$
.
$\rho (H)=0$
. -
(b) If
 $H$
has finite chromatic number, then
where
$H$
has finite chromatic number, then
where \begin{equation*}\min \left \{\frac {b}{2(\chi (H)-1)}, \frac 12\right \}\leq \rho (H)\leq \min \left \{\frac {b}{\chi (H)-1},1\right \},\end{equation*}
\begin{equation*}\min \left \{\frac {b}{2(\chi (H)-1)}, \frac 12\right \}\leq \rho (H)\leq \min \left \{\frac {b}{\chi (H)-1},1\right \},\end{equation*}
 $b$
is the number of infinite components of
$b$
is the number of infinite components of
 $H$
.
$H$
.
-
This theorem answers a question in [Reference DeBiasio and McKenney6], which asks whether for every
![]() $\Delta$
there exists a constant
$\Delta$
there exists a constant
![]() $c\gt 0$
such that every graph with maximum degree at most
$c\gt 0$
such that every graph with maximum degree at most
![]() $\Delta$
has Ramsey upper density at least
$\Delta$
has Ramsey upper density at least
![]() $c$
:
$c$
:
Corollary 1.5.
If
![]() $H$
has maximum degree at most
$H$
has maximum degree at most
![]() $\Delta$
, then
$\Delta$
, then
![]() $\rho (H)\geq 1/(2\Delta )$
.
$\rho (H)\geq 1/(2\Delta )$
.
Let
![]() $P_\infty ^k$
be the
$P_\infty ^k$
be the
![]() $k$
th power of the infinite path, that is, the graph on
$k$
th power of the infinite path, that is, the graph on
![]() $\mathbb{N}$
in which
$\mathbb{N}$
in which
![]() $x$
and
$x$
and
![]() $y$
are connected if
$y$
are connected if
![]() $|x-y|\leq k$
. Elekes, Soukup, Soukup and Szentmiklóssy [Reference Elekes, Soukup, Soukup and Szentmiklóssy7] showed that, in every two-colouring of
$|x-y|\leq k$
. Elekes, Soukup, Soukup and Szentmiklóssy [Reference Elekes, Soukup, Soukup and Szentmiklóssy7] showed that, in every two-colouring of
![]() $K_{\mathbb{N}}$
, the vertex set can be partitioned into at most
$K_{\mathbb{N}}$
, the vertex set can be partitioned into at most
![]() $2^{2k-1}$
monochromatic copies of
$2^{2k-1}$
monochromatic copies of
![]() $P_\infty ^k$
plus a finite set, and the number of copies can be reduced to four for
$P_\infty ^k$
plus a finite set, and the number of copies can be reduced to four for
![]() $P_\infty ^2$
. DeBiasio and McKenney [Reference DeBiasio and McKenney6] pointed out that this implies
$P_\infty ^2$
. DeBiasio and McKenney [Reference DeBiasio and McKenney6] pointed out that this implies
![]() $\rho (P_\infty ^2)\geq 1/4$
and
$\rho (P_\infty ^2)\geq 1/4$
and
![]() $\rho (P_\infty ^k)\geq 2^{1-2k}$
. Theorem 1.4 improves the bound for
$\rho (P_\infty ^k)\geq 2^{1-2k}$
. Theorem 1.4 improves the bound for
![]() $k\geq 3$
to
$k\geq 3$
to
![]() $\rho (P_\infty ^k)\geq 1/(2k)$
.
$\rho (P_\infty ^k)\geq 1/(2k)$
.
The case 2a in Theorem 1.4 connects to a result of Corsten, DeBiasio and McKenney [Reference Corsten, DeBiasio and McKenney5]. While we show that every locally finite graph
![]() $H$
with finitely many components and infinite chromatic number has
$H$
with finitely many components and infinite chromatic number has
![]() $\rho (H)=0$
, they show that these graphs are ‘2-Ramsey-dense’, as they call it (see Corollary 1.7 in their paper). This property means that, in every two-colouring of
$\rho (H)=0$
, they show that these graphs are ‘2-Ramsey-dense’, as they call it (see Corollary 1.7 in their paper). This property means that, in every two-colouring of
![]() $E(K_{\mathbb{N}})$
, there exists a monochromatic copy of
$E(K_{\mathbb{N}})$
, there exists a monochromatic copy of
![]() $H$
with positive upper density. Of course this is not a contradiction, because there exists a sequence of colourings in which the density of the densest monochromatic copy of
$H$
with positive upper density. Of course this is not a contradiction, because there exists a sequence of colourings in which the density of the densest monochromatic copy of
![]() $H$
tends to 0.
$H$
tends to 0.
While no graph
![]() $H$
is known for which the lower bound in 2b is tight and not equal to
$H$
is known for which the lower bound in 2b is tight and not equal to
![]() $1/2$
, the upper bound is tight in the following example. Let
$1/2$
, the upper bound is tight in the following example. Let
![]() $T$
be the tree formed by an infinite path
$T$
be the tree formed by an infinite path
![]() $v_1v_2v_3\dots$
, in which we attach
$v_1v_2v_3\dots$
, in which we attach
![]() $i$
leaves to
$i$
leaves to
![]() $v_i$
for every
$v_i$
for every
![]() $i\in{\mathbb{N}}$
. Then
$i\in{\mathbb{N}}$
. Then
![]() $\rho (b\cdot T+K_a)=b/(a-1)$
for every
$\rho (b\cdot T+K_a)=b/(a-1)$
for every
![]() $1\leq b\lt a$
, where
$1\leq b\lt a$
, where
![]() $b\cdot T+K_a$
denotes the disjoint union of
$b\cdot T+K_a$
denotes the disjoint union of
![]() $b$
copies of
$b$
copies of
![]() $T$
and an
$T$
and an
![]() $a$
-clique. The lower bound will follow from Theorem 3.1.
$a$
-clique. The lower bound will follow from Theorem 3.1.
Another upper bound that applies to all locally finite graphs is related to the expansion of its independent sets:
Theorem 1.6.
Let
![]() $H$
be a locally finite graph. Then
$H$
be a locally finite graph. Then
There are many graphs for which the bound in Theorem 1.6 is tight. The following theorem captures some of them.
Theorem 1.7.
Let
![]() $H$
be a locally finite forest, or a locally finite bipartite graph in which every orbit of the automorphism group acting on
$H$
be a locally finite forest, or a locally finite bipartite graph in which every orbit of the automorphism group acting on
![]() $V(H)$
has infinite size. Then
$V(H)$
has infinite size. Then
This is a particular case of a more general condition on bipartite graphs that is sufficient for Theorem 1.6 to be tight. That condition is stated later as Theorem 4.1. The following corollaries illustrate some examples of graphs for which Theorem 1.7 applies:
Corollary 1.8.
Let
![]() $T_k$
be the infinite
$T_k$
be the infinite
![]() $k$
-ary tree, that is, the rooted tree in which every vertex has
$k$
-ary tree, that is, the rooted tree in which every vertex has
![]() $k$
children. Then
$k$
children. Then
![]() $\rho (T_k)=f(k)$
.
$\rho (T_k)=f(k)$
.
Corollary 1.9.
Let
![]() $\mathrm{Grid}_d$
be the infinite
$\mathrm{Grid}_d$
be the infinite
![]() $d$
-dimensional grid, that is, the graph on
$d$
-dimensional grid, that is, the graph on
![]() $\mathbb{Z}^d$
where two vertices are connected if they are at Euclidean distance 1. Then
$\mathbb{Z}^d$
where two vertices are connected if they are at Euclidean distance 1. Then
![]() $\rho (\mathrm{Grid}_d)=f(1)=(12+\sqrt{8})/17\approx 0.87226$
.
$\rho (\mathrm{Grid}_d)=f(1)=(12+\sqrt{8})/17\approx 0.87226$
.
Corollary 1.10.
Let
![]() $F$
be a finite bipartite graph. Then
$F$
be a finite bipartite graph. Then
 \begin{equation*}\rho (\omega \cdot F)=f\left (\min \limits _{\substack {I\; \text{indep. in } F\\ I\neq \emptyset }}\frac {|N(I)|}{|I|}\right ).\end{equation*}
\begin{equation*}\rho (\omega \cdot F)=f\left (\min \limits _{\substack {I\; \text{indep. in } F\\ I\neq \emptyset }}\frac {|N(I)|}{|I|}\right ).\end{equation*}
In particular, we have
![]() $\rho (C_{2k})=f(1)$
for every
$\rho (C_{2k})=f(1)$
for every
![]() $k\geq 2$
, and for every
$k\geq 2$
, and for every
![]() $1\leq a\leq b$
we have
$1\leq a\leq b$
we have
 \begin{equation*}\rho (\omega \cdot K_{a,b})=f\left (\frac ab\right )=\frac {2\left (\frac ab\right )^2+3\left (\frac ab\right )+7+2\sqrt {\frac ab+1}}{4\left (\frac ab\right )^2+4\left (\frac ab\right )+9}.\end{equation*}
\begin{equation*}\rho (\omega \cdot K_{a,b})=f\left (\frac ab\right )=\frac {2\left (\frac ab\right )^2+3\left (\frac ab\right )+7+2\sqrt {\frac ab+1}}{4\left (\frac ab\right )^2+4\left (\frac ab\right )+9}.\end{equation*}
In a finite bipartite graph
![]() $F$
, there is always an independent set satisfying
$F$
, there is always an independent set satisfying
![]() $|N(I)|\leq |I|$
(one of the two partition classes has this), so the value of
$|N(I)|\leq |I|$
(one of the two partition classes has this), so the value of
![]() $\rho (\omega \cdot F)$
always falls on the range in which
$\rho (\omega \cdot F)$
always falls on the range in which
![]() $f(x)$
is known explicitly.
$f(x)$
is known explicitly.
Finally, we will give two more lower bounds in the particular case of infinite factors
![]() $\omega \cdot F$
. The first one is analogous to Corollary 1.10:
$\omega \cdot F$
. The first one is analogous to Corollary 1.10:
Theorem 1.11.
Let
![]() $F$
be a finite connected graph, and let
$F$
be a finite connected graph, and let
![]() $I\subseteq V(F)$
be a non-empty doubly independent set. Then
$I\subseteq V(F)$
be a non-empty doubly independent set. Then
![]() $\rho (\omega \cdot F)\geq f\left (\frac{|N(I)|}{|I|}\right )$
.
$\rho (\omega \cdot F)\geq f\left (\frac{|N(I)|}{|I|}\right )$
.
If the independent set
![]() $I\subseteq V(F)$
that minimises
$I\subseteq V(F)$
that minimises
![]() $|N(I)|/|I|$
is doubly independent, then Theorems 1.6 and 1.11 together give the exact value for
$|N(I)|/|I|$
is doubly independent, then Theorems 1.6 and 1.11 together give the exact value for
![]() $\rho (\omega \cdot F)$
. This is always true in bipartite graphs, giving another reason why Corollary 1.10 holds. Figure 2 shows four non-bipartite graphs
$\rho (\omega \cdot F)$
. This is always true in bipartite graphs, giving another reason why Corollary 1.10 holds. Figure 2 shows four non-bipartite graphs
![]() $F$
for which this holds. If the graph
$F$
for which this holds. If the graph
![]() $F$
does not contain any non-empty doubly independent sets (such as
$F$
does not contain any non-empty doubly independent sets (such as
![]() $K_3$
), the following lower bound can be used:
$K_3$
), the following lower bound can be used:
Theorem 1.12.
For every finite graph
![]() $F$
, we have
$F$
, we have
This theorem gives the best known lower bound for
![]() $\rho (\omega \cdot K_3)$
. Combining Theorems 1.12 with 1.6 and (2) we obtain
$\rho (\omega \cdot K_3)$
. Combining Theorems 1.12 with 1.6 and (2) we obtain
This paper is organised as follows: we prove the general upper bounds in Section 2, and the general lower bounds in Section 3, besides a lemma that is instead proved in the appendix (the bulk of this proof is a rather long series of calculations without any interesting ideas behind). In Section 4, we discuss the application of the general bounds to particular families of graphs and obtain the remaining results above. In Section 5 we state some open questions. In the appendix, available in the arXiv version of the paper, we prove some properties of
![]() $f(x)$
.
$f(x)$
.

Figure 1. Plot of the function
![]() $f(x)$
on the interval
$f(x)$
on the interval
![]() $[0,1]$
, and the upper and lower bounds elsewhere. The conjectured value is given in blue.
$[0,1]$
, and the upper and lower bounds elsewhere. The conjectured value is given in blue.

Figure 2. Four non-bipartite graphs
![]() $F$
for which
$F$
for which
![]() $\rho (\omega \cdot F)$
equals
$\rho (\omega \cdot F)$
equals
![]() $f(1)$
,
$f(1)$
,
![]() $f(1)$
,
$f(1)$
,
![]() $f(2)$
and
$f(2)$
and
![]() $f(3/2)$
respectively, with their doubly independent sets indicated.
$f(3/2)$
respectively, with their doubly independent sets indicated.
2. General upper bounds
We will prove two upper bounds in this section: the first one implies the upper bound from items 2a and 2b from Theorem 1.4, while the second one is Theorem 1.6. In both cases we will construct a colouring of
![]() $E(K_{\mathbb{N}})$
in which no dense monochromatic copy of
$E(K_{\mathbb{N}})$
in which no dense monochromatic copy of
![]() $H$
exists.
$H$
exists.
Theorem 2.1.
Let
![]() $H$
be a locally finite graph with chromatic number at least
$H$
be a locally finite graph with chromatic number at least
![]() $a$
, such that
$a$
, such that
![]() $V(H)$
is concentrated in at most
$V(H)$
is concentrated in at most
![]() $b$
components. There exists a two-colouring of
$b$
components. There exists a two-colouring of
![]() $E(K_{\mathbb{N}})$
in which every monochromatic copy of
$E(K_{\mathbb{N}})$
in which every monochromatic copy of
![]() $H$
has density at most
$H$
has density at most
![]() $b/(a-1)$
.
$b/(a-1)$
.
Proof. Consider the colouring of
![]() $E(K_{\mathbb{N}})$
in which the edge
$E(K_{\mathbb{N}})$
in which the edge
![]() $uv$
is red iff
$uv$
is red iff
![]() $a-1$
divides
$a-1$
divides
![]() $v-u$
. The graph formed by the blue edges has chromatic number
$v-u$
. The graph formed by the blue edges has chromatic number
![]() $a-1$
and thus does not contain
$a-1$
and thus does not contain
![]() $H$
as a subgraph. Every monochromatic copy
$H$
as a subgraph. Every monochromatic copy
![]() $H'$
of
$H'$
of
![]() $H$
in this colouring is red.
$H$
in this colouring is red.
The red graph consists of
![]() $a-1$
cliques
$a-1$
cliques
![]() $C_1, \dots, C_{a-1}$
, each with
$C_1, \dots, C_{a-1}$
, each with
![]() $\bar d(C_i)=1/(a-1)$
. The
$\bar d(C_i)=1/(a-1)$
. The
![]() $b$
components that concentrate
$b$
components that concentrate
![]() $V(H')$
must be each contained in a clique
$V(H')$
must be each contained in a clique
![]() $C_i$
. Because modifying finitely many elements does not affect the density of a set, we have
$C_i$
. Because modifying finitely many elements does not affect the density of a set, we have
![]() $\bar d(H')\leq \bar d(C_1\cup \dots \cup C_b)=b/(a-1)$
. We conclude that
$\bar d(H')\leq \bar d(C_1\cup \dots \cup C_b)=b/(a-1)$
. We conclude that
![]() $\rho (H)\leq b/(a-1)$
.
$\rho (H)\leq b/(a-1)$
.
Next we will prove Theorem 1.6. As before, the goal is to construct a two-colouring of
![]() $E(K_{\mathbb{N}})$
without dense monochromatic copies of
$E(K_{\mathbb{N}})$
without dense monochromatic copies of
![]() $H$
.
$H$
.
The intuition behind the construction to prove Theorem 1.6 is as follows: suppose that we are trying to find a red copy
![]() $H'$
of
$H'$
of
![]() $H$
. If we have a blue clique
$H$
. If we have a blue clique
![]() $K$
which has fewer than
$K$
which has fewer than
![]() $k$
vertices neighbouring
$k$
vertices neighbouring
![]() $K$
through some red edge, and
$K$
through some red edge, and
![]() $\mu (H,t)=k$
, then we know that fewer than
$\mu (H,t)=k$
, then we know that fewer than
![]() $t$
vertices from
$t$
vertices from
![]() $K$
can be in
$K$
can be in
![]() $H'$
, because those vertices correspond to an independent set in
$H'$
, because those vertices correspond to an independent set in
![]() $H$
. Our goal is to find a construction that maximises the number of vertices from
$H$
. Our goal is to find a construction that maximises the number of vertices from
![]() $[n]$
that can be excluded from a potential red or blue
$[n]$
that can be excluded from a potential red or blue
![]() $H'$
using this method.
$H'$
using this method.
This same approach was used, in the case of the infinite path, by Erdős and Galvin [Reference Erdős and Galvin8]. The improvement that Corsten, DeBiasio, Lamaison and Lang [Reference Corsten, DeBiasio, Lamaison and Lang4] made over their colouring came from a two-step construction: we start with an infinite set of vertices, we first decide the colour of the edges between them and then we choose the element of
![]() $\mathbb{N}$
that will correspond to each vertex. The same two-step technique is used here.
$\mathbb{N}$
that will correspond to each vertex. The same two-step technique is used here.
Proof of Theorem
1.6. Denote
![]() $\lambda =\liminf \limits _{n\rightarrow \infty }\frac{\mu (H,n)}{n}$
. We assume that
$\lambda =\liminf \limits _{n\rightarrow \infty }\frac{\mu (H,n)}{n}$
. We assume that
![]() $\lambda \gt 0$
, as otherwise the statement becomes the trivial inequality
$\lambda \gt 0$
, as otherwise the statement becomes the trivial inequality
![]() $\rho (H)\leq 1$
.
$\rho (H)\leq 1$
.
Let
![]() $\epsilon \gt 0$
. Let
$\epsilon \gt 0$
. Let
![]() $g$
be a 1-Lipschitz function such that the upper limit in (1) is less than
$g$
be a 1-Lipschitz function such that the upper limit in (1) is less than
![]() $h(\gamma )+\epsilon$
, for
$h(\gamma )+\epsilon$
, for
![]() $\gamma =\frac{\lambda -1}{\lambda +1}$
. Take an infinite set of vertices
$\gamma =\frac{\lambda -1}{\lambda +1}$
. Take an infinite set of vertices
![]() $v_1, v_2, \dots$
and arrange them from left to right in this order. Colour these vertices red and blue, in such a way that, for every
$v_1, v_2, \dots$
and arrange them from left to right in this order. Colour these vertices red and blue, in such a way that, for every
![]() $n\in{\mathbb{N}}$
, among the
$n\in{\mathbb{N}}$
, among the
![]() $n$
leftmost vertices there are exactly
$n$
leftmost vertices there are exactly
![]() $\lfloor (n+g(n))/2\rfloor$
red vertices (this is possible because
$\lfloor (n+g(n))/2\rfloor$
red vertices (this is possible because
![]() $g$
is 1-Lipschitz). Form a two-coloured complete graph by giving each edge the colour of its leftmost endpoint.
$g$
is 1-Lipschitz). Form a two-coloured complete graph by giving each edge the colour of its leftmost endpoint.
There must be infinitely many vertices of each colour. Indeed, if there are finitely many red vertices then the non-decreasing function
![]() $\frac{x+g(x)}{2}$
is bounded, while if there are finitely many blue vertices the non-decreasing function
$\frac{x+g(x)}{2}$
is bounded, while if there are finitely many blue vertices the non-decreasing function
![]() $\frac{x-g(x)}{2}$
is bounded. Note that if
$\frac{x-g(x)}{2}$
is bounded. Note that if
![]() $x\pm g(x)$
is bounded, then
$x\pm g(x)$
is bounded, then
![]() $\gamma x\pm g(x)$
has an upper bound, as
$\gamma x\pm g(x)$
has an upper bound, as
![]() $\gamma \leq 1$
. In the first case
$\gamma \leq 1$
. In the first case
![]() $\Gamma ^+_\gamma (g,n)=+\infty$
for every
$\Gamma ^+_\gamma (g,n)=+\infty$
for every
![]() $n$
large enough, while in the second case
$n$
large enough, while in the second case
![]() $\Gamma ^-_\gamma (g,n)=+\infty$
.
$\Gamma ^-_\gamma (g,n)=+\infty$
.
Let the red vertices be
![]() $r_1, r_2, r_3, \dots$
and the blue vertices be
$r_1, r_2, r_3, \dots$
and the blue vertices be
![]() $b_1, b_2, b_3, \dots$
, according to the left-to-right order. Let
$b_1, b_2, b_3, \dots$
, according to the left-to-right order. Let
![]() $\alpha _i$
be the smallest value such that
$\alpha _i$
be the smallest value such that
![]() $r_{\alpha _i}$
has at most
$r_{\alpha _i}$
has at most
![]() $\lambda (\alpha _i-i)$
blue vertices to its left, and
$\lambda (\alpha _i-i)$
blue vertices to its left, and
![]() $\beta _i$
the smallest value such that
$\beta _i$
the smallest value such that
![]() $b_{\beta _i}$
has at most
$b_{\beta _i}$
has at most
![]() $\lambda (\beta _i-i)$
red vertices to its left. The following discussion will not only prove the existence of
$\lambda (\beta _i-i)$
red vertices to its left. The following discussion will not only prove the existence of
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\beta _i$
, but also give a bound on them.
$\beta _i$
, but also give a bound on them.
For a fixed value of
![]() $i$
, let
$i$
, let
![]() $w=\frac{2}{1+\lambda }(\lambda i+2\lambda +2)$
. Let
$w=\frac{2}{1+\lambda }(\lambda i+2\lambda +2)$
. Let
![]() $z^+=\Gamma ^+_\gamma (g,w)$
and
$z^+=\Gamma ^+_\gamma (g,w)$
and
![]() $z^-=\Gamma ^-_\gamma (g,w)$
. By continuity of
$z^-=\Gamma ^-_\gamma (g,w)$
. By continuity of
![]() $g$
and definition of
$g$
and definition of
![]() $\Gamma ^+_\gamma$
and
$\Gamma ^+_\gamma$
and
![]() $\Gamma ^-_\gamma$
, we have
$\Gamma ^-_\gamma$
, we have
One can check that the following identity holds by substution of
![]() $g(z^-)$
:
$g(z^-)$
:
Among the
![]() $\lfloor z^-\rfloor$
leftmost vertices there are
$\lfloor z^-\rfloor$
leftmost vertices there are
![]() $\left \lfloor \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2}\right \rfloor$
red vertices and
$\left \lfloor \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2}\right \rfloor$
red vertices and
![]() $\lfloor z^-\rfloor -\left \lfloor \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2}\right \rfloor$
blue vertices. Observe that
$\lfloor z^-\rfloor -\left \lfloor \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2}\right \rfloor$
blue vertices. Observe that
 \begin{align*} \left \lfloor \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2}\right \rfloor & \leq \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2} \leq \frac{z^-+g(z^-)}{2} \lt \lambda \left (\frac{z^--g(z^-)}{2}-i-2\right )\\[5pt] & \leq \lambda \left (\lfloor z^-\rfloor -\left \lfloor \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2}\right \rfloor -i\right ). \end{align*}
\begin{align*} \left \lfloor \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2}\right \rfloor & \leq \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2} \leq \frac{z^-+g(z^-)}{2} \lt \lambda \left (\frac{z^--g(z^-)}{2}-i-2\right )\\[5pt] & \leq \lambda \left (\lfloor z^-\rfloor -\left \lfloor \frac{\lfloor z^-\rfloor +g(\lfloor z^-\rfloor )}{2}\right \rfloor -i\right ). \end{align*}
If the last blue vertex among those
![]() $\lfloor z^-\rfloor$
is
$\lfloor z^-\rfloor$
is
![]() $b_{\tau }$
, then the number of red vertices to its left is less than
$b_{\tau }$
, then the number of red vertices to its left is less than
![]() $\lambda (\tau -i)$
, meaning that
$\lambda (\tau -i)$
, meaning that
![]() $\beta _{i}\leq \tau$
, and in particular
$\beta _{i}\leq \tau$
, and in particular
![]() $\beta _i$
exists. Hence
$\beta _i$
exists. Hence
Analogously, one has the identity
and the inequality
Hence we find
Adding the two values together, for
![]() $i$
large enough we have
$i$
large enough we have
Let
![]() $\phi\;:\;\mathbb{N}\rightarrow \{v_1, v_2, \dots \}$
be an arbitrary bijection satisfying
$\phi\;:\;\mathbb{N}\rightarrow \{v_1, v_2, \dots \}$
be an arbitrary bijection satisfying
![]() $\phi ([\alpha _j+\beta _j])=\{r_1, r_2, \dots, r_{\alpha _j}, b_1, b_2, \dots, b_{\beta _j}\}$
for every
$\phi ([\alpha _j+\beta _j])=\{r_1, r_2, \dots, r_{\alpha _j}, b_1, b_2, \dots, b_{\beta _j}\}$
for every
![]() $j$
. The function
$j$
. The function
![]() $\phi$
defines a colouring of
$\phi$
defines a colouring of
![]() $E(K_{\mathbb{N}})$
, where the colour of the edge
$E(K_{\mathbb{N}})$
, where the colour of the edge
![]() $ij$
is the colour of the edge
$ij$
is the colour of the edge
![]() $\phi (i)\phi (j)$
.
$\phi (i)\phi (j)$
.
Let
![]() $R$
and
$R$
and
![]() $B$
be the sets of positive integers
$B$
be the sets of positive integers
![]() $i$
whose image
$i$
whose image
![]() $\phi (i)$
is red or blue, respectively. Let
$\phi (i)$
is red or blue, respectively. Let
![]() $H'\subseteq K_{\mathbb{N}}$
be a monochromatic copy of
$H'\subseteq K_{\mathbb{N}}$
be a monochromatic copy of
![]() $H$
in this colouring. Suppose that
$H$
in this colouring. Suppose that
![]() $H'$
is red. Let
$H'$
is red. Let
![]() $n$
be a positive integer, and let
$n$
be a positive integer, and let
![]() $B_n=V(H')\cap [n]\cap B$
. Because the vertices of
$B_n=V(H')\cap [n]\cap B$
. Because the vertices of
![]() $B_n$
form a monochromatic blue clique in our colouring of
$B_n$
form a monochromatic blue clique in our colouring of
![]() $E(K_{\mathbb{N}})$
, the set
$E(K_{\mathbb{N}})$
, the set
![]() $B_n$
must be independent in
$B_n$
must be independent in
![]() $H'$
.
$H'$
.
Let
![]() $j$
be the minimum value such that
$j$
be the minimum value such that
![]() $\phi (B\cap [n])\subseteq \{b_1, b_2, \dots, b_{\beta _j}\}$
. We claim first that there are at least
$\phi (B\cap [n])\subseteq \{b_1, b_2, \dots, b_{\beta _j}\}$
. We claim first that there are at least
![]() $(1-O(\epsilon ))j$
vertices in
$(1-O(\epsilon ))j$
vertices in
![]() $[n]$
which do not belong to
$[n]$
which do not belong to
![]() $H'$
. Indeed, let
$H'$
. Indeed, let
![]() $B'_{\!\!n}=V(H')\cap \phi ^{-1}(\{b_1, b_2, \dots, b_{\beta _{j-1}}\})\subseteq B_n$
. From the construction of the colouring, the vertices that are connected to a vertex of
$B'_{\!\!n}=V(H')\cap \phi ^{-1}(\{b_1, b_2, \dots, b_{\beta _{j-1}}\})\subseteq B_n$
. From the construction of the colouring, the vertices that are connected to a vertex of
![]() $\{b_1, b_2, \dots, b_{\beta _{j-1}}\}$
through a red edge are precisely the red vertices to the left of
$\{b_1, b_2, \dots, b_{\beta _{j-1}}\}$
through a red edge are precisely the red vertices to the left of
![]() $b_{\beta _{j-1}}$
, of which there are at most
$b_{\beta _{j-1}}$
, of which there are at most
![]() $\lambda (\beta _{j-1}-(j-1))$
. This means that
$\lambda (\beta _{j-1}-(j-1))$
. This means that
![]() $\mu (H,|B'_{\!\!n}|)\leq \lambda (\beta _{j-1}-(j-1))$
. For
$\mu (H,|B'_{\!\!n}|)\leq \lambda (\beta _{j-1}-(j-1))$
. For
![]() $j$
large enough, this implies
$j$
large enough, this implies
![]() $|B'_{\!\!n}|\leq (1+o(1))(\beta _{j-1}-(j-1))$
, and since the vertices in
$|B'_{\!\!n}|\leq (1+o(1))(\beta _{j-1}-(j-1))$
, and since the vertices in
![]() $\phi ^{-1}(\{b_1, b_2, \dots, b_{\beta _{j-1}}\})$
which are not in
$\phi ^{-1}(\{b_1, b_2, \dots, b_{\beta _{j-1}}\})$
which are not in
![]() $B'_{\!\!n}$
are not in
$B'_{\!\!n}$
are not in
![]() $V(H')$
,
$V(H')$
,
Since
![]() $\beta _j\leq \alpha _j+\beta _j=O(j)$
by (3), the right hand side in the inequality above is
$\beta _j\leq \alpha _j+\beta _j=O(j)$
by (3), the right hand side in the inequality above is
![]() $(1-o(1))j$
.
$(1-o(1))j$
.
Observe next that we cannot have
![]() $\beta _j=\beta _{j+1}$
. This is because
$\beta _j=\beta _{j+1}$
. This is because
![]() $b_{\beta _j-1}$
, which is to the leftFootnote
3
of
$b_{\beta _j-1}$
, which is to the leftFootnote
3
of
![]() $b_{\beta _j}$
, has more than
$b_{\beta _j}$
, has more than
![]() $\lambda ((\beta _j-1)-j)=\lambda (\beta _j-(j+1))$
red vertices to its left. We thus have, by minimality of
$\lambda ((\beta _j-1)-j)=\lambda (\beta _j-(j+1))$
red vertices to its left. We thus have, by minimality of
![]() $j$
, that
$j$
, that
![]() $b_{\beta _{j+1}}\notin \phi ([n])$
, and by construction of
$b_{\beta _{j+1}}\notin \phi ([n])$
, and by construction of
![]() $\phi$
we have
$\phi$
we have
![]() $\phi ([n])\subset \{r_1,r_2,\dots, r_{\alpha _{j+1}}, b_1, b_2, \dots, b_{\beta _{j+1}}\}$
. This leads to the desired bound:
$\phi ([n])\subset \{r_1,r_2,\dots, r_{\alpha _{j+1}}, b_1, b_2, \dots, b_{\beta _{j+1}}\}$
. This leads to the desired bound:
 \begin{equation*}\frac {|V(H')\cap [n]|}{n}\leq 1-\frac {(1-o(1))j}{n}\leq 1-\frac {(1-o(1))j}{\alpha _{j+1}+\beta _{j+1}}\leq 1-\frac {1-o(1)}{\left (\frac {1-\gamma }{2}h(\gamma )+\epsilon +1\right )\frac {2\lambda }{1+\lambda }}\end{equation*}
\begin{equation*}\frac {|V(H')\cap [n]|}{n}\leq 1-\frac {(1-o(1))j}{n}\leq 1-\frac {(1-o(1))j}{\alpha _{j+1}+\beta _{j+1}}\leq 1-\frac {1-o(1)}{\left (\frac {1-\gamma }{2}h(\gamma )+\epsilon +1\right )\frac {2\lambda }{1+\lambda }}\end{equation*}
which for
![]() $\epsilon$
small enough and
$\epsilon$
small enough and
![]() $n$
large enough can take values arbitrarily close to
$n$
large enough can take values arbitrarily close to
![]() $f(\lambda )$
.
$f(\lambda )$
.
The case in which
![]() $H'$
is monochromatic blue is analogous. Indeed, besides the direction of the rounding, it is equivalent to taking the function
$H'$
is monochromatic blue is analogous. Indeed, besides the direction of the rounding, it is equivalent to taking the function
![]() $-g(x)$
instead of
$-g(x)$
instead of
![]() $g(x)$
.
$g(x)$
.
3. General lower bounds
In this section we will prove three lower bounds. One is item 1 from Theorem 1.4, another is the lower bound of item 2b in the same theorem, and the final one is the following, which will be used in the proof of Theorems 4.1 and 1.11:
Theorem 3.1.
Let
![]() $H$
be a locally finite graph,
$H$
be a locally finite graph,
![]() $a,b,r,s$
be positive integers with
$a,b,r,s$
be positive integers with
![]() $a\gt b$
, and
$a\gt b$
, and
![]() $\Psi\;:\;V(H)\rightarrow [a]$
be a proper colouring. Suppose that there exists an infinitely family of pairwise disjoint doubly independent sets
$\Psi\;:\;V(H)\rightarrow [a]$
be a proper colouring. Suppose that there exists an infinitely family of pairwise disjoint doubly independent sets
![]() $I_1, I_2, \dots$
in
$I_1, I_2, \dots$
in
![]() $H$
, not concentrated in fewer than
$H$
, not concentrated in fewer than
![]() $b$
components and each
$b$
components and each
![]() $I_i$
contained in a single component of
$I_i$
contained in a single component of
![]() $H$
, such that
$H$
, such that
![]() $|I_i|=r$
,
$|I_i|=r$
,
![]() $|N(I_i)|\leq s$
and
$|N(I_i)|\leq s$
and
![]() $\Psi (v)=a$
for all
$\Psi (v)=a$
for all
![]() $v\in N(I_i)$
. Then
$v\in N(I_i)$
. Then
As an example of a graph whose Ramsey density can be computed from Theorem 3.1, but not from the other lower bounds mentioned in this paper, let
![]() $H=b\cdot T+K_a$
be the graph described shortly before the statement of Theorem 1.6. We can define a proper colouring
$H=b\cdot T+K_a$
be the graph described shortly before the statement of Theorem 1.6. We can define a proper colouring
![]() $\Psi\;:\;V(H)\rightarrow [a]$
in which the vertices of
$\Psi\;:\;V(H)\rightarrow [a]$
in which the vertices of
![]() $K_a$
all receive different colours, and the trees
$K_a$
all receive different colours, and the trees
![]() $T$
are properly two-coloured with colours
$T$
are properly two-coloured with colours
![]() $\{1,a\}$
. Then for every
$\{1,a\}$
. Then for every
![]() $r\in{\mathbb{N}}$
there exist infinitely many pairwise disjoint independent sets
$r\in{\mathbb{N}}$
there exist infinitely many pairwise disjoint independent sets
![]() $I$
, in every
$I$
, in every
![]() $T$
-component, where
$T$
-component, where
![]() $N(I)$
is a single vertex with colour
$N(I)$
is a single vertex with colour
![]() $a$
(just take
$a$
(just take
![]() $r$
leaves of a vertex with label greater than
$r$
leaves of a vertex with label greater than
![]() $r$
and colour
$r$
and colour
![]() $a$
). Theorem 3.1 then tells us that
$a$
). Theorem 3.1 then tells us that
![]() $\rho (b\cdot T+K_a)\geq \frac{b}{a-1}f\left (r^{-1}\right )$
for all
$\rho (b\cdot T+K_a)\geq \frac{b}{a-1}f\left (r^{-1}\right )$
for all
![]() $r\in{\mathbb{N}}$
, and so
$r\in{\mathbb{N}}$
, and so
![]() $\rho (b\cdot T+K_a)\geq \frac{b}{a-1}$
. We will have equality here, as this matches the upper bound from Theorem 1.42b.
$\rho (b\cdot T+K_a)\geq \frac{b}{a-1}$
. We will have equality here, as this matches the upper bound from Theorem 1.42b.
Another example is the graph
![]() $2\cdot P_\infty +K_3$
(disjoint union of two infinite paths and a triangle). The graph can be properly coloured with colours
$2\cdot P_\infty +K_3$
(disjoint union of two infinite paths and a triangle). The graph can be properly coloured with colours
![]() $\{1,2,3\}$
in a way that both paths use only colours
$\{1,2,3\}$
in a way that both paths use only colours
![]() $\{1,3\}$
. Then for every
$\{1,3\}$
. Then for every
![]() $r$
, each
$r$
, each
![]() $P_\infty$
-component contains infinitely many pairwise disjoint independent sets
$P_\infty$
-component contains infinitely many pairwise disjoint independent sets
![]() $I$
with
$I$
with
![]() $|I|=r$
,
$|I|=r$
,
![]() $|N(I)|=r+1$
and
$|N(I)|=r+1$
and
![]() $N(I)$
being monochromatic in colour 3 (just take
$N(I)$
being monochromatic in colour 3 (just take
![]() $r$
consecutive vertices receiving colour 1). By Theorem 3.1, we have
$r$
consecutive vertices receiving colour 1). By Theorem 3.1, we have
![]() $\rho (2\cdot P_\infty +K_3)\geq f\left (\frac{r+1}r\right )$
and, by continuity of
$\rho (2\cdot P_\infty +K_3)\geq f\left (\frac{r+1}r\right )$
and, by continuity of
![]() $f(x)$
, we have
$f(x)$
, we have
![]() $\rho (2\cdot P_\infty +K_3)\geq f(1)$
, which matches the upper bound from Theorem 1.6.
$\rho (2\cdot P_\infty +K_3)\geq f(1)$
, which matches the upper bound from Theorem 1.6.
However, for every graph for which we know that Theorem 3.1 produces the correct lower bound, we either have
![]() $a-1=b$
or
$a-1=b$
or
![]() $s/r\rightarrow 0$
, as in the two examples above.
$s/r\rightarrow 0$
, as in the two examples above.
We start with the proof of Theorem 1.41. This result follows easily from the infinite version of Ramsey’s theorem:
Proof of Theorem
1.41. Let
![]() $\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be an edge-colouring. Let
$\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be an edge-colouring. Let
![]() $\mathcal{F}$
be an inclusion-maximal family of pairwise disjoint monochromatic infinite cliques in
$\mathcal{F}$
be an inclusion-maximal family of pairwise disjoint monochromatic infinite cliques in
![]() $\chi$
. Then
$\chi$
. Then
![]() ${\mathbb{N}}\setminus V(\mathcal{F})$
is finite, because otherwise by Ramsey’s theorem there would be an infinite monochromatic clique in
${\mathbb{N}}\setminus V(\mathcal{F})$
is finite, because otherwise by Ramsey’s theorem there would be an infinite monochromatic clique in
![]() $\chi$
restricted to
$\chi$
restricted to
![]() ${\mathbb{N}}\setminus V(\mathcal{F})$
, contradicting the maximality of
${\mathbb{N}}\setminus V(\mathcal{F})$
, contradicting the maximality of
![]() $\mathcal{F}$
. Let
$\mathcal{F}$
. Let
![]() $\mathcal{F}_R$
and
$\mathcal{F}_R$
and
![]() $\mathcal{F}_B$
be the families of red and blue cliques in
$\mathcal{F}_B$
be the families of red and blue cliques in
![]() $\mathcal{F}$
. Since
$\mathcal{F}$
. Since
![]() $\bar d(V(\mathcal{F}_R)\cup V(\mathcal{F}_B))=1$
, we have
$\bar d(V(\mathcal{F}_R)\cup V(\mathcal{F}_B))=1$
, we have
![]() $\max \{\bar d(V(\mathcal{F}_R)),\bar d(V(\mathcal{F}_B))\}\geq 1/2$
. Wlog assume
$\max \{\bar d(V(\mathcal{F}_R)),\bar d(V(\mathcal{F}_B))\}\geq 1/2$
. Wlog assume
![]() $\bar d(\mathcal{F}_R))\geq 1/2$
. We can suppose that
$\bar d(\mathcal{F}_R))\geq 1/2$
. We can suppose that
![]() $\mathcal{F}_R$
contains infinitely many cliques, because otherwise we can take one clique
$\mathcal{F}_R$
contains infinitely many cliques, because otherwise we can take one clique
![]() $K\in \mathcal{F}_R$
and divide it into infinitely many infinite cliques. Let
$K\in \mathcal{F}_R$
and divide it into infinitely many infinite cliques. Let
![]() $K_1, K_2, \dots$
, be the cliques in
$K_1, K_2, \dots$
, be the cliques in
![]() $\mathcal{F}_R$
. We can partition the vertex set of
$\mathcal{F}_R$
. We can partition the vertex set of
![]() $H$
into infinitely many parts
$H$
into infinitely many parts
![]() $S_1, S_2, \dots$
, each of which is made up of infinitely many components of
$S_1, S_2, \dots$
, each of which is made up of infinitely many components of
![]() $H$
. Now take any
$H$
. Now take any
![]() $\Phi\;:\;V(H)\rightarrow V(K_{\mathbb{N}})$
which is a bijection from each
$\Phi\;:\;V(H)\rightarrow V(K_{\mathbb{N}})$
which is a bijection from each
![]() $S_i$
to each
$S_i$
to each
![]() $K_i$
. The image of
$K_i$
. The image of
![]() $H$
is a monochromatic graph
$H$
is a monochromatic graph
![]() $H'$
and
$H'$
and
![]() $\bar d(V(H'))=\bar d(\mathcal{F}_R)\geq 1/2$
.
$\bar d(V(H'))=\bar d(\mathcal{F}_R)\geq 1/2$
.
The proofs of Theorems 1.42b and 3.1 will both be (partially) algorithmic: given a colouring
![]() $\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
, we will define an algorithm that constructs a dense monochromatic copy of
$\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
, we will define an algorithm that constructs a dense monochromatic copy of
![]() $H$
. The algorithms will be similar, so we will first prove Theorem 3.1 and then explain how to adapt the proof to Theorem 1.42b.
$H$
. The algorithms will be similar, so we will first prove Theorem 3.1 and then explain how to adapt the proof to Theorem 1.42b.
Let
![]() $H,a,b,r,s,\Psi$
be as in Theorem 3.1, and let
$H,a,b,r,s,\Psi$
be as in Theorem 3.1, and let
![]() $\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
. Our goal is to find a copy of
$\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
. Our goal is to find a copy of
![]() $H$
in
$H$
in
![]() $K_{\mathbb{N}}$
with density at least
$K_{\mathbb{N}}$
with density at least
![]() $b/(a-1)f(s/r)$
. In order to find such a copy of
$b/(a-1)f(s/r)$
. In order to find such a copy of
![]() $H$
, it will be helpful to also colour the vertices of
$H$
, it will be helpful to also colour the vertices of
![]() $K_{\mathbb{N}}$
, in a way that encodes information about how the vertices are connected through red or blue edges. The following colouring is a variant of one used in [Reference Elekes, Soukup, Soukup and Szentmiklóssy7].
$K_{\mathbb{N}}$
, in a way that encodes information about how the vertices are connected through red or blue edges. The following colouring is a variant of one used in [Reference Elekes, Soukup, Soukup and Szentmiklóssy7].
We denote by
![]() $N_C(v)$
the set of vertices connected to
$N_C(v)$
the set of vertices connected to
![]() $v$
through an edge of colour
$v$
through an edge of colour
![]() $C$
. When
$C$
. When
![]() $C$
is a colour that is either red or blue, we denote the other colour by
$C$
is a colour that is either red or blue, we denote the other colour by
![]() $\bar C$
.
$\bar C$
.
Definition 3.2. Let
![]() $\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be a colouring, and let
$\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be a colouring, and let
![]() $a$
be a positive integer. An
$a$
be a positive integer. An
![]() $a$
-good colouring of
$a$
-good colouring of
![]() $V(K_{\mathbb{N}})$
is a partition
$V(K_{\mathbb{N}})$
is a partition
![]() ${\mathbb{N}}=\cup _{i=1}^a(R_i\cup B_i)\cup X$
into
${\mathbb{N}}=\cup _{i=1}^a(R_i\cup B_i)\cup X$
into
![]() $2a+1$
classes (some of which might be empty), where
$2a+1$
classes (some of which might be empty), where
![]() $X$
is finite, with the following properties:
$X$
is finite, with the following properties:
-
For every colour
 $C\in \{R,B\}$
, every
$C\in \{R,B\}$
, every
 $1\leq i\leq a-1$
and every nonempty finite subset
$1\leq i\leq a-1$
and every nonempty finite subset
 $S\subseteq C_i$
, the set
$S\subseteq C_i$
, the set
 $ (\cap _{v\in S}N_C(v) )\cap C_i$
is infinite.
$ (\cap _{v\in S}N_C(v) )\cap C_i$
is infinite. -
For every colour
 $C\in \{R,B\}$
, every
$C\in \{R,B\}$
, every
 $1\leq i\leq a-1$
and every nonempty finite subset
$1\leq i\leq a-1$
and every nonempty finite subset
 $S\subseteq C_a\cup (\cup _{j=i+1}^{a-1}\bar C_j )$
, the set
$S\subseteq C_a\cup (\cup _{j=i+1}^{a-1}\bar C_j )$
, the set
 $ (\cap _{v\in S}N_C(v) )\cap \bar C_i$
is infinite.
$ (\cap _{v\in S}N_C(v) )\cap \bar C_i$
is infinite.
The colouring from [Reference Elekes, Soukup, Soukup and Szentmiklóssy7] is constructed using ultrafilters. We define ours algorithmically, even though ultrafilters would have worked just as well, in order to make the properties of this colouring more intuitive and, in the process, avoiding an appeal to the axiom of choice.
We call each class
![]() $R_i$
a shade of red and each class
$R_i$
a shade of red and each class
![]() $B_i$
a shade of blue.
$B_i$
a shade of blue.
![]() $X$
can be seen as a residual set, which can be removed without affecting the density of the graph. The choice of
$X$
can be seen as a residual set, which can be removed without affecting the density of the graph. The choice of
![]() $a$
is related to the chromatic number of the monochromatic subgraphs that we can find in this graph. Indeed, say that we want to find a red clique of size
$a$
is related to the chromatic number of the monochromatic subgraphs that we can find in this graph. Indeed, say that we want to find a red clique of size
![]() $a$
containing
$a$
containing
![]() $v\in R_i$
. If
$v\in R_i$
. If
![]() $i\leq a-1$
, then we can set
$i\leq a-1$
, then we can set
![]() $v=v_1$
and then iteratively select
$v=v_1$
and then iteratively select
![]() $v_2, v_3, \dots, v_a\in R_i$
, each adjacent to the previous ones through a red edge. If
$v_2, v_3, \dots, v_a\in R_i$
, each adjacent to the previous ones through a red edge. If
![]() $i=a$
, we can set
$i=a$
, we can set
![]() $v=v_a$
and then iteratively select
$v=v_a$
and then iteratively select
![]() $v_{a-1}, v_{a-2}, \dots, v_1$
, with
$v_{a-1}, v_{a-2}, \dots, v_1$
, with
![]() $v_j\in B_j$
, each adjacent to the previous ones through a red edge.
$v_j\in B_j$
, each adjacent to the previous ones through a red edge.
We denote by
![]() $K_{r,s}^C$
a complete bipartite graph in which all edges have colour
$K_{r,s}^C$
a complete bipartite graph in which all edges have colour
![]() $C$
, all vertices in the part of size
$C$
, all vertices in the part of size
![]() $s$
have colour
$s$
have colour
![]() $C$
and all vertices in the part of size
$C$
and all vertices in the part of size
![]() $r$
have colour
$r$
have colour
![]() $\bar C$
. These subgraphs will be used to embed the sets
$\bar C$
. These subgraphs will be used to embed the sets
![]() $I_i\cup N(I_i)$
in our coloured graph.
$I_i\cup N(I_i)$
in our coloured graph.
The proof of Theorem 3.1 will have three main steps, which are captured by these lemmas:
Lemma 3.3.
Let
![]() $\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be a colouring, and let
$\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be a colouring, and let
![]() $a$
be a positive integer. There exists an
$a$
be a positive integer. There exists an
![]() $a$
-good colouring in which at least two of
$a$
-good colouring in which at least two of
![]() $(R_a\cup B_{a-1})$
,
$(R_a\cup B_{a-1})$
,
![]() $(B_a\cup R_{a-1})$
and
$(B_a\cup R_{a-1})$
and
![]() $X$
are empty.
$X$
are empty.
Lemma 3.4.
Let
![]() $\chi\;:\;E(K_{\mathbb{N}})\cup V(K_{\mathbb{N}})\rightarrow \{R,B\}$
be a colouring, and let
$\chi\;:\;E(K_{\mathbb{N}})\cup V(K_{\mathbb{N}})\rightarrow \{R,B\}$
be a colouring, and let
![]() $r,s$
be positive integers. There exists a colour
$r,s$
be positive integers. There exists a colour
![]() $C$
and a subgraph
$C$
and a subgraph
![]() $W\subseteq K_{\mathbb{N}}$
, with
$W\subseteq K_{\mathbb{N}}$
, with
![]() $\bar d(W)\geq f(s/r)$
, in which every component is either an isolated vertex with colour
$\bar d(W)\geq f(s/r)$
, in which every component is either an isolated vertex with colour
![]() $C$
, or a
$C$
, or a
![]() $K_{r,s}^C$
. Furthermore, if
$K_{r,s}^C$
. Furthermore, if
![]() $V(K_{\mathbb{N}})$
is further subdivided into finitely many shades, then
$V(K_{\mathbb{N}})$
is further subdivided into finitely many shades, then
![]() $W$
can be taken in such a way that each
$W$
can be taken in such a way that each
![]() $K_{r,s}^C$
only uses one shade of each colour.
$K_{r,s}^C$
only uses one shade of each colour.
Lemma 3.5.
Let
![]() $\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be an edge-colouring, let
$\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be an edge-colouring, let
![]() $a\geq a'\geq b$
be positive integers. Let
$a\geq a'\geq b$
be positive integers. Let
![]() ${\mathbb{N}}\rightarrow \{R_1, \dots, R_a, B_1, \dots, B_a, X\}$
be an
${\mathbb{N}}\rightarrow \{R_1, \dots, R_a, B_1, \dots, B_a, X\}$
be an
![]() $a$
-good colouring in which at most
$a$
-good colouring in which at most
![]() $a'$
shades of each colour are non-empty. Let
$a'$
shades of each colour are non-empty. Let
![]() $W\subseteq K_{\mathbb{N}}$
be a subgraph in which every component is either an isolated vertex with colour
$W\subseteq K_{\mathbb{N}}$
be a subgraph in which every component is either an isolated vertex with colour
![]() $C$
, or a
$C$
, or a
![]() $K_{r,s}^C$
which uses only one shade of each colour. Let
$K_{r,s}^C$
which uses only one shade of each colour. Let
![]() $H$
be a graph satisfying the conditions of Theorem 3.1 for some positive integers
$H$
be a graph satisfying the conditions of Theorem 3.1 for some positive integers
![]() $r$
and
$r$
and
![]() $s$
(except possibly
$s$
(except possibly
![]() $a\gt b$
). Then there exists a monochromatic
$a\gt b$
). Then there exists a monochromatic
![]() $H'\subseteq K_{\mathbb{N}}$
of colour
$H'\subseteq K_{\mathbb{N}}$
of colour
![]() $C$
,
$C$
,
![]() $H'\simeq H$
, with
$H'\simeq H$
, with
![]() $\bar d(H')\geq b/a'\bar d(W)$
.
$\bar d(H')\geq b/a'\bar d(W)$
.
It is straightforward to combine these three lemmas to deduce Theorem 3.1:
Proof of Theorem
3.1. Let
![]() $\chi\;:\;E(K_{\mathbb{N}})$
be given. Apply Lemma 3.3 to this edge-colouring to obtain an
$\chi\;:\;E(K_{\mathbb{N}})$
be given. Apply Lemma 3.3 to this edge-colouring to obtain an
![]() $a$
-good colouring where at most
$a$
-good colouring where at most
![]() $a-1$
shades of each colour are non-empty. Assign the colour red to the vertices in
$a-1$
shades of each colour are non-empty. Assign the colour red to the vertices in
![]() $X$
. Apply Lemma 3.4 to obtain
$X$
. Apply Lemma 3.4 to obtain
![]() $C$
and
$C$
and
![]() $W$
. Remove from
$W$
. Remove from
![]() $W$
every component which uses a vertex of
$W$
every component which uses a vertex of
![]() $X$
(this does not affect
$X$
(this does not affect
![]() $\bar d(W)$
because it only removes finitely many vertices). By Lemma 3.5, we can find a monochromatic
$\bar d(W)$
because it only removes finitely many vertices). By Lemma 3.5, we can find a monochromatic
![]() $H'\subseteq K_{\mathbb{N}}$
with
$H'\subseteq K_{\mathbb{N}}$
with
![]() $\bar d(H')\geq b/(a-1)\bar d(W)\geq b/(a-1)f(s/r)$
.
$\bar d(H')\geq b/(a-1)\bar d(W)\geq b/(a-1)f(s/r)$
.
Proof of Lemma
3.3. For each vertex
![]() $v$
, we will denote by
$v$
, we will denote by
![]() $c(v)$
and
$c(v)$
and
![]() $s(v)$
the colour and the shade that we assign to it, respectively. The colour assigned to a vertex might change while the algorithm is running, but the shade of each vertex is final once assigned and it will match the colour that the vertex has at that time.
$s(v)$
the colour and the shade that we assign to it, respectively. The colour assigned to a vertex might change while the algorithm is running, but the shade of each vertex is final once assigned and it will match the colour that the vertex has at that time.
At some points, the shade assigning algorithm will call the basic colouring algorithm to colour an infinite set
![]() $V=\{v_1, v_2, \dots \}$
of vertices. We will first describe this algorithm.
$V=\{v_1, v_2, \dots \}$
of vertices. We will first describe this algorithm.
Basic colouring algorithm: First, the colour
![]() $c(v_1)$
is assigned, satisfying that
$c(v_1)$
is assigned, satisfying that
![]() $N_{c(v_1)}(v_1)\cap V$
is infinite. Once the colours of
$N_{c(v_1)}(v_1)\cap V$
is infinite. Once the colours of
![]() $v_1, \dots, v_{n-1}$
have been assigned, assuming by induction that
$v_1, \dots, v_{n-1}$
have been assigned, assuming by induction that
![]() $ (\cap _{i=1}^{n-1}N_{c(v_i)}(v_i) )\cap V$
is infinite, the colour
$ (\cap _{i=1}^{n-1}N_{c(v_i)}(v_i) )\cap V$
is infinite, the colour
![]() $c(v_n)$
is chosen so that
$c(v_n)$
is chosen so that
![]() $ (\cap _{i=1}^{n}N_{c(v_i)}(v_i) )\cap V$
is infinite.
$ (\cap _{i=1}^{n}N_{c(v_i)}(v_i) )\cap V$
is infinite.
The colouring produced satisfies that
![]() $ (\cap _{i=1}^{n}N_{c(v_i)}(v_i) )\cap V$
is infinite for every
$ (\cap _{i=1}^{n}N_{c(v_i)}(v_i) )\cap V$
is infinite for every
![]() $n$
. We say that a colour
$n$
. We say that a colour
![]() $C$
is dominant in this colouring if, for every
$C$
is dominant in this colouring if, for every
![]() $n$
,
$n$
,
![]() $ (\cap _{i=1}^{n}N_{c(v_i)}(v_i) )\cap V$
contains infinitely many vertices
$ (\cap _{i=1}^{n}N_{c(v_i)}(v_i) )\cap V$
contains infinitely many vertices
![]() $v$
with
$v$
with
![]() $c(v)=C$
. Observe that at least one of the colours is dominant.
$c(v)=C$
. Observe that at least one of the colours is dominant.
Now we define the shade assigning algorithm:
-
1. For every
 $v\in{\mathbb{N}}$
, start with
$v\in{\mathbb{N}}$
, start with
 $c(v)$
and
$c(v)$
and
 $s(v)$
unassigned.
$s(v)$
unassigned. -
2. If finitely many vertices
 $v$
remain with
$v$
remain with
 $s(v)$
unassigned, assign
$s(v)$
unassigned, assign
 $s(v)=X$
and END.
$s(v)=X$
and END. -
3. Let
 $V$
be the set of vertices without a shade. Colour
$V$
be the set of vertices without a shade. Colour
 $V$
with the basic colouring algorithm. Choose a colour
$V$
with the basic colouring algorithm. Choose a colour
 $C$
that is dominant. Let
$C$
that is dominant. Let
 $i$
be the minimum value such that
$i$
be the minimum value such that
 $C_i$
is empty. For every
$C_i$
is empty. For every
 $v\in V$
with
$v\in V$
with
 $c(v)=C$
, set
$c(v)=C$
, set
 $s(v)=C_i$
.
$s(v)=C_i$
. -
4. If
 $i=a-1$
, set
$i=a-1$
, set
 $s(v)=\bar C_a$
for every
$s(v)=\bar C_a$
for every
 $v\in V$
with
$v\in V$
with
 $c(v)=\bar C$
and END. If
$c(v)=\bar C$
and END. If
 $i\neq a-1$
, return to Step 2.
$i\neq a-1$
, return to Step 2.
The algorithm runs the loop
![]() $2$
–
$2$
–
![]() $4$
at most
$4$
at most
![]() $2a-3$
times before ending. Whenever a set
$2a-3$
times before ending. Whenever a set
![]() $C_i$
with
$C_i$
with
![]() $i\leq a-1$
is defined, the colour
$i\leq a-1$
is defined, the colour
![]() $C$
is dominant in the corresponding colouring, meaning that in particular
$C$
is dominant in the corresponding colouring, meaning that in particular
![]() $ (\cap _{v\in S}N_C(v) )\cap C_i$
is infinite for every finite non-empty
$ (\cap _{v\in S}N_C(v) )\cap C_i$
is infinite for every finite non-empty
![]() $S\subseteq C_i$
, as it is a superset of the colour
$S\subseteq C_i$
, as it is a superset of the colour
![]() $C$
vertices of
$C$
vertices of
![]() $ (\cap _{i=1}^nN_{c(v_i)}(v_i) )\cap V$
for
$ (\cap _{i=1}^nN_{c(v_i)}(v_i) )\cap V$
for
![]() $n$
large enough. For the same reason, for any finite subset
$n$
large enough. For the same reason, for any finite subset
![]() $S$
of vertices whose shade is not assigned when
$S$
of vertices whose shade is not assigned when
![]() $C_i$
is defined, we have that
$C_i$
is defined, we have that
![]() $ (\cap _{v\in S}N_{\bar C}(v) )\cap C_i$
is infinite. If
$ (\cap _{v\in S}N_{\bar C}(v) )\cap C_i$
is infinite. If
![]() $C_a$
is defined at some point in the algorithm (namely at the end), then
$C_a$
is defined at some point in the algorithm (namely at the end), then
![]() $\bar C_1, \bar C_2, \dots, \bar C_{a-1}, C_a$
are defined in this order. This proves that the colouring that we obtained is
$\bar C_1, \bar C_2, \dots, \bar C_{a-1}, C_a$
are defined in this order. This proves that the colouring that we obtained is
![]() $a$
-good.
$a$
-good.
To conclude the proof of Lemma 3.3, simply observe that
![]() $X$
is nonempty only if the algorithm terminates at Step 2, the set
$X$
is nonempty only if the algorithm terminates at Step 2, the set
![]() $(R_a\cup B_{a-1})$
is nonempty only if the algorithm terminates at Step 4 with
$(R_a\cup B_{a-1})$
is nonempty only if the algorithm terminates at Step 4 with
![]() $C=B$
and
$C=B$
and
![]() $(B_a\cup R_{a-1})$
is nonempty only if the algorithm terminates at Step 4 with
$(B_a\cup R_{a-1})$
is nonempty only if the algorithm terminates at Step 4 with
![]() $C=R$
.
$C=R$
.
The proof of Lemma 3.4 divides
![]() $K_{\mathbb{N}}$
into infinitely many finite graphs and then combines the regularity lemma and a max flow/min cut argument, to reduce the problem to an optimisation problem equivalent to (1). We will now state the lemmas that we will need for this:
$K_{\mathbb{N}}$
into infinitely many finite graphs and then combines the regularity lemma and a max flow/min cut argument, to reduce the problem to an optimisation problem equivalent to (1). We will now state the lemmas that we will need for this:
Lemma 3.6 (Regularity Lemma [Reference Komlós, Simonovits, Miklós, Sós and Szőnyi9]). For every
![]() $\epsilon \gt 0$
and
$\epsilon \gt 0$
and
![]() $m_0, \ell \geq 1$
there exists
$m_0, \ell \geq 1$
there exists
![]() $M = M(\epsilon,m_0,\ell )$
such that the following holds. Let
$M = M(\epsilon,m_0,\ell )$
such that the following holds. Let
![]() $G$
be a graph on
$G$
be a graph on
![]() $n \geq M$
vertices whose edges are coloured in red and blue and let
$n \geq M$
vertices whose edges are coloured in red and blue and let
![]() $d\gt 0$
. Let
$d\gt 0$
. Let
![]() $\{W_i\}_{i \in [\ell ]}$
be a partition of
$\{W_i\}_{i \in [\ell ]}$
be a partition of
![]() $V(G)$
. Then there exists a partition
$V(G)$
. Then there exists a partition
![]() $\{V_0, \dots, V_m\}$
of
$\{V_0, \dots, V_m\}$
of
![]() $V(G)$
and a subgraph
$V(G)$
and a subgraph
![]() $H$
of
$H$
of
![]() $G$
with vertex set
$G$
with vertex set
![]() $V(G) \setminus V_0$
such that the following holds:
$V(G) \setminus V_0$
such that the following holds:
-
1.
 $m_0 \leq m \leq M$
;
$m_0 \leq m \leq M$
; -
2.
 $\{V_i\}_{i \in [m]}$
refines
$\{V_i\}_{i \in [m]}$
refines
 $\{W_i\cap V(H)\}_{i \in [\ell ]}$
;
$\{W_i\cap V(H)\}_{i \in [\ell ]}$
; -
3.
 $|V_0| \leq \epsilon n$
and
$|V_0| \leq \epsilon n$
and
 $|V_1| = \dots = |V_m| \leq \lceil \epsilon n \rceil$
;
$|V_1| = \dots = |V_m| \leq \lceil \epsilon n \rceil$
; -
4.
 $\deg _{H}(v) \geq \deg _G(v)-(d+\epsilon )n$
for each
$\deg _{H}(v) \geq \deg _G(v)-(d+\epsilon )n$
for each
 $v \in V(G) \setminus V_0$
;
$v \in V(G) \setminus V_0$
; -
5.
 $H[V_i]$
has no edges for
$H[V_i]$
has no edges for
 $i \in [m]$
;
$i \in [m]$
; -
6. all pairs
 $(V_i,V_j)$
are
$(V_i,V_j)$
are
 $\epsilon$
-regular and with density either 0 or at least
$\epsilon$
-regular and with density either 0 or at least
 $d$
in each colour in
$d$
in each colour in
 $H$
.
$H$
.
The max flow-min cut result that we will use can be seen as a weighted version of König’s Theorem:
Lemma 3.7.
Let
![]() $G$
be a finite bipartite graph on
$G$
be a finite bipartite graph on
![]() $V=(X,Y)$
, and let
$V=(X,Y)$
, and let
![]() $r,s$
be positive integers. There exists a unique value of
$r,s$
be positive integers. There exists a unique value of
![]() $D$
for which both of these exist:
$D$
for which both of these exist:
-
A function
 $h\;:\;E(G)\rightarrow{\mathbb{N}}\cup \{0\}$
such that
$h\;:\;E(G)\rightarrow{\mathbb{N}}\cup \{0\}$
such that
 $\sum _{e\ni v}h(e)\leq r$
if
$\sum _{e\ni v}h(e)\leq r$
if
 $v\in X$
,
$v\in X$
,
 $\sum _{e\ni v}h(e)\leq s$
if
$\sum _{e\ni v}h(e)\leq s$
if
 $v\in Y$
and
$v\in Y$
and
 $\sum _{e\in E(G)}h(e)=D$
.
$\sum _{e\in E(G)}h(e)=D$
. -
A vertex cover
 $Z$
of
$Z$
of
 $G$
such that
$G$
such that
 $r|Z\cap X|+s|Z\cap Y|=D$
.
$r|Z\cap X|+s|Z\cap Y|=D$
.
Proof. Take an orientation of every edge in
![]() $G$
from
$G$
from
![]() $X$
to
$X$
to
![]() $Y$
and give it an infinite capacity. Connect every vertex in
$Y$
and give it an infinite capacity. Connect every vertex in
![]() $X$
to a source
$X$
to a source
![]() $\sigma$
through an edge with capacity
$\sigma$
through an edge with capacity
![]() $r$
, and every vertex in
$r$
, and every vertex in
![]() $y$
to a sink
$y$
to a sink
![]() $\tau$
through an edge with capacity
$\tau$
through an edge with capacity
![]() $s$
. Let
$s$
. Let
![]() $D$
be the maximum flow in this network.
$D$
be the maximum flow in this network.
![]() $D$
is the maximum value for which a function
$D$
is the maximum value for which a function
![]() $h$
as in the statement exists (by the integrality theorem, there exists a maximum flow in which the flow of every edge is an integer).
$h$
as in the statement exists (by the integrality theorem, there exists a maximum flow in which the flow of every edge is an integer).
![]() $D$
is also the minimum value for which a cut
$D$
is also the minimum value for which a cut
![]() $(C_1, C_2)$
with
$(C_1, C_2)$
with
![]() $\sigma \in C_1$
and
$\sigma \in C_1$
and
![]() $\tau \in C_2$
exists. Observe that
$\tau \in C_2$
exists. Observe that
![]() $(C_1, C_2)$
is a cut with finite capacity iff
$(C_1, C_2)$
is a cut with finite capacity iff
![]() $(C_2\cap X)\cup (C_1\cap Y)$
is a vertex cover of
$(C_2\cap X)\cup (C_1\cap Y)$
is a vertex cover of
![]() $G$
, in which case the capacity of the cut is
$G$
, in which case the capacity of the cut is
![]() $r|C_2\cap X|+s|C_1\cap Y|$
. Our lemma follows from the Ford–Fulkerson theorem.
$r|C_2\cap X|+s|C_1\cap Y|$
. Our lemma follows from the Ford–Fulkerson theorem.
The next lemma that we will introduce requires the definition of two parameters, which up to a change of coordinates are equivalent to
![]() $\Gamma ^+_\gamma$
and
$\Gamma ^+_\gamma$
and
![]() $\Gamma ^-_\gamma$
. The change of coordinates is a rotation of the axes by 45 degrees, in the following sense: if we denote the 1-Lipschitz function from Definition 1.3 as
$\Gamma ^-_\gamma$
. The change of coordinates is a rotation of the axes by 45 degrees, in the following sense: if we denote the 1-Lipschitz function from Definition 1.3 as
![]() $g$
and the non-decreasing function below as
$g$
and the non-decreasing function below as
![]() $g'$
, then the point
$g'$
, then the point
![]() $(x,y)$
is in the graph of
$(x,y)$
is in the graph of
![]() $g'$
if and only if
$g'$
if and only if
![]() $(x+y, x-y)$
is in the graph of
$(x+y, x-y)$
is in the graph of
![]() $g$
.
$g$
.
Definition 3.8. Let
![]() $g\;:\;[0,+\infty )\rightarrow [0,+\infty )$
be a continuous, non-decreasing function. Let
$g\;:\;[0,+\infty )\rightarrow [0,+\infty )$
be a continuous, non-decreasing function. Let
![]() $\lambda, t$
be positive real numbers. We define the following two parameters:
$\lambda, t$
be positive real numbers. We define the following two parameters:
where we take the minimum of the empty set to be
![]() $+\infty$
.
$+\infty$
.
Lemma 3.9.
For
![]() $\lambda,\epsilon \gt 0$
there exists
$\lambda,\epsilon \gt 0$
there exists
![]() $\gamma \gt 0$
with the following property: for every non-decreasing continuous function
$\gamma \gt 0$
with the following property: for every non-decreasing continuous function
![]() $g\;:\;[0,+\infty )\rightarrow [0, +\infty )$
with
$g\;:\;[0,+\infty )\rightarrow [0, +\infty )$
with
![]() $g(0)=0$
and every
$g(0)=0$
and every
![]() $m\gt 0$
there exists
$m\gt 0$
there exists
![]() $t\in [\gamma m, m]$
such that
$t\in [\gamma m, m]$
such that
The proof of Lemma 3.9 can be found in the appendix. Combining Lemmas 3.7 and 3.9, we can obtain the following:
Lemma 3.10.
For every
![]() $\epsilon, r,s\gt 0$
there exists
$\epsilon, r,s\gt 0$
there exists
![]() $\gamma,\eta \gt 0$
and
$\gamma,\eta \gt 0$
and
![]() $N$
for which the following hold: for every graph
$N$
for which the following hold: for every graph
![]() $G$
on
$G$
on
![]() $[n]$
, with
$[n]$
, with
![]() $n\gt N$
and
$n\gt N$
and
![]() $\delta (G)\geq (1-\eta )n$
, and for every total colouring
$\delta (G)\geq (1-\eta )n$
, and for every total colouring
![]() $\chi\;:\;V(G)\cup E(G)\rightarrow \{R,B\}$
, there exists
$\chi\;:\;V(G)\cup E(G)\rightarrow \{R,B\}$
, there exists
![]() $t\in [\gamma n,n]$
, a colour
$t\in [\gamma n,n]$
, a colour
![]() $C$
, and
$C$
, and
![]() $h\;:\;E(G)\rightarrow{\mathbb{N}}\cup \{0\}$
, such that the following hold:
$h\;:\;E(G)\rightarrow{\mathbb{N}}\cup \{0\}$
, such that the following hold:
-
For every edge
 $e=uv$
, if
$e=uv$
, if
 $h(e)\gt 0$
then
$h(e)\gt 0$
then
 $\chi (e)=C$
and
$\chi (e)=C$
and
 $\chi (u)\neq \chi (v)$
.
$\chi (u)\neq \chi (v)$
. -
 $\sum \limits _{e\ni v}h(e)\leq r$
for every
$\sum \limits _{e\ni v}h(e)\leq r$
for every
 $v$
with
$v$
with
 $\chi (v)=C$
and
$\chi (v)=C$
and
 $\sum \limits _{e\ni v}h(e)\leq s$
for every
$\sum \limits _{e\ni v}h(e)\leq s$
for every
 $v$
with
$v$
with
 $\chi (v)=\bar C$
.
$\chi (v)=\bar C$
. -
 $\frac{|C\cap [t]|}t+\frac{\sum _{v\in (\bar C\cap [t])}\sum _{e\ni v} h(e)}{st}\geq f(s/r)-\epsilon$
.
$\frac{|C\cap [t]|}t+\frac{\sum _{v\in (\bar C\cap [t])}\sum _{e\ni v} h(e)}{st}\geq f(s/r)-\epsilon$
.
Proof. Let
![]() $\lambda =s/r$
. Our constants will follow the hierarchy
$\lambda =s/r$
. Our constants will follow the hierarchy
That is, after
![]() $\epsilon$
and
$\epsilon$
and
![]() $\lambda$
are given we pick
$\lambda$
are given we pick
![]() $\xi$
small enough, after fixing
$\xi$
small enough, after fixing
![]() $\xi$
we pick
$\xi$
we pick
![]() $\kappa$
small enough, and so on.
$\kappa$
small enough, and so on.
For every red vertex
![]() $v$
, we define its blue degree
$v$
, we define its blue degree
![]() $d_B(v)$
as the number of blue vertices
$d_B(v)$
as the number of blue vertices
![]() $w$
such that
$w$
such that
![]() $vw$
is blue. Let
$vw$
is blue. Let
![]() $v_1, v_2, \dots, v_{|R|}$
be the set of red vertices, sorted from smallest to largest blue degree, and let
$v_1, v_2, \dots, v_{|R|}$
be the set of red vertices, sorted from smallest to largest blue degree, and let
![]() $d_i=d_B(v_i)$
. Define additionally
$d_i=d_B(v_i)$
. Define additionally
![]() $d_0=0$
and
$d_0=0$
and
![]() $d_k=d_{|R|}$
for
$d_k=d_{|R|}$
for
![]() $k\gt |R|$
. Let
$k\gt |R|$
. Let
![]() $g\;:\;[0,+\infty )\rightarrow [0,+\infty )$
be the function that satisfies
$g\;:\;[0,+\infty )\rightarrow [0,+\infty )$
be the function that satisfies
![]() $g(k)=d_k$
for every integer
$g(k)=d_k$
for every integer
![]() $k$
and which is linear between every pair of consecutive integers.
$k$
and which is linear between every pair of consecutive integers.
By Lemma 3.9 there exists
![]() $\tau \in [\gamma n, \kappa n ]$
for which
$\tau \in [\gamma n, \kappa n ]$
for which
![]() $\frac{\ell ^+_\lambda (g,\tau )+\ell ^-_\lambda (g,\tau )}{\tau }\geq \frac{f(\lambda )}{1-f(\lambda )}-\xi$
. Adding 1 on each side of the expression,
$\frac{\ell ^+_\lambda (g,\tau )+\ell ^-_\lambda (g,\tau )}{\tau }\geq \frac{f(\lambda )}{1-f(\lambda )}-\xi$
. Adding 1 on each side of the expression,
![]() $\frac{\ell ^+_\lambda (g,\tau )+\ell ^-_\lambda (g,\tau )+\tau }{\tau }\geq \frac{1}{1-f(\lambda )}-\xi$
. Let
$\frac{\ell ^+_\lambda (g,\tau )+\ell ^-_\lambda (g,\tau )+\tau }{\tau }\geq \frac{1}{1-f(\lambda )}-\xi$
. Let
![]() $t=\left (\frac{1}{1-f(\lambda )}-\xi \right )\tau$
. Then, since
$t=\left (\frac{1}{1-f(\lambda )}-\xi \right )\tau$
. Then, since
![]() $t\leq \ell ^+_\lambda (g,\tau )+\ell ^-_\lambda (g,\tau )+\tau$
, we have either
$t\leq \ell ^+_\lambda (g,\tau )+\ell ^-_\lambda (g,\tau )+\tau$
, we have either
![]() $|R\cap [t]|\lt \ell ^-_\lambda (g,\tau )$
or
$|R\cap [t]|\lt \ell ^-_\lambda (g,\tau )$
or
![]() $|B\cap [t]|\leq \ell ^+_\lambda (g,\tau )+\tau$
. We consider both cases, in the former we will have
$|B\cap [t]|\leq \ell ^+_\lambda (g,\tau )+\tau$
. We consider both cases, in the former we will have
![]() $C=B$
and in the latter (mostly)
$C=B$
and in the latter (mostly)
![]() $C=R$
:
$C=R$
:
Case 1:
![]() $|R\cap [t]|\lt \ell ^-(g,\tau )$
. Let
$|R\cap [t]|\lt \ell ^-(g,\tau )$
. Let
![]() $R'=R\cap [t]$
. Let
$R'=R\cap [t]$
. Let
![]() $G'$
be the graph of blue edges in
$G'$
be the graph of blue edges in
![]() $G$
between
$G$
between
![]() $R'$
and
$R'$
and
![]() $B$
. Let
$B$
. Let
![]() $h$
,
$h$
,
![]() $Z$
and
$Z$
and
![]() $D$
be as in Lemma 3.7 applied to
$D$
be as in Lemma 3.7 applied to
![]() $G'$
, with
$G'$
, with
![]() $X=B$
and
$X=B$
and
![]() $Y=R'$
. Suppose that
$Y=R'$
. Suppose that
![]() $D\leq s(|R'|-\tau )$
. Every vertex
$D\leq s(|R'|-\tau )$
. Every vertex
![]() $v\in R'\setminus Z$
must have all its blue neighbours in
$v\in R'\setminus Z$
must have all its blue neighbours in
![]() $B\cap Z$
, and so
$B\cap Z$
, and so
![]() $d_B(v)\leq |B\cap Z|$
. Therefore
$d_B(v)\leq |B\cap Z|$
. Therefore
Setting
![]() $x=|R'|-|Z\cap R'|$
, this expression rearranges to
$x=|R'|-|Z\cap R'|$
, this expression rearranges to
![]() $x-\frac{g(x)}\lambda \geq \tau$
, so by definition of
$x-\frac{g(x)}\lambda \geq \tau$
, so by definition of
![]() $\ell ^-_\lambda$
this means that
$\ell ^-_\lambda$
this means that
![]() $x\geq \ell ^-_\lambda (g,\tau )$
. But this is a contradiction, because
$x\geq \ell ^-_\lambda (g,\tau )$
. But this is a contradiction, because
![]() $x\leq |R'|\lt \ell ^-_\lambda (g,\tau )$
. This means that we have
$x\leq |R'|\lt \ell ^-_\lambda (g,\tau )$
. This means that we have
![]() $D\gt s(|R'|-\tau )$
, and
$D\gt s(|R'|-\tau )$
, and
Case 2:
![]() $|B\cap [t]|\leq \ell ^+(g, \tau )+\tau$
. Let
$|B\cap [t]|\leq \ell ^+(g, \tau )+\tau$
. Let
![]() $B'=B\cap [t]$
. Let
$B'=B\cap [t]$
. Let
![]() $G'$
be the graph of red edges between
$G'$
be the graph of red edges between
![]() $R$
and
$R$
and
![]() $B'$
. Let
$B'$
. Let
![]() $h$
,
$h$
,
![]() $Z$
and
$Z$
and
![]() $D$
be as in Lemma 3.7 applied to
$D$
be as in Lemma 3.7 applied to
![]() $G'$
, with
$G'$
, with
![]() $X=R$
and
$X=R$
and
![]() $Y=B'$
. Suppose that
$Y=B'$
. Suppose that
![]() $D\lt s(|B'|-\tau -\eta n-\frac 1\lambda )$
. Every edge between
$D\lt s(|B'|-\tau -\eta n-\frac 1\lambda )$
. Every edge between
![]() $R\setminus Z$
and
$R\setminus Z$
and
![]() $B'\setminus Z$
is blue. Every vertex
$B'\setminus Z$
is blue. Every vertex
![]() $v$
has at most
$v$
has at most
![]() $\eta n$
vertices to which it is not connected, and so
$\eta n$
vertices to which it is not connected, and so
![]() $d_B(v)\geq |B'\setminus Z|-\eta n$
for all
$d_B(v)\geq |B'\setminus Z|-\eta n$
for all
![]() $v\in R\setminus Z$
.
$v\in R\setminus Z$
.
If
![]() $R\setminus Z$
is empty, then
$R\setminus Z$
is empty, then
![]() $r|R|\leq D\leq s|B'|\leq st\leq s\frac{\tau }{1-f(\lambda )}\leq s\frac{\kappa }{1-f(\lambda )}n$
. This leads to
$r|R|\leq D\leq s|B'|\leq st\leq s\frac{\tau }{1-f(\lambda )}\leq s\frac{\kappa }{1-f(\lambda )}n$
. This leads to
![]() $|R|\leq \frac{\kappa s}{r(1-f(\lambda ))}n\leq (1-f(\lambda ))n$
and
$|R|\leq \frac{\kappa s}{r(1-f(\lambda ))}n\leq (1-f(\lambda ))n$
and
![]() $|B|\geq f(\lambda )n$
. In this case we can take
$|B|\geq f(\lambda )n$
. In this case we can take
![]() $t'=n$
,
$t'=n$
,
![]() $h=0$
and
$h=0$
and
![]() $C=B$
for Lemma 3.10. Thus we can assume that
$C=B$
for Lemma 3.10. Thus we can assume that
![]() $R\setminus Z$
is not empty, and so
$R\setminus Z$
is not empty, and so
![]() $d_{|R\cap Z|+1}\geq |B'\setminus Z|-\eta n$
.
$d_{|R\cap Z|+1}\geq |B'\setminus Z|-\eta n$
.
 \begin{align*} d_{|R\cap Z|+1} &\geq |B'|-|B'\cap Z|-\eta n\geq |B'|-\frac{D-r|R\cap Z|}{s}-\eta n\\[5pt] &=\frac{s|B'|-D}{s}+\frac 1\lambda |R\cap Z|-\eta n\geq \tau +\eta n+\frac 1\lambda +\frac 1\lambda |R\cap Z|-\eta n\\[5pt] &\geq \tau +\frac 1\lambda (|R\cap Z|+1). \end{align*}
\begin{align*} d_{|R\cap Z|+1} &\geq |B'|-|B'\cap Z|-\eta n\geq |B'|-\frac{D-r|R\cap Z|}{s}-\eta n\\[5pt] &=\frac{s|B'|-D}{s}+\frac 1\lambda |R\cap Z|-\eta n\geq \tau +\eta n+\frac 1\lambda +\frac 1\lambda |R\cap Z|-\eta n\\[5pt] &\geq \tau +\frac 1\lambda (|R\cap Z|+1). \end{align*}
Setting
![]() $x=\frac 1\lambda (|R\cap Z|+1)$
, this expression rearranges to
$x=\frac 1\lambda (|R\cap Z|+1)$
, this expression rearranges to
![]() $g(\lambda x)-x\geq \tau$
, so by definition of
$g(\lambda x)-x\geq \tau$
, so by definition of
![]() $\ell ^+_\lambda$
this means that
$\ell ^+_\lambda$
this means that
![]() $x\geq \ell ^+_\lambda (g,\tau )$
. On the other hand,
$x\geq \ell ^+_\lambda (g,\tau )$
. On the other hand,
![]() $x=\frac{|R\cap Z|+1}{\lambda }\leq \frac{D}{s}+\frac 1\lambda \lt |B'|-\tau -\eta n-\frac 1\lambda +\frac 1\lambda \lt |B'|-\tau \leq \ell ^+_\lambda (g,\tau )$
, which is a contradiction. This means that we have
$x=\frac{|R\cap Z|+1}{\lambda }\leq \frac{D}{s}+\frac 1\lambda \lt |B'|-\tau -\eta n-\frac 1\lambda +\frac 1\lambda \lt |B'|-\tau \leq \ell ^+_\lambda (g,\tau )$
, which is a contradiction. This means that we have
![]() $D\geq s(|B'|-\tau -\eta n-\frac 1\lambda )$
, and
$D\geq s(|B'|-\tau -\eta n-\frac 1\lambda )$
, and
To prove Lemma 3.4, we apply the regularity lemma to the graph and use Lemma 3.10. We also use the fact that, by the Kővári-Sós-Turán theorem, every large enough dense bipartite graph contains a large complete bipartite subgraph:
Proof of Lemma
3.4. Let
![]() $\lambda =s/r$
. We first claim that, for every
$\lambda =s/r$
. We first claim that, for every
![]() $\epsilon \gt 0$
, there exists
$\epsilon \gt 0$
, there exists
![]() $\gamma (\epsilon )\gt 0$
and
$\gamma (\epsilon )\gt 0$
and
![]() $N(\epsilon )$
such that, for every
$N(\epsilon )$
such that, for every
![]() $n\gt N$
, there exist
$n\gt N$
, there exist
![]() $t\in [\gamma n,n]$
, a colour
$t\in [\gamma n,n]$
, a colour
![]() $C$
and a subgraph
$C$
and a subgraph
![]() $\mathcal{F}\subseteq K_{\mathbb{N}}$
contained in
$\mathcal{F}\subseteq K_{\mathbb{N}}$
contained in
![]() $[n]$
in which every component is either an isolated vertex of colour
$[n]$
in which every component is either an isolated vertex of colour
![]() $C$
or a
$C$
or a
![]() $K_{r,s}^C$
using only a shade of each colour, with
$K_{r,s}^C$
using only a shade of each colour, with
Let
![]() $a$
be the total number of shades (from both colours). Our constants will follow the hierarchy
$a$
be the total number of shades (from both colours). Our constants will follow the hierarchy
Let
![]() $G$
be the restriction of our colouring to
$G$
be the restriction of our colouring to
![]() $[n]$
. Take a partition of
$[n]$
. Take a partition of
![]() $[n]$
into
$[n]$
into
![]() $\ell =a\lceil \rho ^{-1}\rceil$
parts
$\ell =a\lceil \rho ^{-1}\rceil$
parts
![]() $\{Z_1, \dots, Z_\ell \}$
, such that each
$\{Z_1, \dots, Z_\ell \}$
, such that each
![]() $Z_i$
is contained in one shade, and
$Z_i$
is contained in one shade, and
![]() $\max Z_i-\min Z_i\lt \rho n$
. Applying Lemma 3.6 to
$\max Z_i-\min Z_i\lt \rho n$
. Applying Lemma 3.6 to
![]() $G$
with
$G$
with
![]() $d=2\delta$
, we find a subgraph
$d=2\delta$
, we find a subgraph
![]() $H\subseteq G$
and a partition
$H\subseteq G$
and a partition
![]() $[n]=\{V_0, V_1, \dots, V_m\}$
, with
$[n]=\{V_0, V_1, \dots, V_m\}$
, with
![]() $\ell \leq m\leq M$
, as in the statement of Lemma 3.6, replacing
$\ell \leq m\leq M$
, as in the statement of Lemma 3.6, replacing
![]() $\epsilon$
with
$\epsilon$
with
![]() $\delta$
.
$\delta$
.
We suppose that the labelling of the parts is such that
![]() $\min V_1\lt \min V_2\lt \cdots \lt \min V_m$
. We define an auxilliary graph
$\min V_1\lt \min V_2\lt \cdots \lt \min V_m$
. We define an auxilliary graph
![]() $H'$
as follows: the vertex set is
$H'$
as follows: the vertex set is
![]() $[m]$
. The colour of every vertex
$[m]$
. The colour of every vertex
![]() $i$
is the same as the colour of each of its vertices in
$i$
is the same as the colour of each of its vertices in
![]() $G$
. Between any two vertices
$G$
. Between any two vertices
![]() $ij$
, we draw an edge if the bipartite graph
$ij$
, we draw an edge if the bipartite graph
![]() $V_iV_j$
is nonempty in
$V_iV_j$
is nonempty in
![]() $H$
, and we colour it in the most dense colour in
$H$
, and we colour it in the most dense colour in
![]() $V_iV_j$
.
$V_iV_j$
.
Let
![]() $y=|V_1|=\dots =|V_m|$
. Then
$y=|V_1|=\dots =|V_m|$
. Then
![]() $\frac{(1-\delta )n}{m}\leq y\leq \frac{n}{m}$
. The minimum degree in
$\frac{(1-\delta )n}{m}\leq y\leq \frac{n}{m}$
. The minimum degree in
![]() $H'$
is at least
$H'$
is at least
![]() $(1-\eta )m$
. Indeed, given
$(1-\eta )m$
. Indeed, given
![]() $i$
and
$i$
and
![]() $v\in V_i$
, we have
$v\in V_i$
, we have
![]() $d_{H'}(i)\geq \frac{d_H(v)-\delta n}{y}\geq \frac{d_{G}(v)-4\delta n}{y}\geq (1-\frac{4\delta }{1-\delta })m\gt (1-\eta )m$
.
$d_{H'}(i)\geq \frac{d_H(v)-\delta n}{y}\geq \frac{d_{G}(v)-4\delta n}{y}\geq (1-\frac{4\delta }{1-\delta })m\gt (1-\eta )m$
.
Apply Lemma 3.10 to
![]() $H'$
, with parameters
$H'$
, with parameters
![]() $\epsilon/2, r,s$
to obtain a colour
$\epsilon/2, r,s$
to obtain a colour
![]() $C$
, a function
$C$
, a function
![]() $h\;:\;E(H')\rightarrow{\mathbb{N}}$
and a value
$h\;:\;E(H')\rightarrow{\mathbb{N}}$
and a value
![]() $\tau \in [\gamma m,m]$
as in the statement of Lemma 3.10, replacing
$\tau \in [\gamma m,m]$
as in the statement of Lemma 3.10, replacing
![]() $t$
with
$t$
with
![]() $\tau$
. Subdivide each
$\tau$
. Subdivide each
![]() $V_i$
with colour
$V_i$
with colour
![]() $C$
into
$C$
into
![]() $r$
parts
$r$
parts
![]() $V_{i,1},\dots, V_{i,r}$
, each of size at least
$V_{i,1},\dots, V_{i,r}$
, each of size at least
![]() $\lfloor y/r\rfloor$
and each
$\lfloor y/r\rfloor$
and each
![]() $V_i$
with colour
$V_i$
with colour
![]() $\bar C$
into
$\bar C$
into
![]() $s$
parts
$s$
parts
![]() $V_{i,1},\dots, V_{i,s}$
, each of size at least
$V_{i,1},\dots, V_{i,s}$
, each of size at least
![]() $\lfloor y/s\rfloor$
. Construct a matching
$\lfloor y/s\rfloor$
. Construct a matching
![]() $\mathcal{M}$
of pairs
$\mathcal{M}$
of pairs
![]() $(V_{i,k}, V_{j,k'})$
, where for any fixed values of
$(V_{i,k}, V_{j,k'})$
, where for any fixed values of
![]() $i$
and
$i$
and
![]() $j$
, the number of pairs
$j$
, the number of pairs
![]() $(V_{i,k},V_{j,k'})$
in
$(V_{i,k},V_{j,k'})$
in
![]() $\mathcal{M}$
is
$\mathcal{M}$
is
![]() $h(ij)$
.
$h(ij)$
.
Within each pair
![]() $(V_{i,k}, V_{j,k'})$
, where
$(V_{i,k}, V_{j,k'})$
, where
![]() $V_i$
has colour
$V_i$
has colour
![]() $C$
and
$C$
and
![]() $V_j$
has colour
$V_j$
has colour
![]() $\bar C$
, find a maximum family
$\bar C$
, find a maximum family
![]() $\mathcal{F}_{i,k,j,k'}$
of disjoint copies of
$\mathcal{F}_{i,k,j,k'}$
of disjoint copies of
![]() $K_{r,s}^C$
. Since
$K_{r,s}^C$
. Since
![]() $N\gg M,\delta ^{-1},r,s$
, and therefore
$N\gg M,\delta ^{-1},r,s$
, and therefore
![]() $\delta y\gg r,s$
, then
$\delta y\gg r,s$
, then
![]() $\min \{|V_{i,k}\setminus V(\mathcal{F}_{i,k,j,k'})|,|V_{j,k'}\setminus V(\mathcal{F}_{i,k,j,k'})|\}\lt \delta y$
. That is because otherwise the bipartite graph between
$\min \{|V_{i,k}\setminus V(\mathcal{F}_{i,k,j,k'})|,|V_{j,k'}\setminus V(\mathcal{F}_{i,k,j,k'})|\}\lt \delta y$
. That is because otherwise the bipartite graph between
![]() $V_{i,k}\setminus V(\mathcal{F}_{i,k,j,k'})$
and
$V_{i,k}\setminus V(\mathcal{F}_{i,k,j,k'})$
and
![]() $V_{j,k'}\setminus V(\mathcal{F}_{i,k,j,k'})$
would have density at least
$V_{j,k'}\setminus V(\mathcal{F}_{i,k,j,k'})$
would have density at least
![]() $ \delta$
in the edges of colour
$ \delta$
in the edges of colour
![]() $C$
, and for
$C$
, and for
![]() $\delta y$
large enough this implies the existence of a copy of
$\delta y$
large enough this implies the existence of a copy of
![]() $K_{r,s}^C$
, which would contradict the maximality of
$K_{r,s}^C$
, which would contradict the maximality of
![]() $\mathcal{F}_{i,k,j,k'}$
.
$\mathcal{F}_{i,k,j,k'}$
.
Let
![]() $\mathcal{F}$
be the union of all families
$\mathcal{F}$
be the union of all families
![]() $\mathcal{F}_{i,k,j,k'}$
. Let
$\mathcal{F}_{i,k,j,k'}$
. Let
![]() $t=\min V_\tau$
. We will now bound
$t=\min V_\tau$
. We will now bound
![]() $\frac{|(V(\mathcal{F})\cup C)\cap [t]|}{t}$
. If
$\frac{|(V(\mathcal{F})\cup C)\cap [t]|}{t}$
. If
![]() $v\geq t+\rho n$
, and
$v\geq t+\rho n$
, and
![]() $v\in V_i$
with
$v\in V_i$
with
![]() $i\neq 0$
, then
$i\neq 0$
, then
![]() $\min V_i\gt \max V_i-\rho n\geq v-\rho n\geq t=\min V_\tau$
, and thus
$\min V_i\gt \max V_i-\rho n\geq v-\rho n\geq t=\min V_\tau$
, and thus
![]() $i\gt \tau$
. This means that
$i\gt \tau$
. This means that
![]() $|(\cup _{i=1}^\tau V_i)\setminus [t]|\leq \rho n$
, and
$|(\cup _{i=1}^\tau V_i)\setminus [t]|\leq \rho n$
, and
![]() $t\geq \tau y-\rho n\geq \frac{(1-\delta )\tau n}{m}-\rho n$
. On the other hand, if
$t\geq \tau y-\rho n\geq \frac{(1-\delta )\tau n}{m}-\rho n$
. On the other hand, if
![]() $v\leq t$
then either
$v\leq t$
then either
![]() $v\in V_0$
or
$v\in V_0$
or
![]() $v\in V_i$
with
$v\in V_i$
with
![]() $\min V_i\leq v\leq t=\min V_\tau$
, and thus
$\min V_i\leq v\leq t=\min V_\tau$
, and thus
![]() $i\leq \tau$
. This implies that
$i\leq \tau$
. This implies that
![]() $t\leq \sum _{i=0}^\tau |V_i|\leq \delta n+\tau y\leq \delta n+\frac{\tau n}m$
.
$t\leq \sum _{i=0}^\tau |V_i|\leq \delta n+\tau y\leq \delta n+\frac{\tau n}m$
.
Every
![]() $V_i$
with colour
$V_i$
with colour
![]() $C$
and
$C$
and
![]() $i\in [\tau ]$
will trivially be contained in
$i\in [\tau ]$
will trivially be contained in
![]() $(V(\mathcal F)\cup C)\cap (\cup _{i=1}^\tau V_i)$
. For any
$(V(\mathcal F)\cup C)\cap (\cup _{i=1}^\tau V_i)$
. For any
![]() $V_i$
with colour
$V_i$
with colour
![]() $\bar C$
and
$\bar C$
and
![]() $i\in [\tau ]$
, there are
$i\in [\tau ]$
, there are
![]() $\sum _{e\ni i}h(e)$
parts
$\sum _{e\ni i}h(e)$
parts
![]() $V_{i,k}$
which are paired up with a different part
$V_{i,k}$
which are paired up with a different part
![]() $V_{j,k'}$
. We either have
$V_{j,k'}$
. We either have
![]() $|V_{i,k}\setminus V(\mathcal{F})|\leq \delta y$
or
$|V_{i,k}\setminus V(\mathcal{F})|\leq \delta y$
or
![]() $|V_{j,k'}\setminus V(\mathcal{F})|\leq \delta y$
. In the first case,
$|V_{j,k'}\setminus V(\mathcal{F})|\leq \delta y$
. In the first case,
![]() $|V_{i,k}\cap V(\mathcal{F})|\geq \lfloor y/s\rfloor -\delta y\geq (1/s-1/y-\delta )y$
. In the second case,
$|V_{i,k}\cap V(\mathcal{F})|\geq \lfloor y/s\rfloor -\delta y\geq (1/s-1/y-\delta )y$
. In the second case,
![]() $|V_{j,k'}\cap V(\mathcal{F})|\geq \lfloor y/r\rfloor -\delta y\geq (1/r-1/y-\delta )y$
. But
$|V_{j,k'}\cap V(\mathcal{F})|\geq \lfloor y/r\rfloor -\delta y\geq (1/r-1/y-\delta )y$
. But
![]() $\mathcal{F}$
is a family of copies of
$\mathcal{F}$
is a family of copies of
![]() $K_{r,s}$
, so
$K_{r,s}$
, so
![]() $|V_{i,k}\cap V(\mathcal{F})|=\frac rs|V_{j,k'}\cap V(\mathcal{F})|\geq (1/s-\lambda ^{-1}(1/y+\delta ))y$
. In either case we have
$|V_{i,k}\cap V(\mathcal{F})|=\frac rs|V_{j,k'}\cap V(\mathcal{F})|\geq (1/s-\lambda ^{-1}(1/y+\delta ))y$
. In either case we have
![]() $|V_{i,k}\cap V(\mathcal{F})|\geq (1-\zeta )y/s$
.
$|V_{i,k}\cap V(\mathcal{F})|\geq (1-\zeta )y/s$
.
Putting our bounds together:
 \begin{align*} \frac{|(V(\mathcal{F})\cup C_{G})\cap [t]|}{t} & \geq \frac{|(V(\mathcal{F})\cup C_{G})\cap (\cup _{i=1}^\tau V_i)|-\rho n}{t}\\[5pt] & \geq \frac{y|C_{H'}\cap [\tau ]|}{t}+\left (1-\zeta \right )\frac ys\frac{\sum _{v\in (\bar C_{H'}\cap [\tau ])}\sum _{e\ni v}h(e)}{t}-\frac{\rho n}{t}\\[5pt] & \geq \left (1-\zeta \right )\frac{\tau y}{t}\left (\frac{|C_{H'}\cap [\tau ]|}{\tau }+\frac{\sum _{v\in (\bar C_{H'}\cap [\tau ])}\sum _{e\ni v}h(e)}{s\tau }\right )-\frac{\rho n}{t}\\[5pt] & \geq \left (1-\zeta \right )\frac{\tau y}{t}\left (f(\lambda )-\frac \epsilon 2\right )-\frac{\rho }{\frac{\tau (1-\delta )}{m}-\rho }\\[5pt] & \geq \left (1-\zeta \right )\frac{\tau y}{\delta n+\tau y}\left (f(\lambda )-\frac \epsilon 2\right )-\frac{\rho }{\gamma (1-\delta )-\rho }\\[5pt] & \geq \left (1-\zeta \right )\frac{1}{1+\delta \frac{n}{my}\frac m\tau }\left (f(\lambda )-\frac \epsilon 2\right )-\frac \epsilon 4\\[5pt] & \geq \left (1-\zeta \right )\frac{1}{1+\frac{\delta }{(1-\delta )\gamma }}\left (f(\lambda )-\frac \epsilon 2\right )-\frac \epsilon 4\\[5pt] & \geq f(\lambda )-\epsilon . \end{align*}
\begin{align*} \frac{|(V(\mathcal{F})\cup C_{G})\cap [t]|}{t} & \geq \frac{|(V(\mathcal{F})\cup C_{G})\cap (\cup _{i=1}^\tau V_i)|-\rho n}{t}\\[5pt] & \geq \frac{y|C_{H'}\cap [\tau ]|}{t}+\left (1-\zeta \right )\frac ys\frac{\sum _{v\in (\bar C_{H'}\cap [\tau ])}\sum _{e\ni v}h(e)}{t}-\frac{\rho n}{t}\\[5pt] & \geq \left (1-\zeta \right )\frac{\tau y}{t}\left (\frac{|C_{H'}\cap [\tau ]|}{\tau }+\frac{\sum _{v\in (\bar C_{H'}\cap [\tau ])}\sum _{e\ni v}h(e)}{s\tau }\right )-\frac{\rho n}{t}\\[5pt] & \geq \left (1-\zeta \right )\frac{\tau y}{t}\left (f(\lambda )-\frac \epsilon 2\right )-\frac{\rho }{\frac{\tau (1-\delta )}{m}-\rho }\\[5pt] & \geq \left (1-\zeta \right )\frac{\tau y}{\delta n+\tau y}\left (f(\lambda )-\frac \epsilon 2\right )-\frac{\rho }{\gamma (1-\delta )-\rho }\\[5pt] & \geq \left (1-\zeta \right )\frac{1}{1+\delta \frac{n}{my}\frac m\tau }\left (f(\lambda )-\frac \epsilon 2\right )-\frac \epsilon 4\\[5pt] & \geq \left (1-\zeta \right )\frac{1}{1+\frac{\delta }{(1-\delta )\gamma }}\left (f(\lambda )-\frac \epsilon 2\right )-\frac \epsilon 4\\[5pt] & \geq f(\lambda )-\epsilon . \end{align*}
To conclude the proof of our initial claim, notice that
![]() $t\geq \left (\frac{(1-\delta ) \tau } m-\rho \right )n\geq ((1-\delta )\gamma -\rho ) n\geq \gamma 'n$
for a constant
$t\geq \left (\frac{(1-\delta ) \tau } m-\rho \right )n\geq ((1-\delta )\gamma -\rho ) n\geq \gamma 'n$
for a constant
![]() $\gamma '\gt 0$
.
$\gamma '\gt 0$
.
We are now ready to construct
![]() $W$
. Take a sequence
$W$
. Take a sequence
![]() $f(s/r)\gt \epsilon _1\gt \epsilon _2\gt \cdots \gt 0$
with
$f(s/r)\gt \epsilon _1\gt \epsilon _2\gt \cdots \gt 0$
with
![]() $\epsilon _i\rightarrow 0$
. Start by applying the claim with
$\epsilon _i\rightarrow 0$
. Start by applying the claim with
![]() $\epsilon =\epsilon _1$
and
$\epsilon =\epsilon _1$
and
![]() $n_1=N(\epsilon )$
to obtain a subgraph
$n_1=N(\epsilon )$
to obtain a subgraph
![]() $\mathcal{F}_1$
with colour
$\mathcal{F}_1$
with colour
![]() $C_1$
with density at least
$C_1$
with density at least
![]() $f(s/r)-\epsilon _1$
in
$f(s/r)-\epsilon _1$
in
![]() $[t_1]$
. Now proceed by induction and set
$[t_1]$
. Now proceed by induction and set
![]() $n_i=\max \{N(\epsilon _i/2), 2n_{i-1}(r+s)/(\epsilon _i\gamma (\epsilon _i/2))\}$
. Applying the claim with
$n_i=\max \{N(\epsilon _i/2), 2n_{i-1}(r+s)/(\epsilon _i\gamma (\epsilon _i/2))\}$
. Applying the claim with
![]() $\epsilon =\epsilon _i/2$
we find a subgraph
$\epsilon =\epsilon _i/2$
we find a subgraph
![]() $\mathcal{F}_i'$
with colour
$\mathcal{F}_i'$
with colour
![]() $C_i$
contained in
$C_i$
contained in
![]() $[n_i]$
and with density at least
$[n_i]$
and with density at least
![]() $f(s/r)-\epsilon _i/2$
in
$f(s/r)-\epsilon _i/2$
in
![]() $[t_i]$
, for some
$[t_i]$
, for some
![]() $t_i\in [\gamma (\epsilon )n_i,n_i]$
. Remove from
$t_i\in [\gamma (\epsilon )n_i,n_i]$
. Remove from
![]() $\mathcal{F}_i'$
all components that intersect
$\mathcal{F}_i'$
all components that intersect
![]() $[n_{i-1}]$
(this represents at most
$[n_{i-1}]$
(this represents at most
![]() $n_{i-1}(r+s)$
vertices) to obtain
$n_{i-1}(r+s)$
vertices) to obtain
![]() $\mathcal{F}_i$
. Then
$\mathcal{F}_i$
. Then
![]() $\mathcal{F}_i$
is disjoint from all previous
$\mathcal{F}_i$
is disjoint from all previous
![]() $\mathcal{F}_j$
, and by the choice of
$\mathcal{F}_j$
, and by the choice of
![]() $n_i$
, it still has density at least
$n_i$
, it still has density at least
![]() $f(s/r)-\epsilon _i$
in
$f(s/r)-\epsilon _i$
in
![]() $[t_i]$
.
$[t_i]$
.
Select a colour
![]() $C$
such that
$C$
such that
![]() $C_i=C$
for infinitely many
$C_i=C$
for infinitely many
![]() $i$
. Let
$i$
. Let
![]() $W=\cup _{C_i=C}\mathcal{F}_i$
. Then by construction
$W=\cup _{C_i=C}\mathcal{F}_i$
. Then by construction
![]() $\bar d(W)\geq f(s/r)$
, since the
$\bar d(W)\geq f(s/r)$
, since the
![]() $t_i$
tend to infinity, and the components of
$t_i$
tend to infinity, and the components of
![]() $W$
are isolated vertices of colour
$W$
are isolated vertices of colour
![]() $C$
or
$C$
or
![]() $K_{r,s}^C$
. This concludes the proof of Lemma 3.4.
$K_{r,s}^C$
. This concludes the proof of Lemma 3.4.
Finally, we prove Lemma 3.5 by defining an algorithm that constructs a monochromatic
![]() $H'$
. This algorithm uses enough components from
$H'$
. This algorithm uses enough components from
![]() $W$
(mapping to them either single vertices of
$W$
(mapping to them either single vertices of
![]() $H$
or sets
$H$
or sets
![]() $I_i\cup N(I_i)$
) to keep a fraction of its density and takes advantage of the properties of the
$I_i\cup N(I_i)$
) to keep a fraction of its density and takes advantage of the properties of the
![]() $a$
-good colouring to map the remaining vertices of
$a$
-good colouring to map the remaining vertices of
![]() $H$
.
$H$
.
Proof of Lemma
3.5. Without loss of generality, assume that
![]() $C$
is red, let
$C$
is red, let
![]() $S_j$
denote the vertices in
$S_j$
denote the vertices in
![]() $W$
of shade
$W$
of shade
![]() $R_j$
, plus the blue vertices contained in a copy of
$R_j$
, plus the blue vertices contained in a copy of
![]() $K_{r,s}^R$
in
$K_{r,s}^R$
in
![]() $W$
in which the red side has shade
$W$
in which the red side has shade
![]() $R_j$
. Removing from
$R_j$
. Removing from
![]() $W$
the finite sets
$W$
the finite sets
![]() $S_j$
does not affect its density, so suppose that each
$S_j$
does not affect its density, so suppose that each
![]() $S_j$
is either empty or infinite. We will show that there exists a set
$S_j$
is either empty or infinite. We will show that there exists a set
![]() $J\subseteq [a]$
, of size
$J\subseteq [a]$
, of size
![]() $b$
, such that
$b$
, such that
![]() $\bar d(\cup _{j\in J}S_j)\geq b/a'\bar d(W)$
.
$\bar d(\cup _{j\in J}S_j)\geq b/a'\bar d(W)$
.
By definition of density, there exists a sequence
![]() $n_1\lt n_2\lt \dots$
of positive integers such that
$n_1\lt n_2\lt \dots$
of positive integers such that
![]() $|V(W)\cap [n_i]|/n_i\rightarrow \bar d(W)$
. For each
$|V(W)\cap [n_i]|/n_i\rightarrow \bar d(W)$
. For each
![]() $i$
there exists a subset
$i$
there exists a subset
![]() $J_i\subseteq [a]$
of
$J_i\subseteq [a]$
of
![]() $b$
indices such that
$b$
indices such that
For infinitely many
![]() $i$
, the set
$i$
, the set
![]() $J_i$
is the same, which we denote
$J_i$
is the same, which we denote
![]() $J$
. By taking an appropriate subsequence of
$J$
. By taking an appropriate subsequence of
![]() $n_1, n_2, \dots$
, we can suppose without loss of generality that
$n_1, n_2, \dots$
, we can suppose without loss of generality that
![]() $J_i=J$
for all
$J_i=J$
for all
![]() $i$
and that
$i$
and that
![]() $n_{i+1}/n_i\rightarrow \infty$
. Let
$n_{i+1}/n_i\rightarrow \infty$
. Let
![]() $\mathcal{F}_i$
be the union of components from
$\mathcal{F}_i$
be the union of components from
![]() $W$
contained in some
$W$
contained in some
![]() $S_j$
with
$S_j$
with
![]() $j\in J$
, which contain a vertex from
$j\in J$
, which contain a vertex from
![]() $[n_i]$
but no vertex from
$[n_i]$
but no vertex from
![]() $[n_{i-1}]$
. Let
$[n_{i-1}]$
. Let
![]() $\mathcal{I}=\{I_1, I_2, \dots \}$
be the family of doubly independent sets. We can suppose that the elements in
$\mathcal{I}=\{I_1, I_2, \dots \}$
be the family of doubly independent sets. We can suppose that the elements in
![]() $\mathcal{I}$
are such that the sets
$\mathcal{I}$
are such that the sets
![]() $I_i\cup N(I_i)$
are pairwise disjoint. Indeed, because
$I_i\cup N(I_i)$
are pairwise disjoint. Indeed, because
![]() $H$
is locally finite, each
$H$
is locally finite, each
![]() $I_i\cup N(I_i)$
intersects finitely many sets
$I_i\cup N(I_i)$
intersects finitely many sets
![]() $I_j\cup N(I_j)$
, so we can find an infinite subfamily
$I_j\cup N(I_j)$
, so we can find an infinite subfamily
![]() $\mathcal{I}'$
by including in it only the sets
$\mathcal{I}'$
by including in it only the sets
![]() $I_i$
such that
$I_i$
such that
![]() $I_i\cup N(I_i)$
does not intersect a set
$I_i\cup N(I_i)$
does not intersect a set
![]() $I_j\cup N(I_j)$
for some
$I_j\cup N(I_j)$
for some
![]() $j\lt i$
with
$j\lt i$
with
![]() $I_j\in \mathcal{I'}$
. This does not change the components in which
$I_j\in \mathcal{I'}$
. This does not change the components in which
![]() $\mathcal{I}$
is concentrated.
$\mathcal{I}$
is concentrated.
Let
![]() $J'\subseteq J$
be the set of indices in
$J'\subseteq J$
be the set of indices in
![]() $j$
for which
$j$
for which
![]() $S_j$
is non-empty. We assign to each component
$S_j$
is non-empty. We assign to each component
![]() $\mathcal C\subseteq H$
a number
$\mathcal C\subseteq H$
a number
![]() $\kappa (\mathcal{C})\in J'$
, in such a way that for every
$\kappa (\mathcal{C})\in J'$
, in such a way that for every
![]() $j\in J'$
there are infinitely many sets
$j\in J'$
there are infinitely many sets
![]() $I_i$
in components with
$I_i$
in components with
![]() $\kappa (\mathcal{C})=j$
. Indeed, if finitely many components intersect
$\kappa (\mathcal{C})=j$
. Indeed, if finitely many components intersect
![]() $\mathcal{I}$
, there are at least
$\mathcal{I}$
, there are at least
![]() $b$
components that contain infinitely many elements of
$b$
components that contain infinitely many elements of
![]() $\mathcal{I}$
, so give different values of
$\mathcal{I}$
, so give different values of
![]() $\kappa (\mathcal{C})$
to
$\kappa (\mathcal{C})$
to
![]() $|J'|\leq b$
of them, whereas if there are infinitely many components that intersect
$|J'|\leq b$
of them, whereas if there are infinitely many components that intersect
![]() $\mathcal{I}$
, we can assign each value of
$\mathcal{I}$
, we can assign each value of
![]() $J'$
to infinitely many of them. The purpose of
$J'$
to infinitely many of them. The purpose of
![]() $\kappa (\mathcal{C})$
will be to identify the shade of red to be used in the vertices while embedding
$\kappa (\mathcal{C})$
will be to identify the shade of red to be used in the vertices while embedding
![]() $\mathcal{C}$
in the red edges of
$\mathcal{C}$
in the red edges of
![]() $\chi$
.
$\chi$
.
We will define an injective graph homomorphism
![]() $\Phi\;:\;H\rightarrow K_{\mathbb{N}}$
which maps edges to red edges, whose image contains
$\Phi\;:\;H\rightarrow K_{\mathbb{N}}$
which maps edges to red edges, whose image contains
![]() $\mathcal{F}_i$
for infinitely many
$\mathcal{F}_i$
for infinitely many
![]() $i$
. This is enough to prove Theorem 3.1, because for infinitely many large enough values of
$i$
. This is enough to prove Theorem 3.1, because for infinitely many large enough values of
![]() $i$
we have
$i$
we have
 \begin{align*} \frac{|\Phi (V(H))\cap [n_i]|}{n_i}\geq & \frac{|V(\mathcal{F}_i)\cap [n_i]|}{n_i}\geq \frac{b}{a'}\frac{|V(W)\cap [n_i]|}{n_i}-\frac{(r+s)n_{i-1}}{n_i}\\[5pt]\geq &\frac{b}{a'}\bar d(W)-o(1). \end{align*}
\begin{align*} \frac{|\Phi (V(H))\cap [n_i]|}{n_i}\geq & \frac{|V(\mathcal{F}_i)\cap [n_i]|}{n_i}\geq \frac{b}{a'}\frac{|V(W)\cap [n_i]|}{n_i}-\frac{(r+s)n_{i-1}}{n_i}\\[5pt]\geq &\frac{b}{a'}\bar d(W)-o(1). \end{align*}
We will define
![]() $\Phi$
in steps. Recall that
$\Phi$
in steps. Recall that
![]() $\Psi$
here denotes the proper vertex colouring of
$\Psi$
here denotes the proper vertex colouring of
![]() $H$
from Theorem 3.1. On every step, we will define the image of finitely many vertices of
$H$
from Theorem 3.1. On every step, we will define the image of finitely many vertices of
![]() $H$
. After every step, the following conditions must hold. Let
$H$
. After every step, the following conditions must hold. Let
![]() $u,v$
be two adjacent vertices in some component
$u,v$
be two adjacent vertices in some component
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $H$
, such that
$H$
, such that
![]() $\Phi (v)$
is defined and
$\Phi (v)$
is defined and
![]() $\Phi (u)$
is not. Then:
$\Phi (u)$
is not. Then:
-
If
 $\kappa (\mathcal{C})\neq a$
, then
$\kappa (\mathcal{C})\neq a$
, then
 $\Phi (v)\in R_{\kappa (\mathcal{C})}$
.
$\Phi (v)\in R_{\kappa (\mathcal{C})}$
. -
If
 $\kappa (\mathcal{C})=a$
and
$\kappa (\mathcal{C})=a$
and
 $\Psi (v)=a$
, then
$\Psi (v)=a$
, then
 $\Phi (v)\in R_a$
.
$\Phi (v)\in R_a$
. -
If
 $\kappa (\mathcal{C})=a$
and
$\kappa (\mathcal{C})=a$
and
 $\Psi (v)\neq a$
, then
$\Psi (v)\neq a$
, then
 $\Phi (v)\in B_{\Psi (v)}$
and
$\Phi (v)\in B_{\Psi (v)}$
and
 $\Psi (u)\lt \Psi (v)$
.
$\Psi (u)\lt \Psi (v)$
.
The algorithm will consist of two operations that alternate: defining the image of a vertex
![]() $v\in V(H)$
and adding some
$v\in V(H)$
and adding some
![]() $\mathcal{F}_i$
to the image of
$\mathcal{F}_i$
to the image of
![]() $\Phi$
. If we identify
$\Phi$
. If we identify
![]() $V(H)$
with
$V(H)$
with
![]() $\mathbb{N}$
and always apply the first operation to the least vertex
$\mathbb{N}$
and always apply the first operation to the least vertex
![]() $v$
with undefined
$v$
with undefined
![]() $\Phi (v)$
, at the end of the algorithm
$\Phi (v)$
, at the end of the algorithm
![]() $\Phi (v)$
will be defined for every vertex in
$\Phi (v)$
will be defined for every vertex in
![]() $V(H)$
.
$V(H)$
.
Define the image of a vertex
![]() $v\in V(H)$
: Suppose first that
$v\in V(H)$
: Suppose first that
![]() $v\in \mathcal{C}$
and
$v\in \mathcal{C}$
and
![]() $\kappa (\mathcal{C})=k\neq a$
. Let
$\kappa (\mathcal{C})=k\neq a$
. Let
![]() $w_1, \dots, w_q$
be the neighbours of
$w_1, \dots, w_q$
be the neighbours of
![]() $v$
which have
$v$
which have
![]() $\Phi (w_i)$
defined. By our invariant, the vertices
$\Phi (w_i)$
defined. By our invariant, the vertices
![]() $\Phi (w_i)$
all have shade
$\Phi (w_i)$
all have shade
![]() $R_k$
, and therefore there are infinitely many vertices
$R_k$
, and therefore there are infinitely many vertices
![]() $x$
in shade
$x$
in shade
![]() $R_k$
which are connected to every
$R_k$
which are connected to every
![]() $\Phi (w_i)$
through a red edge. Select one such
$\Phi (w_i)$
through a red edge. Select one such
![]() $x$
which is not yet in the image of
$x$
which is not yet in the image of
![]() $\Phi$
and set
$\Phi$
and set
![]() $\Phi (v)=x$
.
$\Phi (v)=x$
.
Now suppose that
![]() $\kappa (\mathcal{C})=a$
. Let
$\kappa (\mathcal{C})=a$
. Let
![]() $\Psi (v)=k$
. For every edge
$\Psi (v)=k$
. For every edge
![]() $uw$
of
$uw$
of
![]() $H$
, define an orientation
$H$
, define an orientation
![]() $\overrightarrow{uw}$
such that
$\overrightarrow{uw}$
such that
![]() $\Psi (u)\lt \Psi (w)$
. Let
$\Psi (u)\lt \Psi (w)$
. Let
![]() $T$
be the set of vertices that can be reached from
$T$
be the set of vertices that can be reached from
![]() $v$
in this orientation. Because
$v$
in this orientation. Because
![]() $T$
is connected, does not contain a path of length greater than
$T$
is connected, does not contain a path of length greater than
![]() $a$
, and the degree of every vertex is finite,
$a$
, and the degree of every vertex is finite,
![]() $T$
is finite. Also,
$T$
is finite. Also,
![]() $T$
does not have an oriented cycle. Observe that, by our invariant, if
$T$
does not have an oriented cycle. Observe that, by our invariant, if
![]() $\overrightarrow{uw}$
is an edge and
$\overrightarrow{uw}$
is an edge and
![]() $\Phi (u)$
is defined, then
$\Phi (u)$
is defined, then
![]() $\Phi (w)$
is defined.
$\Phi (w)$
is defined.
Now define
![]() $\Phi (w)$
for every
$\Phi (w)$
for every
![]() $w\in T$
for which the image is still undefined, in decreasing order of
$w\in T$
for which the image is still undefined, in decreasing order of
![]() $\Psi (w)$
. If
$\Psi (w)$
. If
![]() $\Psi (w)=a$
, choose an arbitrary vertex
$\Psi (w)=a$
, choose an arbitrary vertex
![]() $x\in R_a$
which is not yet the image of any vertex and set
$x\in R_a$
which is not yet the image of any vertex and set
![]() $\Phi (w)=x$
. If
$\Phi (w)=x$
. If
![]() $\Psi (w)=k\lt a$
, then for every
$\Psi (w)=k\lt a$
, then for every
![]() $w'\in N^+(w)$
the image
$w'\in N^+(w)$
the image
![]() $\Phi (w')$
is defined and in
$\Phi (w')$
is defined and in
![]() $B_{k+1}\cup \dots \cup B_{a-1}\cup R_a$
. By the properties of
$B_{k+1}\cup \dots \cup B_{a-1}\cup R_a$
. By the properties of
![]() $a$
-good colourings, there are infinitely many verticesFootnote
4
$a$
-good colourings, there are infinitely many verticesFootnote
4
![]() $x\in B_k$
which are connected to every
$x\in B_k$
which are connected to every
![]() $\Phi (w')$
through a red edge. Choose one which is not yet in the image of
$\Phi (w')$
through a red edge. Choose one which is not yet in the image of
![]() $\Phi$
and set
$\Phi$
and set
![]() $\Phi (w)=x$
.
$\Phi (w)=x$
.
Add some set
![]() $\mathcal{F}_i$
to the image: Select some
$\mathcal{F}_i$
to the image: Select some
![]() $\mathcal{F}_i$
which is so far disjoint with the image of
$\mathcal{F}_i$
which is so far disjoint with the image of
![]() $\Phi$
. For each
$\Phi$
. For each
![]() $K_{r,s}^R$
component
$K_{r,s}^R$
component
![]() $Z\subseteq \mathcal{F}_i\cap S_j$
, choose a doubly independent set
$Z\subseteq \mathcal{F}_i\cap S_j$
, choose a doubly independent set
![]() $I\in \mathcal{I}$
in a component
$I\in \mathcal{I}$
in a component
![]() $\mathcal{C}$
with
$\mathcal{C}$
with
![]() $\kappa (\mathcal{C})=j$
, such that no vertex from
$\kappa (\mathcal{C})=j$
, such that no vertex from
![]() $I\cup N(I)\cup N(N(I))$
has a defined image. If
$I\cup N(I)\cup N(N(I))$
has a defined image. If
![]() $V(Z)=X\cup Y$
with
$V(Z)=X\cup Y$
with
![]() $|X|=r$
blue and
$|X|=r$
blue and
![]() $|Y|=s$
red, then set
$|Y|=s$
red, then set
![]() $\Phi$
to be bijective from
$\Phi$
to be bijective from
![]() $I$
to
$I$
to
![]() $X$
, and injective from
$X$
, and injective from
![]() $N(I)$
to
$N(I)$
to
![]() $Y$
. The vertices
$Y$
. The vertices
![]() $v$
of
$v$
of
![]() $\mathcal{F}_i\cap S_j$
that remain outside of the image at this point all have shade
$\mathcal{F}_i\cap S_j$
that remain outside of the image at this point all have shade
![]() $R_{j}$
. For each of them, choose a vertex
$R_{j}$
. For each of them, choose a vertex
![]() $w$
with
$w$
with
![]() $\Psi (w)=a$
in a component
$\Psi (w)=a$
in a component
![]() $\mathcal{C}$
with
$\mathcal{C}$
with
![]() $\kappa (\mathcal{C})=j$
(there are infinitely many of these vertices), such that no vertex in
$\kappa (\mathcal{C})=j$
(there are infinitely many of these vertices), such that no vertex in
![]() $w\cup N(w)$
has a defined image and set
$w\cup N(w)$
has a defined image and set
![]() $\Phi (w)=v$
. After doing this for every isolated vertex in
$\Phi (w)=v$
. After doing this for every isolated vertex in
![]() $\mathcal{F}_{i}\cap S_j$
for every
$\mathcal{F}_{i}\cap S_j$
for every
![]() $j\in J'$
, the set
$j\in J'$
, the set
![]() $\mathcal{F}_i$
is contained in the image.
$\mathcal{F}_i$
is contained in the image.
After both steps are applied alternatingly infinitely many times, the image of
![]() $\Phi$
is a monochromatic red graph
$\Phi$
is a monochromatic red graph
![]() $H'\subseteq K_{\mathbb{N}}$
which contains infinitely many sets
$H'\subseteq K_{\mathbb{N}}$
which contains infinitely many sets
![]() $\mathcal{F}_i$
, and therefore
$\mathcal{F}_i$
, and therefore
![]() $\bar d(H')\geq b/a'\bar d(W)$
.
$\bar d(H')\geq b/a'\bar d(W)$
.
To prove the lower bound of Theorem 1.42b, we just need the following variant of Lemma 3.5. The proof is then analogous to the proof of Theorem 3.1, except we bypass completely the use of Lemma 3.4, and we only need that in the
![]() $a$
-good colouring we have
$a$
-good colouring we have
![]() $\max \{\bar d(R), \bar d(B)\}\geq 1/2$
.
$\max \{\bar d(R), \bar d(B)\}\geq 1/2$
.
Lemma 3.11.
Let
![]() $\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be an edge-colouring, let
$\chi\;:\;E(K_{\mathbb{N}})\rightarrow \{R,B\}$
be an edge-colouring, let
![]() $a\geq a'\geq b$
be positive integers. Let
$a\geq a'\geq b$
be positive integers. Let
![]() ${\mathbb{N}}\rightarrow \{R_1, \dots, R_a, B_1, \dots, B_a, X\}$
be an
${\mathbb{N}}\rightarrow \{R_1, \dots, R_a, B_1, \dots, B_a, X\}$
be an
![]() $a$
-good colouring in which at most
$a$
-good colouring in which at most
![]() $a'$
shades of each colour are non-empty. Let
$a'$
shades of each colour are non-empty. Let
![]() $C\in \{R,B\}$
. Let
$C\in \{R,B\}$
. Let
![]() $H$
be a graph with chromatic number
$H$
be a graph with chromatic number
![]() $a$
and at least
$a$
and at least
![]() $b$
infinite components. Then there exists a monochromatic
$b$
infinite components. Then there exists a monochromatic
![]() $H'\subseteq K_{\mathbb{N}}$
of colour
$H'\subseteq K_{\mathbb{N}}$
of colour
![]() $C$
,
$C$
,
![]() $H'\simeq H$
, with
$H'\simeq H$
, with
![]() $\bar d(H')\geq b/a'\bar d(C)$
.
$\bar d(H')\geq b/a'\bar d(C)$
.
Proof. Let
![]() $\Psi\;:\;V(H)\rightarrow [a]$
be a proper colouring, in which in every component of
$\Psi\;:\;V(H)\rightarrow [a]$
be a proper colouring, in which in every component of
![]() $H$
the most common colour is
$H$
the most common colour is
![]() $a$
. Without loss of generality suppose that
$a$
. Without loss of generality suppose that
![]() $C$
is red. As in the proof of Lemma 3.5, there exists
$C$
is red. As in the proof of Lemma 3.5, there exists
![]() $J'$
with
$J'$
with
![]() $|J'|\leq b$
, such that
$|J'|\leq b$
, such that
![]() $\bar d(\cup _{j\in J'}R_j)\geq b/a'$
, and all
$\bar d(\cup _{j\in J'}R_j)\geq b/a'$
, and all
![]() $R_j$
with
$R_j$
with
![]() $j\in J'$
are infinite. Let
$j\in J'$
are infinite. Let
![]() $\mathcal{F}=\cup _{j\in J'}R_j$
. Define a function
$\mathcal{F}=\cup _{j\in J'}R_j$
. Define a function
![]() $\kappa$
from the components of
$\kappa$
from the components of
![]() $H$
to
$H$
to
![]() $J'$
for which the pre-image of every value contains infinitely many vertices. The algorithm now alternates between define the image of a vertex
$J'$
for which the pre-image of every value contains infinitely many vertices. The algorithm now alternates between define the image of a vertex
![]() $v\in V(H)$
, as above, and add a vertex of
$v\in V(H)$
, as above, and add a vertex of
![]() $\mathcal{F}$
to the image. At the end of the procedure, we obtain a red
$\mathcal{F}$
to the image. At the end of the procedure, we obtain a red
![]() $H'\subseteq K_{\mathbb{N}}$
isomorphic to
$H'\subseteq K_{\mathbb{N}}$
isomorphic to
![]() $H$
which contains
$H$
which contains
![]() $\mathcal{F}$
and thus has density at least
$\mathcal{F}$
and thus has density at least
![]() $\bar d(\mathcal{F})\geq b/a'\bar d(R)$
.
$\bar d(\mathcal{F})\geq b/a'\bar d(R)$
.
Add a vertex of
![]() $\mathcal{F}$
to the image: Let
$\mathcal{F}$
to the image: Let
![]() $v\in \mathcal{F}$
be a vertex in
$v\in \mathcal{F}$
be a vertex in
![]() $R_j$
. Choose a vertex
$R_j$
. Choose a vertex
![]() $w$
in a component
$w$
in a component
![]() $\mathcal{C}$
with
$\mathcal{C}$
with
![]() $\kappa (\mathcal{C})=j$
, such that no vertex in
$\kappa (\mathcal{C})=j$
, such that no vertex in
![]() $w\cup N(w)$
has a defined image and with
$w\cup N(w)$
has a defined image and with
![]() $\Psi (w)=a$
and set
$\Psi (w)=a$
and set
![]() $\Phi (w)=v$
.
$\Phi (w)=v$
.
4. Bounds for particular families of graphs
The goal of this section is to prove the remaining results from Section 1. We will start by stating and proving the more general result for bipartite graphs, which will be used to imply Theorem 1.7.
Theorem 4.1.
Let
![]() $H$
be a locally finite bipartite graph, and let
$H$
be a locally finite bipartite graph, and let
![]() $\lambda =\liminf _{n\rightarrow \infty }\frac{\mu (H,n)}{n}$
. Suppose that for every
$\lambda =\liminf _{n\rightarrow \infty }\frac{\mu (H,n)}{n}$
. Suppose that for every
![]() $\lambda '\gt \lambda$
there exist infinitely many pairwise disjoint independent sets
$\lambda '\gt \lambda$
there exist infinitely many pairwise disjoint independent sets
![]() $I_1, I_2, \dots$
, all of the same (finite) size, with
$I_1, I_2, \dots$
, all of the same (finite) size, with
![]() $\frac{|N(I_i)|}{|I_i|}\leq \lambda '$
. Then
$\frac{|N(I_i)|}{|I_i|}\leq \lambda '$
. Then
![]() $\rho (H)=f(\lambda )$
.
$\rho (H)=f(\lambda )$
.
Proof. The upper bound follows from Theorem 1.6. We will show that, for every
![]() $\epsilon \gt 0$
, we have
$\epsilon \gt 0$
, we have
![]() $\rho (H)\geq f(\lambda )-\epsilon$
. Our goal is to show that
$\rho (H)\geq f(\lambda )-\epsilon$
. Our goal is to show that
![]() $H$
satisfies the condition of Theorem 3.1 for
$H$
satisfies the condition of Theorem 3.1 for
![]() $a=2$
,
$a=2$
,
![]() $b=1$
, a certain colouring
$b=1$
, a certain colouring
![]() $\Psi$
and some doubly independent sets
$\Psi$
and some doubly independent sets
![]() $I'_i$
. Let
$I'_i$
. Let
![]() $\Psi\;:\;V(H)\rightarrow \{1,2\}$
be a proper colouring. Choose
$\Psi\;:\;V(H)\rightarrow \{1,2\}$
be a proper colouring. Choose
![]() $\lambda '\gt \lambda$
such that
$\lambda '\gt \lambda$
such that
![]() $f(\lambda ')\gt f(\lambda )-\epsilon$
(it exists by continuity of
$f(\lambda ')\gt f(\lambda )-\epsilon$
(it exists by continuity of
![]() $f$
). There exist infinitely many pairwise disjoint independent sets
$f$
). There exist infinitely many pairwise disjoint independent sets
![]() $I_i$
, all with the same size, such that
$I_i$
, all with the same size, such that
![]() $\frac{|N(I_i)|}{|I_i|}\leq \lambda '$
(by the condition from the statement). Partition each set
$\frac{|N(I_i)|}{|I_i|}\leq \lambda '$
(by the condition from the statement). Partition each set
![]() $I_i$
into non-empty sets
$I_i$
into non-empty sets
![]() $I_{i,1}, \dots, I_{i,k_i}$
, where each vertex
$I_{i,1}, \dots, I_{i,k_i}$
, where each vertex
![]() $v$
is classified according to its colour by
$v$
is classified according to its colour by
![]() $\Psi$
and the component it belongs to. If two vertices
$\Psi$
and the component it belongs to. If two vertices
![]() $v,w$
have a common neighbour, then they are in the same component and
$v,w$
have a common neighbour, then they are in the same component and
![]() $\Psi (u)=\Psi (v)$
. For this reason,
$\Psi (u)=\Psi (v)$
. For this reason,
![]() $|N(I_i)|=\sum _{j=1}^{k_i}|N(I_{i,j})|$
. There exists some
$|N(I_i)|=\sum _{j=1}^{k_i}|N(I_{i,j})|$
. There exists some
![]() $\tau _i$
such that
$\tau _i$
such that
 \begin{equation*}\frac {|N(I_{i,\tau _i})|}{|I_{i,\tau _i}|}\leq \frac {\sum _{j=1}^{k_i}|N(I_{i,j})|}{\sum _{j=1}^{k_i}|I_{i,j}|}=\frac {|N(I_i)|}{|I_i|}\leq \lambda '.\end{equation*}
\begin{equation*}\frac {|N(I_{i,\tau _i})|}{|I_{i,\tau _i}|}\leq \frac {\sum _{j=1}^{k_i}|N(I_{i,j})|}{\sum _{j=1}^{k_i}|I_{i,j}|}=\frac {|N(I_i)|}{|I_i|}\leq \lambda '.\end{equation*}
Set
![]() $I'_i=I_{i,\tau _i}$
. Set
$I'_i=I_{i,\tau _i}$
. Set
![]() $r_i=|I'_i|$
and
$r_i=|I'_i|$
and
![]() $s_i=|N(I'_i)|$
. There is a pair
$s_i=|N(I'_i)|$
. There is a pair
![]() $(r,s)$
satisfying
$(r,s)$
satisfying
![]() $(r,s)=(r_i,s_i)$
for infinitely many values of
$(r,s)=(r_i,s_i)$
for infinitely many values of
![]() $i$
. Considering only the values of
$i$
. Considering only the values of
![]() $i$
for which this equality holds, we have our set of independent sets. Note that, because
$i$
for which this equality holds, we have our set of independent sets. Note that, because
![]() $H$
is bipartite,
$H$
is bipartite,
![]() $N(I'_i)$
is monochromatic and thus independent, meaning that
$N(I'_i)$
is monochromatic and thus independent, meaning that
![]() $I'_i$
is doubly independent. If
$I'_i$
is doubly independent. If
![]() $\Psi (N(I'_i))=2$
does not hold for infinitely many
$\Psi (N(I'_i))=2$
does not hold for infinitely many
![]() $i$
, replace
$i$
, replace
![]() $\Psi$
with
$\Psi$
with
![]() $\bar \Psi =3-\Psi$
. We can now apply Theorem 3.1 to obtain
$\bar \Psi =3-\Psi$
. We can now apply Theorem 3.1 to obtain
![]() $\rho (H)\geq f(s/r)\geq f(\lambda ')$
.
$\rho (H)\geq f(s/r)\geq f(\lambda ')$
.
We will prove Theorem 1.7 using Theorem 4.1. To do this we need to show that, in both graphs with infinite orbits and forests, the condition in the statement of Theorem 4.1 holds.
Proof of Theorem
1.7. Let
![]() $\lambda =\liminf \limits _{n\rightarrow \infty }\frac{\mu (H,n)}{n}$
. Fix
$\lambda =\liminf \limits _{n\rightarrow \infty }\frac{\mu (H,n)}{n}$
. Fix
![]() $\lambda '\gt \lambda$
. We will show that, in both cases, there exist infinitely many pairwise disjoint independent sets
$\lambda '\gt \lambda$
. We will show that, in both cases, there exist infinitely many pairwise disjoint independent sets
![]() $I_1, I_2, \dots$
, all with the same size, with
$I_1, I_2, \dots$
, all with the same size, with
![]() $\frac{|N(I_i)|}{|I_i|}\leq \lambda '$
.
$\frac{|N(I_i)|}{|I_i|}\leq \lambda '$
.
For graphs with infinite orbits: Choose
![]() $n$
such that
$n$
such that
![]() $\frac{\mu (H,n)}{n}\lt \lambda '$
. Let
$\frac{\mu (H,n)}{n}\lt \lambda '$
. Let
![]() $I$
be an independent set of size
$I$
be an independent set of size
![]() $n$
with
$n$
with
![]() $|N(I)|=\mu (H,n)$
. We will show that there are infinitely many automorphisms
$|N(I)|=\mu (H,n)$
. We will show that there are infinitely many automorphisms
![]() $\sigma _i\in \textrm{Aut}(H)$
such that the sets
$\sigma _i\in \textrm{Aut}(H)$
such that the sets
![]() $\sigma _i(I)$
are pairwise disjoint. Then we can take
$\sigma _i(I)$
are pairwise disjoint. Then we can take
![]() $I_i=\sigma _i(I)$
to conlude the proof. We proceed by induction on
$I_i=\sigma _i(I)$
to conlude the proof. We proceed by induction on
![]() $n$
. For
$n$
. For
![]() $n=1$
, if
$n=1$
, if
![]() $I=\{v\}$
, this is equivalent to the orbit of
$I=\{v\}$
, this is equivalent to the orbit of
![]() $v$
being infinite.
$v$
being infinite.
Suppose that the result is true for
![]() $n-1$
. Suppose that we have already found
$n-1$
. Suppose that we have already found
![]() $\sigma _1, \sigma _2, \dots, \sigma _k$
such that the sets
$\sigma _1, \sigma _2, \dots, \sigma _k$
such that the sets
![]() $\sigma _i(I)$
are pairwise disjoint. Let
$\sigma _i(I)$
are pairwise disjoint. Let
![]() $X=\cup _{i=1}^k\sigma _i(I)$
. We will construct
$X=\cup _{i=1}^k\sigma _i(I)$
. We will construct
![]() $\sigma _{k+1}\in \textrm{Aut}(H)$
such that
$\sigma _{k+1}\in \textrm{Aut}(H)$
such that
![]() $\sigma _{k+1}(I)$
is disjoint from
$\sigma _{k+1}(I)$
is disjoint from
![]() $X$
. Choose
$X$
. Choose
![]() $v\in I$
. By the induction hypothesis, there is an infinite family
$v\in I$
. By the induction hypothesis, there is an infinite family
![]() $\{\tau _i\}_{i=1}^\infty \subseteq \textrm{Aut}(H)$
such that the sets
$\{\tau _i\}_{i=1}^\infty \subseteq \textrm{Aut}(H)$
such that the sets
![]() $\tau _i(I-v)$
are pairwise disjoint. If
$\tau _i(I-v)$
are pairwise disjoint. If
![]() $\tau _i(v)\not \in X$
for some
$\tau _i(v)\not \in X$
for some
![]() $i$
, then we can take
$i$
, then we can take
![]() $\sigma _{k+1}=\tau _i$
, and we are done. Therefore, assume that
$\sigma _{k+1}=\tau _i$
, and we are done. Therefore, assume that
![]() $\tau _i(v)\in X$
for every
$\tau _i(v)\in X$
for every
![]() $i$
. By pigeonhole principle, there exists
$i$
. By pigeonhole principle, there exists
![]() $w$
such that
$w$
such that
![]() $\tau _i(v)=w$
for infinitely many
$\tau _i(v)=w$
for infinitely many
![]() $i$
. Choose
$i$
. Choose
![]() $\phi \in \textrm{Aut(H)}$
such that
$\phi \in \textrm{Aut(H)}$
such that
![]() $\phi (w)\not \in X$
(it exists because the orbit of
$\phi (w)\not \in X$
(it exists because the orbit of
![]() $w$
is infinite). The set
$w$
is infinite). The set
![]() $\phi ^{-1}(X)$
intersects finitely many sets
$\phi ^{-1}(X)$
intersects finitely many sets
![]() $\tau _i(I-v)$
, therefore there exists some
$\tau _i(I-v)$
, therefore there exists some
![]() $i$
with
$i$
with
![]() $\tau _i(I-v)$
disjoint from
$\tau _i(I-v)$
disjoint from
![]() $\phi ^{-1}(X)$
and
$\phi ^{-1}(X)$
and
![]() $\tau _i(v)=w$
. Putting this together,
$\tau _i(v)=w$
. Putting this together,
![]() $\phi (\tau _i(I))$
is disjoint from
$\phi (\tau _i(I))$
is disjoint from
![]() $X$
, as we wanted.
$X$
, as we wanted.
For forests: The following lemma will be used to find independent sets of bounded size with bounded expansion within larger independent sets:
Lemma 4.2.
For every
![]() $\lambda '\gt \lambda$
there exists
$\lambda '\gt \lambda$
there exists
![]() $M=M(\lambda,\lambda ')$
such that, for every independent set
$M=M(\lambda,\lambda ')$
such that, for every independent set
![]() $I$
in a forest with
$I$
in a forest with
![]() $|N(I)|\leq \lambda |I|$
, there exists
$|N(I)|\leq \lambda |I|$
, there exists
![]() $I'\subseteq I$
with
$I'\subseteq I$
with
![]() $|N(I')|\leq \lambda '|I'|$
and
$|N(I')|\leq \lambda '|I'|$
and
![]() $|I'|\leq M$
.
$|I'|\leq M$
.
Knowing this lemma, choose
![]() $\lambda ''\lt \lambda '''\in (\lambda,\lambda ')$
and set
$\lambda ''\lt \lambda '''\in (\lambda,\lambda ')$
and set
![]() $M=M(\lambda ''',\lambda ')$
. Suppose that we have already constructed pairwise disjoint independent sets
$M=M(\lambda ''',\lambda ')$
. Suppose that we have already constructed pairwise disjoint independent sets
![]() $I_1, I_2, \dots, I_k$
with
$I_1, I_2, \dots, I_k$
with
![]() $|I_i|\leq M$
and
$|I_i|\leq M$
and
![]() $|N(I_i)|\leq \lambda '|I_i|$
. We will find a new set
$|N(I_i)|\leq \lambda '|I_i|$
. We will find a new set
![]() $I_{k+1}$
, disjoint from the others. Let
$I_{k+1}$
, disjoint from the others. Let
![]() $S=\cup _{i=1}^kI_i$
. There exists
$S=\cup _{i=1}^kI_i$
. There exists
![]() $n$
large enough such that
$n$
large enough such that
![]() $\frac{n}{n-|S|}\leq \frac{\lambda '''}{\lambda ''}$
. By definition of
$\frac{n}{n-|S|}\leq \frac{\lambda '''}{\lambda ''}$
. By definition of
![]() $\liminf$
and
$\liminf$
and
![]() $\mu (H,n)$
, there exists an independent set
$\mu (H,n)$
, there exists an independent set
![]() $I$
with
$I$
with
![]() $|I|\geq n$
and
$|I|\geq n$
and
![]() $|N(I)|\leq \lambda ''|I|$
. Then
$|N(I)|\leq \lambda ''|I|$
. Then
By our claim, there exists
![]() $I_{k+1}\subseteq I\setminus S$
such that
$I_{k+1}\subseteq I\setminus S$
such that
![]() $|I_{k+1}|\leq M$
and
$|I_{k+1}|\leq M$
and
![]() $|N(I_{k+1})|\leq \lambda ' |I_{k+1}|$
. Once we have constructed an infinite family of independent sets
$|N(I_{k+1})|\leq \lambda ' |I_{k+1}|$
. Once we have constructed an infinite family of independent sets
![]() $I_1, I_2, \dots$
, simply take a pair
$I_1, I_2, \dots$
, simply take a pair
![]() $(r,s)$
which is equal to
$(r,s)$
which is equal to
![]() $(|I_i|, |N(I_i)|)$
for infinitely many
$(|I_i|, |N(I_i)|)$
for infinitely many
![]() $i$
(which is possible because this pair can only take finitely many values), and we are done.
$i$
(which is possible because this pair can only take finitely many values), and we are done.
Proof of Lemma
4.2. Let
![]() $\delta =\delta (\lambda,\lambda ')\gt 0$
be small enough, which we will fix later. Let
$\delta =\delta (\lambda,\lambda ')\gt 0$
be small enough, which we will fix later. Let
![]() $F$
be the forest with vertex set
$F$
be the forest with vertex set
![]() $I\cup N(I)$
and containing only the edges between
$I\cup N(I)$
and containing only the edges between
![]() $I$
and
$I$
and
![]() $N(I)$
in our original graph. It is enough to prove our result in
$N(I)$
in our original graph. It is enough to prove our result in
![]() $F$
. Denote
$F$
. Denote
![]() $J=N(I)$
. For every component of
$J=N(I)$
. For every component of
![]() $F$
take a vertex of
$F$
take a vertex of
![]() $I$
as the root.
$I$
as the root.
There exists a set
![]() $S\subseteq V(F)$
with
$S\subseteq V(F)$
with
![]() $|S|\leq \delta |V(F)|$
, satisfying that every component of
$|S|\leq \delta |V(F)|$
, satisfying that every component of
![]() $F\setminus S$
has size at most
$F\setminus S$
has size at most
![]() $\delta ^{-1}$
. Indeed, start with
$\delta ^{-1}$
. Indeed, start with
![]() $S=\emptyset$
and consider the set
$S=\emptyset$
and consider the set
![]() $U$
of vertices whose component in
$U$
of vertices whose component in
![]() $F\setminus S$
contains at least
$F\setminus S$
contains at least
![]() $\delta ^{-1}$
vertices. The rooted forest structure in
$\delta ^{-1}$
vertices. The rooted forest structure in
![]() $F$
induces a rooted forest structure in
$F$
induces a rooted forest structure in
![]() $F\setminus S$
. Let
$F\setminus S$
. Let
![]() $U'$
be the set of vertices in
$U'$
be the set of vertices in
![]() $F\setminus S$
which have at least
$F\setminus S$
which have at least
![]() $\delta ^{-1}-1$
descendants. If
$\delta ^{-1}-1$
descendants. If
![]() $U\neq \emptyset$
then
$U\neq \emptyset$
then
![]() $U'\neq \emptyset$
, because the root of the largest component will be in
$U'\neq \emptyset$
, because the root of the largest component will be in
![]() $U'$
. Select a minimal vertex
$U'$
. Select a minimal vertex
![]() $v$
in
$v$
in
![]() $U'$
and add it to
$U'$
and add it to
![]() $S$
. This removes
$S$
. This removes
![]() $v$
and all its descendants from
$v$
and all its descendants from
![]() $U$
and thus reduces the size of
$U$
and thus reduces the size of
![]() $U$
by at least
$U$
by at least
![]() $\delta ^{-1}$
. After at most
$\delta ^{-1}$
. After at most
![]() $\delta |V(F)|$
steps,
$\delta |V(F)|$
steps,
![]() $U$
will be empty.
$U$
will be empty.
Let
![]() $X$
be the union of
$X$
be the union of
![]() $S$
and the parents of the vertices of
$S$
and the parents of the vertices of
![]() $S\cap J$
. This set has
$S\cap J$
. This set has
![]() $|X|\leq 2|S|\leq 2\delta |V(F)|$
, and every component
$|X|\leq 2|S|\leq 2\delta |V(F)|$
, and every component
![]() $T$
of
$T$
of
![]() $F\setminus X$
(which has the structure of a rooted tree) is adjacent to at most one vertex in
$F\setminus X$
(which has the structure of a rooted tree) is adjacent to at most one vertex in
![]() $X\cap J$
, in which case that vertex is the parent (in
$X\cap J$
, in which case that vertex is the parent (in
![]() $F$
) of the root of
$F$
) of the root of
![]() $T$
. This is because a vertex
$T$
. This is because a vertex
![]() $v$
in
$v$
in
![]() $T$
cannot have a child in
$T$
cannot have a child in
![]() $X\cap J$
, as that child would be in
$X\cap J$
, as that child would be in
![]() $S\cap J$
and
$S\cap J$
and
![]() $v$
would be its parent, and hence in
$v$
would be its parent, and hence in
![]() $X$
. As a consequence, every component of
$X$
. As a consequence, every component of
![]() $F\setminus (X\cap I)$
contains at most one vertex from
$F\setminus (X\cap I)$
contains at most one vertex from
![]() $X\cap J$
.
$X\cap J$
.
Let
![]() $\mathcal{C}=\{C_1, \dots, C_k\}$
be the components of
$\mathcal{C}=\{C_1, \dots, C_k\}$
be the components of
![]() $F\setminus (X\cap I)$
. Then
$F\setminus (X\cap I)$
. Then
 \begin{equation*}\frac {\sum _{j=1}^k|C_i\cap J|}{\sum _{j=1}^k|C_i\cap I|}= \frac {|J|}{|I|-|X\cap I|}\leq \frac {|N(I)|}{|I|-2\delta (|I|+|N(I)|)}\leq \frac {\lambda }{1-2\delta (1+\lambda )}\;=\!:\;\lambda ''.\end{equation*}
\begin{equation*}\frac {\sum _{j=1}^k|C_i\cap J|}{\sum _{j=1}^k|C_i\cap I|}= \frac {|J|}{|I|-|X\cap I|}\leq \frac {|N(I)|}{|I|-2\delta (|I|+|N(I)|)}\leq \frac {\lambda }{1-2\delta (1+\lambda )}\;=\!:\;\lambda ''.\end{equation*}
There exists some component
![]() $C_i$
such that
$C_i$
such that
![]() $|C_i\cap J|\leq \lambda ''|C_i\cap I|$
. If
$|C_i\cap J|\leq \lambda ''|C_i\cap I|$
. If
![]() $C_i\cap I$
has size not greater than
$C_i\cap I$
has size not greater than
![]() $M\;:\!=\;2\delta ^{-1}$
, then set
$M\;:\!=\;2\delta ^{-1}$
, then set
![]() $I'=C_i\cap I$
and we are done, because
$I'=C_i\cap I$
and we are done, because
![]() $N(I')\subseteq C_i\cap J$
. Otherwise
$N(I')\subseteq C_i\cap J$
. Otherwise
![]() $C_i$
has size greater than
$C_i$
has size greater than
![]() $2\delta ^{-1}$
, hence it must contain a (unique) vertex
$2\delta ^{-1}$
, hence it must contain a (unique) vertex
![]() $v\in X\cap J$
. Let
$v\in X\cap J$
. Let
![]() $C'_{\!\!1}, C'_{\!\!2}, \dots, C'_{\!\!r}$
be the components obtained from
$C'_{\!\!1}, C'_{\!\!2}, \dots, C'_{\!\!r}$
be the components obtained from
![]() $C_i$
by removing
$C_i$
by removing
![]() $v$
, labelled in decreasing order of
$v$
, labelled in decreasing order of
![]() $|C'_{\!\!j}\cap J|/|C'_{\!\!j}\cap I|$
. Consider the minimum integer
$|C'_{\!\!j}\cap J|/|C'_{\!\!j}\cap I|$
. Consider the minimum integer
![]() $t$
such that
$t$
such that
![]() $\sum _{j=1}^t|C'_{\!\!j}\cap I|\geq \delta ^{-1}$
. Because every component in
$\sum _{j=1}^t|C'_{\!\!j}\cap I|\geq \delta ^{-1}$
. Because every component in
![]() $F\setminus X$
has size at most
$F\setminus X$
has size at most
![]() $\delta ^{-1}$
, we have
$\delta ^{-1}$
, we have
![]() $\sum _{j=1}^t|C'_{\!\!j}\cap I|\leq \sum _{j=1}^{t-1}|C'_{\!\!j}\cap I|+\delta ^{-1}\leq 2\delta ^{-1}=M$
. Set
$\sum _{j=1}^t|C'_{\!\!j}\cap I|\leq \sum _{j=1}^{t-1}|C'_{\!\!j}\cap I|+\delta ^{-1}\leq 2\delta ^{-1}=M$
. Set
![]() $I'=\cup _{j=1}^t(C'_i\cap I)$
. Then
$I'=\cup _{j=1}^t(C'_i\cap I)$
. Then
 \begin{equation*}\frac {|N(I')|}{|I'|}=\frac {1+\sum _{j=1}^t|C'_{\!\!j}\cap J|}{\sum _{j=1}^t|C'_{\!\!j}\cap I|}\leq \delta +\frac {\sum _{j=1}^r|C'_{\!\!j}\cap J|}{\sum _{j=1}^r|C'_{\!\!j}\cap I|}\leq \delta +\lambda ''.\end{equation*}
\begin{equation*}\frac {|N(I')|}{|I'|}=\frac {1+\sum _{j=1}^t|C'_{\!\!j}\cap J|}{\sum _{j=1}^t|C'_{\!\!j}\cap I|}\leq \delta +\frac {\sum _{j=1}^r|C'_{\!\!j}\cap J|}{\sum _{j=1}^r|C'_{\!\!j}\cap I|}\leq \delta +\lambda ''.\end{equation*}
This proves Lemma 4.2, for
![]() $\delta \gt 0$
small enough such that
$\delta \gt 0$
small enough such that
![]() $\delta +\lambda ''\lt \lambda '$
.
$\delta +\lambda ''\lt \lambda '$
.
Next we will prove Corollaries 1.8–1.10 as direct applications of Theorem 1.7:
Proof of Corollary
1.8. We will show that
![]() $\mu (T_k,n)=kn$
. For every independent set
$\mu (T_k,n)=kn$
. For every independent set
![]() $I$
of size
$I$
of size
![]() $n$
, the set of children of the vertices of
$n$
, the set of children of the vertices of
![]() $I$
has size
$I$
has size
![]() $kn$
and is contained in
$kn$
and is contained in
![]() $N(I)$
, thus
$N(I)$
, thus
![]() $|N(I)|\geq kn$
. Equality can hold, for example for
$|N(I)|\geq kn$
. Equality can hold, for example for
![]() $I=\{v_1, \dots, v_n\}$
where
$I=\{v_1, \dots, v_n\}$
where
![]() $v_1$
is the root of
$v_1$
is the root of
![]() $T_k$
and
$T_k$
and
![]() $v_{i+1}$
is a grandchild of
$v_{i+1}$
is a grandchild of
![]() $v_i$
. We therefore have
$v_i$
. We therefore have
![]() $\mu (T_k,n)=kn$
. Since
$\mu (T_k,n)=kn$
. Since
![]() $T_k$
is a forest, Theorem 1.7 applies and
$T_k$
is a forest, Theorem 1.7 applies and
![]() $\rho (T_k)=f(k)$
.
$\rho (T_k)=f(k)$
.
Proof of Corollary
1.9. Let
![]() $I$
be an independent set. The set
$I$
be an independent set. The set
![]() $I+(1,0,\dots, 0)$
is contained in
$I+(1,0,\dots, 0)$
is contained in
![]() $N(I)$
, so
$N(I)$
, so
![]() $|N(I)|\geq |I|$
and
$|N(I)|\geq |I|$
and
![]() $\mu (\mathrm{Grid}_d,n)\geq n$
for all
$\mu (\mathrm{Grid}_d,n)\geq n$
for all
![]() $n$
. On the other hand, let
$n$
. On the other hand, let
![]() $I_k$
be the set of vertices in
$I_k$
be the set of vertices in
![]() $[2k]^d$
with odd sum of coordinates.
$[2k]^d$
with odd sum of coordinates.
![]() $I_k$
is an independent set of size
$I_k$
is an independent set of size
![]() $(2k)^d/2$
, and
$(2k)^d/2$
, and
![]() $I_k\cup N(I_k)$
is contained in
$I_k\cup N(I_k)$
is contained in
![]() $[2k+2]^d-(1,1,\dots, 1)$
. Since
$[2k+2]^d-(1,1,\dots, 1)$
. Since
![]() $I_k$
and
$I_k$
and
![]() $N(I_k)$
are disjoint,
$N(I_k)$
are disjoint,
which tends to 1 as
![]() $k\rightarrow \infty$
. We have
$k\rightarrow \infty$
. We have
![]() $\liminf \limits _{n\rightarrow \infty }\frac{\mu (\mathrm{Grid_d},n)}{n}=1$
. The graph
$\liminf \limits _{n\rightarrow \infty }\frac{\mu (\mathrm{Grid_d},n)}{n}=1$
. The graph
![]() $\mathrm{Grid}_d$
is vertex-transitive, so by Theorem 1.7 we have
$\mathrm{Grid}_d$
is vertex-transitive, so by Theorem 1.7 we have
![]() $\rho (\mathrm{Grid}_d)=f(1)$
.
$\rho (\mathrm{Grid}_d)=f(1)$
.
Proof of Corollary
1.10. The graph
![]() $\omega \cdot F$
satisfies that every orbit of the automorphism group on
$\omega \cdot F$
satisfies that every orbit of the automorphism group on
![]() $V(\omega \cdot F)$
is infinite (because it intersects every copy of
$V(\omega \cdot F)$
is infinite (because it intersects every copy of
![]() $F$
), so we are in the setting of Theorem 1.7. We need to show that
$F$
), so we are in the setting of Theorem 1.7. We need to show that
![]() $\liminf \limits _{n\rightarrow \infty }\frac{\mu (\omega \cdot F,n)}{n}=\min \limits _{I\subseteq V(F)\text{ indep.}}\frac{|N(I)|}{|I|}$
.
$\liminf \limits _{n\rightarrow \infty }\frac{\mu (\omega \cdot F,n)}{n}=\min \limits _{I\subseteq V(F)\text{ indep.}}\frac{|N(I)|}{|I|}$
.
Let
![]() $I$
be an independent set in
$I$
be an independent set in
![]() $F$
that minimises
$F$
that minimises
![]() $\frac{|N(I)|}{|I|}$
, and let
$\frac{|N(I)|}{|I|}$
, and let
![]() $J\subseteq V(\omega \cdot F)$
be an independent set of size
$J\subseteq V(\omega \cdot F)$
be an independent set of size
![]() $n$
. Partition
$n$
. Partition
![]() $J$
into independent sets
$J$
into independent sets
![]() $J_1, J_2,\dots, J_m$
, according to the component in which the vertices are contained. Then
$J_1, J_2,\dots, J_m$
, according to the component in which the vertices are contained. Then
This implies that
![]() $\frac{\mu (\omega \cdot F,n)}{n}\geq \frac{|N(I)|}{|I|}$
. Equality holds infinitely many times, since for all
$\frac{\mu (\omega \cdot F,n)}{n}\geq \frac{|N(I)|}{|I|}$
. Equality holds infinitely many times, since for all
![]() $n$
divisible by
$n$
divisible by
![]() $I$
we can take the union of the sets
$I$
we can take the union of the sets
![]() $I$
in
$I$
in
![]() $n/|I|$
different copies of
$n/|I|$
different copies of
![]() $F$
. Therefore
$F$
. Therefore
![]() $\rho (\omega \cdot F)=f\left (\liminf \limits _{n\rightarrow \infty }\frac{\mu (\omega \cdot F,n)}{n}\right )=f\left (\frac{|N(I)|}{|I|}\right )$
.
$\rho (\omega \cdot F)=f\left (\liminf \limits _{n\rightarrow \infty }\frac{\mu (\omega \cdot F,n)}{n}\right )=f\left (\frac{|N(I)|}{|I|}\right )$
.
In an even cycle
![]() $C_{2k}$
, each independent set satisfies
$C_{2k}$
, each independent set satisfies
![]() $|N(I)|\geq |I|$
, because
$|N(I)|\geq |I|$
, because
![]() $C_{2k}$
contains a perfect matching. Since each chromatic class in the bipartition satisfies
$C_{2k}$
contains a perfect matching. Since each chromatic class in the bipartition satisfies
![]() $|N(I)|=|I|$
, we have
$|N(I)|=|I|$
, we have
![]() $\rho (\omega \cdot C_{2k})=f(1)$
. For
$\rho (\omega \cdot C_{2k})=f(1)$
. For
![]() $1\leq a\leq b$
, in
$1\leq a\leq b$
, in
![]() $K_{a,b}$
, every independent set has size at most
$K_{a,b}$
, every independent set has size at most
![]() $b$
, and its neighbourhood has size at least
$b$
, and its neighbourhood has size at least
![]() $a$
. Both inequalities are sharp if
$a$
. Both inequalities are sharp if
![]() $I$
is the side of the bipartition with size
$I$
is the side of the bipartition with size
![]() $b$
. Thus
$b$
. Thus
![]() $\frac{|N(I)|}{|I|}\geq \frac ab$
, and
$\frac{|N(I)|}{|I|}\geq \frac ab$
, and
![]() $\rho (\omega \cdot K_{a,b})=f(a/b)$
.
$\rho (\omega \cdot K_{a,b})=f(a/b)$
.
Next we will deduce Theorem 1.11 from Theorem 3.1:
Proof of Theorem
1.11. Let
![]() $a=|V(F)|$
, and let
$a=|V(F)|$
, and let
![]() $b=a-1$
. Let
$b=a-1$
. Let
![]() $\Psi\;:\;V(F)\rightarrow [a]$
be a colouring that assigns the value
$\Psi\;:\;V(F)\rightarrow [a]$
be a colouring that assigns the value
![]() $a$
to every vertex in
$a$
to every vertex in
![]() $N(I)$
, and where the remaining vertices in
$N(I)$
, and where the remaining vertices in
![]() $F$
all get different values in
$F$
all get different values in
![]() $[a-1]$
. Because
$[a-1]$
. Because
![]() $I$
is doubly independent, this is a proper colouring.
$I$
is doubly independent, this is a proper colouring.
![]() $\Psi$
extends to a colouring of
$\Psi$
extends to a colouring of
![]() $\omega \cdot F$
, by colouring all copies of
$\omega \cdot F$
, by colouring all copies of
![]() $F$
equally.
$F$
equally.
Let
![]() $I_1, I_2, \dots$
be the sets
$I_1, I_2, \dots$
be the sets
![]() $I$
of all copies of
$I$
of all copies of
![]() $F$
. Each
$F$
. Each
![]() $I_i$
is contained in a component of
$I_i$
is contained in a component of
![]() $F$
,
$F$
,
![]() $\Psi (N(I_i))=a$
and the family of sets
$\Psi (N(I_i))=a$
and the family of sets
![]() $I_i$
is not concentrated in fewer than
$I_i$
is not concentrated in fewer than
![]() $b$
components. Thus, by Theorem 3.1, setting
$b$
components. Thus, by Theorem 3.1, setting
![]() $r=|I|$
and
$r=|I|$
and
![]() $s=|N(I)|$
, we have
$s=|N(I)|$
, we have
![]() $\rho (\omega \cdot F)\geq f\left (\frac{|N(I)|}{|I|}\right )$
.
$\rho (\omega \cdot F)\geq f\left (\frac{|N(I)|}{|I|}\right )$
.
Finally, we will prove Theorem 1.12 using a result of Burr, Erdős and Spencer [Reference Burr, Erdős and Spencer3] for the Ramsey number of
![]() $n\cdot F$
:
$n\cdot F$
:
Theorem 4.3 ([Reference Burr, Erdős and Spencer3]). Let
![]() $F_1, F_2$
be two finite graphs without isolated vertices. The two-colour Ramsey number
$F_1, F_2$
be two finite graphs without isolated vertices. The two-colour Ramsey number
![]() $R(n\cdot F_1, n\cdot F_2)$
satisfies
$R(n\cdot F_1, n\cdot F_2)$
satisfies
where
![]() $\alpha (G)$
is the size of the largest independent set in
$\alpha (G)$
is the size of the largest independent set in
![]() $G$
. In particular,
$G$
. In particular,
![]() $R(n\cdot F,n\cdot F)=(2|V(F)|-\alpha (F))n+O(1)$
.
$R(n\cdot F,n\cdot F)=(2|V(F)|-\alpha (F))n+O(1)$
.
Proof of Theorem
1.12. Let
![]() $\chi\;:\; E(K_{\mathbb{N}})\rightarrow \{R.B\}$
be a colouring. Let
$\chi\;:\; E(K_{\mathbb{N}})\rightarrow \{R.B\}$
be a colouring. Let
![]() $n_1, n_2, \dots$
be an increasing sequence of positive integers with
$n_1, n_2, \dots$
be an increasing sequence of positive integers with
![]() $n_{i+1}/n_i\rightarrow \infty$
. Let
$n_{i+1}/n_i\rightarrow \infty$
. Let
![]() $k_i$
be the maximum value such that
$k_i$
be the maximum value such that
![]() $R(k_i\cdot F, k_i\cdot F)\leq n_{i+1}-n_i$
. By Theorem 4.3, we have
$R(k_i\cdot F, k_i\cdot F)\leq n_{i+1}-n_i$
. By Theorem 4.3, we have
There exist a family
![]() $\mathcal{F}_i$
of
$\mathcal{F}_i$
of
![]() $k_i$
monochromatic disjoint copies of
$k_i$
monochromatic disjoint copies of
![]() $F$
with vertices in
$F$
with vertices in
![]() $[n_i+1, n_{n+1}]$
, all with the same colour
$[n_i+1, n_{n+1}]$
, all with the same colour
![]() $C_i$
. Choose a colour
$C_i$
. Choose a colour
![]() $C$
which is equal to
$C$
which is equal to
![]() $C_i$
for infinitely many
$C_i$
for infinitely many
![]() $i$
. Then
$i$
. Then
![]() $H'=\cup _{C_i=C}\mathcal{F}_i$
is a copy of
$H'=\cup _{C_i=C}\mathcal{F}_i$
is a copy of
![]() $\omega \cdot F$
with
$\omega \cdot F$
with
5. Open problems and remarks
In a previous version of this paper, we asked to improve the bounds on
![]() $\rho (\omega \cdot K_3)$
: using the results in this paper, from Theorem 1.12 we find a lower bound of
$\rho (\omega \cdot K_3)$
: using the results in this paper, from Theorem 1.12 we find a lower bound of
![]() $3/5$
, and from Theorem 1.6 we find an upper bound of
$3/5$
, and from Theorem 1.6 we find an upper bound of
![]() $f(2)\leq (21+\sqrt{12})/33\approx 0.74133$
. This was answered in a later paper of Balogh and the author [Reference Balogh and Lamaison1], which shows that
$f(2)\leq (21+\sqrt{12})/33\approx 0.74133$
. This was answered in a later paper of Balogh and the author [Reference Balogh and Lamaison1], which shows that
![]() $\rho (\omega \cdot K_3)=f(2)$
, and proves an explicit lower bound
$\rho (\omega \cdot K_3)=f(2)$
, and proves an explicit lower bound
![]() $f(2)\geq 1-1/\sqrt{7}\approx 0.62203$
.
$f(2)\geq 1-1/\sqrt{7}\approx 0.62203$
.
As noted in the introduction,
![]() $f$
depends on the solution of a certain optimisation problem of Lipschitz functions. It would be helpful to remove such dependency and obtain a closed formula for
$f$
depends on the solution of a certain optimisation problem of Lipschitz functions. It would be helpful to remove such dependency and obtain a closed formula for
![]() $f$
(perhaps the upper bound of (2)). In particular, if the upper bound of (2) is sharp then we can observe that the behaviour of
$f$
(perhaps the upper bound of (2)). In particular, if the upper bound of (2) is sharp then we can observe that the behaviour of
![]() $f(x)$
changes at
$f(x)$
changes at
![]() $x=3$
, which corresponds to
$x=3$
, which corresponds to
![]() $\limsup \mu (H,n)/n=3$
(the independent sets have similar expansion ratio as in the infinite ternary graph). The cause of this is that the optimal colouring of
$\limsup \mu (H,n)/n=3$
(the independent sets have similar expansion ratio as in the infinite ternary graph). The cause of this is that the optimal colouring of
![]() $K_{\mathbb{N}}$
changes.
$K_{\mathbb{N}}$
changes.
Problem 5.1. Find a closed formula for
![]() $f(x)$
. In particular, prove or disprove that it matches the upper bound from (2).
$f(x)$
. In particular, prove or disprove that it matches the upper bound from (2).