Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-18T08:46:46.317Z Has data issue: false hasContentIssue false
  • English
  • Français

Easily Testable Graph Properties

Part of: Graph theory

Published online by Cambridge University Press:  02 February 2015

NOGA ALON  and
JACOB FOX
NOGA ALON
Affiliation:
Sackler School of Mathematics and Blavatnik School of Computer Science, Tel Aviv University, Tel Aviv 69978, Israel School of Mathematics, Institute for Advanced Study, Princeton, NJ 08540, USA (e-mail: nogaa@tau.ac.il)
JACOB FOX
Affiliation:
Department of Mathematics, MIT, Cambridge, MA 02139-4307, USA (e-mail: fox@math.mit.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

A graph on n vertices is ε-far from a property 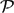$\mathcal{P}$ if one has to add or delete from it at least εn2 edges to get a graph satisfying 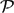$\mathcal{P}$. A graph property 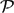$\mathcal{P}$ is strongly testable if for every fixed ε > 0 it is possible to distinguish, with one-sided error, between graphs satisfying 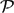$\mathcal{P}$ and ones that are ε-far from 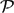$\mathcal{P}$ by inspecting the induced subgraph on a random subset of at most f(ε) vertices. A property is easily testable if it is strongly testable and the function f is polynomial in 1/ε, otherwise it is hard. We consider the problem of characterizing the easily testable graph properties, which is wide open, and obtain several results in its study. One of our main results shows that testing perfectness is hard. The proof shows that testing perfectness is at least as hard as testing triangle-freeness, which is hard. On the other hand, we show that being a cograph, or equivalently, induced P3-freeness where P3 is a path with 3 edges, is easily testable. This settles one of the two exceptional graphs, the other being C4 (and its complement), left open in the characterization by the first author and Shapira of graphs H for which induced H-freeness is easily testable. Our techniques yield a few additional related results, but the problem of characterizing all easily testable graph properties, or even that of formulating a plausible conjectured characterization, remains open.

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C85: Graph algorithms
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 24 , Special Issue 4: Oberwolfach Special Issue Part 1 , July 2015 , pp. 646 - 657
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. (2002) Testing subgraphs in large graphs. Random Struct. Alg. 21 359–370.CrossRefGoogle Scholar
[2]Alon, N., Duke, R. A., Lefmann, H., Rödl, V. and Yuster, R. (1994) The algorithmic aspects of the Regularity Lemma. J. Algorithms 16 80–109.CrossRefGoogle Scholar
[3]Alon, N., Fischer, E., Krivelevich, M. and Szegedy, M. (2000) Efficient testing of large graphs. Combinatorica 20 451–476.CrossRefGoogle Scholar
[4]Alon, N. and Shapira, A. (2006) A characterization of easily testable induced subgraphs. Combin. Probab. Comput. 15 791–805.CrossRefGoogle Scholar
[5]Alon, N. and Shapira, A. (2008) A characterization of the (natural) graph properties testable with one-sided error. SIAM J. Comput. 37 1703–1727.CrossRefGoogle Scholar
[6]Alon, N. and Spencer, J. H. (2008) The Probabilistic Method, third edition, Wiley.CrossRefGoogle Scholar
[7]Behrend, F. A. (1946) On sets of integers which contain no three terms in arithmetic progression. Proc. Nat. Acad. Sci. 32 331–332.CrossRefGoogle Scholar
[8]Chudnovsky, M., Cornuéjols, G., Liu, X., Seymour, P. and Vušković, K. (2005) Recognizing Berge graphs. Combinatorica 25 143–187.CrossRefGoogle Scholar
[9]Chudnovsky, M., Robertson, N., Seymour, P. and Thomas, R. (2006) The strong perfect graph theorem. Ann. of Math. 164 51–229.CrossRefGoogle Scholar
[10]Conlon, D. and Fox, J. (2012) Bounds for graph regularity and removal lemmas. Geom. Funct. Anal. 22 1191–1256.CrossRefGoogle Scholar
[11]Dilworth, R. P. (1950) A decomposition theorem for partially ordered sets. Ann. of Math. 51 161–166.CrossRefGoogle Scholar
[12]Fox, J. (2011) A new proof of the graph removal lemma. Ann. of Math. 174 561–579.CrossRefGoogle Scholar
[13]Gallai, T. (1967) Transitiv orientierbare Graphen. Acta Math. Acad. Sci. Hungar. 18 25–66.CrossRefGoogle Scholar
[14]Goldreich, O., Goldwasser, S. and Ron, D. (1998) Property testing and its applications to learning and approximation. J. Assoc. Comput. Mach. 45 653–750.CrossRefGoogle Scholar
[15]Goldreich, O. and Trevisan, L. (2003) Three theorems regarding testing graph properties. Random Struct. Alg. 23 23–57.CrossRefGoogle Scholar
[16]Grötschel, M., Lovász, L. and Schrijver, A. (1988) Geometric Algorithms and Combinatorial Optimization, Springer.CrossRefGoogle Scholar
[17]Haxell, P. E. (1999) Packing and covering triangles in graphs. Discrete Math. 195 251–254.CrossRefGoogle Scholar
[18]Hoeffding, W. (1963) Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58 13–30.CrossRefGoogle Scholar
[19]McConnell, R. M. and Spinrad, J. P. (1997) Linear-time transitive orientation. In Proc. Eighth Annual ACM–SIAM Symposium on Discrete Algorithms, ACM, pp. 19–25.Google Scholar
[20]Ramírez-Alfonsín, J. L. and Reed, B. A., eds (2001) Perfect Graphs, Wiley.Google Scholar
[21]Roth, K. F. (1953) On certain sets of integers. J. London Math. Soc. 28 104–109.CrossRefGoogle Scholar
[22]Rubinfield, R. and Sudan, M. (1996) Robust characterization of polynomials with applications to program testing. SIAM J. Comput. 25 252–271.CrossRefGoogle Scholar
[23]Ruzsa, I. Z. and Szemerédi, E. (1978) Triple systems with no six points carrying three triangles. In Combinatorics II: Keszthely 1976, Vol. 18 of Colloq. Math. Soc. J. Bolyai, North-Holland, pp. 939–945.Google Scholar
[24]Seinsche, D. (1974) On a property of the class of n-colorable graphs. J. Combin. Theory Ser. B 16 191–193.CrossRefGoogle Scholar