Article contents
Squared Chromatic Number Without Claws or Large Cliques
Published online by Cambridge University Press: 09 January 2019
Abstract
Let 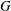 $G$ be a claw-free graph on
$G$ be a claw-free graph on  $n$ vertices with clique number
$n$ vertices with clique number 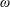 $\unicode[STIX]{x1D714}$, and consider the chromatic number
$\unicode[STIX]{x1D714}$, and consider the chromatic number 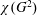 $\unicode[STIX]{x1D712}(G^{2})$ of the square
$\unicode[STIX]{x1D712}(G^{2})$ of the square 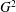 $G^{2}$ of
$G^{2}$ of 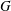 $G$. Writing
$G$. Writing 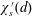 $\unicode[STIX]{x1D712}_{s}^{\prime }(d)$ for the supremum of
$\unicode[STIX]{x1D712}_{s}^{\prime }(d)$ for the supremum of 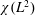 $\unicode[STIX]{x1D712}(L^{2})$ over the line graphs
$\unicode[STIX]{x1D712}(L^{2})$ over the line graphs 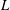 $L$ of simple graphs of maximum degree at most
$L$ of simple graphs of maximum degree at most 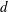 $d$, we prove that
$d$, we prove that 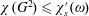 $\unicode[STIX]{x1D712}(G^{2})\leqslant \unicode[STIX]{x1D712}_{s}^{\prime }(\unicode[STIX]{x1D714})$ for
$\unicode[STIX]{x1D712}(G^{2})\leqslant \unicode[STIX]{x1D712}_{s}^{\prime }(\unicode[STIX]{x1D714})$ for 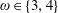 $\unicode[STIX]{x1D714}\in \{3,4\}$. For
$\unicode[STIX]{x1D714}\in \{3,4\}$. For 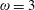 $\unicode[STIX]{x1D714}=3$, this implies the sharp bound
$\unicode[STIX]{x1D714}=3$, this implies the sharp bound 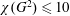 $\unicode[STIX]{x1D712}(G^{2})\leqslant 10$. For
$\unicode[STIX]{x1D712}(G^{2})\leqslant 10$. For 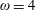 $\unicode[STIX]{x1D714}=4$, this implies
$\unicode[STIX]{x1D714}=4$, this implies 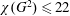 $\unicode[STIX]{x1D712}(G^{2})\leqslant 22$, which is within 2 of the conjectured best bound. This work is motivated by a strengthened form of a conjecture of Erdős and Nešetřil.
$\unicode[STIX]{x1D712}(G^{2})\leqslant 22$, which is within 2 of the conjectured best bound. This work is motivated by a strengthened form of a conjecture of Erdős and Nešetřil.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
Author W. C. v. B. was supported by NWO grant 613.001.217. Author R. J. K. is supported by a NWO Vidi Grant, reference 639.032.614.
References
- 3
- Cited by


