Article contents
Merge Decompositions, Two-sided Krohn–Rhodes, and Aperiodic Pointlikes
Published online by Cambridge University Press: 07 January 2019
Abstract
This paper provides short proofs of two fundamental theorems of finite semigroup theory whose previous proofs were significantly longer, namely the two-sided Krohn-Rhodes decomposition theorem and Henckell’s aperiodic pointlike theorem. We use a new algebraic technique that we call the merge decomposition. A prototypical application of this technique decomposes a semigroup 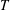 $T$ into a two-sided semidirect product whose components are built from two subsemigroups
$T$ into a two-sided semidirect product whose components are built from two subsemigroups 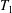 $T_{1}$,
$T_{1}$, 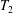 $T_{2}$, which together generate
$T_{2}$, which together generate 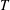 $T$, and the subsemigroup generated by their setwise product
$T$, and the subsemigroup generated by their setwise product 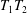 $T_{1}T_{2}$. In this sense we decompose
$T_{1}T_{2}$. In this sense we decompose 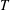 $T$ by merging the subsemigroups
$T$ by merging the subsemigroups 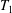 $T_{1}$ and
$T_{1}$ and 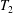 $T_{2}$. More generally, our technique merges semigroup homomorphisms from free semigroups.
$T_{2}$. More generally, our technique merges semigroup homomorphisms from free semigroups.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
Author S. J. v. G. was supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant #655941. Author B. S. was supported by United States–Israel Binational Science Foundation #2012080 and NSA MSP #H98230-16-1-0047.
References
- 3
- Cited by


