Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-28T19:36:51.630Z Has data issue: false hasContentIssue false
  • English
  • Français

Coefficient Bounds in the Lorentz Representation of a Polynomial

Published online by Cambridge University Press:  20 November 2018

D. S. Lubinsky  and
Z. Ziegler
D. S. Lubinsky
Affiliation:
Department of Mathematics, Witwatersrand University, P.O. WITS 2050, Republic of South Africa
Z. Ziegler
Affiliation:
Department of Mathematics, Technion - Israel Institute of Technology, Haifa 32000, Israel
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

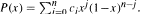Each polynomial P(x) has a "Lorentz representation", of the form This representation becomes unique if we insist that n equals the degree of P. Motivated partly by questions involving polynomials with integer coefficients, we investigate the relationship between

Keywords

26C0541A17PolynomialsCoefficient BoundsLorentz RepresentationMaximum principleChebyshev Polynomials
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 33 , Issue 2 , 01 June 1990 , pp. 197 - 206
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Cheney, E. W., Introduction to Approximation Theory, McGraw Hill, New York, 1966.Google Scholar
2. Erdelyi, T. and Szabados, J., On Polynomials with Positive Coefficients, J. Approx. Theory, 54 (1988), 107–122.Google Scholar
3. Freud, G., Orthogonal Polynomials, Akademiai Kiado/Pergamon Press, Budapest, 1966.Google Scholar
4. Ferguson, LeB. O., Approximation by Polynomials with Integral Coefficients, Math. Surveys, No. 17, Amer. Math. Soc, Providence, 1980.Google Scholar
5. Karlin, S. and Studden, W. J., Tchebycheff Systems: With Applications in Analysis and Statistics, Wiley Interscience, New York, 1966.Google Scholar
6. Lorentz, G. G., Bernstein Polynomials, Toronto University Press, Toronto, 1953.Google Scholar
7. Lorentz, G. G., Approximation of Functions, Holt, Rinehart and Winston, New York, 1966.Google Scholar
8. Lubinsky, D. S., Prolla, J. B. and Ziegler, Z., Extremal Polynomials with Integer Coefficients, in preparation.Google Scholar
9. Natanson, I. P., Constructive Function Theory, Vol. 1, Ungar, New York, 1964.Google Scholar
10. Saff, E. B., Incomplete and Orthogonal Polynomials, (in) “Approximation Theory IV” (C. K. Chui, et al., eds,), pp. 219-256, Academic Press, New York, 1983.Google Scholar
11. Saff, E. B. and Varga, R. S., On Incomplete Polynomials, (in) Numerischen Methoden der Approximationstheorie, Vol. 4 (L. Collatz, et al., eds.), pp. 281-298, I.S.N.M., Vol. 42, Birkhauser, Basel, 1978.Google Scholar