Article contents
Strictly Singular and Cosingular Multiplications
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 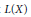 $L(X)$ be the space of bounded linear operators on the Banach space
$L(X)$ be the space of bounded linear operators on the Banach space 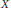 $X$. We study the strict singularity and cosingularity of the two-sided multiplication operators
$X$. We study the strict singularity and cosingularity of the two-sided multiplication operators 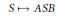 $S\,\mapsto \,ASB$ on
$S\,\mapsto \,ASB$ on 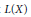 $L(X)$, where
$L(X)$, where 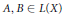 $A,\,B\,\in \,L(X)$ are fixed bounded operators and
$A,\,B\,\in \,L(X)$ are fixed bounded operators and 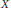 $X$ is a classical Banach space. Let
$X$ is a classical Banach space. Let 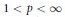 $1\,<\,p\,<\,\infty $ and
$1\,<\,p\,<\,\infty $ and 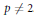 $p\,\ne \,2$. Our main result establishes that the multiplication
$p\,\ne \,2$. Our main result establishes that the multiplication 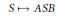 $S\,\mapsto \,ASB$ is strictly singular on
$S\,\mapsto \,ASB$ is strictly singular on 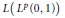 $L\left( {{L}^{p}}\left( 0,\,1 \right) \right)$ if and only if the non-zero operators
$L\left( {{L}^{p}}\left( 0,\,1 \right) \right)$ if and only if the non-zero operators 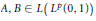 $A,\,B\,\in \,L\left( {{L}^{p}}\left( 0,\,1 \right) \right)$ are strictly singular. We also discuss the case where
$A,\,B\,\in \,L\left( {{L}^{p}}\left( 0,\,1 \right) \right)$ are strictly singular. We also discuss the case where 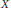 $X$ is a
$X$ is a  ${\mathcal{L}^{1}}-$ or a
${\mathcal{L}^{1}}-$ or a 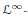 ${{\mathcal{L}}^{\infty }}-$space, as well as several other relevant examples.
${{\mathcal{L}}^{\infty }}-$space, as well as several other relevant examples.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2005
References
- 1
- Cited by


