Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Steiner, A. K.
and
Steiner, E. F.
1970.
Nest generated intersection rings in Tychonoff spaces.
Transactions of the American Mathematical Society,
Vol. 148,
Issue. 2,
p.
589.
Frolík, Zdeněk
1971.
Stone-Weierstrass theorems for 𝐶(𝑋) with the sequential topology.
Proceedings of the American Mathematical Society,
Vol. 27,
Issue. 3,
p.
486.
Hamburger, P.
1971.
On Wallman-type, regular Wallman-type andz-compactifications.
Periodica Mathematica Hungarica,
Vol. 1,
Issue. 4,
p.
303.
Hager, Anthony W.
1971.
An approximation technique for real-valued functions.
General Topology and its Applications,
Vol. 1,
Issue. 2,
p.
127.
Blair, Robert L.
1974.
TOPO 72 — General Topology and its Applications.
Vol. 378,
Issue. ,
p.
46.
Blair, Robert L.
and
Hager, Anthony W.
1974.
Extensions of zero-sets and of real-valued functions.
Mathematische Zeitschrift,
Vol. 136,
Issue. 1,
p.
41.
1975.
Hewitt-Nachbin Spaces.
Vol. 17,
Issue. ,
p.
237.
Bentley, H. L.
and
Taylor, B. J.
1978.
On generalizations of C*-embedding for wallman rings.
Journal of the Australian Mathematical Society,
Vol. 25,
Issue. 2,
p.
215.
Hernández, Salvador
1986.
Algebras of real-valued continuous functions in product spaces.
Topology and its Applications,
Vol. 22,
Issue. 1,
p.
33.
Blasco, J. L.
1988.
A note on inverse-closed subalgebras ofC(X).
Acta Mathematica Hungarica,
Vol. 51,
Issue. 1-2,
p.
47.
Henriksen, Melvin
1989.
Ordered Algebraic Structures.
p.
143.
Vechtomov, E. M.
1994.
Rings of continuous functions. Algebraic aspects.
Journal of Mathematical Sciences,
Vol. 71,
Issue. 2,
p.
2364.
Dimov, Georgi
and
Tironi, Gino
1995.
Compactifications, A-compactifications and proximities.
Annali di Matematica Pura ed Applicata,
Vol. 169,
Issue. 1,
p.
87.
GARRIDO, I.
and
MONTALVO, F.
1996.
Algebraic Properties of the Uniform Closure of Spaces of Continuous Functions.
Annals of the New York Academy of Sciences,
Vol. 788,
Issue. 1,
p.
101.
Bella, A.
and
Yaschenko, I.
1999.
Lindelöf property and absolute embeddings.
Proceedings of the American Mathematical Society,
Vol. 127,
Issue. 3,
p.
907.
Banaschewski, Bernhard
and
Gilmour, Christopher
2001.
Cozero bases of frames.
Journal of Pure and Applied Algebra,
Vol. 157,
Issue. 1,
p.
1.
Hager, Anthony W.
and
Martinez, Jorge
2002.
C-epic compactifications.
Topology and its Applications,
Vol. 117,
Issue. 2,
p.
113.
Yamazaki, Kaori
2003.
Absolute weak C-embedding in Hausdorff spaces.
Topology and its Applications,
Vol. 131,
Issue. 3,
p.
273.
Garrido, M. Isabel
and
Montalvo, Francisco
2005.
Generation of Uniformly Closed Algebras of Functions.
Positivity,
Vol. 9,
Issue. 1,
p.
81.
Dube, Themba
2009.
A Little More on Coz-Unique Frames.
Applied Categorical Structures,
Vol. 17,
Issue. 1,
p.
63.
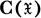 )
)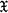 be a completely regular Hausdorff space and C(
be a completely regular Hausdorff space and C(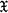 ) the algebra of continuous real-valued functions on
) the algebra of continuous real-valued functions on 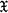 . In attempts to characterize abstractly those algebras that are isomorphic to C(
. In attempts to characterize abstractly those algebras that are isomorphic to C(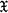 ) for some
) for some 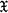 , one produces subalgebras of C(
, one produces subalgebras of C(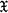 ) which: (a) contain the constant functions, (b) separate points and closed sets in
) which: (a) contain the constant functions, (b) separate points and closed sets in 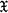 , (c) are closed under uniform convergence, and (d) are closed under inversion in C(
, (c) are closed under uniform convergence, and (d) are closed under inversion in C(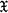 ) (see, for example, (2; 5)).
) (see, for example, (2; 5)).

