Article contents
Lipschitz-free Spaces on Finite Metric Spaces
Published online by Cambridge University Press: 13 February 2019
Abstract
Main results of the paper are as follows:
(1) For any finite metric space 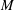 $M$ the Lipschitz-free space on
$M$ the Lipschitz-free space on 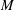 $M$ contains a large well-complemented subspace that is close to
$M$ contains a large well-complemented subspace that is close to 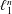 $\ell _{1}^{n}$.
$\ell _{1}^{n}$.
(2) Lipschitz-free spaces on large classes of recursively defined sequences of graphs are not uniformly isomorphic to 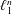 $\ell _{1}^{n}$ of the corresponding dimensions. These classes contain well-known families of diamond graphs and Laakso graphs.
$\ell _{1}^{n}$ of the corresponding dimensions. These classes contain well-known families of diamond graphs and Laakso graphs.
Interesting features of our approach are: (a) We consider averages over groups of cycle-preserving bijections of edge sets of graphs that are not necessarily graph automorphisms. (b) In the case of such recursive families of graphs as Laakso graphs, we use the well-known approach of Grünbaum (1960) and Rudin (1962) for estimating projection constants in the case where invariant projections are not unique.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
Author S. D. was supported by the National Science Foundation under Grant Number DMS–1361461. Authors S. D. and D. K. were supported by the Workshop in Analysis and Probability at Texas A&M University in 2017. Author M. O. was supported by the National Science Foundation under Grant Number DMS–1700176.
References
- 7
- Cited by


