Article contents
Large Irredundant Sets in Operator Algebras
Published online by Cambridge University Press: 07 March 2019
Abstract
A subset 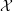 ${\mathcal{X}}$ of a C*-algebra
${\mathcal{X}}$ of a C*-algebra 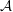 ${\mathcal{A}}$ is called irredundant if no
${\mathcal{A}}$ is called irredundant if no 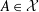 $A\in {\mathcal{X}}$ belongs to the C*-subalgebra of
$A\in {\mathcal{X}}$ belongs to the C*-subalgebra of 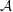 ${\mathcal{A}}$ generated by
${\mathcal{A}}$ generated by 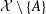 ${\mathcal{X}}\setminus \{A\}$. Separable C*-algebras cannot have uncountable irredundant sets and all members of many classes of nonseparable C*-algebras, e.g., infinite dimensional von Neumann algebras have irredundant sets of cardinality continuum.
${\mathcal{X}}\setminus \{A\}$. Separable C*-algebras cannot have uncountable irredundant sets and all members of many classes of nonseparable C*-algebras, e.g., infinite dimensional von Neumann algebras have irredundant sets of cardinality continuum.
There exists a considerable literature showing that the question whether every AF commutative nonseparable C*-algebra has an uncountable irredundant set is sensitive to additional set-theoretic axioms, and we investigate here the noncommutative case.
Assuming 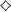 $\diamondsuit$ (an additional axiom stronger than the continuum hypothesis), we prove that there is an AF C*-subalgebra of
$\diamondsuit$ (an additional axiom stronger than the continuum hypothesis), we prove that there is an AF C*-subalgebra of 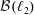 ${\mathcal{B}}(\ell _{2})$ of density
${\mathcal{B}}(\ell _{2})$ of density 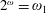 $2^{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}_{1}$ with no nonseparable commutative C*-subalgebra and with no uncountable irredundant set. On the other hand we also prove that it is consistent that every discrete collection of operators in
$2^{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}_{1}$ with no nonseparable commutative C*-subalgebra and with no uncountable irredundant set. On the other hand we also prove that it is consistent that every discrete collection of operators in 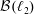 ${\mathcal{B}}(\ell _{2})$ of cardinality continuum contains an irredundant subcollection of cardinality continuum.
${\mathcal{B}}(\ell _{2})$ of cardinality continuum contains an irredundant subcollection of cardinality continuum.
Other partial results and more open problems are presented.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
The research of author C. S. H. was partially supported by doctoral scholarships CAPES: 1427540 and CNPq: 167761/2017-0 and 201213/2016-8. The research of the author P. K. was partially supported by grant PVE Ciência sem Fronteiras - CNPq (406239/2013-4).
References
- 3
- Cited by



