Article contents
Identities and Congruences of theRamanujan Type
Published online by Cambridge University Press: 20 November 2018
Extract
Let P(n) denote the number of unrestricted partitions of the positive integer n. Ramanujan conjectured that
(1.1)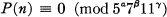
if 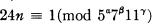 . He also indicated that such congruences could be
deduced from identities of the type
. He also indicated that such congruences could be
deduced from identities of the type
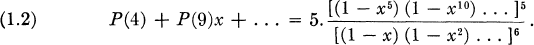
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1950
References
1 Ramanujan, S. Collected papers, Cambridge, 1927.Google Scholar
2 Watson, G. N., Ramanujans Vermutung Über Zerfällungsanzahlen, Jour, für Math., Bd. 179,(1938), p. 97.Google Scholar
3 H., Rademacher The Ramanujan identities under modular substitutions. Trans. Amer. Math. Soc, vol. 51, (1942) p. 609.Google Scholar
4 A11 these are contained in Klein and Fricke, Vorlesungen iiber die Theorie der Elliptischen Modulfunktionen. Bd. 2, p. 64. Also see: Mordell, L. J., Note on certain modular relations considered by Messrs. Ramanujan, Darling, and Rogers. Proc. Lond. Math. Soc. (2), 20 (1922) p. 408.CrossRefGoogle Scholar
5
![]() depends on p. We omit this suffix p in general, but when explicit reference has to be made we write
depends on p. We omit this suffix p in general, but when explicit reference has to be made we write ![]() .
.
6 Watson, loc. cit., pp. 106, 119, 120.
7 There is another method of obtaining expressions for ![]() as polynomials in
as polynomials in ![]() . This will
be published elsewhere.
. This will
be published elsewhere.
8
![]() shall mean summation from i = 1 to a sufficiently large i.
shall mean summation from i = 1 to a sufficiently large i.
9 The construction of the function Fn,v(T) is suggested by the work of Rademacher, p. 622 and 624.
10 To avoid complication we have not shown in ai(n), its dependence on v and p.
- 18
- Cited by


