Article contents
Eigenvalue Optimisation on Flat Tori and Lattice Points in Anisotropically Expanding Domains
Published online by Cambridge University Press: 07 March 2019
Abstract
This paper is concerned with the maximisation of the 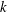 $k$-th eigenvalue of the Laplacian amongst flat tori of unit volume in dimension
$k$-th eigenvalue of the Laplacian amongst flat tori of unit volume in dimension 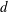 $d$ as
$d$ as 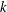 $k$ goes to infinity. We show that in any dimension maximisers exist for any given
$k$ goes to infinity. We show that in any dimension maximisers exist for any given 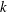 $k$, but that any sequence of maximisers degenerates as
$k$, but that any sequence of maximisers degenerates as 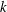 $k$ goes to infinity when the dimension is at most 10. Furthermore, we obtain specific upper and lower bounds for the injectivity radius of any sequence of maximisers. We also prove that flat Klein bottles maximising the
$k$ goes to infinity when the dimension is at most 10. Furthermore, we obtain specific upper and lower bounds for the injectivity radius of any sequence of maximisers. We also prove that flat Klein bottles maximising the 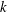 $k$-th eigenvalue of the Laplacian exhibit the same behaviour. These results contrast with those obtained recently by Gittins and Larson, stating that sequences of optimal cuboids for either Dirichlet or Neumann boundary conditions converge to the cube no matter the dimension. We obtain these results via Weyl asymptotics with explicit control of the remainder in terms of the injectivity radius. We reduce the problem at hand to counting lattice points inside anisotropically expanding domains, where we generalise methods of Yu. Kordyukov and A. Yakovlev by considering domains that expand at different rates in various directions.
$k$-th eigenvalue of the Laplacian exhibit the same behaviour. These results contrast with those obtained recently by Gittins and Larson, stating that sequences of optimal cuboids for either Dirichlet or Neumann boundary conditions converge to the cube no matter the dimension. We obtain these results via Weyl asymptotics with explicit control of the remainder in terms of the injectivity radius. We reduce the problem at hand to counting lattice points inside anisotropically expanding domains, where we generalise methods of Yu. Kordyukov and A. Yakovlev by considering domains that expand at different rates in various directions.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
The research of the author was supported by NSERC’s Alexander-Graham-Bell doctoral scholarship.
References
- 4
- Cited by



