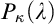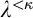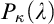1 The original conjecture
Throughout the paper
![]() $\kappa $
will denote a regular uncountable cardinal, and
$\kappa $
will denote a regular uncountable cardinal, and
![]() a cardinal greater than
a cardinal greater than
![]() $\kappa $
. We let
$\kappa $
. We let
![]() denote the collection of all subsets of
denote the collection of all subsets of
![]() of size less than
of size less than
![]() $\kappa $
, and
$\kappa $
, and
![]() the noncofinal ideal on
the noncofinal ideal on
![]() . An ideal J on
. An ideal J on
![]() is fine if
is fine if
![]() . For further definitions see the end of this section.
. For further definitions see the end of this section.
According to Jech [Reference Jech18, p. 409], one of the key concepts in the theory of large cardinals is saturation of ideals. The starting point of our story is Solovay’s seminal result [Reference Solovay58] that for any value of
![]() $\kappa $
, the nonstationary ideal on
$\kappa $
, the nonstationary ideal on
![]() $\kappa $
is nowhere weakly
$\kappa $
is nowhere weakly
![]() $\kappa $
-saturated. There are no large cardinals involved, so how does this fit with Jech’s statement? The first remark to make is that the proof of Solovay’s result needs choice. In fact, by another result of Solovay, under the Axiom of Determinacy, the nonstationary ideal on
$\kappa $
-saturated. There are no large cardinals involved, so how does this fit with Jech’s statement? The first remark to make is that the proof of Solovay’s result needs choice. In fact, by another result of Solovay, under the Axiom of Determinacy, the nonstationary ideal on
![]() $\omega _1$
is prime (i.e., weakly
$\omega _1$
is prime (i.e., weakly
![]() $2$
-saturated). Returning to ZFC, we have Solovay’s result at one end, and measurable cardinals with their normal measures at the other. And in between? For each cardinal
$2$
-saturated). Returning to ZFC, we have Solovay’s result at one end, and measurable cardinals with their normal measures at the other. And in between? For each cardinal
![]() $\rho $
between
$\rho $
between
![]() $2$
and
$2$
and
![]() $\kappa $
, set-theorists carefully determined the exact consistency strength of
$\kappa $
, set-theorists carefully determined the exact consistency strength of
![]() $\kappa $
carrying a (normal or at least)
$\kappa $
carrying a (normal or at least)
![]() $\kappa $
-complete, weakly
$\kappa $
-complete, weakly
![]() $\rho $
-saturated ideal.
$\rho $
-saturated ideal.
In the glorious early days of the study of
![]() (which was seen as a two-cardinal generalization of
(which was seen as a two-cardinal generalization of
![]() $\kappa $
), it was systematically attempted to establish
$\kappa $
), it was systematically attempted to establish
![]() versions of known results on
versions of known results on
![]() $\kappa $
(see, for instance, the problems listed in Section 0 of [Reference Kunen and Pelletier24]). Failures were no problem, since they were seen as productive. By analyzing what went wrong in the attempted generalization, one acquired a better understanding of
$\kappa $
(see, for instance, the problems listed in Section 0 of [Reference Kunen and Pelletier24]). Failures were no problem, since they were seen as productive. By analyzing what went wrong in the attempted generalization, one acquired a better understanding of
![]() and its specificity (for example, see the work of Solovay, Menas [Reference Menas47], and Kunen and Pelletier [Reference Kunen and Pelletier24] on normal measures on
and its specificity (for example, see the work of Solovay, Menas [Reference Menas47], and Kunen and Pelletier [Reference Kunen and Pelletier24] on normal measures on
![]() without the partition property). Thus Menas [Reference Menas46] boldly conjectured that
without the partition property). Thus Menas [Reference Menas46] boldly conjectured that
![]() holds for any possible values of
holds for any possible values of
![]() $\kappa $
and
$\kappa $
and
![]() , where
, where
![]() asserts that the nonstationary ideal
asserts that the nonstationary ideal
![]() on
on
![]() is nowhere weakly
is nowhere weakly
![]() -saturated.
-saturated.
Progress on this two-cardinal version of Solovay’s splitting result was initially slow. As observed by Kanamori in [Reference Kanamori21], most results were about
![]() with
with
![]() replaced by
replaced by
![]() . For example, an early result of Jech [Reference Jech17] stated that if
. For example, an early result of Jech [Reference Jech17] stated that if
![]() $\kappa $
is a successor and
$\kappa $
is a successor and
![]() regular, then
regular, then
![]() is nowhere weakly
is nowhere weakly
![]() -saturated. This was later improved by Baumgartner who proved that for any possible values of
-saturated. This was later improved by Baumgartner who proved that for any possible values of
![]() $\kappa $
and
$\kappa $
and
![]() ,
,
![]() is nowhere weakly
is nowhere weakly
![]() -saturated.
-saturated.
The conjecture was finally refuted by Baumgartner and Taylor [Reference Baumgartner and Taylor3] who showed the consistency of the failure of
![]() $MC_1 (\omega _1, \omega _2)$
. Their result can be revisited as follows. We put
$MC_1 (\omega _1, \omega _2)$
. Their result can be revisited as follows. We put
![]() (
(
![]() $=$
the least size of any subset of
$=$
the least size of any subset of
![]() ) not in
) not in
![]() ).
).
Observation 1.1. If
![]() , then
, then
![]() fails.
fails.
Proof By a result of Shelah [Reference Shelah49],
![]() . Thus there is a stationary subset S of
. Thus there is a stationary subset S of
![]() of size
of size
![]() . Obviously, S can be partitioned into no more than
. Obviously, S can be partitioned into no more than
![]() stationary subsets.
stationary subsets.
Corollary 1.2. Suppose that
![]() and
and
![]() . Then
. Then
![]() fails.
fails.
Proof If
![]() , then
, then
![]() (see, e.g., [Reference Shelah50, p. 86]).
(see, e.g., [Reference Shelah50, p. 86]).
The conjecture somehow survived its refutation by Baumgartner and Taylor, as the so-called splitting problem, the general problem of computing the degree of weak saturation of ideals on
![]() . In how many stationary pieces can this or that stationary subset of
. In how many stationary pieces can this or that stationary subset of
![]() be partitioned? Given a cardinal
be partitioned? Given a cardinal
![]() , what is the consistency strength of the existence of a (normal or maybe just)
, what is the consistency strength of the existence of a (normal or maybe just)
![]() $\kappa $
-complete, weakly
$\kappa $
-complete, weakly
![]() $\rho $
-saturated, fine ideal on
$\rho $
-saturated, fine ideal on
![]() ?
?
Recall that for a fine ideal J on
![]() , Jensen’s diamond principle
, Jensen’s diamond principle
![]() asserts the existence of
asserts the existence of
![]() $s_x$
for
$s_x$
for
![]() such that
such that
![]() $Z_B = \{x : B \cap x = s_x \}$
lies in
$Z_B = \{x : B \cap x = s_x \}$
lies in
![]() $J^+$
for all
$J^+$
for all
![]() . Since
. Since
![]() $\{x \in Z_a : a \subseteq x\} \cap \{x \in Z_b : b \subseteq x\} = \emptyset $
for any two distinct members
$\{x \in Z_a : a \subseteq x\} \cap \{x \in Z_b : b \subseteq x\} = \emptyset $
for any two distinct members
![]() $a, b$
of
$a, b$
of
![]() ,
,
![]() implies that J is not weakly
implies that J is not weakly
![]() -saturated. In [Reference Matsubara43] Matsubara established the consistency of the conjecture by proving that it holds in L. As observed by Shioya [Reference Shioya56], one way to proceed would have been to appeal to the fact that in L, (
-saturated. In [Reference Matsubara43] Matsubara established the consistency of the conjecture by proving that it holds in L. As observed by Shioya [Reference Shioya56], one way to proceed would have been to appeal to the fact that in L, (
![]() and hence)
and hence)
![]() holds for all
holds for all
![]() . Instead, Matsubara relied on the result of Baumgartner in the case when
. Instead, Matsubara relied on the result of Baumgartner in the case when
![]() , and completed his proof by showing that
, and completed his proof by showing that
![]() follows from
follows from
![]() . A new proof of this result can be found in [Reference Matsubara and Shioya45]. Let us recall that an ideal J on
. A new proof of this result can be found in [Reference Matsubara and Shioya45]. Let us recall that an ideal J on
![]() is precipitous if for all generic
is precipitous if for all generic
![]() , the ultrapower
, the ultrapower
![]() is well-founded. By a result of Foreman [Reference Foreman10], any countably complete
is well-founded. By a result of Foreman [Reference Foreman10], any countably complete
![]() -saturated ideal on
-saturated ideal on
![]() is precipitous. As is well-known, any normal, fine, weakly
is precipitous. As is well-known, any normal, fine, weakly
![]() -saturated ideal on
-saturated ideal on
![]() is
is
![]() -saturated (in fact
-saturated (in fact
![]() -saturated) and hence precipitous. In [Reference Matsubara and Shioya45] Matsubara and Shioya establish that no countably complete ideal J on
-saturated) and hence precipitous. In [Reference Matsubara and Shioya45] Matsubara and Shioya establish that no countably complete ideal J on
![]() with
with
![]() $cof (J) = non (J)$
is precipitous. It follows that if
$cof (J) = non (J)$
is precipitous. It follows that if
![]() , then no restriction of
, then no restriction of
![]() is precipitous (and hence
is precipitous (and hence
![]() holds). Let us observe that by pushing the counting argument used in [Reference Matsubara43], one obtains the following.
holds). Let us observe that by pushing the counting argument used in [Reference Matsubara43], one obtains the following.
Observation 1.3. Let J be a fine ideal on
![]() such that
such that
![]() the least size of any C in
the least size of any C in
![]() $J^{\ast }$
. Then
$J^{\ast }$
. Then
![]() holds.
holds.
Proof Select a bijection
![]() . Let
. Let
![]() be a one-to-one enumeration of
be a one-to-one enumeration of
![]() , and pick
, and pick
![]() $C_i \in J^{\ast }$
for
$C_i \in J^{\ast }$
for
![]() such that
such that
![]() . Inductively construct
. Inductively construct
![]() and
and
![]() for
for
![]() as follows. Suppose that
as follows. Suppose that
![]() $a_r$
and
$a_r$
and
![]() $t_{a_r}$
have already been constructed for each
$t_{a_r}$
have already been constructed for each
![]() $r < k$
. Let
$r < k$
. Let
![]() $k = F (i, j)$
. Now select
$k = F (i, j)$
. Now select
![]() $a_k$
in
$a_k$
in
![]() $C_i \setminus \{a_r : r < k \}$
, and put
$C_i \setminus \{a_r : r < k \}$
, and put
![]() $t_{a_k} = A_j$
. Clearly, for any
$t_{a_k} = A_j$
. Clearly, for any
![]() ,
,
![]() (and hence
(and hence
![]() ) lies in
) lies in
![]() $J^+$
.
$J^+$
.
Since
![]() (see [Reference Matet, Péan and Shelah40] for the exact value of
(see [Reference Matet, Péan and Shelah40] for the exact value of
![]() ), it follows that if
), it follows that if
![]() , then (
, then (
![]() holds for every
holds for every
![]() , and hence)
, and hence)
![]() holds.
holds.
If
![]() is a strong limit cardinal with
is a strong limit cardinal with
![]() , then
, then
![]() , so Matsubara’s result shows that for any value of
, so Matsubara’s result shows that for any value of
![]() $\kappa $
, there are always many values of
$\kappa $
, there are always many values of
![]() (of cofinality less than
(of cofinality less than
![]() $\kappa $
) for which
$\kappa $
) for which
![]() holds. Further, Matsubara and Shelah [Reference Matsubara and Shelah44] (see also [Reference Matet and Shelah41]) have shown that if
holds. Further, Matsubara and Shelah [Reference Matsubara and Shelah44] (see also [Reference Matet and Shelah41]) have shown that if
![]() is a strong limit cardinal with
is a strong limit cardinal with
![]() , then no restriction of
, then no restriction of
![]() is precipitous (and hence
is precipitous (and hence
![]() holds). To sum up the results of this section,
holds). To sum up the results of this section,
![]() may consistently fail. On the other hand, we have the following.
may consistently fail. On the other hand, we have the following.
Fact 1.4. Assuming GCH, the following hold:
-
(i) Suppose that either
 $\kappa $
is a successor cardinal, or
$\kappa $
is a successor cardinal, or
 is singular. Then
is singular. Then
 holds.
holds. -
(ii) Suppose that
 $\kappa $
is weakly inaccessible,
$\kappa $
is weakly inaccessible,
 is regular, and
is regular, and
 . Then
. Then
 holds.
holds.
A large cardinal is needed to obtain situations when
![]() [Reference Donder, Koepke and Levinski8] (see also [Reference Kanamori21, p. 345]). Thus Fact 1.4 shows that if GCH holds and there are no large cardinals in an inner model, then
[Reference Donder, Koepke and Levinski8] (see also [Reference Kanamori21, p. 345]). Thus Fact 1.4 shows that if GCH holds and there are no large cardinals in an inner model, then
![]() holds. However the large cardinals in question are of a modest size, since Donder, Koepke, and Levinski [Reference Donder, Koepke and Levinski8] showed that if
holds. However the large cardinals in question are of a modest size, since Donder, Koepke, and Levinski [Reference Donder, Koepke and Levinski8] showed that if
![]() and
and
![]() is
is
![]() $\kappa $
-Erdős, then the set
$\kappa $
-Erdős, then the set
![]() is stationary. We can do better than this. Recall that any normal, fine, weakly
is stationary. We can do better than this. Recall that any normal, fine, weakly
![]() -saturated ideal on
-saturated ideal on
![]() is precipitous. Hence if GCH holds,
is precipitous. Hence if GCH holds,
![]() $\kappa $
is weakly inaccessible,
$\kappa $
is weakly inaccessible,
![]() , and there is no normal, precipitous, fine ideal on
, and there is no normal, precipitous, fine ideal on
![]() , then no normal, fine ideal on
, then no normal, fine ideal on
![]() is weakly
is weakly
![]() -saturated. Now if
-saturated. Now if
![]() carries a precipitous ideal, then by a result of Magidor (see [Reference Matsubara43]), there is a cardinal
carries a precipitous ideal, then by a result of Magidor (see [Reference Matsubara43]), there is a cardinal
![]() $\sigma $
of Mitchell order
$\sigma $
of Mitchell order
![]() $\sigma ^{++}$
in some inner model. Thus the following formulation seems preferable.
$\sigma ^{++}$
in some inner model. Thus the following formulation seems preferable.
Fact 1.5. Assuming GCH, the following hold:
-
(i) Suppose that either
 $\kappa $
is a successor cardinal, or
$\kappa $
is a successor cardinal, or
 is singular. Then
is singular. Then
 holds.
holds. -
(ii) Suppose that
 $\kappa $
is weakly inaccessible,
$\kappa $
is weakly inaccessible,
 is regular, and
is regular, and
 carries no precipitous ideal. Then
carries no precipitous ideal. Then
 holds.
holds.
This discussion is continued in Section 9 where we show that if there are no large cardinals in an inner model, then Menas’s conjecture is equivalent to a weak form of GCH.
Let us at last provide the missing definitions. By an ideal on an infinite set X, we mean a nonempty collection J of subsets of X such that (a)
![]() $X \notin J$
, (b)
$X \notin J$
, (b)
![]() $P(A)\subseteq J$
for all
$P(A)\subseteq J$
for all
![]() $A \in J$
, (c)
$A \in J$
, (c)
![]() $A \cup B \in J$
whenever
$A \cup B \in J$
whenever
![]() $A, B \in J$
, and (d)
$A, B \in J$
, and (d)
![]() $\{x\} \in J$
for all
$\{x\} \in J$
for all
![]() $x \in X$
. Given an ideal J on X, we let
$x \in X$
. Given an ideal J on X, we let
![]() $J^+ = P(X) \setminus J$
,
$J^+ = P(X) \setminus J$
,
![]() $J^{\ast } = \{ A \subseteq X : X \setminus A \in J\}$
, and
$J^{\ast } = \{ A \subseteq X : X \setminus A \in J\}$
, and
![]() $J \vert A = \{ B \subseteq X : B \cap A\in J\}$
for each
$J \vert A = \{ B \subseteq X : B \cap A\in J\}$
for each
![]() $A \in J^+$
. For a cardinal
$A \in J^+$
. For a cardinal
![]() $\rho ,J$
is
$\rho ,J$
is
![]() $\rho $
-complete if
$\rho $
-complete if
![]() $\bigcup Q \in J$
for every
$\bigcup Q \in J$
for every
![]() $Q \subseteq J$
with
$Q \subseteq J$
with
![]() $\vert Q \vert < \rho $
. We let
$\vert Q \vert < \rho $
. We let
![]() $non (J) =$
the least size of a set in
$non (J) =$
the least size of a set in
![]() $J^+$
.
$J^+$
.
![]() $cof (J)$
denotes the least cardinality of any
$cof (J)$
denotes the least cardinality of any
![]() $Q \subseteq J$
such that
$Q \subseteq J$
such that
![]() $J = \bigcup _{A \in Q} P(A)$
. Given an infinite set Y and
$J = \bigcup _{A \in Q} P(A)$
. Given an infinite set Y and
![]() $f : X \rightarrow Y$
, we let
$f : X \rightarrow Y$
, we let
![]() $f (J) = \{ B \subseteq Y : f^{-1} (B) \in J\}$
. For a cardinal
$f (J) = \{ B \subseteq Y : f^{-1} (B) \in J\}$
. For a cardinal
![]() $\sigma $
, J is weakly
$\sigma $
, J is weakly
![]() $\sigma $
-saturated (respectively,
$\sigma $
-saturated (respectively,
![]() $\sigma $
-saturated) if there is no
$\sigma $
-saturated) if there is no
![]() $Q \subseteq J^+$
with
$Q \subseteq J^+$
with
![]() $\vert Q \vert = \sigma $
such that
$\vert Q \vert = \sigma $
such that
![]() $A \cap B = \emptyset $
(respectively,
$A \cap B = \emptyset $
(respectively,
![]() $A \cap B \in J$
) for any two distinct members
$A \cap B \in J$
) for any two distinct members
![]() $A, B$
of Q. J is nowhere weakly
$A, B$
of Q. J is nowhere weakly
![]() $\sigma $
-saturated if for any
$\sigma $
-saturated if for any
![]() $A \in J^+$
,
$A \in J^+$
,
![]() $J \vert A$
is not weakly
$J \vert A$
is not weakly
![]() $\sigma $
-saturated.
$\sigma $
-saturated.
Fact 1.6.
-
(i) (Folklore) Suppose that
 $\sigma $
is singular, and J is nowhere weakly
$\sigma $
is singular, and J is nowhere weakly
 $\tau $
-saturated for every cardinal
$\tau $
-saturated for every cardinal
 $\tau < \sigma $
. Then J is nowhere weakly
$\tau < \sigma $
. Then J is nowhere weakly
 $\sigma $
-saturated.
$\sigma $
-saturated. -
(ii) [Reference Matet, Péan and Shelah40, (proof of) Proposition 2.6] Letting
 $\chi = \min \{\vert C \vert : C \in J^{\ast }\}$
, suppose that
$\chi = \min \{\vert C \vert : C \in J^{\ast }\}$
, suppose that
 . Then
. Then
 $\chi =$
the largest cardinal
$\chi =$
the largest cardinal
 $\tau $
such that J is not weakly
$\tau $
such that J is not weakly
 $\tau $
-saturated.
$\tau $
-saturated. -
(iii) J is weakly
 $\sigma $
-saturated if and only if for every
$\sigma $
-saturated if and only if for every
 $A \in J^+$
,
$A \in J^+$
,
 $J \vert A$
is weakly
$J \vert A$
is weakly
 $\sigma $
-saturated.
$\sigma $
-saturated.
For a regular uncountable cardinal
![]() $\tau $
,
$\tau $
,
![]() $I_{\tau }$
(respectively,
$I_{\tau }$
(respectively,
![]() $NS_{\tau }$
) denotes the noncofinal (respectively, nonstationary) ideal on
$NS_{\tau }$
) denotes the noncofinal (respectively, nonstationary) ideal on
![]() $\tau $
. For each regular cardinal
$\tau $
. For each regular cardinal
![]() $\mu < \tau $
,
$\mu < \tau $
,
![]() $E^{\tau }_{\mu }$
, (respectively,
$E^{\tau }_{\mu }$
, (respectively,
![]() $E^{\tau }_{< \mu }$
) denotes the set of all infinite limit ordinals
$E^{\tau }_{< \mu }$
) denotes the set of all infinite limit ordinals
![]() $\alpha < \tau $
such that
$\alpha < \tau $
such that
![]() $\mathrm {cf}(\alpha ) = \mu $
(respectively,
$\mathrm {cf}(\alpha ) = \mu $
(respectively,
![]() $\mathrm {cf}(\alpha ) < \mu $
).
$\mathrm {cf}(\alpha ) < \mu $
).
2 Second and third versions of the conjecture
In view of the Baumgartner–Taylor result, it is tempting to repair the conjecture by replacing
![]() with the (weaker) assertion
with the (weaker) assertion
![]() that
that
![]() is nowhere weakly
is nowhere weakly
![]() -saturated (notice that since
-saturated (notice that since
![]() ,
,
![]() and
and
![]() are equivalent for
are equivalent for
![]() ). This would be more in line with Solovay’s result, which after all does not assert that
). This would be more in line with Solovay’s result, which after all does not assert that
![]() $NS_{\kappa }$
is nowhere
$NS_{\kappa }$
is nowhere
![]() $\kappa ^{<\kappa }$
-saturated (this holds if and only if
$\kappa ^{<\kappa }$
-saturated (this holds if and only if
![]() $2^{<\kappa } = \kappa $
), but only that it is nowhere
$2^{<\kappa } = \kappa $
), but only that it is nowhere
![]() $cof (I_{\kappa })$
-saturated. However, Gitik [Reference Gitik12] proved that it is consistent relative to a large cardinal that “
$cof (I_{\kappa })$
-saturated. However, Gitik [Reference Gitik12] proved that it is consistent relative to a large cardinal that “
![]() $\kappa $
is inaccessible and
$\kappa $
is inaccessible and
![]() $NS_{\kappa , \kappa ^+} \vert W$
is weakly
$NS_{\kappa , \kappa ^+} \vert W$
is weakly
![]() $\kappa ^+$
-saturated for some W (and hence
$\kappa ^+$
-saturated for some W (and hence
![]() $MC_2 (\kappa , \kappa ^+)$
fails).” Krueger [Reference Krueger23] showed that one could take
$MC_2 (\kappa , \kappa ^+)$
fails).” Krueger [Reference Krueger23] showed that one could take
![]() $W = \{x : o.t (x) = \vert x \cap \kappa \vert ^+ \}$
, and Shioya [Reference Shioya56] obtained a new proof of Gitik’s result starting from the hypothesis that
$W = \{x : o.t (x) = \vert x \cap \kappa \vert ^+ \}$
, and Shioya [Reference Shioya56] obtained a new proof of Gitik’s result starting from the hypothesis that
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa ^+$
-supercompact. Magidor (see [Reference Di Prisco and Marek7]) had shown that for all values of
$\kappa ^+$
-supercompact. Magidor (see [Reference Di Prisco and Marek7]) had shown that for all values of
![]() $\kappa $
and
$\kappa $
and
![]() ,
,
![]() is nowhere weakly
is nowhere weakly
![]() $\kappa $
-saturated, which is thus optimal. Thus Solovay’s result that
$\kappa $
-saturated, which is thus optimal. Thus Solovay’s result that
![]() $NS_{\kappa }$
is nowhere weakly
$NS_{\kappa }$
is nowhere weakly
![]() $\kappa $
-saturated does generalize, but the generalization only asserts that
$\kappa $
-saturated does generalize, but the generalization only asserts that
![]() is nowhere weakly
is nowhere weakly
![]() $\kappa $
-saturated.
$\kappa $
-saturated.
Notice that if
![]() $\kappa $
is
$\kappa $
is
![]() -Shelah and
-Shelah and
![]() , then, as shown by Johnson [Reference Johnson20], the set
, then, as shown by Johnson [Reference Johnson20], the set
![]() $W = \{x : o.t. (x) = \vert x \cap \sigma \vert ^+ \}$
lies in
$W = \{x : o.t. (x) = \vert x \cap \sigma \vert ^+ \}$
lies in
![]() (and hence in
(and hence in
![]() ), but, by another result of Johnson [Reference Johnson19],
), but, by another result of Johnson [Reference Johnson19],
![]() is not weakly
is not weakly
![]() -saturated. Thus the stationarity of
-saturated. Thus the stationarity of
![]() $W = \{x : o.t. (x) = \vert x \cap \kappa \vert ^+ \}$
does not guarantee by itself that
$W = \{x : o.t. (x) = \vert x \cap \kappa \vert ^+ \}$
does not guarantee by itself that
![]() $NS_{\kappa , \kappa ^+} \vert W$
is weakly
$NS_{\kappa , \kappa ^+} \vert W$
is weakly
![]() $\kappa ^+$
-saturated.
$\kappa ^+$
-saturated.
By Gitik’s result,
![]() is still too strong. One way to weaken it would be to require only that
is still too strong. One way to weaken it would be to require only that
![]() is nowhere weakly
is nowhere weakly
![]() -saturated for some S. Now Usuba [Reference Usuba60] established that if
-saturated for some S. Now Usuba [Reference Usuba60] established that if
![]() , then there is a stationary subset S of
, then there is a stationary subset S of
![]() with the property that no normal, fine ideal J on
with the property that no normal, fine ideal J on
![]() with
with
![]() $S \in J^+$
is weakly
$S \in J^+$
is weakly
![]() -saturated. Taking our cue from this, we let
-saturated. Taking our cue from this, we let
![]() assert the existence of S in
assert the existence of S in
![]() such that no normal, fine ideal J on
such that no normal, fine ideal J on
![]() with
with
![]() $S \in J^+$
is weakly
$S \in J^+$
is weakly
![]() -saturated. Then any normal extension of
-saturated. Then any normal extension of
![]() will be nowhere weakly
will be nowhere weakly
![]() -saturated. Clearly, the larger S is, the better.
-saturated. Clearly, the larger S is, the better.
3 Pcf theory
In this section we start working on
![]() using tools of Shelah’s pcf theory.
using tools of Shelah’s pcf theory.
3.1 Pseudo-Kurepa families
For two cardinals
![]() $\sigma $
and
$\sigma $
and
![]() $\pi $
,
$\pi $
,
![]() asserts the existence of
asserts the existence of
![]() with
with
![]() $\vert X \vert = \pi $
such that
$\vert X \vert = \pi $
such that
![]() $\vert X \cap P (b) \vert < \kappa $
for all
$\vert X \cap P (b) \vert < \kappa $
for all
![]() . It is simple to see that (
. It is simple to see that (
![]() , and hence)
, and hence)
![]() holds. These families can be used to strengthen the result of Baumgartner mentioned above. First the case when
holds. These families can be used to strengthen the result of Baumgartner mentioned above. First the case when
![]() $\kappa $
is a successor cardinal:
$\kappa $
is a successor cardinal:
Fact 3.1 [Reference Matet26].
Suppose that
![]() $\kappa $
is a successor cardinal and
$\kappa $
is a successor cardinal and
![]() holds. Then no
holds. Then no
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() is weakly
is weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
Proof The proof is an easy modification of that of Baumgartner. Let J be a
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() . Put
. Put
![]() $\kappa = \nu ^+$
. We can assume that
$\kappa = \nu ^+$
. We can assume that
![]() $\pi $
is greater than or equal to
$\pi $
is greater than or equal to
![]() $\kappa $
(since we have seen that (
$\kappa $
(since we have seen that (
![]() and hence)
and hence)
![]() ) always holds) and (by Fact 1.6(i)) regular. Select
) always holds) and (by Fact 1.6(i)) regular. Select
![]() with
with
![]() $\vert X \vert = \pi $
such that
$\vert X \vert = \pi $
such that
![]() for all
for all
![]() . For
. For
![]() , pick a one-to-one function
, pick a one-to-one function
![]() $f_b : X \cap P (b) \rightarrow \nu $
. By
$f_b : X \cap P (b) \rightarrow \nu $
. By
![]() $\kappa $
-completeness and fineness of J, for each
$\kappa $
-completeness and fineness of J, for each
![]() $x \in X$
, we may find
$x \in X$
, we may find
![]() $S_x \in J^+ \cap P (\{b : x \subseteq b\})$
and
$S_x \in J^+ \cap P (\{b : x \subseteq b\})$
and
![]() $\gamma _x < \nu $
such that
$\gamma _x < \nu $
such that
![]() $f_b (x) = \gamma _x$
for all
$f_b (x) = \gamma _x$
for all
![]() $b \in S_x$
. There must be
$b \in S_x$
. There must be
![]() $\gamma < \nu $
and
$\gamma < \nu $
and
![]() $W \subseteq X$
with
$W \subseteq X$
with
![]() $\vert W \vert = \pi $
such that
$\vert W \vert = \pi $
such that
![]() $\gamma _x = \gamma $
for any
$\gamma _x = \gamma $
for any
![]() $x \in W$
. Then clearly
$x \in W$
. Then clearly
![]() $S_x \cap S_y = \emptyset $
for any two distinct members
$S_x \cap S_y = \emptyset $
for any two distinct members
![]() $x, y$
of W.
$x, y$
of W.
In particular, as observed by Matsubara [Reference Matsubara42] long ago, if
![]() $\kappa $
is a successor cardinal, then no
$\kappa $
is a successor cardinal, then no
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
We use more in the case when
![]() $\kappa $
is weakly inaccessible. Given an ideal J on
$\kappa $
is weakly inaccessible. Given an ideal J on
![]() and a cardinal
and a cardinal
![]() $\tau $
with
$\tau $
with
![]() , J is
, J is
![]() $\tau $
-normal if for any
$\tau $
-normal if for any
![]() $A \in J^+$
and any
$A \in J^+$
and any
![]() $f : A \rightarrow \tau $
such that
$f : A \rightarrow \tau $
such that
![]() $f(a) \in a$
for all
$f(a) \in a$
for all
![]() $a \in A$
, there is
$a \in A$
, there is
![]() $B \in J^+ \cap P(A)$
such that f is constant on B. Notice that
$B \in J^+ \cap P(A)$
such that f is constant on B. Notice that
![]() -normality is the same as normality.
-normality is the same as normality.
Fact 3.2 [Reference Matet28].
Suppose that
![]() $\tau $
and
$\tau $
and
![]() $\pi $
are two cardinals with
$\pi $
are two cardinals with
![]() and
and
![]() $\tau < \pi $
, and J is a
$\tau < \pi $
, and J is a
![]() $\tau $
-normal, fine ideal on
$\tau $
-normal, fine ideal on
![]() . Suppose further that there is
. Suppose further that there is
![]() with
with
![]() $\vert X \vert = \pi $
such that
$\vert X \vert = \pi $
such that
![]() . Then J is not weakly
. Then J is not weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
Note that if X is as in the statement of the fact, then
![]() $\vert X \cap P (c) \vert < \kappa $
for all
$\vert X \cap P (c) \vert < \kappa $
for all
![]() (so X witnesses that
(so X witnesses that
![]() holds). Further note that it follows from Fact 3.2 that if
holds). Further note that it follows from Fact 3.2 that if
![]() $\kappa $
is weakly inaccessible, then no
$\kappa $
is weakly inaccessible, then no
![]() $\kappa $
-normal, fine ideal J on
$\kappa $
-normal, fine ideal J on
![]() with
with
![]() is weakly
is weakly
![]() -saturated. Thus by combining Facts 3.1 and 3.2, we obtain the following.
-saturated. Thus by combining Facts 3.1 and 3.2, we obtain the following.
Proposition 3.3. If
![]() , then
, then
![]() holds.
holds.
Let us return to the special case of Fact 3.2 when
![]() and
and
![]() . If
. If
![]() $\kappa $
is weakly inaccessible,
$\kappa $
is weakly inaccessible,
![]() , and J is a normal, fine, weakly
, and J is a normal, fine, weakly
![]() -saturated ideal on
-saturated ideal on
![]() , then it gives us that the set of all
, then it gives us that the set of all
![]() such that (
such that (
![]() $\vert b \vert> \vert b \cap \tau \vert $
for every cardinal
$\vert b \vert> \vert b \cap \tau \vert $
for every cardinal
![]() $\tau $
with
$\tau $
with
![]() , and hence)
, and hence)
![]() lies in
lies in
![]() $J^{\ast }$
. In the special case when
$J^{\ast }$
. In the special case when
![]() for some regular cardinal
for some regular cardinal
![]() $\sigma < \kappa $
, we can even conclude that
$\sigma < \kappa $
, we can even conclude that
![]() , since it is simple to see that for any cardinal
, since it is simple to see that for any cardinal
![]() $\chi $
with
$\chi $
with
![]() ,
,
![]() .
.
For another remark, letting C denote the set of all
such that (a)
![]() $o.t. (b)$
is an infinite limit ordinal, and (b)
$o.t. (b)$
is an infinite limit ordinal, and (b)
![]() $b \setminus \tau \not = \emptyset $
, then clearly
$b \setminus \tau \not = \emptyset $
, then clearly
, and moreover
for all
![]() $b \in C$
with
$b \in C$
with
. For normal ideals there is the following related result of Usuba (see the proof of Proposition 6.1 in [Reference Usuba59]) who proved it using generic embeddings.
Fact 3.4. Suppose that
![]() is regular, and let J be a normal, fine ideal on
is regular, and let J be a normal, fine ideal on
![]() such that
such that
![]() $S \in J^+$
, where S is the set of all
$S \in J^+$
, where S is the set of all
![]() such that (
such that (
![]() $o.t. (b)$
is an infinite limit ordinal with)
$o.t. (b)$
is an infinite limit ordinal with)
![]() $\mathrm {cf} (o.t. (b)) < o.t. (b)$
. Then J is not weakly
$\mathrm {cf} (o.t. (b)) < o.t. (b)$
. Then J is not weakly
![]() -saturated.
-saturated.
Proof For each infinite limit ordinal
![]() $\delta $
, select an increasing function
$\delta $
, select an increasing function
![]() $t_{\delta } : \mathrm {cf} (\delta ) \rightarrow \delta $
such that
$t_{\delta } : \mathrm {cf} (\delta ) \rightarrow \delta $
such that
![]() $\sup (ran (t_{\delta })) = \delta $
. For
$\sup (ran (t_{\delta })) = \delta $
. For
![]() $b \in S$
, let
$b \in S$
, let
![]() $g_b : o.t. (b) \rightarrow b$
enumerate b in increasing order, and set
$g_b : o.t. (b) \rightarrow b$
enumerate b in increasing order, and set
![]() $\tau _b = \mathrm {cf} (o.t. (b))$
and
$\tau _b = \mathrm {cf} (o.t. (b))$
and
![]() $\xi _b = g_b (\tau _b)$
. By normality of J, we may find
$\xi _b = g_b (\tau _b)$
. By normality of J, we may find
![]() $Y \in J^+ \cap P (S)$
and
$Y \in J^+ \cap P (S)$
and
![]() such that
such that
![]() $\xi _b = \xi $
for all
$\xi _b = \xi $
for all
![]() $b \in Y$
. For
$b \in Y$
. For
![]() $\alpha \in b \in Y$
, put:
$\alpha \in b \in Y$
, put:
-
•
 $F (\alpha , b) =$
the least
$F (\alpha , b) =$
the least
 $\zeta < \tau _b$
such that
$\zeta < \tau _b$
such that
 ;
; -
•
 $\beta ^b_{\alpha } = g_b (t_{o.t. (b)} (F (\alpha , b)))$
;
$\beta ^b_{\alpha } = g_b (t_{o.t. (b)} (F (\alpha , b)))$
; -
•
 $\gamma ^b_{\alpha } = g_b (F (\alpha , b))$
.
$\gamma ^b_{\alpha } = g_b (F (\alpha , b))$
.
Thus
![]() $F (\alpha , b) < \tau _b$
,
$F (\alpha , b) < \tau _b$
,
![]() $\beta ^b_{\alpha } \in b$
and
$\beta ^b_{\alpha } \in b$
and
![]() $\gamma ^b_{\alpha } \in b \cap \xi $
. For
$\gamma ^b_{\alpha } \in b \cap \xi $
. For
![]() , there must be, by normality of J,
, there must be, by normality of J,
![]() $T_{\alpha } \in J^+ \cap P (\{b \in Y : \alpha \in b\})$
,
$T_{\alpha } \in J^+ \cap P (\{b \in Y : \alpha \in b\})$
,
![]() , and
, and
![]() $\gamma _{\alpha } < \xi $
such that for all
$\gamma _{\alpha } < \xi $
such that for all
![]() $b \in T_{\alpha }$
,
$b \in T_{\alpha }$
,
![]() $\beta ^b_{\alpha } = \beta _{\alpha }$
and
$\beta ^b_{\alpha } = \beta _{\alpha }$
and
![]() $\gamma ^b_{\alpha } = \gamma _{\alpha }$
. Since
$\gamma ^b_{\alpha } = \gamma _{\alpha }$
. Since
![]() is regular, we may find
is regular, we may find
![]() and
and
![]() $\gamma < \xi $
such that
$\gamma < \xi $
such that
![]() $\gamma _{\alpha } = \gamma $
for all
$\gamma _{\alpha } = \gamma $
for all
![]() $\alpha \in d$
. Finally, pick
$\alpha \in d$
. Finally, pick
![]() with the property that
with the property that
![]() $\beta _{\alpha } < \alpha '$
whenever
$\beta _{\alpha } < \alpha '$
whenever
![]() $\alpha < \alpha '$
are in e. Given
$\alpha < \alpha '$
are in e. Given
![]() $\alpha < \alpha '$
in e, we claim that
$\alpha < \alpha '$
in e, we claim that
![]() $T_{\alpha } \cap T_{\alpha '} = \emptyset $
. Suppose otherwise, and pick
$T_{\alpha } \cap T_{\alpha '} = \emptyset $
. Suppose otherwise, and pick
![]() $b \in T_{\alpha } \cap T_{\alpha '}$
. Then
$b \in T_{\alpha } \cap T_{\alpha '}$
. Then
![]() $F (\alpha , b) = F (\alpha ', b)$
(since
$F (\alpha , b) = F (\alpha ', b)$
(since
and therefore
![]() . Contradiction.
. Contradiction.
3.2 Scales
To handle the case when
![]() , we will use pcf theory scales. We will first study the effect of one specific scale on weak saturation of ideals on
, we will use pcf theory scales. We will first study the effect of one specific scale on weak saturation of ideals on
![]() , which will keep us busy for a long while (up to the end of Section 5).
, which will keep us busy for a long while (up to the end of Section 5).
Let A be an infinite set of regular cardinals, and let I be an ideal on A such that
![]() $\{A \cap a : a \in A \} \subseteq I$
. We let
$\{A \cap a : a \in A \} \subseteq I$
. We let
![]() $\prod A = \prod _{a \in A} a$
. For
$\prod A = \prod _{a \in A} a$
. For
![]() $f, g \in \prod A$
, we let
$f, g \in \prod A$
, we let
![]() $f <_I g$
if
$f <_I g$
if
![]() $\{a \in A : f (a) \geq g (a) \} \in I$
.
$\{a \in A : f (a) \geq g (a) \} \in I$
.
Let
![]() $\xi \in On$
, and
$\xi \in On$
, and
![]() be an increasing, cofinal sequence in
be an increasing, cofinal sequence in
![]() $(\prod A, <_I)$
. For
$(\prod A, <_I)$
. For
![]() $X \subseteq \xi $
, the sequence
$X \subseteq \xi $
, the sequence
![]() is strongly increasing if there is
is strongly increasing if there is
![]() $Z_{\xi } \in I$
for
$Z_{\xi } \in I$
for
![]() $\xi \in X$
such that
$\xi \in X$
such that
![]() $f_{\beta } (a) < f_{\xi } (a)$
whenever
$f_{\beta } (a) < f_{\xi } (a)$
whenever
![]() $\beta < \xi $
are in X and
$\beta < \xi $
are in X and
![]() $a \in A \setminus (Z_{\beta } \cup Z_{\xi })$
.
$a \in A \setminus (Z_{\beta } \cup Z_{\xi })$
.
An infinite limit ordinal
![]() $\delta < \xi $
is a good point for
$\delta < \xi $
is a good point for
![]() if there is a cofinal subset X of
if there is a cofinal subset X of
![]() $\delta $
such that
$\delta $
such that
![]() is strongly increasing.
is strongly increasing.
Fact 3.5.
-
(i) [Reference Cummings, Foreman and Magidor6, Reference Matet29] If I is
 $\mathrm {cf} (\delta )$
-complete, then
$\mathrm {cf} (\delta )$
-complete, then
 $\delta $
is a good point for
$\delta $
is a good point for
 .
. -
(ii) [Reference Abraham and Magidor1, Lemma 2.7] Suppose that
 $\delta $
is a good point for
$\delta $
is a good point for
 . Then any cofinal subset e of
. Then any cofinal subset e of
 $\delta $
has a cofinal subset X such that the sequence
$\delta $
has a cofinal subset X such that the sequence
 is strongly increasing.
is strongly increasing.
Let
![]() $\pi $
be a regular cardinal greater than
$\pi $
be a regular cardinal greater than
![]() $\sup A$
. An increasing, cofinal sequence
$\sup A$
. An increasing, cofinal sequence
![]() in
in
![]() $(\prod A, <_I)$
is said to be a scale for
$(\prod A, <_I)$
is said to be a scale for
![]() $\sup A$
of length
$\sup A$
of length
![]() $\pi $
. If there is such a sequence, we set
$\pi $
. If there is such a sequence, we set
![]() $\mathrm {tcf} (\prod A / I) = \pi $
.
$\mathrm {tcf} (\prod A / I) = \pi $
.
For a singular cardinal
![]() $\chi $
and a cardinal
$\chi $
and a cardinal
![]() $\sigma $
with
$\sigma $
with
![]() , the pseudopower
, the pseudopower
![]() $\mathrm {pp}_{\sigma } (\chi )$
is defined as the supremum of the set X of all cardinals
$\mathrm {pp}_{\sigma } (\chi )$
is defined as the supremum of the set X of all cardinals
![]() $\pi $
for which one may find A and I such that:
$\pi $
for which one may find A and I such that:
-
• A is a set of regular cardinals smaller than
 $\chi $
;
$\chi $
; -
•
 $\sup A = \chi $
;
$\sup A = \chi $
; -
•
 ;
; -
• I is an ideal on A such that
 $\{A \cap a : a \in A \} \subseteq I$
;
$\{A \cap a : a \in A \} \subseteq I$
; -
•
 $\pi = \mathrm {tcf}( \prod A /I )$
.
$\pi = \mathrm {tcf}( \prod A /I )$
.
The definition is robust in the sense that it will not be affected by minor modifications (such as requiring the ideal I to be prime) (see [Reference Holz, Steffens and Weitz16, p. 270]).
We let
![]() $\mathrm {pp} (\chi ) = \mathrm {pp}_{\mathrm {cf} (\chi )} (\chi )$
.
$\mathrm {pp} (\chi ) = \mathrm {pp}_{\mathrm {cf} (\chi )} (\chi )$
.
Fact 3.6 [Reference Shelah50, Theorem 1.5, p. 50].
Let
![]() $\chi $
be a singular cardinal. Then there is a set A of regular cardinals such that
$\chi $
be a singular cardinal. Then there is a set A of regular cardinals such that
![]() $o.t. (A) = \mathrm {cf} (\chi ) < \min A, \sup A = \chi $
and
$o.t. (A) = \mathrm {cf} (\chi ) < \min A, \sup A = \chi $
and
![]() $\mathrm {tcf} (\prod A/I) = \chi ^+$
, where I is the noncofinal ideal on A.
$\mathrm {tcf} (\prod A/I) = \chi ^+$
, where I is the noncofinal ideal on A.
Thus
![]() $\mathrm {pp} (\chi ) \geq \chi ^+$
for any singular cardinal
$\mathrm {pp} (\chi ) \geq \chi ^+$
for any singular cardinal
![]() $\chi $
.
$\chi $
.
3.3 Large pseudo-Kurepa families from scales
Throughout the remainder of this section and Sections 4 and 5
, we let
![]() $\theta , \pi , A$
, and I be such that:
$\theta , \pi , A$
, and I be such that:
-
•
 $\theta $
and
$\theta $
and
 $\pi $
are two cardinals such that
$\pi $
are two cardinals such that
 and
and
 $\theta < \pi $
;
$\theta < \pi $
; -
• A is a set of regular cardinals smaller than
 $\theta $
such that
$\theta $
such that
 $\vert A \vert < \kappa $
and
$\vert A \vert < \kappa $
and
 $\sup A = \theta $
;
$\sup A = \theta $
; -
• I is an ideal on A with
 $\{A \cap a : a \in A \} \subseteq I$
;
$\{A \cap a : a \in A \} \subseteq I$
; -
•
 $\pi = \mathrm {tcf} (\prod A /I )$
.
$\pi = \mathrm {tcf} (\prod A /I )$
.
Further let
![]() be an increasing, cofinal sequence in
be an increasing, cofinal sequence in
![]() $(\prod A, <_I)$
.
$(\prod A, <_I)$
.
Let
![]() $\Phi $
denote a one-to-one onto function from
$\Phi $
denote a one-to-one onto function from
![]() $On \times On$
to
$On \times On$
to
![]() $On$
such that
$On$
such that
![]() $\Phi " (\sigma \times \sigma ) = \sigma $
for any infinite cardinal
$\Phi " (\sigma \times \sigma ) = \sigma $
for any infinite cardinal
![]() $\sigma $
. We let
$\sigma $
. We let
![]() be defined by:
be defined by:
![]() $y_{\alpha }$
equals
$y_{\alpha }$
equals
![]() $\{\alpha \}$
if
$\{\alpha \}$
if
![]() $\alpha < \theta $
, and
$\alpha < \theta $
, and
![]() $\{\Phi (a, f_{\alpha } (a)) : a \in A \}$
otherwise.
$\{\Phi (a, f_{\alpha } (a)) : a \in A \}$
otherwise.
Observation 3.7. Let
![]() $\delta> \theta $
be a good point for
$\delta> \theta $
be a good point for
![]() $\vec f$
, and let e be a cofinal subset of
$\vec f$
, and let e be a cofinal subset of
![]() $\delta $
of order-type
$\delta $
of order-type
![]() $\mathrm {cf} (\delta )$
. Then
$\mathrm {cf} (\delta )$
. Then
![]() $\vert \bigcup _{\alpha \in e} y_{\alpha } \vert = \max (\vert A \vert , \mathrm {cf} (\delta ))$
.
$\vert \bigcup _{\alpha \in e} y_{\alpha } \vert = \max (\vert A \vert , \mathrm {cf} (\delta ))$
.
Proof By Fact 3.5(ii), we may find a subset X of
![]() $e \setminus \theta $
of order-type
$e \setminus \theta $
of order-type
![]() $\mathrm {cf} (\delta )$
such that the sequence
$\mathrm {cf} (\delta )$
such that the sequence
![]() is strongly increasing. Pick
is strongly increasing. Pick
![]() $Z_{\xi } \in I$
for
$Z_{\xi } \in I$
for
![]() $\xi \in X$
so that
$\xi \in X$
so that
![]() $f_{\beta } (a) < f_{\xi } (a)$
whenever
$f_{\beta } (a) < f_{\xi } (a)$
whenever
![]() $\beta < \xi $
are in X and
$\beta < \xi $
are in X and
![]() $a \in A \setminus (Z_{\beta } \cup Z_{\xi })$
. Now select
$a \in A \setminus (Z_{\beta } \cup Z_{\xi })$
. Now select
![]() $k \in \prod _{\xi \in X} (A \setminus Z_{\xi })$
, and put
$k \in \prod _{\xi \in X} (A \setminus Z_{\xi })$
, and put
![]() $t = \{\Phi (k (\xi ), f_{\xi } (k (\xi ))) : \xi \in X \}$
. It is simple to see that
$t = \{\Phi (k (\xi ), f_{\xi } (k (\xi ))) : \xi \in X \}$
. It is simple to see that
![]() $\vert t \vert = \vert X \vert = \mathrm {cf} (\delta )$
. It follows that
$\vert t \vert = \vert X \vert = \mathrm {cf} (\delta )$
. It follows that
 $$ \begin{align*} \vert \bigcup_{\alpha \in e} y_{\alpha} \vert \geq \vert \bigcup_{\alpha \in X} y_{\alpha} \vert \geq \max (\vert A \vert, \mathrm{cf} (\delta)). \end{align*} $$
$$ \begin{align*} \vert \bigcup_{\alpha \in e} y_{\alpha} \vert \geq \vert \bigcup_{\alpha \in X} y_{\alpha} \vert \geq \max (\vert A \vert, \mathrm{cf} (\delta)). \end{align*} $$
On the other hand, it is readily verified that
![]() .
.
Fact 3.8.
-
(i) [Reference Matet37] There is a closed unbounded subset
 $C_{\vec {f}}$
of
$C_{\vec {f}}$
of
 $\pi $
, consisting of infinite limit ordinals, with the property that any
$\pi $
, consisting of infinite limit ordinals, with the property that any
 $\delta $
in
$\delta $
in
 $C_{\vec {f}}$
satisfying one of the following conditions, where
$C_{\vec {f}}$
satisfying one of the following conditions, where
 $\rho $
denotes the largest limit cardinal less than or equal to
$\rho $
denotes the largest limit cardinal less than or equal to
 $\mathrm {cf} (\delta )$
, is a good point for
$\mathrm {cf} (\delta )$
, is a good point for
 $\vec f$
:
$\vec f$
:-
(a)
 $(\max (\rho , \vert A \vert ))^{+3} < \mathrm {cf} (\delta )$
.
$(\max (\rho , \vert A \vert ))^{+3} < \mathrm {cf} (\delta )$
. -
(b)
 $\rho ^{\vert A \vert } < \mathrm {cf} (\delta )$
.
$\rho ^{\vert A \vert } < \mathrm {cf} (\delta )$
. -
(c)
 $\vert A \vert < \mathrm {cf} (\rho )$
.
$\vert A \vert < \mathrm {cf} (\rho )$
. -
(d)
 $\vert A \vert < \rho $
and I is
$\vert A \vert < \rho $
and I is
 $(\mathrm {cf} (\rho ))^+$
-complete.
$(\mathrm {cf} (\rho ))^+$
-complete. -
(e)
 and
and
 $\mathrm {pp} (\rho ) < \mathrm {cf} (\delta )$
.
$\mathrm {pp} (\rho ) < \mathrm {cf} (\delta )$
.
-
-
(ii) [Reference Matet28] Suppose that
 and there is a closed unbounded subset C of
and there is a closed unbounded subset C of
 $\pi $
such that every
$\pi $
such that every
 $\delta \in C$
of cofinality
$\delta \in C$
of cofinality
 $\kappa $
is a good point for
$\kappa $
is a good point for
 ${\vec f}$
. Then
${\vec f}$
. Then
 holds, as witnessed by
holds, as witnessed by
 $X = \{y_{\alpha } : \alpha < \pi \}$
.
$X = \{y_{\alpha } : \alpha < \pi \}$
.
Thus, for instance,
![]() ${\mathcal A}_{\omega _4,\sigma } (\omega _1, \sigma ^+)$
holds for every uncountable cardinal
${\mathcal A}_{\omega _4,\sigma } (\omega _1, \sigma ^+)$
holds for every uncountable cardinal
![]() $\sigma $
of cofinality
$\sigma $
of cofinality
![]() $\omega $
. On the other hand by a result of Todorcevic (see [Reference Matet28]), if
$\omega $
. On the other hand by a result of Todorcevic (see [Reference Matet28]), if
![]() ,
,
![]() for every cardinal
for every cardinal
![]() $\tau $
with
$\tau $
with
![]() , and
, and
![]() , then
, then
![]() fails.
fails.
The scale
![]() is good if there is a closed unbounded subset C of
is good if there is a closed unbounded subset C of
![]() $\pi $
with the property that every infinite limit ordinal
$\pi $
with the property that every infinite limit ordinal
![]() $\delta $
in C such that
$\delta $
in C such that
![]() $\vert A \vert < \mathrm {cf} (\delta ) <\sup A$
is a good point for
$\vert A \vert < \mathrm {cf} (\delta ) <\sup A$
is a good point for
![]() $\vec f$
.
$\vec f$
.
If
![]() $\pi $
is the successor of a cardinal
$\pi $
is the successor of a cardinal
![]() $\tau $
(possibly greater than
$\tau $
(possibly greater than
![]() $\sup A$
) at which the weak square principle
$\sup A$
) at which the weak square principle
![]() $\square _{\tau }^{\ast }$
holds, then [Reference Cummings, Foreman and Magidor6, Reference Matet31] the scale
$\square _{\tau }^{\ast }$
holds, then [Reference Cummings, Foreman and Magidor6, Reference Matet31] the scale
![]() $\vec f$
is good. Let us recall that the failure of
$\vec f$
is good. Let us recall that the failure of
![]() $\square _{\tau }^{\ast }$
for singular
$\square _{\tau }^{\ast }$
for singular
![]() $\tau $
has, in the words of Jech [Reference Jech18, p. 702] (see also [Reference Cummings5]), the consistency strength of (roughly) at least one Woodin cardinal.
$\tau $
has, in the words of Jech [Reference Jech18, p. 702] (see also [Reference Cummings5]), the consistency strength of (roughly) at least one Woodin cardinal.
3.4 The case

We have seen that if
![]() , then
, then
![]() holds. We give a second proof of this fact now, under the extra assumption that
holds. We give a second proof of this fact now, under the extra assumption that
![]() is the length of a scale.
is the length of a scale.
Lemma 3.9. Suppose that
![]() , and let
, and let
![]() be such that:
be such that:
-
•
 $\sup b \notin b$
.
$\sup b \notin b$
. -
• Either
 $\sup b$
is a good point for
$\sup b$
is a good point for
 ${\vec f}$
of cofinality greater than
${\vec f}$
of cofinality greater than
 $ \vert A \vert $
, or I is
$ \vert A \vert $
, or I is
 $\mathrm {cf} (\sup b)$
-complete.
$\mathrm {cf} (\sup b)$
-complete. -
•
 $ran (f_{\alpha }) \subseteq b$
for all
$ran (f_{\alpha }) \subseteq b$
for all
 $\alpha \in b$
.
$\alpha \in b$
.
Then
![]() .
.
Proof Set
![]() $\tau = \mathrm {cf} (\sup b)$
. Select an order type
$\tau = \mathrm {cf} (\sup b)$
. Select an order type
![]() $\tau $
subset c of b with supremum
$\tau $
subset c of b with supremum
![]() $\sup b$
. Let us first suppose that
$\sup b$
. Let us first suppose that
![]() $\sup b$
is a good point of
$\sup b$
is a good point of
![]() ${\vec f}$
of cofinality greater than
${\vec f}$
of cofinality greater than
![]() $ \vert A \vert $
. By Fact 3.5(ii), we may find
$ \vert A \vert $
. By Fact 3.5(ii), we may find
![]() $d \in [c]^{\tau }$
and
$d \in [c]^{\tau }$
and
![]() $w_{\gamma } \in I$
for
$w_{\gamma } \in I$
for
![]() $\gamma \in d$
such that
$\gamma \in d$
such that
![]() $f_{\beta } (a) < f_{\alpha } (a)$
whenever
$f_{\beta } (a) < f_{\alpha } (a)$
whenever
![]() $\beta < \alpha $
are in d and
$\beta < \alpha $
are in d and
![]() $a \in A \setminus (w_{\beta } \cup w_{\alpha })$
. For
$a \in A \setminus (w_{\beta } \cup w_{\alpha })$
. For
![]() $\alpha \in d$
, pick
$\alpha \in d$
, pick
![]() $a_{\alpha } \in A \setminus w_{\alpha }$
. There must be
$a_{\alpha } \in A \setminus w_{\alpha }$
. There must be
![]() $a \in A$
and
$a \in A$
and
![]() $e \in [d]^{\tau }$
such that
$e \in [d]^{\tau }$
such that
![]() $a_{\alpha } = a$
for all
$a_{\alpha } = a$
for all
![]() $\alpha \in e$
. Then
$\alpha \in e$
. Then
![]() is an increasing sequence of length
is an increasing sequence of length
![]() $\tau $
with all its terms in
$\tau $
with all its terms in
![]() $b \cap \theta $
.
$b \cap \theta $
.
Next suppose that I is
![]() $\tau $
-complete. For
$\tau $
-complete. For
![]() $\beta < \alpha $
in c, select
$\beta < \alpha $
in c, select
![]() $u_{\beta \alpha } \in I$
such that
$u_{\beta \alpha } \in I$
such that
![]() $f_{\beta } (a) < f_{\alpha } (a)$
whenever
$f_{\beta } (a) < f_{\alpha } (a)$
whenever
![]() $a \in A \setminus u_{\beta \alpha }$
. For each
$a \in A \setminus u_{\beta \alpha }$
. For each
![]() $\gamma \in c$
, pick
$\gamma \in c$
, pick
![]() $a_{\gamma }$
in
$a_{\gamma }$
in
![]() $A \setminus (\bigcup \{u_{\beta \alpha } : \beta < \alpha < \gamma $
and
$A \setminus (\bigcup \{u_{\beta \alpha } : \beta < \alpha < \gamma $
and
![]() $\beta , \alpha \in c \})$
. Then
$\beta , \alpha \in c \})$
. Then
![]() is an increasing sequence of length
is an increasing sequence of length
![]() $o.t. (c \cap \gamma )$
with all its terms in
$o.t. (c \cap \gamma )$
with all its terms in
![]() $b \cap \theta $
, so
$b \cap \theta $
, so
![]() . It follows that
. It follows that
![]() .
.
Proposition 3.10. Suppose that
![]() , and J is a normal, fine ideal on
, and J is a normal, fine ideal on
![]() such that either
such that either
![]() $S_1 \in J^+$
, or
$S_1 \in J^+$
, or
![]() $S_2 \in J^+$
, where
$S_2 \in J^+$
, where
![]() $S_1$
is the set of all
$S_1$
is the set of all
![]() such that
such that
![]() $\sup b$
is a good point for
$\sup b$
is a good point for
![]() ${\vec f}$
of cofinality greater than
${\vec f}$
of cofinality greater than
![]() $ \vert A \vert $
, and
$ \vert A \vert $
, and
![]() $S_2$
the set of all
$S_2$
the set of all
![]() such that I is
such that I is
![]() $\mathrm {cf} (\sup b)$
-complete. Then J is not weakly
$\mathrm {cf} (\sup b)$
-complete. Then J is not weakly
![]() -saturated.
-saturated.
Proof Let C be the set of all
![]() such that:
such that:
-
•
 $\sup b \notin b$
;
$\sup b \notin b$
; -
•
 $ran (f_{\alpha }) \subseteq b$
for all
$ran (f_{\alpha }) \subseteq b$
for all
 $\alpha \in b$
;
$\alpha \in b$
; -
•
 $b \setminus \theta \not = \emptyset $
.
$b \setminus \theta \not = \emptyset $
.
Then clearly,
![]() . Hence, for
. Hence, for
![]() $i = 1, 2$
,
$i = 1, 2$
,
![]() $C \cap S_i \in J^+$
. Moreover by Lemma 3.9,
$C \cap S_i \in J^+$
. Moreover by Lemma 3.9,
![]() $\mathrm {cf} (o.t. (b)) < o.t. (b)$
for all
$\mathrm {cf} (o.t. (b)) < o.t. (b)$
for all
![]() $b \in C \cap S_i$
. The result is now immediate from Fact 3.4.
$b \in C \cap S_i$
. The result is now immediate from Fact 3.4.
3.5 The isomorphism method
One way to show that an ideal J on
![]() is not weakly
is not weakly
![]() $\pi $
-saturated is to establish that it is isomorphic to some ideal K on
$\pi $
-saturated is to establish that it is isomorphic to some ideal K on
![]() $P_{\kappa } (\pi )$
that is itself not weakly
$P_{\kappa } (\pi )$
that is itself not weakly
![]() $\pi $
-saturated. In this subsection we consider some situations when this can (or cannot) be done.
$\pi $
-saturated. In this subsection we consider some situations when this can (or cannot) be done.
For
![]() $i = 1, 2$
, let
$i = 1, 2$
, let
![]() $X_i$
be an infinite set, and let
$X_i$
be an infinite set, and let
![]() $K_i$
be an ideal on
$K_i$
be an ideal on
![]() $X_i$
. We say that
$X_i$
. We say that
![]() $K_1$
is isomorphic to
$K_1$
is isomorphic to
![]() $K_2$
if there are
$K_2$
if there are
![]() $W_1 \in K_1^{\ast }$
,
$W_1 \in K_1^{\ast }$
,
![]() $W_2 \in K_2^{\ast }$
, and a bijection
$W_2 \in K_2^{\ast }$
, and a bijection
![]() $k : W_1 \rightarrow W_2$
such that
$k : W_1 \rightarrow W_2$
such that
![]() $K_1^{\ast } = \{D \subseteq W_1 : k"D \in K_2^{\ast }\}$
.
$K_1^{\ast } = \{D \subseteq W_1 : k"D \in K_2^{\ast }\}$
.
Notice that
![]() $K_1$
is isomorphic to
$K_1$
is isomorphic to
![]() $K_2$
if and only if there are
$K_2$
if and only if there are
![]() $W_1 \in K_1^{\ast }$
,
$W_1 \in K_1^{\ast }$
,
![]() $W_2 \in K_2^{\ast }$
, and a bijection
$W_2 \in K_2^{\ast }$
, and a bijection
![]() $k : W_1 \rightarrow W_2$
such that (a)
$k : W_1 \rightarrow W_2$
such that (a)
![]() $\{k"D : D \in K_1^{\ast } \cap P (W_1)\} \subseteq K_2^{\ast }$
, and (b)
$\{k"D : D \in K_1^{\ast } \cap P (W_1)\} \subseteq K_2^{\ast }$
, and (b)
![]() $\{k^{- 1} (B) : B \in K_2^{\ast } \cap P (W_2)\} \subseteq K_1^{\ast }$
. It easily follows that
$\{k^{- 1} (B) : B \in K_2^{\ast } \cap P (W_2)\} \subseteq K_1^{\ast }$
. It easily follows that
![]() $K_1$
is isomorphic to
$K_1$
is isomorphic to
![]() $K_2$
just in case
$K_2$
just in case
![]() $K_2$
is isomorphic to
$K_2$
is isomorphic to
![]() $K_1$
.
$K_1$
.
For a cardinal
![]() $\sigma> \kappa $
and a
$\sigma> \kappa $
and a
![]() $\kappa $
-complete ideal G on
$\kappa $
-complete ideal G on
![]() $P_{\kappa } (\sigma )$
,
$P_{\kappa } (\sigma )$
,
![]() $\overline {\mathrm {cof}} (G)$
denotes the least cardinality of any
$\overline {\mathrm {cof}} (G)$
denotes the least cardinality of any
![]() $Q \subseteq G$
such that for any
$Q \subseteq G$
such that for any
![]() $B \in G$
, there is
$B \in G$
, there is
![]() $Z \in P_{\kappa } (Q)$
with
$Z \in P_{\kappa } (Q)$
with
![]() $B \subseteq \bigcup Z$
.
$B \subseteq \bigcup Z$
.
Observation 3.11. For
![]() $i = 0, 1$
, let
$i = 0, 1$
, let
![]() $\sigma _i$
be a cardinal greater than
$\sigma _i$
be a cardinal greater than
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $K_i$
be a fine ideal on
$K_i$
be a fine ideal on
![]() $P_{\kappa } (\sigma _i)$
. Suppose that
$P_{\kappa } (\sigma _i)$
. Suppose that
![]() $K_1$
is
$K_1$
is
![]() $\kappa $
-complete, and
$\kappa $
-complete, and
![]() $K_1$
and
$K_1$
and
![]() $K_2$
are isomorphic. Then
$K_2$
are isomorphic. Then
![]() $K_2$
is
$K_2$
is
![]() $\kappa $
-complete, and moreover
$\kappa $
-complete, and moreover
![]() $\overline {\mathrm {cof}} (K_1) = \overline {\mathrm {cof}} (K_2)$
.
$\overline {\mathrm {cof}} (K_1) = \overline {\mathrm {cof}} (K_2)$
.
Fact 3.12 [Reference Matet36].
The following are equivalent:
-
(i)
 $f (K_1) = K_2$
for some one-to-one
$f (K_1) = K_2$
for some one-to-one
 $f : X_1 \rightarrow X_2$
.
$f : X_1 \rightarrow X_2$
. -
(ii) There are
 $W_2 \in K_2^{\ast }$
and a bijection
$W_2 \in K_2^{\ast }$
and a bijection
 $k : X_1 \rightarrow W_2$
such that
$k : X_1 \rightarrow W_2$
such that
 $K_1^{\ast } = \{D \subseteq W_1 : k"D \in K_2^{\ast }\}$
.
$K_1^{\ast } = \{D \subseteq W_1 : k"D \in K_2^{\ast }\}$
.
We use the isomorphism method to give new versions of Facts 3.1 and 3.2. Let us start with the situation when
![]() $\kappa $
is a successor cardinal. There is a more informative proof of Fact 3.1 which runs as follows. For the first case, when
$\kappa $
is a successor cardinal. There is a more informative proof of Fact 3.1 which runs as follows. For the first case, when
![]() , proceed as in the original proof. Now for the second case, suppose that
, proceed as in the original proof. Now for the second case, suppose that
![]() $\kappa $
is a successor cardinal, J is a
$\kappa $
is a successor cardinal, J is a
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() ,
,
![]() , and X is a size
, and X is a size
![]() $\pi $
subset of
$\pi $
subset of
![]() with the property that
with the property that
![]() $\vert X \cap P (b) \vert < \kappa $
for all
$\vert X \cap P (b) \vert < \kappa $
for all
![]() . Letting
. Letting
![]() be a one-to-one enumeration of X, define
be a one-to-one enumeration of X, define
![]() by
by
![]() $f (b) = b \cup \{\alpha : x_{\alpha } \subseteq b \}$
. Clearly, f is one-to-one, so by Fact 3.12, J and
$f (b) = b \cup \{\alpha : x_{\alpha } \subseteq b \}$
. Clearly, f is one-to-one, so by Fact 3.12, J and
![]() $f (J)$
are isomorphic. Since by the first case,
$f (J)$
are isomorphic. Since by the first case,
![]() $f (J)$
is not weakly
$f (J)$
is not weakly
![]() $\pi $
-saturated, J is not weakly
$\pi $
-saturated, J is not weakly
![]() $\pi $
-saturated either. It is worth stressing that, as the following shows, there are situations when the condition on the existence of an X as above cannot be dispensed with.
$\pi $
-saturated either. It is worth stressing that, as the following shows, there are situations when the condition on the existence of an X as above cannot be dispensed with.
Observation 3.13. Suppose that
![]() $\kappa $
is a successor cardinal, and some
$\kappa $
is a successor cardinal, and some
![]() $\kappa $
-complete, fine ideal J on
$\kappa $
-complete, fine ideal J on
![]() with
with
![]() is isomorphic to some fine ideal K on
is isomorphic to some fine ideal K on
![]() $P_{\kappa } (\pi )$
. Then
$P_{\kappa } (\pi )$
. Then
![]() holds.
holds.
Proof By Observation 3.11, K is
![]() $\kappa $
-complete, and moreover
$\kappa $
-complete, and moreover
![]() . By Proposition 5.7 in [Reference Matet, Péan and Shelah39], the desired conclusion follows.
. By Proposition 5.7 in [Reference Matet, Péan and Shelah39], the desired conclusion follows.
Observation 3.13 can be applied with
![]() . More interestingly, suppose that
. More interestingly, suppose that
![]() is a strong limit cardinal of cofinality less than
is a strong limit cardinal of cofinality less than
![]() $\kappa $
. Then by a result of Shelah [Reference Shelah53],
$\kappa $
. Then by a result of Shelah [Reference Shelah53],
![]() for some
for some
![]() , so
, so
![]() and moreover since
and moreover since
![]() is nowhere
is nowhere
![]() -saturated by Fact 1.6(ii), so is
-saturated by Fact 1.6(ii), so is
![]() . Thus if GCH holds,
. Thus if GCH holds,
![]() $\kappa $
is a successor cardinal,
$\kappa $
is a successor cardinal,
![]() , and
, and
![]() fails, we cannot use the isomorphism trick to show that
fails, we cannot use the isomorphism trick to show that
![]() is not weakly
is not weakly
![]() saturated.
saturated.
Let us now turn to the case when
![]() $\kappa $
is weakly inaccessible.
$\kappa $
is weakly inaccessible.
Observation 3.14. Suppose that
![]() ,
,
![]() $\kappa $
is weakly inaccessible,
$\kappa $
is weakly inaccessible,
![]() $\sigma $
is a cardinal with
$\sigma $
is a cardinal with
![]() , and J is a
, and J is a
![]() $\sigma $
-normal, fine ideal on
$\sigma $
-normal, fine ideal on
![]() . Suppose further that there exist a closed unbounded subset C of
. Suppose further that there exist a closed unbounded subset C of
![]() $\pi $
and
$\pi $
and
![]() $D \in J^+$
such that
$D \in J^+$
such that
![]() $\delta $
is a good point for
$\delta $
is a good point for
![]() $\vec {f}$
whenever
$\vec {f}$
whenever
![]() $\delta \in C \cap E^{\pi }_{\vert b \cap \sigma \vert ^+}$
for some
$\delta \in C \cap E^{\pi }_{\vert b \cap \sigma \vert ^+}$
for some
![]() $b \in D$
. Then J is not weakly
$b \in D$
. Then J is not weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
Proof Recall that
![]() is defined by:
is defined by:
![]() $y_{\alpha }$
equals
$y_{\alpha }$
equals
![]() $\{\alpha \}$
if
$\{\alpha \}$
if
![]() $\alpha < \theta $
, and
$\alpha < \theta $
, and
![]() $\{\Phi (a, f_{\alpha } (a)) : a \in A \}$
otherwise. Define
$\{\Phi (a, f_{\alpha } (a)) : a \in A \}$
otherwise. Define
![]() by
by
Notice that
![]() $g (b) \cap \theta = b \cap \theta $
. It follows that g is one-to-one in case
$g (b) \cap \theta = b \cap \theta $
. It follows that g is one-to-one in case
![]() .
.
Claim. Let
![]() $b \in D$
. Then
$b \in D$
. Then
![]() $\vert g (b) \vert = \vert b \cap \sigma \vert $
.
$\vert g (b) \vert = \vert b \cap \sigma \vert $
.
Proof of the claim
Suppose otherwise. Pick a subset e of
![]() $g (b) \setminus \sigma $
of order-type
$g (b) \setminus \sigma $
of order-type
![]() $\vert b \cap \sigma \vert ^+$
, and put
$\vert b \cap \sigma \vert ^+$
, and put
![]() $\delta = \sup e$
. Then clearly,
$\delta = \sup e$
. Then clearly,
![]() $\delta \in C \cap E^{\pi }_{\vert b \cap \sigma \vert ^+}$
, and therefore
$\delta \in C \cap E^{\pi }_{\vert b \cap \sigma \vert ^+}$
, and therefore
![]() $\delta $
is a good point for
$\delta $
is a good point for
![]() $\vec {f}$
. But then by Observation 3.7,
$\vec {f}$
. But then by Observation 3.7,
This is a contradiction, since
![]() $\bigcup _{\alpha \in e} y_{\alpha } \subseteq b \cap \theta $
, which completes the proof of the claim.
$\bigcup _{\alpha \in e} y_{\alpha } \subseteq b \cap \theta $
, which completes the proof of the claim.
Set
![]() $K = g (J \vert D)$
and
$K = g (J \vert D)$
and
![]() $Z = g" (D)$
. Then, as is readily checked, K is a
$Z = g" (D)$
. Then, as is readily checked, K is a
![]() $\sigma $
-normal, fine ideal on
$\sigma $
-normal, fine ideal on
![]() $P_{\kappa } (\pi )$
, and moreover
$P_{\kappa } (\pi )$
, and moreover
![]() $Z \in K^{\ast }$
. By the claim,
$Z \in K^{\ast }$
. By the claim,
![]() $\vert x \vert $
=
$\vert x \vert $
=
![]() $\vert x \cap \sigma \vert $
for all
$\vert x \cap \sigma \vert $
for all
![]() $x \in Z$
, so by Fact 3.2, K is not weakly
$x \in Z$
, so by Fact 3.2, K is not weakly
![]() $\pi $
-saturated, and hence neither is J.
$\pi $
-saturated, and hence neither is J.
Corollary 3.15. Suppose that
![]() ,
,
![]() $\kappa $
is weakly inaccessible,
$\kappa $
is weakly inaccessible,
![]() $\sigma $
is a cardinal with
$\sigma $
is a cardinal with
![]() , and J is a weakly
, and J is a weakly
![]() $\pi $
-saturated,
$\pi $
-saturated,
![]() $\sigma $
-normal, fine ideal on
$\sigma $
-normal, fine ideal on
![]() .Then
.Then
![]() $\Upsilon \in J^{\ast }$
, where
$\Upsilon \in J^{\ast }$
, where
![]() $\Upsilon $
denotes the set of all
$\Upsilon $
denotes the set of all
![]() for which there are stationarily many
for which there are stationarily many
![]() $\delta < \pi $
such that (a)
$\delta < \pi $
such that (a)
![]() $\delta $
is not a good point for
$\delta $
is not a good point for
![]() ${\vec f}$
, and (b)
${\vec f}$
, and (b)
![]() $\mathrm {cf} (\delta ) = \vert b \cap \sigma \vert ^+$
.
$\mathrm {cf} (\delta ) = \vert b \cap \sigma \vert ^+$
.
Proof Suppose otherwise, and let
![]() . Let T be the set of all
. Let T be the set of all
![]() $\delta < \pi $
such that either
$\delta < \pi $
such that either
![]() $\delta \notin E^{\pi }_{\vert b \cap \sigma \vert ^+}$
for every
$\delta \notin E^{\pi }_{\vert b \cap \sigma \vert ^+}$
for every
![]() $b \in D$
, or
$b \in D$
, or
![]() $\delta $
is a good point for
$\delta $
is a good point for
![]() $\vec {f}$
. Then
$\vec {f}$
. Then
![]() $\pi \setminus T$
must be stationary. Hence we may find
$\pi \setminus T$
must be stationary. Hence we may find
![]() $\mu < \pi $
, and a stationary subset W of
$\mu < \pi $
, and a stationary subset W of
![]() $\pi \setminus T$
, such that (a)
$\pi \setminus T$
, such that (a)
![]() $\mu = \vert b \cap \sigma \vert ^+$
for some
$\mu = \vert b \cap \sigma \vert ^+$
for some
![]() $b \in D$
, and (b)
$b \in D$
, and (b)
![]() $W \subseteq E^{\pi }_{\mu }$
. Notice that for any
$W \subseteq E^{\pi }_{\mu }$
. Notice that for any
![]() $\delta \in W$
,
$\delta \in W$
,
![]() $\delta $
is not a good point for
$\delta $
is not a good point for
![]() $\vec {f}$
. Thus
$\vec {f}$
. Thus
![]() $b \in \Upsilon $
. Contradiction.
$b \in \Upsilon $
. Contradiction.
The corollary extends several known results, including one by Shelah (see [Reference Eisworth9, Theorem 4.63]) asserting that above a supercompact
![]() $\chi $
, there is no good scale at any cardinal
$\chi $
, there is no good scale at any cardinal
![]() $\rho $
of cofinality smaller than
$\rho $
of cofinality smaller than
![]() $\chi $
, and a more detailed result of Sinapova [Reference Sinapova57, Lemma 8] for the special case when
$\chi $
, and a more detailed result of Sinapova [Reference Sinapova57, Lemma 8] for the special case when
![]() $\rho < \chi ^{+ \chi }$
.
$\rho < \chi ^{+ \chi }$
.
4 The function
 $\psi $
$\psi $
Throughout the section it is assumed that
![]() . We need a new method to handle situations when the results established so far do not apply. In this quest the function
. We need a new method to handle situations when the results established so far do not apply. In this quest the function
![]() $\psi $
considered in this section will play a key role.
$\psi $
considered in this section will play a key role.
Define
![]() $\varphi : P_{\theta } (\pi ) \rightarrow \prod A$
by:
$\varphi : P_{\theta } (\pi ) \rightarrow \prod A$
by:
![]() $\varphi (w) (a)$
equals
$\varphi (w) (a)$
equals
![]() $\sup (w \cap a)$
if
$\sup (w \cap a)$
if
![]() $\sup (w \cap a) < a$
, and
$\sup (w \cap a) < a$
, and
![]() $0$
otherwise. Further define
$0$
otherwise. Further define
![]() $\psi : P_{\theta } (\pi ) \rightarrow \pi $
by
$\psi : P_{\theta } (\pi ) \rightarrow \pi $
by
![]() $\psi (w) =$
the least
$\psi (w) =$
the least
![]() $\alpha $
such that
$\alpha $
such that
![]() .
.
To show that an ideal K on
![]() is not weakly
is not weakly
![]() $\pi $
-saturated, it will suffice to prove that the ideal
$\pi $
-saturated, it will suffice to prove that the ideal
![]() on
on
![]() $\pi $
is (included in some ideal on
$\pi $
is (included in some ideal on
![]() $\pi $
that is) not weakly
$\pi $
that is) not weakly
![]() $\pi $
-saturated. As a first step, in this section we compare
$\pi $
-saturated. As a first step, in this section we compare
![]() $\psi \vert P_{\kappa } (\pi )$
and the sup function on
$\psi \vert P_{\kappa } (\pi )$
and the sup function on
![]() $P_{\kappa } (\pi )$
. The main results are Observation 4.7, which will be used in Section 5, and Observation 4.3.
$P_{\kappa } (\pi )$
. The main results are Observation 4.7, which will be used in Section 5, and Observation 4.3.
A subset C of
![]() $P_{\kappa } (\pi )$
is strongly closed if
$P_{\kappa } (\pi )$
is strongly closed if
![]() $\bigcup X \in C$
for all
$\bigcup X \in C$
for all
![]() $X \in P_{\kappa }(C) \setminus \{\emptyset \}$
.
$X \in P_{\kappa }(C) \setminus \{\emptyset \}$
.
![]() $SNS_{\kappa , \pi }$
denotes the collection of all
$SNS_{\kappa , \pi }$
denotes the collection of all
![]() $B \subseteq P_{\kappa }(\pi )$
such that
$B \subseteq P_{\kappa }(\pi )$
such that
![]() $B \cap C = \emptyset $
for some strongly closed C in
$B \cap C = \emptyset $
for some strongly closed C in
![]() $I^+_{\kappa , \pi }$
. It is easy to see that
$I^+_{\kappa , \pi }$
. It is easy to see that
![]() $SNS_{\kappa , \pi }$
is a
$SNS_{\kappa , \pi }$
is a
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() $P_{\kappa } (\pi )$
. Furthermore,
$P_{\kappa } (\pi )$
. Furthermore,
![]() $SNS_{\kappa , \pi } \subset NS_{\kappa , \pi }$
.
$SNS_{\kappa , \pi } \subset NS_{\kappa , \pi }$
.
Observation 4.1.
![]() $\{x \in P_{\kappa } (\pi ) : \psi (x) \geq \sup x\} \in SNS^{\ast }_{\kappa ,\pi }$
.
$\{x \in P_{\kappa } (\pi ) : \psi (x) \geq \sup x\} \in SNS^{\ast }_{\kappa ,\pi }$
.
Proof It suffices to note that
![]() $\{x \in P_{\kappa } (\pi ) : \forall \xi \in x (ran (f_{\xi }) \subseteq x)\} \in SNS^{\ast }_{\kappa ,\pi }$
.
$\{x \in P_{\kappa } (\pi ) : \forall \xi \in x (ran (f_{\xi }) \subseteq x)\} \in SNS^{\ast }_{\kappa ,\pi }$
.
Let
![]() $\mu $
be a regular cardinal less than
$\mu $
be a regular cardinal less than
![]() $\kappa $
. An ideal K on
$\kappa $
. An ideal K on
![]() $P_{\kappa } (\pi )$
is
$P_{\kappa } (\pi )$
is
![]() $(\mu , \kappa )$
-normal if for any
$(\mu , \kappa )$
-normal if for any
![]() $G \in K^+$
and any
$G \in K^+$
and any
![]() $k : G \rightarrow P_{\mu } (\pi )$
with the property that
$k : G \rightarrow P_{\mu } (\pi )$
with the property that
![]() $k (x) \subseteq x$
for every
$k (x) \subseteq x$
for every
![]() $x \in G$
, there is d in
$x \in G$
, there is d in
![]() $P_{\kappa } (\pi )$
and
$P_{\kappa } (\pi )$
and
![]() $H \in K^+ \cap P (G)$
such that
$H \in K^+ \cap P (G)$
such that
![]() $f (x) \subseteq d$
for all
$f (x) \subseteq d$
for all
![]() $x \in H$
. We let
$x \in H$
. We let
![]() denote the smallest fine,
denote the smallest fine,
![]() $\kappa $
-complete,
$\kappa $
-complete,
![]() $(\mu , \kappa )$
-normal ideal on
$(\mu , \kappa )$
-normal ideal on
![]() . As observed in [Reference Matet33], the set of all
. As observed in [Reference Matet33], the set of all
![]() $x \in P_{\kappa } (\pi )$
such that
$x \in P_{\kappa } (\pi )$
such that
![]() $\sup e \in x$
for all
$\sup e \in x$
for all
![]() $e \in P_{\mu } (x)$
lies in
$e \in P_{\mu } (x)$
lies in
![]() $NS_{\mu , \kappa , \pi }^{\ast }$
. Furthermore, the set of all
$NS_{\mu , \kappa , \pi }^{\ast }$
. Furthermore, the set of all
![]() $x \in P_{\kappa } (\pi )$
such that
$x \in P_{\kappa } (\pi )$
such that
![]() $\sup x$
is a limit ordinal of cofinality
$\sup x$
is a limit ordinal of cofinality
![]() $\mu $
lies in
$\mu $
lies in
![]() $NS_{\mu , \kappa , \pi }^+$
.
$NS_{\mu , \kappa , \pi }^+$
.
A subset C of
![]() $P_{\kappa } (\pi )$
is
$P_{\kappa } (\pi )$
is
![]() $\mu $
-closed if
$\mu $
-closed if
![]() $\bigcup _{i < \mu } c_i \in C$
for every increasing sequence
$\bigcup _{i < \mu } c_i \in C$
for every increasing sequence
![]() in
in
![]() $(C, \subset )$
. A subset D of
$(C, \subset )$
. A subset D of
![]() $P_{\kappa } (\pi )$
is a
$P_{\kappa } (\pi )$
is a
![]() $\mu $
-club if it is a
$\mu $
-club if it is a
![]() $\mu $
-closed, cofinal subset of
$\mu $
-closed, cofinal subset of
![]() $P_{\kappa } (\pi )$
. We let
$P_{\kappa } (\pi )$
. We let
![]() $N\mu $
-
$N\mu $
-
![]() $S_{\kappa ,\pi }$
be the set of all
$S_{\kappa ,\pi }$
be the set of all
![]() $H \subseteq P_{\kappa } (\pi )$
such that
$H \subseteq P_{\kappa } (\pi )$
such that
![]() $H \cap D = \emptyset $
for some
$H \cap D = \emptyset $
for some
![]() $\mu $
-club
$\mu $
-club
![]() $D \subseteq P_{\kappa } (\pi )$
. Let
$D \subseteq P_{\kappa } (\pi )$
. Let
![]() $Y_{\mu }^{\kappa , \pi }$
denote the set of all nonempty
$Y_{\mu }^{\kappa , \pi }$
denote the set of all nonempty
![]() $x \in P_{\kappa }(\pi )$
such that:
$x \in P_{\kappa }(\pi )$
such that:
-
• For any
 $\alpha \in x$
,
$\alpha \in x$
,
 $\alpha + 1 \in x$
.
$\alpha + 1 \in x$
. -
• For any regular infinite cardinal
 $\sigma \in \kappa \setminus \{\mu \}$
, and any increasing sequence
$\sigma \in \kappa \setminus \{\mu \}$
, and any increasing sequence
 of elements of x,
of elements of x,
 $\sup \{\beta _{\xi } : \xi < \sigma \} \in x$
.
$\sup \{\beta _{\xi } : \xi < \sigma \} \in x$
.
Notice that for any
![]() $x \in Y_{\mu }^{\kappa , \pi }$
and any cardinal
$x \in Y_{\mu }^{\kappa , \pi }$
and any cardinal
![]() of cofinality greater than or equal to
of cofinality greater than or equal to
![]() $\kappa $
,
$\kappa $
,
![]() $\sup (x \cap \tau )$
is a limit ordinal of cofinality
$\sup (x \cap \tau )$
is a limit ordinal of cofinality
![]() $\mu $
. It is remarked in [Reference Matet30] that
$\mu $
. It is remarked in [Reference Matet30] that
![]() $Y^{\kappa , \pi }_{\mu }$
and the set
$Y^{\kappa , \pi }_{\mu }$
and the set
![]() $\{x \in P_{\kappa } (\pi ):\vert x\vert = \vert x \cap \kappa \vert \geq \mu \}$
are both
$\{x \in P_{\kappa } (\pi ):\vert x\vert = \vert x \cap \kappa \vert \geq \mu \}$
are both
![]() $\mu $
-clubs.
$\mu $
-clubs.
Lemma 4.2.
-
(i) Suppose that
 $\vert A \vert < \mu $
. Then
$\vert A \vert < \mu $
. Then
 .
. -
(ii) Suppose that I is
 $\mu ^+$
-complete. Then
$\mu ^+$
-complete. Then
 -
-
 $S_{\kappa ,\pi })^{\ast }$
.
$S_{\kappa ,\pi })^{\ast }$
.
Proof (i): Suppose toward a contradiction that the set
![]() $X = \{x \in P_{\kappa } (\pi ) : \psi (x)> \sup x\}$
lies in
$X = \{x \in P_{\kappa } (\pi ) : \psi (x)> \sup x\}$
lies in
![]() $NS_{\mu , \kappa , \pi }^+$
. For
$NS_{\mu , \kappa , \pi }^+$
. For
![]() $x \in X$
, set
$x \in X$
, set
![]() $e_x = \{a \in A : \sup (x \cap a)> f_{\sup x} (a)\}$
, and select
$e_x = \{a \in A : \sup (x \cap a)> f_{\sup x} (a)\}$
, and select
![]() $s_x : e_x \rightarrow x$
so that
$s_x : e_x \rightarrow x$
so that
![]() $f_{\sup x} (a) < s_x (a) < a$
for all
$f_{\sup x} (a) < s_x (a) < a$
for all
![]() $a \in e_x$
. There must be
$a \in e_x$
. There must be
![]() $T \in NS_{\mu , \kappa , \pi }^+ \cap P (X)$
and
$T \in NS_{\mu , \kappa , \pi }^+ \cap P (X)$
and
![]() such that
such that
![]() $ran (s_x) \subseteq w$
for all
$ran (s_x) \subseteq w$
for all
![]() $x \in T$
. Pick
$x \in T$
. Pick
![]() $x \in T$
such that
$x \in T$
such that
![]() . Then
. Then
![]() . On the other hand for any
. On the other hand for any
![]() $a \in e_x$
,
$a \in e_x$
,
![]() $\sup (w \cap a) \geq s_x (a)> f_{\sup x} (a)$
. This is a contradiction, since
$\sup (w \cap a) \geq s_x (a)> f_{\sup x} (a)$
. This is a contradiction, since
![]() $e_x \in I^+$
.
$e_x \in I^+$
.
(ii): We first establish the following.
Claim. Let
![]() be an increasing sequence in
be an increasing sequence in
![]() $(P_{\kappa } (\pi ), \subset )$
. Then
$(P_{\kappa } (\pi ), \subset )$
. Then
![]() .
.
Proof of the claim
For
![]() $i < \mu $
, put
$i < \mu $
, put
![]() $v_i = \{a \in A : \sup (c_i \cap a)> f_{\psi (c_i)} (a)\}$
and
$v_i = \{a \in A : \sup (c_i \cap a)> f_{\psi (c_i)} (a)\}$
and
![]() $w_i = \{a \in A : f_{\psi (c_i)} (a)> f_{\sup \{\psi (c_r) : r < \mu \}} (a)\}$
. Then
$w_i = \{a \in A : f_{\psi (c_i)} (a)> f_{\sup \{\psi (c_r) : r < \mu \}} (a)\}$
. Then
![]() $\bigcup _{i < \mu } (v_i \cup w_i) \in I$
, and moreover for any
$\bigcup _{i < \mu } (v_i \cup w_i) \in I$
, and moreover for any
![]() $a \in A \setminus (\bigcup _{i < \mu } (v_i \cup w_i))$
,
$a \in A \setminus (\bigcup _{i < \mu } (v_i \cup w_i))$
,
![]() , which completes the proof of the claim.
, which completes the proof of the claim.
By the claim, the set
![]() is
is
![]() $\mu $
-closed. To show that it is cofinal, fix
$\mu $
-closed. To show that it is cofinal, fix
![]() $z \in P_{\kappa } (\pi )$
. Inductively define
$z \in P_{\kappa } (\pi )$
. Inductively define
![]() $c_i \in P_{\kappa } (\pi )$
for
$c_i \in P_{\kappa } (\pi )$
for
![]() $i < \mu $
so that:
$i < \mu $
so that:
-
•
 $c_0 = z$
.
$c_0 = z$
. -
•
 $c_i \cup \{\psi (c_i)\} \subset c_{i + 1}$
for all
$c_i \cup \{\psi (c_i)\} \subset c_{i + 1}$
for all
 $i < \mu $
.
$i < \mu $
.
Put
![]() $c = \bigcup _{i < \mu } c_i$
. Then clearly,
$c = \bigcup _{i < \mu } c_i$
. Then clearly,
![]() $z \subseteq c$
. Moreover by the claim,
$z \subseteq c$
. Moreover by the claim,
![]() , so
, so
![]() $c \in C$
.
$c \in C$
.
Observation 4.3.
-
(i) Suppose that
 $\vert A \vert < \mu $
. Then
$\vert A \vert < \mu $
. Then
 $ \{x \in P_{\kappa } (\pi ) : \psi (x) = \sup x\} \in NS_{\mu , \kappa , \pi }^{\ast }$
.
$ \{x \in P_{\kappa } (\pi ) : \psi (x) = \sup x\} \in NS_{\mu , \kappa , \pi }^{\ast }$
. -
(ii) Suppose that I is
 $\mu ^+$
-complete. Then
$\mu ^+$
-complete. Then
 $ \{x \in P_{\kappa } (\pi ) : \psi (x) = \sup x\} \in (N\mu $
-
$ \{x \in P_{\kappa } (\pi ) : \psi (x) = \sup x\} \in (N\mu $
-
 $S_{\kappa ,\pi })^{\ast }$
.
$S_{\kappa ,\pi })^{\ast }$
.
Observation 4.3 is of no use in the (critical) case when
![]() $\vert A \vert = \mu $
, which must be handled separately. In what follows we present Shelah’s approach, which is based on Namba combinatorics (that is, properties of trees of height
$\vert A \vert = \mu $
, which must be handled separately. In what follows we present Shelah’s approach, which is based on Namba combinatorics (that is, properties of trees of height
![]() $\omega $
). So from here on to Observation 4.7 we suppose that (
$\omega $
). So from here on to Observation 4.7 we suppose that (
![]() $\mathrm {cf} (\theta ) = \omega $
and)
$\mathrm {cf} (\theta ) = \omega $
and)
![]() $\vert A \vert = \aleph _0$
. Let
$\vert A \vert = \aleph _0$
. Let
![]() be a one-to-one enumeration of A, and set
be a one-to-one enumeration of A, and set
![]() ${\cal I} = u (I)$
, where
${\cal I} = u (I)$
, where
![]() $u : A \rightarrow \omega $
is defined by:
$u : A \rightarrow \omega $
is defined by:
![]() $u (\theta _i) = i$
.
$u (\theta _i) = i$
.
An ideal H on
![]() $\omega $
is a P-point if for any
$\omega $
is a P-point if for any
![]() $F : \omega \rightarrow H$
, there is
$F : \omega \rightarrow H$
, there is
![]() $G \in H^{\ast }$
such that
$G \in H^{\ast }$
such that
![]() $G \cap F (j)$
is finite for all
$G \cap F (j)$
is finite for all
![]() $j < \omega $
.
$j < \omega $
.
Assume that
![]() ${\cal I}$
is a P-point (i.e., that given
${\cal I}$
is a P-point (i.e., that given
![]() $B_n \in I$
for
$B_n \in I$
for
![]() $n < \omega $
, there is
$n < \omega $
, there is
![]() $C \in I^{\ast }$
that meets each
$C \in I^{\ast }$
that meets each
![]() $B_n$
in a finite set). For
$B_n$
in a finite set). For
![]() $\alpha < \pi $
, define
$\alpha < \pi $
, define
![]() $F_{\alpha } \in \prod _{i < \omega } \theta _i$
by
$F_{\alpha } \in \prod _{i < \omega } \theta _i$
by
![]() $F_{\alpha } (i) = f_{\alpha } (\theta _i)$
.
$F_{\alpha } (i) = f_{\alpha } (\theta _i)$
.
![]() ${\cal T}_{\pi }$
denotes the collection of all nonempty
${\cal T}_{\pi }$
denotes the collection of all nonempty
![]() $T\subseteq \bigcup _{n < \omega } {}^n\pi $
such that for any
$T\subseteq \bigcup _{n < \omega } {}^n\pi $
such that for any
![]() $t \in T$
,
$t \in T$
,
![]() $\{ t \vert n : n < \mathrm {dom} (t) \} \subseteq T$
and
$\{ t \vert n : n < \mathrm {dom} (t) \} \subseteq T$
and
![]() $\vert \{\alpha < \pi : t \cup \{(\mathrm {dom} (t), \alpha )\} \in T \} \vert = \pi $
.
$\vert \{\alpha < \pi : t \cup \{(\mathrm {dom} (t), \alpha )\} \in T \} \vert = \pi $
.
Let
![]() $T \in {\mathcal T}_{\pi }$
. Set
$T \in {\mathcal T}_{\pi }$
. Set
![]() $[T] = \{ f\in {}^{\omega }\pi : \forall n < \omega (f \vert n \in T)\}$
. For
$[T] = \{ f\in {}^{\omega }\pi : \forall n < \omega (f \vert n \in T)\}$
. For
![]() $t \in T$
, put
$t \in T$
, put
![]() $T\ast t = \{ s \in T : s \subseteq t$
or
$T\ast t = \{ s \in T : s \subseteq t$
or
![]() $t \subseteq s\}$
.
$t \subseteq s\}$
.
![]() $[T]$
is endowed with the topology obtained by taking as basic open sets the members of the family
$[T]$
is endowed with the topology obtained by taking as basic open sets the members of the family
![]() $\{ [T \ast t] : t \in T \}$
.
$\{ [T \ast t] : t \in T \}$
.
Fact 4.4 [Reference Rubin and Shelah48, Lemma 2.14].
Suppose that
![]() $T \in {\cal T}_{\pi }$
,
$T \in {\cal T}_{\pi }$
,
![]() $\sigma < \pi $
is a cardinal, and
$\sigma < \pi $
is a cardinal, and
![]() $[T] = \bigcup _{\beta < \sigma } H_{\beta }$
, where each
$[T] = \bigcup _{\beta < \sigma } H_{\beta }$
, where each
![]() $H_{\beta }$
is Borel. Then there is
$H_{\beta }$
is Borel. Then there is
![]() $T' \in {\cal T}_{\pi } \cap P(T)$
and
$T' \in {\cal T}_{\pi } \cap P(T)$
and
![]() $\beta < \sigma $
such that
$\beta < \sigma $
such that
![]() $[T'] \subseteq H_{\beta }$
.
$[T'] \subseteq H_{\beta }$
.
Let
![]() $\sigma $
be a cardinal greater than
$\sigma $
be a cardinal greater than
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $\mu $
be a regular cardinal less than
$\mu $
be a regular cardinal less than
![]() $\kappa $
. For
$\kappa $
. For
![]() $Q \subseteq P_{\kappa } (\sigma )$
,
$Q \subseteq P_{\kappa } (\sigma )$
,
![]() $G_{\kappa ,\sigma }^{\mu } (Q)$
denotes the following two-person game consisting of
$G_{\kappa ,\sigma }^{\mu } (Q)$
denotes the following two-person game consisting of
![]() $\mu $
moves. At step
$\mu $
moves. At step
![]() $\alpha < \mu $
, player I selects
$\alpha < \mu $
, player I selects
![]() $a_{\alpha } \in P_{\kappa } (\sigma )$
, and II replies by playing
$a_{\alpha } \in P_{\kappa } (\sigma )$
, and II replies by playing
![]() $b_{\alpha } \in P_{\kappa } (\sigma )$
. The players must follow the rule that for
$b_{\alpha } \in P_{\kappa } (\sigma )$
. The players must follow the rule that for
![]() $\beta < \alpha < \mu $
,
$\beta < \alpha < \mu $
,
![]() $b_{\beta }\subseteq a_{\alpha } \subseteq b_{\alpha }$
. II wins if and only if
$b_{\beta }\subseteq a_{\alpha } \subseteq b_{\alpha }$
. II wins if and only if
![]() $\bigcup _{\alpha < \mu } a_{\alpha }\in Q$
.
$\bigcup _{\alpha < \mu } a_{\alpha }\in Q$
.
![]() $NG_{\kappa ,\sigma }^{\mu }$
denotes the collection of all
$NG_{\kappa ,\sigma }^{\mu }$
denotes the collection of all
![]() $Q \subseteq P_{\kappa } (\sigma )$
such that II has a winning strategy in
$Q \subseteq P_{\kappa } (\sigma )$
such that II has a winning strategy in
![]() $G_{\kappa ,\sigma }^{\mu } (P_{\kappa } (\sigma ) \setminus Q)$
.
$G_{\kappa ,\sigma }^{\mu } (P_{\kappa } (\sigma ) \setminus Q)$
.
Fact 4.5 [Reference Matet25, Reference Matet30, Reference Matet35].
-
(i)
 $NG_{\kappa ,\sigma }^{\mu }$
is a
$NG_{\kappa ,\sigma }^{\mu }$
is a
 $(\mu , \kappa )$
-normal ideal on
$(\mu , \kappa )$
-normal ideal on
 $P_{\kappa } (\sigma )$
.
$P_{\kappa } (\sigma )$
. -
(ii)
 $N\mu $
-
$N\mu $
-
 $S_{\kappa ,\sigma } \subseteq NG_{\kappa ,\sigma }^{\mu }$
.
$S_{\kappa ,\sigma } \subseteq NG_{\kappa ,\sigma }^{\mu }$
. -
(iii) Let
 $\tau> \sigma $
be a cardinal. Then
$\tau> \sigma $
be a cardinal. Then
 $NG_{\kappa ,\sigma }^{\mu } = q (NG_{\kappa ,\tau }^{\mu })$
, where
$NG_{\kappa ,\sigma }^{\mu } = q (NG_{\kappa ,\tau }^{\mu })$
, where
 $q : P_{\kappa } (\tau ) \rightarrow P_{\kappa } (\sigma )$
is defined by
$q : P_{\kappa } (\tau ) \rightarrow P_{\kappa } (\sigma )$
is defined by
 $q (x) = x \cap \sigma $
.
$q (x) = x \cap \sigma $
. -
(iv) If
 $\kappa = \omega _1$
(and
$\kappa = \omega _1$
(and
 $\mu = \omega $
), then
$\mu = \omega $
), then
 $NG_{\kappa ,\sigma }^{\mu } = NS_{\kappa ,\sigma }$
.
$NG_{\kappa ,\sigma }^{\mu } = NS_{\kappa ,\sigma }$
. -
(v) There is a one-to-one function
 $y : \sigma ^{< \kappa } \rightarrow P_{\kappa } (\sigma )$
such that (a) for any
$y : \sigma ^{< \kappa } \rightarrow P_{\kappa } (\sigma )$
such that (a) for any
 $\beta \in \sigma $
,
$\beta \in \sigma $
,
 $\beta \in y (\beta )$
, and
$\beta \in y (\beta )$
, and
 $(b) \ NG^{\omega }_{\kappa ,\sigma } = {\overline y} (NS_{\omega _1, \sigma ^{< \kappa }})$
, where
$(b) \ NG^{\omega }_{\kappa ,\sigma } = {\overline y} (NS_{\omega _1, \sigma ^{< \kappa }})$
, where
 ${\overline y} : P_{\omega _1} ( \sigma ^{< \kappa } )\rightarrow P_{\kappa } (\sigma )$
is defined by
${\overline y} : P_{\omega _1} ( \sigma ^{< \kappa } )\rightarrow P_{\kappa } (\sigma )$
is defined by
 ${\overline y} (x) = \bigcup _{\delta \in x} y(\delta )$
.
${\overline y} (x) = \bigcup _{\delta \in x} y(\delta )$
.
The following generalizes a result of Shelah [Reference Shelah54] (in which
![]() $\pi = \theta ^+$
and
$\pi = \theta ^+$
and
![]() ${\cal I} = I_{\omega }$
).
${\cal I} = I_{\omega }$
).
Lemma 4.6. Let
![]() $S \in NS_{\pi }^+ \cap P (E_{\omega }^{\pi })$
. Then
$S \in NS_{\pi }^+ \cap P (E_{\omega }^{\pi })$
. Then
Proof Fix a closed unbounded subset C of
![]() $P_{\omega _1} (\pi )$
. Pick
$P_{\omega _1} (\pi )$
. Pick

so that:
-
• For
 $h : \omega \rightarrow \pi $
,
$h : \omega \rightarrow \pi $
,
 $k (h) = \bigcup _{n < \omega } k (h \vert n)$
.
$k (h) = \bigcup _{n < \omega } k (h \vert n)$
. -
• For
 $t : m + 1 \rightarrow \pi $
,
$t : m + 1 \rightarrow \pi $
,
 $\{ t (m) \} \cup k (t \vert m) \subseteq k (t)$
.
$\{ t (m) \} \cup k (t \vert m) \subseteq k (t)$
.
Clearly, if
![]() $h \in {}^{\omega }\pi $
,
$h \in {}^{\omega }\pi $
,
![]() $i \in \omega $
, and
$i \in \omega $
, and
![]() $\beta \in \theta _i$
are such that
$\beta \in \theta _i$
are such that
![]() $\varphi (k(h)) (\theta _i)> \beta $
, then
$\varphi (k(h)) (\theta _i)> \beta $
, then
![]() $\varphi (k(h \vert m)) (\theta _i)> \beta $
for some m with
$\varphi (k(h \vert m)) (\theta _i)> \beta $
for some m with
![]() . Hence, using Fact 4.4, we may construct inductively
. Hence, using Fact 4.4, we may construct inductively
![]() $T \in {\cal T}_{\pi }$
and
$T \in {\cal T}_{\pi }$
and
![]() $\chi : T \rightarrow \theta $
such that for any
$\chi : T \rightarrow \theta $
such that for any
![]() $t \in T$
and any
$t \in T$
and any
![]() $h \in [T\ast t]$
,
$h \in [T\ast t]$
,
![]() .
.
We define a strategy
![]() $\tau $
for player II in
$\tau $
for player II in
![]() $G_{\kappa ,\pi }^{\omega } (P_{\kappa } (\pi ))$
as follows. Consider a play of the game where I’s successive moves are
$G_{\kappa ,\pi }^{\omega } (P_{\kappa } (\pi ))$
as follows. Consider a play of the game where I’s successive moves are
![]() $d_0, d_1, \dots $
. Using her strategy
$d_0, d_1, \dots $
. Using her strategy
![]() $\tau $
, II will successively play
$\tau $
, II will successively play
![]() $e_0, e_1, \dots $
so that:
$e_0, e_1, \dots $
so that:
-
•
 $d_j \cup \{ \psi (d_j) \} \subseteq e_j$
.
$d_j \cup \{ \psi (d_j) \} \subseteq e_j$
. -
•
 $\sup e_j$
is an infinite limit ordinal greater than
$\sup e_j$
is an infinite limit ordinal greater than
 $\sup d_j$
.
$\sup d_j$
. -
• For any
 $t \in T$
with
$t \in T$
with
 $\mathrm {ran} (t) \subseteq e_j$
,
$\mathrm {ran} (t) \subseteq e_j$
,
 $\chi (t) \in e_j$
, and moreover
$\chi (t) \in e_j$
, and moreover  $$ \begin{align*} \sup \{ \gamma \in e_j : t \cup \{ (\mathrm{dom} (t), \gamma)\} \in T \} = \sup e_j. \end{align*} $$
$$ \begin{align*} \sup \{ \gamma \in e_j : t \cup \{ (\mathrm{dom} (t), \gamma)\} \in T \} = \sup e_j. \end{align*} $$
Now
![]() $\{ b \in P_{\omega _1} (\pi ) : \sup b \in S \} \in NS_{\omega _1, \pi }^+$
, so by Fact 4.5(iv),
$\{ b \in P_{\omega _1} (\pi ) : \sup b \in S \} \in NS_{\omega _1, \pi }^+$
, so by Fact 4.5(iv),
![]() $\tau $
is not a winning strategy for II in
$\tau $
is not a winning strategy for II in
![]() $G_{\kappa ,\pi }^{\omega } (\{ b \in P_{\omega _1} (\pi ) : \sup b \notin S \})$
. Hence there must be a play of this game where I’s successive moves are
$G_{\kappa ,\pi }^{\omega } (\{ b \in P_{\omega _1} (\pi ) : \sup b \notin S \})$
. Hence there must be a play of this game where I’s successive moves are
![]() $d_0, d_1, \dots $
, II successively plays
$d_0, d_1, \dots $
, II successively plays
![]() $e_0, e_1, \dots $
using her strategy
$e_0, e_1, \dots $
using her strategy
![]() $\tau $
, and I wins. Thus
$\tau $
, and I wins. Thus
![]() $\sup e \in S$
, where
$\sup e \in S$
, where
![]() $e = \bigcup _{j < \omega } e_j$
. Put
$e = \bigcup _{j < \omega } e_j$
. Put
![]() $\delta = \sup e$
. Notice that for any
$\delta = \sup e$
. Notice that for any
![]() $j < \omega $
,
$j < \omega $
,
![]() . It follows that
. It follows that
![]() , since
, since
![]() $\psi (d_{j + 1}) \in e_{j + 1}$
. Define
$\psi (d_{j + 1}) \in e_{j + 1}$
. Define
![]() $\unicode{x0142} :\omega \rightarrow {\cal I }$
by
$\unicode{x0142} :\omega \rightarrow {\cal I }$
by
![]() $\unicode{x0142} (j) = \{ i < \omega : \varphi (e_j) (\theta _i)> F_{\delta } (i) \}$
. By P-pointness of
$\unicode{x0142} (j) = \{ i < \omega : \varphi (e_j) (\theta _i)> F_{\delta } (i) \}$
. By P-pointness of
![]() ${\cal I}$
, there must be
${\cal I}$
, there must be
![]() $G \in {\cal I}^{\ast }$
such that
$G \in {\cal I}^{\ast }$
such that
![]() $G \cap \unicode{x0142} (j)$
is finite for all
$G \cap \unicode{x0142} (j)$
is finite for all
![]() $j < \omega $
. Pick an increasing sequence
$j < \omega $
. Pick an increasing sequence
![]() $< n_j : j < \omega>$
of elements of
$< n_j : j < \omega>$
of elements of
![]() $\omega $
so that
$\omega $
so that
![]() whenever
whenever
![]() $j < \omega $
and
$j < \omega $
and
![]() $i \in G \setminus n_j$
. Now construct
$i \in G \setminus n_j$
. Now construct
![]() $h \in [T]$
so that
$h \in [T]$
so that
![]() $\{h (i) : i < n_0\} \subseteq e_0$
, and for any
$\{h (i) : i < n_0\} \subseteq e_0$
, and for any
![]() $j < \omega $
:
$j < \omega $
:
-
•
 $h(i) \in e_j$
whenever
$h(i) \in e_j$
whenever
 ;
; -
•
 $h(n_{j + 1})> \sup (e_j)$
.
$h(n_{j + 1})> \sup (e_j)$
.
Put
![]() $b = k (h)$
. Then clearly,
$b = k (h)$
. Then clearly,
![]() $b \in C$
, and moreover
$b \in C$
, and moreover
![]() $\mathrm {ran} (h) \subseteq b$
. It follows that
$\mathrm {ran} (h) \subseteq b$
. It follows that
![]() .
.
Claim. Let
![]() $j < \omega $
and
$j < \omega $
and
![]() $i \in G$
with
$i \in G$
with
![]() . Then
. Then
![]() .
.
Proof of the claim
Since
![]() $\mathrm {ran} (h \vert i) \subseteq e_j$
,
$\mathrm {ran} (h \vert i) \subseteq e_j$
,
![]() $\chi (h \vert i) \in e_j \cap \theta _i$
. Hence,
$\chi (h \vert i) \in e_j \cap \theta _i$
. Hence,
![]() , which completes the proof of the claim.
, which completes the proof of the claim.
It follows from the claim that
![]() . Thus,
. Thus,
![]() , so
, so
![]() $\sup b = \psi (b)$
.
$\sup b = \psi (b)$
.
Observation 4.7. Let
![]() $S \in NS_{\pi }^+ \cap P (E_{\omega }^{\pi })$
. Then
$S \in NS_{\pi }^+ \cap P (E_{\omega }^{\pi })$
. Then
Proof For
![]() $\kappa = \omega _1$
, this is just Lemma 4.6. Let us now assume that
$\kappa = \omega _1$
, this is just Lemma 4.6. Let us now assume that
![]() $\kappa> \omega _1$
. Set
$\kappa> \omega _1$
. Set
Then by Fact 4.5(iii) and (iv) and Lemma 4.6,
![]() $Q \in NS_{\omega _1,\pi ^{< \kappa }}^+$
. By Fact 4.5(v), we may find
$Q \in NS_{\omega _1,\pi ^{< \kappa }}^+$
. By Fact 4.5(v), we may find
![]() $y : \pi ^{< \kappa } \rightarrow P_{\kappa } (\pi )$
such that (a) for any
$y : \pi ^{< \kappa } \rightarrow P_{\kappa } (\pi )$
such that (a) for any
![]() $\beta \in \pi $
,
$\beta \in \pi $
,
![]() $\beta \in y (\beta )$
, and (b)
$\beta \in y (\beta )$
, and (b)
![]() $NG^{\omega }_{\kappa ,\pi } = {\overline y} (NS_{\omega _1, \pi ^{< \kappa }})$
, where
$NG^{\omega }_{\kappa ,\pi } = {\overline y} (NS_{\omega _1, \pi ^{< \kappa }})$
, where
![]() ${\overline y} : P_{\omega _1} ( \pi ^{< \kappa } )\rightarrow P_{\kappa } (\pi )$
is defined by
${\overline y} : P_{\omega _1} ( \pi ^{< \kappa } )\rightarrow P_{\kappa } (\pi )$
is defined by
![]() ${\overline y} (x) = \bigcup _{\delta \in x} y(\delta )$
. Note that
${\overline y} (x) = \bigcup _{\delta \in x} y(\delta )$
. Note that
![]() $x \cap \pi \subseteq {\overline y} (x)$
for all
$x \cap \pi \subseteq {\overline y} (x)$
for all
![]() $x \in P_{\omega _1} (\pi ^{< \kappa })$
. Put
$x \in P_{\omega _1} (\pi ^{< \kappa })$
. Put
![]() $c = \{ i < \omega : \theta _i \geq \kappa \}$
. Note that
$c = \{ i < \omega : \theta _i \geq \kappa \}$
. Note that
![]() $c \in {\cal I}^{\ast }$
. Let C denote the set of all infinite
$c \in {\cal I}^{\ast }$
. Let C denote the set of all infinite
![]() $x \in P_{\omega _1} (\pi ^{< \kappa })$
such that:
$x \in P_{\omega _1} (\pi ^{< \kappa })$
such that:
-
• For any
 $\eta \in x$
and any
$\eta \in x$
and any
 $i \in c$
, there is
$i \in c$
, there is
 $\beta \in x \cap \theta _i$
with
$\beta \in x \cap \theta _i$
with
 $\sup (y (\eta ) \cap \theta _i) < \beta $
.
$\sup (y (\eta ) \cap \theta _i) < \beta $
. -
• For any
 $\eta \in x$
, there is
$\eta \in x$
, there is
 $\beta \in x \cap \pi $
with
$\beta \in x \cap \pi $
with
 $\sup (y (\eta )) < \beta $
.
$\sup (y (\eta )) < \beta $
.
Then clearly, C is a closed unbounded subset of
![]() $P_{\omega _1} (\pi ^{< \kappa })$
. Furthermore for any
$P_{\omega _1} (\pi ^{< \kappa })$
. Furthermore for any
![]() $x \in C$
,
$x \in C$
,
![]() $\psi (x \cap \pi ) = \psi ({\overline y} (x))$
and
$\psi (x \cap \pi ) = \psi ({\overline y} (x))$
and
![]() $\sup (x \cap \pi ) = \sup ({\overline y} (x))$
. Thus
$\sup (x \cap \pi ) = \sup ({\overline y} (x))$
. Thus
![]() ${\overline y}" (Q \cap C)$
lies in
${\overline y}" (Q \cap C)$
lies in
![]() $(NG^{\omega }_{\kappa ,\pi })^+$
, and moreover it is included in the set
$(NG^{\omega }_{\kappa ,\pi })^+$
, and moreover it is included in the set
![]() $\{ w \in P_{\kappa } (\pi ) : \sup w \in S$
and
$\{ w \in P_{\kappa } (\pi ) : \sup w \in S$
and
![]() $\psi (w)= \sup w\}$
.
$\psi (w)= \sup w\}$
.
For any
![]() $S \in (NS_{\pi } \vert E_{\omega }^{\pi })^+$
,
$S \in (NS_{\pi } \vert E_{\omega }^{\pi })^+$
,
![]() $\{ w \in P_{\kappa } (\pi ) : \psi (w) \in S\} \in (NG^{\omega }_{\kappa ,\pi })^+$
by Observation 4.7, and therefore
$\{ w \in P_{\kappa } (\pi ) : \psi (w) \in S\} \in (NG^{\omega }_{\kappa ,\pi })^+$
by Observation 4.7, and therefore
![]() by Fact 4.5(iii). Thus
by Fact 4.5(iii). Thus
![]() . Let us observe that it is not necessarily the case that
. Let us observe that it is not necessarily the case that
![]() $\psi " W \in NS_{\pi }^+$
for all
$\psi " W \in NS_{\pi }^+$
for all
![]() . To see this, recall that the bounding number
. To see this, recall that the bounding number
![]() $\mathfrak {b}_{\pi }$
denotes the least cardinality of any
$\mathfrak {b}_{\pi }$
denotes the least cardinality of any
![]() $F \subseteq {}^{\pi } \pi $
with the property that there is no
$F \subseteq {}^{\pi } \pi $
with the property that there is no
![]() $g \in {}^{\pi } \pi $
such that
$g \in {}^{\pi } \pi $
such that
![]() $\vert \{\beta < \pi : f (\beta ) \geq g (\beta \} \vert < \pi $
for all
$\vert \{\beta < \pi : f (\beta ) \geq g (\beta \} \vert < \pi $
for all
![]() $f \in F$
.
$f \in F$
.
Fact 4.8 [Reference Balcar and Simon2].
![]() $\mathfrak {b}_{\pi }$
is the least cardinality of any collection F of closed unbounded subsets of
$\mathfrak {b}_{\pi }$
is the least cardinality of any collection F of closed unbounded subsets of
![]() $\pi $
such that for any
$\pi $
such that for any
![]() $B \in [\pi ]^{\pi }$
, there is
$B \in [\pi ]^{\pi }$
, there is
![]() $C \in F$
with
$C \in F$
with
![]() $\vert B \setminus C \vert = \pi $
.
$\vert B \setminus C \vert = \pi $
.
Observation 4.9. Let K be an ideal on
![]() such that
such that
![]() and
and
![]() $\overline {\mathrm {cof}} (K) < \mathfrak {b}_{\pi }$
. Then there is
$\overline {\mathrm {cof}} (K) < \mathfrak {b}_{\pi }$
. Then there is
![]() $D \in NS_{\pi }^{\ast }$
such that
$D \in NS_{\pi }^{\ast }$
such that
![]() .
.
Proof Put
![]() $\sigma = \overline {\mathrm {cof}} (K)$
. We have that
$\sigma = \overline {\mathrm {cof}} (K)$
. We have that
![]() . Now
. Now
![]() , so we may find
, so we may find
![]() $C_{\alpha } \in NS_{\pi }^{\ast }$
for
$C_{\alpha } \in NS_{\pi }^{\ast }$
for
![]() $\alpha < \sigma $
such that for any
$\alpha < \sigma $
such that for any
![]() , there is
, there is
![]() $z \in P_{\kappa } (\sigma ) \setminus \{\emptyset \}$
with the property that
$z \in P_{\kappa } (\sigma ) \setminus \{\emptyset \}$
with the property that
![]() $(\bigcap _{\alpha \in z} C_{\alpha }\big ) \cap E_{\omega }^{\pi } \subseteq X$
. Using Fact 4.8, select
$(\bigcap _{\alpha \in z} C_{\alpha }\big ) \cap E_{\omega }^{\pi } \subseteq X$
. Using Fact 4.8, select
![]() $D \in NS_{\pi }^{\ast }$
so that
$D \in NS_{\pi }^{\ast }$
so that
![]() $\vert D \setminus C_{\alpha } \vert < \pi $
for every
$\vert D \setminus C_{\alpha } \vert < \pi $
for every
![]() $\alpha < \sigma $
. Now fix
$\alpha < \sigma $
. Now fix
![]() $T \in I_{\pi }^+ \cap P(D\cap E_{\omega }^{\pi })$
. Clearly
$T \in I_{\pi }^+ \cap P(D\cap E_{\omega }^{\pi })$
. Clearly
![]() $T \setminus \bigcup _{\alpha \in z} (D \setminus C_{\alpha }) \subseteq \bigcap _{\alpha \in z} C_{\alpha }$
for every
$T \setminus \bigcup _{\alpha \in z} (D \setminus C_{\alpha }) \subseteq \bigcap _{\alpha \in z} C_{\alpha }$
for every
![]() $z \in P_{\kappa } (\sigma ) \setminus \{\emptyset \}$
, so
$z \in P_{\kappa } (\sigma ) \setminus \{\emptyset \}$
, so
![]() $T \cap X \not = \emptyset $
for all
$T \cap X \not = \emptyset $
for all
![]() . Hence
. Hence
![]() .
.
Set
![]() and
and
![]() . Then
. Then
![]() , so by Observation 4.9, there must be
, so by Observation 4.9, there must be
![]() $D \in NS_{\pi }^{\ast }$
such that
$D \in NS_{\pi }^{\ast }$
such that
![]() . Select T in
. Select T in
![]() $I_{\pi }^+ \cap NS_{\pi } \cap P (D \cap E^{\pi }_{\omega })$
, and put
$I_{\pi }^+ \cap NS_{\pi } \cap P (D \cap E^{\pi }_{\omega })$
, and put
![]() . Then clearly,
. Then clearly,
![]() , and moreover
, and moreover
![]() $\psi " W \in NS_{\pi }$
.
$\psi " W \in NS_{\pi }$
.
Another comment is in order. In contrast to Observation 4.3, the conclusion of Observation 4.7 does not assert that the set
![]() $\{ w \in P_{\kappa } (\pi ) : \sup w \in S$
and
$\{ w \in P_{\kappa } (\pi ) : \sup w \in S$
and
![]() $\psi (w)= \sup w\}$
lies in the dual filter (
$\psi (w)= \sup w\}$
lies in the dual filter (
![]() $(NG^{\omega }_{\kappa ,\pi })^{\ast }$
), but only that it does not lie in the ideal (
$(NG^{\omega }_{\kappa ,\pi })^{\ast }$
), but only that it does not lie in the ideal (
![]() $(NG^{\omega }_{\kappa ,\pi })$
). There is a good reason for this. In fact if
$(NG^{\omega }_{\kappa ,\pi })$
). There is a good reason for this. In fact if
![]() $\mu = \vert A \vert = \mathrm {cf} (\theta )$
,
$\mu = \vert A \vert = \mathrm {cf} (\theta )$
,
![]() $\theta ^{< \mu } < \pi $
, and
$\theta ^{< \mu } < \pi $
, and
![]() $Z \in NS_{\pi }^+ \cap P(E_{\mu }^{\pi })$
lies in the approachable ideal
$Z \in NS_{\pi }^+ \cap P(E_{\mu }^{\pi })$
lies in the approachable ideal
![]() $I [\pi ]$
, then by a result of [Reference Matet30], for any
$I [\pi ]$
, then by a result of [Reference Matet30], for any
![]() $\ell : \pi \rightarrow \pi $
,
$\ell : \pi \rightarrow \pi $
,
On the other hand, we have the following.
Observation 4.10. Let
![]() $X \subseteq P_{\kappa } (\pi )$
be such that
$X \subseteq P_{\kappa } (\pi )$
be such that
![]() $\vert \{x \in X : \sup x = \beta \} \vert < \pi $
for all
$\vert \{x \in X : \sup x = \beta \} \vert < \pi $
for all
![]() $\beta < \pi $
. Then there is
$\beta < \pi $
. Then there is
![]() $\ell : \pi \rightarrow \pi $
with the property that
$\ell : \pi \rightarrow \pi $
with the property that
![]() for all
for all
![]() $x \in X$
.
$x \in X$
.
Proof For
![]() $\beta < \pi $
, put
$\beta < \pi $
, put
![]() $e_{\beta } = \{x \in X : \sup x = \beta \}$
. Now define
$e_{\beta } = \{x \in X : \sup x = \beta \}$
. Now define
![]() $\ell : \pi \rightarrow \pi $
by:
$\ell : \pi \rightarrow \pi $
by:
![]() $\ell (\beta )$
equals
$\ell (\beta )$
equals
![]() $\sup \{\psi (x) : x \in e_{\beta }\}$
if
$\sup \{\psi (x) : x \in e_{\beta }\}$
if
![]() $e_{\beta } \not = \emptyset $
, and
$e_{\beta } \not = \emptyset $
, and
![]() $0$
otherwise.
$0$
otherwise.
Note that if
![]() $V = L$
, then by a result of Dieter Donder, for any stationary
$V = L$
, then by a result of Dieter Donder, for any stationary
![]() $Y \subseteq P_{\kappa } (\pi )$
, there exists a stationary
$Y \subseteq P_{\kappa } (\pi )$
, there exists a stationary
![]() $X \subseteq Y$
such that
$X \subseteq Y$
such that
![]() for all
for all
![]() $\beta < \pi $
.
$\beta < \pi $
.
Let us finally observe that if
![]() $x = ran (f_{\alpha })$
, where
$x = ran (f_{\alpha })$
, where
![]() $\alpha < \pi $
, then obviously
$\alpha < \pi $
, then obviously
![]() $\psi (x) = \alpha $
. This shows that
$\psi (x) = \alpha $
. This shows that
![]() $\psi (x)$
needs not be a limit ordinal. On the other hand, by Observation 4.7 (respectively, Observation 4.3), if
$\psi (x)$
needs not be a limit ordinal. On the other hand, by Observation 4.7 (respectively, Observation 4.3), if
![]() $\vert A \vert = \mu = \omega $
(respectively,
$\vert A \vert = \mu = \omega $
(respectively,
![]() $\vert A \vert < \mu $
or I is
$\vert A \vert < \mu $
or I is
![]() $\mu ^+$
-complete), the set of all x such that
$\mu ^+$
-complete), the set of all x such that
![]() $\psi (x)$
is a limit ordinal of cofinality
$\psi (x)$
is a limit ordinal of cofinality
![]() $\mathrm {cf} (\vert x \cap \theta \vert ) (= \mu )$
lies in
$\mathrm {cf} (\vert x \cap \theta \vert ) (= \mu )$
lies in
![]() $(NG_{\kappa ,\pi }^{\mu })^+$
(respectively,
$(NG_{\kappa ,\pi }^{\mu })^+$
(respectively,
![]() $(NG_{\kappa ,\pi }^{\mu })^{\ast }$
). One intriguing question which is left unanswered by the results of the next section is whether the set of all x such that
$(NG_{\kappa ,\pi }^{\mu })^{\ast }$
). One intriguing question which is left unanswered by the results of the next section is whether the set of all x such that
![]() $\psi (x)$
is a limit ordinal of cofinality
$\psi (x)$
is a limit ordinal of cofinality
![]() $(\mathrm {cf} (\vert x \cap \theta \vert ))^+$
lies in
$(\mathrm {cf} (\vert x \cap \theta \vert ))^+$
lies in
![]() $J^{\ast }$
for any weakly
$J^{\ast }$
for any weakly
![]() $\pi $
-saturated, normal, fine ideal J on
$\pi $
-saturated, normal, fine ideal J on
![]() .
.
5 The way of Usuba
As in the preceding section, we assume in this one that
![]() , and we look for strategies to deal with situations when our ideal J on
, and we look for strategies to deal with situations when our ideal J on
![]() cannot be shown to be isomorphic to a nice ideal on
cannot be shown to be isomorphic to a nice ideal on
![]() $P_{\kappa } (\pi )$
. Sticking with ideals, we could attempt to bypass
$P_{\kappa } (\pi )$
. Sticking with ideals, we could attempt to bypass
![]() $P_{\kappa } (\pi )$
and associate J with an ideal on
$P_{\kappa } (\pi )$
and associate J with an ideal on
![]() $\pi $
of the form
$\pi $
of the form
![]() $h (J)$
for some
$h (J)$
for some
![]() . But there are obvious difficulties. One is that
. But there are obvious difficulties. One is that
![]() $h (J)$
will be
$h (J)$
will be
![]() $\kappa $
-complete (when we would be more comfortable with
$\kappa $
-complete (when we would be more comfortable with
![]() $\pi $
-completeness). Another is that if
$\pi $
-completeness). Another is that if
![]() , then J and
, then J and
![]() $h (J)$
will not be isomorphic. So instead we will follow Usuba [Reference Usuba60] whose method consists in moving from J (to its projection on
$h (J)$
will not be isomorphic. So instead we will follow Usuba [Reference Usuba60] whose method consists in moving from J (to its projection on
![]() $P_{\kappa } (\theta )$
and then) to an ideal K on
$P_{\kappa } (\theta )$
and then) to an ideal K on
![]() $P_{\kappa } (\theta )$
with which is associated a function h taking its values in
$P_{\kappa } (\theta )$
with which is associated a function h taking its values in
![]() $\pi $
. The crux of the matter is that if J is weakly
$\pi $
. The crux of the matter is that if J is weakly
![]() $\pi $
-saturated, then so is K.
$\pi $
-saturated, then so is K.
An ideal on
![]() $P_{\kappa } (\sigma )$
, where
$P_{\kappa } (\sigma )$
, where
![]() $\sigma $
is a cardinal greater than or equal to
$\sigma $
is a cardinal greater than or equal to
![]() $\theta $
, is adequate if it is
$\theta $
, is adequate if it is
![]() $\kappa $
-complete in case
$\kappa $
-complete in case
![]() $\kappa $
is a successor cardinal, and
$\kappa $
is a successor cardinal, and
![]() $\theta $
-normal otherwise.
$\theta $
-normal otherwise.
Let J be an adequate, fine ideal on
![]() . We put
. We put
![]() ${\cal J} = p (J)$
, where
${\cal J} = p (J)$
, where
![]() is defined by
is defined by
![]() $p (c) = c \cap \theta $
.
$p (c) = c \cap \theta $
.
Observation 5.1.
-
(i)
 ${\cal J}$
is an adequate, fine ideal on
${\cal J}$
is an adequate, fine ideal on
 $P_{\kappa } (\theta )$
.
$P_{\kappa } (\theta )$
. -
(ii) If J is
 $\theta $
-normal, then
$\theta $
-normal, then
 ${\cal J}$
is normal.
${\cal J}$
is normal. -
(iii) If J is weakly
 $\pi $
-saturated, then so is
$\pi $
-saturated, then so is
 ${\cal J}$
.
${\cal J}$
.
Fact 5.2 [Reference Usuba60].
-
(i) There exist a function
 $h : P_{\kappa } (\theta ) \rightarrow On$
and an adequate ideal K on
$h : P_{\kappa } (\theta ) \rightarrow On$
and an adequate ideal K on
 $P_{\kappa } (\theta )$
extending
$P_{\kappa } (\theta )$
extending
 ${\cal J}$
such that:
${\cal J}$
such that:-
• For any
 $X \in K^+$
and any
$X \in K^+$
and any
 $g \in \prod _{b \in X} h (b)$
, there is
$g \in \prod _{b \in X} h (b)$
, there is
 $\beta < \pi $
with
$\beta < \pi $
with
 .
. -
• For each
 $\gamma < \pi $
,
$\gamma < \pi $
,
 $\{ b \in P_{\kappa } (\theta ) : h (b)> \gamma \} \in K^{\ast }$
.
$\{ b \in P_{\kappa } (\theta ) : h (b)> \gamma \} \in K^{\ast }$
.
-
-
(ii) K is weakly
 $\pi $
-saturated if and only if for any
$\pi $
-saturated if and only if for any
 $X \in K^{\ast }$
and any
$X \in K^{\ast }$
and any
 $g \in \prod _{b \in X} h (b)$
, there is
$g \in \prod _{b \in X} h (b)$
, there is
 $\beta < \pi $
with
$\beta < \pi $
with
 .
. -
(iii) If
 ${\cal J}$
is weakly
${\cal J}$
is weakly
 $\pi $
-saturated, then so is K.
$\pi $
-saturated, then so is K. -
(iv) If (
 $\kappa $
is a successor and)
$\kappa $
is a successor and)
 ${\cal J}$
is normal, then so is K.
${\cal J}$
is normal, then so is K.
We should stress that
![]() $\psi $
(or, for that matter, the fact that
$\psi $
(or, for that matter, the fact that
![]() $\theta $
is singular) does not play any role in the definition of h and K.
$\theta $
is singular) does not play any role in the definition of h and K.
Observation 5.3.
-
(i)
 .
. -
(ii) Let C be a closed unbounded subset of
 $\pi $
. Then
$\pi $
. Then
 $h^{- 1} (C) \in K^{\ast }$
.
$h^{- 1} (C) \in K^{\ast }$
. -
(iii) Let
 $C_{\vec {f}}$
be as in the statement of Fact 3.8(i). Then
$C_{\vec {f}}$
be as in the statement of Fact 3.8(i). Then
 $\{b \in P_{\kappa } (\theta ) : h (b) \in C_{\vec {f}}\} \in K^{\ast }$
.
$\{b \in P_{\kappa } (\theta ) : h (b) \in C_{\vec {f}}\} \in K^{\ast }$
. -
(iv) Suppose that K is weakly
 $\pi $
-saturated, and let W be a stationary subset of
$\pi $
-saturated, and let W be a stationary subset of
 $\pi $
such that
$\pi $
such that
 $\mathrm {cf} (\gamma ) < \kappa $
for all
$\mathrm {cf} (\gamma ) < \kappa $
for all
 $\gamma \in W$
. Then the set of all
$\gamma \in W$
. Then the set of all
 $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
 $W \cap h (b)$
is stationary in
$W \cap h (b)$
is stationary in
 $h (b)$
lies in
$h (b)$
lies in
 $K^{\ast }$
.
$K^{\ast }$
.
Proof For (i) (respectively, (ii) and (iv)), the proof is a straightforward modification of that of Proposition 4.1 (respectively, 4.2 and 4.3) of [Reference Usuba60]. As for (iii), it is immediate from (ii).
Concerning (iv), notice that by
![]() $\kappa $
-completeness of K, we can actually simultaneously reflect less than
$\kappa $
-completeness of K, we can actually simultaneously reflect less than
![]() $\kappa $
many stationary sets. By Theorem 2.13 in [Reference Hayut and Lambie-Hanson15], it follows that if J (and hence K) is weakly
$\kappa $
many stationary sets. By Theorem 2.13 in [Reference Hayut and Lambie-Hanson15], it follows that if J (and hence K) is weakly
![]() $\pi $
-saturated, then the square principle
$\pi $
-saturated, then the square principle
![]() $\square (\pi , < \sigma )$
fails for every regular cardinal
$\square (\pi , < \sigma )$
fails for every regular cardinal
![]() $\sigma < \kappa $
.
$\sigma < \kappa $
.
Observation 5.4. Suppose that K is weakly
![]() $\pi $
-saturated. Then the set of all
$\pi $
-saturated. Then the set of all
![]() $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
![]() $\mathrm {cf} (h (b))> o.t. (b)$
lies in
$\mathrm {cf} (h (b))> o.t. (b)$
lies in
![]() $K^{\ast }$
.
$K^{\ast }$
.
Proof Suppose otherwise. Then the set Q of all
![]() $b \in P_{\kappa } (\theta )$
with
$b \in P_{\kappa } (\theta )$
with
![]() lies in
lies in
![]() $K^+$
. Define
$K^+$
. Define
![]() $r : P_{\kappa } (\theta ) \rightarrow P_{\kappa } (\theta )$
by:
$r : P_{\kappa } (\theta ) \rightarrow P_{\kappa } (\theta )$
by:
![]() $r (b)$
equals b if
$r (b)$
equals b if
![]() $\kappa $
is weakly inaccessible, and
$\kappa $
is weakly inaccessible, and
![]() $\nu $
if
$\nu $
if
![]() $\kappa = \nu ^+$
. For
$\kappa = \nu ^+$
. For
![]() $b \in Q$
, pick
$b \in Q$
, pick
![]() $t_b : r (b) \rightarrow h (b)$
such that
$t_b : r (b) \rightarrow h (b)$
such that
![]() $\sup (ran (t_b)) = h (b)$
. Let
$\sup (ran (t_b)) = h (b)$
. Let
![]() $\chi = \theta $
if
$\chi = \theta $
if
![]() $\kappa $
is weakly inaccessible, and
$\kappa $
is weakly inaccessible, and
![]() $\chi = \nu $
if
$\chi = \nu $
if
![]() $\kappa = \nu ^+$
. We define
$\kappa = \nu ^+$
. We define
![]() $s : \chi \rightarrow \pi $
, and
$s : \chi \rightarrow \pi $
, and
![]() $Q_{\gamma } \in (K \vert Q)^{\ast } \cap P (Q)$
for
$Q_{\gamma } \in (K \vert Q)^{\ast } \cap P (Q)$
for
![]() $\gamma < \chi $
, as follows. Put
$\gamma < \chi $
, as follows. Put
![]() $W = \{b \in P_{\kappa } (\theta ) : h (b)> 0\}$
. Notice that
$W = \{b \in P_{\kappa } (\theta ) : h (b)> 0\}$
. Notice that
![]() $W \in K^{\ast }$
. Given
$W \in K^{\ast }$
. Given
![]() $\gamma < \chi $
, set
$\gamma < \chi $
, set
![]() $W_{\gamma } = W \cap \{b \in P_{\kappa } (\theta ) : \gamma \in b\}$
, and define
$W_{\gamma } = W \cap \{b \in P_{\kappa } (\theta ) : \gamma \in b\}$
, and define
![]() $g_{\gamma } \in \prod _{b \in W_{\gamma }} h (b)$
by:
$g_{\gamma } \in \prod _{b \in W_{\gamma }} h (b)$
by:
![]() $g_{\gamma } (b)$
equals
$g_{\gamma } (b)$
equals
![]() $t_b (\gamma )$
if
$t_b (\gamma )$
if
![]() $b \in Q$
, and
$b \in Q$
, and
![]() $0$
otherwise. Since K is weakly
$0$
otherwise. Since K is weakly
![]() $\pi $
-saturated, we may find
$\pi $
-saturated, we may find
![]() $\xi _{\gamma } < \pi $
such that
$\xi _{\gamma } < \pi $
such that
![]() $X_{\gamma } \in K^{\ast }$
, where
$X_{\gamma } \in K^{\ast }$
, where
![]() . We now let
. We now let
![]() $s (\gamma ) = \xi _{\gamma }$
. Notice that
$s (\gamma ) = \xi _{\gamma }$
. Notice that
![]() for all
for all
![]() $b \in Q \cap X_{\gamma }$
.
$b \in Q \cap X_{\gamma }$
.
Since K is adequate, the set of all
![]() $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
![]() $b \in X_{\gamma }$
for all
$b \in X_{\gamma }$
for all
![]() $\gamma \in b \cap \chi $
lies in
$\gamma \in b \cap \chi $
lies in
![]() $K^{\ast }$
. Hence we may select
$K^{\ast }$
. Hence we may select
![]() $b \in Q$
such that (a)
$b \in Q$
such that (a)
![]() $h (b)> \sup (ran (s))$
, and (b)
$h (b)> \sup (ran (s))$
, and (b)
![]() $b \in X_{\gamma }$
for all
$b \in X_{\gamma }$
for all
![]() $\gamma \in r (b)$
. Then
$\gamma \in r (b)$
. Then
Contradiction.
Observation 5.5.
-
(i) Let
 $z_{\alpha } \in P_{\kappa } (\theta )$
for
$z_{\alpha } \in P_{\kappa } (\theta )$
for
 $\alpha < \pi $
. Then
$\alpha < \pi $
. Then  $$ \begin{align*} \{ b \in P_{\kappa} (\theta) : \sup \{ \alpha < h (b) : z_{\alpha} \subseteq b \}= h (b) \} \in K^{\ast}. \end{align*} $$
$$ \begin{align*} \{ b \in P_{\kappa} (\theta) : \sup \{ \alpha < h (b) : z_{\alpha} \subseteq b \}= h (b) \} \in K^{\ast}. \end{align*} $$
-
(ii) Suppose that there is
 $z_{\alpha } \in P_{\kappa } (\theta )$
for
$z_{\alpha } \in P_{\kappa } (\theta )$
for
 $\alpha < \pi $
so that the set of all
$\alpha < \pi $
so that the set of all
 $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
 lies in
lies in
 $K^{\ast }$
.Then the set of all
$K^{\ast }$
.Then the set of all
 $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
 $\vert b \vert \geq \mathrm {cf} (h (b))$
lies in
$\vert b \vert \geq \mathrm {cf} (h (b))$
lies in
 $K^{\ast }$
.
$K^{\ast }$
.
Observation 5.6. Suppose that K is weakly
![]() $\pi $
-saturated. Then the set of all
$\pi $
-saturated. Then the set of all
![]() $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
![]() $h (b)$
is not a good point for
$h (b)$
is not a good point for
![]() ${\vec f}$
lies in
${\vec f}$
lies in
![]() $K^{\ast }$
.
$K^{\ast }$
.
Proof Recall from Section 3 that for
![]() $\alpha < \pi $
,
$\alpha < \pi $
,
![]() $y_{\alpha }$
equals
$y_{\alpha }$
equals
![]() $\{\alpha \}$
if
$\{\alpha \}$
if
![]() $\alpha < \theta $
, and
$\alpha < \theta $
, and
![]() $\{\Phi (a, f_{\alpha } (a)) : a \in A \}$
otherwise. Assume toward a contradiction that the desired conclusion fails. Then by Observations 5.4 and 5.5(i), we may find
$\{\Phi (a, f_{\alpha } (a)) : a \in A \}$
otherwise. Assume toward a contradiction that the desired conclusion fails. Then by Observations 5.4 and 5.5(i), we may find
![]() $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
![]() $\mathrm {cf} (h (b))> o.t. (b)$
,
$\mathrm {cf} (h (b))> o.t. (b)$
,
![]() $h (b)$
is a good point for
$h (b)$
is a good point for
![]() ${\vec f}$
, and
${\vec f}$
, and
![]() $\sup z = h (b)$
, where
$\sup z = h (b)$
, where
![]() $z = \{ \alpha < h (b) : y_{\alpha } \subseteq b \}$
. Then, by Observation 3.7,
$z = \{ \alpha < h (b) : y_{\alpha } \subseteq b \}$
. Then, by Observation 3.7,
![]() $\vert \bigcup _{\alpha \in z} y_{\alpha } \vert \geq \mathrm {cf} (h (b))> \vert b \vert $
. Contradiction.
$\vert \bigcup _{\alpha \in z} y_{\alpha } \vert \geq \mathrm {cf} (h (b))> \vert b \vert $
. Contradiction.
Observation 5.7. Suppose that K is weakly
![]() $\pi $
-saturated. Then the set of all
$\pi $
-saturated. Then the set of all
![]() $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
![]() lies in
lies in
![]() $K^{\ast }$
.
$K^{\ast }$
.
Proof Assume that the conclusion fails. By [Reference Matet28, Lemmas 4.2 and 4.7], there is an increasing, cofinal sequence
![]() in
in
![]() $(\prod A, <_I)$
with the property that for any cardinal
$(\prod A, <_I)$
with the property that for any cardinal
![]() $\sigma $
with
$\sigma $
with
![]() $\vert A \vert < \sigma < \theta $
, and any order-type
$\vert A \vert < \sigma < \theta $
, and any order-type
![]() $\sigma ^{+ 3}$
subset v of
$\sigma ^{+ 3}$
subset v of
![]() $\pi $
, there is an order-type
$\pi $
, there is an order-type
![]() $\sigma $
subset w of v such that the sequence
$\sigma $
subset w of v such that the sequence
![]() is strongly increasing. For
is strongly increasing. For
![]() $\alpha < \pi $
, put
$\alpha < \pi $
, put
![]() $z_{\alpha } =\{\Phi (a, k_{\alpha } (a)) : a \in A \}$
. By Observation 5.5(i), there must be
$z_{\alpha } =\{\Phi (a, k_{\alpha } (a)) : a \in A \}$
. By Observation 5.5(i), there must be
![]() $b \in P_{\kappa } (\theta )$
such that:
$b \in P_{\kappa } (\theta )$
such that:
-
•
 $\vert b \vert \geq \vert A \vert $
.
$\vert b \vert \geq \vert A \vert $
. -
•
 $\mathrm {cf} (h (b))> \vert b \vert ^{+ 3}$
.
$\mathrm {cf} (h (b))> \vert b \vert ^{+ 3}$
. -
•
 $\sup \{ \alpha < h (b) : z_{\alpha } \subseteq b \}= h (b)$
.
$\sup \{ \alpha < h (b) : z_{\alpha } \subseteq b \}= h (b)$
.
Now select an order-type
![]() $(\vert b \vert ^+)^{+ 3}$
subset v of
$(\vert b \vert ^+)^{+ 3}$
subset v of
![]() $\{ \alpha < h (b) : z_{\alpha } \subseteq b \}$
. We may find an order-type
$\{ \alpha < h (b) : z_{\alpha } \subseteq b \}$
. We may find an order-type
![]() $\vert b \vert ^+$
subset w of v, and
$\vert b \vert ^+$
subset w of v, and
![]() $Z_{\xi } \in I$
for
$Z_{\xi } \in I$
for
![]() $\xi \in w$
such that
$\xi \in w$
such that
![]() $k_{\xi _1} (a) < k_{\xi _2} (a)$
whenever
$k_{\xi _1} (a) < k_{\xi _2} (a)$
whenever
![]() $a \in A \setminus (Z_{\xi _1} \cup Z_{\xi _2})$
. Pick
$a \in A \setminus (Z_{\xi _1} \cup Z_{\xi _2})$
. Pick
![]() $t \in \prod _{\xi \in w} (A \setminus Z_{\xi })$
, and set
$t \in \prod _{\xi \in w} (A \setminus Z_{\xi })$
, and set
![]() $c = \{\Phi (t (\xi ), k_{\xi } (t (\xi ))) : \xi \in w \}$
. Then clearly,
$c = \{\Phi (t (\xi ), k_{\xi } (t (\xi ))) : \xi \in w \}$
. Then clearly,
![]() $c \subseteq b$
. However
$c \subseteq b$
. However
![]() $\vert c \vert = \vert b \vert ^+$
, which is a contradiction.
$\vert c \vert = \vert b \vert ^+$
, which is a contradiction.
The ideal
![]() ${\cal K} = h (K)$
does have some interesting properties, but it is not clear what can be gained by considering it. By Fact 5.2 and Observations 5.3 and 5.6, the following hold:
${\cal K} = h (K)$
does have some interesting properties, but it is not clear what can be gained by considering it. By Fact 5.2 and Observations 5.3 and 5.6, the following hold:
-
•
 ${\cal K}$
is a
${\cal K}$
is a
 $\kappa $
-complete ideal on
$\kappa $
-complete ideal on
 $\pi $
extending
$\pi $
extending
 $NS_{\pi }$
.
$NS_{\pi }$
. -
• If K is weakly
 $\pi $
-saturated, then so is
$\pi $
-saturated, then so is
 ${\cal K}$
.
${\cal K}$
. -
• For any
 $X \in {\cal K}^+$
and any
$X \in {\cal K}^+$
and any
 $g : X \rightarrow \pi $
such that
$g : X \rightarrow \pi $
such that
 $g (\gamma ) < \gamma $
for all
$g (\gamma ) < \gamma $
for all
 $\gamma \in X$
, there is
$\gamma \in X$
, there is
 $\beta < \pi $
with
$\beta < \pi $
with
 .
. -
• Suppose that K is weakly
 $\pi $
-saturated. Then (a) for any
$\pi $
-saturated. Then (a) for any
 $X \in {\cal K}^{\ast }$
and any
$X \in {\cal K}^{\ast }$
and any
 $g : X \rightarrow \pi $
such that
$g : X \rightarrow \pi $
such that
 $g (\gamma ) < \gamma $
for all
$g (\gamma ) < \gamma $
for all
 $\gamma \in X$
, there is
$\gamma \in X$
, there is
 $\beta < \pi $
with
$\beta < \pi $
with
 , and (b) the set of all
, and (b) the set of all
 $\gamma \in \pi $
such that
$\gamma \in \pi $
such that
 $\gamma $
is not a good point for
$\gamma $
is not a good point for
 ${\vec f}$
lies in
${\vec f}$
lies in
 ${\cal K}^{\ast }$
.
${\cal K}^{\ast }$
.
A function
![]() $g \in \prod A$
is an exact upper bound for some
$g \in \prod A$
is an exact upper bound for some
![]() $F \subseteq \{ f_{\alpha } : \alpha < \pi \}$
if (a)
$F \subseteq \{ f_{\alpha } : \alpha < \pi \}$
if (a)
![]() for all
for all
![]() $f \in F$
, and (b) for any
$f \in F$
, and (b) for any
![]() $k \in \prod A$
with
$k \in \prod A$
with
![]() $k <_I g$
, there is
$k <_I g$
, there is
![]() $f \in F$
with
$f \in F$
with
![]() $k <_I f$
.
$k <_I f$
.
Fact 5.8 ([Reference Shelah50, Claim 1.6, p. 52] (see also [Reference Abraham and Magidor1, Exercise 2.6])).
Let e be a subset of
![]() $\pi $
such that
$\pi $
such that
![]() $\sup e \notin e$
and
$\sup e \notin e$
and
![]() $\mathrm {cf} (\sup e)> \vert A \vert $
. Then the following are equivalent:
$\mathrm {cf} (\sup e)> \vert A \vert $
. Then the following are equivalent:
-
(i)
 $\sup e$
is a good point for
$\sup e$
is a good point for
 ${\vec f}$
.
${\vec f}$
. -
(ii) The sequence
 has an exact upper bound g such that the set of all
has an exact upper bound g such that the set of all
 $a \in A$
such that
$a \in A$
such that
 $g (a)$
is a limit ordinal of cofinality
$g (a)$
is a limit ordinal of cofinality
 $\mathrm {cf} (\sup e)$
lies in
$\mathrm {cf} (\sup e)$
lies in
 $I^{\ast }$
.
$I^{\ast }$
.
An infinite limit ordinal
![]() $\delta < \pi $
is a more-than-good point for
$\delta < \pi $
is a more-than-good point for
![]() $\vec f$
if there is a cofinal subset X of
$\vec f$
if there is a cofinal subset X of
![]() $\delta $
, and
$\delta $
, and
![]() $Z_{\xi } \in I$
for
$Z_{\xi } \in I$
for
![]() $\xi \in X$
such that
$\xi \in X$
such that
![]() $f_{\beta } (a) < f_{\xi } (a)$
whenever
$f_{\beta } (a) < f_{\xi } (a)$
whenever
![]() $\beta < \xi $
are in X and
$\beta < \xi $
are in X and
![]() $a \in A \setminus Z_{\xi }$
. By results of Shelah, for any regular cardinal
$a \in A \setminus Z_{\xi }$
. By results of Shelah, for any regular cardinal
![]() $\mu $
with
$\mu $
with
![]() $\vert A \vert < \mu < \theta $
, the set of all good points for
$\vert A \vert < \mu < \theta $
, the set of all good points for
![]() ${\vec f}$
of cofinality
${\vec f}$
of cofinality
![]() $\mu $
is stationary in
$\mu $
is stationary in
![]() $\pi $
. This is also true of more-than-good points.
$\pi $
. This is also true of more-than-good points.
Observation 5.9. Let
![]() $\mu $
be a regular cardinal with
$\mu $
be a regular cardinal with
![]() $\vert A \vert < \mu < \kappa $
. Then the set of all
$\vert A \vert < \mu < \kappa $
. Then the set of all
![]() $x \in P_{\kappa } (\pi )$
such that
$x \in P_{\kappa } (\pi )$
such that
![]() $\sup x$
is a more-than-good point for
$\sup x$
is a more-than-good point for
![]() ${\vec f}$
lies in
${\vec f}$
lies in
![]() $(NS_{\mu , \kappa , \pi } \vert \{x : \mathrm {cf} (\sup x) = \mu \})^{\ast }$
.
$(NS_{\mu , \kappa , \pi } \vert \{x : \mathrm {cf} (\sup x) = \mu \})^{\ast }$
.
Proof For
![]() $e \in P_{\mu } (\pi )$
, define
$e \in P_{\mu } (\pi )$
, define
![]() $g_e \in \prod A$
by:
$g_e \in \prod A$
by:
![]() $g_e (a)$
equals
$g_e (a)$
equals
![]() $\sup \{f_{\beta } (a) : \beta \in e \}$
if
$\sup \{f_{\beta } (a) : \beta \in e \}$
if
![]() $a \geq \mu $
, and 0 otherwise. Let X be the set of all
$a \geq \mu $
, and 0 otherwise. Let X be the set of all
![]() $x \in P_{\kappa } (\pi )$
such that for any
$x \in P_{\kappa } (\pi )$
such that for any
![]() $e \in P_{\mu } (x)$
, there is
$e \in P_{\mu } (x)$
, there is
![]() $\alpha \in x$
with
$\alpha \in x$
with
![]() $g_e <_I f_{\alpha }$
.
$g_e <_I f_{\alpha }$
.
Claim.
![]() $X \in NS_{\mu , \kappa , \pi }^{\ast }$
.
$X \in NS_{\mu , \kappa , \pi }^{\ast }$
.
Proof of the claim
Suppose otherwise. For
![]() $x \in P_{\kappa } (\pi ) \setminus X$
, select
$x \in P_{\kappa } (\pi ) \setminus X$
, select
![]() $e_x \in P_{\mu } (x)$
such that there is no
$e_x \in P_{\mu } (x)$
such that there is no
![]() $\alpha \in x$
with
$\alpha \in x$
with
![]() $g_{e_x} <_I f_{\alpha }$
. We may find
$g_{e_x} <_I f_{\alpha }$
. We may find
![]() $W \in NS_{\mu , \kappa , \pi }^+$
and
$W \in NS_{\mu , \kappa , \pi }^+$
and
![]() $b \in P_{\kappa } (\pi )$
such that
$b \in P_{\kappa } (\pi )$
such that
![]() $e_x \subseteq b$
for all
$e_x \subseteq b$
for all
![]() $x \in W$
. Define
$x \in W$
. Define
![]() $\unicode{x0142} \in \prod A$
by:
$\unicode{x0142} \in \prod A$
by:
![]() $\unicode{x0142} (a)$
equals
$\unicode{x0142} (a)$
equals
![]() $\sup \{f_{\gamma } (a) : \gamma \in b \}$
if
$\sup \{f_{\gamma } (a) : \gamma \in b \}$
if
![]() $a \geq \kappa $
, and 0 otherwise. Pick
$a \geq \kappa $
, and 0 otherwise. Pick
![]() $\alpha < \pi $
with
$\alpha < \pi $
with
![]() $\unicode{x0142} <_I f_{\alpha }$
. Now there must be
$\unicode{x0142} <_I f_{\alpha }$
. Now there must be
![]() $x \in W$
with
$x \in W$
with
![]() $\alpha \in x$
. This contradiction completes the proof of the claim.
$\alpha \in x$
. This contradiction completes the proof of the claim.
Given
![]() $x \in X$
with
$x \in X$
with
![]() $\mathrm {cf} (\sup x) = \mu $
, pick an increasing sequence
$\mathrm {cf} (\sup x) = \mu $
, pick an increasing sequence
![]() of ordinals with supremum
of ordinals with supremum
![]() $\sup x$
. Inductively define
$\sup x$
. Inductively define
![]() $\alpha _i \in x \setminus \xi _i$
and
$\alpha _i \in x \setminus \xi _i$
and
![]() $Z_i \in I$
for
$Z_i \in I$
for
![]() $i < \mu $
so that for any
$i < \mu $
so that for any
![]() $i < \mu $
and any
$i < \mu $
and any
![]() $a \in A \setminus Z_i$
,
$a \in A \setminus Z_i$
,
![]() $g_{\{\alpha _j : j < i\}} (a) < f_{\alpha _i} (a)$
. Then clearly,
$g_{\{\alpha _j : j < i\}} (a) < f_{\alpha _i} (a)$
. Then clearly,
![]() $f_{\alpha _j} (a) < f_{\alpha _i} (a)$
whenever
$f_{\alpha _j} (a) < f_{\alpha _i} (a)$
whenever
![]() $j < i < \mu $
and
$j < i < \mu $
and
![]() $a \in A \setminus Z_i$
.
$a \in A \setminus Z_i$
.
Corollary 5.10. Let
![]() $\mu $
be a regular cardinal with
$\mu $
be a regular cardinal with
![]() $\vert A \vert < \mu < \theta $
. Then there are stationarily many more-than-good points for
$\vert A \vert < \mu < \theta $
. Then there are stationarily many more-than-good points for
![]() ${\vec f}$
of cofinality
${\vec f}$
of cofinality
![]() $\mu $
.
$\mu $
.
For
![]() $b \in P_{\kappa } (\theta )$
, let
$b \in P_{\kappa } (\theta )$
, let
![]() $d_b$
be the set of all
$d_b$
be the set of all
![]() $\delta \in b$
such that
$\delta \in b$
such that
![]() $o.t. (b \cap \delta )$
is a regular cardinal greater than
$o.t. (b \cap \delta )$
is a regular cardinal greater than
![]() $\vert A \vert $
. For
$\vert A \vert $
. For
![]() $\delta \in d_b$
, let
$\delta \in d_b$
, let
![]() $G^b_{\delta }$
be the set of all
$G^b_{\delta }$
be the set of all
![]() $\beta < h (b)$
with
$\beta < h (b)$
with
![]() $\mathrm {cf} (\beta ) = o.t. (b \cap \delta )$
with the property that
$\mathrm {cf} (\beta ) = o.t. (b \cap \delta )$
with the property that
![]() $\beta $
is a good point for
$\beta $
is a good point for
![]() . Let
. Let
![]() $\Omega $
be the set of all
$\Omega $
be the set of all
![]() $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
![]() $G^b_{\delta }$
is stationary in
$G^b_{\delta }$
is stationary in
![]() $h (b)$
for all
$h (b)$
for all
![]() $\delta \in d_b$
.
$\delta \in d_b$
.
Lemma 5.11. Suppose that K is weakly
![]() $\pi $
-saturated. Then
$\pi $
-saturated. Then
![]() $\Omega \in K^{\ast }$
.
$\Omega \in K^{\ast }$
.
Proof The proof is a modification of that of Claim 5.2 in [Reference Usuba60]. Suppose that the conclusion fails. Then we may find
![]() $X \in K^+$
,
$X \in K^+$
,
![]() $\tau < \theta $
, and
$\tau < \theta $
, and
![]() $c_b$
for
$c_b$
for
![]() $b \in X$
such that for each
$b \in X$
such that for each
![]() $b \in X$
, (a)
$b \in X$
, (a)
![]() $\tau \in d_b$
, (b)
$\tau \in d_b$
, (b)
![]() $c_b$
is a closed unbounded subset of
$c_b$
is a closed unbounded subset of
![]() $h (b)$
of order type
$h (b)$
of order type
![]() $\mathrm {cf} (h (b))$
, and (c)
$\mathrm {cf} (h (b))$
, and (c)
![]() $G^b_{\tau } \cap c_b = \emptyset $
.
$G^b_{\tau } \cap c_b = \emptyset $
.
Claim.
![]() $\tau $
is a regular cardinal.
$\tau $
is a regular cardinal.
Proof of the claim
It suffices to observe the following:
Case when
![]() $\kappa $
is a successor cardinal, say
$\kappa $
is a successor cardinal, say
![]() $\kappa = \nu ^+$
. Pick
$\kappa = \nu ^+$
. Pick
![]() $x \in X$
with
$x \in X$
with
![]() $\nu + 1 \subseteq x$
. We must have
$\nu + 1 \subseteq x$
. We must have
![]() , since otherwise
, since otherwise
![]() $\nu < o.t. (x \cap \tau ) = \vert x \cap \tau \vert = \nu $
. But then
$\nu < o.t. (x \cap \tau ) = \vert x \cap \tau \vert = \nu $
. But then
![]() $x \cap \tau = \tau = o.t. (x \cap \tau )$
.
$x \cap \tau = \tau = o.t. (x \cap \tau )$
.
Case when
![]() $\kappa $
is weakly inaccessible. Given
$\kappa $
is weakly inaccessible. Given
![]() $q \subseteq \tau $
and an increasing function
$q \subseteq \tau $
and an increasing function
![]() $k : q \rightarrow \tau $
with the property that
$k : q \rightarrow \tau $
with the property that
![]() $\sup (ran (k)) = \sup \tau $
, the set of all
$\sup (ran (k)) = \sup \tau $
, the set of all
![]() $b \in P_{\kappa } (\theta )$
with
$b \in P_{\kappa } (\theta )$
with
![]() $\sup (k" (b \cap q)) = \sup (b \cap \tau )$
lies in
$\sup (k" (b \cap q)) = \sup (b \cap \tau )$
lies in
![]() $NS^{\ast }_{\kappa , \theta }$
.
$NS^{\ast }_{\kappa , \theta }$
.
It is simple to see that
![]() $\tau> \vert A \vert $
. Inductively construct
$\tau> \vert A \vert $
. Inductively construct
![]() $u_{\xi } \in P_{\tau } (\pi )$
,
$u_{\xi } \in P_{\tau } (\pi )$
,
![]() $\delta _{\xi } < \pi $
and
$\delta _{\xi } < \pi $
and
![]() $T_{\xi } \in (K \vert X)^{\ast }$
for
$T_{\xi } \in (K \vert X)^{\ast }$
for
![]() $\xi < \tau $
such that:
$\xi < \tau $
such that:
-
•
 $u_{\xi } \subseteq u_{\xi + 1}$
.
$u_{\xi } \subseteq u_{\xi + 1}$
. -
•
 $u_{\xi } = \bigcup _{\zeta < \xi } u_{\zeta }$
in case
$u_{\xi } = \bigcup _{\zeta < \xi } u_{\zeta }$
in case
 $\xi $
is an infinite limit ordinal.
$\xi $
is an infinite limit ordinal. -
•
 $\varphi (u_{\xi }) <_I f_{\delta _{\xi }}$
.
$\varphi (u_{\xi }) <_I f_{\delta _{\xi }}$
. -
•
 $ran (f_{\delta _{\xi }}) \subseteq u_{\xi + 1}$
.
$ran (f_{\delta _{\xi }}) \subseteq u_{\xi + 1}$
. -
• For any
 $b \in X \cap T_{\xi }$
,
$b \in X \cap T_{\xi }$
,
 $h (b)> \sup u_{\xi }$
, and moreover the least
$h (b)> \sup u_{\xi }$
, and moreover the least
 $\eta \in c_b$
with
$\eta \in c_b$
with
 $\eta \geq \sup u_{\xi }$
is less than
$\eta \geq \sup u_{\xi }$
is less than
 $\sup u_{\xi + 1}$
.
$\sup u_{\xi + 1}$
.
We may find
![]() $b \in X$
such that (1)
$b \in X$
such that (1)
![]() $\mathrm {cf} (h (b))> o.t. (b)$
, and (2)
$\mathrm {cf} (h (b))> o.t. (b)$
, and (2)
![]() $b \in T_{\xi }$
for all
$b \in T_{\xi }$
for all
![]() $\xi \in b \cap \tau $
. Set
$\xi \in b \cap \tau $
. Set
![]() $\beta = \sup (\bigcup _{\xi < \sup (b \cap \tau )} u_{\xi })$
. Clearly,
$\beta = \sup (\bigcup _{\xi < \sup (b \cap \tau )} u_{\xi })$
. Clearly,
![]() $\mathrm {cf} (\beta ) = o.t. (b \cap \tau )$
. Moreover, since
$\mathrm {cf} (\beta ) = o.t. (b \cap \tau )$
. Moreover, since
![]() $o.t. (c_b) = \mathrm {cf} (h (b))> o.t. (b) \geq o.t. (b \cap \tau )$
, we have that
$o.t. (c_b) = \mathrm {cf} (h (b))> o.t. (b) \geq o.t. (b \cap \tau )$
, we have that
![]() $\beta \in c_b$
. Pick
$\beta \in c_b$
. Pick
![]() $e \subseteq \sup (b \cap \tau )$
so that
$e \subseteq \sup (b \cap \tau )$
so that
![]() $o.t. (e) = \mathrm {cf} (\beta )$
and
$o.t. (e) = \mathrm {cf} (\beta )$
and
![]() $\sup e = \sup (b \cap \tau )$
. For
$\sup e = \sup (b \cap \tau )$
. For
![]() $\xi \in e$
,
$\xi \in e$
,
![]() , so there is
, so there is
![]() $Z_{\xi } \in I$
such that
$Z_{\xi } \in I$
such that
![]() $A \cap \kappa \subseteq Z_{\xi }$
, and moreover
$A \cap \kappa \subseteq Z_{\xi }$
, and moreover
![]() for all
for all
![]() $a \in A \setminus Z_{\xi }$
. Now let
$a \in A \setminus Z_{\xi }$
. Now let
![]() $\zeta < \xi $
in e. Then for any
$\zeta < \xi $
in e. Then for any
![]() $a \in A \setminus (Z_{\delta } \cup Z_{\xi })$
,
$a \in A \setminus (Z_{\delta } \cup Z_{\xi })$
,
![]() . Thus
. Thus
![]() $\beta $
is a good point for
$\beta $
is a good point for
![]() . Contradiction.
. Contradiction.
For
![]() $b \in P_{\kappa } (\theta )$
, let
$b \in P_{\kappa } (\theta )$
, let
![]() $w_b$
be the set of all those
$w_b$
be the set of all those
![]() $\delta < h (b)$
of cofinality
$\delta < h (b)$
of cofinality
![]() $\vert b \vert ^+$
that are good points for
$\vert b \vert ^+$
that are good points for
![]() . Assuming that K is weakly
. Assuming that K is weakly
![]() $\pi $
-saturated, it is easy to show that, in contrast to Lemma 5.11, the set of all
$\pi $
-saturated, it is easy to show that, in contrast to Lemma 5.11, the set of all
![]() $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
![]() $w_b$
is stationary in
$w_b$
is stationary in
![]() $h (b)$
lies in K. Suppose otherwise. By Observations 5.4 and 5.5(i), there must be
$h (b)$
lies in K. Suppose otherwise. By Observations 5.4 and 5.5(i), there must be
![]() $b \in P_{\kappa } (\theta )$
such that (a)
$b \in P_{\kappa } (\theta )$
such that (a)
![]() $w_b$
is stationary in
$w_b$
is stationary in
![]() $h (b)$
, (b)
$h (b)$
, (b)
![]() $\sup \{\alpha < h (b) : y_{\alpha } \subseteq b\} = h (b)$
(where
$\sup \{\alpha < h (b) : y_{\alpha } \subseteq b\} = h (b)$
(where
![]() is the sequence defined in Section 3), and (c)
is the sequence defined in Section 3), and (c)
![]() $\mathrm {cf} (h (b))> \vert b \vert \geq \vert A \vert $
. Pick
$\mathrm {cf} (h (b))> \vert b \vert \geq \vert A \vert $
. Pick
![]() $z \subseteq \{ \alpha < h (b) : y_{\alpha } \subseteq b \}$
with
$z \subseteq \{ \alpha < h (b) : y_{\alpha } \subseteq b \}$
with
![]() $o.t. (z) = \mathrm {cf} (h (b))$
and
$o.t. (z) = \mathrm {cf} (h (b))$
and
![]() $\sup z = h (b)$
. We may find
$\sup z = h (b)$
. We may find
![]() $\delta \in w_b$
such that
$\delta \in w_b$
such that
![]() $\sup (z \cap \delta ) = \delta $
. But then by Observation 3.7,
$\sup (z \cap \delta ) = \delta $
. But then by Observation 3.7,
![]() $\vert \bigcup \{y_{\alpha } : \alpha \in z \cap \delta \} \vert \geq \mathrm {cf} (\delta )> \vert b \vert $
, which yields the desired contradiction.
$\vert \bigcup \{y_{\alpha } : \alpha \in z \cap \delta \} \vert \geq \mathrm {cf} (\delta )> \vert b \vert $
, which yields the desired contradiction.
Let
![]() $\Xi $
be the set of all
$\Xi $
be the set of all
![]() $b \in P_{\kappa } (\theta )$
with the property that
$b \in P_{\kappa } (\theta )$
with the property that
![]() has an exact upper bound g such that
has an exact upper bound g such that
![]() for each regular cardinal
for each regular cardinal
![]() $\sigma $
with
$\sigma $
with
![]() .
.
Lemma 5.12. Suppose that
![]() $\vert A \vert ^+ < \kappa $
and K is weakly
$\vert A \vert ^+ < \kappa $
and K is weakly
![]() $\pi $
-saturated. Then
$\pi $
-saturated. Then
![]() $\Xi \in K^{\ast }$
.
$\Xi \in K^{\ast }$
.
Proof Let B be the set of all
![]() $b \in \Omega $
such that
$b \in \Omega $
such that
![]() $\sup b = \theta $
and
$\sup b = \theta $
and
![]() $\vert A \vert < \vert b \vert < \mathrm {cf} (h (b))$
. By Observation 5.4 and Lemma 5.11,
$\vert A \vert < \vert b \vert < \mathrm {cf} (h (b))$
. By Observation 5.4 and Lemma 5.11,
![]() $B \in K^{\ast }$
. We will show that
$B \in K^{\ast }$
. We will show that
![]() $B \subseteq \Xi $
. Thus let
$B \subseteq \Xi $
. Thus let
![]() $b \in B$
.
$b \in B$
.
Claim. Let
![]() $\sigma $
be a regular cardinal with
$\sigma $
be a regular cardinal with
![]() . Then there are stationarily many good points for
. Then there are stationarily many good points for
![]() of cofinality
of cofinality
![]() $\sigma $
.
$\sigma $
.
Proof of the claim
We have that
![]() , so
, so
![]() $\sigma < o.t. (b)$
. Hence there must be
$\sigma < o.t. (b)$
. Hence there must be
![]() $\delta \in b$
such that
$\delta \in b$
such that
![]() $o.t. (b \cap \delta ) = \sigma $
. Since
$o.t. (b \cap \delta ) = \sigma $
. Since
![]() $b \in \Omega $
, the claim follows.
$b \in \Omega $
, the claim follows.
By Lemmas 15 and 16 of [Reference Kojman22], it follows from the claim that
![]() $b \in \Xi $
.
$b \in \Xi $
.
Lemma 5.13.
![]() $\Theta \in K^{\ast }$
, where
$\Theta \in K^{\ast }$
, where
![]() $\Theta $
denotes the set of all
$\Theta $
denotes the set of all
![]() $b \in P_{\kappa } (\theta )$
such that if g is an exact upper bound for
$b \in P_{\kappa } (\theta )$
such that if g is an exact upper bound for
![]() , then
, then
Proof The proof is a straightforward modification of that of Lemma 4.5 in [Reference Usuba60].
Observation 5.14. Suppose that
![]() $\vert A \vert ^+ < \kappa $
and K is weakly
$\vert A \vert ^+ < \kappa $
and K is weakly
![]() $\pi $
-saturated. Then
$\pi $
-saturated. Then
![]() ${\mathfrak A} \in K^{\ast }$
, where
${\mathfrak A} \in K^{\ast }$
, where
![]() ${\mathfrak A}$
denotes the set of all
${\mathfrak A}$
denotes the set of all
![]() $b \in P_{\kappa } (\theta )$
such that
$b \in P_{\kappa } (\theta )$
such that
![]() $(a) \ \vert b \vert $
is a singular cardinal of cofinality at most
$(a) \ \vert b \vert $
is a singular cardinal of cofinality at most
![]() $\vert A \vert $
,
$\vert A \vert $
,
![]() $(b) \ I$
is not
$(b) \ I$
is not
![]() $(\mathrm {cf} (\vert b \vert ))^+$
-complete, and
$(\mathrm {cf} (\vert b \vert ))^+$
-complete, and
![]() $(c) \ \mathrm {pp} (\vert b \vert ) \geq \mathrm {cf} (h (b))$
.
$(c) \ \mathrm {pp} (\vert b \vert ) \geq \mathrm {cf} (h (b))$
.
Proof Let B be the set of all
![]() $b \in \Xi \cap \Theta $
such that:
$b \in \Xi \cap \Theta $
such that:
-
•
 .
. -
•
 $h (b) \in C_{\vec f}$
.
$h (b) \in C_{\vec f}$
. -
•
 $h (b)$
is not a good point for
$h (b)$
is not a good point for
 ${\vec f}$
.
${\vec f}$
.
Then by Observations 5.3(iii), 5.4, 5.6, and 5.7 and Lemmas 5.12 and 5.13,
![]() $B \in K^{\ast }$
. Let us show that
$B \in K^{\ast }$
. Let us show that
![]() $B \subseteq {\mathfrak A}$
. Thus fix
$B \subseteq {\mathfrak A}$
. Thus fix
![]() $b \in B$
. Since
$b \in B$
. Since
![]() $b \in \Xi $
,
$b \in \Xi $
,
![]() has an exact upper bound g such that
has an exact upper bound g such that
![]() for each regular cardinal
for each regular cardinal
![]() $\sigma $
with
$\sigma $
with
![]() . On the other hand,
. On the other hand,
![]() $b \in \Theta $
, so the set of all a such that
$b \in \Theta $
, so the set of all a such that
![]() lies in
lies in
![]() $I^{\ast }$
. It follows that
$I^{\ast }$
. It follows that
![]() $\vert b \vert $
is not regular. As
$\vert b \vert $
is not regular. As
![]() ,
,
![]() $\vert b \vert $
must be the largest limit cardinal less than or equal to
$\vert b \vert $
must be the largest limit cardinal less than or equal to
![]() $\mathrm {cf} (h (b))$
. Now
$\mathrm {cf} (h (b))$
. Now
![]() $h (b)$
lies in
$h (b)$
lies in
![]() $C_{\vec f}$
, and moreover it is not a good point for
$C_{\vec f}$
, and moreover it is not a good point for
![]() ${\vec f}$
. Hence
${\vec f}$
. Hence
![]() , I is not
, I is not
![]() $(\mathrm {cf} (\vert b \vert ))^+$
-complete, and (c)
$(\mathrm {cf} (\vert b \vert ))^+$
-complete, and (c)
![]() .
.
Theorem 5.15.
-
(i) Suppose that
 $\kappa $
is weakly inaccessible and J is weakly
$\kappa $
is weakly inaccessible and J is weakly
 $\pi $
-saturated. Then
$\pi $
-saturated. Then
 ${\mathcal X} \in J^{\ast }$
, where
${\mathcal X} \in J^{\ast }$
, where
 ${\mathcal X}$
denotes the set of all
${\mathcal X}$
denotes the set of all
 such that
such that
 $(a) \ \vert x \cap \theta \vert $
is a singular cardinal of cofinality less than or equal to
$(a) \ \vert x \cap \theta \vert $
is a singular cardinal of cofinality less than or equal to
 $\vert A \vert $
and
$\vert A \vert $
and
 $(b) \ I$
is not
$(b) \ I$
is not
 $(\mathrm {cf} (\vert x \cap \theta \vert ))^+$
-complete.
$(\mathrm {cf} (\vert x \cap \theta \vert ))^+$
-complete. -
(ii) Suppose that
 $\kappa $
is a successor cardinal, say
$\kappa $
is a successor cardinal, say
 $\kappa = \nu ^+$
, and J is weakly
$\kappa = \nu ^+$
, and J is weakly
 $\pi $
-saturated. Then either
$\pi $
-saturated. Then either
 $\nu = \vert A \vert $
, or
$\nu = \vert A \vert $
, or
 and I is not
and I is not
 $(\mathrm {cf} (\nu ))^+$
-complete.
$(\mathrm {cf} (\nu ))^+$
-complete.
Proof
Corollary 5.16.
-
(i) Suppose that
 $\kappa $
is weakly inaccessible, J is weakly
$\kappa $
is weakly inaccessible, J is weakly
 $\pi $
-saturated, and (
$\pi $
-saturated, and (
 $\vert A \vert = \mathrm {cf} (\theta )$
and) I is
$\vert A \vert = \mathrm {cf} (\theta )$
and) I is
 $\vert A \vert $
-complete. Then the set of all
$\vert A \vert $
-complete. Then the set of all
 such that
such that
 $\mathrm {cf} (\vert x \cap \theta \vert ) = \mathrm {cf} (\theta )$
lies in
$\mathrm {cf} (\vert x \cap \theta \vert ) = \mathrm {cf} (\theta )$
lies in
 $J^{\ast }$
.
$J^{\ast }$
. -
(ii) Suppose that
 $\kappa $
is a successor cardinal, say
$\kappa $
is a successor cardinal, say
 $\kappa = \nu ^+$
, J is weakly
$\kappa = \nu ^+$
, J is weakly
 $\pi $
-saturated, and (
$\pi $
-saturated, and (
 $\vert A \vert = \mathrm {cf} (\theta )$
and) I is
$\vert A \vert = \mathrm {cf} (\theta )$
and) I is
 $\vert A \vert $
-complete. Then
$\vert A \vert $
-complete. Then
 $\mathrm {cf} (\nu ) = \mathrm {cf} (\theta )$
.
$\mathrm {cf} (\nu ) = \mathrm {cf} (\theta )$
.
Here is one result that specifically addresses the situation when
![]() $\mathrm {pp} (\theta ) > \theta ^+$
.
$\mathrm {pp} (\theta ) > \theta ^+$
.
Observation 5.17. Suppose that
![]() $\kappa $
is weakly inaccessible, J is normal, and
$\kappa $
is weakly inaccessible, J is normal, and
![]() $M \in J^+$
, where M denotes the set of all
$M \in J^+$
, where M denotes the set of all
![]() such that
such that
![]() $\vert x \vert \geq \vert x \cap \theta \vert ^{+ 3}$
. Then J is not weakly
$\vert x \vert \geq \vert x \cap \theta \vert ^{+ 3}$
. Then J is not weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
Claim. There is a cardinal
![]() $\sigma $
such that the set
$\sigma $
such that the set
![]() $N_{\sigma }$
of all
$N_{\sigma }$
of all
![]() $x \in M$
with
$x \in M$
with
![]() $\vert x \cap \sigma \vert = \vert x \cap \theta \vert ^{+ 3}$
lies in
$\vert x \cap \sigma \vert = \vert x \cap \theta \vert ^{+ 3}$
lies in
![]() $J^+$
.
$J^+$
.
Proof of the claim
Suppose that
![]() . Then by normality of J, we may find
. Then by normality of J, we may find
![]() $X \in J^+ \cap P (M)$
and
$X \in J^+ \cap P (M)$
and
![]() such that for any
such that for any
![]() $x \in X$
,
$x \in X$
,
![]() $\gamma \in x$
, and moreover
$\gamma \in x$
, and moreover
![]() $o.t. (x \cap \gamma ) = \vert x \cap \theta \vert ^{+ 3}$
. Put
$o.t. (x \cap \gamma ) = \vert x \cap \theta \vert ^{+ 3}$
. Put
![]() $\tau _1 = \vert \gamma \vert $
and
$\tau _1 = \vert \gamma \vert $
and
![]() $\tau _2 = \tau _1^+$
. Since
$\tau _2 = \tau _1^+$
. Since
![]() , there must be
, there must be
![]() $j \in \{1, 2\}$
and
$j \in \{1, 2\}$
and
![]() $D \in J^+ \cap P (X)$
such that
$D \in J^+ \cap P (X)$
such that
![]() $\vert x \cap \gamma \vert = \vert x \cap \tau _j \vert $
for all
$\vert x \cap \gamma \vert = \vert x \cap \tau _j \vert $
for all
![]() $x \in D$
. Set
$x \in D$
. Set
![]() $\sigma = \tau _j$
. Then clearly,
$\sigma = \tau _j$
. Then clearly,
![]() $D \subseteq N_{\sigma }$
, which completes the proof of the claim.
$D \subseteq N_{\sigma }$
, which completes the proof of the claim.
By Theorem 5.15(i), the set Q of all
![]() such that
such that
![]() $\vert x \cap \theta \vert $
is a singular cardinal greater than
$\vert x \cap \theta \vert $
is a singular cardinal greater than
![]() $\vert A \vert $
lies in
$\vert A \vert $
lies in
![]() $J^{\ast }$
. By Corollary 3.15, we may find
$J^{\ast }$
. By Corollary 3.15, we may find
![]() $x \in Q \cap N_{\sigma }$
and
$x \in Q \cap N_{\sigma }$
and
![]() $\delta \in C_{\vec {f}}$
such that (a)
$\delta \in C_{\vec {f}}$
such that (a)
![]() $\delta $
is not a good point for
$\delta $
is not a good point for
![]() $\vec {f}$
, and (b)
$\vec {f}$
, and (b)
![]() $\mathrm {cf} (\delta ) = \vert x \cap \sigma \vert ^+ = \vert x \cap \theta \vert ^{+ 4}$
. But clearly,
$\mathrm {cf} (\delta ) = \vert x \cap \sigma \vert ^+ = \vert x \cap \theta \vert ^{+ 4}$
. But clearly,
![]() $\vert x \cap \theta \vert $
is the largest limit cardinal less than or equal to
$\vert x \cap \theta \vert $
is the largest limit cardinal less than or equal to
![]() $\mathrm {cf} (\delta )$
. By Fact 3.8(i), this yields the desired contradiction.
$\mathrm {cf} (\delta )$
. By Fact 3.8(i), this yields the desired contradiction.
In situations when the scale is not good and
![]() $\mathrm {cf} (\vert x \cap \theta \vert ) = \vert A \vert $
, the following approach will help.
$\mathrm {cf} (\vert x \cap \theta \vert ) = \vert A \vert $
, the following approach will help.
Pick a sequence
![]() of pairwise disjoint stationary subsets of
of pairwise disjoint stationary subsets of
![]() $\{ \alpha < \pi : \mathrm {cf} (\alpha ) < \kappa \}$
. For
$\{ \alpha < \pi : \mathrm {cf} (\alpha ) < \kappa \}$
. For
![]() $\beta < \pi $
with
$\beta < \pi $
with
![]() $\mathrm {cf} (\beta ) < \theta $
, let
$\mathrm {cf} (\beta ) < \theta $
, let
![]() $e_{\beta }$
be the set of all
$e_{\beta }$
be the set of all
![]() $\xi < \theta $
such that
$\xi < \theta $
such that
![]() $W_{\xi } \cap \beta $
is stationary in
$W_{\xi } \cap \beta $
is stationary in
![]() $\beta $
. Note that
$\beta $
. Note that
![]() . Let
. Let
![]() $C_{\psi }$
be the set of all
$C_{\psi }$
be the set of all
![]() $x \in P_{\kappa } (\pi )$
such that
$x \in P_{\kappa } (\pi )$
such that
![]() $\psi (e_{\beta }) < \sup x$
for all
$\psi (e_{\beta }) < \sup x$
for all
![]() $\beta < \sup x$
with
$\beta < \sup x$
with
![]() $\mathrm {cf} (\beta ) < \theta $
. Strictly speaking,
$\mathrm {cf} (\beta ) < \theta $
. Strictly speaking,
![]() $C_{\psi }$
also depends on the sequence
$C_{\psi }$
also depends on the sequence
![]() . The reason that this is not reflected in our notation is that in the proofs below, it does not matter which specific sequence we choose. The same remark applies to
. The reason that this is not reflected in our notation is that in the proofs below, it does not matter which specific sequence we choose. The same remark applies to
![]() $W_{\psi }$
and
$W_{\psi }$
and
![]() $S_{\psi }$
to be introduced shortly. It is simple to see that
$S_{\psi }$
to be introduced shortly. It is simple to see that
![]() $C_{\psi } \in NS_{\kappa , \pi }^{\ast }$
. Let
$C_{\psi } \in NS_{\kappa , \pi }^{\ast }$
. Let
![]() $T_{\psi }$
be the set of all
$T_{\psi }$
be the set of all
![]() $x \in P_{\kappa } (\pi )$
such that (a)
$x \in P_{\kappa } (\pi )$
such that (a)
![]() $\sup x \notin x$
, (b)
$\sup x \notin x$
, (b)
![]() $\sup x = \psi (x)$
, and (c)
$\sup x = \psi (x)$
, and (c)
![]() .
.
Fact 5.18 [Reference Menas46].
![]() $NS_{\kappa , \theta } = q (NS_{\kappa , \pi })$
, where
$NS_{\kappa , \theta } = q (NS_{\kappa , \pi })$
, where
![]() $q : P_{\kappa } (\pi ) \rightarrow P_{\kappa } (\theta )$
is defined by
$q : P_{\kappa } (\pi ) \rightarrow P_{\kappa } (\theta )$
is defined by
![]() $q (x) = x \cap \theta $
.
$q (x) = x \cap \theta $
.
Set
![]() $W_{\psi } = \{ x \cap \theta : x \in T_{\psi } \cap C_{\psi } \}$
. Note that by Fact 5.18, if
$W_{\psi } = \{ x \cap \theta : x \in T_{\psi } \cap C_{\psi } \}$
. Note that by Fact 5.18, if
![]() $T_{\psi } \in NS_{\kappa , \pi }^+$
, then
$T_{\psi } \in NS_{\kappa , \pi }^+$
, then
![]() $W_{\psi } \in NS_{\kappa , \theta }^+$
.
$W_{\psi } \in NS_{\kappa , \theta }^+$
.
Observation 5.19. Suppose that
![]() ${\cal J}$
is normal, and K is weakly
${\cal J}$
is normal, and K is weakly
![]() $\pi $
-saturated. Then
$\pi $
-saturated. Then
![]() $W_{\psi } \in K$
.
$W_{\psi } \in K$
.
Proof Suppose otherwise. Then by Observations 5.3, 5.4, and 5.7, we may find
![]() $b \in W_{\psi }$
such that:
$b \in W_{\psi }$
such that:
-
•
 .
. -
•
 $\theta> \mathrm {cf} (h (b)) > \vert b \vert $
.
$\theta> \mathrm {cf} (h (b)) > \vert b \vert $
. -
•
 $b \subseteq e_{h (b)}$
.
$b \subseteq e_{h (b)}$
.
Select
![]() $x \in T_{\psi } \cap C_{\psi }$
such that
$x \in T_{\psi } \cap C_{\psi }$
such that
![]() $b = x \cap \theta $
. Then
$b = x \cap \theta $
. Then
so
![]() $h (b) < \psi (b) = \sup x$
. Hence,
$h (b) < \psi (b) = \sup x$
. Hence,
![]() . Contradiction.
. Contradiction.
Set
![]() . Notice that if
. Notice that if
![]() $T_{\psi }$
lies in
$T_{\psi }$
lies in
![]() $NS_{\kappa , \pi }^+$
(respectively,
$NS_{\kappa , \pi }^+$
(respectively,
![]() $(NG^{\mu }_{\kappa , \pi })^+$
,
$(NG^{\mu }_{\kappa , \pi })^+$
,
![]() $(NG^{\mu }_{\kappa , \pi })^{\ast }$
for some regular cardinal
$(NG^{\mu }_{\kappa , \pi })^{\ast }$
for some regular cardinal
![]() $\mu < \kappa $
), then by Facts 5.18 and 4.5(iii),
$\mu < \kappa $
), then by Facts 5.18 and 4.5(iii),
![]() $S_{\psi }$
lies in
$S_{\psi }$
lies in
![]() (respectively,
(respectively,
![]() ,
,
![]() ).
).
Corollary 5.20. Suppose that J is
![]() $\theta $
-normal, and
$\theta $
-normal, and
![]() $S_{\psi } \in J^{\ast }$
. Then J is not weakly
$S_{\psi } \in J^{\ast }$
. Then J is not weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
Proof Suppose otherwise. By Observation 5.1,
![]() ${\cal J}$
is normal. Moreover, it is weakly
${\cal J}$
is normal. Moreover, it is weakly
![]() $\pi $
-saturated, and by Fact 5.2(iii), so is K. Now clearly,
$\pi $
-saturated, and by Fact 5.2(iii), so is K. Now clearly,
![]() $W_{\psi }$
lies in
$W_{\psi }$
lies in
![]() ${\cal J}^{\ast }$
, and hence in
${\cal J}^{\ast }$
, and hence in
![]() $K^{\ast }$
. This contradicts Observation 5.19.
$K^{\ast }$
. This contradicts Observation 5.19.
How large is
![]() $S_{\psi }$
? The following provides some answer.
$S_{\psi }$
? The following provides some answer.
Observation 5.21. Let
![]() $\mu $
be a regular cardinal less than
$\mu $
be a regular cardinal less than
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $q : P_{\kappa } (\pi ) \rightarrow P_{\kappa } (\theta )$
be defined by
$q : P_{\kappa } (\pi ) \rightarrow P_{\kappa } (\theta )$
be defined by
![]() $q (x) = x \cap \theta $
. Then the following hold:
$q (x) = x \cap \theta $
. Then the following hold:
-
(i) Suppose that
 $\vert A \vert < \mu $
. Then
$\vert A \vert < \mu $
. Then
 $S_{\psi }$
lies in
$S_{\psi }$
lies in
 $(q (NS_{\mu , \kappa , \pi } \vert \{x : \vert x \vert = \vert x \cap \theta \vert \}))^{\ast }$
(and hence in
$(q (NS_{\mu , \kappa , \pi } \vert \{x : \vert x \vert = \vert x \cap \theta \vert \}))^{\ast }$
(and hence in
 by Fact 4.5
by Fact 4.5
 $(i)$
and
$(i)$
and
 $(iii))$
.
$(iii))$
. -
(ii) Suppose that I is
 $\mu ^+$
-complete. Then
$\mu ^+$
-complete. Then
 $S_{\psi }$
lies in
$S_{\psi }$
lies in
 $(q (N\mu $
-
$(q (N\mu $
-
 $S_{\kappa ,\pi }))^{\ast }$
(and hence in
$S_{\kappa ,\pi }))^{\ast }$
(and hence in
 by Fact 4.5
by Fact 4.5
 $(ii)$
and
$(ii)$
and
 $(iii))$
.
$(iii))$
.
Proof By Observation 4.3.
6 Recapitulation
We have been working so far with a fixed scale
![]() ${\vec f}$
. In this brief section we let the scale vary and recapitulate the corresponding results. For this we need to introduce some more members of the large family of
${\vec f}$
. In this brief section we let the scale vary and recapitulate the corresponding results. For this we need to introduce some more members of the large family of
![]() $\mathrm {pp}$
functions.
$\mathrm {pp}$
functions.
Given two infinite cardinals
![]() $\eta $
and
$\eta $
and
![]() $\chi $
such that
$\chi $
such that
![]() , and an ideal I on
, and an ideal I on
![]() $\eta $
, we put
$\eta $
, we put
![]() $\mathrm {pp}_I^{\ast }(\chi ) = \sup Y$
, where Y is the set of all cardinals
$\mathrm {pp}_I^{\ast }(\chi ) = \sup Y$
, where Y is the set of all cardinals
![]() $\pi $
for which one can find a sequence
$\pi $
for which one can find a sequence
![]() of regular infinite cardinals less than
of regular infinite cardinals less than
![]() $\chi $
with supremum
$\chi $
with supremum
![]() $\chi $
such that
$\chi $
such that
![]() for all
for all
![]() $\xi < \chi $
, and
$\xi < \chi $
, and
![]() $\mathrm {tcf} (\prod _{i < \eta } \chi _i / I ) = \pi $
.
$\mathrm {tcf} (\prod _{i < \eta } \chi _i / I ) = \pi $
.
Fact 6.1 (See, e.g., [Reference Holz, Steffens and Weitz16, Lemma 9.1.1]).
![]() $\mathrm {pp}_{\sigma } (\chi ) = \sup T$
, where T is the set of all cardinals
$\mathrm {pp}_{\sigma } (\chi ) = \sup T$
, where T is the set of all cardinals
![]() $\nu $
for which one may find an infinite cardinal
$\nu $
for which one may find an infinite cardinal
![]() and an ideal I on
and an ideal I on
![]() $\eta $
such that
$\eta $
such that
![]() $\nu = \mathrm {pp}_I^{\ast }(\chi )$
.
$\nu = \mathrm {pp}_I^{\ast }(\chi )$
.
Given three infinite cardinals
![]() $\rho $
,
$\rho $
,
![]() $\tau $
, and
$\tau $
, and
![]() $\chi $
with
$\chi $
with
![]() , let
, let
![]() $\mathrm {PP}_{\Gamma (\tau , \rho )} (\chi )$
be the collection of all cardinals
$\mathrm {PP}_{\Gamma (\tau , \rho )} (\chi )$
be the collection of all cardinals
![]() $\pi $
such that
$\pi $
such that
![]() $\pi = \mathrm {tcf} (\prod A /I )$
for some set A of regular cardinals smaller than
$\pi = \mathrm {tcf} (\prod A /I )$
for some set A of regular cardinals smaller than
![]() $\chi $
with
$\chi $
with
![]() $\vert A \vert < \tau $
and
$\vert A \vert < \tau $
and
![]() $\sup A = \chi $
, and some
$\sup A = \chi $
, and some
![]() $\rho $
-complete ideal I on A with
$\rho $
-complete ideal I on A with
![]() $\{A \cap a : a \in A \} \subseteq I$
. We let
$\{A \cap a : a \in A \} \subseteq I$
. We let
![]() $\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi ) = \sup \mathrm {PP}_{\Gamma (\tau , \rho )} (\chi )$
.
$\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi ) = \sup \mathrm {PP}_{\Gamma (\tau , \rho )} (\chi )$
.
We let
![]() $\mathrm {pp}^+_{\Gamma (\tau , \rho )} (\chi )$
equal
$\mathrm {pp}^+_{\Gamma (\tau , \rho )} (\chi )$
equal
![]() $(\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi ))^+$
if
$(\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi ))^+$
if
![]() $\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi ) \in \mathrm {PP}_{\Gamma (\tau , \rho )} (\chi )$
, and
$\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi ) \in \mathrm {PP}_{\Gamma (\tau , \rho )} (\chi )$
, and
![]() $\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi )$
otherwise. Notice that
$\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi )$
otherwise. Notice that
![]() $\mathrm {pp}^+_{\Gamma (\tau , \rho )} (\chi )$
equals
$\mathrm {pp}^+_{\Gamma (\tau , \rho )} (\chi )$
equals
![]() $(\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi ))^+$
if
$(\mathrm {pp}_{\Gamma (\tau , \rho )} (\chi ))^+$
if
![]() $\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi )$
is a successor cardinal, and
$\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi )$
is a successor cardinal, and
![]() $\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi )$
if
$\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi )$
if
![]() $\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi )$
is a singular cardinal.
$\mathrm {pp}_{\Gamma (\tau , \sigma )} (\chi )$
is a singular cardinal.
![]() $\mathrm {pp}_I^{\ast +}(\chi )$
,
$\mathrm {pp}_I^{\ast +}(\chi )$
,
![]() $\mathrm {pp}^+_{\sigma } (\chi )$
, and
$\mathrm {pp}^+_{\sigma } (\chi )$
, and
![]() $\mathrm {pp}^+ (\chi )$
are defined in the same way.
$\mathrm {pp}^+ (\chi )$
are defined in the same way.
Proposition 6.2. Suppose that
![]() $\kappa $
is a successor cardinal, say
$\kappa $
is a successor cardinal, say
![]() $\kappa = \nu ^+$
, and
$\kappa = \nu ^+$
, and
![]() $\theta $
and
$\theta $
and
![]() $\pi $
are two cardinals such that
$\pi $
are two cardinals such that
![]() . Then the following hold:
. Then the following hold:
-
(i) Suppose that
 $\mathrm {cf} (\theta ) < \mathrm {cf} (\nu )$
and
$\mathrm {cf} (\theta ) < \mathrm {cf} (\nu )$
and
 $\pi < \mathrm {pp}^+ (\theta )$
. Then there is no
$\pi < \mathrm {pp}^+ (\theta )$
. Then there is no
 $\kappa $
-complete, fine, weakly
$\kappa $
-complete, fine, weakly
 $\pi $
-saturated ideal on
$\pi $
-saturated ideal on
 .
. -
(ii) Suppose that
 $\mathrm {cf} (\theta )\not = \mathrm {cf} (\nu )$
and
$\mathrm {cf} (\theta )\not = \mathrm {cf} (\nu )$
and
 $\pi < \mathrm {pp}^+_{\Gamma ((\mathrm {cf} (\theta ))^+, (\mathrm {cf} (\nu ))^+)} (\theta )$
. Then there is no
$\pi < \mathrm {pp}^+_{\Gamma ((\mathrm {cf} (\theta ))^+, (\mathrm {cf} (\nu ))^+)} (\theta )$
. Then there is no
 $\kappa $
-complete, fine, weakly
$\kappa $
-complete, fine, weakly
 $\pi $
-saturated ideal on
$\pi $
-saturated ideal on
 .
. -
(iii) Suppose that
 $\mathrm {cf} (\theta ) = \mathrm {cf} (\nu )> \omega $
. Then for any regular cardinal
$\mathrm {cf} (\theta ) = \mathrm {cf} (\nu )> \omega $
. Then for any regular cardinal
 $\mu < \mathrm {cf} (\theta )$
such that
$\mu < \mathrm {cf} (\theta )$
such that
 $\pi < \mathrm {pp}^+_{\Gamma ((\mathrm {cf} (\theta ))^+, \mu ^+)} (\theta )$
, there is
$\pi < \mathrm {pp}^+_{\Gamma ((\mathrm {cf} (\theta ))^+, \mu ^+)} (\theta )$
, there is
 such that no
such that no
 $\theta $
-normal, fine ideal H on
$\theta $
-normal, fine ideal H on
 with
with
 $S \in H^+$
is weakly
$S \in H^+$
is weakly
 $\pi $
-saturated.
$\pi $
-saturated. -
(iv) Suppose that
 $\mathrm {cf} (\theta ) = \mathrm {cf} (\nu ) < \nu $
and
$\mathrm {cf} (\theta ) = \mathrm {cf} (\nu ) < \nu $
and
 $\pi < \mathrm {pp}^+ (\theta )$
. Then for any regular cardinal
$\pi < \mathrm {pp}^+ (\theta )$
. Then for any regular cardinal
 $\mu $
with
$\mu $
with
 $\mathrm {cf} (\theta ) <\mu < \nu $
, there is
$\mathrm {cf} (\theta ) <\mu < \nu $
, there is
 such that no
such that no
 $\theta $
-normal, fine ideal H on
$\theta $
-normal, fine ideal H on
 with
with
 $S \in H^+$
is weakly
$S \in H^+$
is weakly
 $\pi $
-saturated.
$\pi $
-saturated. -
(v) Suppose that
 $\mathrm {cf} (\theta ) = \mathrm {cf} (\nu ) = \omega $
, and
$\mathrm {cf} (\theta ) = \mathrm {cf} (\nu ) = \omega $
, and
 $\pi < \mathrm {pp}^{\ast +}_I (\theta )$
for some P-point ideal I on
$\pi < \mathrm {pp}^{\ast +}_I (\theta )$
for some P-point ideal I on
 $\omega $
. Then there is
$\omega $
. Then there is
 such that no
such that no
 $\theta $
-normal, fine ideal H on
$\theta $
-normal, fine ideal H on
 with
with
 $S \in H^+$
is weakly
$S \in H^+$
is weakly
 $\pi $
-saturated.
$\pi $
-saturated.
Proof
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
: By Theorem 5.15
$(ii)$
: By Theorem 5.15
![]() $(i)$
.
$(i)$
.
![]() $(iii)$
and
$(iii)$
and
![]() $(iv)$
: By Corollary 5.20 and Observation 5.21.
$(iv)$
: By Corollary 5.20 and Observation 5.21.
Proposition 6.3. Suppose that
![]() $\kappa $
is weakly inaccessible, and
$\kappa $
is weakly inaccessible, and
![]() $\theta $
and
$\theta $
and
![]() $\pi $
are two cardinals such that
$\pi $
are two cardinals such that
![]() . Then the following hold:
. Then the following hold:
-
(i) Suppose that
 $\pi < \mathrm {pp}^+ (\theta )$
, and let S be the set of all
$\pi < \mathrm {pp}^+ (\theta )$
, and let S be the set of all
 such that
such that
 $\mathrm {cf} (\vert x \cap \theta \vert )> \mathrm {cf} (\theta )$
. Then no
$\mathrm {cf} (\vert x \cap \theta \vert )> \mathrm {cf} (\theta )$
. Then no
 $\theta $
-normal, fine ideal H on
$\theta $
-normal, fine ideal H on
 with
with
 $S \in H^+$
is weakly
$S \in H^+$
is weakly
 $\pi $
-saturated.
$\pi $
-saturated. -
(ii) Suppose that
 $\pi < \mathrm {pp}^+_{\Gamma ((\mathrm {cf} (\theta ))^+, \tau )} (\theta )$
, where
$\pi < \mathrm {pp}^+_{\Gamma ((\mathrm {cf} (\theta ))^+, \tau )} (\theta )$
, where
 $\tau $
is an uncountable cardinal less than or equal to
$\tau $
is an uncountable cardinal less than or equal to
 $\mathrm {cf} (\theta )$
, and let S be the set of all
$\mathrm {cf} (\theta )$
, and let S be the set of all
 such that
such that
 $\mathrm {cf} (\vert x \cap \theta \vert ) < \tau $
. Then no
$\mathrm {cf} (\vert x \cap \theta \vert ) < \tau $
. Then no
 $\theta $
-normal, fine ideal H on
$\theta $
-normal, fine ideal H on
 with
with
 $S \in H^+$
is weakly
$S \in H^+$
is weakly
 $\pi $
-saturated.
$\pi $
-saturated.
Proof By Theorem 5.15
![]() $(i)$
.
$(i)$
.
7 More on
 $\mathrm {pp} (\theta )$
and weak saturation
$\mathrm {pp} (\theta )$
and weak saturation
In this section, we have a closer look at the situation when
![]() and describe some cases when no adequate, fine ideal on
and describe some cases when no adequate, fine ideal on
![]() is weakly
is weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
Fact 7.1 [Reference Matet31].
Let
![]() $\tau $
,
$\tau $
,
![]() $\theta $
, and
$\theta $
, and
![]() $\pi $
be three infinite cardinals such that
$\pi $
be three infinite cardinals such that
![]() , and let I be an ideal on
, and let I be an ideal on
![]() $\tau $
. Suppose that
$\tau $
. Suppose that
![]() , and
, and
![]() $\pi $
is either singular, or the successor of a regular cardinal. Then there is
$\pi $
is either singular, or the successor of a regular cardinal. Then there is
![]() $k_{\alpha } : \tau \rightarrow \theta $
for
$k_{\alpha } : \tau \rightarrow \theta $
for
![]() $\alpha < \pi $
with the property that for any
$\alpha < \pi $
with the property that for any
![]() $e \in P_{\theta ^+} (\pi )$
, there is
$e \in P_{\theta ^+} (\pi )$
, there is
![]() $g : e \rightarrow I$
such that
$g : e \rightarrow I$
such that
![]() $k_{\alpha } (i) < k_{\beta } (i)$
whenever
$k_{\alpha } (i) < k_{\beta } (i)$
whenever
![]() $\alpha < \beta $
are in e and
$\alpha < \beta $
are in e and
![]() $i \in \tau \setminus ( g(\alpha ) \cup g(\beta ))$
.
$i \in \tau \setminus ( g(\alpha ) \cup g(\beta ))$
.
Observation 7.2. Let
![]() $\sigma $
,
$\sigma $
,
![]() $\theta $
, and
$\theta $
, and
![]() $\pi $
be three infinite cardinals such that
$\pi $
be three infinite cardinals such that
![]() . Suppose that
. Suppose that
![]() $\pi $
is either singular, or the successor of a regular cardinal. Then there is
$\pi $
is either singular, or the successor of a regular cardinal. Then there is
![]() $z_{\alpha } \subseteq \theta $
with
$z_{\alpha } \subseteq \theta $
with
![]() for
for
![]() with the property that
with the property that
![]() for any
for any
![]() $b \in P_{\kappa } (\theta )$
.
$b \in P_{\kappa } (\theta )$
.
Proof Let us first suppose that
![]() $\pi $
is the successor of a regular cardinal. By Fact 6.1, we may find an infinite cardinal
$\pi $
is the successor of a regular cardinal. By Fact 6.1, we may find an infinite cardinal
![]() and an ideal I on
and an ideal I on
![]() $\tau $
such that
$\tau $
such that
![]() . By Fact 7.1, there must be
. By Fact 7.1, there must be
![]() $k_{\alpha } : \tau \rightarrow \theta $
for
$k_{\alpha } : \tau \rightarrow \theta $
for
![]() $\alpha < \pi $
with the property that for any
$\alpha < \pi $
with the property that for any
![]() $e \in P_{\theta ^+} (\pi )$
, there is
$e \in P_{\theta ^+} (\pi )$
, there is
![]() $g : e \rightarrow I$
such that
$g : e \rightarrow I$
such that
![]() $k_{\alpha } (i) < k_{\beta } (i)$
whenever
$k_{\alpha } (i) < k_{\beta } (i)$
whenever
![]() $\alpha < \beta $
are in e and
$\alpha < \beta $
are in e and
![]() $i \in \tau \setminus ( g(\alpha ) \cup g(\beta ))$
. For
$i \in \tau \setminus ( g(\alpha ) \cup g(\beta ))$
. For
![]() , let
, let
![]() $z_{\alpha } = \{\Phi (i, k_{\alpha } (i)) : i < \tau \}$
(recall that
$z_{\alpha } = \{\Phi (i, k_{\alpha } (i)) : i < \tau \}$
(recall that
![]() $\Phi $
denotes a one-to-one onto function from
$\Phi $
denotes a one-to-one onto function from
![]() $On \times On$
to
$On \times On$
to
![]() $On$
such that
$On$
such that
![]() $\Phi " (\sigma \times \sigma ) = \sigma $
for any infinite cardinal
$\Phi " (\sigma \times \sigma ) = \sigma $
for any infinite cardinal
![]() $\sigma $
). Let
$\sigma $
). Let
![]() $b \in P_{\kappa } (\theta )$
. Assume toward a contradiction that
$b \in P_{\kappa } (\theta )$
. Assume toward a contradiction that
![]() $\vert \{\alpha \in \pi \setminus \theta : z_{\alpha } \subseteq b\} \vert> \vert b \vert $
. Pick
$\vert \{\alpha \in \pi \setminus \theta : z_{\alpha } \subseteq b\} \vert> \vert b \vert $
. Pick
![]() $e \subseteq \pi \setminus \theta $
with
$e \subseteq \pi \setminus \theta $
with
![]() $\kappa \geq \vert e \vert> \vert b \vert $
such that
$\kappa \geq \vert e \vert> \vert b \vert $
such that
![]() $\bigcup _{\alpha \in e} z_{\alpha } \subseteq b$
. There must be
$\bigcup _{\alpha \in e} z_{\alpha } \subseteq b$
. There must be
![]() $g : e \rightarrow I$
such that
$g : e \rightarrow I$
such that
![]() $k_{\alpha } (i) < k_{\beta } (i)$
whenever
$k_{\alpha } (i) < k_{\beta } (i)$
whenever
![]() $\alpha < \beta $
are in e and
$\alpha < \beta $
are in e and
![]() $i \in \tau \setminus ( g(\alpha ) \cup g(\beta ))$
. For
$i \in \tau \setminus ( g(\alpha ) \cup g(\beta ))$
. For
![]() $\alpha \in e$
, select
$\alpha \in e$
, select
![]() $i_{\alpha }$
in
$i_{\alpha }$
in
![]() $\tau \setminus g(\alpha )$
. Then the function
$\tau \setminus g(\alpha )$
. Then the function
![]() $s : e \rightarrow b \cap \theta $
defined by
$s : e \rightarrow b \cap \theta $
defined by
![]() $s (\alpha ) = \Phi (i_{\alpha }, k_{\alpha } (i_{\alpha }))$
is one-to-one. Contradiction.
$s (\alpha ) = \Phi (i_{\alpha }, k_{\alpha } (i_{\alpha }))$
is one-to-one. Contradiction.
Now suppose that
![]() $\pi $
is singular. Pick an increasing sequence
$\pi $
is singular. Pick an increasing sequence
![]() of successors of regular cardinals greater than
of successors of regular cardinals greater than
![]() with supremum
with supremum
![]() $\pi $
. For each
$\pi $
. For each
![]() $j < \mathrm {cf} (\pi )$
, there must be
$j < \mathrm {cf} (\pi )$
, there must be
![]() $z^j_{\alpha } \subseteq \theta $
with
$z^j_{\alpha } \subseteq \theta $
with
![]() for
for
![]() with the property that
with the property that
![]() for any
for any
![]() $c \in P_{\kappa } (\theta )$
. Hence by Proposition 3.3 of [Reference Matet28], we may find
$c \in P_{\kappa } (\theta )$
. Hence by Proposition 3.3 of [Reference Matet28], we may find
![]() $z_{\alpha } \subseteq \theta $
with
$z_{\alpha } \subseteq \theta $
with
![]() for
for
![]() with the property that
with the property that
![]() for any
for any
![]() $d \in P_{\kappa } (\theta )$
.
$d \in P_{\kappa } (\theta )$
.
Proposition 7.3. Let
![]() $\sigma $
,
$\sigma $
,
![]() $\theta $
, and
$\theta $
, and
![]() $\pi $
be as in the statement of Observation 7.2, and let J be an adequate (in the sense given to this term in Section 5), fine ideal on
$\pi $
be as in the statement of Observation 7.2, and let J be an adequate (in the sense given to this term in Section 5), fine ideal on
![]() . Then J is not weakly
. Then J is not weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
Proof We use the isomorphism method of Section 3. Set
![]() $H = p (J)$
, where
$H = p (J)$
, where
![]() is defined by
is defined by
![]() $p (x) = x \cap \theta $
. By Observation 7.2, there must be
$p (x) = x \cap \theta $
. By Observation 7.2, there must be
![]() $z_{\alpha } \subseteq \theta $
with
$z_{\alpha } \subseteq \theta $
with
![]() for
for
![]() so that
so that
![]() for any
for any
![]() $b \in P_{\kappa } (\theta )$
. Put
$b \in P_{\kappa } (\theta )$
. Put
![]() $z_{\alpha } = \{\alpha \}$
for
$z_{\alpha } = \{\alpha \}$
for
![]() $\alpha < \theta $
. Define
$\alpha < \theta $
. Define
![]() $g : P_{\kappa } (\theta ) \rightarrow P (\pi )$
by
$g : P_{\kappa } (\theta ) \rightarrow P (\pi )$
by
![]() $g (b) = \{\alpha < \pi : z_{\alpha } \subseteq b\}$
. Notice that
$g (b) = \{\alpha < \pi : z_{\alpha } \subseteq b\}$
. Notice that
![]() $\vert g (b) \vert = \vert b \vert $
for any
$\vert g (b) \vert = \vert b \vert $
for any
![]() $b \in P_{\kappa } (\theta )$
. Now
$b \in P_{\kappa } (\theta )$
. Now
![]() $g (H)$
is an adequate, fine ideal on
$g (H)$
is an adequate, fine ideal on
![]() $P_{\kappa } (\pi )$
, which is not weakly
$P_{\kappa } (\pi )$
, which is not weakly
![]() $\pi $
-saturated by Facts 3.1 and 3.2. It follows that H (and hence J) is not weakly
$\pi $
-saturated by Facts 3.1 and 3.2. It follows that H (and hence J) is not weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
Corollary 7.4. Let
![]() $\sigma $
,
$\sigma $
,
![]() $\theta $
, and
$\theta $
, and
![]() $\tau $
be three infinite cardinals such that
$\tau $
be three infinite cardinals such that
![]() . Then no adequate, fine ideal on
. Then no adequate, fine ideal on
![]() is weakly
is weakly
![]() $\tau $
-saturated.
$\tau $
-saturated.
Proof Apply Proposition 7.3 with
![]() $\pi = \tau $
if
$\pi = \tau $
if
![]() $\tau $
is singular, and
$\tau $
is singular, and
![]() $\pi = \tau ^+$
otherwise.
$\pi = \tau ^+$
otherwise.
Proposition 7.3 can also be used to show that weak saturation makes scales short.
Corollary 7.5. Let
![]() $\sigma $
,
$\sigma $
,
![]() $\theta $
, and
$\theta $
, and
![]() $\tau $
be three infinite cardinals such that
$\tau $
be three infinite cardinals such that
![]() . Suppose that there exists an adequate, fine, weakly
. Suppose that there exists an adequate, fine, weakly
![]() $\tau ^{++}$
-saturated ideal on
$\tau ^{++}$
-saturated ideal on
![]() . Then
. Then
![]() .
.
Proof Apply Proposition 7.3 with
![]() $\pi = \tau ^{++}$
.
$\pi = \tau ^{++}$
.
8 More of Usuba
As indicated in its title, [Reference Usuba60] is mostly concerned with the case when
![]() has small cofinality. However its techniques can also be used in the situation when
has small cofinality. However its techniques can also be used in the situation when
![]() is regular. Take, for instance, the result of Burke and Matsubara [Reference Burke and Matsubara4] that if
is regular. Take, for instance, the result of Burke and Matsubara [Reference Burke and Matsubara4] that if
![]() is regular and there exists a
is regular and there exists a
![]() -saturated,
-saturated,
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() , then for each regular cardinal
, then for each regular cardinal
![]() $\mu < \kappa $
, any stationary subset of
$\mu < \kappa $
, any stationary subset of
![]() reflects.
reflects.
Observation 8.1. Suppose that (
![]() $\kappa $
is weakly inaccessible,)
$\kappa $
is weakly inaccessible,)
![]() is regular, and J is a weakly
is regular, and J is a weakly
![]() -saturated,
-saturated,
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() . Then the following hold.
. Then the following hold.
-
(i) Any stationary subset of
 reflects (and in fact, we can simultaneously reflect less than
reflects (and in fact, we can simultaneously reflect less than
 $\kappa $
many stationary subsets of
$\kappa $
many stationary subsets of
 ).
). -
(ii) Suppose that (J is normal or just that) for any
 $X \in J^+$
and any
$X \in J^+$
and any
 such that
such that
 $g (b) < \sup b$
for all
$g (b) < \sup b$
for all
 $b \in X$
, there is
$b \in X$
, there is
 with
with
 . Then
. Then
 (that is,
(that is,
 for any
for any
 ), and
), and
 $(b)$
for any stationary subset T of
$(b)$
for any stationary subset T of
 , the set of all
, the set of all
 with the property that
with the property that
 $T \cap \sup b$
is stationary in
$T \cap \sup b$
is stationary in
 $\sup b$
lies in
$\sup b$
lies in
 $J^{\ast }$
.
$J^{\ast }$
.
Proof
![]() $(i)$
: By Propositions 3.7 and 3.10 of [Reference Usuba60], we may find a function
$(i)$
: By Propositions 3.7 and 3.10 of [Reference Usuba60], we may find a function
and a
![]() $\kappa $
-complete, fine ideal H on
$\kappa $
-complete, fine ideal H on
extending J such that
for all
and
![]() $(2)$
for any
$(2)$
for any
such that
![]() $\{ b : g (b) < k( b) \} \in H^{\ast }$
, there is
$\{ b : g (b) < k( b) \} \in H^{\ast }$
, there is
with
. It is simple to see that
Now follow the proof of Proposition 4.2 of [Reference Usuba60] to establish that
![]() , and that of Proposition 4.3 of [Reference Usuba60] to establish that for any stationary subset T of
, and that of Proposition 4.3 of [Reference Usuba60] to establish that for any stationary subset T of
![]() , the set of all
, the set of all
![]() with the property that
with the property that
![]() $T \cap k (b)$
is stationary in
$T \cap k (b)$
is stationary in
![]() $k (b)$
lies in
$k (b)$
lies in
![]() $H^{\ast }$
.
$H^{\ast }$
.
![]() $(ii)$
: Notice that
$(ii)$
: Notice that
![]() for all
for all
![]() , and
, and
![]() for each
for each
![]() with the property that
with the property that
![]() for all
for all
![]() . Hence by Proposition 3.10 of [Reference Usuba60], for any
. Hence by Proposition 3.10 of [Reference Usuba60], for any
![]() such that
such that
![]() $\{ b : g (b) < \sup b \} \in J^{\ast }$
, there is
$\{ b : g (b) < \sup b \} \in J^{\ast }$
, there is
![]() with
with
![]() . Now proceed as in the proof of Proposition 4.2 of [Reference Usuba60] for
. Now proceed as in the proof of Proposition 4.2 of [Reference Usuba60] for
![]() $(a)$
, and as in the proof of Proposition 4.3 of [Reference Usuba60] for
$(a)$
, and as in the proof of Proposition 4.3 of [Reference Usuba60] for
![]() $(b)$
.
$(b)$
.
Thus, appealing again to Theorem 2.13 in [Reference Hayut and Lambie-Hanson15] (see also [Reference Fuchs and Lambie-Hanson11]), if
![]() is regular and there exists a weakly
is regular and there exists a weakly
![]() -saturated,
-saturated,
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() , then
, then
![]() fails for every cardinal
fails for every cardinal
![]() $\sigma < \kappa $
.
$\sigma < \kappa $
.
Usuba also proved the following.
Fact 8.2 [Reference Usuba59].
Suppose that
![]() is regular, and let J be a normal, fine ideal on
is regular, and let J be a normal, fine ideal on
![]() such that
such that
![]() $T \in J^+$
, where T is the set of all
$T \in J^+$
, where T is the set of all
![]() such that (
such that (
![]() $\sup x$
is an infinite limit ordinal and) x is not stationary in
$\sup x$
is an infinite limit ordinal and) x is not stationary in
![]() $\sup x$
. Then J is not weakly
$\sup x$
. Then J is not weakly
![]() -saturated.
-saturated.
9 The case when

For the case when
![]() is singular of cofinality greater than or equal to
is singular of cofinality greater than or equal to
![]() $\kappa $
, the following can be used.
$\kappa $
, the following can be used.
Observation 9.1. Suppose that
![]() is singular,
is singular,
![]() is an increasing sequence of regular cardinals greater than
is an increasing sequence of regular cardinals greater than
![]() $\kappa $
with supremum
$\kappa $
with supremum
![]() , and J is an ideal on
, and J is an ideal on
![]() . Suppose further that for any
. Suppose further that for any
![]() and any
and any
![]() $S \in J^+$
,
$S \in J^+$
,
![]() $p_i (J \vert S)$
is not weakly
$p_i (J \vert S)$
is not weakly
![]() -saturated, where
-saturated, where
![]() is defined by
is defined by
![]() . Then J is not weakly
. Then J is not weakly
![]() -saturated.
-saturated.
Proof By our assumption, for any
![]() , J is nowhere weakly
, J is nowhere weakly
![]() -saturated. By Fact 1.6
-saturated. By Fact 1.6
![]() $(i)$
, the desired conclusion follows.
$(i)$
, the desired conclusion follows.
10 Paradise in heaven
Shelah’s Strong Hypothesis (SSH) asserts that
![]() $\mathrm {pp}(\chi ) = \chi ^+$
for every singular cardinal
$\mathrm {pp}(\chi ) = \chi ^+$
for every singular cardinal
![]() $\chi $
.
$\chi $
.
Shelah [Reference Shelah49] (see also [Reference Matet27]) showed SSH to be equivalent to the statement that for any value of
![]() $\kappa $
and any value of
$\kappa $
and any value of
![]() ,
,
![]() equals
equals
![]() if
if
![]() , and
, and
![]() otherwise.
otherwise.
Large cardinals are needed in order to negate SSH. The exact consistency strength of the failure of SSH is not known, but it is conjectured to be roughly the same as that of the failure of SCH (the Singular Cardinal Hypothesis) that has been shown by Gitik [Reference Gitik13] to be equiconsistent with the existence of a measurable cardinal
![]() $\chi $
of Mitchell order
$\chi $
of Mitchell order
![]() $\chi ^{++}$
.
$\chi ^{++}$
.
On the other hand, just as GCH, SSH may fail everywhere (that is, it is consistent relative to a large large cardinal that
![]() $\mathrm {pp} (\sigma )> \sigma ^+$
for every singular cardinal
$\mathrm {pp} (\sigma )> \sigma ^+$
for every singular cardinal
![]() $\sigma $
[Reference Matet38]).
$\sigma $
[Reference Matet38]).
Observation 10.1. Suppose that the following hold:
-
• SSH.
-
• If
 $\kappa $
is weakly inaccessible and
$\kappa $
is weakly inaccessible and
 regular, then there is no normal, fine, precipitous ideal on
regular, then there is no normal, fine, precipitous ideal on
 .
. -
• If
 , then
, then
 holds (or just there is a good scale for
holds (or just there is a good scale for
 ).
).
Then no normal, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
Proof Case when
![]() $\kappa $
is a successor and
$\kappa $
is a successor and
![]() : By Fact 3.1.
: By Fact 3.1.
Case when
![]() $\kappa $
is weakly inaccessible and
$\kappa $
is weakly inaccessible and
![]() is regular: Recall that any normal, fine, weakly
is regular: Recall that any normal, fine, weakly
![]() -saturated ideal on
-saturated ideal on
![]() is precipitous.
is precipitous.
Case when
![]() $\kappa $
is weakly inaccessible and
$\kappa $
is weakly inaccessible and
![]() : For any regular cardinal
: For any regular cardinal
![]() $\chi $
with
$\chi $
with
![]() , we have by (the proof of) the preceding case that no normal, fine ideal on
, we have by (the proof of) the preceding case that no normal, fine ideal on
![]() $P_{\kappa } (\chi )$
is weakly
$P_{\kappa } (\chi )$
is weakly
![]() $\chi $
-saturated. Now apply Observation 9.1.
$\chi $
-saturated. Now apply Observation 9.1.
Case when
![]() : Then
: Then
![]() , and moreover
, and moreover
![]() . Now appeal to Fact 3.8
. Now appeal to Fact 3.8
![]() $(ii)$
if
$(ii)$
if
![]() $\kappa $
is a successor, and to Observation 3.14 otherwise.
$\kappa $
is a successor, and to Observation 3.14 otherwise.
Corollary 10.2. Suppose that there are no inner models with large cardinals. Then no normal, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
Corollary 10.3. Suppose that there are no inner models with large cardinals. Then the following are equivalent:
-
(i) For any values of
 $\kappa $
and
$\kappa $
and
 , no normal, fine ideal on
, no normal, fine ideal on
 is weakly
is weakly
 -saturated.
-saturated. -
(ii) Menas’s conjecture.
-
(iii)
 for any infinite cardinal
for any infinite cardinal
 $\tau $
.
$\tau $
.
Proof
-
(i)
 $\rightarrow \ (\mathrm{ii})$
: Trivial.
$\rightarrow \ (\mathrm{ii})$
: Trivial. -
(ii)
 $\rightarrow \ (\mathrm{iii})$
: Assume Menas’s conjecture, and let
$\rightarrow \ (\mathrm{iii})$
: Assume Menas’s conjecture, and let
 $\tau $
be an infinite cardinal. Set
$\tau $
be an infinite cardinal. Set
 $\kappa = \tau ^+$
and
$\kappa = \tau ^+$
and
 . Then by Observation 1.1, so
. Then by Observation 1.1, so
 .
.
-
(iii)
 $\rightarrow \ (\mathrm{i})$
: Assume
$\rightarrow \ (\mathrm{i})$
: Assume
 $(iii)$
. By Corollary 10.2, it suffices to show that for any values of
$(iii)$
. By Corollary 10.2, it suffices to show that for any values of
 $\kappa $
and
$\kappa $
and
 ,
,
 , or equivalently
, or equivalently
 , since
, since
 . Now if
. Now if
 $\kappa $
is a successor, say
$\kappa $
is a successor, say
 $\kappa = \tau ^+$
, then
$\kappa = \tau ^+$
, then
 . And if
. And if
 $\kappa $
is weakly inaccessible, then
$\kappa $
is weakly inaccessible, then 
SSH is the hard core of GCH, in the sense that [Reference Matet36] GCH = SSH + GCH at regular cardinals (i.e.,
![]() $2^{\sigma } = \sigma ^+$
for any regular cardinal
$2^{\sigma } = \sigma ^+$
for any regular cardinal
![]() $\sigma $
(this is the soft part, easily destroyed by forcing
$\sigma $
(this is the soft part, easily destroyed by forcing
![]() $))$
. Thus we would expect SSH to substitute for GCH in many articles in contemporary set-theoretic mathematics. But this is not the case, one possible explanation being that authors are often frightened of pcf theory (who isn’t?). But, to take a similar situation, the fact that they are intimidated by forcing does not prevent researchers to use it in their proofs, encouraged as they are by black box presentations of forcing that make it more accessible. Maybe something analogous should be done for pcf theory.
$))$
. Thus we would expect SSH to substitute for GCH in many articles in contemporary set-theoretic mathematics. But this is not the case, one possible explanation being that authors are often frightened of pcf theory (who isn’t?). But, to take a similar situation, the fact that they are intimidated by forcing does not prevent researchers to use it in their proofs, encouraged as they are by black box presentations of forcing that make it more accessible. Maybe something analogous should be done for pcf theory.
11 Paradise on earth (but only for the shortsighted)
In this section we show (in ZFC) that if
![]() $\kappa $
is greater than
$\kappa $
is greater than
![]() $\omega _1$
and
$\omega _1$
and
![]() close enough to
close enough to
![]() $\kappa $
, then
$\kappa $
, then
![]() holds. The crucial point is that in this setting, we have, just like under SSH, that if
holds. The crucial point is that in this setting, we have, just like under SSH, that if
![]() is regular and greater than
is regular and greater than
![]() , then it is the length of some scale. We start with the easier case, when
, then it is the length of some scale. We start with the easier case, when
![]() $\kappa $
is a successor cardinal.
$\kappa $
is a successor cardinal.
For a cardinal k,
![]() $FP (k)$
denotes the least fixed point of the aleph function greater than k.
$FP (k)$
denotes the least fixed point of the aleph function greater than k.
Fact 11.1 [Reference Matet34, Theorem 3.9 and Corollary 3.13].
Suppose that
![]() $\kappa $
is a successor cardinal, say
$\kappa $
is a successor cardinal, say
![]() $\kappa = \nu ^+$
, and
$\kappa = \nu ^+$
, and
![]() . Then
. Then
![]() is not a weakly inaccessible cardinal, and moreover there is a cardinal
is not a weakly inaccessible cardinal, and moreover there is a cardinal
![]() such that:
such that:
-
•
 and
and
 .
. -
•
 .
. -
•
 for any cardinal
for any cardinal
 $\chi $
with
$\chi $
with
 .
. -
•
 .
. -
• If
 , then
, then
 .
.
Theorem 11.2. Suppose that
![]() $\kappa $
is a successor cardinal greater than
$\kappa $
is a successor cardinal greater than
![]() $\omega _1$
, and
$\omega _1$
, and
![]() . Then
. Then
![]() holds.
holds.
Proof Let
![]() $\kappa = \nu ^+$
.
$\kappa = \nu ^+$
.
Case when
![]() . Then
. Then
![]() holds, so by Fact 3.1, no
holds, so by Fact 3.1, no
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
Notice that if
![]() is a regular cardinal greater than
is a regular cardinal greater than
![]() , then by Fact 11.1 it is a successor cardinal.
, then by Fact 11.1 it is a successor cardinal.
Case when
![]() and
and
![]() is either singular, or the successor of a regular cardinal. Then by Observation 7.2,
is either singular, or the successor of a regular cardinal. Then by Observation 7.2,
![]() holds, so by Fact 3.1, no
holds, so by Fact 3.1, no
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
Case when
![]() ,
,
![]() is the successor of a singular cardinal and
is the successor of a singular cardinal and
![]() . Then by Proposition 6.2
. Then by Proposition 6.2
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
, no
$(ii)$
, no
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
Case when
![]() ,
,
![]() is the successor of a singular cardinal, and
is the successor of a singular cardinal, and
![]() . Then by Proposition 6.2
. Then by Proposition 6.2
![]() $((iv)$
if
$((iv)$
if
![]() $\mathrm {cf} (\nu ) = \omega $
, and
$\mathrm {cf} (\nu ) = \omega $
, and
![]() $(iii)$
and
$(iii)$
and
![]() $(iv)$
otherwise), for any regular cardinal
$(iv)$
otherwise), for any regular cardinal
![]() , there is
, there is
![]() such that no
such that no
![]() -normal, fine ideal H on
-normal, fine ideal H on
![]() with
with
![]() $S \in H^+$
is weakly
$S \in H^+$
is weakly
![]() -saturated.
-saturated.
Our results are far more modest in the case when
![]() $\kappa $
is weakly inaccessible. This is due to our approach in [Reference Matet34] where this case is reduced to the successor case (with the successor cardinal in question being at the first stage
$\kappa $
is weakly inaccessible. This is due to our approach in [Reference Matet34] where this case is reduced to the successor case (with the successor cardinal in question being at the first stage
![]() $\kappa ^+$
).
$\kappa ^+$
).
Fact 11.3 [Reference Matet34].
Suppose that
![]() $\kappa $
is weakly inaccessible, and let
$\kappa $
is weakly inaccessible, and let
![]() $n < \omega $
. Then the following hold:
$n < \omega $
. Then the following hold:
-
(i)
 $u (\kappa , \kappa ^{+(\kappa \cdot n)}) = \kappa ^{+(\kappa \cdot n)}$
.
$u (\kappa , \kappa ^{+(\kappa \cdot n)}) = \kappa ^{+(\kappa \cdot n)}$
. -
(ii) Suppose that
 and
and
 . Then
. Then
 is a successor cardinal, and moreover
is a successor cardinal, and moreover
 .
.
Theorem 11.4. Suppose that
![]() $\kappa $
is weakly inaccessible, and
$\kappa $
is weakly inaccessible, and
![]() . Then
. Then
![]() holds.
holds.
Proof Let
![]() $n < \omega $
be such that
$n < \omega $
be such that
![]() .
.
Case when
![]() and
and
![]() is regular. Let S be the set of all
is regular. Let S be the set of all
![]() such that (
such that (
![]() $o.t. (x)$
is an infinite limit ordinal and) either
$o.t. (x)$
is an infinite limit ordinal and) either
![]() $\mathrm {cf} (o.t. (x)) < o.t. (x)$
, or x is not stationary in
$\mathrm {cf} (o.t. (x)) < o.t. (x)$
, or x is not stationary in
![]() $\sup x$
. Then by Facts 3.4 and 8.2, no normal, fine ideal J on
$\sup x$
. Then by Facts 3.4 and 8.2, no normal, fine ideal J on
![]() with
with
![]() $S \in J^+$
is weakly
$S \in J^+$
is weakly
![]() -saturated.
-saturated.
Case when
![]() and
and
![]() . Then
. Then
![]() . For
. For
![]() $i < \kappa $
, set
$i < \kappa $
, set
![]() $\alpha _i = \kappa \cdot (n - 1) + i$
and
$\alpha _i = \kappa \cdot (n - 1) + i$
and
![]() . Put
. Put
![]() , where
, where
![]() $S_i$
is the set of all
$S_i$
is the set of all
![]() with the property that
with the property that
![]() $o.t. (a)$
is an infinite limit ordinal such that either
$o.t. (a)$
is an infinite limit ordinal such that either
![]() $\mathrm {cf} (o.t. (a)) < o.t. (a)$
, or a is not stationary in
$\mathrm {cf} (o.t. (a)) < o.t. (a)$
, or a is not stationary in
![]() $\sup a$
.
$\sup a$
.
Claim.
![]() .
.
Proof of the claim
Fix a closed unbounded subset C of
![]() . For
. For
![]() , set
, set
![]() $e_x = \{ i < \kappa : x \setminus \kappa ^{+ \alpha _i} \not = \emptyset \}$
. Inductively define
$e_x = \{ i < \kappa : x \setminus \kappa ^{+ \alpha _i} \not = \emptyset \}$
. Inductively define
![]() and
and
![]() $c_n \in C$
for
$c_n \in C$
for
![]() $n < \omega $
so that:
$n < \omega $
so that:
-
•
 $x_0 = \omega _1$
.
$x_0 = \omega _1$
. -
•
 $x_n \subseteq c_n$
.
$x_n \subseteq c_n$
. -
•
 .
.
Finally, set
![]() $x = \bigcup _{n < \omega } x_n$
. The following are readily checked:
$x = \bigcup _{n < \omega } x_n$
. The following are readily checked:
-
•
 $x \in C$
.
$x \in C$
. -
•
 $e_x = x \cap \kappa $
.
$e_x = x \cap \kappa $
. -
•
 $x \cap \kappa $
is a limit ordinal of cofinality
$x \cap \kappa $
is a limit ordinal of cofinality
 $\omega $
.
$\omega $
. -
•
 $\sup x = \kappa ^{+ \alpha _{x \cap \kappa }}$
.
$\sup x = \kappa ^{+ \alpha _{x \cap \kappa }}$
. -
•
 for all
for all
 $i \in e_x$
.
$i \in e_x$
. -
• For any
 $i \in \kappa \setminus e_x$
,
$i \in \kappa \setminus e_x$
,
 (and hence
(and hence
 ).
).
Thus
![]() $x \in C \cap S$
, which completes the proof of the claim.
$x \in C \cap S$
, which completes the proof of the claim.
Finally by Observation 9.1, no normal, fine ideal J on
![]() with
with
![]() $S \in J^+$
is weakly
$S \in J^+$
is weakly
![]() -saturated.
-saturated.
Case when
![]() . Then by Facts 11.1 and 11.3,
. Then by Facts 11.1 and 11.3,
![]() is a successor cardinal, and moreover
is a successor cardinal, and moreover
![]() , where
, where
![]() $\chi $
is the successor cardinal
$\chi $
is the successor cardinal
![]() $\kappa ^{+(\kappa \cdot n) + 1}$
. Notice that
$\kappa ^{+(\kappa \cdot n) + 1}$
. Notice that
![]() , so
, so
![]() . Let S be the set of all
. Let S be the set of all
![]() such that
such that
![]() . Then by Proposition 6.3, no
. Then by Proposition 6.3, no
![]() -normal, fine ideal J on
-normal, fine ideal J on
![]() with
with
![]() $S \in J^+$
is weakly
$S \in J^+$
is weakly
![]() -saturated.
-saturated.
To conclude this section we remark that if
![]() ,
,
![]() is close to
is close to
![]() $\kappa $
and there are no inner models with large large cardinals, then no normal, fine ideal J on
$\kappa $
and there are no inner models with large large cardinals, then no normal, fine ideal J on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
Observation 11.5. Suppose that
![]() , and
, and
![]() $\square _{\tau }^{\ast }$
holds for every singular cardinal
$\square _{\tau }^{\ast }$
holds for every singular cardinal
![]() $\tau $
with
$\tau $
with
![]() . Then the following hold:
. Then the following hold:
-
(i) If
 $\kappa $
is a successor cardinal, and
$\kappa $
is a successor cardinal, and
 , then no
, then no
 $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
 is weakly
is weakly
 -saturated.
-saturated. -
(ii) If
 $\kappa $
is weakly inaccessible, and
$\kappa $
is weakly inaccessible, and
 , then no normal, fine ideal on
, then no normal, fine ideal on
 is weakly
is weakly
 -saturated.
-saturated.
Proof To start with we define
![]() $\chi $
by:
$\chi $
by:
![]() $\chi $
equals
$\chi $
equals
![]() $\kappa $
if
$\kappa $
if
![]() $\kappa $
is a successor cardinal, and
$\kappa $
is a successor cardinal, and
![]() $\kappa ^{+ (\kappa \cdot n + 1)}$
, where
$\kappa ^{+ (\kappa \cdot n + 1)}$
, where
![]() , otherwise. By Fact 11.1 and the proof of Theorem 11.4, the following hold:
, otherwise. By Fact 11.1 and the proof of Theorem 11.4, the following hold:
-
•
 .
. -
•
 .
. -
•
 is not a weakly inaccessible cardinal.
is not a weakly inaccessible cardinal.
Case when
![]() is either singular, or the successor of a regular cardinal. Then by Proposition 7.3, we have the following:
is either singular, or the successor of a regular cardinal. Then by Proposition 7.3, we have the following:
-
• If
 $\kappa $
is a successor cardinal, then no
$\kappa $
is a successor cardinal, then no
 $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
 is weakly
is weakly
 -saturated.
-saturated. -
• If
 $\kappa $
is weakly inaccessible, then no
$\kappa $
is weakly inaccessible, then no
 -normal, fine ideal on
-normal, fine ideal on
 is weakly
is weakly
 -saturated.
-saturated.
Case when
![]() is the successor of a singular cardinal
is the successor of a singular cardinal
![]() $\tau $
. Then
$\tau $
. Then
![]() for some A and I such that:
for some A and I such that:
-
• A is a set of regular cardinals smaller than
 such that
such that
 and
and
 .
. -
• I is an ideal on A with
 $\{A \cap a : a \in A \} \subseteq I$
.
$\{A \cap a : a \in A \} \subseteq I$
.
Select an increasing, cofinal sequence
![]() $\vec {f}$
in
$\vec {f}$
in
![]() $(\prod A, <_I)$
. We know that
$(\prod A, <_I)$
. We know that
![]() $\square _{\tau }^{\ast }$
holds, so by the remark at the end of Section 3.3, the scale
$\square _{\tau }^{\ast }$
holds, so by the remark at the end of Section 3.3, the scale
![]() $\vec {f}$
is good. Now if
$\vec {f}$
is good. Now if
![]() $\kappa $
is a successor cardinal, then
$\kappa $
is a successor cardinal, then
![]() holds by Fact 3.8
holds by Fact 3.8
![]() $(ii)$
, and consequently by Fact 3.1, no
$(ii)$
, and consequently by Fact 3.1, no
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() is weakly
is weakly
![]() -saturated. Finally, if
-saturated. Finally, if
![]() $\kappa $
is weakly inaccessible, then by Observation 3.14, no
$\kappa $
is weakly inaccessible, then by Observation 3.14, no
![]() -normal, fine ideal on
-normal, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
12 A poor man’s version
The top-down approach (stating an optimal-looking result and then trying to prove it) did not work so well, so let us see whether we fare better with the bottom-up approach (formulating a result corresponding to the available proofs). We have already seen how to handle the case when
![]() . So our starting point is a situation in which
. So our starting point is a situation in which
![]() and we have a normal, fine ideal J on
and we have a normal, fine ideal J on
![]() . The way we see it, our first problem is to produce large disjoint families in
. The way we see it, our first problem is to produce large disjoint families in
![]() $J^+$
. Once this is achieved, it will be time to see whether we can actually find such families of size
$J^+$
. Once this is achieved, it will be time to see whether we can actually find such families of size
![]() .
.
Adding yet a new
![]() $\mathrm {pp}$
function to the already long list of existing ones, we let
$\mathrm {pp}$
function to the already long list of existing ones, we let
We let
![]() assert the existence of S in
assert the existence of S in
![]() with the property that no normal, fine ideal J on
with the property that no normal, fine ideal J on
![]() with
with
![]() $S \in J^+$
is weakly
$S \in J^+$
is weakly
![]() -saturated.
-saturated.
Given four cardinals
![]() $\rho _1, \rho _2, \rho _3, \rho _4$
with
$\rho _1, \rho _2, \rho _3, \rho _4$
with
![]() $\rho _1 \geq \rho _2 \geq \rho _3 \geq \omega $
and
$\rho _1 \geq \rho _2 \geq \rho _3 \geq \omega $
and
![]() $\rho _3 \geq \rho _4 \geq 2$
, the covering number
$\rho _3 \geq \rho _4 \geq 2$
, the covering number
![]() $\mathrm {cov} (\rho _1, \rho _2, \rho _3, \rho _4)$
denotes the least cardinality of any
$\mathrm {cov} (\rho _1, \rho _2, \rho _3, \rho _4)$
denotes the least cardinality of any
![]() $X \subseteq P_{\rho _2}(\rho _1)$
such that for any
$X \subseteq P_{\rho _2}(\rho _1)$
such that for any
![]() $a \in P_{\rho _3}(\rho _1)$
, there is
$a \in P_{\rho _3}(\rho _1)$
, there is
![]() $Q \in P_{\rho _4}(X)$
with
$Q \in P_{\rho _4}(X)$
with
![]() $a \subseteq \bigcup Q$
.
$a \subseteq \bigcup Q$
.
Note that
![]() .
.
Fact 12.1. Let
![]() $\tau $
and
$\tau $
and
![]() $\chi $
be two cardinals such that
$\chi $
be two cardinals such that
![]() . Then the following hold:
. Then the following hold:
-
(i) [Reference Shelah50, 15.7]
 $\mathrm {cf} (\mathrm {pp}_{\tau } (\chi ))> \tau $
.
$\mathrm {cf} (\mathrm {pp}_{\tau } (\chi ))> \tau $
. -
(ii) [Reference Shelah50, Theorem 5.4, p. 87]
 .
.
Observation 12.2.
![]() .
.
Proof Let
![]() $\tau $
and
$\tau $
and
![]() $\chi $
be two cardinals such that
$\chi $
be two cardinals such that
![]() . Then by Fact 12.1
. Then by Fact 12.1
![]() $(ii)$
,
$(ii)$
,
 .
.
Thus
![]() is a weaker variant of
is a weaker variant of
![]() . Too little is known about how
. Too little is known about how
![]() and
and
![]() compare. For instance it is tempting to think that
compare. For instance it is tempting to think that
![]() if and only if
if and only if
![]() , but we do not know whether this holds.
, but we do not know whether this holds.
13 Which way to paradise, please?
In the next section we will attempt to establish that
![]() holds for any values of
holds for any values of
![]() $\kappa $
and
$\kappa $
and
![]() , but will fail to do so, and will end up proving something weaker. The case we have trouble with is when
, but will fail to do so, and will end up proving something weaker. The case we have trouble with is when
![]() , which, we recall, is
, which, we recall, is
![]() with
with
![]() $\sigma = \omega $
, is greater than
$\sigma = \omega $
, is greater than
![]() and weakly inaccessible. In the present section we show that, as often in pcf theory, the situation is more manageable when
and weakly inaccessible. In the present section we show that, as often in pcf theory, the situation is more manageable when
![]() $\sigma $
is uncountable.
$\sigma $
is uncountable.
Observation 13.1. Let
![]() $\theta , k, \rho $
, and
$\theta , k, \rho $
, and
![]() $\sigma $
be four cardinals with
$\sigma $
be four cardinals with
![]() $\theta \geq k \geq \rho> \sigma = \mathrm {cf} (\sigma ) > \omega $
. Suppose that
$\theta \geq k \geq \rho> \sigma = \mathrm {cf} (\sigma ) > \omega $
. Suppose that
![]() $\mathrm {cov} (\theta , k, \rho , \sigma )$
is weakly inaccessible and greater than
$\mathrm {cov} (\theta , k, \rho , \sigma )$
is weakly inaccessible and greater than
![]() $\theta $
. Then there is a cardinal
$\theta $
. Then there is a cardinal
![]() $\chi $
such that
$\chi $
such that
![]() and
and
![]() and a cardinal
and a cardinal
![]() $\pi \geq \mathrm {cov} (\theta , k, \rho , \sigma )$
such that
$\pi \geq \mathrm {cov} (\theta , k, \rho , \sigma )$
such that
![]() $\pi \in \mathrm {PP}_{\Gamma (\rho , \sigma )} (\chi )$
.
$\pi \in \mathrm {PP}_{\Gamma (\rho , \sigma )} (\chi )$
.
Proof By [Reference Shelah50, Theorem 5.4, pp. 87–88], we may find an infinite cardinal
![]() $\tau < \rho $
, a
$\tau < \rho $
, a
![]() $\sigma $
-complete ideal J on
$\sigma $
-complete ideal J on
![]() $\tau $
, and a sequence
$\tau $
, and a sequence
![]() of regular cardinals greater than
of regular cardinals greater than
![]() $\rho $
and less than or equal to
$\rho $
and less than or equal to
![]() $\theta $
, and a cardinal
$\theta $
, and a cardinal
![]() $\pi \geq \mathrm {cov} (\theta , k, \rho , \sigma )$
such that
$\pi \geq \mathrm {cov} (\theta , k, \rho , \sigma )$
such that
![]() $\pi = \mathrm {tcf}(\prod _{i < \tau } \nu _i /J )$
. Select an increasing, cofinal sequence
$\pi = \mathrm {tcf}(\prod _{i < \tau } \nu _i /J )$
. Select an increasing, cofinal sequence
![]() in
in
![]() $\prod _{i < \tau } \nu _i /J$
.
$\prod _{i < \tau } \nu _i /J$
.
Let
![]() $\chi $
be the least cardinal
$\chi $
be the least cardinal
![]() $\mu $
such that
$\mu $
such that
![]() . Note that
. Note that
![]() . Set
. Set
![]() $e = \{i < \tau : \nu _i = \chi \}$
.
$e = \{i < \tau : \nu _i = \chi \}$
.
Claim 1.
![]() $e \in J$
.
$e \in J$
.
Proof of Claim 1
Suppose otherwise. Then clearly,
![]() $\chi $
is regular. For
$\chi $
is regular. For
![]() $\alpha < \pi $
, put
$\alpha < \pi $
, put
![]() $\delta _{\alpha } = \sup \{ f_{\alpha } (i) : i \in e \}$
. Note that
$\delta _{\alpha } = \sup \{ f_{\alpha } (i) : i \in e \}$
. Note that
![]() $\delta _{\alpha } < \chi $
, since
$\delta _{\alpha } < \chi $
, since
![]() . Define
. Define
![]() $g_{\alpha } : e \rightarrow \chi $
by:
$g_{\alpha } : e \rightarrow \chi $
by:
![]() $g_{\alpha } (i) = \delta _{\alpha }$
for all
$g_{\alpha } (i) = \delta _{\alpha }$
for all
![]() $i \in e$
. Since
$i \in e$
. Since
![]() , we may find
, we may find
![]() $\delta < \chi $
and
$\delta < \chi $
and
![]() $d \subseteq \pi $
with
$d \subseteq \pi $
with
![]() $\vert d \vert = \pi $
such that
$\vert d \vert = \pi $
such that
![]() $\delta _{\alpha } = \delta $
for all
$\delta _{\alpha } = \delta $
for all
![]() $\alpha \in d$
. Now setting
$\alpha \in d$
. Now setting
![]() $K = J \vert e$
,
$K = J \vert e$
,
![]() is cofinal in
is cofinal in
![]() $\prod _{i \in e} \nu _i /K$
, and hence so are
$\prod _{i \in e} \nu _i /K$
, and hence so are
![]() and
and
![]() . But if we define
. But if we define
![]() $k : e \rightarrow \chi $
by:
$k : e \rightarrow \chi $
by:
![]() $k (i) = \delta + 1$
for all
$k (i) = \delta + 1$
for all
![]() $i \in e$
, then for all
$i \in e$
, then for all
![]() $\alpha \in d$
and all
$\alpha \in d$
and all
![]() $i \in e$
,
$i \in e$
,
![]() $g_{\alpha } (i) < k (i)$
. This contradiction completes the proof of the claim.
$g_{\alpha } (i) < k (i)$
. This contradiction completes the proof of the claim.
Set
![]() and
and
![]() $K = J \vert w$
. Then by Lemma 3.1.7 in [Reference Holz, Steffens and Weitz16],
$K = J \vert w$
. Then by Lemma 3.1.7 in [Reference Holz, Steffens and Weitz16],
![]() $\pi = \mathrm {tcf}(\prod _{i \in w} \nu _i /K )$
. Note that by the definition of
$\pi = \mathrm {tcf}(\prod _{i \in w} \nu _i /K )$
. Note that by the definition of
![]() $\chi $
,
$\chi $
,
![]() $\sup \{ \nu _i : i \in w \} = \chi $
. It follows that
$\sup \{ \nu _i : i \in w \} = \chi $
. It follows that
![]() . Furthermore,
. Furthermore,
![]() by
by
![]() $\sigma $
-completeness of K.
$\sigma $
-completeness of K.
Put
![]() $A = \{ \nu _i : i \in w \}$
, and for each
$A = \{ \nu _i : i \in w \}$
, and for each
![]() $a \in A$
,
$a \in A$
,
![]() $t_a = \{ i \in w : \nu _i = a \}$
. Define
$t_a = \{ i \in w : \nu _i = a \}$
. Define
![]() $s : w \rightarrow A$
by
$s : w \rightarrow A$
by
![]() $s (i) = \nu _i$
, and let
$s (i) = \nu _i$
, and let
![]() $I = s (K)$
. Then clearly, I is a
$I = s (K)$
. Then clearly, I is a
![]() $\sigma $
-complete ideal on A. Note that by the minimality of
$\sigma $
-complete ideal on A. Note that by the minimality of
![]() $\chi $
,
$\chi $
,
![]() $\{A \cap a : a \in A \} \subseteq I$
. Define
$\{A \cap a : a \in A \} \subseteq I$
. Define
![]() $G : \prod _{i \in w} \nu _i \rightarrow \prod A$
by:
$G : \prod _{i \in w} \nu _i \rightarrow \prod A$
by:
![]() $G (f) (a) = \sup \{ f (i) : i \in t_a \}$
.
$G (f) (a) = \sup \{ f (i) : i \in t_a \}$
.
Claim 2. Let
![]() $r \in \prod A$
. Then there is
$r \in \prod A$
. Then there is
![]() $u \in \prod _{i \in w} \nu _i$
with the property that
$u \in \prod _{i \in w} \nu _i$
with the property that
![]() $r <_I G (q)$
for any
$r <_I G (q)$
for any
![]() $q \in \prod _{i \in w} \nu _i$
with
$q \in \prod _{i \in w} \nu _i$
with
![]() .
.
Proof of Claim 2
Define
![]() $u \in \prod _{i \in w} \nu _i$
by
$u \in \prod _{i \in w} \nu _i$
by
![]() $u (i) = r (\nu _i) + 1$
. Now fix
$u (i) = r (\nu _i) + 1$
. Now fix
![]() $q \in \prod _{i \in w} \nu _i$
with
$q \in \prod _{i \in w} \nu _i$
with
![]() . Set
. Set
![]() and
and
![]() $c = s"b$
. Then
$c = s"b$
. Then
![]() $c \in I^{\ast }$
, since
$c \in I^{\ast }$
, since
![]() $b \in K^{\ast }$
. It is simple to see that
$b \in K^{\ast }$
. It is simple to see that
![]() $r (a) < G (f) (a)$
for all
$r (a) < G (f) (a)$
for all
![]() $a \in c$
. Thus
$a \in c$
. Thus
![]() $r <_I G (f)$
, which completes the proof of the claim.
$r <_I G (f)$
, which completes the proof of the claim.
By Lemma 3.1.10 of [Reference Holz, Steffens and Weitz16], it follows from Claim 2 that
![]() $\mathrm {tcf}(\prod A /I )$
exists and is equal to
$\mathrm {tcf}(\prod A /I )$
exists and is equal to
![]() $\mathrm {tcf}(\prod _{i \in w} \nu _i /K )$
. Thus
$\mathrm {tcf}(\prod _{i \in w} \nu _i /K )$
. Thus
![]() $\pi \in \mathrm {PP}_{\Gamma (\rho , \sigma )} (\chi )$
.
$\pi \in \mathrm {PP}_{\Gamma (\rho , \sigma )} (\chi )$
.
Observation 13.2. Suppose that
![]() is greater than
is greater than
![]() and weakly inaccessible. Then there is
and weakly inaccessible. Then there is
![]() such that no normal, fine ideal H on
such that no normal, fine ideal H on
![]() with
with
![]() $S \in H^+$
is weakly
$S \in H^+$
is weakly
![]() -saturated.
-saturated.
Proof By Observation 13.1, we may find two cardinals
![]() $\chi $
and
$\chi $
and
![]() $\pi $
such that:
$\pi $
such that:
-
•
 .
. -
•
 .
. -
•
 $\pi \in \mathrm {PP}_{\Gamma (\kappa , \omega _1)} (\chi )$
.
$\pi \in \mathrm {PP}_{\Gamma (\kappa , \omega _1)} (\chi )$
.
Case when
![]() $\kappa $
is weakly inaccessible. Put
$\kappa $
is weakly inaccessible. Put
![]() . Then by Corollary 5.16, no
. Then by Corollary 5.16, no
![]() $\chi $
-normal, fine ideal H on
$\chi $
-normal, fine ideal H on
![]() with
with
![]() $S \in H^+$
is weakly
$S \in H^+$
is weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
Case when
![]() $\kappa $
is a successor cardinal. By Corollary 5.20 and Observation 5.21, there is
$\kappa $
is a successor cardinal. By Corollary 5.20 and Observation 5.21, there is
![]() with the property that no
with the property that no
![]() $\chi $
-normal, fine ideal H on
$\chi $
-normal, fine ideal H on
![]() with
with
![]() $S \in H^+$
is weakly
$S \in H^+$
is weakly
![]() $\pi $
-saturated.
$\pi $
-saturated.
14 Paradise not found
In this section we establish that
![]() holds for many values of
holds for many values of
![]() $\kappa $
and
$\kappa $
and
![]() . We start by computing
. We start by computing
![]() . We will show that if
. We will show that if
![]() , then
, then
![]() for some cardinal
for some cardinal
![]() $\theta $
with
$\theta $
with
![]() . We need some facts from pcf theory.
. We need some facts from pcf theory.
Fact 14.1 [Reference Shelah50, Conclusion 2.3(2), p. 57].
Let
![]() $\sigma , \tau $
and
$\sigma , \tau $
and
![]() $\chi $
be three infinite cardinals such that
$\chi $
be three infinite cardinals such that
![]() . Then
. Then
![]() .
.
Fact 14.2 [Reference Matet34].
Let
![]() $\theta $
, A, I, and
$\theta $
, A, I, and
![]() $\pi $
be such that:
$\pi $
be such that:
-
•
 $\theta $
is a singular cardinal of cofinality
$\theta $
is a singular cardinal of cofinality
 $\omega $
.
$\omega $
. -
• A is a set of regular cardinals less than
 $\theta $
with
$\theta $
with
 $\sup A = \theta $
and
$\sup A = \theta $
and
 $\vert A \vert < \min A$
.
$\vert A \vert < \min A$
. -
• I is an ideal on A with
 $\{A \cap a : a \in A\} \subseteq I$
.
$\{A \cap a : a \in A\} \subseteq I$
. -
•
 $\mathrm {tcf}(\prod A/I) = \pi $
.
$\mathrm {tcf}(\prod A/I) = \pi $
. -
•
 $\mathrm {pp}_{\vert A \vert } (\chi ) < \theta $
for any singular cardinal
$\mathrm {pp}_{\vert A \vert } (\chi ) < \theta $
for any singular cardinal
 $\chi $
with
$\chi $
with
 and
and
 $\min A < \chi < \theta $
.
$\min A < \chi < \theta $
.
Then
![]() $\mathrm {tcf}(\prod B/J) = \pi $
for some countable set B of regular cardinals less than
$\mathrm {tcf}(\prod B/J) = \pi $
for some countable set B of regular cardinals less than
![]() $\theta $
with
$\theta $
with
![]() and
and
![]() $\sup B = \theta $
, and some ideal J on B with
$\sup B = \theta $
, and some ideal J on B with
![]() $\{B \cap b : b \in B\} \subseteq J$
.
$\{B \cap b : b \in B\} \subseteq J$
.
Fact 14.3 [Reference Shelah50, Conclusion 1.6(3), p. 321].
Let
![]() $\tau $
and
$\tau $
and
![]() $\theta $
be two cardinals such that
$\theta $
be two cardinals such that
![]() . Suppose that
. Suppose that
![]() $\mathrm {pp}_{\tau } (\chi ) < \theta $
for any large enough singular cardinal
$\mathrm {pp}_{\tau } (\chi ) < \theta $
for any large enough singular cardinal
![]() $\chi < \theta $
with
$\chi < \theta $
with
![]() . Then
. Then
Fact 14.4 [Reference Shelah50, Theorem 5.4, pp. 87–88].
Let
![]() $\theta , k, \rho $
, and
$\theta , k, \rho $
, and
![]() $\sigma $
be four cardinals with
$\sigma $
be four cardinals with
![]() $\theta \geq k \geq \rho> \sigma = \mathrm {cf} (\sigma ) > \omega $
. Then
$\theta \geq k \geq \rho> \sigma = \mathrm {cf} (\sigma ) > \omega $
. Then
where Q denotes the set of all cardinals
![]() $\chi $
such that
$\chi $
such that
![]() and
and
![]() .
.
Observation 14.5. Suppose that
![]() . Let
. Let
![]() be the least cardinal
be the least cardinal
![]() $\chi $
such that for some
$\chi $
such that for some
![]() $\tau $
,
$\tau $
,
![]() and
and
![]() , and let
, and let
![]() be the least such
be the least such
![]() $\tau $
. Then the following hold:
$\tau $
. Then the following hold:
-
(i) Let
 $\tau $
and
$\tau $
and
 $\chi $
be two cardinals such that
$\chi $
be two cardinals such that
 and
and
 . Then
. Then
 .
. -
(ii) Let
 $\tau $
and
$\tau $
and
 $\chi $
be two cardinals such that
$\chi $
be two cardinals such that
 . Then
. Then
 .
. -
(iii) Suppose
 . Then
. Then
 ,
,
 ,
,
 , and
, and
 for any cardinal
for any cardinal
 $\tau $
with
$\tau $
with
 .
. -
(iv) Suppose
 . Then
. Then
 ,
,
 ,
,
 , and
, and
 for any cardinal
for any cardinal
 $\tau $
with
$\tau $
with
 .
.
Proof
-
(i): This follows from Fact 14.1, since
 .
. -
(ii): Suppose otherwise. Then, by Fact 14.1,
 . Contradiction.
. Contradiction. -
(iii): Let us first show that
 . Suppose otherwise. Then we may find A and I such that:
. Suppose otherwise. Then we may find A and I such that:-
• A is a set of regular infinite cardinals smaller than
 .
. -
•
 .
. -
•
 $\min A> \kappa $
.
$\min A> \kappa $
. -
•
 .
. -
• I is a prime ideal on A such that
 $\{A \cap a : a \in A \} \subseteq I$
$\{A \cap a : a \in A \} \subseteq I$
-
•
 .
.
-
By
![]() $(ii)$
,
$(ii)$
,
![]() for any singular cardinal
for any singular cardinal
![]() $\chi $
with
$\chi $
with
![]() and
and
![]() . Hence, by Fact 14.2,
. Hence, by Fact 14.2,
![]() $\mathrm {tcf}(\prod B/J) = \mathrm {tcf}(\prod A /I )$
for some countable set B of regular cardinals less than
$\mathrm {tcf}(\prod B/J) = \mathrm {tcf}(\prod A /I )$
for some countable set B of regular cardinals less than
![]() with
with
![]() and
and
![]() , and some ideal J on B with
, and some ideal J on B with
![]() $\{B \cap b : b \in B\} \subseteq J$
. Contradiction.
$\{B \cap b : b \in B\} \subseteq J$
. Contradiction.
Clearly,
![]() . By Fact 12.1
. By Fact 12.1
![]() $(ii)$
,
$(ii)$
,
![]() . Furthermore by
. Furthermore by
![]() $(ii)$
,
$(ii)$
,
![]() whenever
whenever
![]() $\tau $
and
$\tau $
and
![]() $\chi $
are two cardinals such that
$\chi $
are two cardinals such that
![]() and
and
![]() .
.
Claim. Let
![]() $\tau $
be a cardinal such that
$\tau $
be a cardinal such that
![]() $\omega < \tau < \kappa $
. Then
$\omega < \tau < \kappa $
. Then
![]() .
.
Proof of the claim
Suppose otherwise. Then we may find A and I such that:
-
• A is a set of regular infinite cardinals smaller than
 $\theta $
.
$\theta $
. -
•
 .
. -
•
 $\min A> \kappa $
.
$\min A> \kappa $
. -
•
 $\vert A \vert> \aleph _0$
.
$\vert A \vert> \aleph _0$
. -
• I is a prime ideal on A such that
 $\{A \cap a : a \in A \} \subseteq I$
.
$\{A \cap a : a \in A \} \subseteq I$
. -
•
 .
.
By
![]() $(ii)$
,
$(ii)$
,
![]() for any singular cardinal
for any singular cardinal
![]() $\chi $
with
$\chi $
with
![]() and
and
![]() . Hence by Fact 14.2,
. Hence by Fact 14.2,
![]() $\mathrm {tcf}(\prod B/J) = \mathrm {tcf}(\prod A /I )$
for some countable set B of regular cardinals less than
$\mathrm {tcf}(\prod B/J) = \mathrm {tcf}(\prod A /I )$
for some countable set B of regular cardinals less than
![]() with
with
![]() and
and
![]() , and some ideal J on B with
, and some ideal J on B with
![]() $\{B \cap b : b \in B\} \subseteq J$
. This contradiction completes the proof of the claim.
$\{B \cap b : b \in B\} \subseteq J$
. This contradiction completes the proof of the claim.
Note that by Fact 12.1
![]() $(i)$
, we can deduce from the claim that
$(i)$
, we can deduce from the claim that
![]() . Finally, by the claim and
. Finally, by the claim and
![]() $(i)$
,
$(i)$
,
![]() whenever
whenever
![]() $\tau $
and
$\tau $
and
![]() $\chi $
are two cardinals such that
$\chi $
are two cardinals such that
![]() and
and
![]() .
.
-
(iv): Let
 $\tau $
be an infinite cardinal less than
$\tau $
be an infinite cardinal less than
 $\kappa $
. Then
$\kappa $
. Then
 for any cardinal
for any cardinal
 $\chi $
such that
$\chi $
such that
 and
and
 . If
. If
 , then by
, then by
 $(ii)$
and Fact 14.3,
$(ii)$
and Fact 14.3,
 .
.
It follows that
![]() , that
, that
![]() (by Fact 12.1
(by Fact 12.1
![]() $(i))$
, and also (by
$(i))$
, and also (by
![]() $(i))$
that
$(i))$
that
![]() for any cardinal
for any cardinal
![]() $\chi $
such that
$\chi $
such that
![]() and
and
![]() . Now suppose that
. Now suppose that
![]() , and
, and
![]() $\chi $
is a cardinal such that
$\chi $
is a cardinal such that
![]() and
and
![]() . Then
. Then
![]() . We can now conclude that
. We can now conclude that
![]() .
.
Finally, let Q be the set of all cardinals
![]() $\chi $
such that
$\chi $
such that
![]() and
and
![]() . Then for any
. Then for any
![]() $\chi \in Q$
,
$\chi \in Q$
,
 . Hence by Fact 14.4,
. Hence by Fact 14.4,
![]() .
.
Thus
can be defined more simply by
Let us next see how
![]() and
and
![]() compare.
compare.
Observation 14.6. Suppose that
![]() . Then the following hold:
. Then the following hold:
-
(i) Suppose
 . Then
. Then
 .
. -
(ii) Suppose
 . Then
. Then
 .
.
Proof It is simple to see that since
![]() ,
,
![]() .
.
Claim.
-
(a) Let
 $\tau $
and
$\tau $
and
 $\chi $
be two cardinals such that
$\chi $
be two cardinals such that
 . Then
. Then
 .
. -
(b) Let
 $\tau $
and
$\tau $
and
 $\chi $
be two cardinals such that
$\chi $
be two cardinals such that
 and
and
 . Then
. Then
 .
.
Proof of the claim
-
(a): By the definition of
 ,
,
 .
. -
(b): This is immediate from the definition of
 , which completes the proof of the claim.
, which completes the proof of the claim.
Let Q denote the set of all cardinals
![]() $\chi $
such that
$\chi $
such that
. By the claim,
for all
![]() $\chi \in Q$
. Hence by Fact 14.4,
$\chi \in Q$
. Hence by Fact 14.4,
Now suppose that
. Then
, and consequently
.
Observation 14.7. Suppose that
![]() . Then
. Then
![]() .
.
Proof Suppose otherwise. Then by Fact 14.4, we may find a cardinal
![]() $\chi $
such that
$\chi $
such that
![]() and
and
![]() . Hence there must exist a cardinal
. Hence there must exist a cardinal
![]() $\tau $
such that
$\tau $
such that
![]() and
and
![]() . But then
. But then
![]() . Contradiction.
. Contradiction.
Theorem 14.8.
-
(i) Suppose that either
 , or
, or
 is singular, or
is singular, or
 is the successor of a regular cardinal. Then
is the successor of a regular cardinal. Then
 holds.
holds. -
(ii) Suppose that
 $\kappa> \omega _1$
,
$\kappa> \omega _1$
,
 , and either
, and either
 is the successor of a singular cardinal, or
is the successor of a singular cardinal, or
 is weakly inaccessible and
is weakly inaccessible and
 . Then
. Then
 holds.
holds. -
(iii) For any cardinal
 , no
, no
 -normal, fine ideal on
-normal, fine ideal on
 is weakly
is weakly
 $\pi $
-saturated.
$\pi $
-saturated.
Proof
![]() $(i)$
and
$(i)$
and
![]() $(ii)$
: Let us first assume that
$(ii)$
: Let us first assume that
![]() $\kappa $
is a successor cardinal, say
$\kappa $
is a successor cardinal, say
![]() $\kappa = \nu ^+$
. The proof is in large part similar to that of Theorem 11.2, so we will skip some details.
$\kappa = \nu ^+$
. The proof is in large part similar to that of Theorem 11.2, so we will skip some details.
Claim 1. Suppose that one of the following holds:
-
(a)
 .
. -
(b)
 and
and
 is either singular, or the successor of a regular cardinal.
is either singular, or the successor of a regular cardinal. -
(c)
 ,
,
 is the successor of a singular cardinal and
is the successor of a singular cardinal and
 .
. -
(d)
 ,
,
 is the successor of a singular cardinal, and
is the successor of a singular cardinal, and
 .
.
Then no
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
Proof of Claim 1
-
(a): By Fact 3.1, since
 holds.
holds. -
(b): By Proposition 7.3.
-
(c): By Proposition 6.2
 $(i)$
.
$(i)$
. -
(d): By Proposition 6.2
 $(ii)$
.
$(ii)$
.
This completes the proof of the claim.
Claim 2. Suppose that
![]() ,
,
![]() is the successor of a singular cardinal, and
is the successor of a singular cardinal, and
![]() . Let
. Let
![]() $\mu $
be a regular cardinal less than
$\mu $
be a regular cardinal less than
![]() $\kappa $
with
$\kappa $
with
![]() . Then there is
. Then there is
![]() such that no
such that no
![]() -normal, fine ideal H on
-normal, fine ideal H on
![]() with
with
![]() $S \in H^+$
is weakly
$S \in H^+$
is weakly
![]() -saturated.
-saturated.
Proof of Claim 2
By Proposition 6.2
![]() $(iv)$
if
$(iv)$
if
![]() (note that then
(note that then
![]() $\nu \geq \mu> \mathrm {cf} (\nu )$
, so
$\nu \geq \mu> \mathrm {cf} (\nu )$
, so
![]() $\nu $
is singular), and Proposition 6.2
$\nu $
is singular), and Proposition 6.2
![]() $(iii))$
otherwise.
$(iii))$
otherwise.
Claim 3. Suppose that
![]() ,
,
![]() is weakly inaccessible, and
is weakly inaccessible, and
![]() . Then there is
. Then there is
![]() such that no normal, fine ideal H on
such that no normal, fine ideal H on
![]() with
with
![]() $S \in H^+$
is weakly
$S \in H^+$
is weakly
![]() -saturated.
-saturated.
Proof of Claim 3
By Observation 14.6,
![]() . Now apply Observation 13.2. This completes the proof of Claim 3.
. Now apply Observation 13.2. This completes the proof of Claim 3.
Let us now assume that
![]() $\kappa $
is weakly inaccessible.
$\kappa $
is weakly inaccessible.
Claim 4.
-
(a) Suppose that
 and
and
 is regular. Let S be the set of all
is regular. Let S be the set of all
 such that (
such that (
 $o.t. (x)$
is an infinite limit ordinal and) either
$o.t. (x)$
is an infinite limit ordinal and) either
 $\mathrm {cf} (o.t. (x)) < o.t. (x)$
, or x is not stationary in
$\mathrm {cf} (o.t. (x)) < o.t. (x)$
, or x is not stationary in
 $\sup x$
. Then no normal, fine ideal J on
$\sup x$
. Then no normal, fine ideal J on
 with
with
 $S \in J^+$
is weakly
$S \in J^+$
is weakly
 -saturated.
-saturated. -
(b) Suppose that
 and
and
 . Select an increasing sequence
. Select an increasing sequence
 of regular cardinals greater than
of regular cardinals greater than
 $\kappa $
with supremum
$\kappa $
with supremum
 , and set
, and set
 , where
, where
 $S_i$
is the set of all
$S_i$
is the set of all
 with the property that
with the property that
 $o.t. (a)$
is an infinite limit ordinal such that either
$o.t. (a)$
is an infinite limit ordinal such that either
 $\mathrm {cf} (o.t. (a)) < o.t. (a)$
, or a is not stationary in
$\mathrm {cf} (o.t. (a)) < o.t. (a)$
, or a is not stationary in
 $\sup a$
. Then no normal, fine ideal J on
$\sup a$
. Then no normal, fine ideal J on
 with
with
 $S \in J^+$
is weakly
$S \in J^+$
is weakly
 -saturated.
-saturated.
Proof of Claim 4
As in the proof of Theorem 11.4.
Claim 5. Suppose that
![]() , and
, and
![]() is either singular, or the successor of a regular cardinal. Then no
is either singular, or the successor of a regular cardinal. Then no
![]() -normal, fine ideal on
-normal, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
Proof of Claim 5
By Proposition 7.3.
Claim 6. Suppose that
![]() and
and
![]() is the successor of a singular cardinal. Let S be the set of all
is the successor of a singular cardinal. Let S be the set of all
![]() such that
such that
![]() . Then no
. Then no
![]() -normal, fine ideal H on
-normal, fine ideal H on
![]() with
with
![]() $S \in H^+$
is weakly
$S \in H^+$
is weakly
![]() -saturated.
-saturated.
Proof of Claim 6
Case when
![]() . Use Corollary 5.16
. Use Corollary 5.16
![]() $(i)$
.
$(i)$
.
Case when
![]() . By Observation 14.5,
. By Observation 14.5,
![]() . Since
. Since
![]() is a successor cardinal, we have that
is a successor cardinal, we have that
![]()
![]() . Now apply Proposition 6.3.
. Now apply Proposition 6.3.
Claim 7. Suppose that
![]() ,
,
![]() is weakly inaccessible and
is weakly inaccessible and
![]() . Let S be the set of all
. Let S be the set of all
![]() such that
such that
![]() is a singular cardinal of cofinality
is a singular cardinal of cofinality
![]() $\omega $
. Then no normal, fine ideal H on
$\omega $
. Then no normal, fine ideal H on
![]() with
with
![]() $S \in H^+$
is weakly
$S \in H^+$
is weakly
![]() -saturated.
-saturated.
![]() $(iii)$
: By Corollary 7.4.
$(iii)$
: By Corollary 7.4.
For models with a singular cardinal
![]() $\theta $
such that
$\theta $
such that
![]() $\mathrm {pp} (\theta )$
is a weakly inaccessible cardinal, see [Reference Gitik14] (note however that in these models,
$\mathrm {pp} (\theta )$
is a weakly inaccessible cardinal, see [Reference Gitik14] (note however that in these models,
![]() $\mathrm {pp} (\theta )$
is the length of some scale, so that
$\mathrm {pp} (\theta )$
is the length of some scale, so that
![]() $\mathrm {pp}^+ (\theta ) = (\mathrm {pp} (\theta ))^+$
).
$\mathrm {pp}^+ (\theta ) = (\mathrm {pp} (\theta ))^+$
).
Theorem 14.8 says little in the case when
![]() $\kappa = \omega _1$
, to which we will return in Section 16. Assuming
$\kappa = \omega _1$
, to which we will return in Section 16. Assuming
![]() $\kappa> \omega _1$
, the theorem tells us that
$\kappa> \omega _1$
, the theorem tells us that
![]() holds unless
holds unless
![]() is weakly inaccessible and
is weakly inaccessible and
![]() , and even this one case could be claimed to be a near miss, since for any
, and even this one case could be claimed to be a near miss, since for any
![]() , no normal, fine ideal on
, no normal, fine ideal on
![]() is weakly
is weakly
![]() $\pi $
-saturated. However these are mere theoretical considerations. In practice it is not that easy to compute either
$\pi $
-saturated. However these are mere theoretical considerations. In practice it is not that easy to compute either
![]() , or
, or
![]() , so Theorem 14.8 is of limited applicability. In this respect the following result, with only one, easy to check, condition, is more appealing.
, so Theorem 14.8 is of limited applicability. In this respect the following result, with only one, easy to check, condition, is more appealing.
Theorem 14.9. Suppose that
![]() $\kappa> \omega _1$
. Then there is S in
$\kappa> \omega _1$
. Then there is S in
![]() with the property that no normal, fine ideal J on
with the property that no normal, fine ideal J on
![]() with
with
![]() $S \in J^+$
is weakly
$S \in J^+$
is weakly
![]() -saturated.
-saturated.
On the other hand,
![]() may be quite small. For example, if
may be quite small. For example, if
![]() , then by results of Shelah [Reference Shelah50, pp. 86–88],
, then by results of Shelah [Reference Shelah50, pp. 86–88],
![]() .
.
Finally, let us compare the results of this section with those of Section 11.
Observation 14.10.
-
(i) Suppose that
 $\kappa $
is a successor cardinal and
$\kappa $
is a successor cardinal and
 (recall that
(recall that
 $FP (\kappa )$
denotes the least fixed point of the aleph function greater than
$FP (\kappa )$
denotes the least fixed point of the aleph function greater than
 $\kappa $
). Then
$\kappa $
). Then
 . Furthermore if
. Furthermore if
 , then
, then
 .
. -
(ii) Suppose that
 $\kappa $
is weakly inaccessible and
$\kappa $
is weakly inaccessible and
 . Then
. Then
 .
.
Proof
![]() $(i)$
: If
$(i)$
: If
equals
, then so does
by Observation 12.2. Now assume that
. Then by Fact 11.1,
, so
. If this inequality were strict, then setting
![]() $\kappa = \nu ^+$
, we would have
$\kappa = \nu ^+$
, we would have
Contradiction.
![]() $(ii)$
: If
$(ii)$
: If
equals
, then as above so does
. Suppose now that
, and let
![]() $n < \omega $
be such that
$n < \omega $
be such that
. Then by definition,
where
and
Now by Fact 11.3 and Observation 12.2,
Furthermore by Facts 11.1 and 11.3,
, so
.
This leaves us confused, since it implies that
![]() and
and
![]() are one and the same statement in case
are one and the same statement in case
![]() is close to
is close to
![]() $\kappa $
, so that results of this section can be seen as generalizations of those of Section 11. Now is it because we are missing the very last step, which would establish that
$\kappa $
, so that results of this section can be seen as generalizations of those of Section 11. Now is it because we are missing the very last step, which would establish that
![]() is always equal to
is always equal to
![]() ? Or rather because the general statement should indeed be formulated in terms of
? Or rather because the general statement should indeed be formulated in terms of
![]() which, so to speak by accident, happens to be equal to
which, so to speak by accident, happens to be equal to
![]() when
when
![]() is close to
is close to
![]() $\kappa $
?
$\kappa $
?
15 Situations when

We have already observed that in the case when
![]() , it was not easy to compute
, it was not easy to compute
![]() , and thus to determine its cofinality (which is crucial for applying Theorem 14.8), or whether it is a fixed point of the aleph function (if it is not, then by a result of Shelah [Reference Shelah50, Theorem 2.2, p. 373],
, and thus to determine its cofinality (which is crucial for applying Theorem 14.8), or whether it is a fixed point of the aleph function (if it is not, then by a result of Shelah [Reference Shelah50, Theorem 2.2, p. 373],
![]() cannot be weakly inaccessible). Of course the computation is easy if, for instance,
cannot be weakly inaccessible). Of course the computation is easy if, for instance,
![]() is a strong limit cardinal, or under SSH. In this section we show that there are many situations when
is a strong limit cardinal, or under SSH. In this section we show that there are many situations when
![]() . We start by recalling a few facts.
. We start by recalling a few facts.
Fact 15.1 [Reference Shelah50, pp. 85–86].
Let
![]() $\rho _1, \rho _2, \rho _3$
, and
$\rho _1, \rho _2, \rho _3$
, and
![]() $\rho _4$
be four cardinals such that
$\rho _4$
be four cardinals such that
![]() $\rho _1 \geq \rho _2 \geq \rho _3 \geq \omega $
and
$\rho _1 \geq \rho _2 \geq \rho _3 \geq \omega $
and
![]() $\rho _3 \geq \rho _4 \geq 2$
. Then the following hold:
$\rho _3 \geq \rho _4 \geq 2$
. Then the following hold:
-
(i)
 $\mathrm {cov} (\rho _1, \rho _2, \rho _3, \rho _4) = \mathrm {cov} (\rho _1, \rho _2, \rho _3, \max \{\omega , \rho _4\})$
.
$\mathrm {cov} (\rho _1, \rho _2, \rho _3, \rho _4) = \mathrm {cov} (\rho _1, \rho _2, \rho _3, \max \{\omega , \rho _4\})$
. -
(ii) If
 $\rho _3> \rho _4 \geq \omega $
, then
$\rho _3> \rho _4 \geq \omega $
, then 
-
(iii) Suppose that
 $\rho _3> \mathrm {cf} (\rho _2) \geq \rho _4$
and
$\rho _3> \mathrm {cf} (\rho _2) \geq \rho _4$
and
 $\mathrm {cf} (\rho _3) \not = \mathrm {cf} (\rho _2)$
. Then
$\mathrm {cf} (\rho _3) \not = \mathrm {cf} (\rho _2)$
. Then
 $\mathrm {cov} (\rho _1, \rho _2, \rho _3, \rho _4) = \mathrm {cov} (\rho _1, \rho , \rho _3, \rho _4)$
for some cardinal
$\mathrm {cov} (\rho _1, \rho _2, \rho _3, \rho _4) = \mathrm {cov} (\rho _1, \rho , \rho _3, \rho _4)$
for some cardinal
 $\rho $
with
$\rho $
with
 $\rho _2> \rho \geq \rho _3$
.
$\rho _2> \rho \geq \rho _3$
.
Given a cardinal
![]() $\sigma $
and a set Q of regular cardinals,
$\sigma $
and a set Q of regular cardinals,
![]() $\sup Q =^+ \sigma $
means that
$\sup Q =^+ \sigma $
means that
![]() $\sup Q = \sigma $
and moreover either
$\sup Q = \sigma $
and moreover either
![]() $\sigma \in Q$
, or
$\sigma \in Q$
, or
![]() $\sup Q$
is a singular cardinal.
$\sup Q$
is a singular cardinal.
Fact 15.2 [Reference Shelah55, Lemma 18.13], [Reference Matet32].
Assume that:
-
(1)
 $\theta $
is a cardinal such that
$\theta $
is a cardinal such that
 $\omega < \mathrm {cf} (\theta ) < \theta $
.
$\omega < \mathrm {cf} (\theta ) < \theta $
. -
(2)
 is an increasing, continuous sequence of cardinals greater than
is an increasing, continuous sequence of cardinals greater than
 $\mathrm {cf} (\theta )$
with supremum
$\mathrm {cf} (\theta )$
with supremum
 $\theta $
.
$\theta $
. -
(3)
 $\mathrm {cov} (\theta _i,\theta _i, (\mathrm {cf} (\theta ))^+, 2) < \theta $
for all
$\mathrm {cov} (\theta _i,\theta _i, (\mathrm {cf} (\theta ))^+, 2) < \theta $
for all
 $i < \mathrm {cf} (\theta )$
.
$i < \mathrm {cf} (\theta )$
.
Then the following hold:
-
•
 $\mathrm {pp} (\theta ) =^+ \mathrm {cov} (\theta , \theta , (\mathrm {cf} (\theta ))^+, 2)$
.
$\mathrm {pp} (\theta ) =^+ \mathrm {cov} (\theta , \theta , (\mathrm {cf} (\theta ))^+, 2)$
. -
•
 $\mathrm {pp}_{I_{\mathrm {cf} (\theta )}}^{\ast }(\theta ) = \mathrm {cov} (\theta ,\theta , (\mathrm {cf} (\theta ))^+, 2))$
.
$\mathrm {pp}_{I_{\mathrm {cf} (\theta )}}^{\ast }(\theta ) = \mathrm {cov} (\theta ,\theta , (\mathrm {cf} (\theta ))^+, 2))$
. -
•
 $\{i < \mathrm {cf} (\theta ) : \mathrm {pp}_{I_{\mathrm {cf} (i)}}^{\ast }(\theta _i) = \mathrm {cov} (\theta _i, \theta _i, (\mathrm {cf} (\theta ))^+, 2)\}$
contains a closed unbounded set.
$\{i < \mathrm {cf} (\theta ) : \mathrm {pp}_{I_{\mathrm {cf} (i)}}^{\ast }(\theta _i) = \mathrm {cov} (\theta _i, \theta _i, (\mathrm {cf} (\theta ))^+, 2)\}$
contains a closed unbounded set.
Observation 15.3. Suppose that
![]() , and
, and
![]() for any cardinal
for any cardinal
![]() $\tau < \kappa $
and any cardinal
$\tau < \kappa $
and any cardinal
![]() $\chi $
with
$\chi $
with
![]() . Then the following hold:
. Then the following hold:
-
(i)
 .
. -
(ii)
 .
. -
(iii) There is a closed unbounded subset D of
 with the following properties:
with the following properties:-
(1) D consists of cardinals
 $\rho $
with
$\rho $
with
 $\mathrm {cf} (\rho ) < \kappa < \rho = \theta (\kappa , \rho )$
.
$\mathrm {cf} (\rho ) < \kappa < \rho = \theta (\kappa , \rho )$
. -
(2) For any
 $\rho \in D$
,
$\rho \in D$
,
 .
.
-
Proof
Claim 1. Let
![]() $\chi $
be a cardinal such that
$\chi $
be a cardinal such that
![]() . Then
. Then
![]() .
.
Proof of Claim 1
Let us assume that
![]() $\kappa $
is weakly inaccessible, since otherwise the result is trivial. By Fact 15.1,
$\kappa $
is weakly inaccessible, since otherwise the result is trivial. By Fact 15.1,
Now the sequence
![]() is nondecreasing, so its supremum must be less than
is nondecreasing, so its supremum must be less than
![]() , which completes the proof of Claim 1.
, which completes the proof of Claim 1.
Pick an increasing, continuous sequence
![]() of cardinals greater than
of cardinals greater than
![]() $\kappa $
with supremum
$\kappa $
with supremum
![]() .
.
Claim 2. There is a closed unbounded subset
![]() $C_1$
of
$C_1$
of
![]() with the property that
with the property that
![]() whenever
whenever
![]() $j < i$
are in
$j < i$
are in
![]() $C_1$
.
$C_1$
.
Proof of Claim 2
Suppose otherwise. Then the set
is stationary, so we may find
and a stationary
![]() $W \subseteq T$
such that
$W \subseteq T$
such that
for all
![]() $i \in W$
with
$i \in W$
with
![]() $i> k$
. But then
$i> k$
. But then
. This contradiction completes the proof of Claim 2.
Claim 3. There is a stationary subset S of
![]() $C_1$
such that
$C_1$
such that
![]() for all
for all
![]() $k \in S$
.
$k \in S$
.
Proof of Claim 3
By Fact 15.1, for any limit point i of
![]() $C_1$
, there is
$C_1$
, there is
![]() $j < i$
such that
$j < i$
such that
![]() . Claim 3 easily follows.
. Claim 3 easily follows.
Claim 4. There is a closed unbounded subset
![]() $C_2$
of
$C_2$
of
![]() $C_1$
consisting of limit ordinals such that
$C_1$
consisting of limit ordinals such that
![]() whenever
whenever
![]() $j < i$
are in
$j < i$
are in
![]() $C_2$
and
$C_2$
and
![]() $\chi $
is a cardinal with
$\chi $
is a cardinal with
![]() and
and
![]() $\mathrm {cf} (\chi ) < \kappa $
.
$\mathrm {cf} (\chi ) < \kappa $
.
Proof of Claim 4
Let
![]() $C_2$
be the set of all limit points of S. Now suppose that
$C_2$
be the set of all limit points of S. Now suppose that
![]() $j < i$
are in
$j < i$
are in
![]() $C_2$
, and
$C_2$
, and
![]() $\chi $
is a cardinal with
$\chi $
is a cardinal with
![]() and
and
![]() $\mathrm {cf} (\chi ) < \kappa $
. There must be
$\mathrm {cf} (\chi ) < \kappa $
. There must be
![]() $k \in S$
such that
$k \in S$
such that
![]() . Then
. Then
 , which completes the proof of Claim 4.
, which completes the proof of Claim 4.
Notice that for any
![]() $i \in C_2$
,
$i \in C_2$
,
![]() , so
, so
![]() .
.
Claim 5. Let
![]() $\tau $
be an infinite cardinal less than
$\tau $
be an infinite cardinal less than
![]() $\kappa $
. Then there is
$\kappa $
. Then there is
![]() $j \in C_2$
such that
$j \in C_2$
such that
![]() for each cardinal
for each cardinal
![]() $\chi $
with
$\chi $
with
![]() and
and
![]() .
.
Proof of Claim 5
Suppose otherwise, and let
![]() $\rho $
be the least cardinal
$\rho $
be the least cardinal
![]() $\chi $
such that
$\chi $
such that
![]() ,
,
![]() and
and
![]() . By Fact 12.1
. By Fact 12.1
![]() $(ii)$
,
$(ii)$
,
![]() , so we may find
, so we may find
![]() $j \in C_2$
with
$j \in C_2$
with
![]() . Now by Fact 14.1, for each cardinal
. Now by Fact 14.1, for each cardinal
![]() $\sigma $
with
$\sigma $
with
![]() and
and
![]() ,
,
![]() . This contradiction completes the proof of the claim.
. This contradiction completes the proof of the claim.
Claim 6. There is
![]() $k \in C_2$
such that
$k \in C_2$
such that
![]() for any infinite cardinal
for any infinite cardinal
![]() $\tau < \kappa $
and any cardinal
$\tau < \kappa $
and any cardinal
![]() $\chi $
with
$\chi $
with
![]() and
and
![]() .
.
Proof of Claim 6
We can assume that
![]() $\kappa $
is weakly inaccessible, since otherwise the result is immediate from Claim 5. For each infinite cardinal
$\kappa $
is weakly inaccessible, since otherwise the result is immediate from Claim 5. For each infinite cardinal
![]() $\tau < \kappa $
, set
$\tau < \kappa $
, set
![]() $i_{\tau } =$
the least
$i_{\tau } =$
the least
![]() $j \in C_2$
such that
$j \in C_2$
such that
![]() for each cardinal
for each cardinal
![]() $\chi $
with
$\chi $
with
![]() and
and
![]() . Since the sequence
. Since the sequence
![]() is nondecreasing, its supremum k must be less than
is nondecreasing, its supremum k must be less than
![]() , which completes the proof of the claim.
, which completes the proof of the claim.
Set
![]() $C_3 = C_2 \setminus k$
.
$C_3 = C_2 \setminus k$
.
Claim 7. Let
![]() $i \in C_3$
. Then
$i \in C_3$
. Then
![]() .
.
Proof of Claim 7
Let
![]() $\tau $
be an infinite cardinal less than
$\tau $
be an infinite cardinal less than
![]() $\kappa $
, and let
$\kappa $
, and let
![]() $\chi $
be a cardinal such that
$\chi $
be a cardinal such that
and
. If
, then
. Otherwise, put
and
![]() $r = \min (C_2 \setminus (\ell + 1))$
. Then by Fact 12.1
$r = \min (C_2 \setminus (\ell + 1))$
. Then by Fact 12.1
![]() $(ii)$
,
$(ii)$
,
which completes the proof of Claim 7.
It easily follows from Claim 7 that
. Furthermore by Observation 14.5 and Fact 15.2,
By Fact 15.2, there is a closed unbounded subset
![]() $C_4$
of
$C_4$
of
![]() $C_3$
with the property that
$C_3$
with the property that
for all
![]() $i \in C_4$
. Now by Observation 14.5
$i \in C_4$
. Now by Observation 14.5
![]() $(iv)$
, for any
$(iv)$
, for any
![]() $i \in C_4$
of uncountable cofinality,
$i \in C_4$
of uncountable cofinality,
Finally, given
![]() $i \in C_4$
of cofinality
$i \in C_4$
of cofinality
![]() $\omega $
, we have by Fact 6.1 that
$\omega $
, we have by Fact 6.1 that
. Furthermore by Observation 14.5
![]() $(iii)$
,
$(iii)$
,
Thus, in this case too,
Let us make some comments. First, notice that if
![]() and D are as in the statement of Observation 15.3, then by Theorem 14.8,
and D are as in the statement of Observation 15.3, then by Theorem 14.8,
![]() holds, and so does
holds, and so does
![]() $MC_4 (\kappa , \rho )$
for every
$MC_4 (\kappa , \rho )$
for every
![]() $\rho \in D$
of uncountable cofinality. Furthermore if
$\rho \in D$
of uncountable cofinality. Furthermore if
![]() is not a fixed point of the aleph function, then for any large enough
is not a fixed point of the aleph function, then for any large enough
![]() $\rho $
in D (of cofinality
$\rho $
in D (of cofinality
![]() $\omega $
), (
$\omega $
), (
![]() $\rho $
is not a fixed point of the aleph function and)
$\rho $
is not a fixed point of the aleph function and)
![]() $\mathrm {pp}_{I_{\mathrm {cf} (\rho )}}^{\ast }(\rho )$
is not weakly inaccessible, and hence
$\mathrm {pp}_{I_{\mathrm {cf} (\rho )}}^{\ast }(\rho )$
is not weakly inaccessible, and hence
![]() $MC_4 (\kappa , \rho )$
holds. Notice further that if in the statement of the observation, we make the stronger assumption that
$MC_4 (\kappa , \rho )$
holds. Notice further that if in the statement of the observation, we make the stronger assumption that
![]() for any cardinal
for any cardinal
![]() , then we may find a closed unbounded subset
, then we may find a closed unbounded subset
![]() $D'$
of D such that
$D'$
of D such that
![]() $\chi ^{< \kappa } < \rho $
whenever
$\chi ^{< \kappa } < \rho $
whenever
![]() $\rho \in D'$
and
$\rho \in D'$
and
![]() $\chi $
is a cardinal less than
$\chi $
is a cardinal less than
![]() $\rho $
. Now by results of Shelah (see, e.g., Theorems 9.1.2 and 9.1.3 in [Reference Holz, Steffens and Weitz16]), if
$\rho $
. Now by results of Shelah (see, e.g., Theorems 9.1.2 and 9.1.3 in [Reference Holz, Steffens and Weitz16]), if
![]() $\tau $
and
$\tau $
and
![]() $\sigma $
are two cardinals such that
$\sigma $
are two cardinals such that
![]() ,
,
![]() $(b) \ \chi ^{\tau } < \sigma $
for any cardinal
$(b) \ \chi ^{\tau } < \sigma $
for any cardinal
![]() $\chi < \sigma $
, and
$\chi < \sigma $
, and
![]() $(c)$
either
$(c)$
either
![]() $\mathrm {cf} (\sigma )> \omega $
, or
$\mathrm {cf} (\sigma )> \omega $
, or
![]() $\sigma $
is not a fixed point of the aleph function, then
$\sigma $
is not a fixed point of the aleph function, then
![]() $\mathrm {pp}_{\tau } (\sigma ) = \sigma ^{\tau }$
. Hence for any
$\mathrm {pp}_{\tau } (\sigma ) = \sigma ^{\tau }$
. Hence for any
![]() ,
,
![]() $(a) \ \mathrm {pp} (\kappa , \sigma ) = \sigma ^{< \kappa } = u (\kappa , \sigma )$
and
$(a) \ \mathrm {pp} (\kappa , \sigma ) = \sigma ^{< \kappa } = u (\kappa , \sigma )$
and
![]() $(b) \ MC_3 (\kappa , \sigma )$
holds if
$(b) \ MC_3 (\kappa , \sigma )$
holds if
![]() $\mathrm {cf} (\sigma )> \omega $
. Moreover if
$\mathrm {cf} (\sigma )> \omega $
. Moreover if
![]() is not a fixed point of the aleph function, then
is not a fixed point of the aleph function, then
![]() $MC_3 (\kappa , \sigma )$
holds for any large enough
$MC_3 (\kappa , \sigma )$
holds for any large enough
![]() $\sigma $
in
$\sigma $
in
![]() $D'$
(of cofinality
$D'$
(of cofinality
![]() $\omega $
).
$\omega $
).
16 The case
 $\kappa = \omega _1$
$\kappa = \omega _1$
What is so special about the case
![]() $\kappa = \omega _1$
is that there is only one possible cofinality (for, e.g.,
$\kappa = \omega _1$
is that there is only one possible cofinality (for, e.g.,
![]() ), namely
), namely
![]() $\omega $
, which is thus unavoidable.
$\omega $
, which is thus unavoidable.
As we have seen, one problem we have to deal with for any value of
![]() $\kappa $
is the possibility of the weak inaccessibility of
$\kappa $
is the possibility of the weak inaccessibility of
![]() (with
(with
![]() ). For
). For
![]() $\kappa = \omega _1$
, we may appeal to Theorem 14.8
$\kappa = \omega _1$
, we may appeal to Theorem 14.8
![]() $(i)$
and
$(i)$
and
![]() $(iii)$
. Further, Observation 4.7 and Corollary 5.20 give us the following.
$(iii)$
. Further, Observation 4.7 and Corollary 5.20 give us the following.
Observation 16.1. Suppose that
![]() $(a) \ \kappa = \omega _1$
,
$(a) \ \kappa = \omega _1$
,
![]() ,
,
![]() is the successor of a singular cardinal, and
is the successor of a singular cardinal, and
![]() for some P-point ideal I on
for some P-point ideal I on
![]() $\omega $
. Then
$\omega $
. Then
![]() holds, and in fact there is
holds, and in fact there is
![]() such that no
such that no
![]() -normal, fine ideal H on
-normal, fine ideal H on
![]() with
with
![]() $S \in H^+$
is weakly
$S \in H^+$
is weakly
![]() -saturated.
-saturated.
Here we have a second problem, due to the P-pointness condition. It turns out that if
![]() is close to
is close to
![]() $\kappa $
, this condition can be removed. Recall that the pseudointersection number
$\kappa $
, this condition can be removed. Recall that the pseudointersection number
![]() $\frak {p}$
is the least size of any collection Z of infinite subsets of
$\frak {p}$
is the least size of any collection Z of infinite subsets of
![]() $\omega $
such that
$\omega $
such that
![]() $(a) \ \vert \bigcap w \vert = \aleph _0$
for any
$(a) \ \vert \bigcap w \vert = \aleph _0$
for any
![]() $w \subseteq Z$
with
$w \subseteq Z$
with
![]() $0 < \vert w \vert < \aleph _0$
, and
$0 < \vert w \vert < \aleph _0$
, and
![]() $(b)$
there is no infinite
$(b)$
there is no infinite
![]() $A \subseteq \omega $
such that
$A \subseteq \omega $
such that
![]() $\vert A \setminus B \vert < \aleph _0$
for all
$\vert A \setminus B \vert < \aleph _0$
for all
![]() $B \in Z$
. The following, which was pointed out to the author by Todd Eisworth, is largely due to Shelah (see [Reference Shelah50, Remark 1.6B, p. 322] and [Reference Shelah52]).
$B \in Z$
. The following, which was pointed out to the author by Todd Eisworth, is largely due to Shelah (see [Reference Shelah50, Remark 1.6B, p. 322] and [Reference Shelah52]).
Fact 16.2 [Reference Matet32].
Let
![]() $\theta $
and
$\theta $
and
![]() $\pi $
be two infinite cardinals such that
$\pi $
be two infinite cardinals such that
![]() $\omega = \mathrm {cf}(\theta ) < \theta < \pi = \mathrm {cf}( \pi ) < \min (\mathrm {pp}^+(\theta ), \theta ^{+ \frak {p}})$
. Then there is a set u of regular cardinals such that
$\omega = \mathrm {cf}(\theta ) < \theta < \pi = \mathrm {cf}( \pi ) < \min (\mathrm {pp}^+(\theta ), \theta ^{+ \frak {p}})$
. Then there is a set u of regular cardinals such that
![]() $\sup u = \theta $
,
$\sup u = \theta $
,
![]() $\vert u \vert = \aleph _0 < \min u$
and
$\vert u \vert = \aleph _0 < \min u$
and
![]() $\mathrm {tcf} (\prod u / I_u) = \pi $
.
$\mathrm {tcf} (\prod u / I_u) = \pi $
.
Observation 16.3. Suppose that
![]() $\kappa = \omega _1$
and
$\kappa = \omega _1$
and
![]() . Then
. Then
![]() holds.
holds.
Proof Case when
![]() . Then by Fact 3.1, no
. Then by Fact 3.1, no
![]() $\kappa $
-complete, fine ideal on
$\kappa $
-complete, fine ideal on
![]() is weakly
is weakly
![]() -saturated.
-saturated.
Case when
![]() . By Observation 14.10
. By Observation 14.10
![]() $(i)$
,
$(i)$
,
![]() (and hence
(and hence
![]() and
and
![]() assert the same thing). Furthermore by Fact 11.1,
assert the same thing). Furthermore by Fact 11.1,
![]() is not weakly inaccessible. Now
is not weakly inaccessible. Now
![]() holds by Observation 16.1 and Fact 16.2 if
holds by Observation 16.1 and Fact 16.2 if
![]() is the successor of a singular cardinal, and by Theorem 14.8
is the successor of a singular cardinal, and by Theorem 14.8
![]() $(i)$
otherwise.
$(i)$
otherwise.
17 A small, private, devotional altar to pcf theory
The original conjecture of Menas is not only consistently false, by the result of Baumgartner and Taylor [Reference Baumgartner and Taylor3], but it is also, as seen in Corollary 10.3, heavily dependent on cardinal arithmetic. A weaker statement, which looks more reasonable, asserts that the nonstationary ideal
![]() is nowhere weakly
is nowhere weakly
![]() -saturated (where
-saturated (where
![]() denotes the least size of any cofinal subset of
denotes the least size of any cofinal subset of
![]() ), but by the result of Gitik [Reference Gitik12], this assertion too is relative to a (large) large cardinal, consistently false. If there are no large cardinals in an inner model, and either
), but by the result of Gitik [Reference Gitik12], this assertion too is relative to a (large) large cardinal, consistently false. If there are no large cardinals in an inner model, and either
![]() , or
, or
![]() is the successor of a singular cardinal of cofinality less than
is the successor of a singular cardinal of cofinality less than
![]() $\kappa $
, the assertion does hold by Observation 10.1 and Proposition 3.8, and in fact no normal, fine ideal on
$\kappa $
, the assertion does hold by Observation 10.1 and Proposition 3.8, and in fact no normal, fine ideal on
![]() is weakly
is weakly
![]() -saturated (so, contrary to Gitik, we are not taking advantage of the specificity of
-saturated (so, contrary to Gitik, we are not taking advantage of the specificity of
![]() ). By Facts 3.4 and 8.2, and Observations 8.1 and 10.1, a similar result holds in the case when (
). By Facts 3.4 and 8.2, and Observations 8.1 and 10.1, a similar result holds in the case when (
![]() $\kappa $
is weakly inaccessible,)
$\kappa $
is weakly inaccessible,)
![]() (and
(and
![]() is not the successor of a cardinal of cofinality less than
is not the successor of a cardinal of cofinality less than
![]() $\kappa $
). However with such statements we are far from the (unconditional) spirit of Menas’s conjecture. So how much of the original conjecture is true in ZFC? By Theorems 11.2 and 11.4, if
$\kappa $
). However with such statements we are far from the (unconditional) spirit of Menas’s conjecture. So how much of the original conjecture is true in ZFC? By Theorems 11.2 and 11.4, if
![]() $\kappa> \omega _1$
and
$\kappa> \omega _1$
and
![]() is close to
is close to
![]() $\kappa $
, then there is
$\kappa $
, then there is
![]() such that no normal extension of
such that no normal extension of
![]() is weakly
is weakly
![]() -saturated. This can be generalized to some extent. If
-saturated. This can be generalized to some extent. If
![]() $\kappa> \omega _1$
and
$\kappa> \omega _1$
and
![]() is not weakly inaccessible (where
is not weakly inaccessible (where
![]() ), then by Theorem 14.8, there is
), then by Theorem 14.8, there is
![]() such that no normal extension of
such that no normal extension of
![]() is weakly
is weakly
![]() -saturated. Much remains to be clarified. What about the case when
-saturated. Much remains to be clarified. What about the case when
![]() $\kappa = \omega _1$
? Is it consistent that
$\kappa = \omega _1$
? Is it consistent that
![]() ? That
? That
![]() is weakly inaccessible and greater than
is weakly inaccessible and greater than
![]() ?
?
There are problems that are intractable in ZFC alone, but have a shadow version that can be established using the tools of pcf theory. Some people are not impressed, pointing out that the original problems remain unresolved. For others it is a way of showing that ZFC is not so desperately incomplete as it may seem. The most prominent such problem is the Generalized Continuum Hypothesis revisited by Shelah in [Reference Shelah51]. Our goal in the present paper was to show, on a more modest scale, that Menas’s Conjecture is also amenable to an analysis of this type. Hopefully, future will tell which is the correct formulation for its shadow variant: should it be
![]() ,
,
![]() or maybe some other assertion?
or maybe some other assertion?
Acknowledgement
The author is most grateful to the referee for an indefatigable dedication and extensive lists of corrections and suggestions for improvement.