This thesis divides naturally into two parts, each concerned with the extent to which the theory of 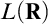$L(\mathbf {R})$ can be changed by forcing.

The first part focuses primarily on applying generic-absoluteness principles to how that definable sets of reals enjoy regularity properties. The work in Part I is joint with Itay Neeman and is adapted from our paper Happy and mad families in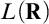 $L(\mathbf {R})$ , JSL, 2018. The project was motivated by questions about mad families, maximal families of infinite subsets of 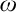$\omega $ of which any two have only finitely many members in common. We begin, in the spirit of Mathias, by establishing (Theorem 2.8) a strong Ramsey property for sets of reals in the Solovay model, giving a new proof of Törnquist’s theorem that there are no infinite mad families in the Solovay model.

In Chapter 3 we stray from the main line of inquiry to briefly study a game-theoretic characterization of filters with the Baire Property.

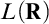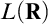Neeman and Zapletal showed, assuming roughly the existence of a proper class of Woodin cardinals, that the boldface theory of $L(\mathbf {R})$ cannot be changed by proper forcing. They call their result the Embedding Theorem, because they conclude that in fact there is an elementary embedding from the $L(\mathbf {R})$ of the ground model to that of the proper forcing extension. With a view toward analyzing mad families under $\mathsf {AD}^+$ and in 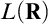$L(\mathbf {R})$ under large-cardinal hypotheses, in Chapter 4 we establish triangular versions of the Embedding Theorem. 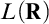These are enough for us to use Mathias’s methods to show (Theorem 4.5) that there are no infinite mad families in $L(\mathbf {R})$ under large cardinals and (Theorem 4.9) that 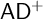$\mathsf {AD}^+$ implies that there are no infinite mad families. These are again corollaries of theorems about strong Ramsey properties under large-cardinal assumptions and $\mathsf {AD}^+$ , respectively. 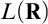Our first theorem improves the large-cardinal assumption under which Todorcevic established the nonexistence of infinite mad families in $L(\mathbf {R})$ . Part I concludes with Chapter 5, a short list of open questions.

In the second part of the thesis, we undertake a finer analysis of the Embedding Theorem and its consistency strength. Schindler found that the the Embedding Theorem is consistent relative to much weaker assumptions than the existence of Woodin cardinals. He defined remarkable cardinals, which can exist even in L, and showed that the Embedding Theorem is equiconsistent with the existence of a remarkable cardinal. His theorem resembles a theorem of Harrington–Shelah and Kunen from the 1980s: the absoluteness of the theory of 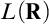$L(\mathbf {R})$ to ccc forcing extensions is equiconsistent with a weakly compact cardinal. Joint with Itay Neeman, we improve Schindler’s theorem by showing that absoluteness for $\sigma $ -closed 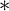$\ast $ ccc posets—instead of the larger class of proper posets—implies the remarkability of 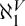$\aleph _1^V$ in L. This requires a fundamental change in the proof, since Schindler’s lower-bound argument uses Jensen’s reshaping forcing, which, though proper, need not be 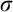$\sigma $ -closed 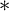$\ast $ ccc in that context. Our proof bears more resemblance to that of Harrington–Shelah than to Schindler’s.

The proof of Theorem 6.2 splits naturally into two arguments. In Chapter 7 we extend the Harrington–Shelah method of coding reals into a specializing function to allow for trees with uncountable levels that may not belong to L. This culminates in Theorem 7.4, which asserts that if there are 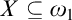$X\subseteq \omega _1$ and a tree 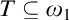$T\subseteq \omega _1$ of height $\omega _1$ such that X is codable along T (see Definition 7.3), then 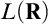$L(\mathbf {R})$ -absoluteness for ccc posets must fail.

We complete the argument in Chapter 8, where we show that if in any 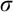$\sigma $ -closed extension of V there is no 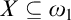$X\subseteq \omega _1$ codable along a tree T, then 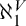$\aleph _1^V$ must be remarkable in L.

In Chapter 9 we review Schindler’s proof of generic absoluteness from a remarkable cardinal to show that the argument gives a level-by-level upper bound: a strongly 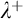$\lambda ^+$ -remarkable cardinal is enough to get 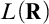$L(\mathbf {R})$ -absoluteness for 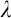$\lambda $ -linked proper posets.

Chapter 10 is devoted to partially reversing the level-by-level upper bound of Chapter 9. Adapting the methods of Neeman, Hierarchies of forcing axioms II, we are able to show that 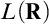$L(\mathbf {R})$ -absoluteness for $\left |\mathbf {R}\right |\cdot \left |\lambda \right |$ -linked posets implies that the interval 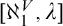$[\aleph _1^V,\lambda ]$ is $\Sigma ^2_1$ -remarkable in L.

Abstract prepared by Zach Norwood.

E-mail: zachnorwood@gmail.com