Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T09:19:52.283Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison of non-linear models to describe the lactation curves for milk yield and composition in buffaloes (Bubalus bubalis)

Published online by Cambridge University Press:  10 September 2015

N. Ghavi Hossein-Zadeh
N. Ghavi Hossein-Zadeh*
Affiliation:
Department of Animal Science, Faculty of Agricultural Sciences, University of Guilan, PO Box 41635-1314, Rasht, Iran
*
†E-mail: nhosseinzadeh@guilan.ac.ir or navid.hosseinzadeh@gmail.com
Get access

Abstract

In order to describe the lactation curves of milk yield (MY) and composition in buffaloes, seven non-linear mathematical equations (Wood, Dhanoa, Sikka, Nelder, Brody, Dijkstra and Rook) were used. Data were 116 117 test-day records for MY, fat (FP) and protein (PP) percentages of milk from the first three lactations of buffaloes which were collected from 893 herds in the period from 1992 to 2012 by the Animal Breeding Center of Iran. Each model was fitted to monthly production records of dairy buffaloes using the NLIN and MODEL procedures in SAS and the parameters were estimated. The models were tested for goodness of fit using adjusted coefficient of determination (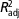 $$_{{{\rm adj}}}^{2} $$ ), root means square error (RMSE), Durbin–Watson statistic and Akaike’s information criterion (AIC). The Dijkstra model provided the best fit of MY and PP of milk for the first three parities of buffaloes due to the lower values of RMSE and AIC than other models. For the first-parity buffaloes, Sikka and Brody models provided the best fit of FP, but for the second- and third-parity buffaloes, Sikka model and Brody equation provided the best fit of lactation curve for FP, respectively. The results of this study showed that the Wood and Dhanoa equations were able to estimate the time to the peak MY more accurately than the other equations. In addition, Nelder and Dijkstra equations were able to estimate the peak time at second and third parities more accurately than other equations, respectively. Brody function provided more accurate predictions of peak MY over the first three parities of buffaloes. There was generally a positive relationship between 305-day MY and persistency measures and also between peak yield and 305-day MY, calculated by different models, within each lactation in the current study. Overall, evaluation of the different equations used in the current study indicated the potential of the non-linear models for fitting monthly productive records of buffaloes.

Keywords

dairy buffalolactation curvemathematical modelmilk yieldpersistency of lactation
Type
Research Article
Information
animal , Volume 10 , Issue 2 , February 2016 , pp. 248 - 261
Copyright
© The Animal Consortium 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdel-Salam, SAM, Mekkawy, W, Hafez, YM, Zaki, AA and Abou-Bakr, S 2011. Fitting lactation curve of Egyptian buffalo using three different models. Egyptian Journal of Animal Production 48 (2), 119–133.Google Scholar
Aziz, MA, Shalaby, NA, El-Shafie, OM, Mahdy, AT and Nishida, A 2006. Comparison between the shapes of lactation curve of Egyptian buffalo milk yield estimated by the incomplete gamma function and a new model. Livestock Research for Rural Developement 18 (5), 1–12.Google Scholar
Barbosa, SBP, Pereira, RGA, Santoro, KR, Batista, AMV and Ribeiro Neto, AC 2007. Lactation curve of cross-bred buffalo under two production systems in the Amazonian region of Brazil. Italian Journal of Animal Science 6 (suppl. 2), 1075–1078.Google Scholar
Brody, S, Ragsdale, AC and Turner, CW 1923. The rate of decline of milk secretion with the advance of the period of lactation. The Journal of General Physiology 5, 441–444.Google Scholar
Catillo, G, Macciotta, NPP, Carretta, A and Cappio-Borlino, A 2002. Effects of age and calving season on lactation curves of milk production traits in Italian water buffaloes. Journal of Dairy Science 85, 1298–1306.Google Scholar
Cobuci, JA, Euclydes, RF, Pereira, CS, Torres R de, A, Costa, CN and Lopes, PS 2003. Persistency in lactation – a review. Archivos Latinoamericanos de Produccion Animal 11, 163–173.Google Scholar
Cole, JB and Null, DJ 2009. Genetic evaluation of lactation persistency for five breeds of dairy cattle. Journal of Dairy Science 92, 2248–2258.Google Scholar
Coulon, JB, Perochon, L and Lescourret, F 1995. Modelling the effect of the stage of pregnancy on dairy cows’ milk yield. Animal Science 60, 401–408.Google Scholar
Dekkers, JCM, Ten Hag, JH and Weersink, A 1998. Economic aspects of persistency of lactation in dairy cattle. Livestock Production Science 53, 237–252.Google Scholar
Dematawewa, CMB and Dekkers, JCM 2014. Lactation curve modeling for Murrah and Surti buffalo breeds in Sri Lanka. Paper presented at the 10th World Congress of Genetics Applied to Livestock Production, 17–22 August, Vancouver, BC, Canada.Google Scholar
Dhanoa, MS 1981. A note on an alternative form of the lactation model of Wood. Animal Production 32, 349–351.Google Scholar
Dijkstra, J, France, J, Dhanoa, MS, Maas, JA, Hanigan, MD, Rook, AJ and Beever, DE 1997. A model to describe growth patterns of the mammary gland during pregnancy and lactation. Journal of Dairy Science 80, 2340–2354.Google Scholar
Dimauro, C, Catillo, G, Bacciu, N and Macciotta, NPP 2005. Fit of different linear models to the lactation curve of Italian water buffalo. Italian Journal of Animal Science 4 (suppl. 2), 22–24.Google Scholar
Fernandez, C, Sanchez, A and Garces, C 2002. Modeling the lactation curve for test-day milk yield in Murciano-Granadina goats. Small Ruminant Research 46, 29–41.Google Scholar
Flores, EB, Kinghorn, BP and van der Werf, J 2013. Predicting lactation yields in dairy buffaloes by interpolation and multiple trait prediction. Livestock Science 151, 97–107.CrossRefGoogle Scholar
Gahlot, GC, Gahlot, RS and Jairath, LK 1988. Pattern of lactation curve in Rathi cattle. Indian Journal of Animal Science 58 (9), 1112–1114.Google Scholar
Gengler, N 1996. Persistency of lactation yields: a review. Interbull Bulletin 12, 87–95.Google Scholar
Ghavi Hossein-Zadeh, N 2014a. Comparison of non-linear models to describe the lactation curves of milk yield and composition in Iranian Holsteins. The Journal of Agricultural Science 152, 309–324.Google Scholar
Ghavi Hossein-Zadeh, N 2014b. Linear and threshold analysis of direct and maternal genetic effects for secondary sex ratio in Iranian buffaloes. Journal of Applied Genetics 55, 365–372.Google Scholar
Ghavi Hossein-Zadeh, N, Madad, M, Shadparvar, AA and Kianzad, D 2012. An observational analysis of secondary sex ratio, stillbirth and birth weight in Iranian buffaloes (Bubalus bubalis). Journal of Agricultural Science and Technology 14, 1477–1484.Google Scholar
Gołębiewski, M, Brzozowski, P and Gołębiewski, Ł 2011. Analysis of lactation curves, milk constituents, somatic cell count and urea in milk of cows by the mathematical model of Wood. Acta Veterinaria Brno 80, 73–80.Google Scholar
Johansson, I and Hansson, A 1940. Causes of variation in milk and butterfat yield on dairy cows. Kongl Landtbruks-akademiens handlingar och tidskrift 79, 1–127.Google Scholar
Macciotta, NPP, Miglior, F, Cappio-Borlino, A and Schaeffer, LR 2008. Issues in modelling lactation curves with regression splines. Journal of Dairy Science 91 (E-suppl.1), 544. (abstract).Google Scholar
Nelder, JA 1966. Inverse polynomials, a useful group of multi-factor response functions. Biometrics 22, 128–141.Google Scholar
Papajcsik, IA and Bodero, J 1988. Modeling lactation curves of Friesian cow in a subtropical climate. Animal Production 47, 201–207.Google Scholar
Pulina, G and Nudda, A 2001. La produzione del latte. In L’alimentazione degli ovini da latte (ed. G Pulina), pp. 9–31. Avenue Media, Bologna, Italy.Google Scholar
Rook, AJ, France, J and Dhanoa, MS 1993. On the mathematical description of lactation curves. The Journal of Agricultural Science 121, 97–102.Google Scholar
SAS Institute 2002. SAS user’s guide v. 9.1: Statistics. SAS Institute Inc., Cary, NC, USA.Google Scholar
Sikka, LC 1950. A study of lactation as affected by heredity and environment. Journal of Dairy Research 17, 231–252.Google Scholar
Silvestre, ADM, Martins, AM, Santos, MM, Ginja, JA and Colaco, JA 2009. Lactation curves for milk, fat and protein in dairy cows: a full approach. Livestock Science 122, 308–313.Google Scholar
Steri, R, Dimauro, C, Canavesi, F, Nicolazzi, EL and Macciotta, NPP 2012. Analysis of lactation shapes in extended lactations. Animal 6 (10), 1572–1582.Google Scholar
Tekerli, M, Akinci, Z, Dogan, I and Akcan, A 2000. Factors affecting the shape of lactation curves of Holstein cows from the Balikesir Province of Turkey. Journal of Dairy Science 83, 1381–1386.Google Scholar
Weller, JI, Ezra, E and Leitner, G 2006. Genetic analysis of persistency in the Israeli Holstein population by the multitrait animal model. Journal of Dairy Science 89, 2738–2746.Google Scholar
Wood, PDP 1967. Algebraic models of the lactation curves in cattle. Nature 216, 164–165.Google Scholar