Introduction
The present programmes of genetic improvement in beef cattle in Brazil have aimed to incorporate within their selection criteria, traits related to fertility and sexual precocity. Studies have shown the importance of these traits to obtain profitability in the beef cattle business (Melton, Reference Melton1995).
Age at first calving is an easily measurable reproductive trait that has been widely studied. However, the management used can interfere in a decisive manner with the expression of this trait, especially the use of limited breeding season. An analysis by linear models would only make sense if all females had the continuous opportunity to become pregnant, otherwise the females that do not become pregnant within the breeding season could not be evaluated. This is more severe in zebu breeds, when the females are exposed too young and the great majority cannot become pregnant. The heritability found for age at first calving is low (Lôbo et al., Reference Lôbo, Madalena and Vieira2000) but the methods used in the analyses are not very adequate.
Survival analysis is a class of statistical methods ideal for studying the occurrence of events in time. It provides adequate statistical treatment for censored records (i.e. animals that did not express the event of interest until the end of the study) and also takes into account data from non-linear traits (Ducrocq and Casella, Reference Ducrocq and Casella1996). Therefore, this kind of analysis could be applied to study time to first calving (or conception), considering restricted breeding seasons as is the case for beef cattle. Vargas et al. (Reference Vargas, Van der Lende, Baaijen and Van Arendonk1998) used survival analysis to study age at first calving in dairy cattle, considering as censored the records of those of females lacking the date of first calving.
However, the non-linearity regarding the parameters of interest makes the implementation and interpretation of the results of survival analysis more complicated, since the effects act in a multiplicative fashion in hazard functions (Guo, Reference Guo1999). On the other hand, linear models are widely used in genetic evaluations due to ease of implementation and interpretation. Thus, some linear models have been proposed for censored traits (Korsgaard et al., Reference Korsgaard, Sorensen and Gianola1998; Sorensen et al., Reference Sorensen, Gianola and Korsgaard1998). Sorensen et al. (Reference Sorensen, Gianola and Korsgaard1998), using the technique of data augmentation in Bayesian analyses, obtained all posterior conditional distributions in a standard form, which facilitated the implementation of the Gibbs sampling. A limitation in the linear model, however, is the impossibility of using time-dependent covariates as in the survival analysis.
The binary trait ‘heifer pregnancy’ has been widely studied in beef cattle for evaluation of sexual precocity in Brazil, and is already used in publications such as sire evaluation catalogues for the Nellore breed. Heifer pregnancy and age at first conception are similar traits, because both are related to ‘conception rate’, the ability to conceive. Heifer pregnancy also includes censored data (‘zero’ values) and non-censored (‘one’ values), and therefore, a comparative study between the binary and the continuous trait is pertinent.
The aim of the present work was to compare three approaches for evaluation of sexual precocity in the Nellore breed, with the use of survival and censored linear models for the continuous trait of age at first conception and a threshold model for the binary trait of heifer pregnancy.
Material and methods
Data
Initially, a database with 12 566 Nellore females, born between 1991 and 1999, was used. These data were from six farms of Agropecuária CFM Ltd, located in the states of São Paulo, Mato Grosso do Sul and Goiás. The animals were raised in a pasture regime without supplementation. The breeding season started in October and ended in January with a mean duration of 100 days for heifers. Natural breeding was used, and at the end of each breeding season open cows were culled, except for 14-month-old heifers, which had the opportunity to enter the next season. For this study, however, only data from the first breeding season of the heifers were used.
Contemporary groups were defined as: farm of birth+year of birth+weaning management group+18-months management groups+breeding farm (farm where heifers were exposed to the bulls). Each management group was composed of heifers, born within a (approximately) 30-day period, that were treated similarly regarding feed and management, from birth to weaning or from weaning to 18 months. Data from females with unknown parents and belonging to contemporary groups with no variability (i.e. groups having only censored records or with only one observation) were eliminated, leaving 6699 records for the analysis.
The studied traits were heifer pregnancy (HP14) and age at first conception (AFC14) in days. For both traits the data file had similar structure, although age at first conception was a continuous trait (‘continuous’ for period in study) and heifer pregnancy was binary. The females in question were exposed to sires for the first time at about 14 months of age (between 11 and 16 months). HP14 received a value of one (success) or zero (failure) as the pregnancy was confirmed or not by calving in the next year. For AFC14, the data from females that did not have a record for calving date the next year following first exposure to the sire were censored. For these females the value was calculated as: age at the beginning of the breeding season (in days)+100 days (duration of the breeding season). Therefore, it was known that these females were not pregnant up to this age. For animals with an available calving record (non-censored) the age at conception was equal to the age at first calving (in days) minus 290 days (average pregnancy period in these herds) (Pereira et al., Reference Pereira, Eler and Ferraz2002). It must be clear that if the female conceived within the 100 days of the breeding season, its record was not censored (since the failure, that is, conception occurred within the period of study), otherwise it was considered censored (censoring to the right). From the values obtained in such a way for AFC14, the minimum value for age at first conception observed in the file minus one (403 days), was then subtracted, aiming to adjust the data to the Weibull distribution, since one of the frequent causes for data not adjusting to this distribution is the lack of observations between the origin and a given point t0 (V. Ducrocq, 2002, personal communication). The same values (subtracted from the minimum minus one) were used for the censored linear model, although it was not a requirement for this model. Table 1 shows a summary of the final data set used in analysis.
Table 1 Descriptive summary of the final dataset of the Nellore heifers used in analysis
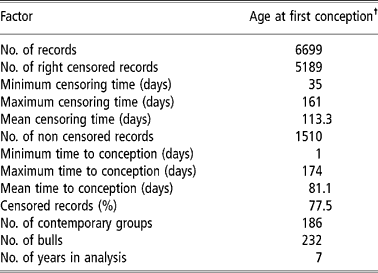
† To know the real value (in days) you may add 403 days.
Mathematical models
Survival model
For survival analysis the following model was used:
where: λ(t;z) is the hazard function of an individual depending on time t (age at first conception in days), remembering that the time scale was shifted to avoid a long period of time where no failure occurs, as described previously.
λ0(t) is the baseline hazard function; it was assumed that it followed a Weibull hazard distribution (λ0(t) = λρ(λt)ρ − 1) with parameters of shape and scale ρ and λ, respectively.
β is a vector that contains the fixed and random effects (possibly time-dependent) that affect the hazard, with z(t)' being the corresponding vector of incidence.
The effects included in the model were: contemporary group: as defined previously, time-independent fixed effect; period: time-dependent fixed effect, with three classes (the definition of these classes is explained below); sire and maternal grandsire (mgs): time-independent random effects, and mgs = 0.5(sire effect). It was assumed that the effects followed a multinormal distribution with mean zero and variance 

The sire-mgs model was initially used to obtain the variance component of sire together with the ρ parameter of shape of Weibull. The sire variance component obtained was multiplied by four and fixed to obtain the expected progeny differences (EPDs) by animal model, in a posterior analysis. For the referred analysis, it was assumed that the animal effect (a time-independent random effect that substituted the sire/mgs effect) followed multinormal distribution with mean zero and variance 

The adequacy of the Weibull model was verified according to Pereira et al. (Reference Pereira, Oliveira, Eler, Silva and Van Melis2006), that used the graphic verification, by plotting ln[-ln S(t)] × ln(t), where ln is the natural logarithm, S(t) the estimate of the Kaplan-Meyer function of survival (S(t) = exp( − (λt)ρ) and t is the age at first conception in days. To show the adequacy, this graph should be ‘roughly’ linear. The graphic inspection showed no linearity of ln[ − ln S(t)] × ln(t) over the whole period of age of heifers, leading to the conclusion that one Weibull distribution was not adequate to describe data over the whole period. However, it allowed distinguishing three periods in which linearity was observed. Within each of these periods the assumption of a Weibull model was plausible. The limits of these periods represent ages at which abruptly changes occur in the chance of the heifers becoming pregnant (until 14 months, from 14 to 15 months and after 15 months). As suggested by V. Ducrocq (2003, personal communication) a time dependent effect (period) was defined to account for these features, leading to the supposition of one shape parameter (ρ), but different scale parameter (λ) for the different periods.
To perform the survival analysis the Survival Kit (Ducrocq and Sölkner, Reference Ducrocq and Sölkner1998) was used, which makes use of an empirical Bayesian approximation in the estimation of parameters. The heritability for the sire-mgs model was calculated in logarithmic scale as 


Censored linear model
The following mixed linear model was used:
in which y = vector of AFC14 observations, transformed for logarithmic scale (this transformation is made internally by the program); b = vector of fixed effects (in this case, including only contemporary groups, as defined previously); X = matrix of incidence associating b with y; u = vector of random effects of direct additive genetic value of animal; Z = matrix of incidence associating u with y; e = vector of residual effects.
It was assumed that 





Minimum and maximum values were attributed for the uniform distributions of b, 

Gibbs sampling was implemented with censored data using the procedure of data augmentation (Sorensen et al., Reference Sorensen, Gianola and Korsgaard1998). The other procedures were similar to those described by Sorensen et al. (Reference Sorensen, Gianola and Korsgaard1998), adapted to the animal model.
To perform this analysis a Fortran program was used, granted by Professor Daniel Sorensen. Convergence analysis followed the algorithm of Raferty and Lewis (1995). In this algorithm the user must inform the precision required. The program gives back the number of iterations required to estimate the cumulative density function a posteriori of the q-quantile of the quantity of interest (a function of parameters) within the interval ± r with probability s. Values of r = 0.0125, s = 0.95 and q = 0.975 were used.
Threshold model
For HP14, the mathematical model included the fixed effects of contemporary groups (as described previously) and the covariate Julian date of birth (number of days, from the 1 January of the year the female was born). The later along the year the female is born in general the more difficult it will be for her to become pregnant during the first breeding season. The random effects considered were the animal additive genetic (with 18 043 animals in the numerator relationship matrix) and the residual. The components of variance were estimated by the R method (Reverter et al., Reference Reverter, Golden, Bourdon and Brinks1994), and the genetic values were predicted using a maximum likelihood a posteriori threshold model (MAP; Gianola, Reference Gianola1982) in an underlying genetic scale. For this analysis the ABTK 2.0 package was used (Golden et al., Reference Golden, Snelling and Mallinckrodt1992).
Additional analysis
Aiming to verify if the addition of information, resulting from the substitution of the binary (HP14) by the continuous data (AFC14), had impact in the EPDs, regression analyses of the EPDs in some of sire's parameters were performed. The parameters considered were pregnancy rates and mean ages at conception and censoring of the daughters of the sires. For these analyses only sires with EPDs of greater accuracy (with 5 or more non-censored daughters, a total of 59 sires) were considered.
Regression analysis, Spearman and Pearson correlations between sire' EPDs were calculated using Statistical Analysis Systems Institute (1995).
Initially, we supposed that the analysis of age at first conception using the survival model was a standard, because age at first conception is a continuous trait (thus, it may add some information compared with the binary trait) and the survival model allow to include time-dependent effects, which is not possible in the linear one. Comparisons are made within the trait age at first conception (comparing survival × linear models) and between the traits age at first conception and heifer pregnancy. The final aim was to know if there were advantages in substitute the binary trait by the continuous one, and, showed this advantage, if we could use the linear model for the analysis of the continuous trait without a great loss in selection response in relation to the survival model. So, graphic inspection concerning loss in selection response using other approaches in comparison to survival analysis was made using Microsoft Excel®.
Results and discussion
Genetic parameters
Table 2 shows the parameters obtained by survival analysis. The value of ρ (2.09 ± 0.12) greater than 1 indicates that the baseline hazard rate increases with time, what is logical, since the older the heifers become, a greater hazard they have of reaching puberty and becoming pregnant.
Table 2 Estimates of parameters for age at first conception in Nellore cattle obtained by survival analysis

† The convergence criterion utilised was 10− 9.
The interpretation of heritability in the case of survival analysis has been object of debate (Korsgaard et al., Reference Korsgaard, Andersen and Jensen1999), since it is not straightforward as in the case of the linear model. The heritability in logarithmic scale is not adequate to obtain the EPD accuracies, being preferable to use the heritability in original scale (Yazdi et al., Reference Yazdi, Visscher, Ducrocq and Thompson2002).
Tables 3 and 4 show the results for censored linear and threshold models, respectively.
Table 3 Posterior mean (PM), posterior standard deviation (PSD), minimum (MIN) and maximum (MAX) estimates and dependence factor (FD) for genetic parameters of age at first conception obtained by censored linear model using Gibbs sampling†
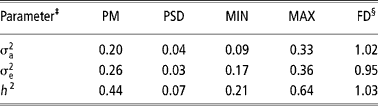
† Chain length = 2 010 000, with burn-in of 10 000 and sampling interval of 1000, resulting in 2000 estimates.
‡ 

§ Value that measure the dependence of values in the final chain (2000 estimates); values close to 1 indicate low serial correlations (Raftery and Lewis, Reference Raftery, Lewis, Gilks, Spiegelhalter and Richardson1995)
Table 4 Estimates of mean, standard deviation, medium and mode of heritability for the trait heifer pregnancy in Nellore cattle, obtained by threshold model (HP14)

† Values obtained with 542 random 50% subsamples and convergence criterion equal to 10− 10.
The heritability obtained by the censored linear model (Table 3) was lower than that obtained by the survival analysis, although heritability in logarithmic scale, which has a more straightforward comparison, has been close to that of the linear model. This result is similar to that obtained by Schneider et al. (Reference Schneider, Strandberg, Ducrocq and Roth2005), in dairy cattle.
The value of heritability found by survival analysis (0.76 in original scale) was also higher than the estimate obtained for HP14 in this work (0.56) and in others (Snelling et al., Reference Snelling, MacNeil and Golden1996; Evans et al., Reference Evans, Golden, Bourdon and Long1999; Eler et al., Reference Eler, Silva, Ferraz, Dias, Oliveira, Evans and Golden2002). Boettcher et al. (Reference Boettcher, Jairath and Dekkers1999), studying longevity in dairy cattle, also observed that the estimate of heritability obtained by survival analysis was superior to those obtained by the linear and threshold models (for binary traits), that could result from a better adjustment of the data to the survival model. In a more recent study, Carlén et al. (Reference Carlén, Schneider and Strandberg2005), working with Swedish Holstein data, reported a higher estimate of heritability for the continuous trait (time to first mastitis or censoring - TFM), analysed by survival model, in relation to the binary one (mastitis - MAST), analysed by mixed linear model, suggesting that this result was probably partly due to an increased observed variation among cows using the trait TFM (more continuously distributed than MAST).
However, it must be taken into account that in the present study a sire-maternal grandsire model was used for the survival analysis (to obtain the heritability), while an animal model was used for the other analysis. Nevertheless, in a recent study, Eler et al. (Reference Eler, Silva, Evans, Ferraz, Dias and Golden2004) also found high heritability for HP14 even with the animal model (0.68).
Analysis of EPDs
By means of regression analyses using the F test, it was observed that the pregnancy rates in daughters of the sires was significant for their respective EPDs for HP14 and AFC14 by the censored linear and survival models (P < 0.05). On the other hand, the mean age at censoring (for daughters that did not conceive within the breeding season) was not significant (P>0.05) for none of the EPDs of the sires. However, the mean age at conception of non-censored daughters was significant for the EPDs of AFC14 by the survival and censored linear models (P < 0.05), but not for the EPDs of HP14 (P>0.05). This last result indicates that the information on age at first conception (in days) of non-censored daughters (that is, that had conception within the breeding season) is important to explain the variation of the EPD for AFC14 of sires, which do not occur with the EPD for HP14, indicating a possible advantage of the continuous trait in relation to the binary one.
Correlations
Table 5 shows the Spearman (ranking) and Pearson correlations between animals' EPDs obtained by the three approaches in the study. The negative values of the correlations occur because of different scales of measurements.
Table 5 Spearman (Spear)† and Pearson (Pear) correlations between heifer pregnancy (HP14) and age at first conception EPDs in Nellore heifers. EPDs for age at first conception were obtained using survival (Surv.) and censored linear (Lin.) models

† Based in survival analysis rank.
‡ Minimum accuracy = 0.55.
In general, it can be observed that the rankings were similar. Considering the 513 sires the correlations were high. However, these were smaller when only the best 5 to 10% of sires were considered, showing a greater change in the positions, especially between HP14 and the other two approaches. However, it is necessary to remember that the lower the number of sires considered, the more sensitive is the Spearman correlation to slight changes in classification, what is observed to a lesser extent in the correlation between the EPDs values (Pearson), which is always higher.
It can be observed that the correlations between EPDs of the binary (HP14) and the continuous (AFC14) traits were, in general, lower than those obtained comparing the two models for the continuous trait. This reflects a greater difference between classifications of sires for HP14 in relation to AFC14.
Analysing the 59 sires of greater accuracy (Rwei>0.55), it was observed that the correlations obtained were higher (values above 0.95) than the majority of the other correlations. Thus, the greater changes in positions observed between the 5 and 10% best sires can be attributed to sires of reduced accuracy, as a consequence of the low number of non-censored progeny.
Correlations in the order of 0.90 among the EPDs obtained by the three approaches in question have been previously reported. Guo (Reference Guo1999), studying longevity and prolificacy in Landrace pigs, found high ranking correlations between the EPDs of boars, comparing the censored linear and survival models (0.90 to 0.96). Similar results were reported by González-Recio et al. (Reference González-Recio, Chang, Gianola and Weigel2006), in a study with dairy cattle that showed sires' rank correlation equal to 0.98, between evaluations for the trait ‘days open’ obtained by survival and censored linear models. When comparing binary and continuous traits the sires' rank correlations found in the literature were, in general, lower, indicating a moderate reranking of sires, which is in agreement with the present study. Boettcher et al. (Reference Boettcher, Jairath and Dekkers1999), analysing longevity in dairy cattle by threshold (binary trait) and survival models (continuous trait), found a ranking correlation between EPDs of sires equal to 0.90. Carlén et al. (Reference Carlén, Schneider and Strandberg2005) found correlations of 0.93, 0.89 and 0.88 (for lactations 1 to 3), between EPDs of sires obtained for the continuous trait (time to first mastitis or censoring) analysed by survival analysis and for the binary one (mastitis) analysed by mixed linear model.
Response to selection
Considering survival analysis as a standard (by incorporating time-dependent covariables, it makes the modelling more adequate for the data (Boettcher et al., Reference Boettcher, Jairath and Dekkers1999)), a comparative graph was elaborated (Figure 1) to verify whether there would be loss in regard to mean EPD obtained by survival analysis, performing sire selection based on EPDs for HP14 or AFC14 by censored linear model. In other words, the classification of animals by EPD using survival analysis was considered ideal and the consequence was verified, in terms of means of the EPDs of selected animals, if the selection was based on EPDs for other traits.

Figure 1 Average superiority in risk ratio (RR) for age at first conception (AFC14) in the next generation (F1) according to the percentage of sires selected, if up to 10% of the best sires (51 sires) are selected by different criteria.
To better understand the results, instead of the EDPs for AFC14, the relative risk ratios (RR) were used, which are equal to the exponential of the estimate of EDPs. Both values are provided by the Survival Kit. The RR are expressed in relation to the founder animals the pedigree (in the case of the animal model), to whom are given, arbitrarily, a hazard value equal to 1. The RR is the ratio between the hazard of every animal and the founder animals. In the case of sires, the more daughters and/or relatives with high RR they have, better they will be. Sires with high RR (or EPDs) for AFC14 will have daughters with a greater chance of becoming pregnant (when exposed to a sire at about 14 months of age) than the daughters of sires with lower RR (or EPDs).
A reduction in the response to selection in AFC14 will be observed if the selection is made based on HP14. This reduction in risk ratio, depending on the fraction selected, reaches in average to 0.5. This indicates, for example, that when the mean of the selected animals by AFC14 is of approximately 4.5, selecting by HP14 would lead to a reduction in 11% in the response in RR.
On the other hand, selection based on EPDs of the censored linear model will lead to a response to selection similar to that made based on the survival model directly. The greater difference between RR is observed when selecting three sires, since the third sire in the classification of the censored linear model is only the seventh by survival analysis. This sire has 43 daughters, of which 16 are non-censored and 27 are censored. The reason for the change in classification seems to be a greater weight given by the linear model (to obtain the EPDs) to the mean age at conception of the non-censored daughters, which for this animal was very low (thus improving the classification of the sire). Thus, selecting the three first sires classified by the linear model would lead to an 11% loss in the response in RR. However, this loss is diluted with the increase of the fraction selected being that at 10% (51 sires) it is practically nil.
Conclusions
The high heritabilities found indicate the use of heifer pregnancy and age at first conception as selection criteria aiming for greater sexual precocity in Nellore breed. However, the results showed that the use of the continuous trait in substitution to the binary trait can bring greater precision to the analysis, with impact in the classification of sires and, consequently, the response to selection.
The use of the censored linear model allowed results to be obtained very similar to those of survival analysis, thus indicating that this kind of model can be explored for traits that have censored observations, by its greater ease of implementation and interpretation, as well as the possibility of its use in multiple trait context (for example, production and fertility traits). However, the survival model has advantages as the permission of use of time-dependent effects. So, the choice between survival or linear models may be influenced mainly by the implementation problems.








