Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-30T07:47:53.934Z Has data issue: false hasContentIssue false
  • English
  • Français

Poisson approximations for runs and patterns of rare events

Published online by Cambridge University Press:  01 July 2016

Anant P. Godbole
Anant P. Godbole*
Affiliation:
Michigan Technological University
*
∗Postal address: Department of Mathematical Sciences, Michigan Technological University, Houghton, Michigan 49931, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

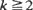Consider a sequence of Bernoulli trials with success probability p, and let Nn,k denote the number of success runs of length among the first n trials. The Stein–Chen method is employed to obtain a total variation upper bound for the rate of convergence of Nn,k to a Poisson random variable under the standard condition npk→λ. This bound is of the same order, O(p), as the best known for the case k = 1, i.e. for the classical binomial-Poisson approximation. Analogous results are obtained for occurrences of word patterns, where, depending on the nature of the word, the corresponding rate is at most O(pk–m) for some m = 0, 2, ···, k – 1. The technique is adapted for use with two-state Markov chains. Applications to reliability systems and tests for randomness are discussed.

Keywords

SUCCESS RUNSWORD PATIERNSSTEIN-CHEN METHODCONSECUTIVE k-OUT-OF-N : F RELIABILITY SYSTEMSMARKOV-BINOMIAL RANDOM VARIABLES
Type
Research Article
Information
Advances in Applied Probability , Volume 23 , Issue 4 , December 1991 , pp. 851 - 865
Copyright
Copyright © Applied Probability Trust 1991 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agin, M. A. and Godbole, A. P. (1991) A new exact runs test for randomness. Proc. Interface 1990 Conference. To appear.Google Scholar
Aldous, D. (1989) Probability Approximations via the Poisson Clumping Heuristic. Springer-Verlag, New York.Google Scholar
Arratia, R. and Waterman, M. (1985) Critical phenomena in sequence matching. Ann. Prob. 13, 1236–1249.CrossRefGoogle Scholar
Arratia, R. and Waterman, M. (1989) The Erdös–Rényi strong law for pattern matching with a given proportion of mismatches. Ann. Prob. 17, 1152–1169.CrossRefGoogle Scholar
Arratia, R., Goldstein, L. and Gordon, L. (1989) Two moments suffice for Poisson approximations: the Chen–Stein method. Ann. Prob. 17, 9–25.Google Scholar
Banjevic, D. (1988) On some statistics connected with runs in Markov chains. J. Appl. Prob. 25, 815–821.CrossRefGoogle Scholar
Barbour, A. D. (1987) Asymptotic expansions in the Poisson limit theorem. Ann. Prob. 15, 748–766.Google Scholar
Barbour, A. D. and Eagleson, G. K. (1983) Poisson approximation for some statistics based on exchangeable trials. Adv. Appl. Prob. 15, 585–600.Google Scholar
Barbour, A. D. and Eagleson, G. K. (1984) Poisson convergence for dissociated statistics. J. R. Statist. Soc. 46, 397–402.Google Scholar
Barbour, A. D. and Hall, P. (1984) On the rate of Poisson convergence. Math. Proc. Camb. Phil. Soc. 95, 473–480.Google Scholar
Barbour, A. D. and Holst, L. (1989) Some applications of the Stein–Chen method for proving Poisson convergence. Adv. Appl. Prob. 21, 74–90.Google Scholar
Barbour, A. D., Holst, L. and Janson, S. (1991) Poisson approximations. To appear.Google Scholar
Bartlett, M. S. (1978) An Introduction to Stochastic Processes , 3rd edn. Cambridge University Press.Google Scholar
Benevento, R. (1984) The occurrence of sequence patterns in ergodic Markov chains. Stoch. Proc. Appl. 17, 369–373.Google Scholar
Blom, G. (1982) On the mean number of random digits until a given sequence occurs. J. Appl. Prob. 19, 136–143.Google Scholar
Blom, G. and Thorburn, D. (1982) How many random digits are required until given sequences are obtained? J. Appl. Prob. 19, 518–531.Google Scholar
Breen, S., Waterman, M. and Zhang, N. (1985) Renewal theory for several patterns. J. Appl. Prob. 22, 228–234.Google Scholar
Burr, E. J. and Cane, G. (1961) Longest run of consecutive observations having a specified attribute. Biometrika 48, 461–465.Google Scholar
Chen, L. (1975) Poisson approximation for dependent trials. Ann. Prob. 3, 534–545.Google Scholar
Chryssaphinou, O. and Papastavridis, S. (1988a) A limit theorem for the number of non-overlapping occurrences of a pattern in a sequence of independent trials. J. Appl. Prob. 25, 428–431.Google Scholar
Chryssaphinou, O. and Papastavridis, S. (1988b) A limit theorem on the number of overlapping appearances of a pattern in a sequence of independent trials. Prob. Theory Rel. Fields 79, 129–143.Google Scholar
David, F. N. and Barton, D. E. (1962) Combinatorial Chance. Griffin, London.CrossRefGoogle Scholar
Deheuvels, P., Devroye, L. and Lynch, J. (1986) Exact convergence rate in the limit theorems of Erdös–Rényi and Shepp. Ann. Prob. 14, 209–223.CrossRefGoogle Scholar
Erdös, P. and Renyi, A. (1970) On a new law of large numbers. J. Analyse Math. 23, 103–111.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications , Vol. 1, 3rd edn. Wiley, New York.Google Scholar
Földes, A. (1979) The limit distribution of the length of the longest head run. Period. Math. Hungar. 10, 301–310.Google Scholar
Fu, J. C. (1985) Reliability of a large consecutive-k-out-of-n: F system. IEEE Trans. Reliability 34, 127–130.Google Scholar
Gani, J. (1982) On the probability generating function of the sum of Markov Bernoulli random variables. J. Appl. Prob. 19A, 321–326.Google Scholar
Gerber, H. U. and Li, S.-Y. R. (1981) The occurrence of sequence patterns in repeated experiments and hitting times in a Markov chain. Stoch. Proc. Appl. 11, 101–108.Google Scholar
Gibbons, J. D. (1971) Nonparametric Statistical Inference. McGraw-Hill, New York.Google Scholar
Godbole, A. P. (1990a) Specific formulae for some success run distributions. Statist. Probab. Lett. 10, 119–124.Google Scholar
Godbole, A. P. (1990b) Degenerate and Poisson convergence criteria for success runs. Statist. Probab. Lett. 10, 247–255.Google Scholar
Godbole, A. P. (1990c) Poisson approximations for recurrent runs of rare events. Michigan Technological University, Mathematical Sciences Technical Report MS-TR 90–1.Google Scholar
Griffith, W. S. (1986) On consecutive k-out-of-n failure systems and their generalizations. In Reliability and Quality Control , ed. Basu, A. P. Elsevier, Amsterdam.Google Scholar
Guibas, L. and Odlyzko, A. (1980) Long repetitive patterns in random sequences. Z. Wahrscheinlichkeitsth. 53, 241–262.CrossRefGoogle Scholar
Guibas, L. and Odlyzko, A. (1981a) Periods in strings. J. Combinatorial Theory A 30, 19–42.Google Scholar
Guibas, L. and Odlyzko, A. (1981b) String overlaps, pattern matching, and nontransitive games. J. Combinatorial Theory A 30, 183–208.Google Scholar
Ivanov, V. A. and Novikov, A. E. (1977) On the distribution of the time up to the first occurrence of a given number of different l-tuple series. Theory Prob. Appl. 22, 533–542.Google Scholar
Kusolitsch, N. (1982) Longest runs in Markov chains. Prob. Statist. Inference 223–230.Google Scholar
Li, S. (1980) A martingale approach to the study of occurrence of sequence patterns in repeated experiments. Ann. Prob. 8, 1171–1176.Google Scholar
Ling, K. (1988) On binomial distributions of order k. Statist. Prob. Lett. 6, 247–250.Google Scholar
Mosteller, F. (1941) Note on an application of runs to quality control charts. Ann. Math. Statist. 12, 228–232.Google Scholar
Mood, A. (1940) The distribution theory of runs. Ann. Math. Statist. 11, 367–392.Google Scholar
Nemetz, T. and Kusolitsch, N. (1982) On the longest run of coincidences. Z. Wahrscheinlichkeitsth. 61, 59–73.Google Scholar
Olmstead, P. S. (1958) Runs determined in a sample by an arbitrary cut. Bell System Tech. J. 37, 55–82.Google Scholar
Papastavridis, S. (1986) Upper and lower bounds for the reliability of a consecutive-k-out-of-w: F system. IEEE Trans. Reliability 35, 607–610.Google Scholar
Papastavridis, S. (1990) m-Consecutive-k-out-of-n: F systems. IEEE Trans. Reliability. 39, 386–388.CrossRefGoogle Scholar
Papastavridis, S. and Chryssaphinou, O. (1991) A limit theorem on the number of appearances of a pattern in a sequence of independent trials. Submitted to J. Appl. Prob. Google Scholar
Pawlowski, J. (1989) Poisson theorem for non-homogeneous Markov chains. J. Appl. Prob. 26, 637–642.Google Scholar
Philippou, A. N. and Makri, F. (1986) Successes, runs and longest runs. Statist. Prob. Lett. 4, 211–215.Google Scholar
Philippou, A. N., Georghiou, C. and Philippou, G. (1983) A generalized geometric distribution and some of its properties. Statist. Prob. Lett. 1, 171–175.Google Scholar
Rajarshi, M. (1974) Success runs in a two-state Markov chain. J. Appl. Prob. 11, 190–192.Google Scholar
Samarova, S. (1981) On the length of the longest head run for a Markov chain with two states. Theory Prob. Appl. 26, 498–509.Google Scholar
Schwager, S. (1983) Run probabilities in sequences of Markov-dependent trials. J. Amer. Statist. Assoc. 78, 168–175.Google Scholar
Sevastyanov, B. A. (1972) Poisson limit law for a scheme of sums of dependent random variables. Theory Prob. Appl. 17, 695–699.Google Scholar
Solovev, A. D. (1966) A combinatorial identity and its application to the problems concerning the first occurrence of a rare event. Theory Prob. Appl. 11, 276–282.Google Scholar
Soltani, A. Reza and Khodadadi, A. (1986) Run probabilities and the motion of a particle on a given path. J. Appl. Prob. 23, 28–41.Google Scholar
Thorburn, D. (1983) On the mean number of trials until the last trials satisfy a given condition. Stoch. Proc. Appl. 16, 211–217.Google Scholar
Wang, Y. H. (1981) On the limit of the Markov binomial distribution. J. Appl. Prob. 18, 937–942.Google Scholar
Wolfowitz, J. (1944) Asymptotic distribution of runs up and down. Ann. Math. Statist. 15, 163–172.Google Scholar
Zubkov, A. M. and Mikhailov, V. G. (1974) Limit distributions of random variables associated with long duplications in a sequence of independent trials. Theory Prob. Appl. 19, 172–179.Google Scholar