Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Down, D.
and
Meyn, S.P.
1994.
Piecewise linear test functions for stability of queueing networks.
Vol. 3,
Issue. ,
p.
2069.
Botvich, Dimitri
Fayolle, Guy
and
Malyshev, Vadim
1994.
11th International Conference on Analysis and Optimization of Systems Discrete Event Systems.
Vol. 199,
Issue. ,
p.
463.
Kumar, P.R.
and
Meyn, S.
1994.
Duality and linear programs for stability and performance analysis of queueing networks and scheduling policies.
Vol. 1,
Issue. ,
p.
524.
Down, D.
and
Meyn, S.
1994.
11th International Conference on Analysis and Optimization of Systems Discrete Event Systems.
Vol. 199,
Issue. ,
p.
490.
Williams, R. J.
1995.
Stochastic Networks.
Vol. 71,
Issue. ,
p.
125.
Aspandiiaroy, Sanjar
1995.
On the convergence of 2-dimensional markov chains in quadrants with boundary reflection.
Stochastics and Stochastic Reports,
Vol. 53,
Issue. 3-4,
p.
275.
Kumar, P.R.
and
Meyn, S.P.
1996.
Duality and linear programs for stability and performance analysis of queuing networks and scheduling policies.
IEEE Transactions on Automatic Control,
Vol. 41,
Issue. 1,
p.
4.
Aspandiiarov, S.
Iasnogorodski, R.
and
Menshikov, M.
1996.
Passage-time moments for nonnegative stochastic processes and an application to reflected random walks in a quadrant.
The Annals of Probability,
Vol. 24,
Issue. 2,
Tanikawa, A.
1996.
The rate of convergence of a homogeneous Markov chain arising from two-queue networks.
Computers & Mathematics with Applications,
Vol. 31,
Issue. 2,
p.
103.
Малышев, Вадим Александрович
and
Malyshev, Vadim Aleksandrovich
1997.
Взаимодействующие цепочки символов.
Успехи математических наук,
Vol. 52,
Issue. 2,
p.
59.
Куркова, Ирина Анатольевна
and
Kurkova, Irina Anatol'evna
1999.
Граница Пуассона для однородных случайных блужданий.
Успехи математических наук,
Vol. 54,
Issue. 2,
p.
177.
Budhiraja, Amarjit
and
Dupuis, Paul
1999.
Simple Necessary and Sufficient Conditions for the Stability of Constrained Processes.
SIAM Journal on Applied Mathematics,
Vol. 59,
Issue. 5,
p.
1686.
Atar, Rami
Budhiraja, Amarjit
and
Dupuis, Paul
2001.
On Positive Recurrence of Constrained Diffusion Processes.
The Annals of Probability,
Vol. 29,
Issue. 2,
Gamarnik, David
2001.
On deciding stability of constrained random walks and queueing systems.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 28,
Issue. 4,
p.
39.
Gamarnik, David
2002.
Computing stationary probability distributions and large deviation rates for constrained random walks..
ACM SIGMETRICS Performance Evaluation Review,
Vol. 30,
Issue. 3,
p.
38.
Gamarnik, David
2002.
On Deciding Stability of Constrained Homogeneous Random Walks and Queueing Systems.
Mathematics of Operations Research,
Vol. 27,
Issue. 2,
p.
272.
Robert, Philippe
2003.
Stochastic Networks and Queues.
p.
231.
Kovalevskii, A. P.
Topchii, V. A.
and
Foss, S. G.
2005.
On the Stability of a Queueing System with Uncountably Branching Fluid Limits.
Problems of Information Transmission,
Vol. 41,
Issue. 3,
p.
254.
Dimakis, Antonis
and
Walrand, Jean
2006.
Sufficient conditions for stability of longest-queue-first scheduling: second-order properties using fluid limits.
Advances in Applied Probability,
Vol. 38,
Issue. 2,
p.
505.
Gamarnik, David
2007.
On the Undecidability of Computing Stationary Distributions and Large Deviation Rates for Constrained Random Walks.
Mathematics of Operations Research,
Vol. 32,
Issue. 2,
p.
257.
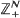 or Markovian models for queueing networks with identical customers is introduced. It is based on the analysis of the intrinsic dynamical system associated with the random walk. Earlier results for small dimensions are presented from this novel point of view. We give proofs of new results for higher dimensions related to the existence of a continuous invariant measure for the underlying dynamical system. Two constants are shown to be important: the free energy M < 0 corresponds to ergodicity, the Lyapounov exponent L < 0 defines recurrence. General conjectures, examples, unsolved problems and surprising connections with ergodic theory, classical dynamical systems and their random perturbations are largely presented. A useful notion naturally arises, the so-called scaled random perturbation of a dynamical system.
or Markovian models for queueing networks with identical customers is introduced. It is based on the analysis of the intrinsic dynamical system associated with the random walk. Earlier results for small dimensions are presented from this novel point of view. We give proofs of new results for higher dimensions related to the existence of a continuous invariant measure for the underlying dynamical system. Two constants are shown to be important: the free energy M < 0 corresponds to ergodicity, the Lyapounov exponent L < 0 defines recurrence. General conjectures, examples, unsolved problems and surprising connections with ergodic theory, classical dynamical systems and their random perturbations are largely presented. A useful notion naturally arises, the so-called scaled random perturbation of a dynamical system.

