Article contents
Approach to Stationarity of the Bernoulli–Laplace Diffusion Model
Published online by Cambridge University Press: 01 July 2016
Abstract
Two urns initially contain r red balls and n – r black balls respectively. At each time epoch a ball is chosen randomly from each urn and the balls are switched. Effectively the same process arises in many other contexts, notably for a symmetric exclusion process and random walk on the Johnson graph. If Y(·) counts the number of black balls in the first urn then we give a direct asymptotic analysis of its transition probabilities to show that (when run at rate (n – r)/n in continuous time) for 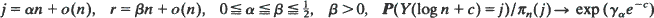 as n →∞, where π n denotes the equilibrium distribution of Y(·) and γ α = 1 – α /β (1 – β). Thus for large n the transient probabilities approach their equilibrium values at time log n + log|γ α | (≦log n) in a particularly sharp manner. The same is true of the separation distance between the transient distribution and the equilibrium distribution. This is an explicit analysis of the so-called cut-off phenomenon associated with a wide variety of Markov chains.
as n →∞, where π n denotes the equilibrium distribution of Y(·) and γ α = 1 – α /β (1 – β). Thus for large n the transient probabilities approach their equilibrium values at time log n + log|γ α | (≦log n) in a particularly sharp manner. The same is true of the separation distance between the transient distribution and the equilibrium distribution. This is an explicit analysis of the so-called cut-off phenomenon associated with a wide variety of Markov chains.
Keywords
- Type
- General Applied Probability
- Information
- Copyright
- Copyright © Applied Probability Trust 1994
References
- 12
- Cited by


