Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-18T16:45:29.177Z Has data issue: false hasContentIssue false
  • English
  • Français

A new class of markov processes for image encoding

Published online by Cambridge University Press:  01 July 2016

Michael F. Barnsley  and
John H. Elton
Michael F. Barnsley*
Affiliation:
Georgia Institute of Technology
John H. Elton*
Affiliation:
Georgia Institute of Technology
*
Postal address for both authors: School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332, USA.
Postal address for both authors: School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

A new class of iterated function systems is introduced, which allows for the computation of non-compactly supported invariant measures, which may represent, for example, greytone images of infinite extent. Conditions for the existence and attractiveness of invariant measures for this new class of randomly iterated maps, which are not necessarily contractions, in metric spaces such as , are established. Estimates for moments of these measures are obtained.

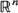Special conditions are given for existence of the invariant measure in the interesting case of affine maps on . For non-singular affine maps on 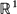, the support of the measure is shown to be an infinite interval, but Fourier transform analysis shows that the measure can be purely singular even though its distribution function is strictly increasing.

Keywords

RANDOM MAPSFRACTALS
Type
Research Article
Information
Advances in Applied Probability , Volume 20 , Issue 1 , March 1988 , pp. 14 - 32
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barnsley, M. (1986) Fractal functions and interpolation. Constructive Approximation 2, 303–329.CrossRefGoogle Scholar
[2] Barnsley, M. and Demko, S. (1985) Iterated function systems and the global construction of fractals, Proc. R. Soc. London A 399, 243–275.Google Scholar
[3] Barnsley, M., Demko, S., Elton, J. and Geronimo, J. Attractors for iterated function systems with place dependent probabilities. In preparation.Google Scholar
[4] Barnsley, M., Ervin, V., Hardin, D. and Lancaster, J. (1986) Solution of an inverse problem for fractals and other sets. Proc. Nat. Acad. Sci. U.S.A. 83, 1975–1977.CrossRefGoogle ScholarPubMed
[5] Breiman, L. (1968) Probability. Addison-Wesley, Reading, Mass.Google Scholar
[6] Demko, S., Hodges, L. and Naylor, B. (1985) Construction of fractal objects with iterated function systems. Computer Graphics 19, 271–278.CrossRefGoogle Scholar
[7] Diaconis, P. and Shashahani, M. (1986) Products of random matrices and computer image generation. Contemporary Math. 50, 173–182.CrossRefGoogle Scholar
[8] Dubins, L. E. and Freedman, D. A. (1966) Invariant probabilities for certain Markov processes. Ann. Math. Statist. 32, 837–848.CrossRefGoogle Scholar
[9] Erdös, P. (1939) On a family of symmetric Bernoulli convolutions. Amer. J. Math. 61, 974–976.CrossRefGoogle Scholar
[10] Garsia, A. (1962) Arithmetic properties of Bernoulli convolutions. Trans. Amer. Math. Soc. 102, 409–432.CrossRefGoogle Scholar
[11] Hewitt, E. and Stromberg, K. (1965) Real and Abstract Analysis. Springer-Verlag, New York.Google Scholar
[12] Hutchinson, J. (1981) Fractals and self-similarity. Indiana U. J. Math. 30, 713–747.CrossRefGoogle Scholar
[13] Karlin, S. (1953) Some random walks arising in learning models. Pacific J. Math. 3, 725–756.CrossRefGoogle Scholar
[14] Mandelbrot, B. (1982) The Fractal Geometry of Nature. W. H. Freeman, San Francisco.Google Scholar
[15] Riesz, F. and Sz.-Nagy, B. (1955) Functional Analysis. Frederick Ungar, New York.Google Scholar