Hostname: page-component-7bb8b95d7b-5mhkq Total loading time: 0 Render date: 2024-09-18T03:45:35.388Z Has data issue: false hasContentIssue false
  • English
  • Français

New better than used processes

Published online by Cambridge University Press:  01 July 2016

Albert W. Marshall  and
Moshe Shared
Albert W. Marshall*
Affiliation:
University of British Columbia
Moshe Shared*
Affiliation:
University of Arizona
*
∗Postal address: Department of Mathematics, University of British Columbia, Vancouver, B.C., Canada V6T 1Y4.
∗∗Postal address: Department of Mathematics, University of Arizona, Tucson, AZ 85721, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

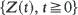A stochastic process , such that P{Z(0) = 0} = 1, is said to be new better than used (NBU) if, for every x, the first-passage time Tx = inf {t: Z(t) > x} satisfies P{TX > s + t} 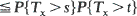for everys 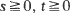. In this paper it is shown that many useful processes are NBU. Examples of such processes include processes with shocks and recovery, processes with random repair-times, various Gaver–Miller processes and some strong Markov processes. Applications in reliability theory, queueing, dams, inventory and electrical activity of neurons are indicated. It is shown that various waiting times for clusters of events and for short and wide gaps in some renewal processes are NBU random variables. The NBU property of processes and random variables can be used to obtain bounds on various probabilistic quantities of interest; this is illustrated numerically.

Keywords

RELIABILITY THEORYQUEUESDAMSINVENTORYSHOCK MODELSGENERAL RELEASE OR RECOVERY RULESWIDE AND SHORT GAPS IN A RENEWAL PROCESSCLUSTERS OF RENEWAL EVENTSRANDOM REPAIR-TIMES PROCESSESGAVER–MILLER PROCESSESMARKOV PROCESSES
Type
Research Article
Information
Advances in Applied Probability , Volume 15 , Issue 3 , September 1983 , pp. 601 - 615
Copyright
Copyright © Applied Probability Trust 1983 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported in part by the National Science Foundation at Stanford University, and in part by the National Sciences and Engineering Research Council, Canada.

Supported in part by National Science Foundation Grant MCS-79-27150.

References

A-Hameed, M. S. and Proschan, F. (1975) Shock models with underlying birth process. J. Appl. Prob, 12, 18–28.CrossRefGoogle Scholar
Barlow, R. E. and Proschan, F. (1976) Theory of maintained systems: distribution of time to first system failure. Math. Operat. Res. 1, 32–42.CrossRefGoogle Scholar
Block, H. W. and Savits, T. H. (1978) Shock models with NBUE survival. J. Appl. Prob. 15, 621–628.CrossRefGoogle Scholar
Brown, M. and Rao, C. N. (1980) On the first passage time distribution for a class of Markov chains. Technical Report M552, Department of Statistics, Florida State University, Tallahassee.CrossRefGoogle Scholar
Clarotti, C. A. (1981) Markov processes in partially ordered spaces, NBU property for the exit-time from increasing sets. Technical report, Institute of Mathematics, University of Rome.Google Scholar
Derman, C., Ross, S. M. and Schechner, Z. (1979) A note on first passage times in birth and death and nonnegative diffusion processes. Technical Report ORC 79-15, Operations Research Center, University of California, Berkeley.CrossRefGoogle Scholar
El-Neweihi, E., Proschan, F. and Sethuraman, J. (1978) Multistate coherent systems. J. Appl. Prob. 15, 675–688.CrossRefGoogle Scholar
Esary, J. D., Marshall, A. W. and Proschan, F. (1973) Shock models and wear processes. Ann. Prob. 1, 627–650.CrossRefGoogle Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2, 2nd edn. Wiley, New York.Google Scholar
Gaver, D. P. and Miller, R. G. (1962) Limiting distributions for some storage problems. In Studies in Applied Probability and Management Science, ed. Arrow, K. J., Karlin, S. and Scarf, H., Stanford University Press, 110–126.Google Scholar
Gilbert, E. N. and Pollar, H. O. (1957) Coincidences in Poisson patterns. Bell System Tech. J. 36, 1005–1033.Google Scholar
Keilson, J. (1979) Markov Chain Models–Rarity and Exponentiality. Springer-Verlag, New York.CrossRefGoogle Scholar
Leslie, R. T. (1969) Recurrence times of clusters of Poisson points. J. Appl. Prob. 6, 372–388.CrossRefGoogle Scholar
Marshall, A. W. and Proschan, F. (1972) Classes of distributions applicable in replacement with renewal theory implications. Proc. 6th Berkeley Symp. Math. Statist. Prob. 1, 395–415.Google Scholar
Moran, P. A. P. (1959) The Theory of Storage. Methuen, London.Google Scholar
Prabhu, N. U. (1965) Queues and Inventories, Wiley, New York.Google Scholar
Rösler, U. (1980) Unimodality of passage times for one-dimensional strong Markov processes. Ann. Prob. 8, 853–859.CrossRefGoogle Scholar
Ross, S. M. (1979) Multivalued state component systems. Ann. Prob. 7, 379–383.Google Scholar
Ross, S. M. (1981) Generalized Poisson shock models. Ann. Prob. 9, 896–898.CrossRefGoogle Scholar
Smith, N. M. H. and Yeo, G. F. (1981) On a general storage problem and its approximating solution. Adv. Appl. Prob. 13, 567–602.CrossRefGoogle Scholar