Article contents
Hyperplans poissoniens et compacts de Steiner
Published online by Cambridge University Press: 01 July 2016
Abstract
A compact convex set in RN is Steiner if it is a finite Minkowski sum of line segments, or a limit of such finite sums, and then satisfies an extension of the Steiner formula. With each Poisson hyperplane stationary process A is uniquely associated a Steiner set M, and for any linear variety V, the Steiner set associated with 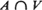 is the projection of M on V. The density of the order k network Ak (i.e., the set of the intersections of k hyperplanes belonging to A) is linked with simple geometrical properties of M. In the isotropic case, the expression of the covariance measures associated with Ak is derived and compared with the analogous results obtained for (N — k)-dimensional Poisson flats.
is the projection of M on V. The density of the order k network Ak (i.e., the set of the intersections of k hyperplanes belonging to A) is linked with simple geometrical properties of M. In the isotropic case, the expression of the covariance measures associated with Ak is derived and compared with the analogous results obtained for (N — k)-dimensional Poisson flats.
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1974
References
Bibliographie
- 10
- Cited by


