Article contents
Exact sampling for some multi-dimensional queueing models with renewal input
Published online by Cambridge University Press: 15 November 2019
Abstract
Using a result of Blanchet and Wallwater (2015) for exactly simulating the maximum of a negative drift random walk queue endowed with independent and identically distributed (i.i.d.) increments, we extend it to a multi-dimensional setting and then we give a new algorithm for simulating exactly the stationary distribution of a first-in–first-out (FIFO) multi-server queue in which the arrival process is a general renewal process and the service times are i.i.d.: the FIFO GI/GI/c queue with 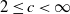 $ 2 \leq c \lt \infty$
. Our method utilizes dominated coupling from the past (DCFP) as well as the random assignment (RA) discipline, and complements the earlier work in which Poisson arrivals were assumed, such as the recent work of Connor and Kendall (2015). We also consider the models in continuous time, and show that with mild further assumptions, the exact simulation of those stationary distributions can also be achieved. We also give, using our FIFO algorithm, a new exact simulation algorithm for the stationary distribution of the infinite server case, the GI/GI/
$ 2 \leq c \lt \infty$
. Our method utilizes dominated coupling from the past (DCFP) as well as the random assignment (RA) discipline, and complements the earlier work in which Poisson arrivals were assumed, such as the recent work of Connor and Kendall (2015). We also consider the models in continuous time, and show that with mild further assumptions, the exact simulation of those stationary distributions can also be achieved. We also give, using our FIFO algorithm, a new exact simulation algorithm for the stationary distribution of the infinite server case, the GI/GI/ $\infty$
model. Finally, we even show how to handle fork–join queues, in which each arriving customer brings c jobs, one for each server.
$\infty$
model. Finally, we even show how to handle fork–join queues, in which each arriving customer brings c jobs, one for each server.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2019
References
- 3
- Cited by


