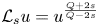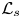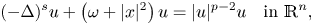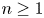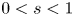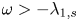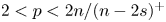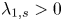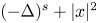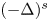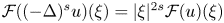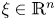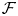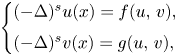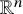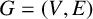193 results in 35Rxx
Early warning signs for SPDEs with continuous spectrum
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ASYMPTOTIC BEHAVIOUR OF THE LEAST ENERGY SOLUTIONS TO FRACTIONAL NEUMANN PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-32
-
- Article
-
- You have access
- HTML
- Export citation
On a localization-in-frequency approach for a class of elliptic problems with singular boundary data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation
Opinion formation on evolving network: the DPA method applied to a nonlocal cross-diffusion PDE-ODE system
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic profiles of a nonlocal dispersal SIS epidemic model with saturated incidence
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-33
-
- Article
-
- You have access
- HTML
- Export citation
Optimal decay for solutions of nonlocal semilinear equations with critical exponent in homogeneous groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unified framework for the separation property in binary phase-segregation processes with singular entropy densities
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Threshold dynamics scenario of a plants-pollinators cooperative system with impulsive effect on a periodically evolving domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Propagation of anisotropic Gabor wave front sets
- Part of
- General quantum mechanics and problems of quantization
- Partial differential equations on manifolds; differential operators
- Groups and semigroups of linear operators, their generalizations and applications
- Partial differential equations
- Distributions, generalized functions, distribution spaces
- Integral, integro-differential, and pseudodifferential operators
- Miscellaneous topics - Partial differential equations
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 April 2024, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
A finite-volume scheme for fractional diffusion on bounded domains
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the fractional powers of a Schrödinger operator with a Hardy-type potential
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 460-507
-
- Article
-
- You have access
- HTML
- Export citation
Uniqueness of ground states to fractional nonlinear elliptic equations with harmonic potential
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
On the reconstruction of unknown driving forces from low-mode observations in the 2D Navier–Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-24
-
- Article
-
- You have access
- HTML
- Export citation
Qualitative properties of solutions for system involving the fractional Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
On determining and breaking the gauge class in inverse problems for reaction-diffusion equations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 February 2024, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GLOBAL HYPOELLIPTICITY OF SUMS OF SQUARES ON COMPACT MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1-35
-
- Article
-
- You have access
- HTML
- Export citation
On Calderon's problem for the connection Laplacian
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 05 January 2024, pp. 1-26
-
- Article
-
- You have access
- HTML
- Export citation
Systems involving mean value formulas on trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 January 2024, pp. 1-33
-
- Article
-
- You have access
- HTML
- Export citation
Variational inequalities arising from credit rating migration with buffer zone
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 14 December 2023, pp. 515-532
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME GLOBAL EXISTENCE RESULTS ON LOCALLY FINITE GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 November 2023, pp. 1-17
-
- Article
-
- You have access
- HTML
- Export citation