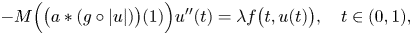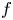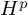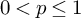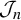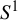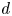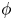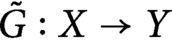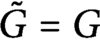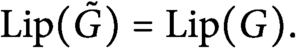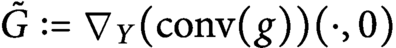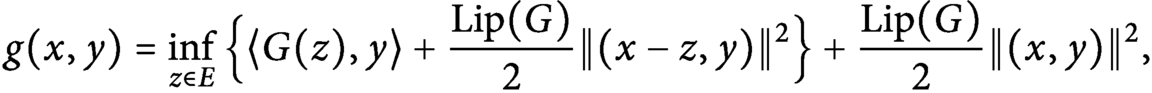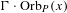117 results in 47Hxx
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
-
- You have access
- HTML
- Export citation
The geometry of monotone operator splitting methods
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 487-632
- Print publication:
- July 2024
-
- Article
-
- You have access
- Export citation
Theoretical study of a
 $\varphi $-Hilfer fractional differential system in Banach spaces
$\varphi $-Hilfer fractional differential system in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 27 February 2024, pp. 742-759
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRILINEAR FOURIER MULTIPLIERS ON HARDY SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 15 February 2024, pp. 1-62
-
- Article
-
- You have access
- HTML
- Export citation
A NOTE ON BRØNDSTED’S FIXED POINT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 31 August 2023, pp. 161-166
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
A strongly convergent algorithm for solving multiple set split equality equilibrium and fixed point problems in Banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 15 June 2023, pp. 475-515
-
- Article
-
- You have access
- HTML
- Export citation
Dynamics of iteration operators on self-maps of locally compact Hausdorff spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 03 May 2023, pp. 749-768
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
CONTRACTIVE SEMIGROUPS IN TOPOLOGICAL VECTOR SPACES, ON THE 100TH ANNIVERSARY OF STEFAN BANACH’S CONTRACTION PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 331-338
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
Existence of exponentially and superexponentially spatially localized breather solutions for nonlinear klein–gordon lattices in ℤd, d ≥ 1
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 16 June 2022, pp. 480-499
-
- Article
- Export citation
SOLUTIONS TO DIFFERENTIAL EQUATIONS VIA FIXED POINT APPROACHES: NEW MATHEMATICAL FOUNDATIONS AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 163-164
- Print publication:
- August 2022
-
- Article
-
- You have access
- HTML
- Export citation
Proof Mining with the Bounded Functional Interpretation
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 265-266
- Print publication:
- June 2022
-
- Article
-
- You have access
- Export citation
Bounds for a nonlinear ergodic theorem for Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 18 February 2022, pp. 1570-1593
- Print publication:
- May 2023
-
- Article
- Export citation
An asynchronous inertial algorithm for solving convex feasibility problems with strict pseudo-contractions in Hilbert spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 February 2022, pp. 229-243
-
- Article
- Export citation
Existence results for a nonlinear nonautonomous transmission problem via domain perturbation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1451-1476
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamic aspects of tumour–immune system interaction under a periodic immunotherapy
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 606-645
-
- Article
- Export citation
NOTES ON ORTHOGONAL-COMPLETE METRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 154-160
- Print publication:
- February 2022
-
- Article
- Export citation
INVARIANT MEANS AND ACTIONS OF SEMITOPOLOGICAL SEMIGROUPS ON COMPLETELY REGULAR SPACES AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 10 June 2020, pp. 162-173
- Print publication:
- February 2021
-
- Article
- Export citation
Kirszbraun’s Theorem via an Explicit Formula
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 29 April 2020, pp. 142-153
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- Export citation
Orbits of homogeneous polynomials on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1627-1655
- Print publication:
- June 2021
-
- Article
- Export citation
Steady-state solutions of one-dimensional competition models in an unstirred chemostat via the fixed point index theory
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 240-264
- Print publication:
- February 2021
-
- Article
- Export citation