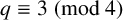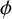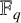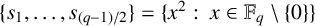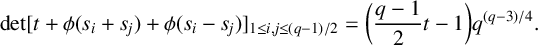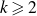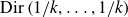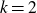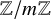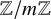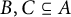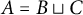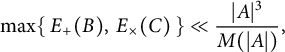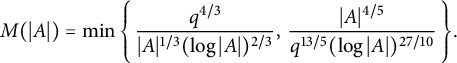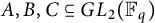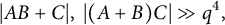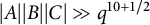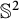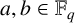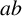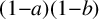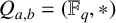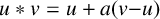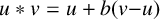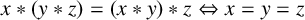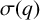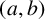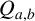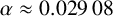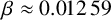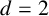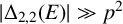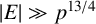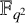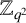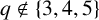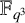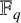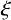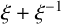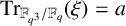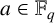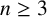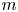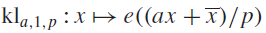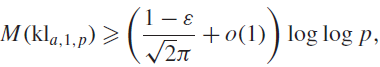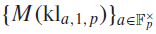97 results in 11Txx
A CONJECTURE OF ZHI-WEI SUN ON MATRICES CONCERNING MULTIPLICATIVE SUBGROUPS OF FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 September 2024, pp. 1-7
-
- Article
-
- You have access
- HTML
- Export citation
Random walks and the “Euclidean” association scheme in finite vector spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric structures in pseudo-random graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1-31
-
- Article
-
- You have access
- HTML
- Export citation
Relative rank and regularization
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 March 2024, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet law for factorisation of integers, polynomials and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 06 September 2023, pp. 649-676
- Print publication:
- November 2023
-
- Article
-
- You have access
- HTML
- Export citation
Weil Sums over Small Subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 39-53
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
Decidability of the class of all the rings
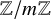 $\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
$\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An energy decomposition theorem for matrices and related questions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1280-1295
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
On the stability of ring relative equilibria in the N-body problem on
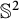 $\mathbb {S}^2$ with Hodge potential
$\mathbb {S}^2$ with Hodge potential
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 03 March 2023, pp. 495-518
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
ON THE NUMBER OF QUADRATIC ORTHOMORPHISMS THAT PRODUCE MAXIMALLY NONASSOCIATIVE QUASIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 20 February 2023, pp. 311-336
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUPER CATALAN NUMBERS AND FOURIER SUMMATIONS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 12 December 2022, p. 170
- Print publication:
- February 2023
-
- Article
-
- You have access
- HTML
- Export citation
Nearly sharp Lang–Weil bounds for a hypersurface
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 October 2022, pp. 654-664
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomials over structured grids
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 284-298
-
- Article
- Export citation
ON THE TWO-PARAMETER ERDŐS–FALCONER DISTANCE PROBLEM IN FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 29 September 2022, pp. 502-506
- Print publication:
- June 2023
-
- Article
- Export citation
ON LINEARISED POLYNOMIALS, SIDON ARRAYS AND FAST CONSTRUCTION OF SIDON SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 376-384
- Print publication:
- December 2022
-
- Article
- Export citation
PRIMITIVE ELEMENT PAIRS WITH A PRESCRIBED TRACE IN THE CUBIC EXTENSION OF A FINITE FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 458-462
- Print publication:
- December 2022
-
- Article
- Export citation
Corrections to “Value sets of sparse polynomials”
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 November 2021, pp. 1071-1073
- Print publication:
- December 2022
-
- Article
- Export citation
The distribution of the maximum of partial sums of Kloosterman sums and other trace functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 28 June 2021, pp. 1610-1651
- Print publication:
- July 2021
-
- Article
- Export citation
GENERATORS OF FINITE FIELDS WITH PRESCRIBED TRACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 27 May 2021, pp. 355-366
- Print publication:
- June 2022
-
- Article
- Export citation
On the size of the maximum of incomplete Kloosterman sums
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 15 April 2021, pp. 563-590
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation