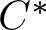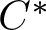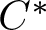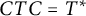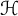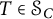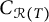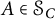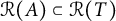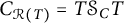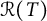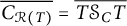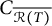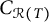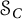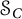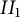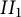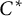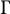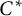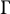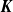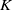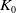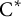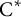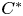363 results in 46Lxx
CUNTZ–KRIEGER ALGEBRAS ASSOCIATED TO SELF-SIMILAR GROUPOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 September 2024, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Coactions and skew products for topological quivers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-26
-
- Article
-
- You have access
- HTML
- Export citation
Homology and K-theory of dynamical systems IV. Further structural results on groupoid homology
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 15 May 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tensorially absorbing inclusions of C*-algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 April 2024, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Range inclusion and diagonalization of complex symmetric operators
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 04 April 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
DYNAMICAL MCDUFF-TYPE PROPERTIES FOR GROUP ACTIONS ON VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A classification of anomalous actions through model action absorption
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tracial weights on topological graph algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 05 March 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The degree one Laguerre–Pólya class and the shuffle-word-embedding conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 760-767
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Actions of discrete amenable groups into the normalizers of full groups of ergodic transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 February 2024, pp. 3290-3315
- Print publication:
- November 2024
-
- Article
-
- You have access
- HTML
- Export citation
Tracial oscillation zero and stable rank one
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 January 2024, pp. 1-68
-
- Article
-
- You have access
- HTML
- Export citation
THE RIEFFEL CORRESPONDENCE FOR EQUIVALENT FELL BUNDLES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Goldie dimension for C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 200-223
-
- Article
-
- You have access
- HTML
- Export citation
Unitary groups,
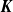 $\boldsymbol{K}$-theory, and traces
$\boldsymbol{K}$-theory, and traces
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 15 December 2023, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANY DUAL OPERATOR SPACE IS WEAKLY LOCALLY REFLEXIVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 158-160
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
A dynamical classification for crossed products of fiberwise essentially minimal zero-dimensional dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 2229-2256
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivariant
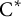 $\textrm {C}^*$-correspondences and compact quantum group actions on Pimsner algebras
$\textrm {C}^*$-correspondences and compact quantum group actions on Pimsner algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 05 December 2023, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ISOMETRIES AND HERMITIAN OPERATORS ON SPACES OF VECTOR-VALUED LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 1857-1874
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reconstruction of topological graphs and their Hilbert bimodules
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tensor algebras of subproduct systems and noncommutative function theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation