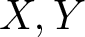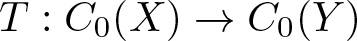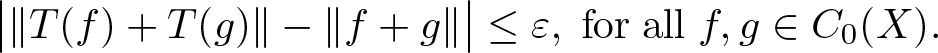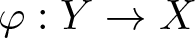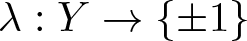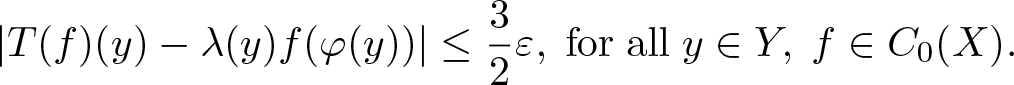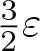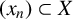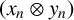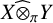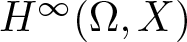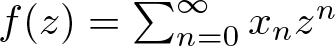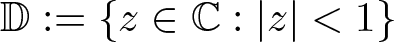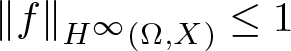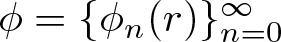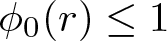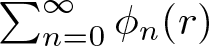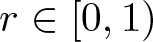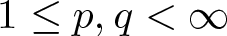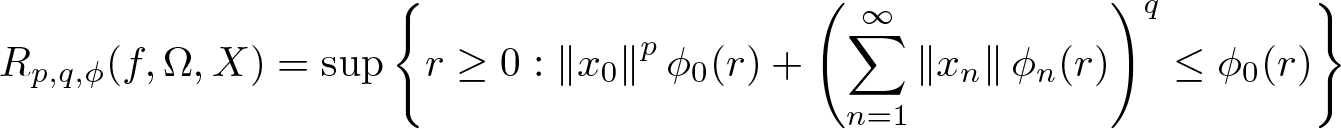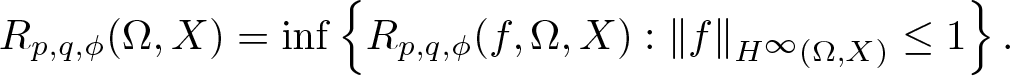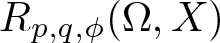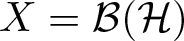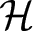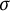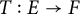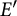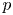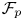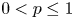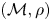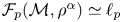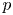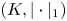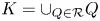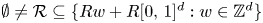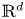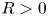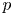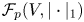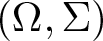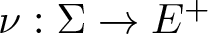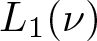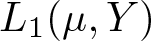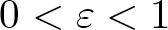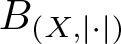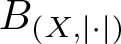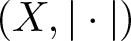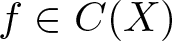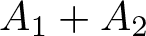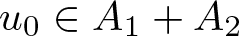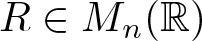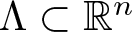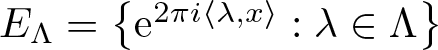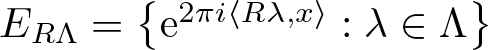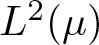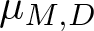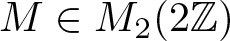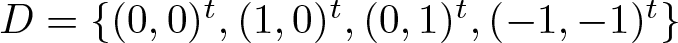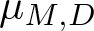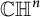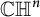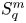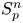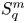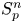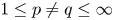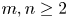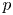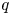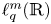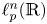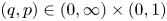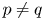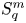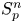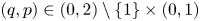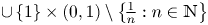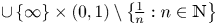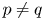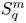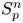271 results in 46Bxx
Perturbations of norm-additive maps between continuous function spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 October 2024, pp. 1-16
-
- Article
-
- You have access
- HTML
- Export citation
Note on almost isometric ideals and local retracts in Banach and metric spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-25
-
- Article
-
- You have access
- HTML
- Export citation
THE SET OF ELEMENTARY TENSORS IS WEAKLY CLOSED IN PROJECTIVE TENSOR PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1-8
-
- Article
-
- You have access
- HTML
- Export citation
THE WIGNER PROPERTY OF SMOOTH NORMED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 09 May 2024, pp. 1-9
-
- Article
-
- You have access
- HTML
- Export citation
Symmetric and antisymmetric tensor products for the function-theoretic operator theorist
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACES OF BANACH SPACES: COMPLEXITY OF ISOMETRY AND ISOMORPHISM CLASSES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1919-1957
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remarks on Naimark dilation theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 469-477
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
ISOMETRIES AND HERMITIAN OPERATORS ON SPACES OF VECTOR-VALUED LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 1857-1874
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr radius for Banach spaces on simply connected domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 113-141
-
- Article
-
- You have access
- HTML
- Export citation
Some results on various types of compactness of weak* Dunford–Pettis operators on Banach lattices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 403-414
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Lipschitz-free spaces and subsets of finite-dimensional spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On weakly almost square Banach spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 05 October 2023, pp. 979-997
-
- Article
-
- You have access
- HTML
- Export citation
Order continuity of Arens extensions of regular multilinear operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 September 2023, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
A Chebyshev-type alternation theorem for best approximation by a sum of two algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 01 September 2023, pp. 971-978
-
- Article
-
- You have access
- HTML
- Export citation
A NOTE ON BRØNDSTED’S FIXED POINT THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 31 August 2023, pp. 161-166
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
The spectral eigenmatrix problems of planar self-affine measures with four digits
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 897-918
-
- Article
-
- You have access
- HTML
- Export citation
Assembling RKHS with Pick kernels and assembling polyhedra in
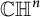 $\mathbb {CH} ^{n}$
$\mathbb {CH} ^{n}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON REAL NONISOMORPHIC BANACH SPACES WITH HOMEOMORPHIC GEOMETRIC STRUCTURE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 26 July 2023, pp. 562-570
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak weight-semi-greedy Markushevich bases
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1118-1179
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation
On isometric embeddability of $S_q^m$
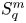 into $S_p^n$
into $S_p^n$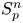 as non-commutative quasi-Banach spaces
as non-commutative quasi-Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 June 2023, pp. 1180-1203
- Print publication:
- August 2024
-
- Article
-
- You have access
- HTML
- Export citation