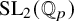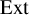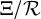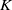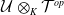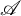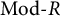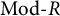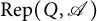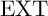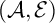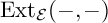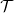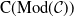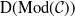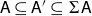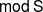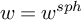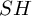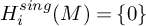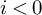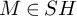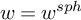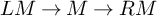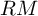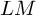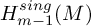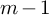118 results in 18Exx
Stability in the category of smooth mod-p representations of
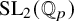 ${\mathrm {SL}}_2(\mathbb {Q}_p)$
${\mathrm {SL}}_2(\mathbb {Q}_p)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Largest exact structures and almost split sequences on hearts of twin cotorsion pairs
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 April 2024, pp. 1-30
-
- Article
-
- You have access
- HTML
- Export citation
A NONCOMMUTATIVE ANALOGUE OF CLAUSEN’S VIEW ON THE IDÈLE CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-48
-
- Article
-
- You have access
- HTML
- Export citation
Triangular matrix categories over quasi-hereditary categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
On tau-tilting subcategories
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-38
-
- Article
-
- You have access
- HTML
- Export citation
A classification of some thick subcategories in locally noetherian Grothendieck categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 23 November 2023, pp. 175-182
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
EXACT SUBCATEGORIES, SUBFUNCTORS OF
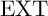 ${\operatorname{EXT}}$, AND SOME APPLICATIONS
${\operatorname{EXT}}$, AND SOME APPLICATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 254 / June 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 379-419
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized tilting theory in functor categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 July 2023, pp. 595-611
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Co-t-structures, cotilting and cotorsion pairs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 10 March 2023, pp. 89-106
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Rouquier dimension of wrapped Fukaya categories and a conjecture of Orlov
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 01 March 2023, pp. 437-487
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANNIHILATORS AND DIMENSIONS OF THE SINGULARITY CATEGORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 06 January 2023, pp. 533-548
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
COSUPPORT FOR COMPACTLY GENERATED TRIANGULATED CATEGORIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 13 December 2022, pp. 128-144
- Print publication:
- February 2024
-
- Article
- Export citation
ON MORPHISMS KILLING WEIGHTS AND STABLE HUREWICZ-TYPE THEOREMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 October 2022, pp. 521-556
- Print publication:
- March 2024
-
- Article
- Export citation
Uniqueness of enhancements for derived and geometric categories
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 October 2022, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A BRICK VERSION OF A THEOREM OF AUSLANDER
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 249 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 88-106
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intervals of s-torsion pairs in extriangulated categories with negative first extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 451-469
- Print publication:
- May 2023
-
- Article
- Export citation
Calabi–Yau properties of Postnikov diagrams
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 July 2022, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON HIGHER TORSION CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 May 2022, pp. 823-848
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived categories of skew-gentle algebras and orbifolds
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 31 January 2022, pp. 649-674
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tilting pairs in extriangulated categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 26 October 2021, pp. 947-981
-
- Article
- Export citation