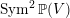 $\operatorname{Sym}^{2}\mathbb{P}(V)$
$\operatorname{Sym}^{2}\mathbb{P}(V)$
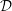 ${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS
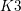 $K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
$K3$ surfaces, O’Grady’s filtration, and zero-cycles on holomorphic symplectic varieties
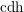 $\operatorname{cdh}$- AND
$\operatorname{cdh}$- AND 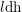 $l\operatorname{dh}$-COHOMOLOGIES
$l\operatorname{dh}$-COHOMOLOGIES
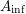 $A_{\text{inf}}$-cohomology in the semistable case
$A_{\text{inf}}$-cohomology in the semistable case
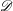 $\mathscr{D}$-MODULES
$\mathscr{D}$-MODULES